Control of Dynamic Positioning System with Disturbance Observer for Autonomous Marine Surface Vessels
Abstract
1. Introduction
2. Formulation of the Problem of Steering the Ship at Low Speed
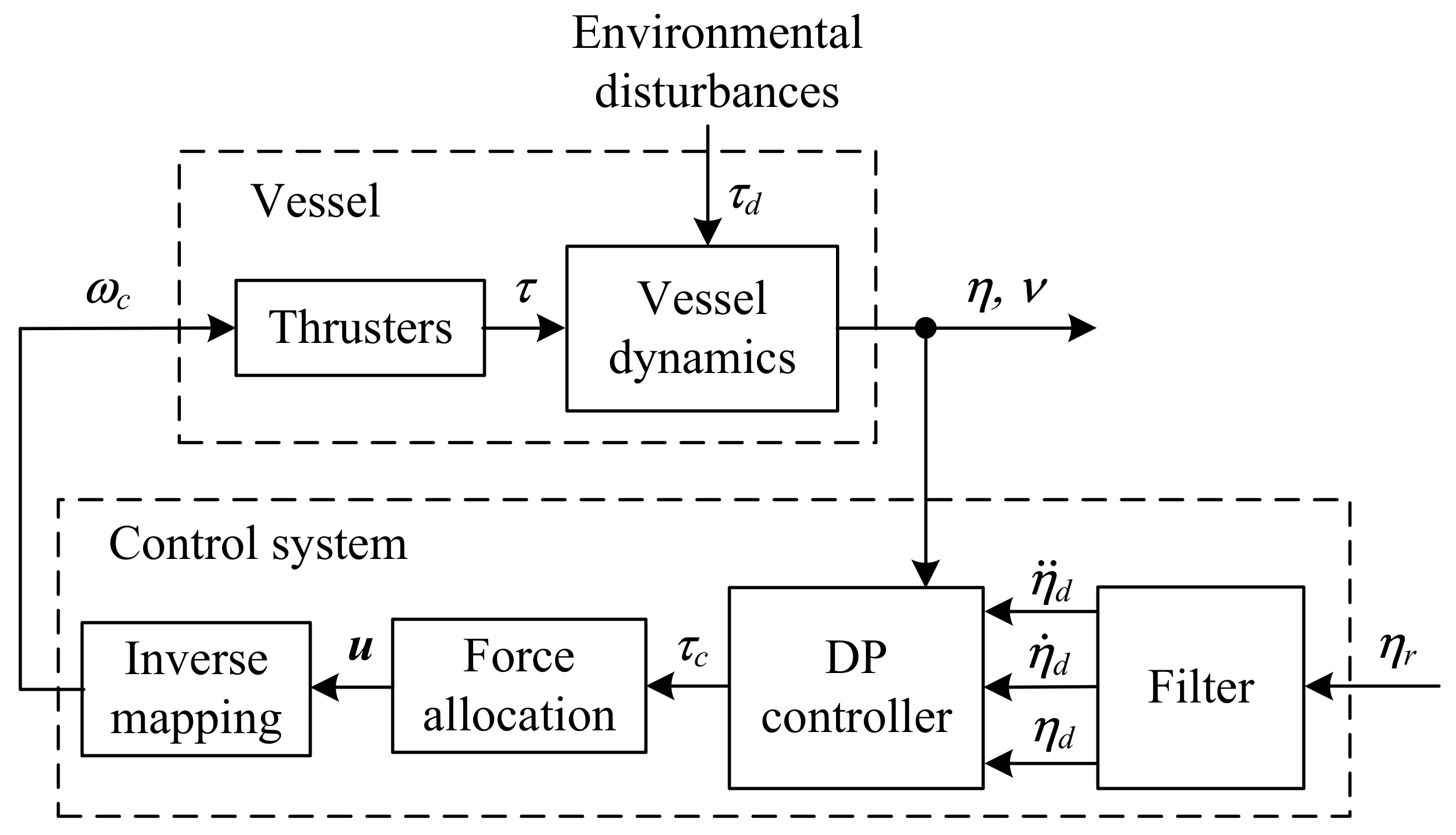
3. Control Algorithms in the Dynamic Positioning System
3.1. Backstepping Method with Disturbance Observer
3.2. Nonlinear PID Controller
3.3. Unconstrained Control Allocation
4. Simulations
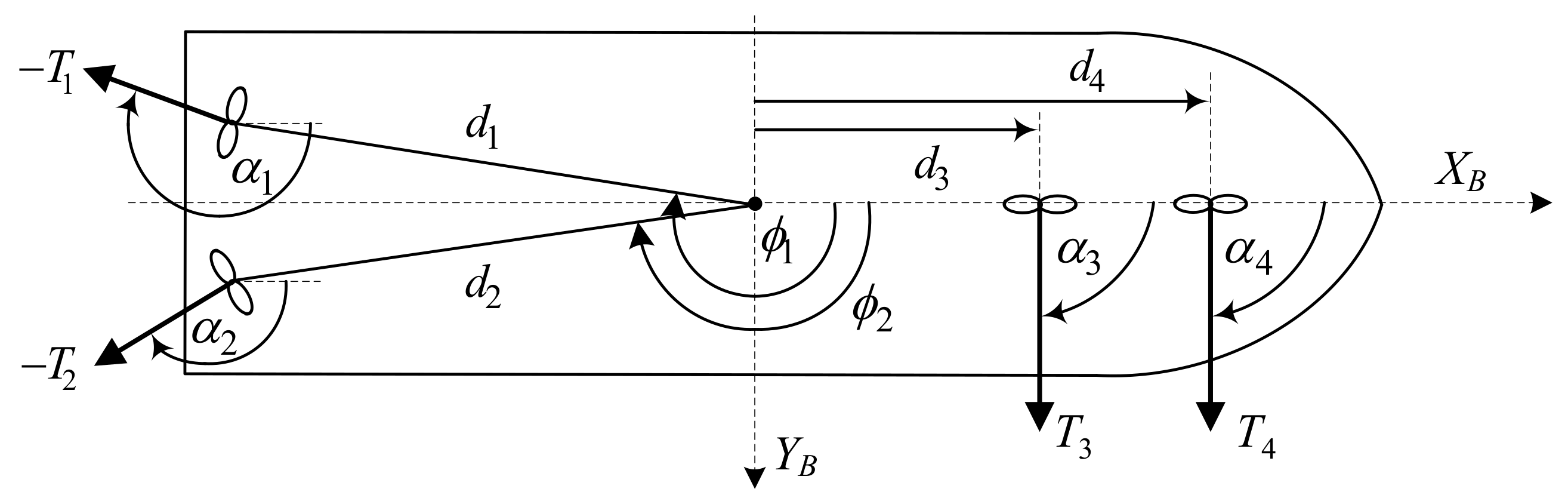
4.1. Ship Model
4.2. Parameters of Control Systems
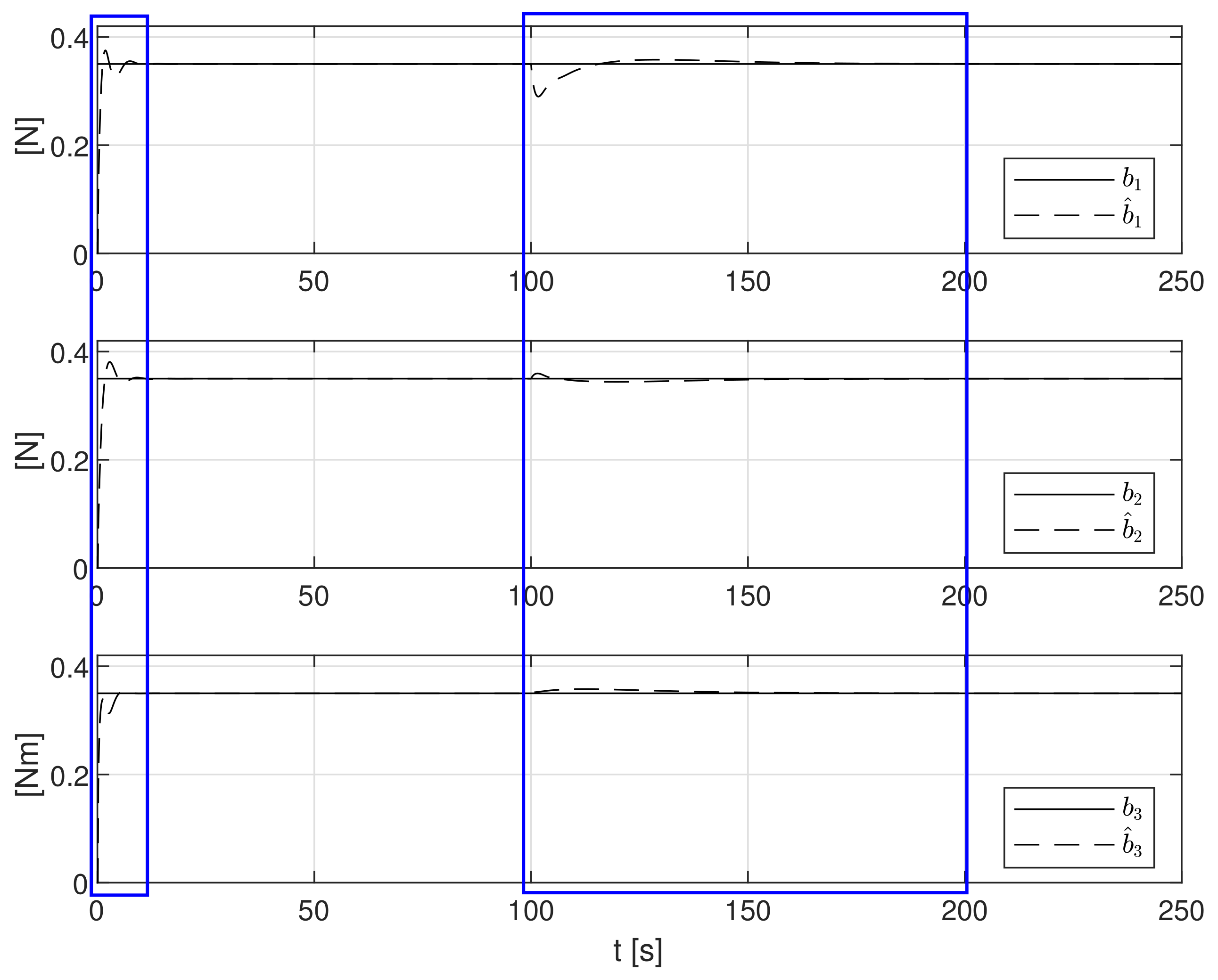
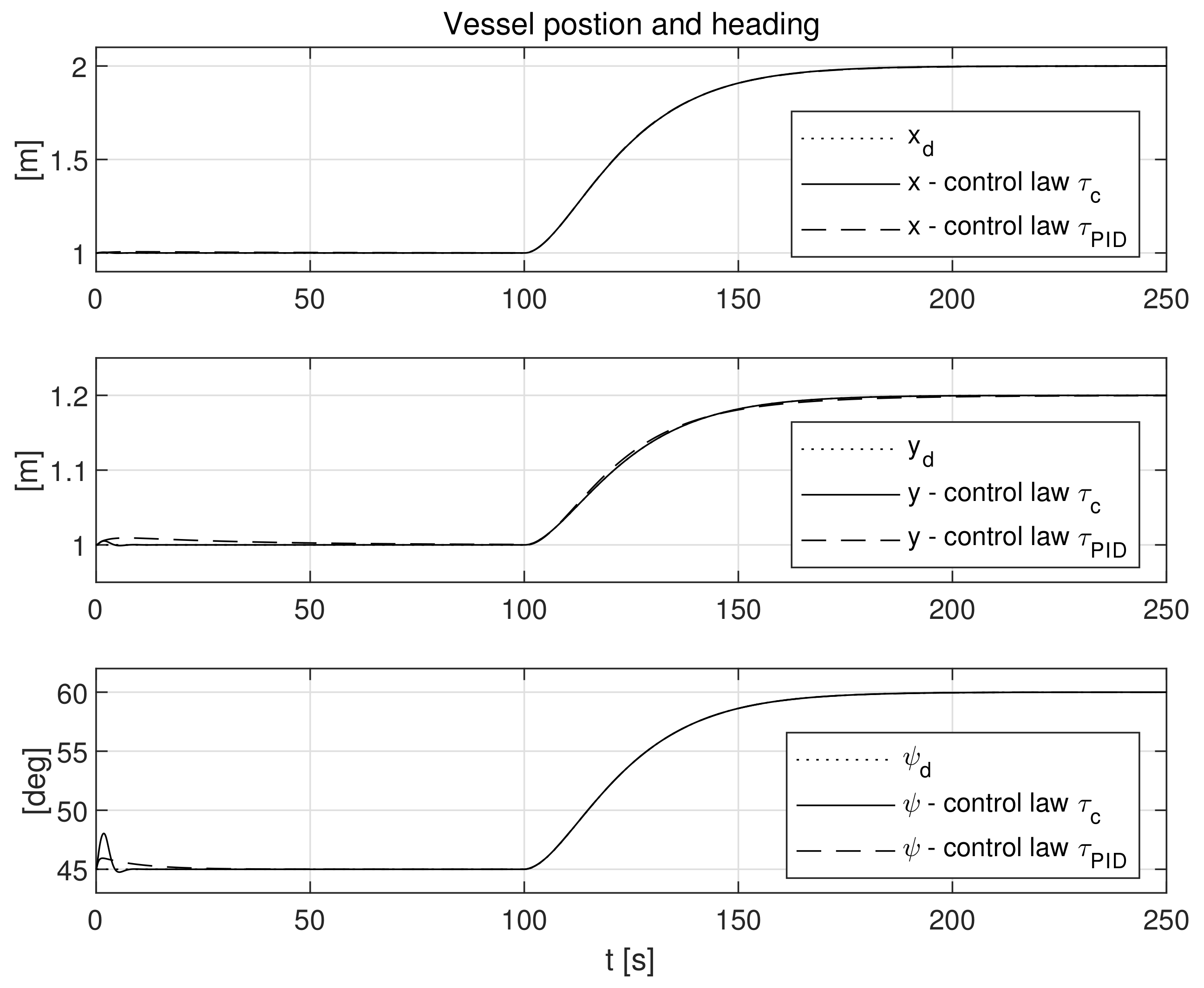
4.3. Case 1—Constant Disturbances
4.4. Case 2—Stochastic and Time-Varying Disturbances
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| MASS | Maritime Autonomous Surface Ship |
| DP | Dynamic Positioning |
| FPSO | Floating Production Storage and Offloading |
| LQG | Linear Quadratic–Gaussian |
| NTNU | Norwegian University of Science and Technology |
| PID | Proportional–Integral–Derivative |
References
- Shi, Y.; Shen, C.; Fang, H.; Li, H. Advanced control in marine mechatronic systems: A survey. IEEE/ASME Trans. Mechatron. 2017, 22, 1121–1131. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, Y.; Yu, X.; Yuan, C. Unmanned surface vehicles: An overview of developments and challenges. Annu. Rev. Control 2016, 41, 71–93. [Google Scholar] [CrossRef]
- Zereik, E.; Bibuli, M.; Mišković, N.; Ridao, P.; Pascoal, A. Challenges and future trends in marine robotics. Annu. Rev. Control 2018, 46, 350–368. [Google Scholar] [CrossRef]
- Rak, A.; Gierusz, W. Reinforcement learning in discrete and continuous domains applied to ship trajectory generation. Pol. Marit. Res. 2012, 19, 31–36. [Google Scholar] [CrossRef][Green Version]
- Szymak, P. Comparison of fuzzy system with neural aggregation FSNA with classical TSK fuzzy system in anti-collision problem of USV. Pol. Marit. Res. 2017, 24, 3–14. [Google Scholar] [CrossRef][Green Version]
- Lazarowska, A. Comparison of discrete artificial potential field algorithm and wave-front algorithm for autonomous ship trajectory planning. IEEE Access 2020, 8, 221013–221026. [Google Scholar] [CrossRef]
- Lisowski, J.; Mohamed-Seghir, M. Comparison of computational intelligence methods based on fuzzy sets and game theory in the synthesis of safe ship control based on information from a radar ARPA system. Remote Sens. 2019, 11, 82. [Google Scholar] [CrossRef]
- Lisowski, J. Multi-criteria optimisation of multi-stage positional game of vessels. Pol. Marit. Res. 2020, 27, 46–52. [Google Scholar] [CrossRef]
- Miller, A.; Walczak, S. Maritime autonomous surface ship’s path approximation using Bézier curves. Symmetry 2020, 12, 1704. [Google Scholar] [CrossRef]
- Miller, A.; Rybczak, M.; Rak, A. Towards the autonomy: Control systems for the ship in confined and open waters. Sensors 2021, 21, 2286. [Google Scholar] [CrossRef] [PubMed]
- Song, L.; Chen, H.; Xiong, W.; Dong, Z.; Mao, P.; Xiang, Z.; Hu, K. Method of emergency collision avoidance for unmanned surface vehicle (USV) based on motion ability database. Pol. Marit. Res. 2019, 26, 55–67. [Google Scholar] [CrossRef]
- Szłapczyński, R.; Ghaemi, H. Framework of an evolutionary multi-objective optimisation method for planning a safe trajectory for a marine autonomous surface ship. Pol. Marit. Res. 2019, 26, 69–79. [Google Scholar] [CrossRef]
- Śmierzchalski, R.; Łebkowski, A. Evolutionary-Fuzzy Hybrid System of Steering the Moveable Object in Dynamic Invironment. In Proceedings of the 6th IFAC Conference Control Application in Marine Craft, Girona, Spain, 17–19 September 2003; pp. 235–240. [Google Scholar]
- Vagale, A.; Oucheikh, R.; Bye, R.T.; Osen, O.L.; Fossen, T.I. Path planning and collision avoidance for autonomous surface vehicles I: A review. J. Mar. Sci. Technol. 2021, 1–15. [Google Scholar] [CrossRef]
- Vagale, A.; Bye, R.T.; Oucheikh, R.; Osen, O.L.; Fossen, T.I. Path planning and collision avoidance for autonomous surface vehicles II: A comparative study of algorithms. J. Mar. Sci. Technol. 2021, 1–17. [Google Scholar] [CrossRef]
- Skjetne, R.; Smogeli, O.; Fossen, T.I. Modeling, Identification, and Adaptive Maneuvering of Cybership II: A Complete Design with Experiments. In Proceedings of the IFAC Conference on the Control and Application in Marine Systems, Ancona, Italy, 7–9 July 2004; pp. 203–208. [Google Scholar]
- Strand, J.P. Nonlinear Position Control Systems Design for Marine Vessels. Ph.D. Thesis, Department of Engineering Cybernetics, Norwegian University Science and Technology, Trondheim, Norway, 1999. [Google Scholar]
- Lindegaard, K.-P. Acceleration Feedback in Dynamic Positioning. Ph.D. Thesis, Department of Engineering Cybernetics, Norwegian University Science and Technology, Trondheim, Norway, 2003. [Google Scholar]
- Sørensen, A.J. A survey of dynamic positioning control systems. Annu. Rev. Control 2011, 35, 123–136. [Google Scholar] [CrossRef]
- Wang, Y.-L.; Han, Q.-L.; Fei, M.-R.; Peng, C. Network-based TS fuzzy dynamic positioning controller design for unmanned marine vehicles. IEEE Trans. Cybern. 2018, 48, 2168–2267. [Google Scholar] [CrossRef]
- Mehrzadi, M.; Terriche, Y.; Su, C.L.; Othman, M.B.; Vasquez, J.C.; Guerrero, J.M. Review of dynamic positioning control in maritime microgrid systems. Energies 2020, 13, 3188. [Google Scholar] [CrossRef]
- van Amerongen, J. Adaptive Steering of Ships: A Model- Reference Approach to Improved Manoeuvring and Economical Course Keeping. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 1982. [Google Scholar]
- Fossen, T.I. Guidance and Control of Ocean Vehicles; John Wiley & Sons: Chichester, UK, 1994. [Google Scholar]
- Li, Z.; Sun, J. Disturbance compensating model predictive control with application to ship heading control. IEEE Trans. Control Syst. Technol. 2012, 20, 257–265. [Google Scholar] [CrossRef]
- Zwierzewicz, Z. On the ship course-keeping control system design by using robust feedback linearization. Pol. Marit. Res. 2013, 20, 70–76. [Google Scholar] [CrossRef]
- Borkowski, P. Ship course stabilization by feedback linearization with adaptive object model. Pol. Marit. Res. 2014, 21, 14–19. [Google Scholar] [CrossRef]
- Liu, Z. Adaptive sliding mode control for ship autopilot with speed keeping. Pol. Marit. Res. 2018, 25, 21–29. [Google Scholar] [CrossRef]
- Miao, R.; Dong, Z.; Lei, W.; Zeng, J. Heading control system design for a micro-USV based on an adaptive expert S-PID algorithm. Pol. Marit. Res. 2018, 25, 6–13. [Google Scholar] [CrossRef]
- Kula, K.S. Automatic control of ship motion conducting search in open waters. Pol. Marit. Res. 2020, 27, 157–169. [Google Scholar] [CrossRef]
- Zhang, Q.; Ding, Z.; Zhang, M. Adaptive self-regulation pid control of course-keeping for ships. Pol. Marit. Res. 2020, 27, 39–45. [Google Scholar] [CrossRef]
- Holzhüter, T. LQG approach for the high-precision track control of ships. IET Control Theory Appl. 1997, 144, 121–127. [Google Scholar] [CrossRef]
- Ashrafiuon, H.; Muske, K.R.; McNinch, L.C. Review of Nonlinear Tracking and Setpoint Control Approaches for Autonomous Underactuated Marine Vehicles. In Proceedings of the 2010 American Control Conference, Baltimore, MD, USA, 30 June–2 July 2010; pp. 5203–5211. [Google Scholar]
- Kula, K.S. Model-Based Controller for Ship Track-Keeping Using Neural Network. In Proceedings of the 2nd IEEE International Conference on Cybernetics, Gdynia, Poland, 24–26 June 2015; pp. 178–183. [Google Scholar]
- Abdelaal, M.; Fränzle, M.; Hahn, A. Nonlinear model predictive control for trajectory tracking and collision avoidance of underactuated vessels with disturbances. Ocean Eng. 2018, 160, 168–180. [Google Scholar] [CrossRef]
- Liu, Y.; Bu, R.; Gao, X. Ship trajectory tracking control system design based on sliding mode control algorithm. Pol. Marit. Res. 2018, 25, 26–34. [Google Scholar] [CrossRef]
- Wang, S.; Tuo, Y. Robust trajectory tracking control of underactuated surface vehicles with prescribed performance. Pol. Marit. Res. 2020, 27, 148–156. [Google Scholar] [CrossRef]
- Breivik, M.; Fossen, T.I. Path Following for Marine Surface Vessels. In Proceedings of the MTS/IEEE Techno-Ocean ’04, Kobe, Japan, 9–12 November 2004; pp. 2282–2289. [Google Scholar]
- Aguiar, A.P.; Hespanha, J.P. Trajectory-tracking and path-following of underactuated autonomous vehicles with parametric modeling uncertainty. IEEE Trans. Autom. Control 2007, 52, 1362–1379. [Google Scholar] [CrossRef]
- Liu, T.; Dong, Z.; Du, H.; Song, L.; Mao, Y. Path following control of the underactuated USV on the improved lineof-sight guidance algorithm. Pol. Marit. Res. 2017, 24, 3–11. [Google Scholar] [CrossRef]
- Liu, Z. Pre-filtered backstepping control for underactuated ship path following. Pol. Marit. Res. 2019, 26, 68–75. [Google Scholar] [CrossRef]
- Ghassemi, H.; Dadmarzi, F.H.; Ghadimi, P.; Ommani, B. Neural network-PID controller for roll fin stabilizer. Pol. Marit. Res. 2010, 17, 23–28. [Google Scholar] [CrossRef][Green Version]
- Koshkouei, A.J.; Nowak, L. Stabilisation of ship roll motion via switched controllers. Ocean Eng. 2012, 49, 66–75. [Google Scholar] [CrossRef]
- Karakas, S.C.; Ucer, E.; Pesman, E. Control design of fin roll stabilization in beam seas based on Lyapunov’s direct method. Pol. Marit. Res. 2012, 19, 25–30. [Google Scholar] [CrossRef]
- Lu, Y.; Zhang, G.; Sun, Z.; Zhang, W. Robust adaptive formation control of underactuated autonomous surface vessels based on MLP and DOB. Nonlinear Dyn. 2018, 94, 503–519. [Google Scholar] [CrossRef]
- Dong, Z.; Liu, Y.; Wang, H.; Qin, T. Method of cooperative formation control for underactuated usvs based on nonlinear backstepping and cascade system theory. Pol. Marit. Res. 2021, 28, 149–162. [Google Scholar] [CrossRef]
- Fannemel, Å.V. Dynamic Positioning by Nonlinear Model Predictive Control. Master’s Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2008. [Google Scholar]
- Sargent, J.S.; Cowgill, P.N. Design Considerations for Dynamically Positioned Utility Vessels. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 3–6 May 1976. [Google Scholar]
- Balchen, J.G.; Jenssen, N.A.; Saelid, S. Dynamic Positioning Using Kalman Filtering and Optimal Control Theory. In Proceedings of the IFAC/IFIP Symposium on Automation in Offshore Oil Field Operation, Bergen, Norway, 14–17 June 1976; pp. 183–186. [Google Scholar]
- Grimble, M.J.; Patton, R.J.; Wise, D.A. Use of Kalman filtering techniques in dynamic positioning systems. IEE Proc. D (Control Theory Appl.) 1980, 127, 93–102. [Google Scholar] [CrossRef]
- Saelid, S.; Jenssen, N.A.; Balchen, J.G. Design and analysis of a dynamic positioning system based on Kalman filtering and optimal control. IEEE Trans. Autom. Control 1983, 28, 331–339. [Google Scholar] [CrossRef]
- Fung, P.; Grimble, M. Dynamic ship positioning using self-tuning Kalman filter. IEEE Trans. Autom. Control 1983, 28, 339–350. [Google Scholar] [CrossRef]
- Grøvlen, A.; Fossen, T.I. Nonlinear Control of Dynamic Positioned Ships Using only Position Feedback: An Observer Backstepping Approach. In Proceedings of the 35th IEEE Conference on Decision and Control, Kobe, Japan, 13 December 1996; pp. 3388–3393. [Google Scholar]
- Fossen, T.I.; Grovlen, A. Nonlinear output feedback control of dynamic positioned ships using vectorial observer backstepping. IEEE Trans. Control Syst. Technol. 1998, 6, 121–128. [Google Scholar] [CrossRef]
- Loria, A.; Fossen, T.I.; Panteley, E. A separation principle for dynamic positioning of ships: Theoretical and experimental results. IEEE Trans. Control Syst. Technol. 2000, 8, 332–343. [Google Scholar] [CrossRef]
- Donha, D.C.; Desanj, D.S.; Katebi, M.R.; Grimble, M.J. Non-Linear Ship Positioning System Design Using an H2 Controller. In Proceedings of the IFAC European Control Conference, Brussels, Belgium, 1–4 July 1997; pp. 2276–2281. [Google Scholar]
- Katebi, M.R.; Grimble, M.J.; Zhang, Y. H∞ robust control design for dynamic ship positioning. IEE Proc. D (Control Theory Appl.) 1997, 144, 110–120. [Google Scholar] [CrossRef]
- Katebi, M.R.; Yamamoto, I.; Matsuura, M.; Grimble, M.J.; Hirayama, H.; Okamoto, N. Robust dynamic ship positioning control system design and applications. Int. J. Robust Nonlin. 2001, 11, 1257–1284. [Google Scholar] [CrossRef]
- Rybczak, M. Linear Matrix Inequalities in multivariable ship’s steering. Pol. Marit. Res. 2012, 19, 37–44. [Google Scholar] [CrossRef][Green Version]
- Hassani, V.; Sørensen, A.J.; Pascoal, A.M. A Novel Methodology for Robust Dynamic Positioning of Marine Vessels: Theory and Experiments. In Proceedings of the American Control Conference, Washington, DC, USA, 17–19 June 2013; pp. 560–565. [Google Scholar]
- Hassani, V.; Sørensen, A.J.; Pascoal, A.M.; Athans, M. Robust dynamic positioning of offshore vessels using mixed-μ synthesis modeling, design, and practice. Ocean Eng. 2017, 129, 389–400. [Google Scholar] [CrossRef]
- Hu, X.; Du, J.; Sun, Y. Robust adaptive control for dynamic positioning of ships. IEEE J. Ocean. Eng. 2017, 42, 826–835. [Google Scholar] [CrossRef]
- Hu, X.; Du, J. Robust nonlinear control design for dynamic positioning of marine vessels with thruster system dynamics. Nonlinear Dyn. 2018, 94, 365–376. [Google Scholar] [CrossRef]
- Gierusz, W.; Rybczak, M. Effectiveness of multidimensional controllers designated to steering of the motions of ship at low speed. Sensors 2020, 20, 3533. [Google Scholar] [CrossRef]
- Martin, P.; Katebi, R. Multivariable PID tuning of dynamic ship positioning control systems. J. Mar. Eng. Technol. 2005, 4, 11–24. [Google Scholar] [CrossRef]
- Bańka, S.; Dworak, P.; Jaroszewski, K. Linear adaptive structure for control of a nonlinear MIMO dynamic plant. Int. J. Appl. Math. Comput. Sci. 2013, 23, 47–63. [Google Scholar] [CrossRef][Green Version]
- Tannuri, E.A.; Kubota, L.K.; Pesce, C.P. Adaptive techniques applied to offshore dynamic positioning systems. J. Braz. Soc. Mech. Sci. Eng. 2006, 28, 323–330. [Google Scholar] [CrossRef]
- Chen, H.; Wan, L.; Wang, F.; Zhang, G. Model predictive controller design for the dynamic positioning system of a semisubmersible platform. J. Mar. Sci. Appl. 2012, 11, 361–367. [Google Scholar] [CrossRef]
- Sotnikova, M.V.; Veremey, E.I. Dynamic positioning based on nonlinear MPC. IFAC Proc. Vol. 2013, 46, 37–42. [Google Scholar] [CrossRef]
- Veksler, A.; Johansen, T.A.; Borrelli, F.; Realfsen, B. Dynamic positioning with model predictive control. IEEE Trans. Control Syst. Technol. 2016, 24, 1340–1353. [Google Scholar] [CrossRef]
- Shah, M. Dynamic Positioning of Ships: A Nonlinear Control Design Study. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2012. [Google Scholar]
- Sharma, S.K.; Sutton, R.; Motwani, A.; Annamalai, A. Non-linear control algorithms for an unmanned surface vehicle. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2014, 228, 146–155. [Google Scholar] [CrossRef]
- Krstić, M.; Kanellakopoulos, I.; Kokotović, P. Nonlinear and Adaptive Control Design; John Wiley & Sons, Inc.: New York, NY, USA, 1995. [Google Scholar]
- Aarset, M.F.; Strand, J.P.; Fossen, T.I. Nonlinear Vectorial Observer Backstepping with Integral Action and Wave Filtering for Ships. In Proceedings of the IFAC Conference on Control Applications in Marine Systems, Fukuoka, Japan, 27–30 October 1998; pp. 83–88. [Google Scholar]
- Strand, J.P.; Fossen, T.I. Nonlinear Output Feedback and Locally Optimal Control of Dynamically Possitioned Ships: Experimental Results. Proceedings of IFAC Conference on Control Applications in Marine Systems, Fukuoka, Japan, 27–30 October 1998; pp. 89–94. [Google Scholar]
- Zakartchouk, A., Jr.; Morishita, H.M. A backstepping controller for dynamic positioning of ships: Numerical and experimental results for a shuttle tanker model. IFAC Proc. Vol. 2009, 42, 394–399. [Google Scholar] [CrossRef]
- Zhang, C.D.; Wang, X.H.; Xiao, J.M. Ship dynamic positioning system based on backstepping control. J. Theor. Appl. Inf. Technol. 2013, 51, 129–136. [Google Scholar]
- Witkowska, A. Dynamic Positioning System with Vectorial Backstepping Controller. In Proceedings of the 18th International Conference on Methods and Models in Automation and Robotics, Międzyzdroje, Poland, 26–29 August 2013; pp. 842–847. [Google Scholar]
- Witkowska, A.; Śmierzchalski, R. Adaptive backstepping tracking control for an over-actuated DP marine vessel with inertia uncertainties. Int. J. Appl. Math. Comput. Sci. 2018, 28, 679–693. [Google Scholar] [CrossRef]
- Swaroop, D.; Hedrick, J.K.; Yip, P.P.; Gerdes, J.C. Dynamic surface control for a class of nonlinear systems. IEEE Trans. Automat. Control 2000, 45, 1893–1899. [Google Scholar] [CrossRef]
- Yang, Y.; Du, J.; Li, G.; Li, W.; Guo, C. Dynamic surface control for nonlinear dynamic positioning system of ship. In Mechanical Engineering and Technology; Zhang, T., Ed.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 237–244. [Google Scholar]
- Fu, M.; Xu, Y.; Zhou, L. Bio-Inspired Trajectory Tracking Algorithm for Dynamic Positioning Ship with System Uncertainties. In Proceedings of the 35th Chinese Control Conference, Chengdu, China, 27–29 July 2016; pp. 4562–4566. [Google Scholar]
- Kjerstad, Ø.K.; Skjetne, R. Modeling and control for dynamic positioned marine vessels in drifting managed sea ice. Model. Identif. Control. 2014, 35, 249–262. [Google Scholar] [CrossRef][Green Version]
- Tomera, M. Dynamic positioning system for a ship on harbor manoeuvring with different observers. Experimental results. Pol. Marit. Res. 2014, 21, 13–24. [Google Scholar] [CrossRef]
- Donaire, A.; Perez, T. Dynamic positioning of marine craft using a port-Hamiltonian framework. Automatica 2012, 48, 851–856. [Google Scholar] [CrossRef]
- Agostinho, A.C.; Moratelli, L.; Tannuri, E.A.; Morishita, H.M. Sliding mode control applied to offshore dynamic positioning systems. IFAC Proc. Vol. 2009, 42, 237–242. [Google Scholar] [CrossRef]
- Tannuri, E.A.; Agostinho, A.C.; Morishita, H.M.; Moratelli, L. Dynamic positioning systems: An experimental analysis of sliding mode control. Control Eng. Pract. 2010, 18, 1121–1132. [Google Scholar] [CrossRef]
- Esfahani, H.N.; Szłapczyński, R. Model predictive super-twisting sliding mode control for an autonomous surface vehicle. Pol. Marit. Res. 2019, 26, 163–171. [Google Scholar] [CrossRef]
- Nguyen, D.T.; Sorensen, A.J. Switching control for thrust-assisted mooring. Control Eng. Pract. 2009, 17, 985–994. [Google Scholar] [CrossRef]
- Panagou, D.; Kyriakopoulos, K.J. Dynamic positioning for an underactuated marine vehicle using hybrid control. Int. J. Control 2014, 87, 264–280. [Google Scholar] [CrossRef]
- Brodtkorb, A.H.; Værnø, S.A.; Teel, A.R.; Sørensen, A.J.; Skjetne, R. Hybrid controller concept for dynamic positioning of marine vessels with experimental results. Automatica 2018, 93, 489–497. [Google Scholar] [CrossRef]
- Stephens, R.I.; Burnham, K.J.; Reeve, P.J. A practical approach to the design of fuzzy controllers with application to dynamic ship positioning. IFAC Proc. Vol. 1995, 28, 370–377. [Google Scholar] [CrossRef]
- Broel-Plater, B. Fuzzy Control for Vessel Motion. In Proceedings of the 5th International Symposium on Method and Models in Automation and Robotics, Międzyzdroje, Poland, 25–29 August 1998; pp. 2.697–2.702. [Google Scholar]
- Chang, W.-J.; Chen, G.-J.; Yeh, Y.-L. Fuzzy control of dynamic positioning systems for ships. J. Mar. Sci. Technol. 2002, 10, 47–53. [Google Scholar] [CrossRef]
- Lee, T.H.; Cao, Y.S.; Lin, Y.M. Dynamic positioning of drilling vessels with a fuzzy logic controller. Int. J. Syst. Sci. 2002, 33, 979–993. [Google Scholar] [CrossRef]
- Ho, W.H.; Chen, S.H.; Chou, J.H. Optimal control of Takagi–Sugeno fuzzy-model-based systems representing dynamic ship positioning systems. Appl. Soft Comput. 2013, 13, 3197–3210. [Google Scholar] [CrossRef]
- Hu, X.; Du, J.; Shi, J. Adaptive fuzzy controller design for dynamic positioning system of vessels. Appl. Ocean Res. 2015, 53, 46–53. [Google Scholar] [CrossRef]
- Lin, X.; Nie, J.; Jiao, Y.; Liang, K.; Li, H. Nonlinear adaptive fuzzy output-feedback controller design for dynamic positioning system of ships. Ocean Eng. 2018, 158, 186–195. [Google Scholar] [CrossRef]
- Gu, M.X.; Pao, Y.H.; Yip, P.P.C. Neural-net computing for real-time control of a ship’s dynamic positioning at sea. Control Eng. Pract. 1993, 1, 305–314. [Google Scholar]
- Du, J.; Yang, Y.; Wang, D.; Guo, C. A robust adaptive neural networks controller for maritime dynamic positioning system. Neurocomputing 2013, 110, 128–136. [Google Scholar] [CrossRef]
- Fang, M.C.; Lee, Z.Y. Portable dynamic positioning control system on a barge in short-crested waves using the neural network algorithm. China Ocean Eng. 2013, 27, 469–480. [Google Scholar] [CrossRef]
- Bańka, S.; Dworak, P.; Jaroszewski, K. Design of a multivariable neural controller for control of a nonlinear mimo plant. Int. J. Appl. Math. Comput. Sci. 2013, 24, 357–369. [Google Scholar] [CrossRef]
- Zhang, G.; Cai, Y.; Zhang, W. Robust neural control for dynamic positioning ships with the optimum-seeking guidance. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 1500–1509. [Google Scholar] [CrossRef]
- Witkowska, A.; Niksa-Rynkiewicz, T. Dynamically positioned ship steering making use of backstepping method and artificial neural networks. Pol. Marit. Res. 2018, 25, 5–12. [Google Scholar] [CrossRef]
- Meng, W.; Sheng, L.H.; Qing, M.; Rong, B.G. Intelligent control algorithm for ship dynamic positioning. Arch. Control Sci. 2014, 24, 479–497. [Google Scholar] [CrossRef]
- Fang, M.C.; Lee, Z.Y. Application of neuro-fuzzy algorithm to portable dynamic positioning control system for ships. Int. J. Nav. Arch. Ocean 2016, 8, 38–52. [Google Scholar] [CrossRef]
- Lindfords, I. Thrust Allocation Method for the Dynamic Positioning System. In Proceedings of the 10th International Ship Control Systems Symposium, Ottawa, ON, Canada, 25–29 October 1993; pp. 93–106. [Google Scholar]
- Berge, S.P.; Fossen, T.I. Robust Control Allocation of Overactuated Ships: Experiments with a Model Ship. In Proceedings of the 4th IFAC Conference on Manoeuvering and Control of Marine Craft, Brijuni, Croatia, 10–12 September 1997; pp. 166–171. [Google Scholar]
- Sordalen, O.J. Optimal thrust allocation for marine vessels. Control Eng. Pract. 1997, 5, 1223–1231. [Google Scholar] [CrossRef]
- Liang, C.C.; Cheng, H. The optimum control of thruster system for dynamically positioned vessels. Ocean Eng. 2004, 31, 97–110. [Google Scholar] [CrossRef]
- Gierusz, W.; Tomera, M. Logic thrust allocation applied to multivariable control of the training ship. Control Eng. Pract. 2006, 14, 511–524. [Google Scholar] [CrossRef]
- Johansen, T.A.; Fuglseth, T.P.; Tøndel, P.; Fossen, T.I. Optimal constrained control allocation in marine surface vessels with rudders. Control Eng. Pract. 2008, 16, 457–464. [Google Scholar] [CrossRef]
- Tjønnås, J.; Johansen, T.A. Adaptive control allocation. Automatica 2008, 44, 2754–2765. [Google Scholar] [CrossRef]
- Ruth, E. Propulsion Control and Thrust Allocation on Marine Vessels. Ph.D. Thesis, Norwegian University of Science and Technology, Department of Marine Technology, Trondheim, Norway, 2008. [Google Scholar]
- Shi, X.; Wei, Y.; Ning, J.; Fu, M. Constrained Control Allocation Using Cascading Generalized Inverse for Dynamic Positioning of Ships. In Proceedings of the 2011 IEEE International Conference on Mechatronics and Automation, Beijing, China, 7–10 August 2011; pp. 1636–1640. [Google Scholar]
- Ji, S.W.; Bui, V.P.; Balachandran, B.; Kim, Y.B. Robust control allocation design for marine vessel. Ocean Eng. 2013, 63, 105–111. [Google Scholar] [CrossRef]
- Skjetne, R.; Kjerstad, Ø.K. Recursive nullspace-based control allocation with strict prioritrization for marine craft. IFAC Proc. Vol. 2013, 46, 49–54. [Google Scholar] [CrossRef]
- Wei, Y.; Fu, M.; Ning, J.; Sun, X. Quadratic programming thrust allocation and management for dynamic positioning ships. Telkomnika 2013, 11, 1632–1638. [Google Scholar] [CrossRef]
- Zhao, L.; Roh, M.I. A thrust a method for efficient dynamic positioning of a semisubmersible drilling rig based on the hybrid optimization algorithm. Math. Probl. Eng. 2015, 2015, 183705. [Google Scholar] [CrossRef]
- Torben, T.R.; Brodtkorb, A.H.; Sørensen, A.J. Control allocation for double-ended ferries with full-scale experimental results. Int. J. Control Autom. Syst. 2020, 18, 556–563. [Google Scholar] [CrossRef]
- Lindegaard, K.-P.; Fossen, T.I. Fuel efficient rudder and propeller control allocation for marine craft: Experiments with model ship. IEEE Trans. Control Syst. Technol. 2003, 11, 850–862. [Google Scholar] [CrossRef]
- Fossen, T.I. A Survey of Control Allocation Methods for Ships and Underwater Vehicles. In Proceedings of the 14th IEEE Mediterriannen Conference on Control and Automation, Ancona, Italy, 28–30 June 2006. [Google Scholar]
- Johansen, T.A.; Fossen, T.I. Control allocation—A survey. Automatica 2013, 49, 1087–1103. [Google Scholar] [CrossRef]
- Fossen, T.I.; Strand, J.P. Passive nonlinear observer design for ships using Lyapunov methods: Full-scale experiments with a supply vessel. Automatica 1999, 35, 3–16. [Google Scholar] [CrossRef]
- Torsetnes, G.; Jouffroy, J.; Fossen, T.I. Nonlinear Dynamic Positioning of Ships with Gain-Scheduled Wave Filtering. In Proceedings of the 43rd IEEE Conference on Decision and Control, Nassau, Bahamas, 14–17 December 2004. [Google Scholar]
- Hassani, V.; Sørensen, A.J.; Pascoal, A.M.; Aguiar, A.P. Multiple Model Adaptive Wave Filtering for Dynamic Positioning of Marine Vessels. In Proceedings of the American Control Conference, Montreal, QC, Canada, 27–29 June 2012; pp. 6222–6228. [Google Scholar]
- Hassani, V.; Pascoal, A.M. Wave Filtering and Dynamic Positioning of Marine Vessels Using a Linear Design Model: Theory and Experiments; Ocampo-Martinez, C., Negenborn, R., Eds.; Transport of Water versus Transport over Water; Operations Research/Computer Science Interfaces Series; Springer: Cham, Switzerland, 2015; Volume 58. [Google Scholar]
- Fossen, T.I. Handbook of Marine Craft Hydrodynamics and Motion Control; John Wiley & Sons, Ltd.: Chichester, UK, 2011. [Google Scholar]
- Do, K.D. Practical control of underactuated ships. Ocean Eng. 2010, 37, 1111–1119. [Google Scholar] [CrossRef]
- McGookin, E.W. Optimisation of Sliding Mode Controllers for Marine Applications: A Study of Methods and Implementation Issues. Ph.D. Thesis, Department of Electronics and Electrical Engineering, University of Glasgow, Glasgow, Scotland, 1997. [Google Scholar]
- Alfaro-Cid, E. Optimisation of Time Domain Controllers for Supply Ships Using Genetic Algorithms and Genetic Programming. Ph.D. Thesis, Department of Electronics and Electrical Engineering of the University of Glasgow, Glasgow, Scotland, 2003. [Google Scholar]
- Johansen, T.A.; Fossen, T.I.; Tondel, P. Efficient optimal constrained control allocation via multiparametric programming. J. Guid. Control Dynam. 2005, 28, 506–515. [Google Scholar] [CrossRef]
- Tomera, M. Switching-Based Multi-Operational Control of Ship Motion; Academic Publishing House EXIT: Warsaw, Poland, 2018. [Google Scholar]



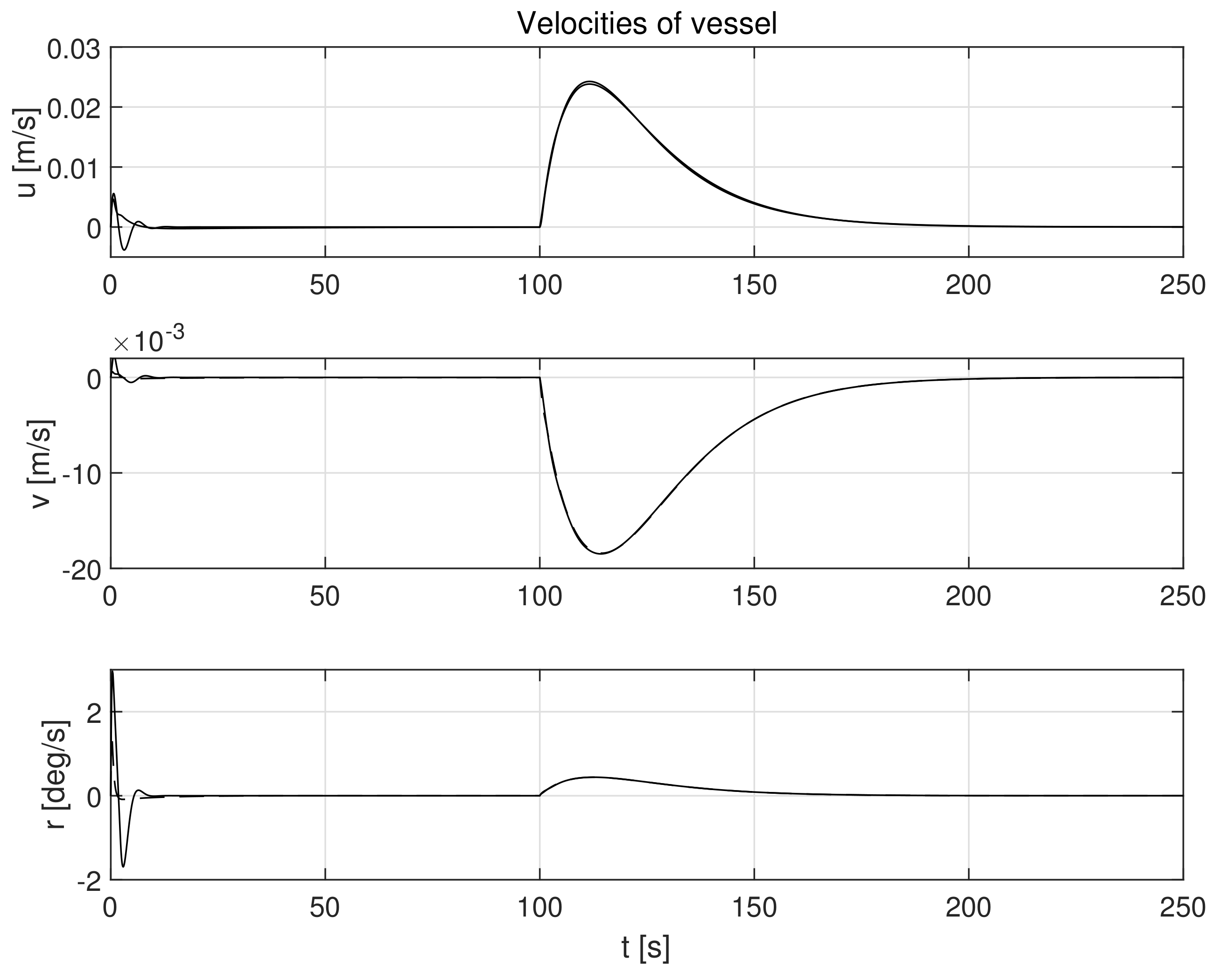


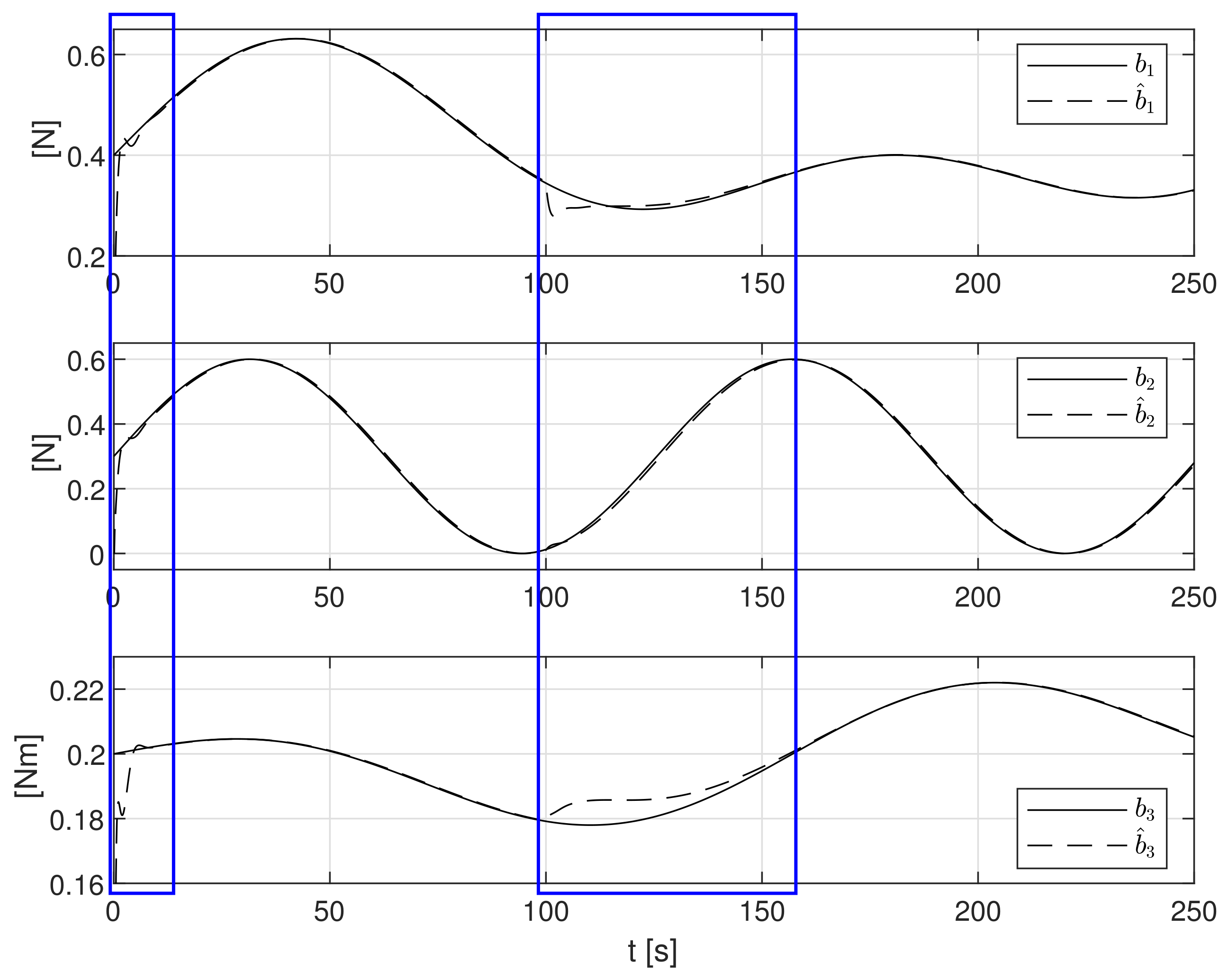






| Disturbances | Constant | Stochastic and Time-Varying | ||
|---|---|---|---|---|
| Controller | τc | τPID | τc | τPID |
| 0.1948 | 6.8797 | 0.4237 | 11.7068 | |
| 0.1564 | 1.3406 | 0.6250 | 2.8474 | |
| 80.7763 | 105.9706 | 45.6141 | 80.5418 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tomera, M.; Podgórski, K. Control of Dynamic Positioning System with Disturbance Observer for Autonomous Marine Surface Vessels. Sensors 2021, 21, 6723. https://doi.org/10.3390/s21206723
Tomera M, Podgórski K. Control of Dynamic Positioning System with Disturbance Observer for Autonomous Marine Surface Vessels. Sensors. 2021; 21(20):6723. https://doi.org/10.3390/s21206723
Chicago/Turabian StyleTomera, Mirosław, and Kamil Podgórski. 2021. "Control of Dynamic Positioning System with Disturbance Observer for Autonomous Marine Surface Vessels" Sensors 21, no. 20: 6723. https://doi.org/10.3390/s21206723
APA StyleTomera, M., & Podgórski, K. (2021). Control of Dynamic Positioning System with Disturbance Observer for Autonomous Marine Surface Vessels. Sensors, 21(20), 6723. https://doi.org/10.3390/s21206723






