Wearable Vibration Sensor for Measuring the Wing Flapping of Insects
Abstract
:1. Introduction
2. Problem Statement
- a wearable vibration sensor for an insect is developed,
- the flapping of the insect wings is measured with a vibration sensor, and
- changes in flapping during the insect’s behavior are analyzed.
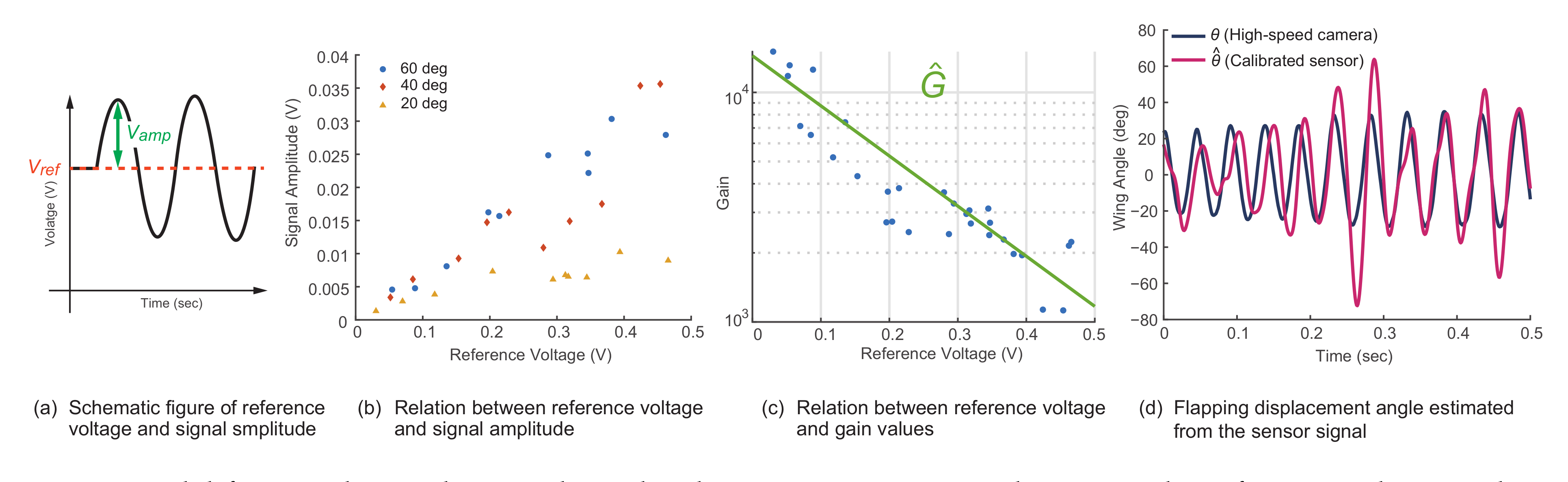
3. Development of the Wearable Vibration Sensor
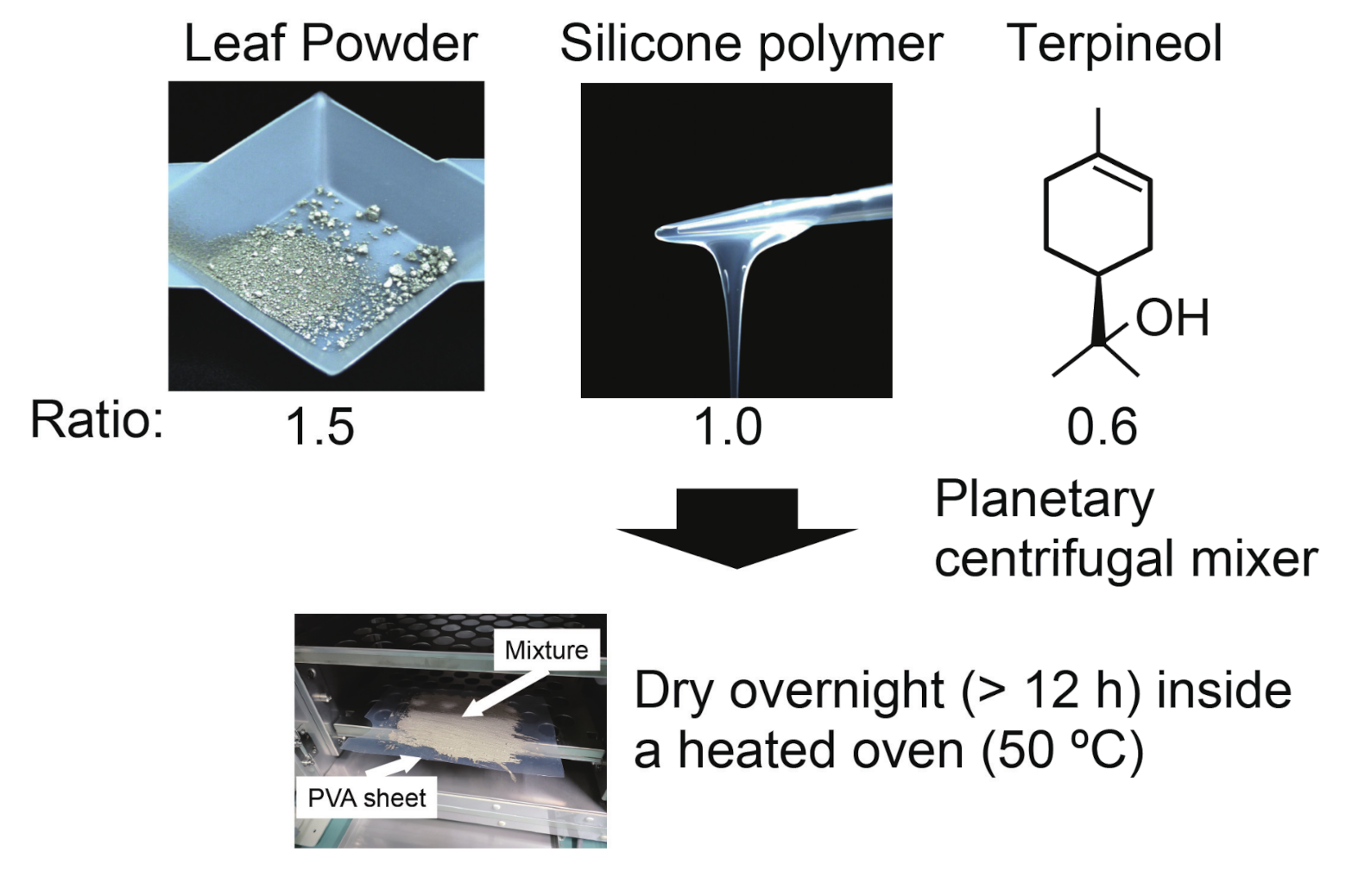
3.1. Fabrication of the Silver Leaf Powder-Silicon Vibration Sensor
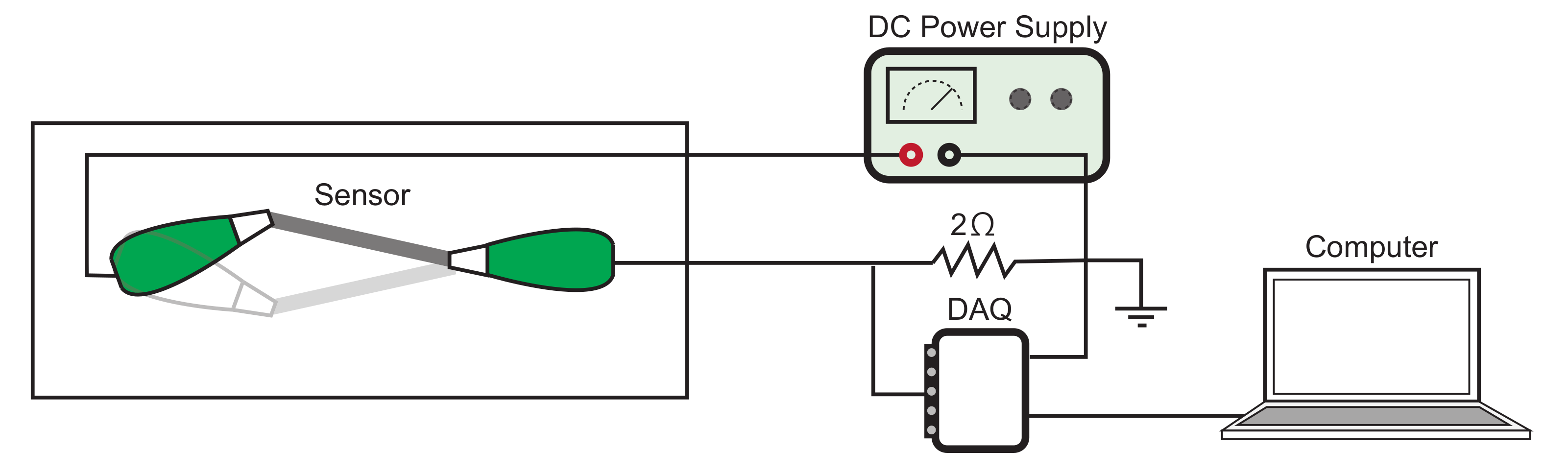
3.2. Property Evaluation of the Thin Vibration Sensor
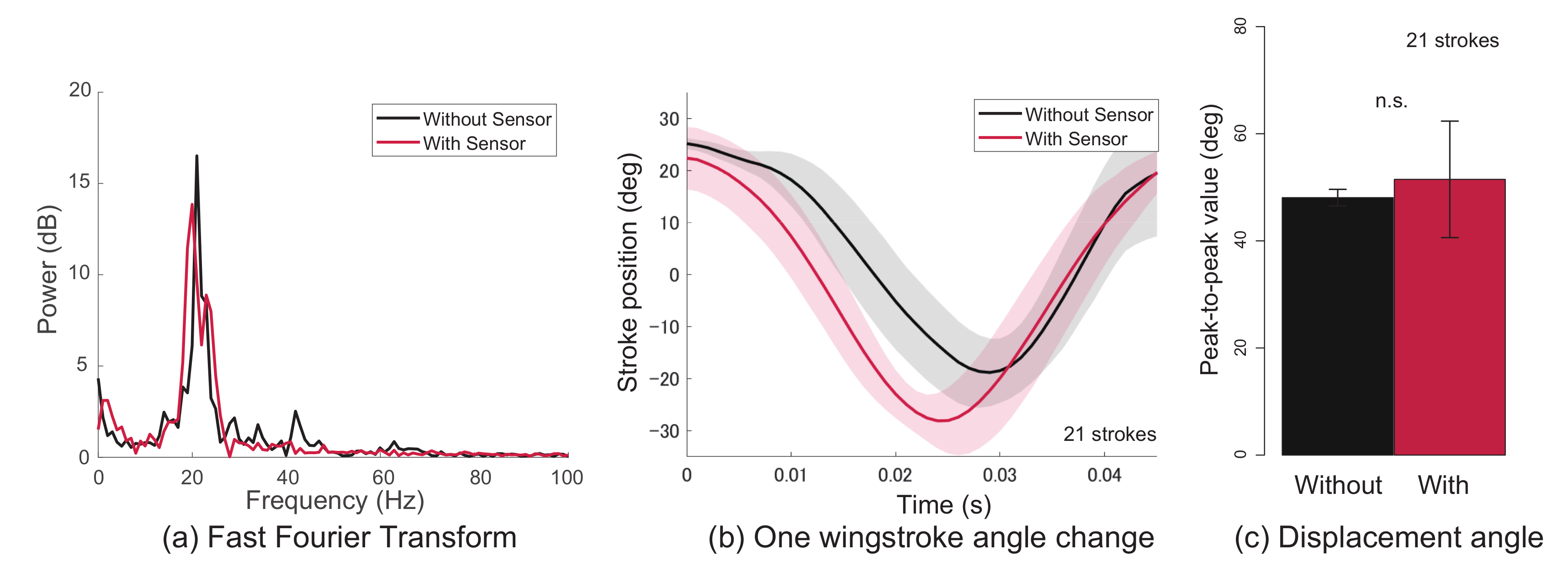
3.3. Experimental Evaluation of the Sensor Response
4. Measurement of Insect Wing Flapping with a Wearable Vibration Sensor
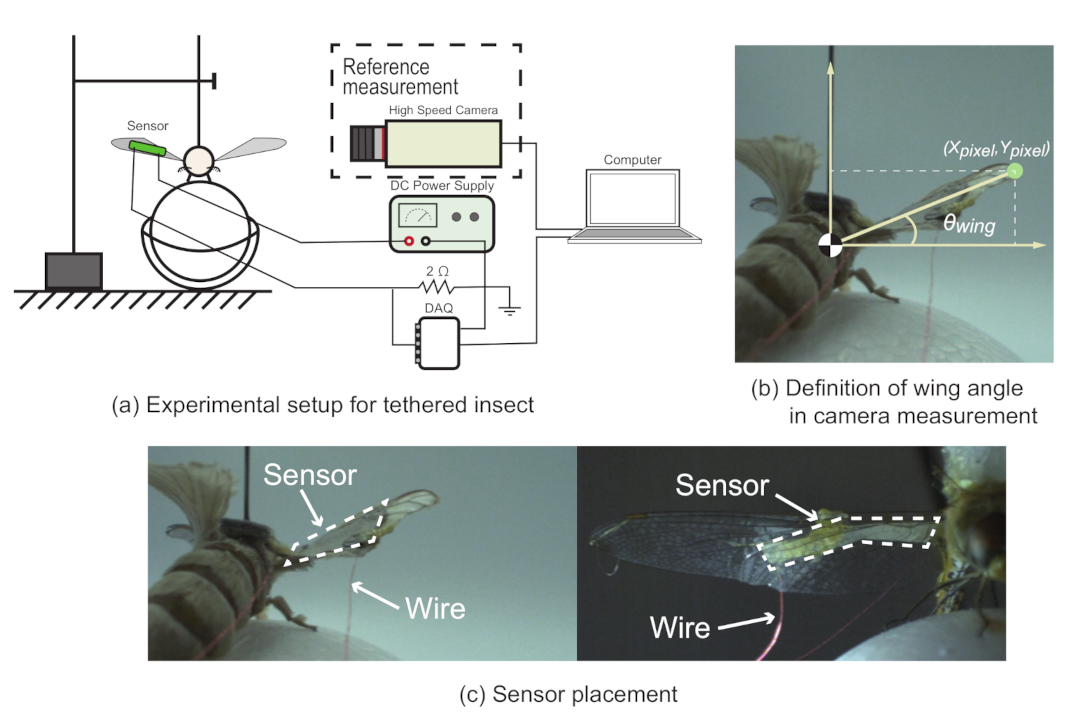
4.1. Experimental Conditions
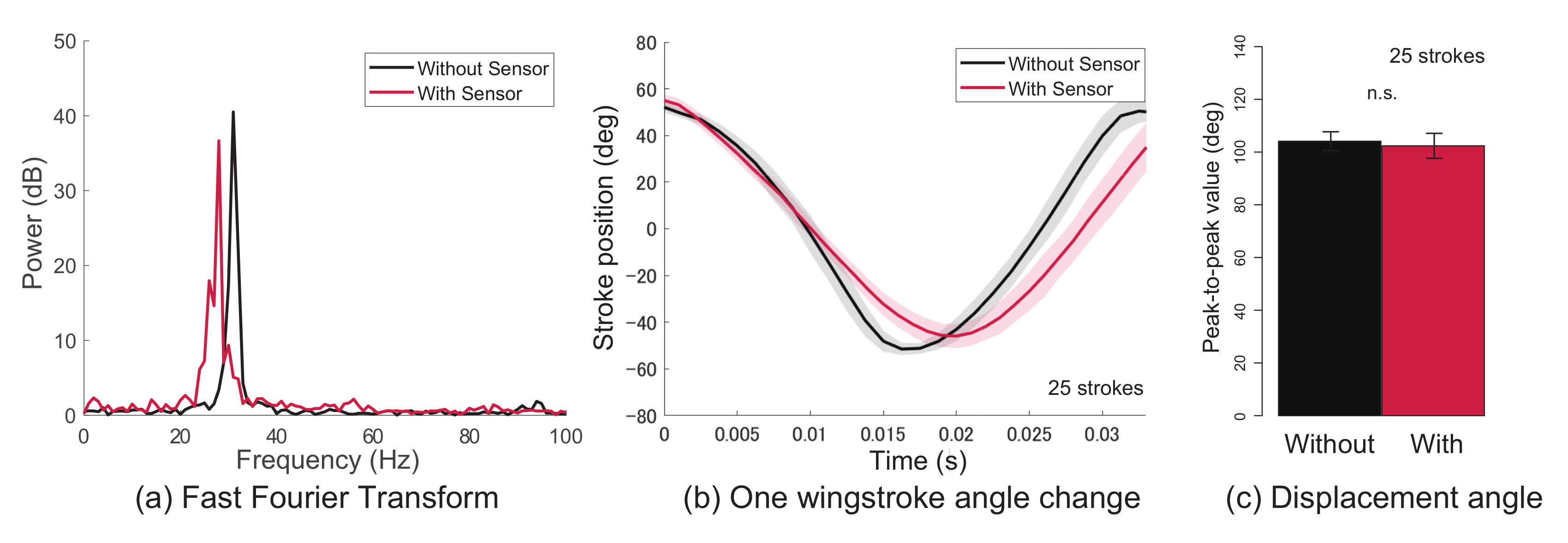
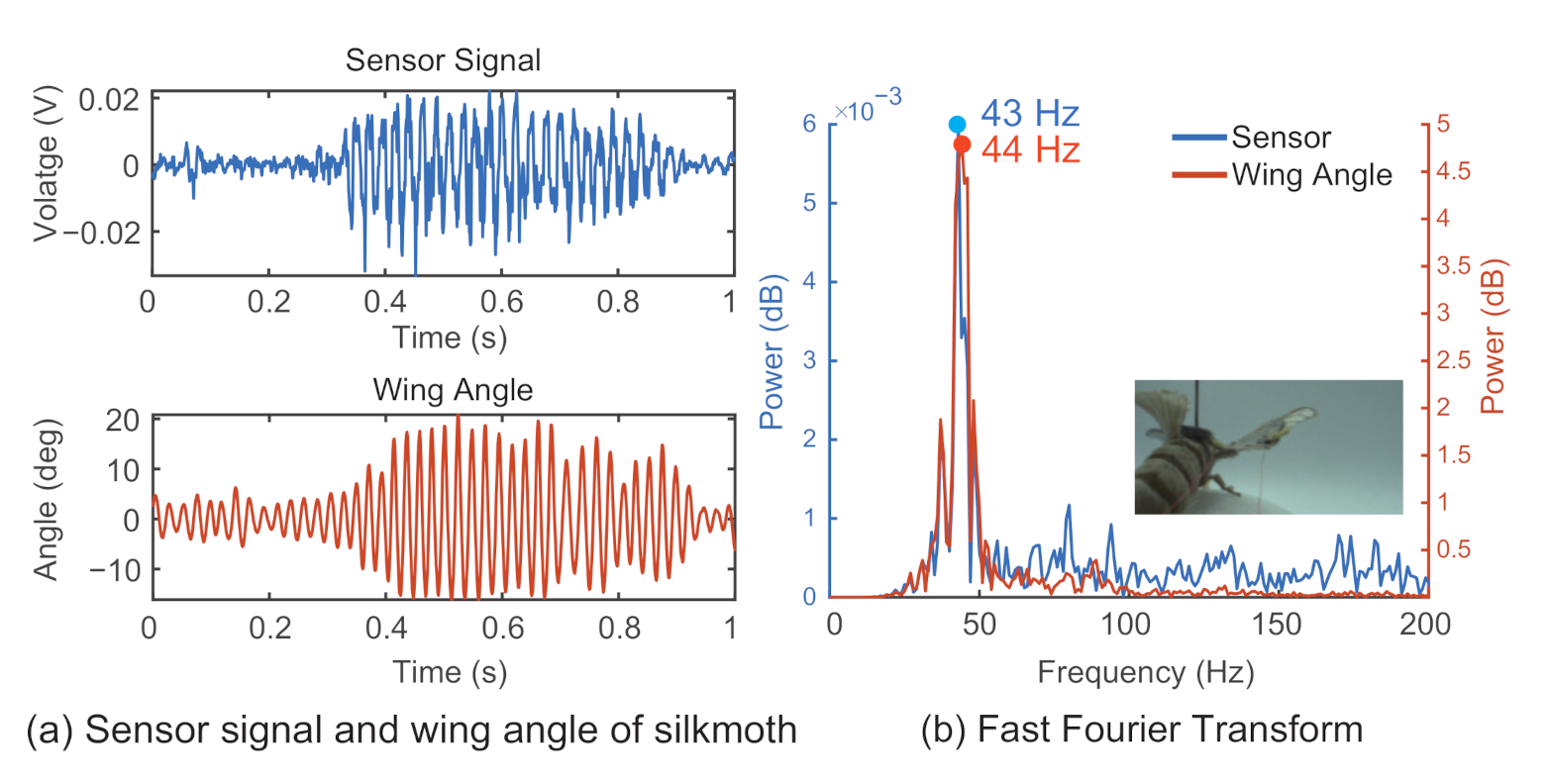
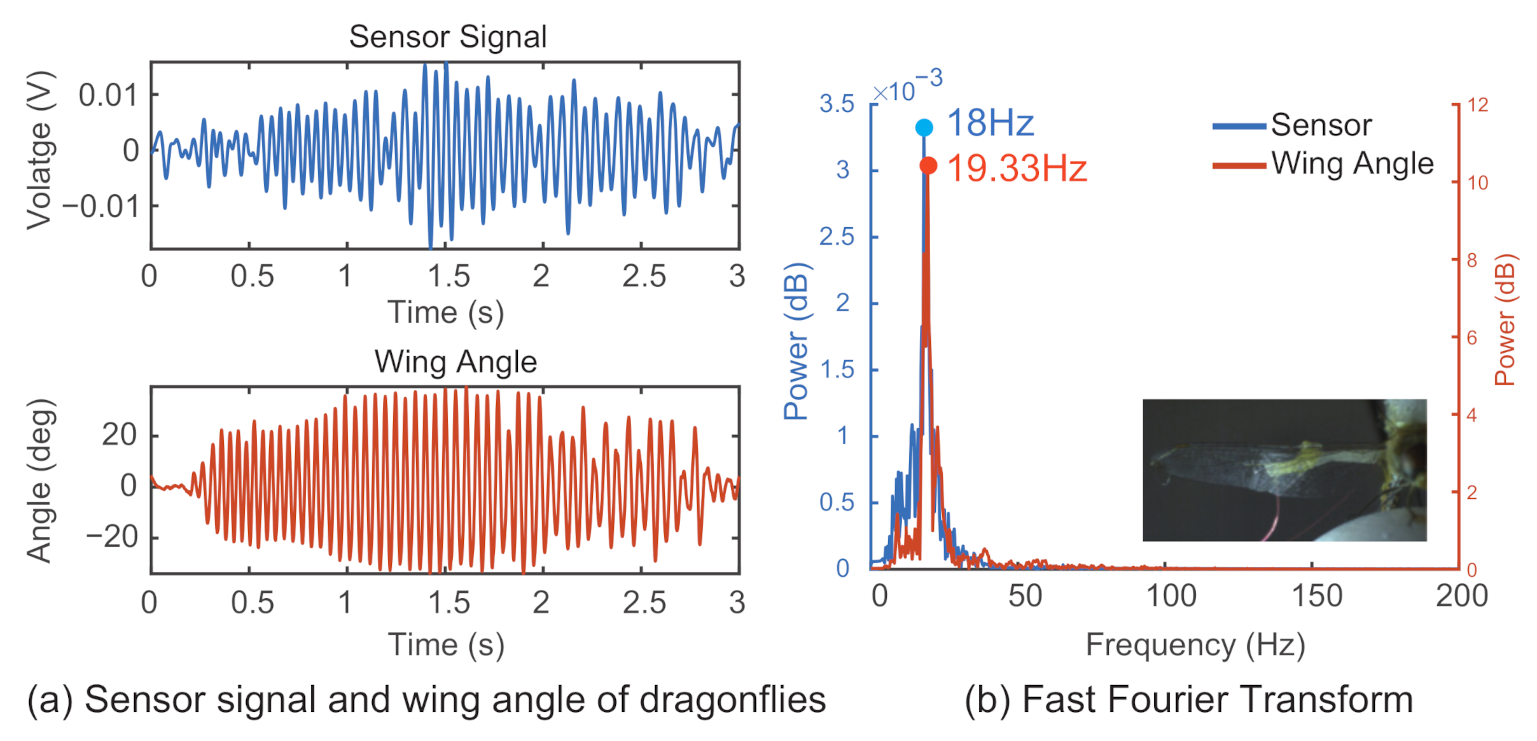
4.2. Results
5. Analysis of Flapping Changes with Behavior
5.1. Experimental Conditions
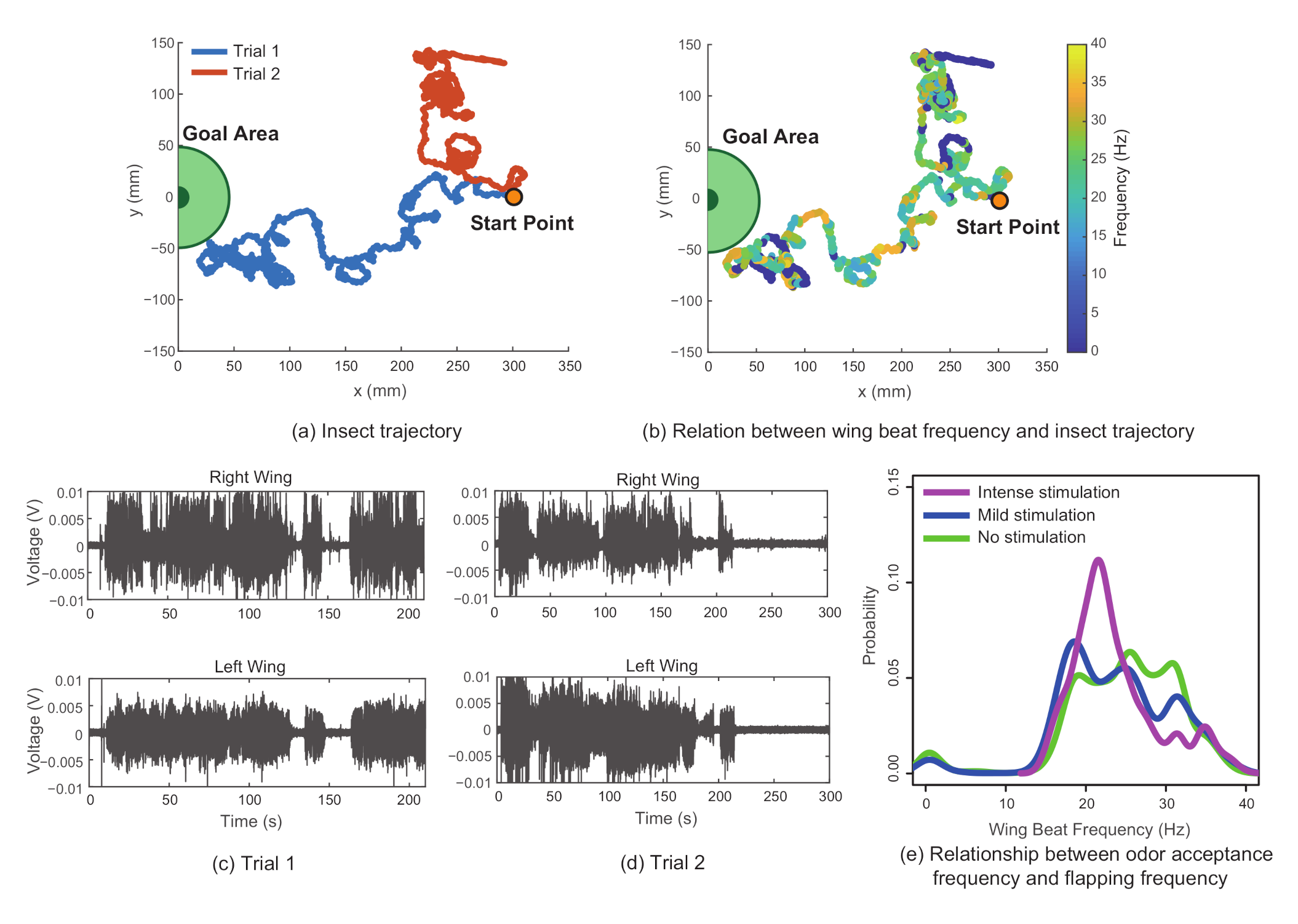
5.2. Experimental Results
6. Discussion
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| FFT | Fast Fourier transform |
| PDMS | Polydimethylsiloxane |
References
- Pfeifer, R.; Lungarella, M.; Iida, F. Self-organization, embodiment, and biologically inspired robotics. Science 2007, 318, 1088–1093. [Google Scholar]
- Jafferis, N.T.; Helbling, E.F.; Karpelson, M.; Wood, R.J. Untethered flight of an insect-sized flapping-wing microscale aerial vehicle. Nature 2019, 570, 491–495. [Google Scholar]
- Shigaki, S.; Sakurai, T.; Ando, N.; Kurabayashi, D.; Kanzaki, R. Time-varying moth-inspired algorithm for chemical plume tracing in turbulent environment. IEEE Robot. Autom. Lett. 2017, 3, 76–83. [Google Scholar]
- Ribak, G.; Barkan, S.; Soroker, V. The aerodynamics of flight in an insect flight-mill. PLoS ONE 2017, 12, e0186441. [Google Scholar]
- Naranjo, S.E. Assessing insect flight behavior in the laboratory: A primer on flight mill methodology and what can be learned. Ann. Entomol. Soc. Am. 2019, 112, 182–199. [Google Scholar]
- Minter, M.; Pearson, A.; Lim, K.S.; Wilson, K.; Chapman, J.W.; Jones, C.M. The tethered flight technique as a tool for studying lifehistory strategies associated with migration in insects. Ecol. Entomol. 2018, 43, 397–411. [Google Scholar]
- Chauncy, G. Mems & High Speed Vision Development and Application to Reverse-Engineer Drosophila Flight Control. Ph.D. Dissertation, ETH Zurich, Zürich, Switzerland, 2008. [Google Scholar]
- Nasir, M.; Dickinson, M.; Liepmann, D. Measurement of insect flight forces using a mems based physical sensor. In Proceedings of the Hilton Head 2006: A Solid State Sensors, Actuators and Microsystems Workshop, Hilton Head Island, SC, USA, 4–8 June 2006. [Google Scholar]
- Nasir, M.; Dickinson, M.; Liepmann, D. Multidirectional force and torque sensor for insect flight research. In Proceedings of the International Electronic Packaging Technical Conference and Exhibition, San Francisco, CA, USA, 17–22 July 2005; Volume 42002, pp. 1625–1630. [Google Scholar]
- Wood, R.J.; Fearing, R.S. Flight force measurements for a micromechanical flying insect. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Maui, HI, USA, 29 October–3 November 2001; Volume 1, pp. 355–362. [Google Scholar]
- Meresman, Y.; Husak, J.; Ben-Shlomo, R.; Ribak, G. Morphological diversification has led to inter-specific variation in elastic wing deformation during flight in scarab beetles. R. Soc. Open Sci. 2020, 7, 200277. [Google Scholar]
- Koehler, C.; Liang, Z.; Gaston, Z.; Wan, H.; Dong, H. 3d reconstruction and analysis of wing deformation in free-flying dragonflies. J. Exp. Biol. 2012, 215, 3018–3027. [Google Scholar]
- Chen, M.W.; Zhang, Y.L.; Sun, M. Wing and body motion and aerodynamic and leg forces during take-off in droneflies. J. R. Soc. Interface 2013, 10, 20130808. [Google Scholar]
- Liu, Y.; Sun, M. Wing kinematics measurement and aerodynamics of hovering droneflies. J. Exp. Biol. 2008, 211, 2014–2025. [Google Scholar]
- Wallace, I.D.; Lawson, N.J.; Harvey, A.R.; Jones, J.D.; Moore, A.J. Highspeed photogrammetry system for measuring the kinematics of insect wings. Appl. Opt. 2006, 45, 4165–4173. [Google Scholar]
- Pannequin, R.; Jouaiti, M.; Boutayeb, M.; Lucas, P.; Martinez, D. Automatic tracking of free-flying insects using a cable-driven robot. Sci. Robot. 2020, 5, eabb2890. [Google Scholar]
- Kang, C.K.; Cranford, J.; Sridhar, M.K.; Kodali, D.L.; Rum, D.B.; Slegers, N. Experimental characterization of a butterfly in climbing flight. AIAA J. 2018, 56, 15–24. [Google Scholar]
- Chen, Y.; Why, A.; Batista, G.; Mafra-Neto, A.; Keogh, E. Flying insect classification with inexpensive sensors. J. Insect Behav. 2014, 27, 657–677. [Google Scholar]
- Potamitis, I.; Rigakis, I. Large aperture optoelectronic devices to record and timestamp insects’ wingbeats. IEEE Sens. J. 2016, 16, 6053–6061. [Google Scholar]
- Jansson, S.; Brydegaard, M. Passive khz lidar for the quantification of insect activity and dispersal. Anim. Biotelemetry 2018, 6, 1–10. [Google Scholar]
- Mullen, E.R.; Rutschman, P.; Pegram, N.; Patt, J.M.; Adamczyk, J.J. Laser system for identification, tracking, and control of flying insects. Opt. Express 2016, 24, 828–838. [Google Scholar]
- Matsuhisa, N.; Inoue, D.; Zalar, P.; Jin, H.; Matsuba, Y.; Itoh, A.; Yokota, T.; Hashizume, D.; Someya, T. Printable elastic conductors by in situ formation of silver nanoparticles from silver flakes. Nat. Mater. 2017, 16, 834–840. [Google Scholar]
- Pang, C.; Lee, C.; Suh, K.Y. Recent advances in flexible sensors for wearable and implantable devices. J. Appl. Polym. Sci. 2013, 130, 1429–1441. [Google Scholar]
- Li, H.; Zhang, J.; Chen, J.; Luo, Z.; Zhang, J.; Alh Arish, Y.; Liu, Q.; Tang, W.; Wang, L. A supersensitive, multidimensional flexible strain gauge sensor based on ag/pdms for human activities monitoring. Sci. Rep. 2020, 10, 1–9. [Google Scholar]
- Segev-Bar, M.; Haick, H. Flexible sensors based on nanoparticles. ACS Nano 2013, 7, 8366–8378. [Google Scholar]
- Miao, P.; Wang, J.; Zhang, C.; Sun, M.; Cheng, S.; Liu, H. Graphene nanostructure-based tactile sensors for electronic skin applications. Nano-Micro Lett. 2019, 11, 71. [Google Scholar]
- Kinovea. Available online: https://www.kinovea.org/ (accessed on 30 December 2020).
- Kumar, A.; Kumar, N.; Das, R.; Lakhani, P.; Bhushan, B. In vivo structural dynamic analysis of the dragonfly wing: The effect of stigma as its modulator. Philos. Trans. R. Soc. 2019, 377, 20190132. [Google Scholar]
- Buten, T.A.; Beckmann, R.; Hecker, E. Über den sexuallockstoff des seidenspinners, i. der biologische test und die isolierung des reinen sexuallockstoffes bombykol. Hoppe-Seyler Z. FÜR Physiol. Chem. 1961, 324, 71–83. [Google Scholar]
- Loudon, C.; Koehl, M.A. Sniffing by a silkworm moth: Wing fanning enhances air penetration through and pheromone interception by antennae. J. Exp. Biol. 2000, 203, 2977–2990. [Google Scholar]
- Li, Q.; Zheng, M.; Pan, T.; Su, G. Experimental and numerical investigation on dragonfly wing and body motion during voluntary take-off. Sci. Rep. 2018, 8, 1–16. [Google Scholar]
- Obara, Y. Bombyx mori mationg dance: An essential in locationg the female. Appl. Entomol. Zool. 1979, 14, 130–132. [Google Scholar]
- Yamada, M.; Shigaki, S.; Ohashi, H.; Shimizu, M.; Hosoda, K.; Kurabayashi, D. Measurement and Analysis of Odor Source Search Behavior of Insect Using Virtual Reality System. In Proceedings of the SICE Annual Conference, Chiang Mai, Thailand, 23–26 September 2020. [Google Scholar]
- Kanzaki, R.; Sugi, N.; Shibuya, T. Self-generated Zigzag Turning of Bombyx mori Males during Pheromone-mediated Upwind Walking. Zool. Sci. 1992, 9, 515–527. [Google Scholar]
- Shigaki, S.; Shiota, Y.; Kurabayashi, D.; Kanzaki, R. Modeling of the Adaptive Chemical Plume Tracing Algorithm of an Insect Using Fuzzy Inference. IEEE Trans. Fuzzy Syst. 2019, 28, 72–84. [Google Scholar]
- Kanzaki, R. Coordination of wing motion and walking suggests common control of zigzag motor program in a male silkworm moth. J. Comp. Physiol. A 1998, 182, 267–276. [Google Scholar]
- Shigaki, S.; Fukushima, S.; Kurabayashi, D.; Sakurai, T.; Kanzaki, R. A novel method for full locomotion compensation of an untethered walking insect. Bioinspiration Biomimetics 2016, 12, 016005. [Google Scholar]

| Angle (deg) | True Freq. (Hz) | Sensor Freq. (Hz) | Difference Freq. (Hz) |
|---|---|---|---|
| 20 | 2.5 ± 0.0 | 2.5 ± 0.0 | 0.0 ± 0.0 |
| 40 | 1.3 ± 0.0 | 1.0 ± 0.0 | 0.3 ± 0.0 |
| 60 | 0.83 ± 0.0 | 1.0 ± 0.0 | 0.17 ± 0.0 |
| ID | Trial | True Freq. (Hz) | Sensor Freq. (Hz) | Difference Freq. (Hz) |
|---|---|---|---|---|
| 1 | 26 | 26 | 0 | |
| SM1 | 2 | 19 | 20 | 1 |
| 3 | 18 | 18 | 0 | |
| 1 | 28 | 30 | 2 | |
| SM2 | 2 | 26 | 26 | 0 |
| 3 | 18 | 21 | 3 | |
| 1 | 17 | 17 | 0 | |
| SM3 | 2 | 16 | 19 | 3 |
| 3 | 17 | 18 | 1 | |
| 1 | 31 | 31 | 0 | |
| SM4 | 2 | 23 | 23 | 0 |
| 3 | 23 | 23 | 0 | |
| 1 | 43 | 43 | 0 | |
| SM5 | 2 | 41 | 41 | 0 |
| 3 | 40 | 40 | 0 |
| Trial | True Freq. (Hz) | Sensor Freq. (Hz) | Difference freq. (Hz) |
|---|---|---|---|
| 1 | 19 | 19 | 0 |
| 2 | 19 | 18 | 1 |
| 3 | 20 | 20 | 0 |
| 4 | 19 | 19 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yanagisawa, R.; Shigaki, S.; Yasui, K.; Owaki, D.; Sugimoto, Y.; Ishiguro, A.; Shimizu, M. Wearable Vibration Sensor for Measuring the Wing Flapping of Insects. Sensors 2021, 21, 593. https://doi.org/10.3390/s21020593
Yanagisawa R, Shigaki S, Yasui K, Owaki D, Sugimoto Y, Ishiguro A, Shimizu M. Wearable Vibration Sensor for Measuring the Wing Flapping of Insects. Sensors. 2021; 21(2):593. https://doi.org/10.3390/s21020593
Chicago/Turabian StyleYanagisawa, Ryota, Shunsuke Shigaki, Kotaro Yasui, Dai Owaki, Yasuhiro Sugimoto, Akio Ishiguro, and Masahiro Shimizu. 2021. "Wearable Vibration Sensor for Measuring the Wing Flapping of Insects" Sensors 21, no. 2: 593. https://doi.org/10.3390/s21020593
APA StyleYanagisawa, R., Shigaki, S., Yasui, K., Owaki, D., Sugimoto, Y., Ishiguro, A., & Shimizu, M. (2021). Wearable Vibration Sensor for Measuring the Wing Flapping of Insects. Sensors, 21(2), 593. https://doi.org/10.3390/s21020593







