MNP-Enhanced Microwave Medical Imaging by Means of Pseudo-Noise Sensing
Abstract
:1. Introduction
2. Materials and Methods
2.1. Magnetic Susceptibility of MNPs in the Microwave Frequency Range
2.2. UWB M-Sequence Radar
2.3. Investigation of the MNP Response Depending on the Viscosity and the Magnetic Field Intensity
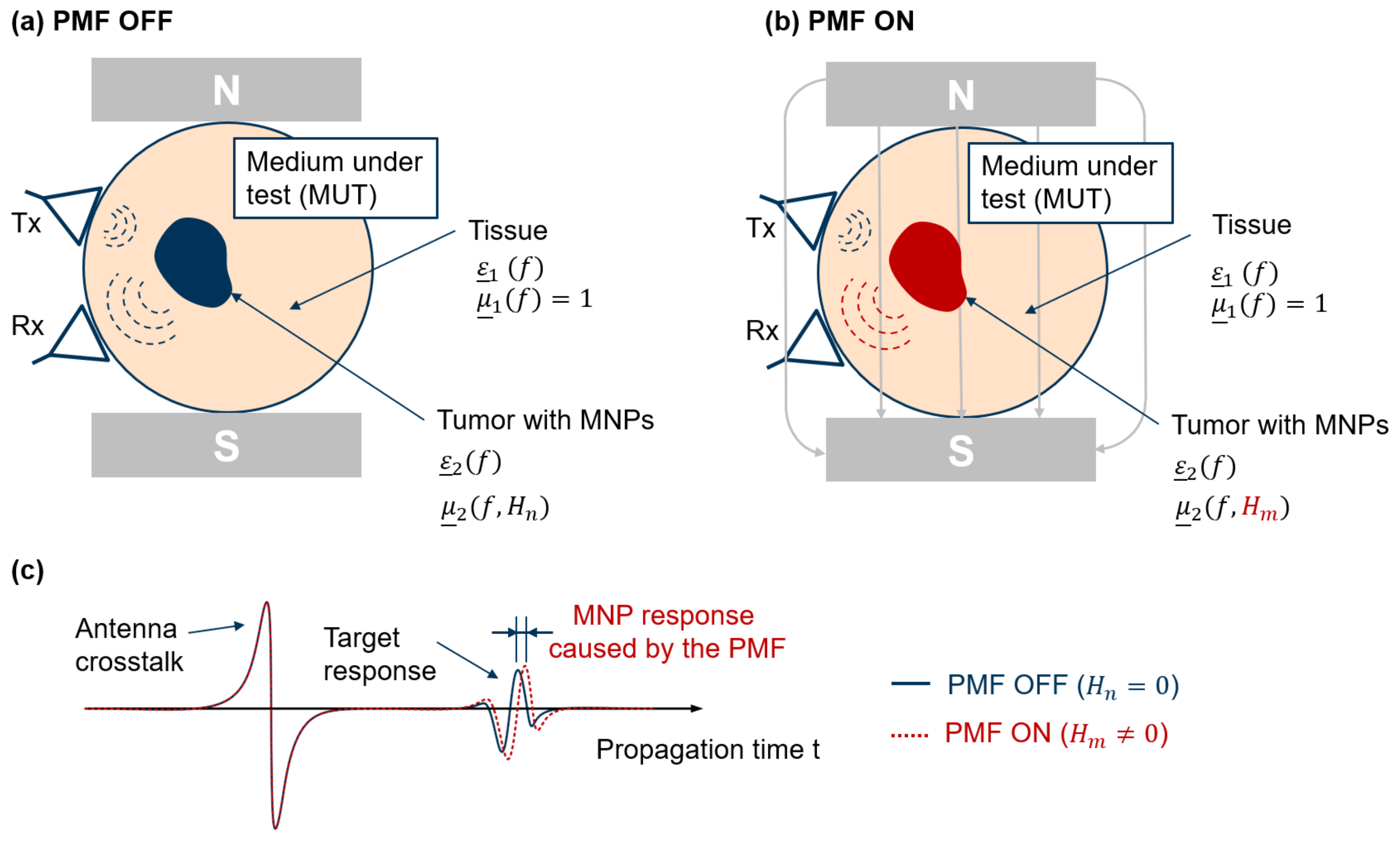
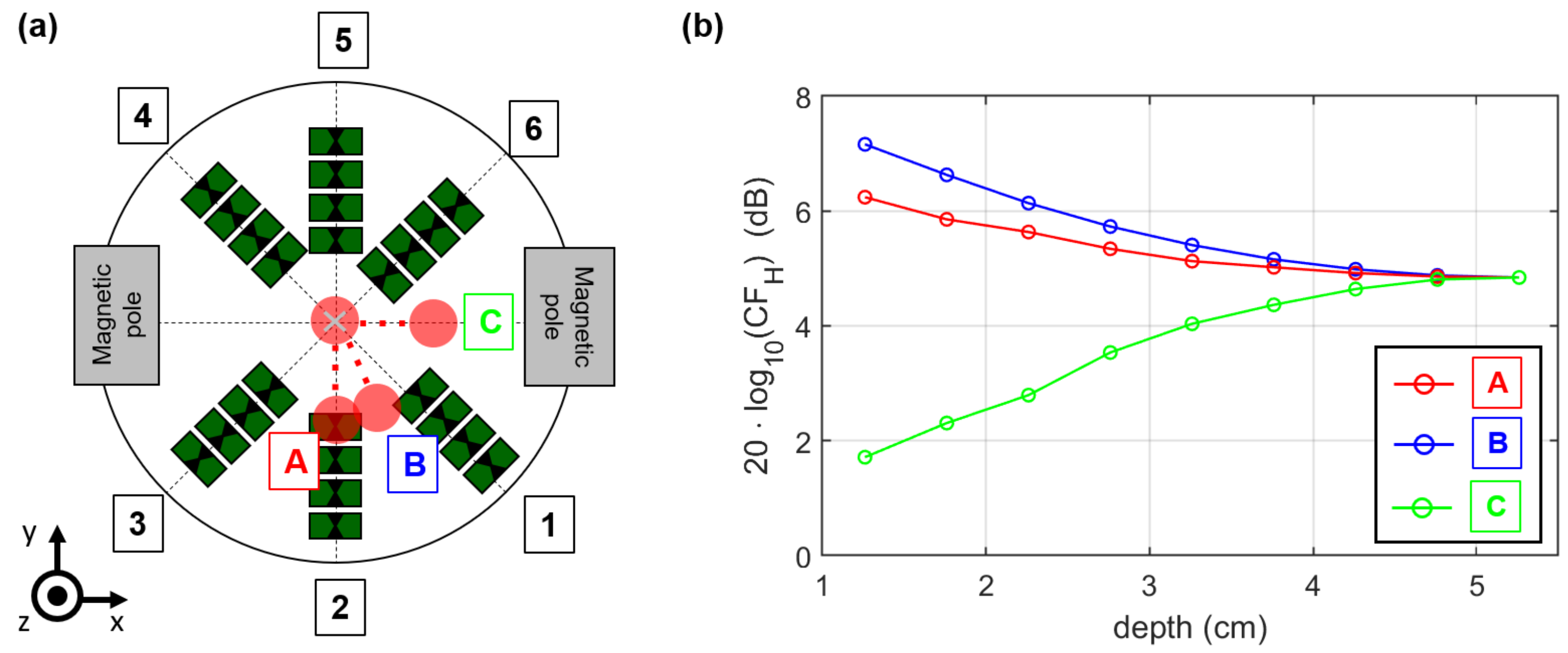
2.4. MNP Differential Microwave Imaging Setup
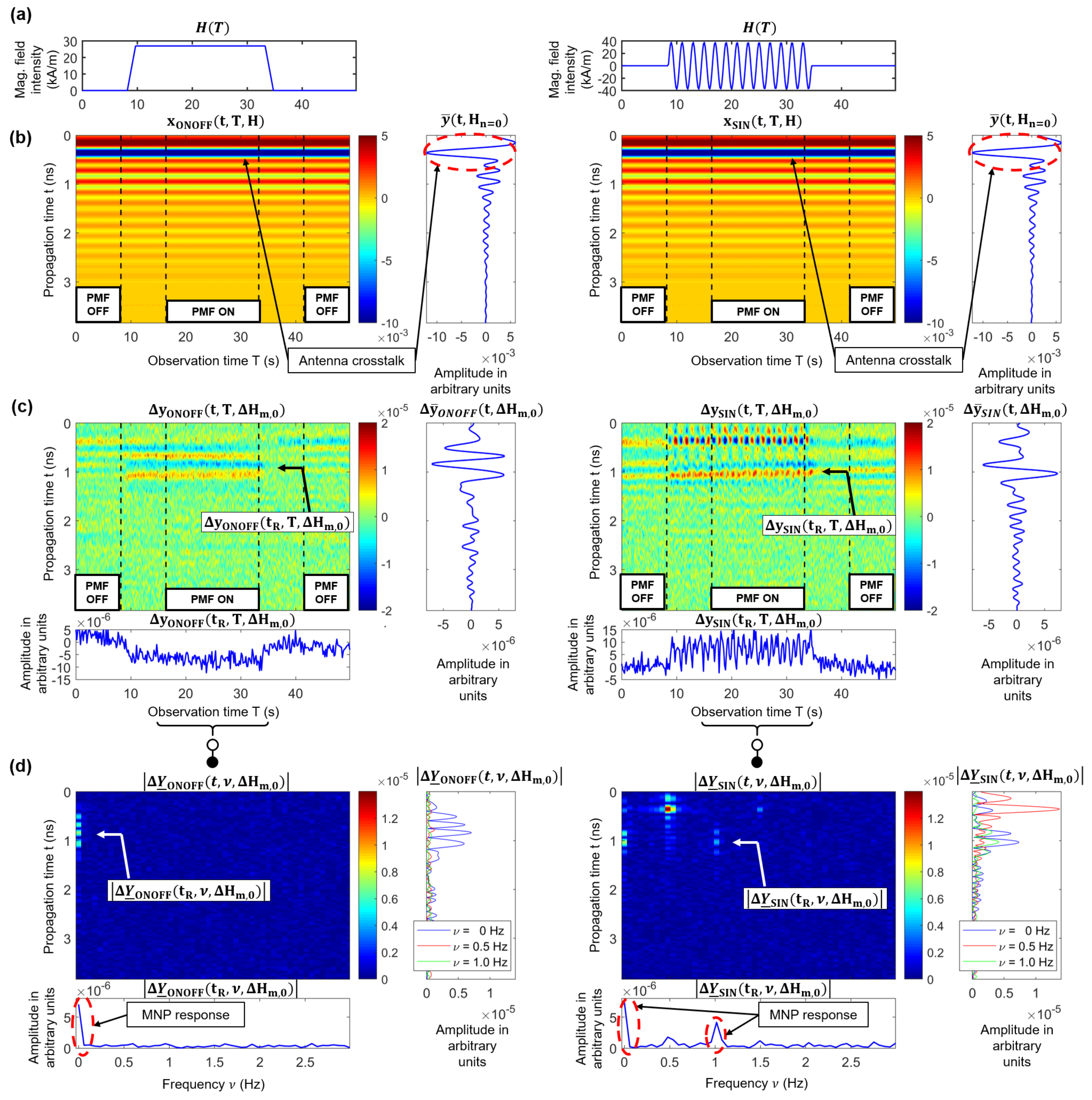
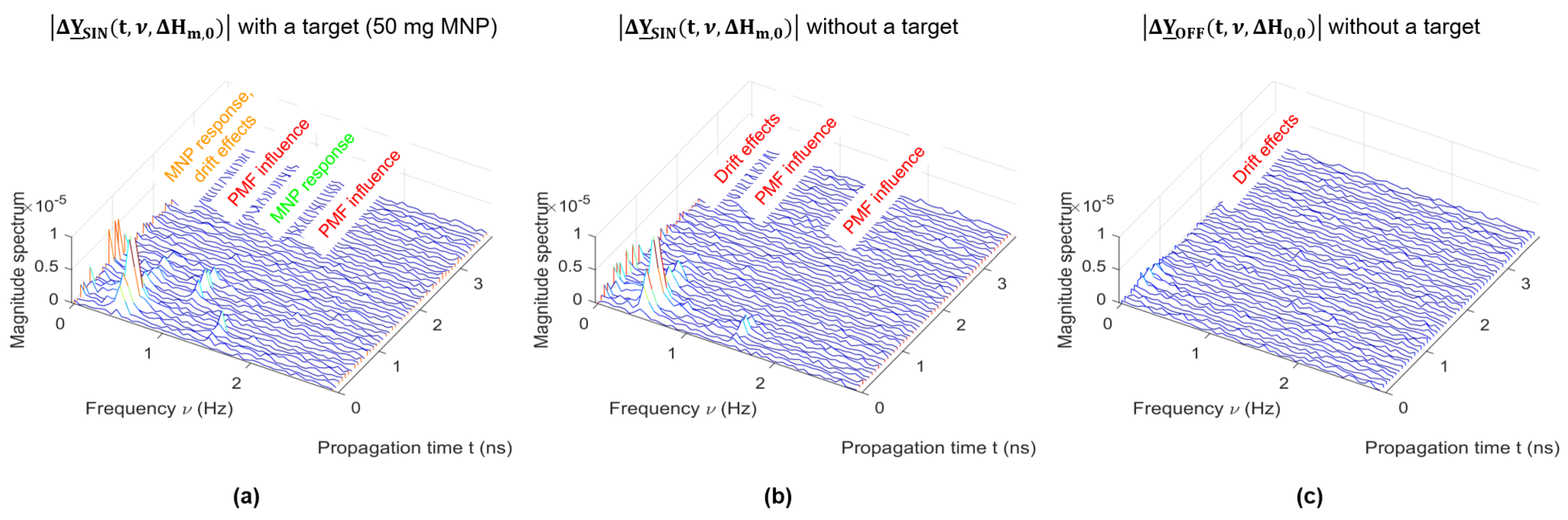
2.5. Signal Processing and Clutter Removal
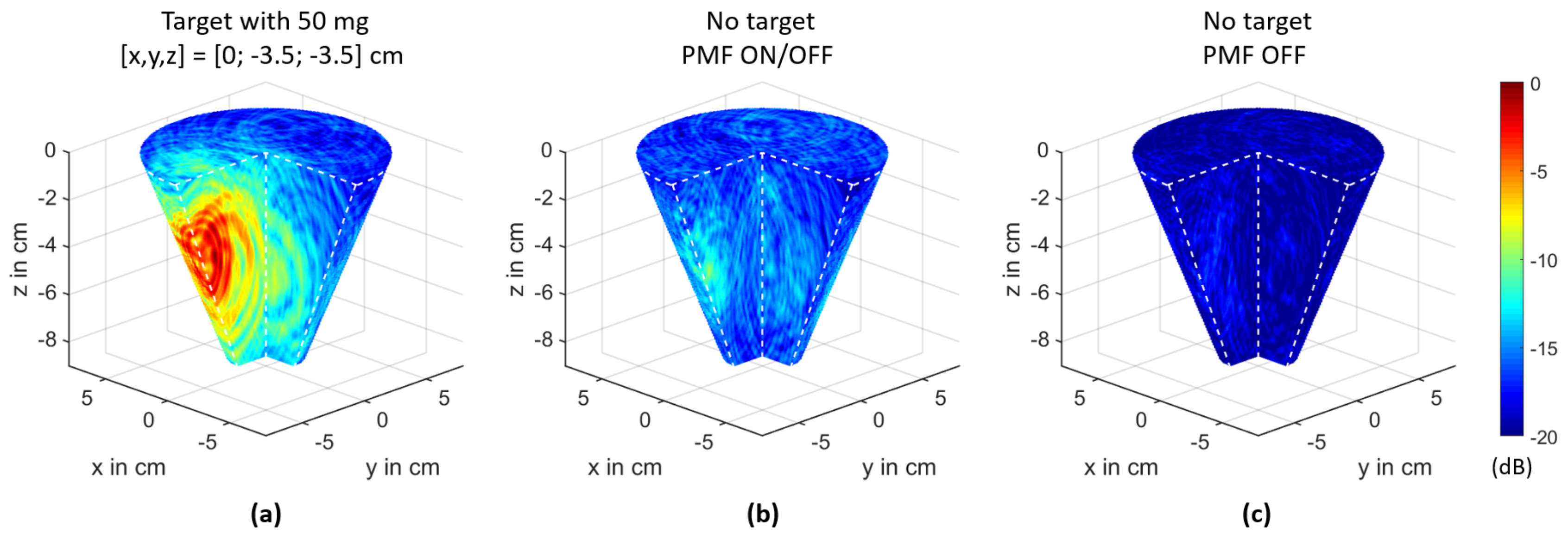
2.6. MNP Imaging
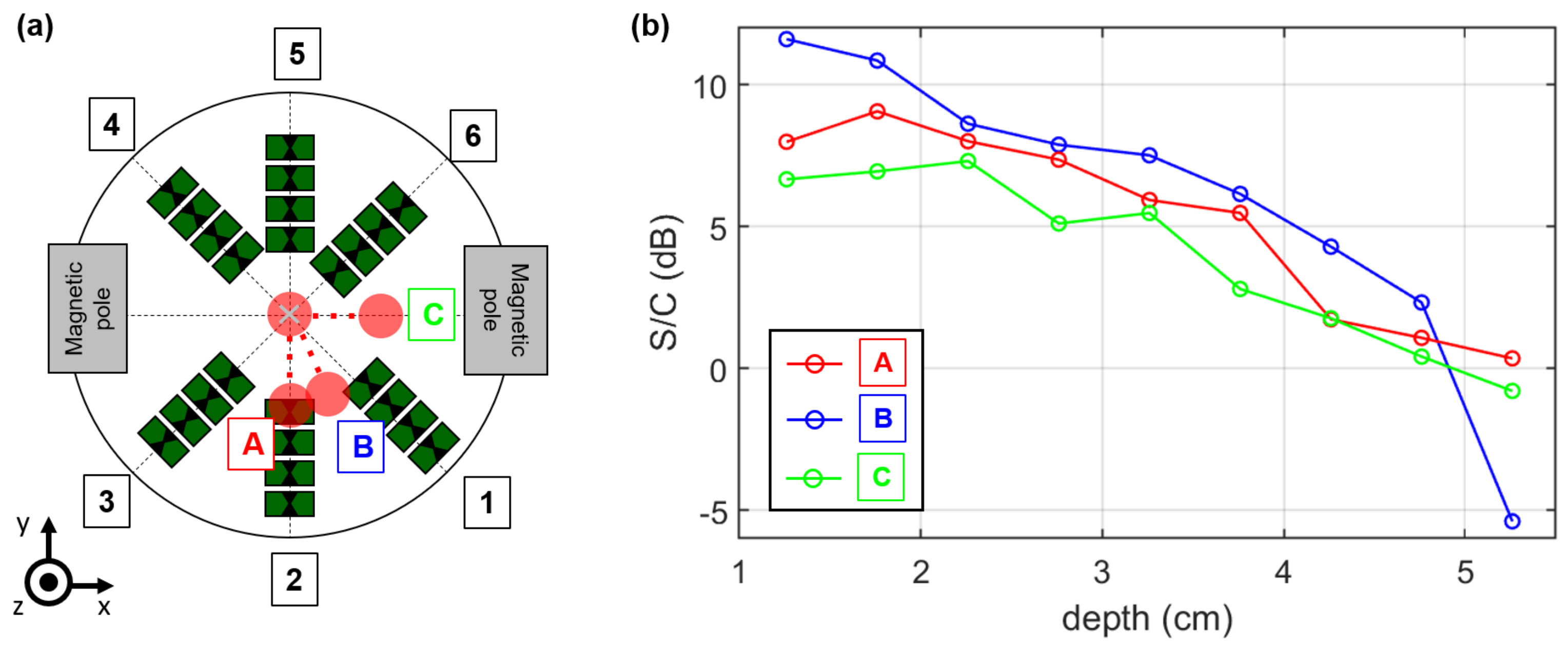
2.7. Magnetic Field Analysis
3. Results
3.1. Influence of Viscosity and Magnetic Field Intensity
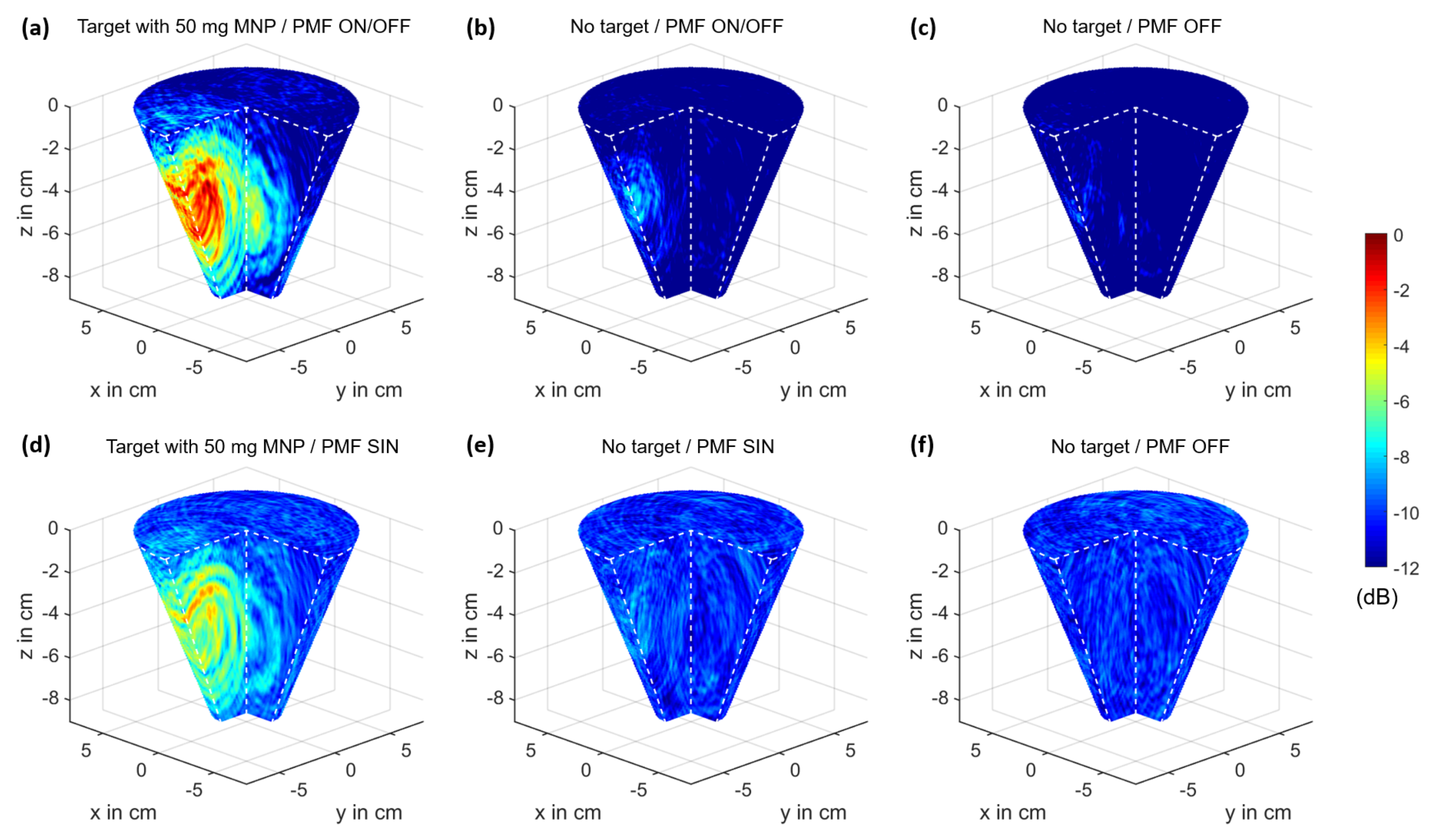
3.2. MNP Imaging
3.3. Magnetic Field Influence
3.4. PMF Modulation
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| 3D | Three-dimensional |
| DAS | Delay-and-sum |
| DC | Direct current |
| IRF | Impulse response function |
| MIMO | Multiple-in and multiple-out |
| MNPs | Magnetic nanoparticles |
| MPI | Magnetic particle imaging |
| MRI | Magnetic resonance imaging |
| MRX | Magnetorelaxometry |
| MUT | Medium under test |
| MWI | Microwave imaging |
| OG | Oil–gelatin |
| PMF | Polarizing magnetic field |
| UWB | Ultra-wideband |
References
- Cheng, H.W.; Tsao, H.Y.; Chiang, C.S.; Chen, S.Y. Advances in Magnetic Nanoparticle-Mediated Cancer Immune-Theranostics. Adv. Healthc. Mater. 2021, 10, 2001451. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.; Kim, D.I.; Kwon, S.H.; Park, S. Magnetically Actuated Drug Delivery Helical Microrobot with Magnetic Nanoparticle Retrieval Ability. ACS Appl. Mater. Interfaces 2021, 13, 19633–19647. [Google Scholar] [CrossRef]
- Wells, J.; Ortega, D.; Steinhoff, U.; Dutz, S.; Garaio, E.; Sandre, O.; Natividad, E.; Cruz, M.M.; Brero, F.; Southern, P.; et al. Challenges and recommendations for magnetic hyperthermia characterization measurements. Int. J. Hyperth. 2021, 38, 447–460. [Google Scholar] [CrossRef] [PubMed]
- Campanile, R.; Scardapane, E.; Forente, A.; Granata, C.; Germano, R.; Di Girolamo, R.; Minopoli, A.; Velotta, R.; Della Ventura, B.; Iannotti, V. Core-Shell Magnetic Nanoparticles for Highly Sensitive Magnetoelastic Immunosensor. Nanomaterials 2020, 10, 1526. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Ouyang, M.; Ray, A.; Liu, T.; Kong, J.; Bai, B.; Kim, D.; Guziak, A.; Luo, Y.; Feizi, A.; et al. Computational cytometer based on magnetically modulated coherent imaging and deep learning. Light Sci. Appl. 2019, 8, 91. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jin, Y.; Jia, C.; Huang, S.W.; O’Donnell, M.; Gao, X. Multifunctional nanoparticles as coupled contrast agents. Nat. Commun. 2010, 1, 41. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Anker, J.N.; Kopelman, R. Magnetically modulated optical nanoprobes. Appl. Phys. Lett. 2003, 82, 1102–1104. [Google Scholar] [CrossRef] [Green Version]
- Pankhurst, Q.A.; Connolly, J.; Jones, S.K.; Dobson, J. Applications of magnetic nanoparticles in biomedicine. J. Phys. D Appl. Phys. 2003, 36, R167–R181. [Google Scholar] [CrossRef] [Green Version]
- Weizenecker, J.; Gleich, B.; Rahmer, J.; Dahnke, H.; Borgert, J. Three-dimensional real-time in vivo magnetic particle imaging. Phys. Med. Biol. 2009, 54, L1–L10. [Google Scholar] [CrossRef]
- Wiekhorst, F.; Steinhoff, U.; Eberbeck, D.; Trahms, L. Magnetorelaxometry Assisting Biomedical Applications of Magnetic Nanoparticles. Pharm. Res. 2011, 29, 1189–1202. [Google Scholar] [CrossRef] [Green Version]
- Bellizzi, G.; Bucci, O.M.; Catapano, I. Microwave Cancer Imaging Exploiting Magnetic Nanoparticles as Contrast Agent. IEEE Trans. Biomed. Eng. 2011, 58, 2528–2536. [Google Scholar] [CrossRef]
- Ley, S.; Sachs, J.; Helbig, M. MNP enhanced microwave breast cancer imaging based on ultra-wideband pseudo-noise sensing. In Proceedings of the 2017 11th European Conference on Antennas and Propagation (EUCAP), Paris, France, 19–24 March 2017; pp. 2754–2757. [Google Scholar]
- Dulińska-Litewka, J.; Łazarczyk, A.; Hałubiec, P.; Szafrański, O.; Karnas, K.; Karewicz, A. Superparamagnetic Iron Oxide Nanoparticles—Current and Prospective Medical Applications. Materials 2019, 12, 617. [Google Scholar] [CrossRef] [Green Version]
- Bao, Y.; Wen, T.; Samia, A.C.S.; Khandhar, A.; Krishnan, K.M. Magnetic nanoparticles: Material engineering and emerging applications in lithography and biomedicine. J. Mater. Sci. 2016, 51, 513–553. [Google Scholar] [CrossRef] [Green Version]
- Liebl, M.; Wiekhorst, F.; Eberbeck, D.; Radon, P.; Gutkelch, D.; Baumgarten, D.; Steinhoff, U.; Trahms, L. Magnetorelaxometry procedures for quantitative imaging and characterization of magnetic nanoparticles in biomedical applications. Biomed. Eng./Biomed. Tech. 2015, 60, 427–443. [Google Scholar] [CrossRef]
- Schier, P.; Liebl, M.; Steinhoff, U.; Handler, M.; Wiekhorst, F.; Baumgarten, D. Optimizing Excitation Coil Currents for Advanced Magnetorelaxometry Imaging. J. Math. Imaging Vis. 2020, 62, 238–252. [Google Scholar] [CrossRef] [Green Version]
- Bucci, O.M.; Bellizzi, G.; Costanzo, S.; Crocco, L.; Di Massa, G.; Scapaticci, R. Experimental Characterization of Spurious Signals in Magnetic Nanoparticles Enhanced Microwave Imaging of Cancer. Sensors 2021, 21, 2820. [Google Scholar] [CrossRef]
- Ley, S.; Helbig, M.; Sachs, J.; Frick, S.; Hilger, I. First trials towards contrast enhanced microwave breast cancer detection by magnetic modulated nanoparticles. In Proceedings of the 2015 9th European Conference on Antennas and Propagation (EuCAP), Lisbon, Portugal, 13–17 April 2015; pp. 1–4. [Google Scholar]
- Fannin, P.C.; Kinsella, L.; Charles, S.W. On the influence of a uniform magnetic field on the Néel relaxation of a colloidal suspension of nanometre-sized particles. J. Phys. D Appl. Phys. 1997, 30, 2292–2297. [Google Scholar] [CrossRef]
- Raikher, Y.; Shliomis, M. The Effective-Field Method in the Orientational Kinetics of Magnetic Fluids and Liquid-Crystals. Relax. Phenom. Condens. Matter 2007, 87, 595–751. [Google Scholar] [CrossRef]
- Bellizzi, G.; Bucci, O.M. A Novel Measurement Technique for the Broadband Characterization of Diluted Water Ferrofluids for Biomedical Applications. IEEE Trans. Magn. 2013, 49, 2903–2912. [Google Scholar] [CrossRef]
- Coffey, W.T.; Kalmykov, Y.P.; Massawe, E.S. The Effective Eigenvalue Method and Its Application to Stochastic Problems in Conjunction with the Nonlinear Langevin Equation; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1993. [Google Scholar] [CrossRef]
- Coffey, W.; Cregg, P.J.; Kalmykov, Y. On the theory of Debye and Néel relaxation of single domain ferromagnetic particles. Adv. Chem. Phys. 1993, 83, 263–464. [Google Scholar]
- Fannin, P.; Kinsella, L.; Charles, S. The high-frequency complex susceptibility of ferrofluids deduced from fits to lower frequency measurements. J. Phys. D Appl. Phys. 1997, 30, 533. [Google Scholar] [CrossRef]
- Fannin, P.C. Magnetic spectroscopy as an aide in understanding magnetic fluids. J. Magn. Magn. Mater. 2002, 252, 59–64. [Google Scholar] [CrossRef]
- Fannin, P.; Scaife, B.; Giannitsis, A.; Oireachtaigh, C. High frequency ferromagnetic resonance measurements in magnetic fluids. J. Magn. Magn. Mater. 2005, 289, 159–161. [Google Scholar] [CrossRef]
- Fannin, P.C.; Scaife, B.K.P.; Giannitsis, A.T.; Charles, S.W. Determination of the radius of nano-particles in a magnetic fluid by means of a constant frequency measurement technique. J. Phys. D Appl. Phys. 2002, 35, 1305–1310. [Google Scholar] [CrossRef]
- Bucci, O.M.; Bellizzi, G.; Bellizzi, G.G. Microwave Broadband Characterization of a Diluted Water-Based Ferrofluid in Presence of a Polarizing Magnetic Field. IEEE Trans. Magn. 2017, 53, 1–8. [Google Scholar] [CrossRef]
- Sachs, J.; Helbig, M.; Herrmann, R.; Kmec, M.; Schilling, K.; Zaikov, E. Remote vital sign detection for rescue, security, and medical care by ultra-wideband pseudo-noise radar. Ad Hoc Netw. 2014, 13, 42–53. [Google Scholar] [CrossRef]
- Sachs, J. Handbook of Ultra-Wideband Short-Range Sensing; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2012. [Google Scholar]
- Ley, S.; Faenger, B.; Sachs, J.; Hilger, I.; Helbig, M. Investigation of Influences on the Detectability of Magnetic Nanoparticles by Means of Microwaves for Biomedical Applications. In Proceedings of the 2020 14th European Conference on Antennas and Propagation (EuCAP), Copenhagen, Denmark, 15–20 March 2020; pp. 1–4. [Google Scholar] [CrossRef]
- Lazebnik, M.; Madsen, E.L.; Frank, G.R.; Hagness, S.C. Tissue-mimicking phantom materials for narrowband and ultrawideband microwave applications. Phys. Med. Biol. 2005, 50, 4245–4258. [Google Scholar] [CrossRef] [PubMed]
- Ley, S.; Faenger, B.; Hilger, I.; Helbig, M. MNP Enhanced Microwave Imaging by Means of Pseudo-Noise Sensing with Different External Magnetic Field Modulations. In Proceedings of the 2020 42nd Annual International Conference of the IEEE Engineering in Medicine Biology Society (EMBC), Montreal, QC, Canada, 20–24 July 2020; pp. 1795–1798. [Google Scholar] [CrossRef]
- Prokhorova, A.; Ley, S.; Helbig, M. Quantitative Interpretation of UWB Radar Images for Non-Invasive Tissue Temperature Estimation during Hyperthermia. Diagnostics 2021, 11, 818. [Google Scholar] [CrossRef]
- Bucci, O.M.; Bellizzi, G.; Costanzo, S.; Crocco, L.; Di Massa, G.; Scapaticci, R. Assessing Detection Limits in Magnetic Nanoparticle Enhanced Microwave Imaging. IEEE Access 2018, 6, 43192–43202. [Google Scholar] [CrossRef]
- Fear, E.C.; Li, X.; Hagness, S.C.; Stuchly, M.A. Confocal microwave imaging for breast cancer detection: Localization of tumors in three dimensions. IEEE Trans. Biomed. Eng. 2002, 49, 812–822. [Google Scholar] [CrossRef] [Green Version]
- Helbig, M.; Kmec, M.; Sachs, J.; Geyer, C.; Hilger, I.; Rimkus, G. Aspects of antenna array configuration for UWB breast imaging. In Proceedings of the 6th European Conference on Antennas and Propagation, EuCAP 2012, Prague, Czech Republic, 26–30 March 2012; pp. 1737–1741. [Google Scholar] [CrossRef]
- Massey, F.J. The Kolmogorov-Smirnov Test for Goodness of Fit. J. Am. Stat. Assoc. 1951, 46, 68–78. [Google Scholar] [CrossRef]
- Helbig, M.; Dahlke, K.; Hilger, I.; Kmec, M.; Sachs, J. Design and Test of an Imaging System for UWB Breast Cancer Detection. Frequenz 2012, 66, 387–394. [Google Scholar] [CrossRef] [Green Version]
- Bellizzi, G.; Bellizzi, G.G.; Bucci, O.M.; Crocco, L.; Helbig, M.; Ley, S.; Sachs, J. Optimization of the Working Conditions for Magnetic Nanoparticle-Enhanced Microwave Diagnostics of Breast Cancer. IEEE Trans. Biomed. Eng. 2018, 65, 1607–1616. [Google Scholar] [CrossRef]
- Dutz, S.; Kettering, M.; Hilger, I.; Robert, M. Magnetic multicore nanoparticles for hyperthermia—Influence of particle immobilization in tumour tissue on magnetic properties. Nanotechnology 2011, 22, 265102. [Google Scholar] [CrossRef]







| PMF | ON/OFF | SIN ( Hz) | OFF | ||
|---|---|---|---|---|---|
| Target | 50 mg (2 mL) | No Target | 50 mg (2 mL) | No Target | No Target |
| Hz | 5.7 dB | 1.8 dB | 4.9 dB | 2.7 dB | 0.9 dB |
| Hz | dB | dB | 3.4 dB | 0.1 dB | 0 dB |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ley, S.; Sachs, J.; Faenger, B.; Hilger, I.; Helbig, M. MNP-Enhanced Microwave Medical Imaging by Means of Pseudo-Noise Sensing. Sensors 2021, 21, 6613. https://doi.org/10.3390/s21196613
Ley S, Sachs J, Faenger B, Hilger I, Helbig M. MNP-Enhanced Microwave Medical Imaging by Means of Pseudo-Noise Sensing. Sensors. 2021; 21(19):6613. https://doi.org/10.3390/s21196613
Chicago/Turabian StyleLey, Sebastian, Jürgen Sachs, Bernd Faenger, Ingrid Hilger, and Marko Helbig. 2021. "MNP-Enhanced Microwave Medical Imaging by Means of Pseudo-Noise Sensing" Sensors 21, no. 19: 6613. https://doi.org/10.3390/s21196613
APA StyleLey, S., Sachs, J., Faenger, B., Hilger, I., & Helbig, M. (2021). MNP-Enhanced Microwave Medical Imaging by Means of Pseudo-Noise Sensing. Sensors, 21(19), 6613. https://doi.org/10.3390/s21196613






