Study of Forward and Backward Modes in Double-Sided Dielectric-Filled Corrugated Waveguides
Abstract
:1. Introduction
2. Parametric Study of the Structure
2.1. Effect of Breaking the Symmetry
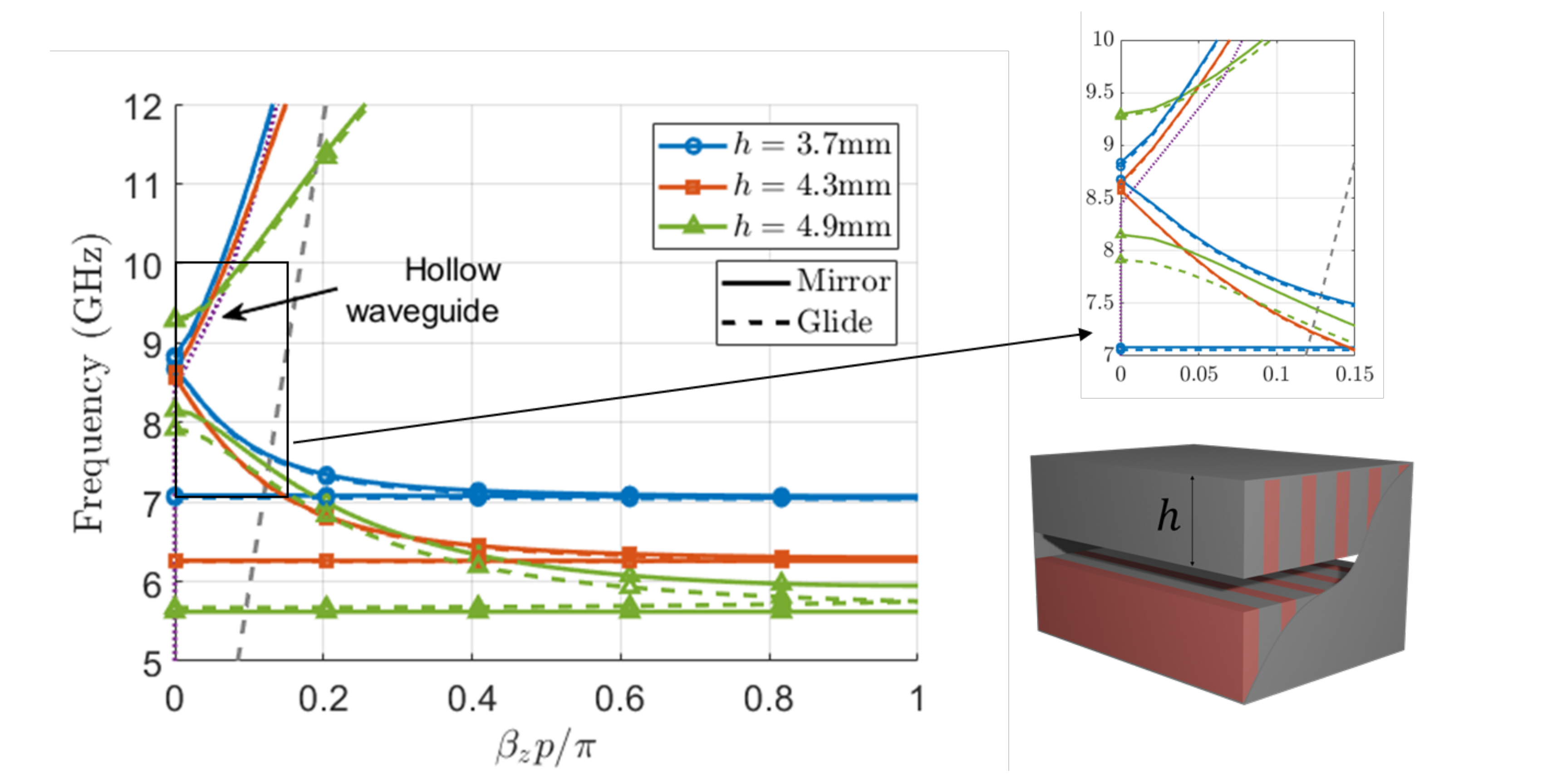
2.2. Effect of Corrugations Height
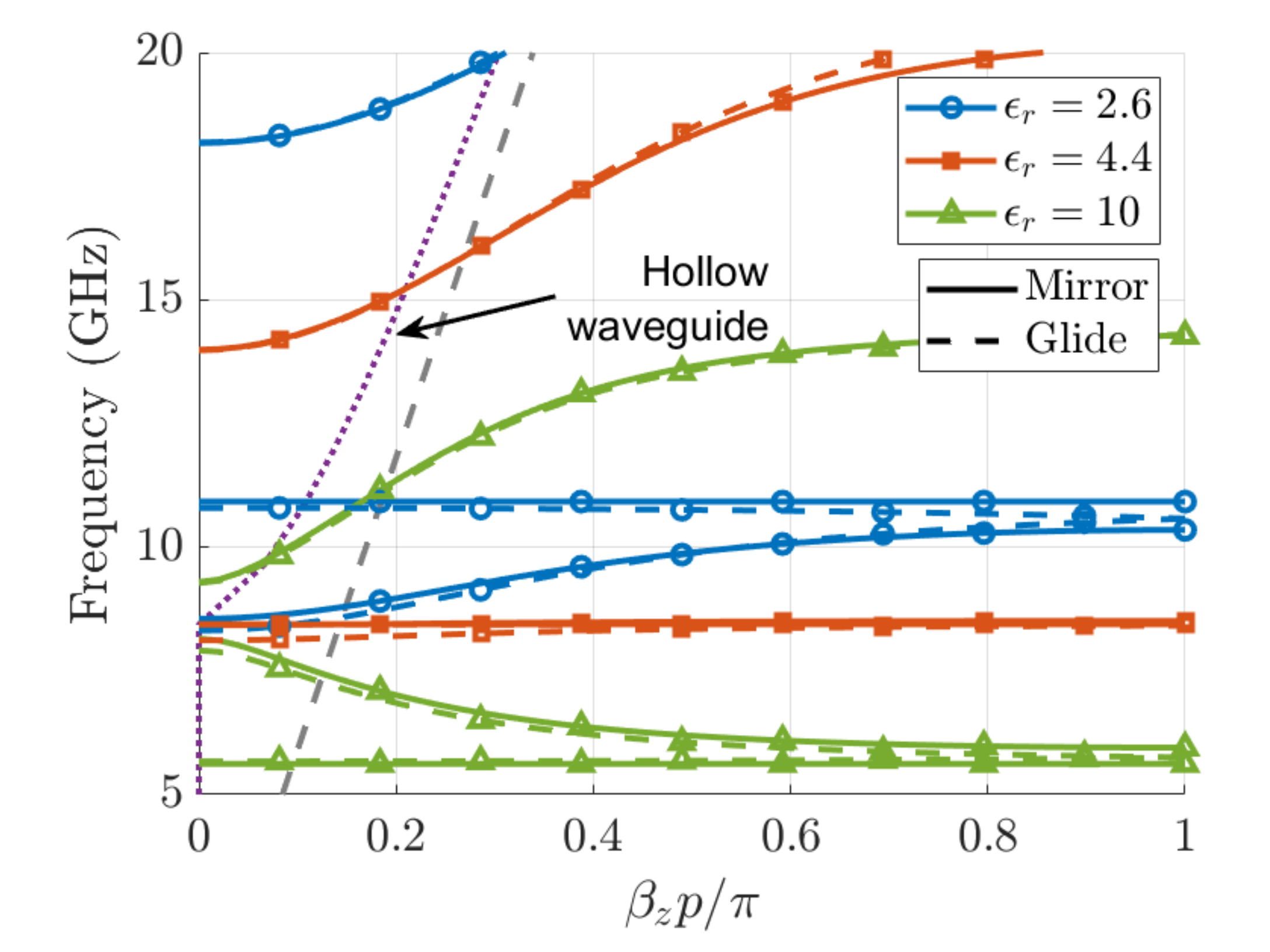
2.3. Effect of the Permittivity
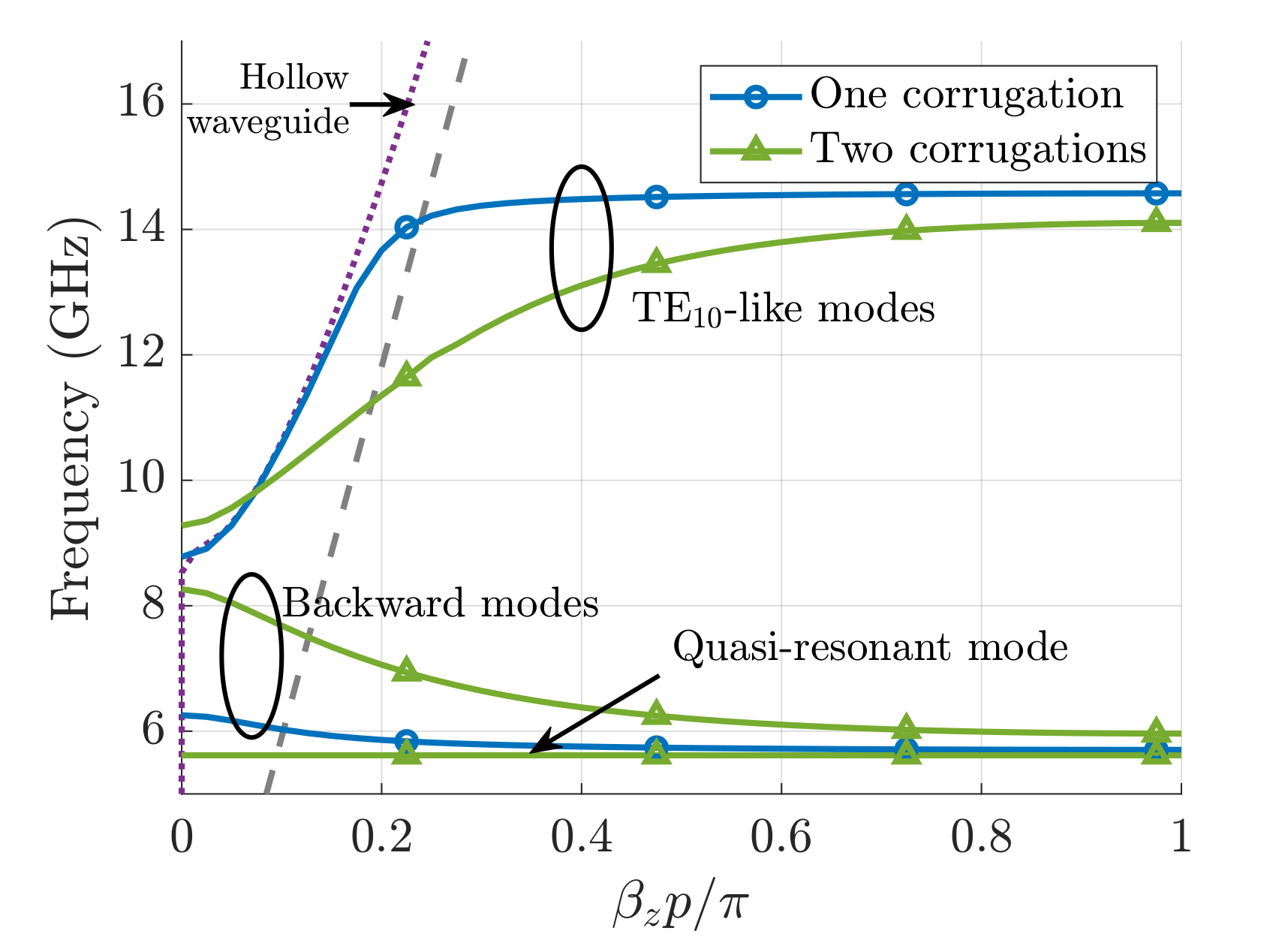
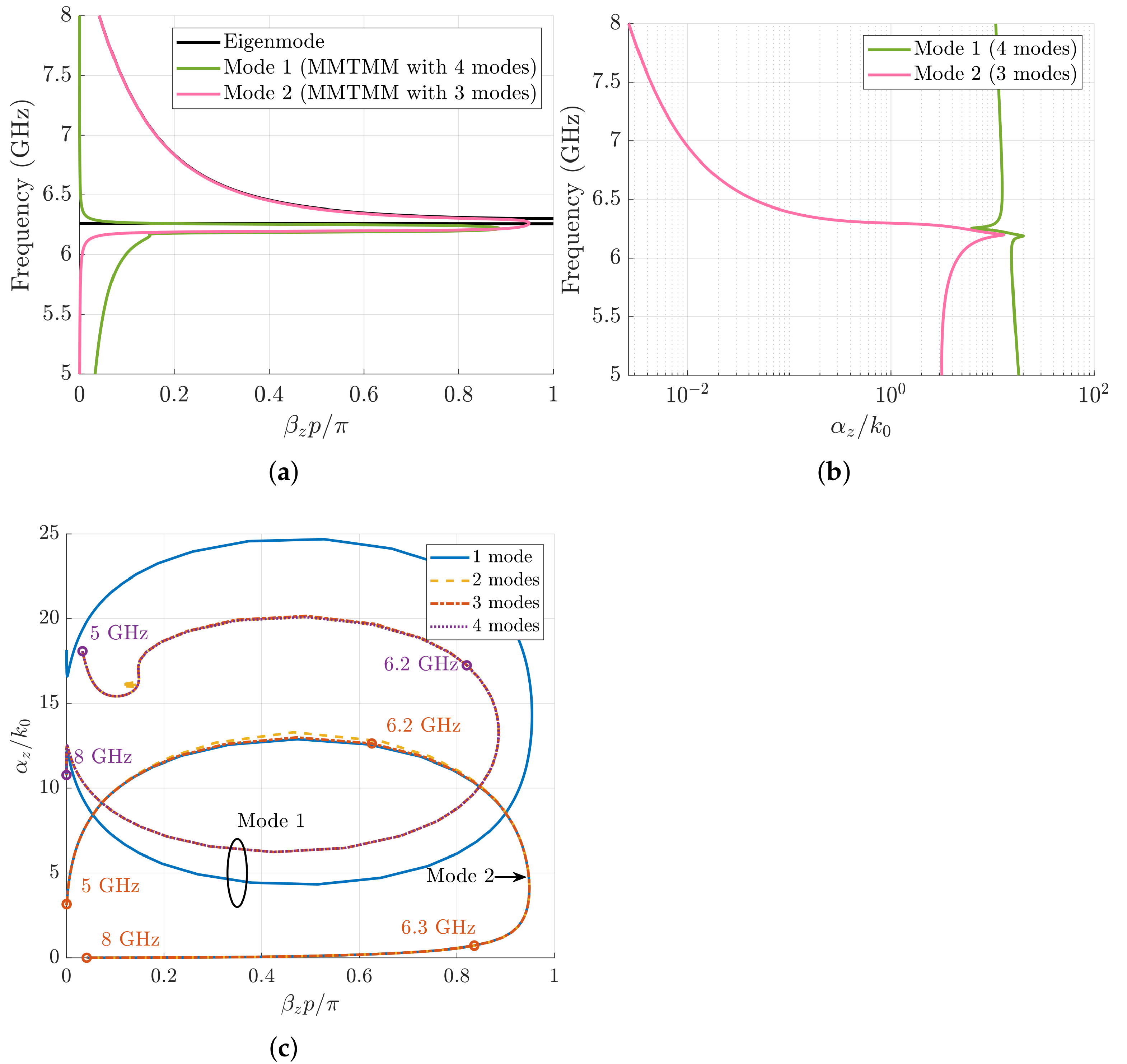
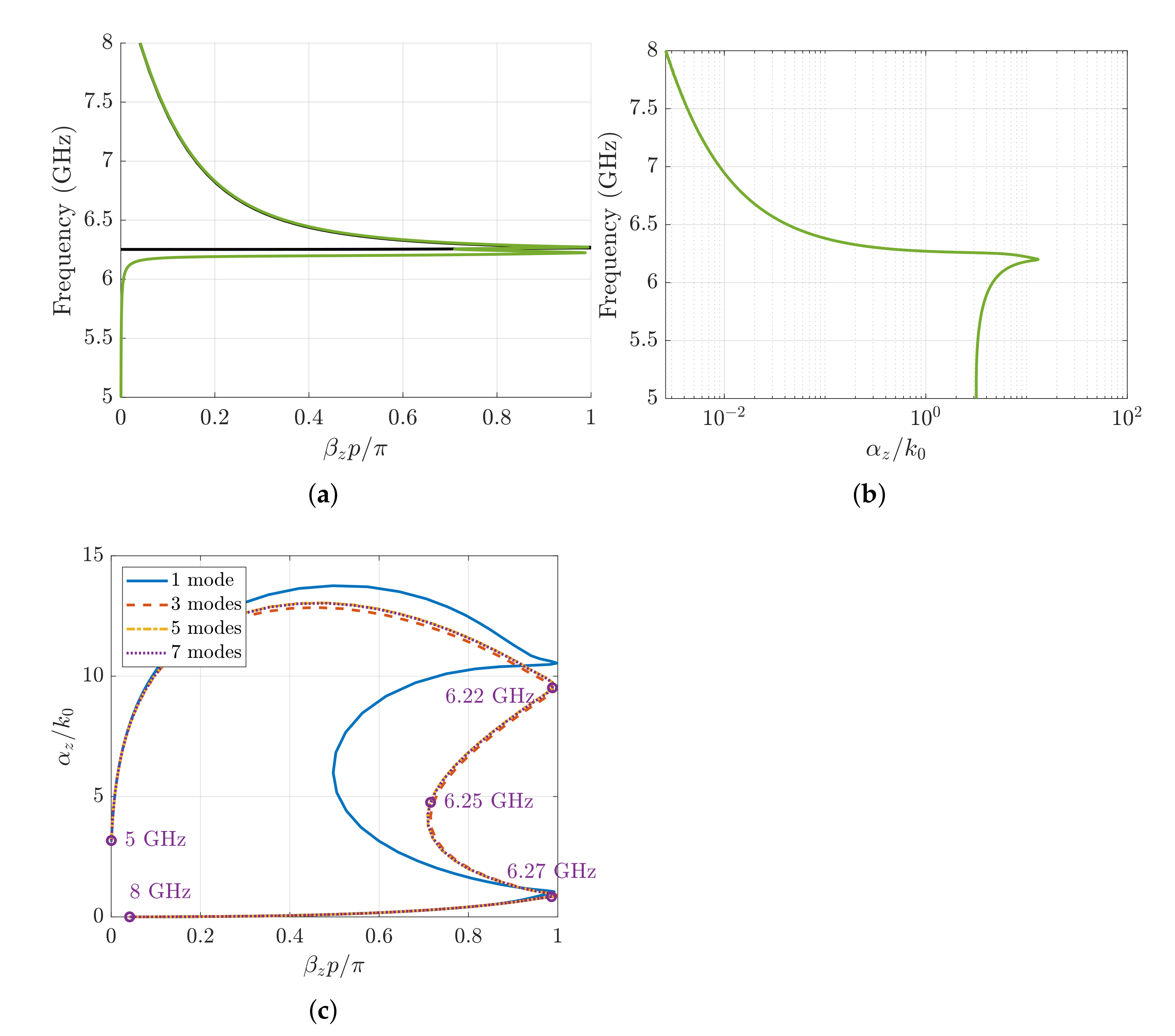
3. Multi-Mode Transfer Matrix Method (MMTMM)
3.1. Numerical Results
3.2. Convergence Study
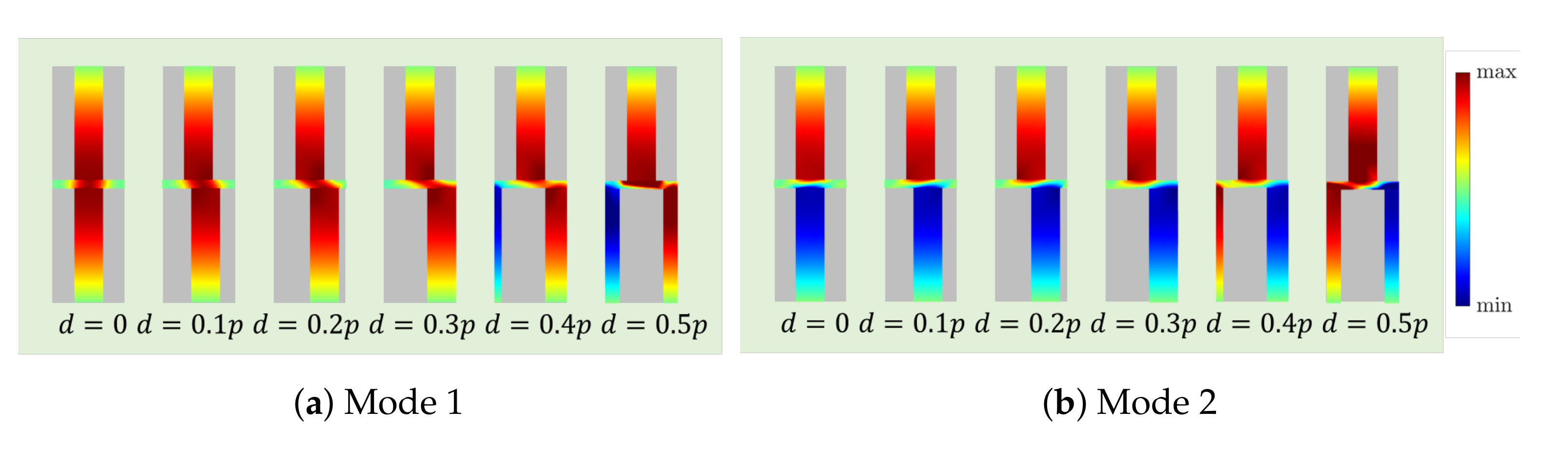
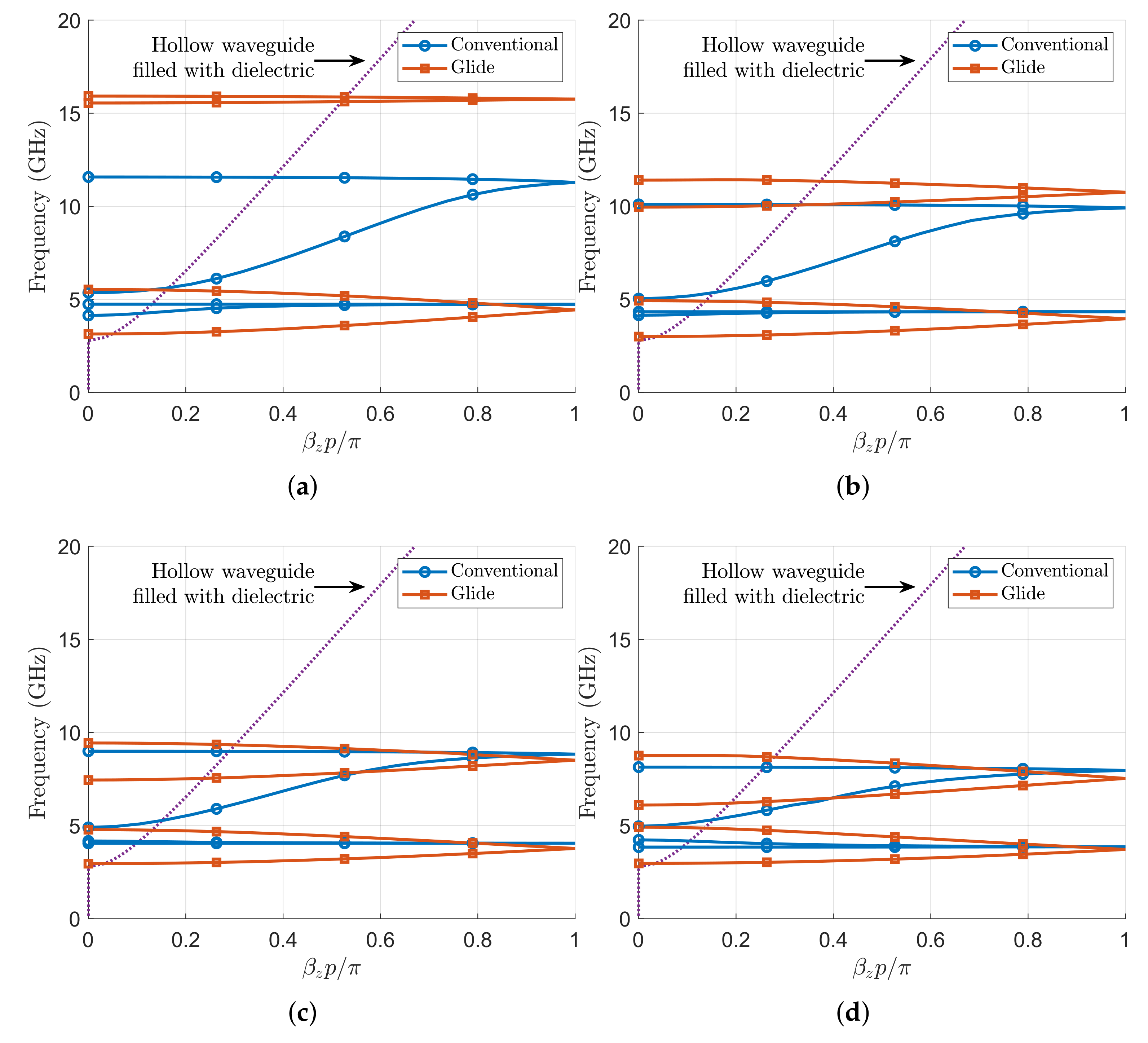
4. Interleaved Corrugations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pozar, D. Microwave Engineering, 4th ed.; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Marqués, R.; Martel, J.; Mesa, F.; Medina, F. Left-Handed-Media Simulation and Transmission of EM Waves in Subwavelength Split-Ring-Resonator-Loaded Metallic Waveguides. Phys. Rev. Lett. 2002, 89, 183901. [Google Scholar] [CrossRef]
- Esteban, J.; Camacho-Peñalosa, C.; Page, J.E.; Martín-Guerrero, T.M.; Márquez-Segura, E. Simulation of negative permittivity and negative permeability by means of evanescent waveguide modes—Theory and experiment. IEEE Trans. Microw. Theory Tech. 2005, 53, 1506–1513. [Google Scholar] [CrossRef]
- Hrabar, S.; Bartolic, J.; Sipus, Z. Waveguide miniaturization using uniaxial negative permeability metamaterial. IEEE Trans. Antennas Propag. 2005, 53, 110–119. [Google Scholar] [CrossRef]
- Quevedo-Teruel, O.; Rajo-Iglesias, E.; Kehn, N.M.M. Numerical and experimental studies of split ring resonators loaded on the sidewalls of rectangular waveguides. IET Microw. Antennas Propagat. 2009, 3, 1262–1270. [Google Scholar] [CrossRef]
- Navarro-Tapia, M.; Esteban, J.; Camacho-Peñalosa, C. On the actual possibilities of applying the composite right/left-handed waveguide technology to slot array antennas. IEEE Trans. Antennas Propag. 2012, 60, 2183–2193. [Google Scholar] [CrossRef]
- Navarro-Tapia, M.; Esteban, J.; Camacho-Peñalosa, C. Broadband slot array antenna with full-space steerable pattern in a composite right/left-handed waveguide. Radio Sci. 2013, 48, 406–415. [Google Scholar] [CrossRef]
- Eshrah, I.A.; Kishk, A.A.; Yakovlev, A.B.; Glisson, A.W. Rectangular waveguide with dielectric-filled corrugations supporting backward waves. IEEE Trans. Microw. Theory Tech. 2005, 53, 3298–3304. [Google Scholar] [CrossRef]
- Eshrah, I.A.; Kishk, A.A.; Yakovlev, A.B.; Glisson, A.W. Spectral analysis of left-handed rectangular waveguides with dielectric-filled corrugations. IEEE Trans. Antennas Propag. 2005, 53, 3673–3683. [Google Scholar] [CrossRef]
- Xu, L.L.; Gong, Y.; Fan, Y.X.; Tao, Z.Y. A High-Resolution Terahertz Electric Field Sensor Using a Corrugated Liquid Crystal Waveguide. Crystals 2019, 9, 302. [Google Scholar] [CrossRef] [Green Version]
- Xue, J.L.; Xu, L.L.; Wang, T.T.; Fan, Y.X.; Tao, Z.Y. Terahertz Thermal Sensing by Using a Defect-Containing Periodically Corrugated Gold Waveguide. Appl. Sci. 2020, 10, 4365. [Google Scholar] [CrossRef]
- Hessel, A.; Chen, M.H.; Li, R.C.M.; Oliner, A.A. Propagation in periodically loaded waveguides with higher symmetries. Proc. IEEE 1973, 61, 183–195. [Google Scholar] [CrossRef]
- Quesada, R.; Martín-Cano, D.; García-Vidal, F.J.; Bravo-Abad, J. Deep-subwavelength negative-index waveguiding enabled by coupled conformal surface plasmons. Opt. Lett. 2014, 39, 2990–2993. [Google Scholar] [CrossRef]
- Quevedo-Teruel, O.; Chen, Q.; Mesa, F.; Fonseca, N.J.G.; Valerio, G. On the Benefits of Glide Symmetries for Microwave Devices. IEEE J. Microw. 2021, 1, 457–469. [Google Scholar] [CrossRef]
- Quevedo-Teruel, O.; Miao, J.; Mattsson, M.; Algaba-Brazalez, A.; Johansson, M.; Manholm, L. Glide-Symmetric Fully Metallic Luneburg Lens for 5G Communications at Ka-Band. IEEE Antennas Wirel. Propag. Lett. 2018, 17, 1588–1592. [Google Scholar] [CrossRef]
- Arnberg, P.; Barreira Petersson, O.; Zetterstrom, O.; Ghasemifard, F.; Quevedo-Teruel, O. High Refractive Index Electromagnetic Devices in Printed Technology Based on Glide-Symmetric Periodic Structures. Appl. Sci. 2020, 10, 3216. [Google Scholar] [CrossRef]
- Chen, Q.; Zetterstrom, O.; Pucci, E.; Palomares-Caballero, A.; Padilla, P.; Quevedo-Teruel, O. Glide-Symmetric Holey Leaky-Wave Antenna With Low Dispersion for 60 GHz Point-to-Point Communications. IEEE Trans. Antennas Propag. 2020, 68, 1925–1936. [Google Scholar] [CrossRef]
- Ebrahimpouri, M.; Quevedo-Teruel, O. Ultrawideband Anisotropic Glide-Symmetric Metasurfaces. IEEE Antennas Wirel. Propag. Lett. 2019, 18, 1547–1551. [Google Scholar] [CrossRef]
- Chen, Q.; Giusti, F.; Valerio, G.; Mesa, F.; Quevedo-Teruel, O. Anisotropic glide-symmetric substrate-integrated-holey metasurface for a compressed ultrawideband Luneburg lens. Appl. Phys. Lett. 2021, 118, 084102. [Google Scholar] [CrossRef]
- Ebrahimpouri, M.; Herran, L.F.; Quevedo-Teruel, O. Wide-Angle Impedance Matching Using Glide-Symmetric Metasurfaces. IEEE Microw. Wirel. Compon. Lett. 2020, 30, 8–11. [Google Scholar] [CrossRef]
- Ebrahimpouri, M.; Rajo-Iglesias, E.; Sipus, Z.; Quevedo-Teruel, O. Cost-Effective Gap Waveguide Technology Based on Glide-Symmetric Holey EBG Structures. IEEE Trans. Microw. Theory Tech. 2018, 66, 927–934. [Google Scholar] [CrossRef] [Green Version]
- Monje-Real, A.; Fonseca, N.J.G.; Zetterstrom, O.; Pucci, E.; Quevedo-Teruel, O. Holey Glide-Symmetric Filters for 5G at Millimeter-Wave Frequencies. IEEE Microw. Wirel. Compon. Lett. 2020, 30, 31–34. [Google Scholar] [CrossRef]
- Ebrahimpouri, M.; Algaba Brazalez, A.; Manholm, L.; Quevedo-Teruel, O. Using Glide-Symmetric Holes to Reduce Leakage Between Waveguide Flanges. IEEE Microw. Wirel. Compon. Lett. 2018, 28, 473–475. [Google Scholar] [CrossRef]
- Amari, S.; Vahldieck, R.; Bornemann, J.; Leuchtmann, P. Spectrum of corrugated and periodically loaded waveguides from classical matrix eigenvalues. IEEE Trans. Microw. Theory Tech. 2000, 48, 453–460. [Google Scholar] [CrossRef] [Green Version]
- Bandlow, B.; Schuhmann, R.; Lubkowski, G.; Weiland, T. Analysis of single-cell modeling of periodic metamaterial structures. IEEE Trans. Magn. 2008, 44, 1662–1665. [Google Scholar] [CrossRef]
- Coves, Á.; Marini, S.; Gimeno, B.; Boria, V. Full-wave analysis of periodic dielectric frequency-selective surfaces under plane wave excitation. IEEE Trans. Antennas Propag. 2012, 60, 2760–2769. [Google Scholar] [CrossRef]
- Bagherias, M.; Quevedo-Teruel, O.; Valerio, G. Bloch Analysis of Artificial Lines and Surfaces Exhibiting Glide Symmetry. IEEE Trans. Microw. Theory Tech. 2019, 67, 2618–2628. [Google Scholar] [CrossRef] [Green Version]
- Mesa, F.; Valerio, G.; Rodriguez-Berral, R.; Quevedo-Teruel, O. Simulation-Assisted Approach to Efficiently Compute the Dispersion Diagram of Periodic Structures. IEEE Antennas Propag. Mag. 2020. [Google Scholar] [CrossRef]
- Sihvola, A. Metamaterials in Electromagnetics. Metamaterials 2007, 1, 2–11. [Google Scholar] [CrossRef]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Castillo-Tapia, P.; Mesa, F.; Yakovlev, A.; Valerio, G.; Quevedo-Teruel, O. Study of Forward and Backward Modes in Double-Sided Dielectric-Filled Corrugated Waveguides. Sensors 2021, 21, 6293. https://doi.org/10.3390/s21186293
Castillo-Tapia P, Mesa F, Yakovlev A, Valerio G, Quevedo-Teruel O. Study of Forward and Backward Modes in Double-Sided Dielectric-Filled Corrugated Waveguides. Sensors. 2021; 21(18):6293. https://doi.org/10.3390/s21186293
Chicago/Turabian StyleCastillo-Tapia, Pilar, Francisco Mesa, Alexander Yakovlev, Guido Valerio, and Oscar Quevedo-Teruel. 2021. "Study of Forward and Backward Modes in Double-Sided Dielectric-Filled Corrugated Waveguides" Sensors 21, no. 18: 6293. https://doi.org/10.3390/s21186293
APA StyleCastillo-Tapia, P., Mesa, F., Yakovlev, A., Valerio, G., & Quevedo-Teruel, O. (2021). Study of Forward and Backward Modes in Double-Sided Dielectric-Filled Corrugated Waveguides. Sensors, 21(18), 6293. https://doi.org/10.3390/s21186293






