Identification of Multiple Cracks in Composite Laminated Beams Using Perturbation to Dynamic Equilibrium
Abstract
:1. Introduction
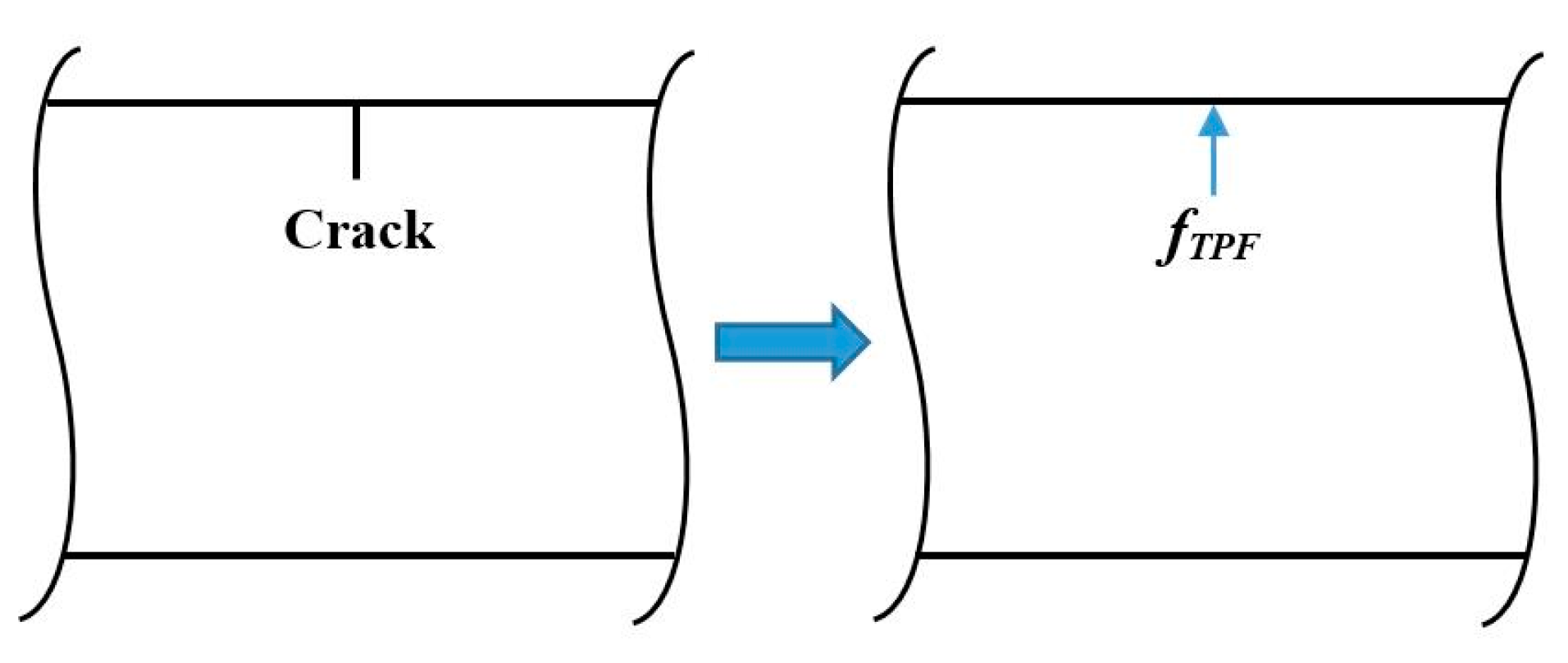
2. Identification of Multiple Cracks Using Perturbation to Dynamic Equilibrium
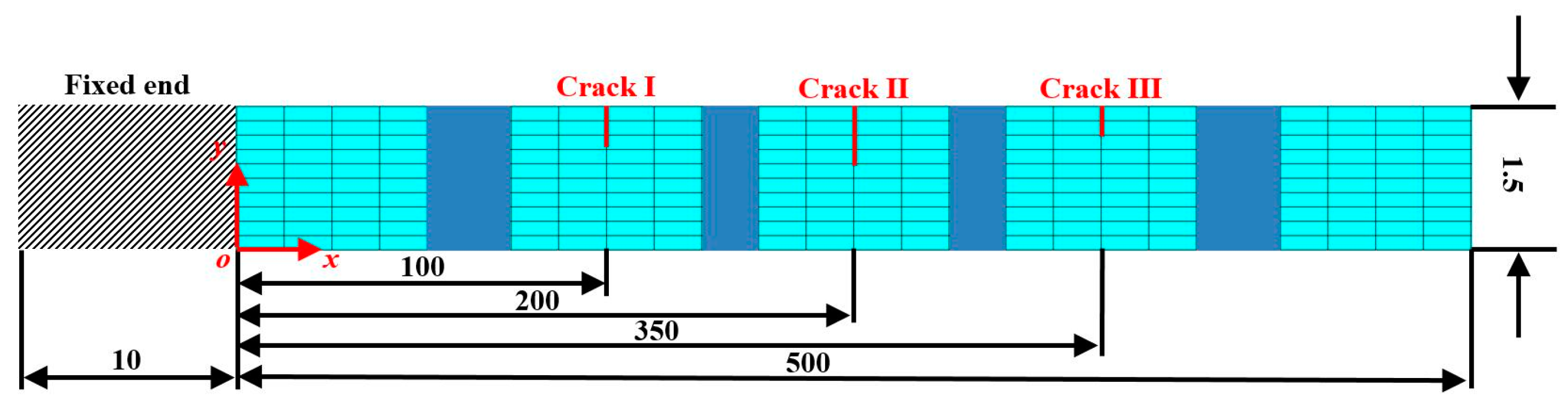
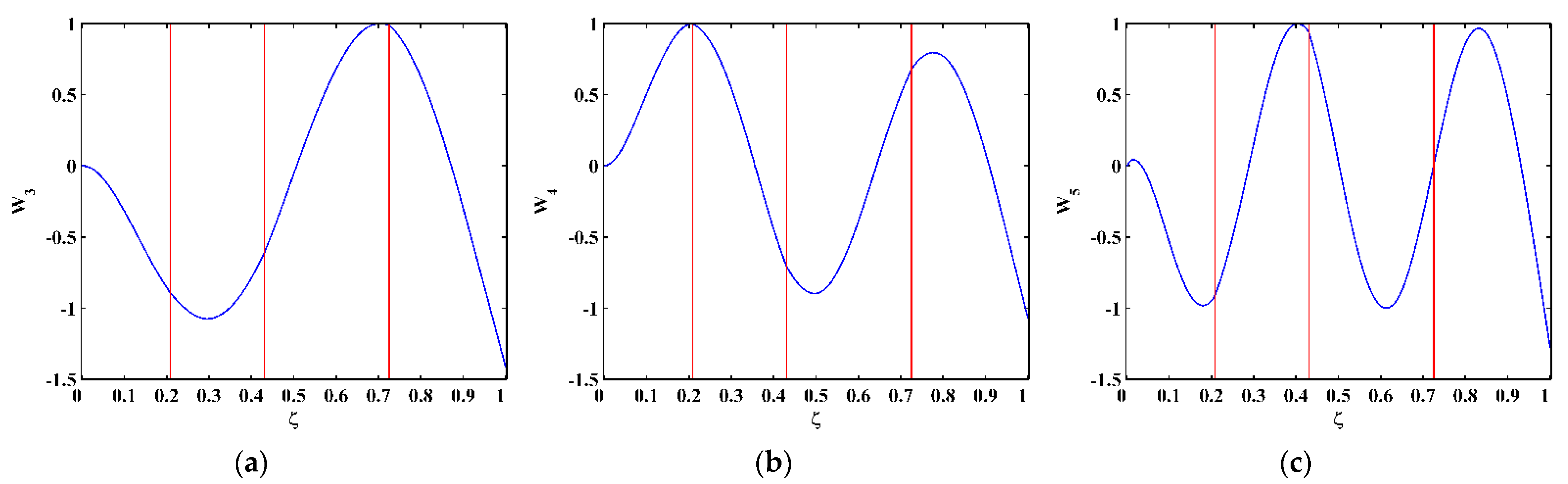
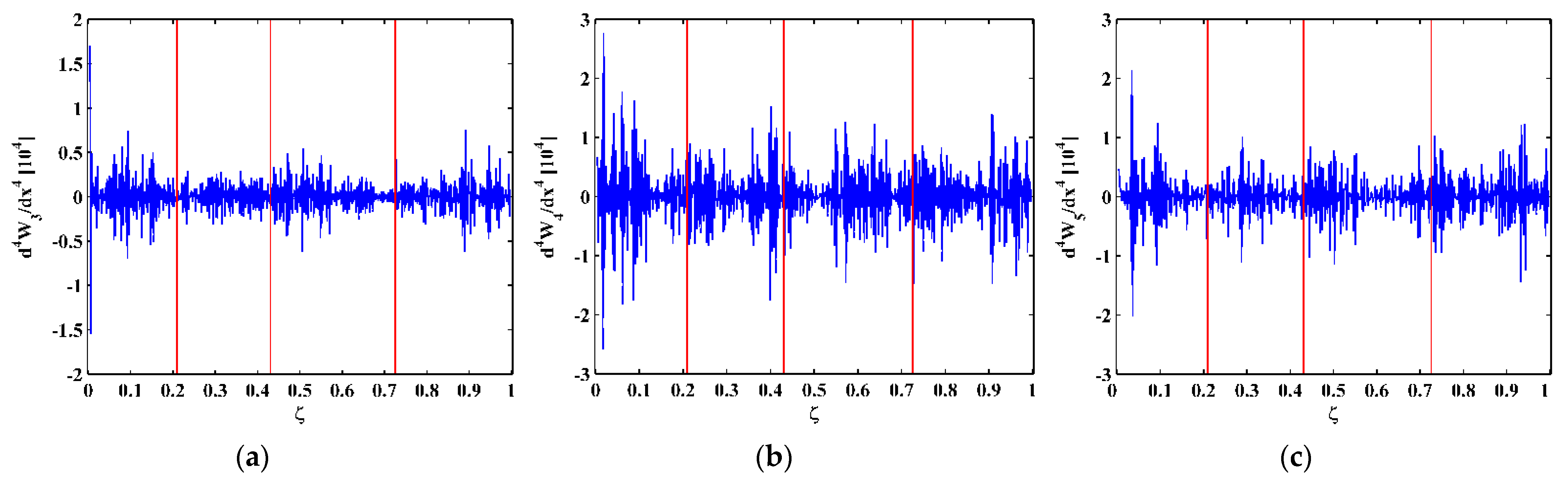
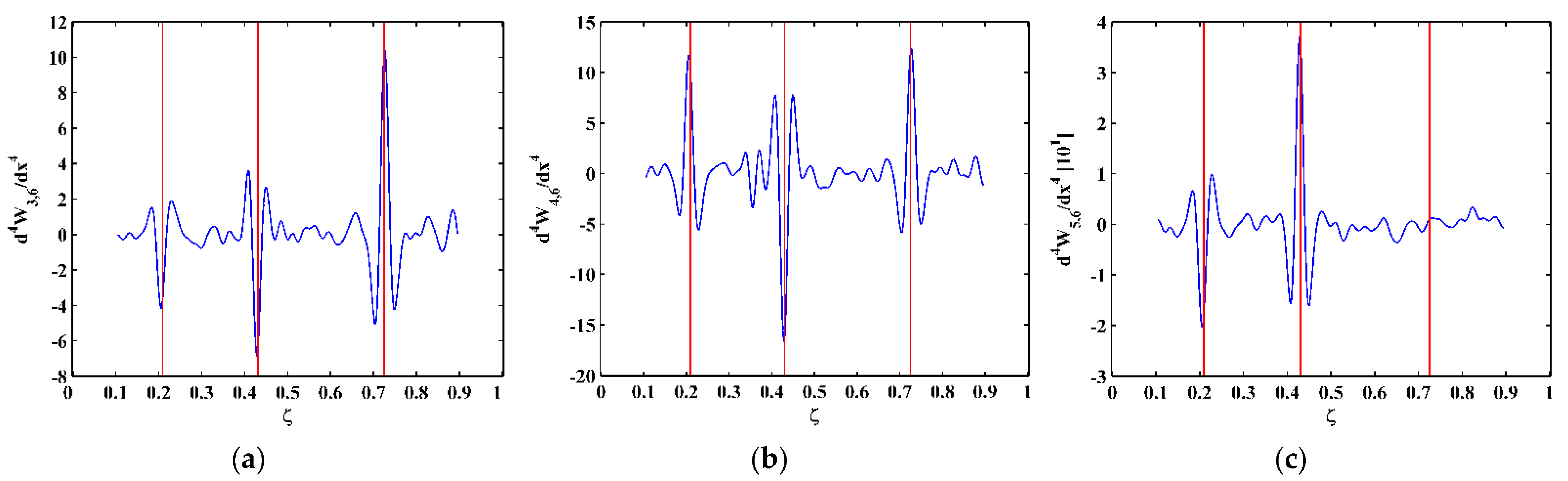
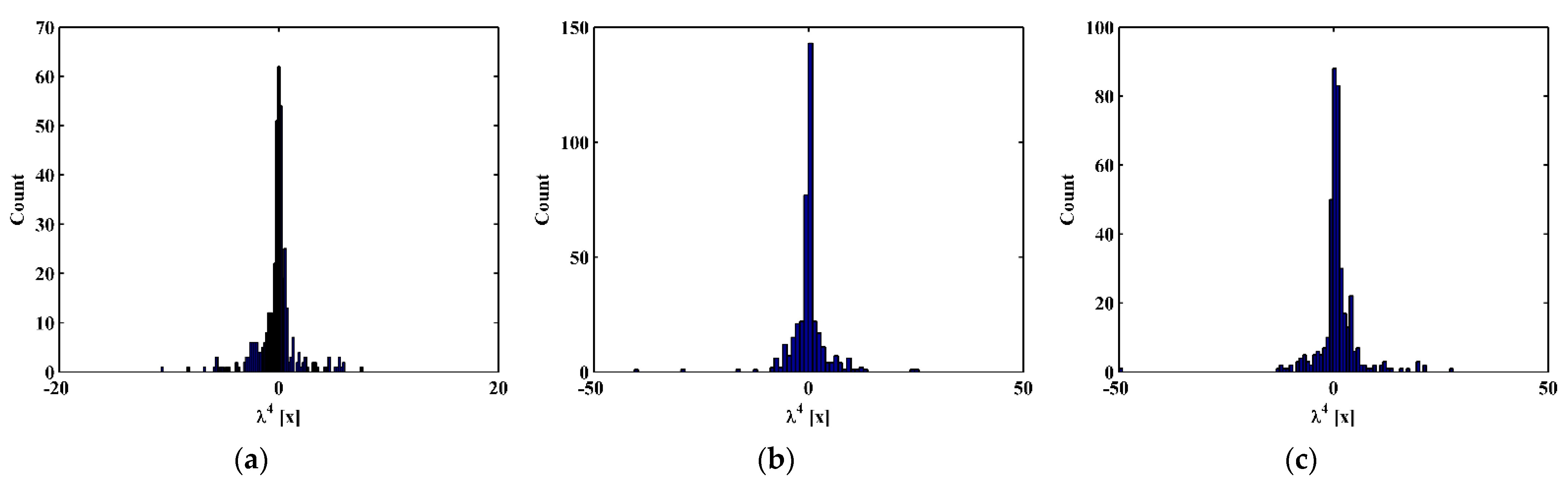
3. Numerical Verification
3.1. Numerical Model
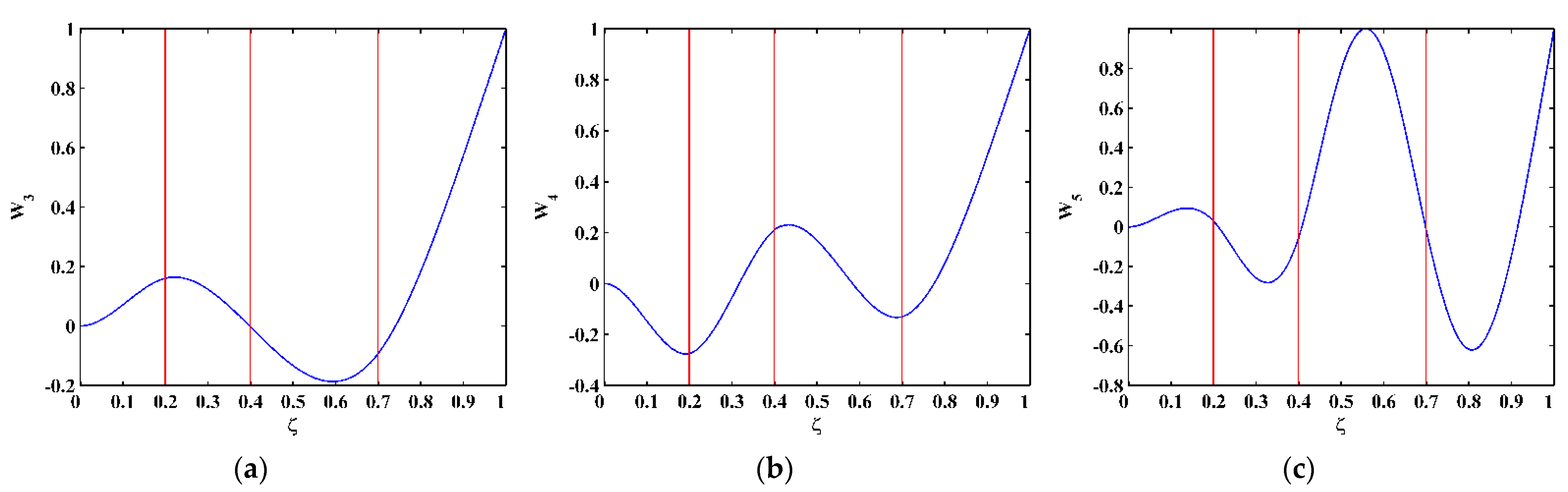
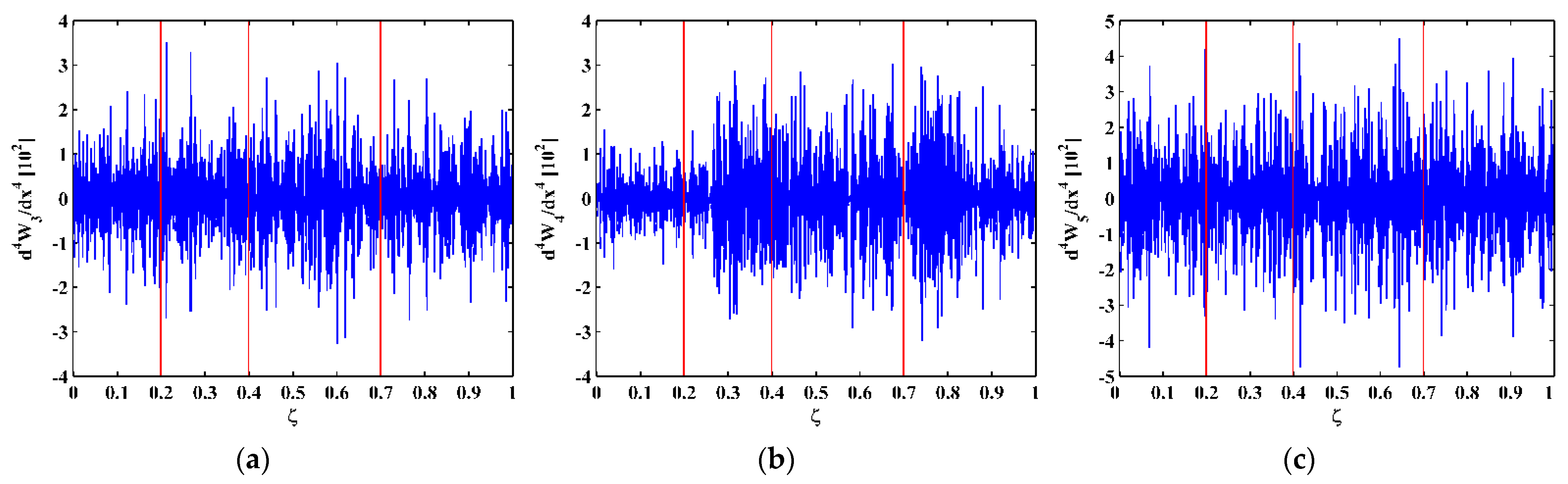
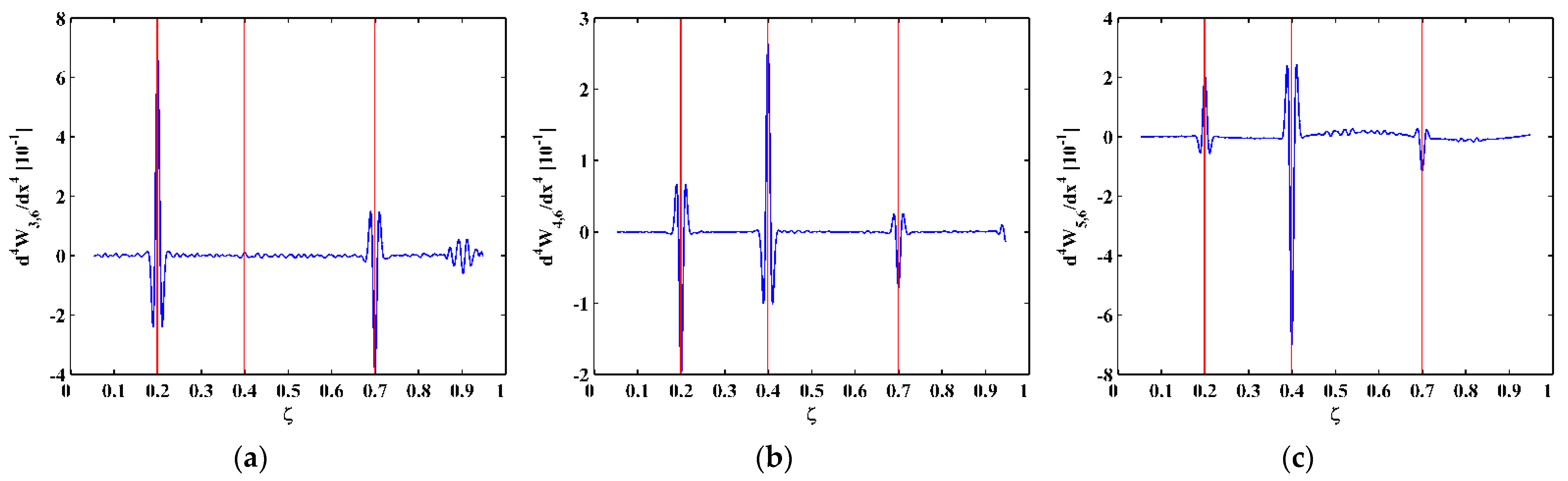
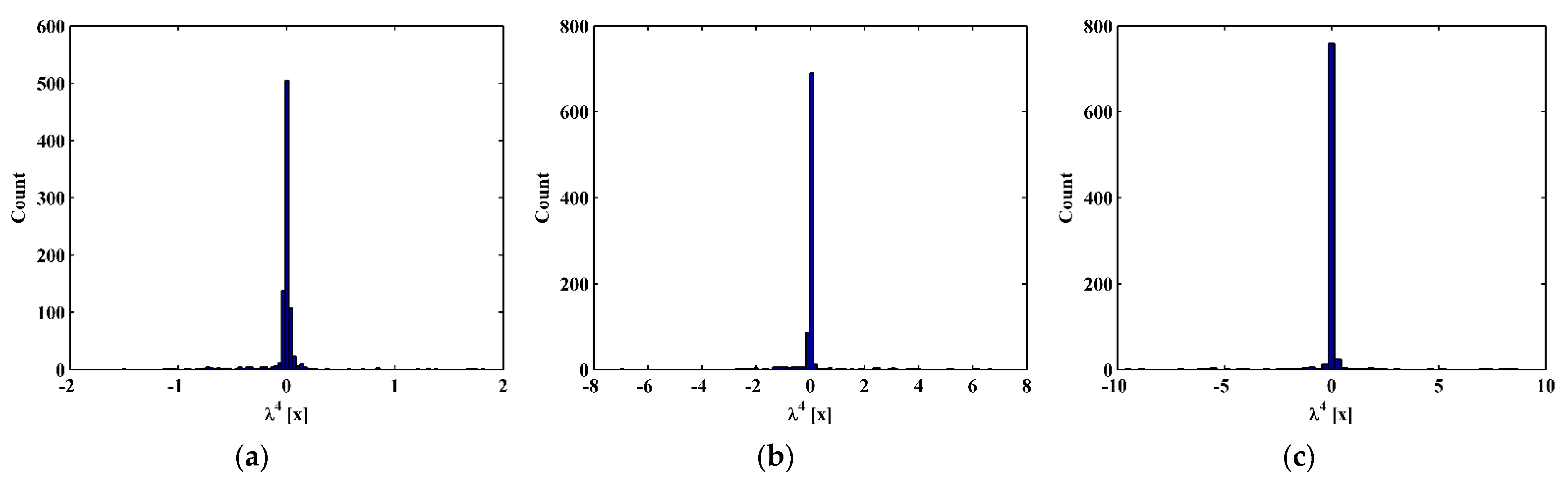
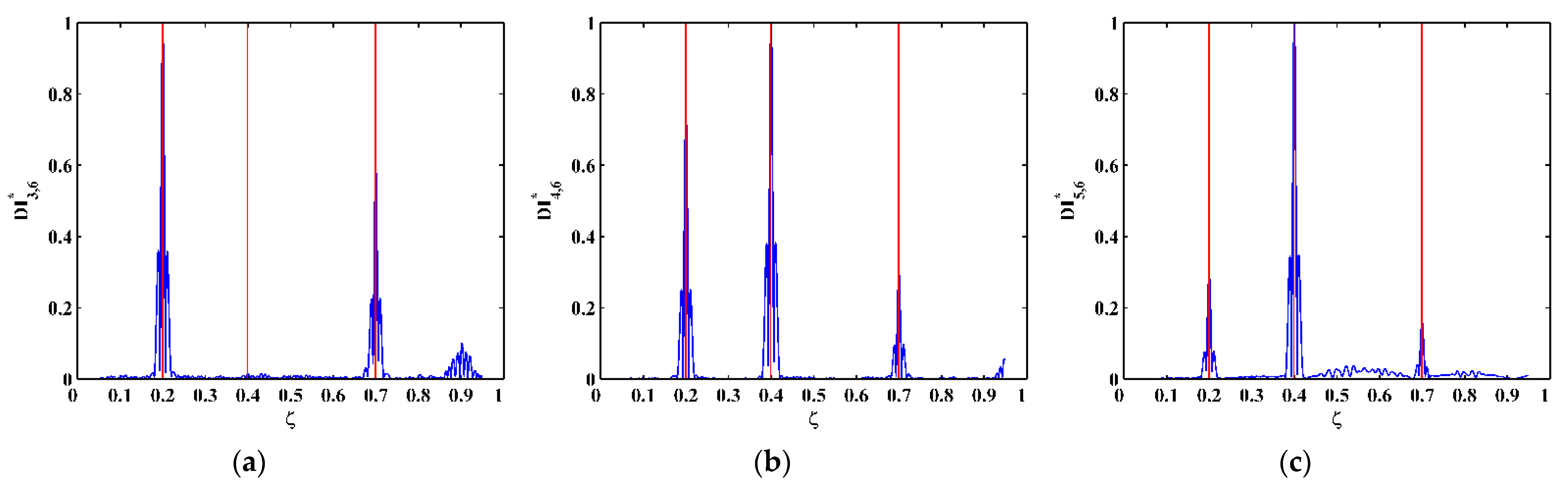
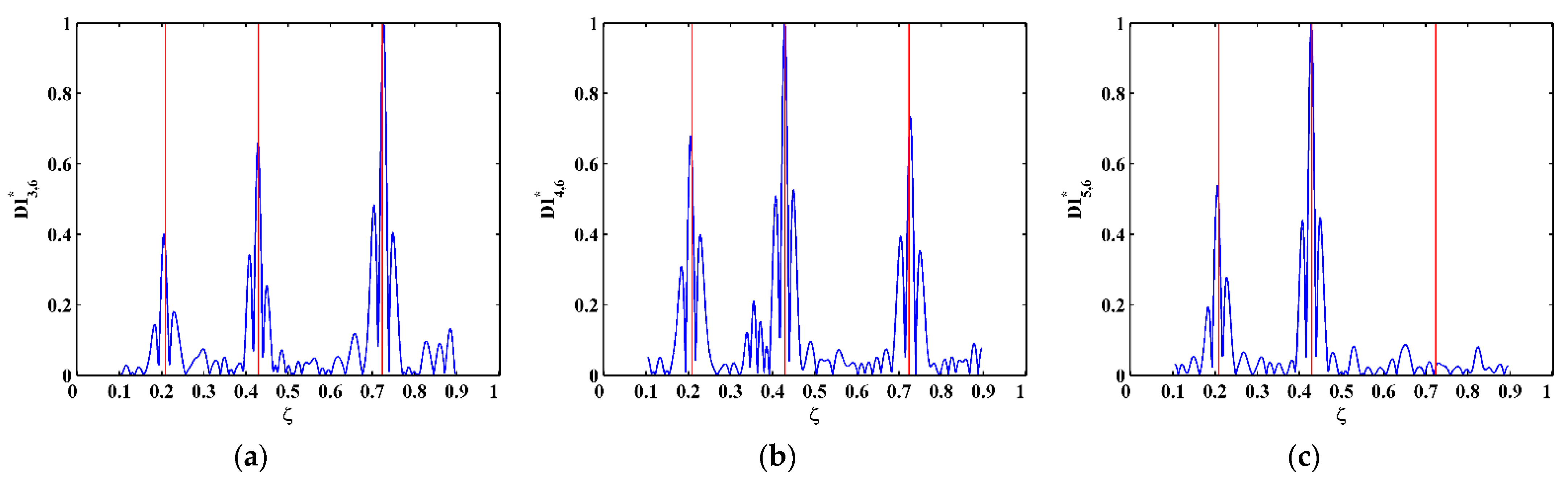
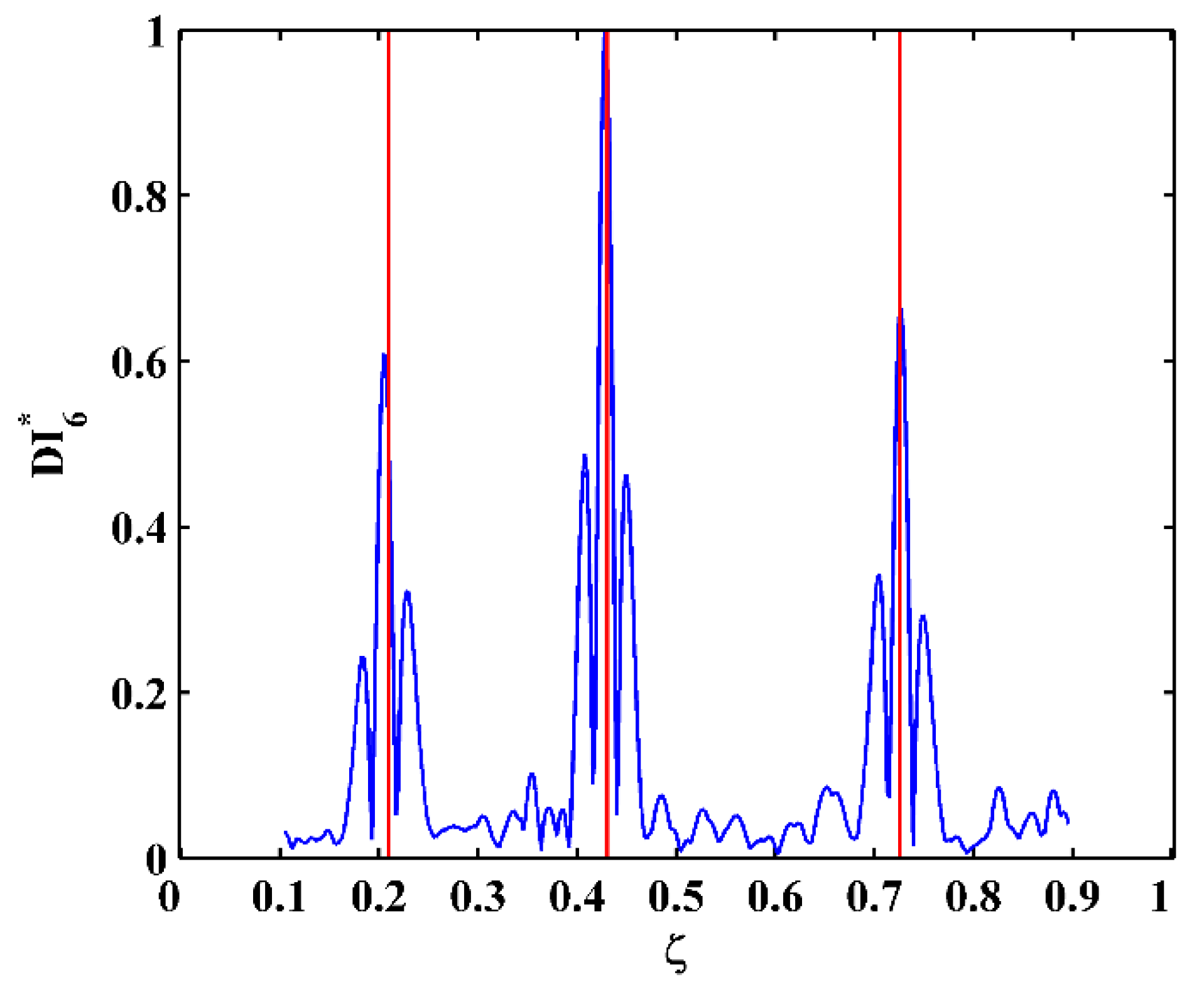
3.2. Numerical Results
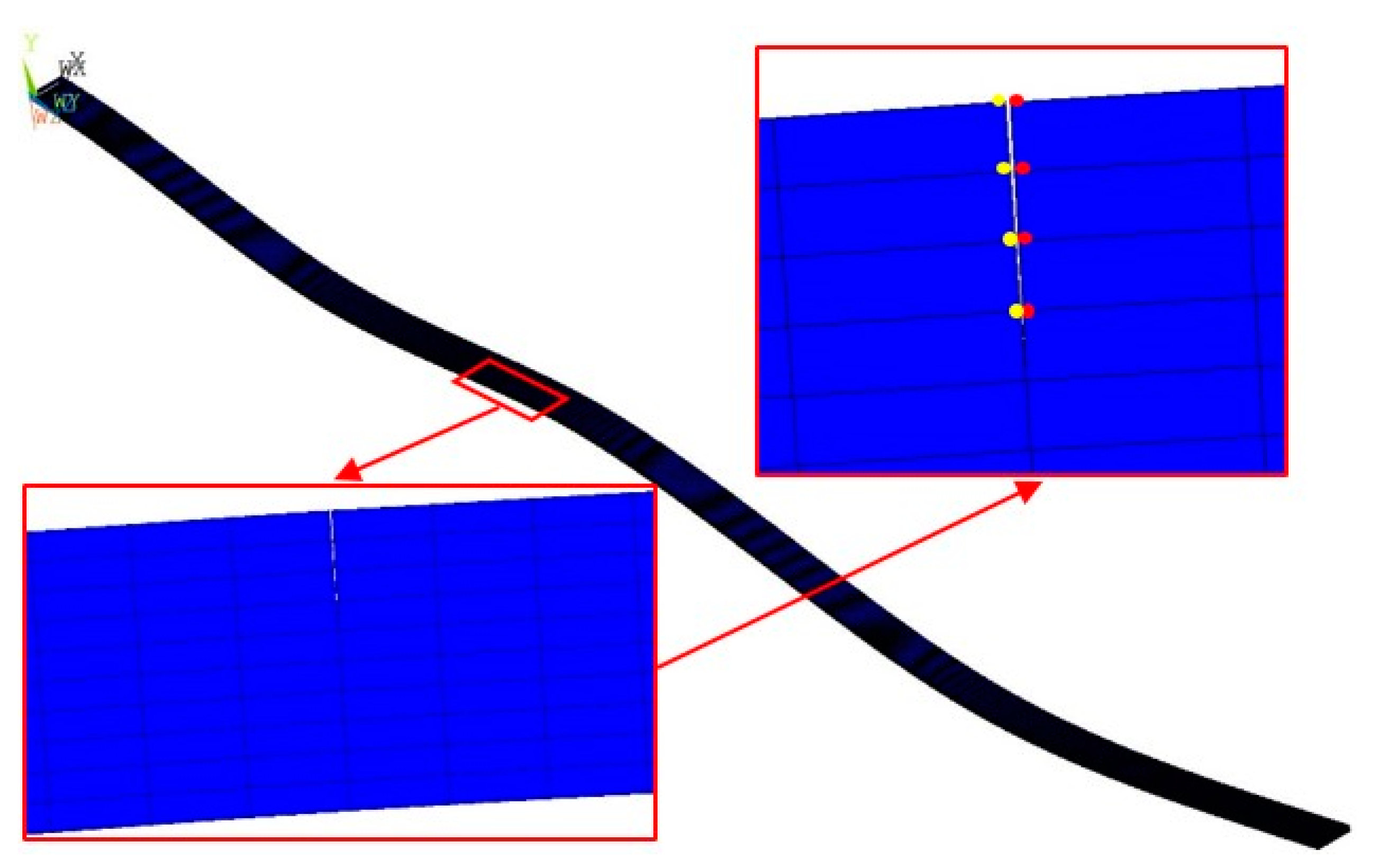
4. Experimental Validation
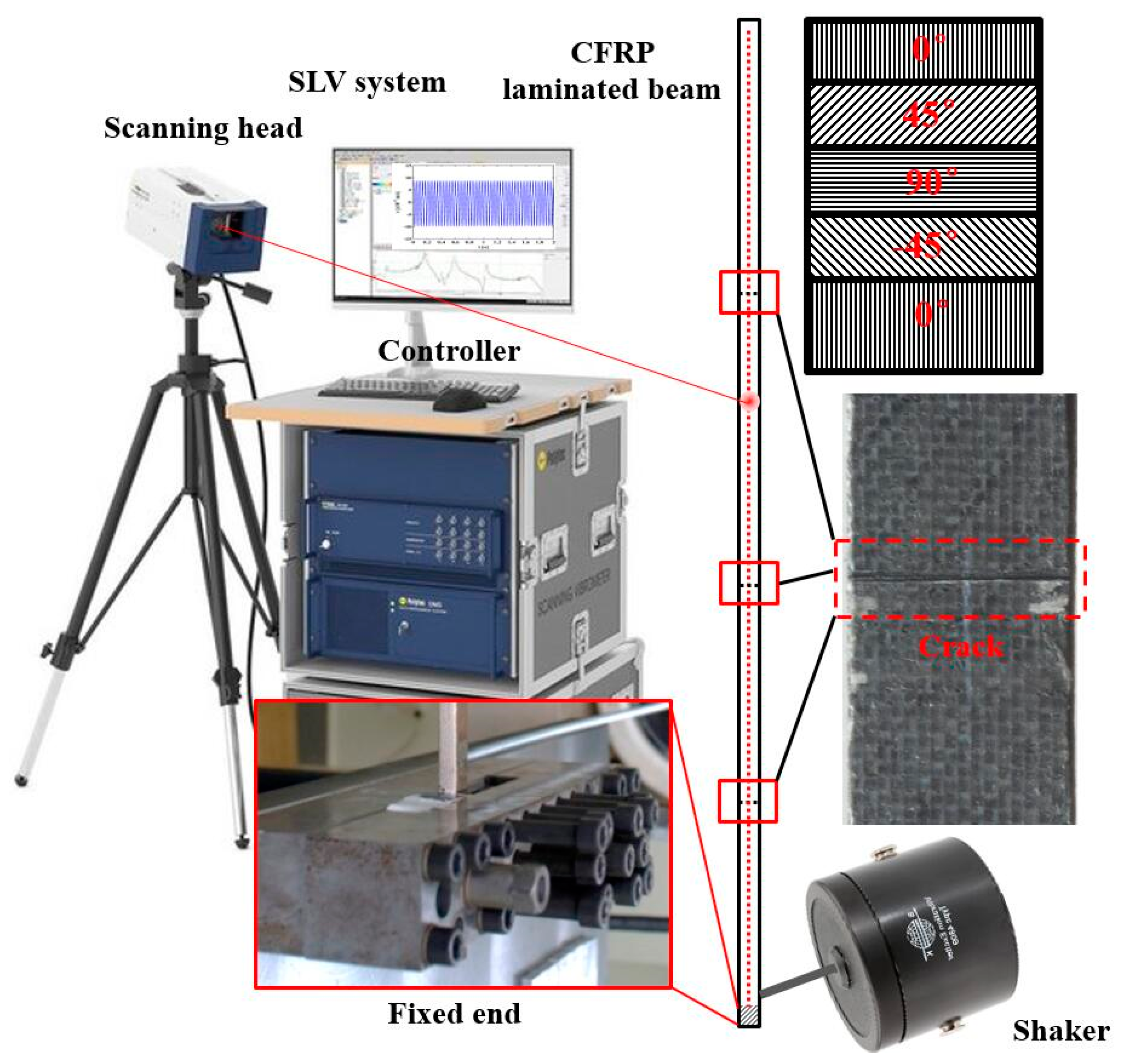
4.1. Experimental Specimen and Setup
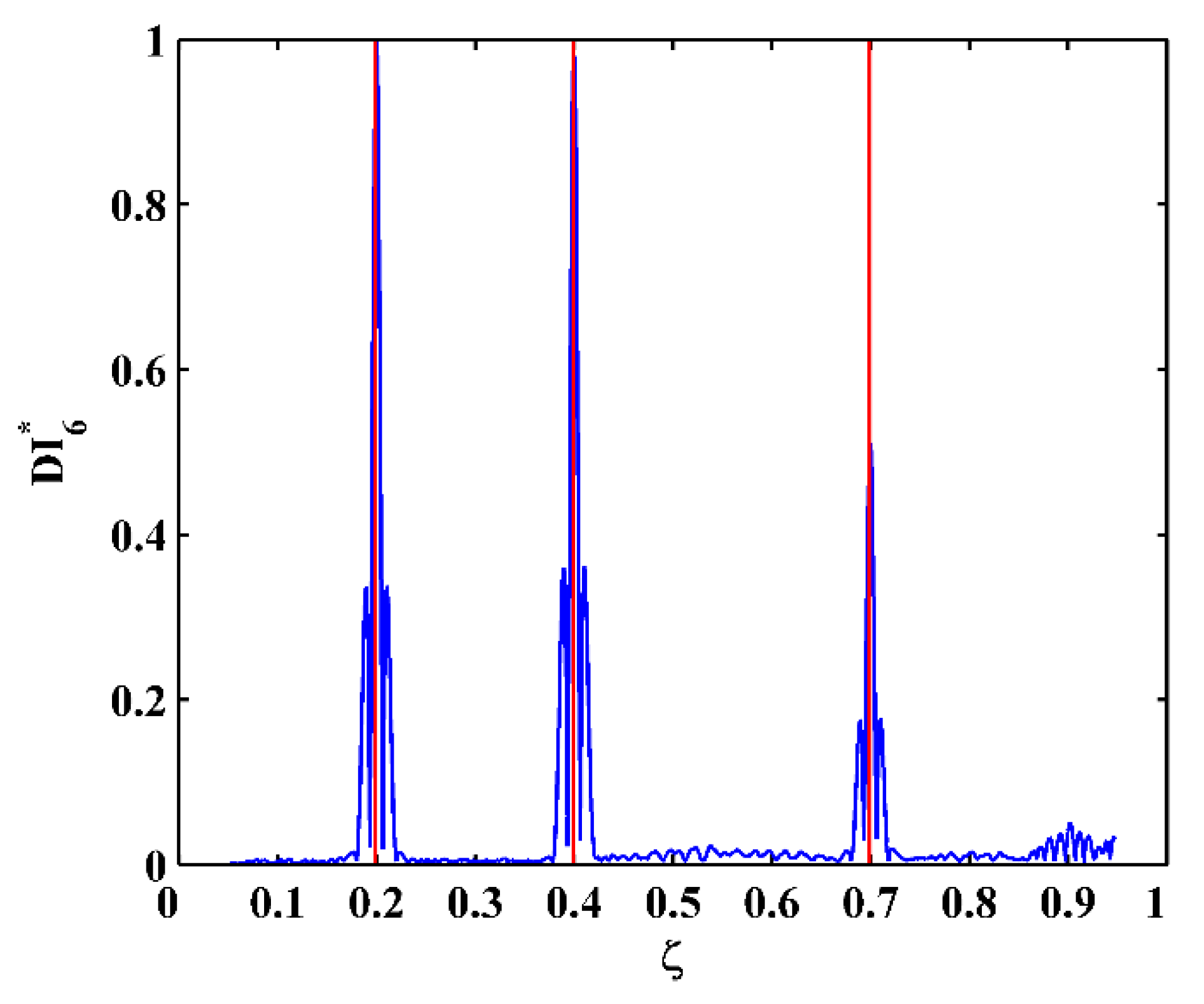
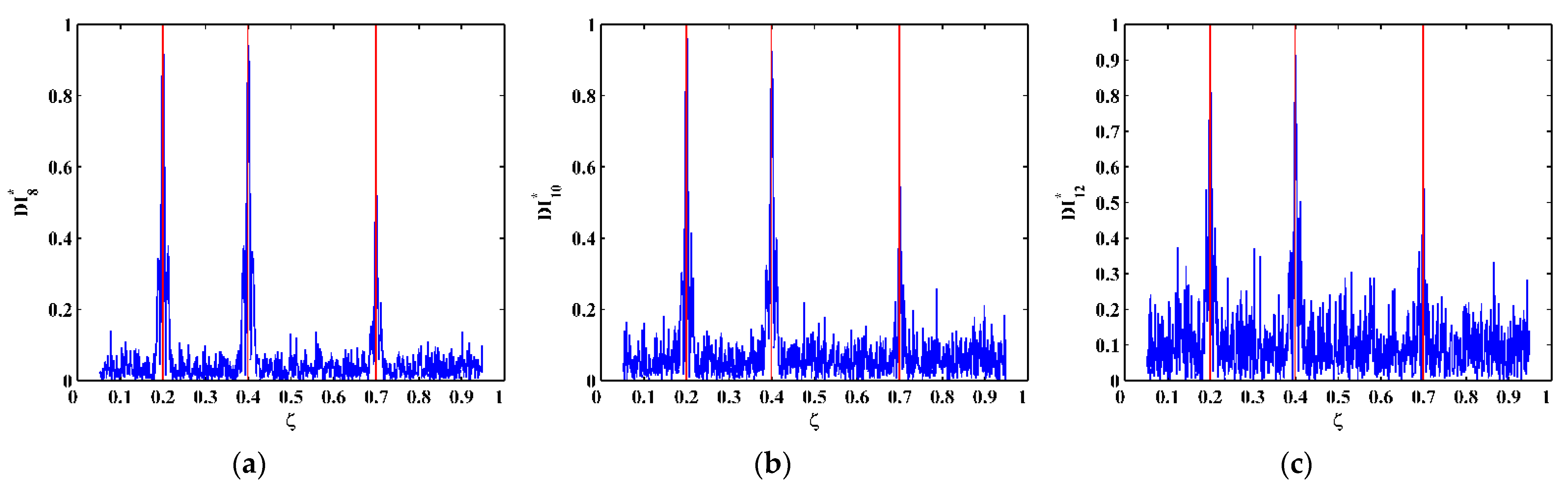
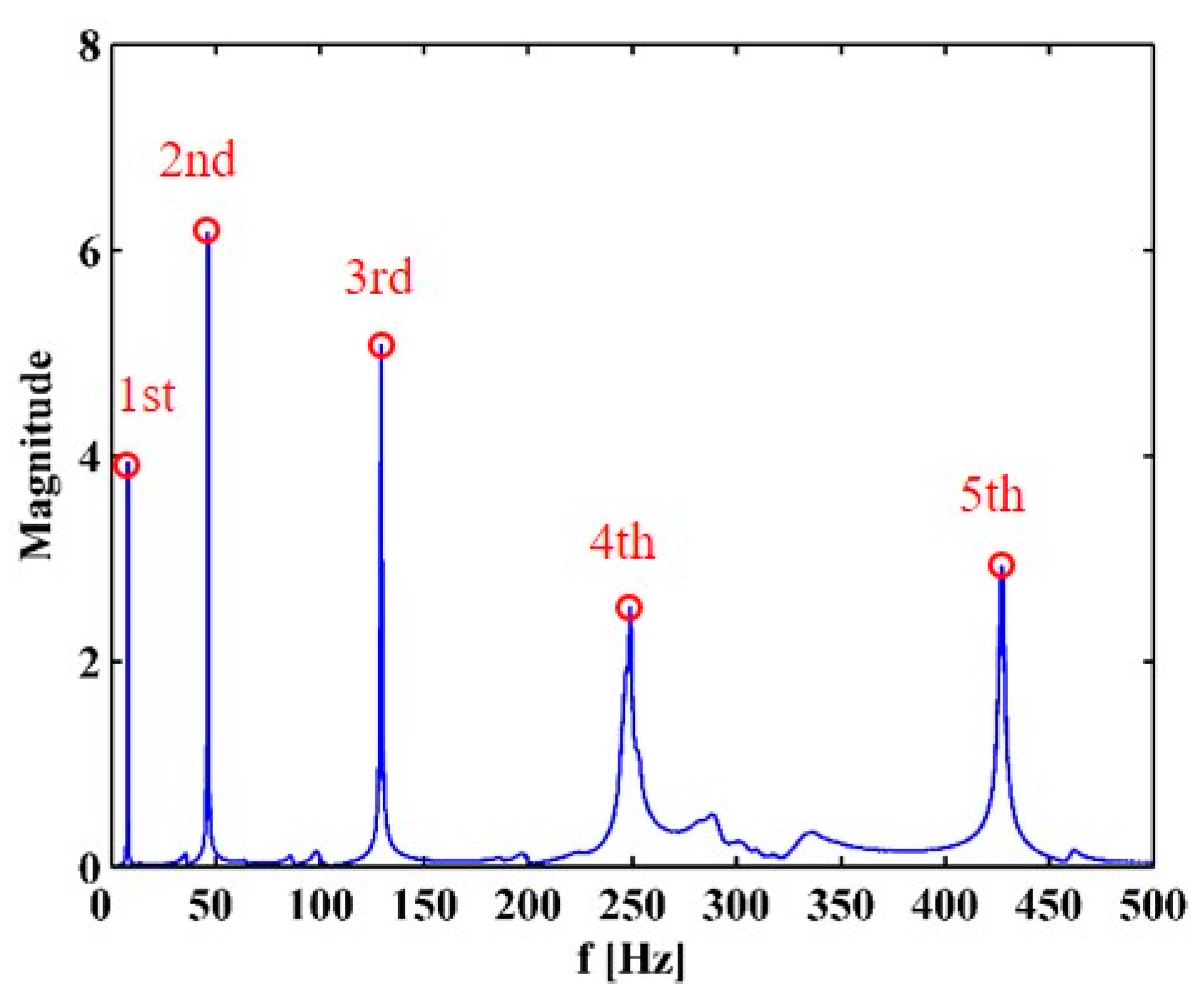
4.2. Experimental Results
5. Concluding Remarks
- (1)
- The TPF exists at the crack locations only and vanishes at intact locations, based on which the DI is established using the absolute value of the amplitude of the TPF. The occurrence of multiple cracks can be manifested by the singularity peaks in the DI. Furthermore, cracks can be pinpointed by the locations of the peaks.
- (2)
- To enhance the robustness of the DI against noise interference, multi-scale analysis is integrated into the DI. By sliding a scaled Gaussian window function along a mode shape signal, the “region-by-region” manner is utilized to average noise components in the noisy mode shape. On the other hand, crack-induced singularity peaks in the MDIs are naturally retained for the identification of cracks.
- (3)
- To deal with unknown material and structural parameters that are required to formulate TPFs in composite laminated beams, a statistic manner is utilized to estimate the constants of the TPFs related to the material and structural parameters. In this regard, the proposed approach is a baseline-free approach, feasible to real scenarios in the absence of material and structural information.
- (4)
- To remove the node effect that hinders the identification of multiple cracks in beams, an integrating scheme is utilized to fuse identification results associated with multiple mode shapes, whereby even cracks in the vicinity of nodes of mode shapes can be evidently identified.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xu, W.; Su, Z.; Radzieński, M.; Cao, M.; Ostachowicz, W. Nonlinear pseudo-force in a breathing crack to generate harmonics. J. Sound Vib. 2021, 492, 115734. [Google Scholar] [CrossRef]
- Xu, Z.; Cao, M.; Bai, R.; Xu, H.; Xu, W. Evaluation of high-order modes and damage effects of multi-crack beams using enhanced spectral element method. J. Vib. Control 2018, 24, 5186–5200. [Google Scholar] [CrossRef]
- Morassi, A.; Rollo, M. Identification of two cracks in a simple supported beam from minimal frequency measurements. J. Vib. Control 2001, 7, 729–739. [Google Scholar] [CrossRef]
- Patil, D.P.; Maiti, S.K. Detection of multiple cracks using frequency measurements. Eng. Fract. Mech. 2003, 70, 1553–1572. [Google Scholar] [CrossRef]
- Patil, D.P.; Maiti, S.K. Experimental verification of a method of detection of multiple cracks in beams based on frequency measurements. J. Sound Vib. 2005, 281, 439–451. [Google Scholar] [CrossRef]
- Murigendrappa, S.M.; Maiti, S.K.; Srirangarajan, H.R. Frequency-based experimental and theoretical identification of multiple cracks in straight pipes filled with fluid. NDT E Int. 2004, 37, 431–438. [Google Scholar] [CrossRef]
- Lee, J. Identification of multiple cracks in a beam using vibration amplitudes. J. Sound Vib. 2009, 326, 205–212. [Google Scholar] [CrossRef]
- Khiem, N.T.; Lien, T.V. Multi-crack detection for beam by the natural frequencies. J. Sound Vib. 2004, 273, 175–184. [Google Scholar] [CrossRef]
- Singh, S.K.; Tiwari, R. Identification of a multi-crack in a shaft system using transverse frequency response functions. Mech. Mach. Theory 2010, 45, 1813–1827. [Google Scholar] [CrossRef]
- Lin, R.; Cheng, F. Multiple crack identification of a free-free beam with uniform material property variation and varied noised frequency. Eng. Struct. 2008, 30, 909–929. [Google Scholar] [CrossRef]
- Dawari, V.B.; Vesmawala, G.R. Modal curvature and modal flexibility methods for honey comb identification in reinforced concrete beams. Procedia Eng. 2013, 51, 119–124. [Google Scholar] [CrossRef] [Green Version]
- Abdel Wahab, M.M.; De Roeck, G. Damage detection in bridges using modal curvatures: Application to a real damage scenario. J. Sound Vib. 1999, 226, 217–235. [Google Scholar] [CrossRef]
- Sung, S.H.; Jung, H.J.; Jung, H.Y. Damage detection for beam-like structures using the normalized curvature of a uniform load surface. J. Sound Vib. 2013, 332, 1501–1519. [Google Scholar] [CrossRef]
- Cao, M.; Xu, W.; Ren, W.; Ostachowicz, W.; Sha, G.; Pan, L. A concept of complex-wavelet modal curvature for detecting multiple cracks in beams under noisy conditions. Mech. Syst. Signal Process. 2016, 76–77, 555–575. [Google Scholar] [CrossRef]
- Cao, M.; Radzieński, M.; Xu, W.; Ostachowicz, W. Identification of multiple damage in beams based on robust curvature mode shapes. Mech. Syst. Signal Process. 2014, 46, 468–480. [Google Scholar] [CrossRef]
- Sha, G.; Radzieński, M.; Soman, R.; Cao, M.; Ostachowicz, W.; Xu, W. Multiple damage detection in composite laminated beams by data fusion of Teager energy operator-wavelet transform mode shapes. Compos. Struct. 2020, 235, 111798. [Google Scholar] [CrossRef]
- Xu, W.; Cao, M.; Ding, K.; Radzieński, M.; Ostachowicz, W. Crack identification in CFRP laminated beams using multi-resolution modal Teager–Kaiser energy under noisy environments. Materials 2017, 10, 656. [Google Scholar] [CrossRef] [Green Version]
- Pezerat, C.; Guyader, J. Two inverse methods for localization of external sources exciting a beam. Acta Acust. 1995, 3, 1–10. [Google Scholar]
- Xu, H.; Cheng, L.; Su, Z.; Guyader, J.L. Identification of structural damage based on locally perturbed dynamic equilibrium with an application to beam component. J. Sound Vib. 2011, 330, 5963–5981. [Google Scholar] [CrossRef]
- Cao, M.; Cheng, L.; Su, Z.; Xu, H. A multi-scale pseudo-force model in wavelet domain for identification of damage in structural components. Mech. Syst. Signal Process. 2012, 28, 638–659. [Google Scholar] [CrossRef]
- Cao, M.; Su, Z.; Cheng, L.; Xu, H. A multi-scale pseudo-force model for characterization of damage in beam components with unknown material and structural parameters. J. Sound Vib. 2013, 332, 5566–5583. [Google Scholar] [CrossRef]
- Xu, H.; Su, Z.; Cheng, L.; Guyader, J.L. A “pseudo-excitation” approach for structural damage identification: From “strong” to “weak” modality. J. Sound Vib. 2015, 337, 181–198. [Google Scholar] [CrossRef]
- Zhang, C.; Ji, H.; Qiu, J.; Cheng, L.; Yao, W.; Wu, Y. A local specific stiffness identification method based on a multi-scale “weak” formulation. Mech. Syst. Signal Process. 2020, 140, 106650. [Google Scholar] [CrossRef]
- Xu, H.; Su, Z.; Cheng, L.; Guyader, J.L.; Hamelin, P. Reconstructing interfacial force distribution for identification of multi-debonding in steel-reinforced concrete structures using noncontact laser vibrometry. Struct. Health Monit. Int. J. 2013, 12, 507–521. [Google Scholar] [CrossRef]
- Cao, S.; Ouyang, H.; Xu, C. Robust baseline-free damage localization by using locally perturbed dynamic equilibrium and data fusion technique. Sensors 2020, 20, 5964. [Google Scholar] [CrossRef]
- Leissa, A.; Qatu, M. Vibration of Continuous Systems; McGraw Hill: New York, NY, USA, 2011. [Google Scholar]
- Mallat, S. A Wavelet Tour of Signal Processing; Academic Press: Salt Lake City, UT, USA, 2008. [Google Scholar]
- Xu, W.; Zhu, W.; Su, Z.; Cao, M.; Xu, H. A novel structural damage identification approach using damage-induced perturbation in longitudinal vibration. J. Sound Vib. 2021, 496, 115932. [Google Scholar] [CrossRef]
- Xu, H.; Zeng, Z.; Wu, Z.; Zhou, L.; Su, Z.; Liao, Y.; Liu, M. Broadband dynamic responses of flexible carbon black/poly (vinylidene fluoride) nanocomposites: A sensitivity study. Compos. Sci. Technol. 2017, 149, 246–253. [Google Scholar] [CrossRef]
- Schwarz, B.J.; Richardson, M.H. Introduction to operating deflection shapes. CSI Reliab. Week 1999, 10, 121–126. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, A.; Cao, M.; Lu, Q.; Xu, W. Identification of Multiple Cracks in Composite Laminated Beams Using Perturbation to Dynamic Equilibrium. Sensors 2021, 21, 6171. https://doi.org/10.3390/s21186171
Deng A, Cao M, Lu Q, Xu W. Identification of Multiple Cracks in Composite Laminated Beams Using Perturbation to Dynamic Equilibrium. Sensors. 2021; 21(18):6171. https://doi.org/10.3390/s21186171
Chicago/Turabian StyleDeng, Aimin, Maosen Cao, Qitian Lu, and Wei Xu. 2021. "Identification of Multiple Cracks in Composite Laminated Beams Using Perturbation to Dynamic Equilibrium" Sensors 21, no. 18: 6171. https://doi.org/10.3390/s21186171
APA StyleDeng, A., Cao, M., Lu, Q., & Xu, W. (2021). Identification of Multiple Cracks in Composite Laminated Beams Using Perturbation to Dynamic Equilibrium. Sensors, 21(18), 6171. https://doi.org/10.3390/s21186171






