Simulation and Optimization Studies of the LHCb Beetle Readout ASIC and Machine Learning Approach for Pulse Shape Reconstruction
Abstract
1. Introduction
2. Materials and Methods
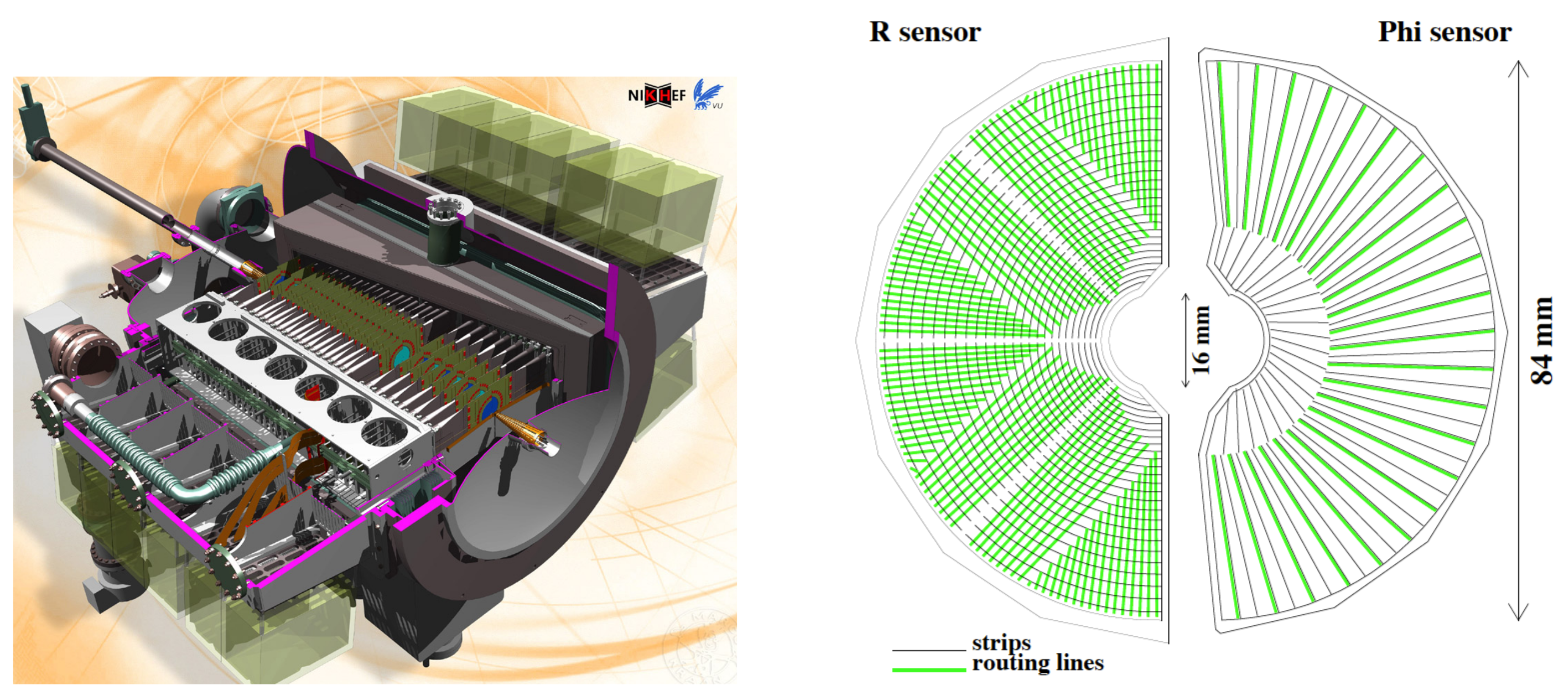
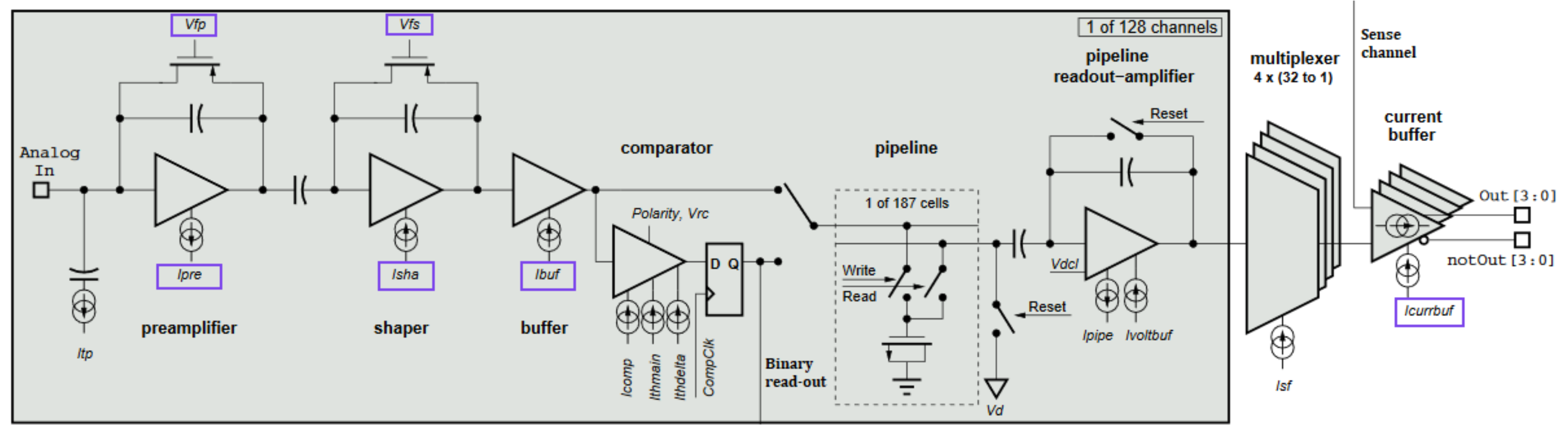
2.1. The Beetle Readout Chip
2.2. Pulse Shape Reconstruction
2.3. Modeling the Pulse Shape
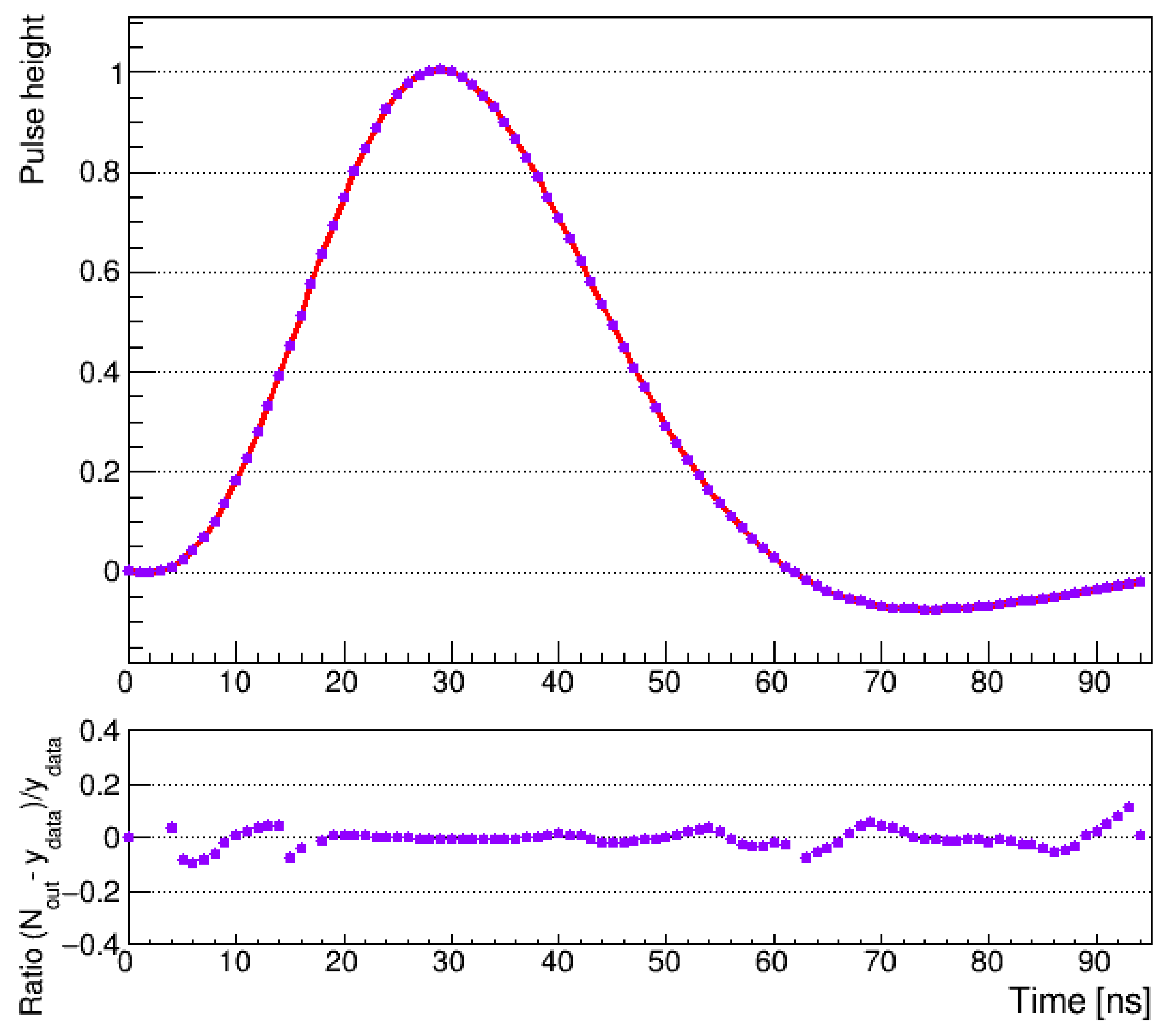
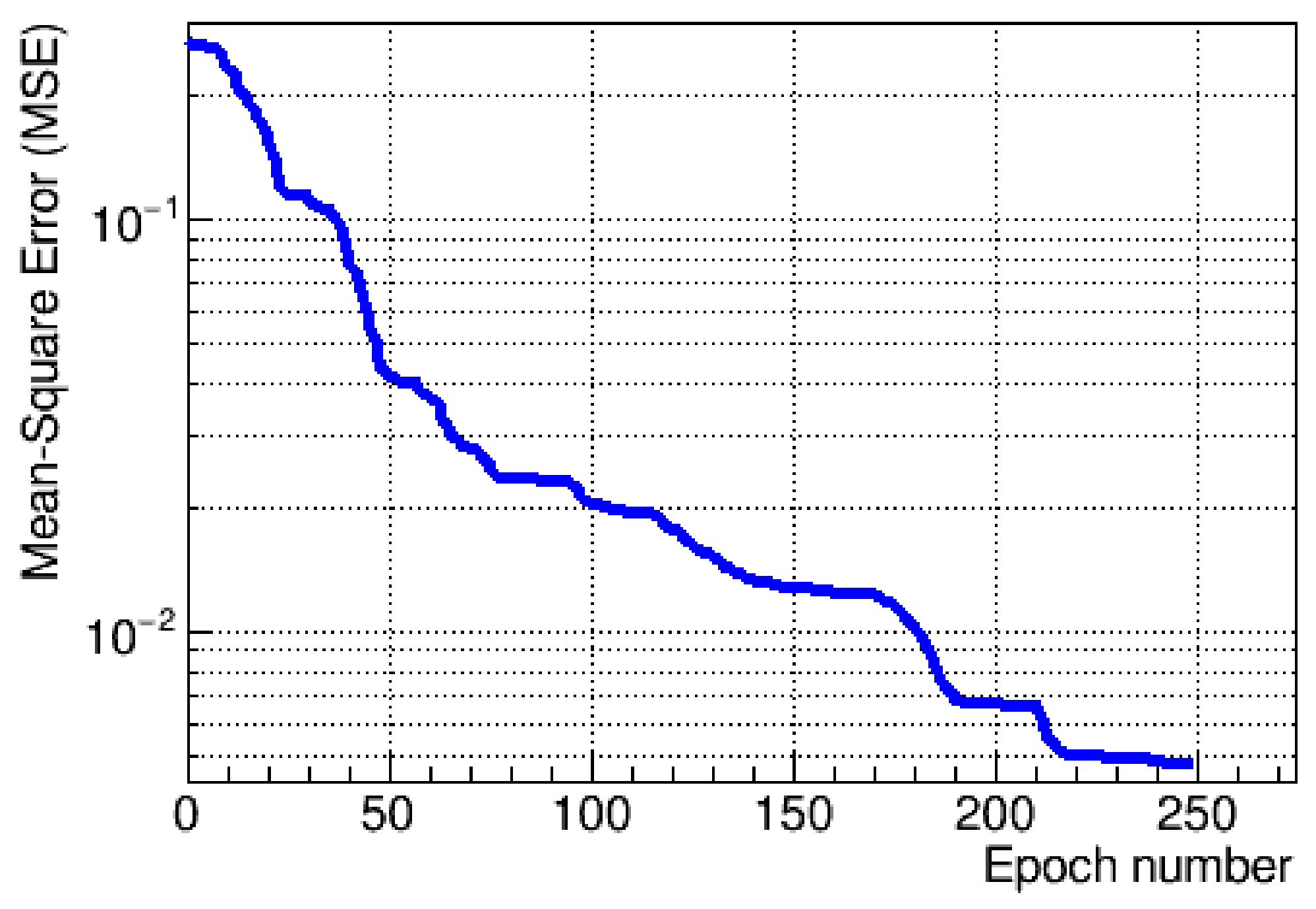
3. Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Löchner, S.; Schmelling, M. The Beetle Reference Manual. In LHCb-2005-105; CERN: Geneva, Switzerland, 2006. [Google Scholar]
- Belyaev, I.; Carboni, G.; Harnew, N.; Matteuzzi, C.; Teubert, F. The history of LHCb. Eur. Phys. J. H 2021, 46, 1–53. [Google Scholar] [CrossRef]
- Libby, J. VELO: The LHCb vertex detector. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2002, 494, 113–119. [Google Scholar] [CrossRef][Green Version]
- LHCb Collaboration. LHCb VELO (VErtex LOcator): Technical Design Report, Tech. Rep. In CERN-LHCC-2001-011; CERN: Geneva, Switzerland, 2001. [Google Scholar]
- Affolder, A.; Akiba, K.; Alexander, M.; Ali, S.; Artuso, M.; Benton, J.; van Beuzekom, M.; Bjornstad, P.M.; Bogdanova, G.; Borghi, S.; et al. Radiation damage in the LHCb Vertex Locator. J. Instrum. 2013, 8, P08002. [Google Scholar] [CrossRef]
- Alexander, M.; Barter, W.; Bay, A.; Bel, L.J.; van Beuzekom, M.; Bogdanova, G.; Borghi, S.; Bowcock, T.J.V.; Buchanan, E.; Buytaert, J.; et al. Mapping the material in the LHCb vertex locator using secondary hadronic interactions. J. Instrum. 2018, 13, P06008. [Google Scholar] [CrossRef]
- Beck, G.; Viehhauser, G. Analytic model of thermal runaway in silicon detectors. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2010, 618, 131–138. [Google Scholar] [CrossRef]
- Oblakowska-Mucha, A. The LHCb Vertex Locator-performance and radiation damage. J. Instrum. 2014, 9, C01065. [Google Scholar] [CrossRef]
- Bourilkov, D. Machine and deep learning applications in particle physics. Mod. Phys. A 2020, 34, 1930019. [Google Scholar] [CrossRef]
- Carleo, G.; Cirac, I.; Cranmer, K.; Daudet, L.; Schuld, M.; Tishby, N.; Vogt-Maranto, L.; Zdeborova, L. Machine learning and the physical sciences. Rev. Mod. Phys. 2019, 91, 045002. [Google Scholar] [CrossRef]
- Guest, D.; Cranmer, K.; Whiteson, D. Deep Learning and its application to LHC physics. Annu. Rev. Nucl. Part. Sci. 2018, 68, 161–181. [Google Scholar] [CrossRef]
- Siviero, F.; Arcidiacono, R.; Cartiglia, N.; Costa, M.; Ferrero, M.; Legger, F.; Mandurrino, M.; Sola, V.; Staiano, A.; Tornago, M. First application of machine learning algorithms to the position reconstruction in Resistive Silicon Detectors. J. Instrum. 2021, 16, P03019. [Google Scholar] [CrossRef]
- Holl, P.; Hauertmann, L.; Majorovits, B.; Schulz, O.; Schuster, M.; Zsigmond, A.J. Deep learning based pulse shape discrimination for germanium detectors. Eur. Phys. J. C 2021, 79, P03019. [Google Scholar] [CrossRef]
- LHCb Collaboration. LHCb collaboration. LHCb Tracker Upgrade, Tech. Rep. In CERN-LHCC-2014-001; CERN: Geneva, Switzerland, 2014. [Google Scholar]
- Steinkamp, O. The Upstream Tracker for the LHCb upgrade. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2016, 831, 367–369. [Google Scholar] [CrossRef]
- Rudolph, M. The LHCb Upstream Tracker Upgrade. Proc. Sci. 2020, 378. [Google Scholar] [CrossRef]
- LHCb Collaboration. The LHCb detector at the LHC. J. Instrum. 2008, 3, S08005. [Google Scholar]
- LHCb Collaboration. LHCb detector performance. Int. J. Mod. Phys. A 2015, 30, 1530022. [Google Scholar] [CrossRef]
- Aaij, R.; Affolder, A.; Akiba, K.; Alexander, M.; Ali, S.; Appleby, R.B.; Artuso, M.; Bates, A.; Bay, A.; Behrendt, O.; et al. Performance of the LHCb vertex locator. J. Instrum. 2014, 9, P09007. [Google Scholar] [CrossRef]
- LHCb Collaboration. LHCb trigger system: Technical Design Report, Tech. Rep. In CERN-LHCC-2003-031; CERN: Geneva, Switzerland, 2003. [Google Scholar]
- LHCb Collaboration. LHCb VELO Upgrade Technical Design Report, Tech. Rep. In CERN-LHCC-2013-031; CERN: Geneva, Switzerland, 2013. [Google Scholar]
- Poikela, T.; De Gaspari, M.; Plosila, J.; Westerlund, T.; Ballabriga, R.; Buytaert, J.; Campbell, M.; Llopart, X.; Wyllie, K.; Gromov, V.; et al. VeloPix: The pixel ASIC for the LHCb upgrade. J. Instrum. 2015, 10, C01057. [Google Scholar] [CrossRef]
- Aaij, R.; Akar, S.; Albrecht, J.; Alexander, M.; Alfonso Albero, A.; Amerio, S.; Anderlini, L.; d’Argent, P.; Baranov, A.; Barter, W.; et al. Design and performance of the LHCb trigger and full real-time reconstruction in Run 2 of the LHC. J. Instrum. 2019, 14, P04013. [Google Scholar] [CrossRef]
- Muheim, F.; The LHCb Collaboration. LHCb Upgrade Plans. Nucl. Phys. B-Proc. Suppl. 2007, 170, 317–322. [Google Scholar] [CrossRef]
- Piucci, A. The LHCb Upgrade. J. Phys. Conf. Ser. 2017, 878. [Google Scholar] [CrossRef]
- Williams, M. Upgrade of the LHCb VELO detector. J. Instrum. 2017, 12. [Google Scholar] [CrossRef]
- Eklund, L. The LHCb VELO Upgrade. Nucl. Part. Phys. Proc. 2016, 273–275, 1079–1083. [Google Scholar] [CrossRef]
- LHCb Collaboration. LHCb Trigger and Online Upgrade Technical Design Report, Tech. Rep. In CERN-LHCC-2014-016; CERN: Geneva, Switzerland, 2014. [Google Scholar]
- LHCb Collaboration. LHCb Upgrade GPU High Level Trigger Technical Design Report, Tech. Rep. In CERN-LHCC-2020-006; CERN: Geneva, Switzerland, 2020. [Google Scholar]
- Dutta, D. The LHCb VELO Upgrade. In Proceedings of the 27th International Workshop on Vertex Detectors (VERTEX2018), Chennai, India, 21–26 October 2018. [Google Scholar]
- Kopciewicz, P.; Szumlak, T.; Majewski, M.; Akiba, K.; Augusto, O.; Back, J.; Bobulska, D.S.; Bogdanova, G.; Borghi, S.; Bowcock, T.; et al. The upgrade I of LHCb VELO-towards an intelligent monitoring platform. J. Instrum. 2020, 15, C06009. [Google Scholar] [CrossRef]
- Zyla, P.A.; Barnett, R.M.; Beringer, J.; Bonventre, R.J.; Dahl, O.; Dwyer, D.A.; Groom, D.E.; Lin, C.J.; Lugovsky, K.S.; Pianori, E. (Particle Data Group). Prog. Theor. Exp. Phys. 2020, 083C01, Update in 2021. [Google Scholar]
- Szumlak, T. VETRA-offline analysis and monitoring software platform for the LHCb vertex locator. J. Phys. Conf. Ser. 2010, 219, 032058. [Google Scholar] [CrossRef]
- Barrand, G.; Belyaev, I.; Binko, P.; Cattaneo, M.; Chytracek, R.; Corti, G.; Frank, M.; Gracia, G.; Harvey, J.; van Hervijnen, E.; et al. Gaudi-a software architecture and framework for building hep data processing applications. Comput. Phys. Commun. 2001, 140, 40–45. [Google Scholar] [CrossRef]
- Marsden, M. Cubic spline interpolation of continuous functions. J. Approx. Theory 2001, 10, 103–111. [Google Scholar] [CrossRef]
- Hocker, A.; Speckmayer, P.; Stelzer, J.; Therhaag, J.; von Toerne, E.; Voss, H.; Backes, M.; Carli, T.; Cohen, O.; Christov, A.; et al. TMVA-Toolkit for Multivariate Data Analysis. In CERN-OPEN-2007-007; CERN: Geneva, Switzerland, 2007. [Google Scholar]
- Landau, L.D. On the energy loss of fast particles by ionization. J. Phys. 1944, 8, 201–205. [Google Scholar]
- Bugiel, S.; Dasgupta, R.; Firlej, M.; Fiutowski, T.; Idzik, M.; Kuczynska, M.; Moron, J.; Swientek, K.; Szumlak, T. SALT, a dedicated readout chip for high precision tracking silicon strip detectors at the LHCb Upgrade. J. Instrum. 2016, 11, C02028. [Google Scholar] [CrossRef]

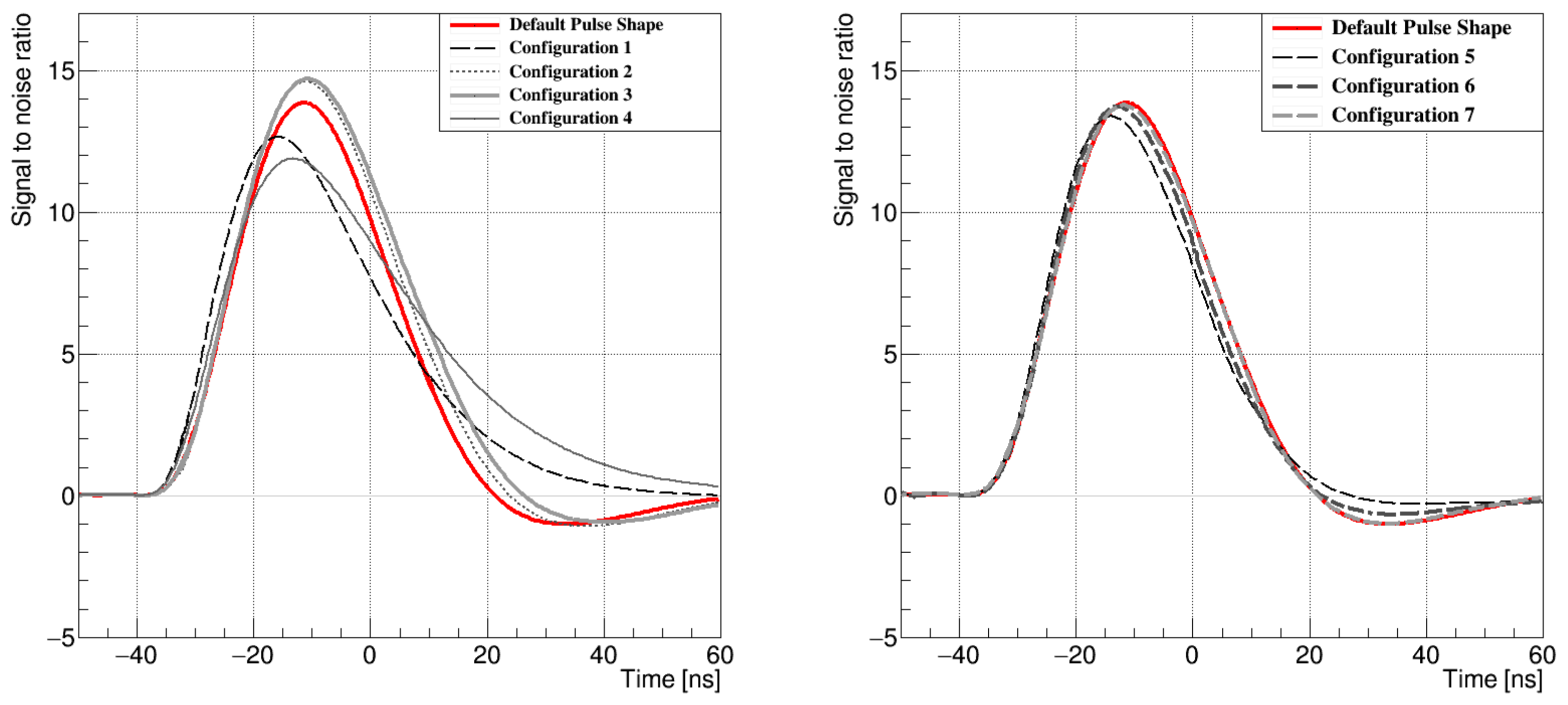
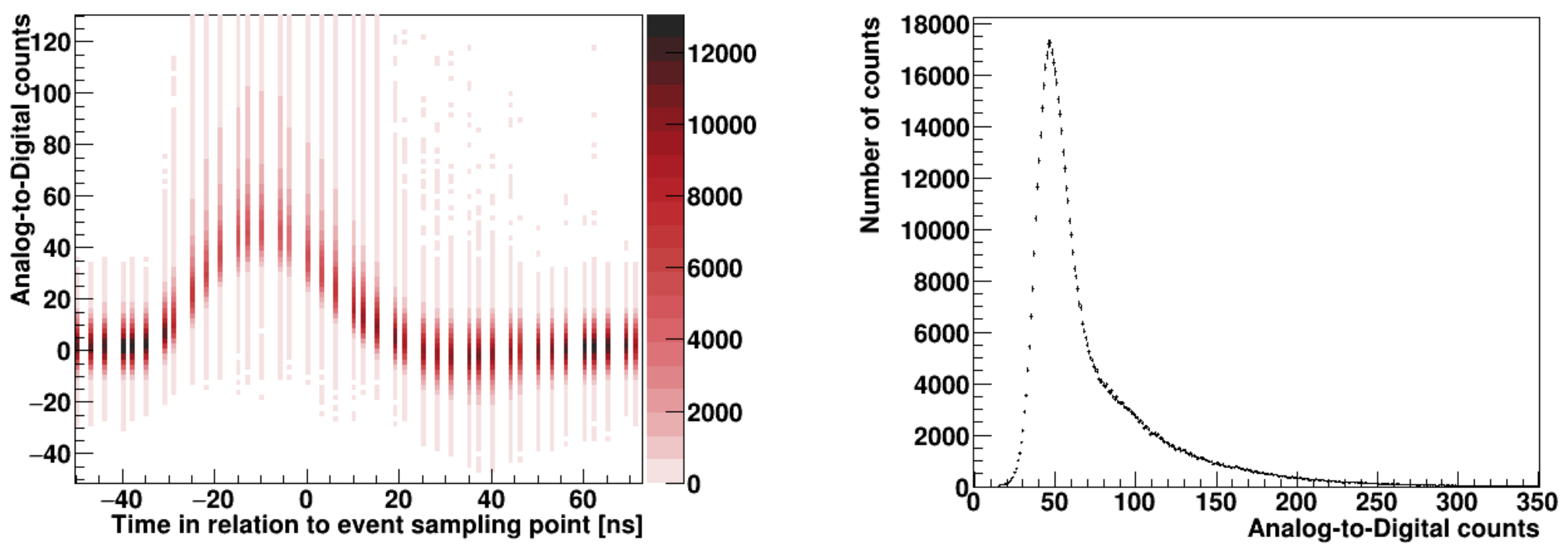
| Configuration | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Parameter | Default | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| [A] | 600 | 800 | 640 | 496 | 400 | 600 | 536 | 600 | |
| [A] | 80 | 80 | 80 | 200 | 200 | 80 | 112 | 80 | |
| [] | 510 | 600 | 600 | 600 | 700 | 510 | 510 | 510 | |
| [] | 150 | 300 | 400 | 300 | 600 | 150 | 100 | 140 | |
| [A] | 80 | 80 | 80 | 80 | 80 | 80 | 80 | 80 | |
| [A] | 824 | 744 | 744 | 744 | 744 | 744 | 744 | 744 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kopciewicz, P.; Akiba, K.C.; Szumlak, T.; Sitko, S.; Barter, W.; Buytaert, J.; Eklund, L.; Hennessy, K.; Koppenburg, P.; Latham, T.; et al. Simulation and Optimization Studies of the LHCb Beetle Readout ASIC and Machine Learning Approach for Pulse Shape Reconstruction. Sensors 2021, 21, 6075. https://doi.org/10.3390/s21186075
Kopciewicz P, Akiba KC, Szumlak T, Sitko S, Barter W, Buytaert J, Eklund L, Hennessy K, Koppenburg P, Latham T, et al. Simulation and Optimization Studies of the LHCb Beetle Readout ASIC and Machine Learning Approach for Pulse Shape Reconstruction. Sensors. 2021; 21(18):6075. https://doi.org/10.3390/s21186075
Chicago/Turabian StyleKopciewicz, Pawel, Kazuyoshi Carvalho Akiba, Tomasz Szumlak, Sebastian Sitko, William Barter, Jan Buytaert, Lars Eklund, Karol Hennessy, Patrick Koppenburg, Thomas Latham, and et al. 2021. "Simulation and Optimization Studies of the LHCb Beetle Readout ASIC and Machine Learning Approach for Pulse Shape Reconstruction" Sensors 21, no. 18: 6075. https://doi.org/10.3390/s21186075
APA StyleKopciewicz, P., Akiba, K. C., Szumlak, T., Sitko, S., Barter, W., Buytaert, J., Eklund, L., Hennessy, K., Koppenburg, P., Latham, T., Majewski, M., Oblakowska-Mucha, A., Parkes, C., Qian, W., Velthuis, J., & Williams, M. (2021). Simulation and Optimization Studies of the LHCb Beetle Readout ASIC and Machine Learning Approach for Pulse Shape Reconstruction. Sensors, 21(18), 6075. https://doi.org/10.3390/s21186075






