Real-Time 3D Reconstruction Method Based on Monocular Vision
Abstract
:1. Introduction
- There are many cameras and various sensors required for reconstruction, which are expensive and poor in portability.
- The reconstruction speed is slow. The reconstruction method is computationally expensive and time-consuming. It cannot meet real-time requirements.
- The reconstruction error is large, especially for the depth error. The reconstruction model effect is poor.
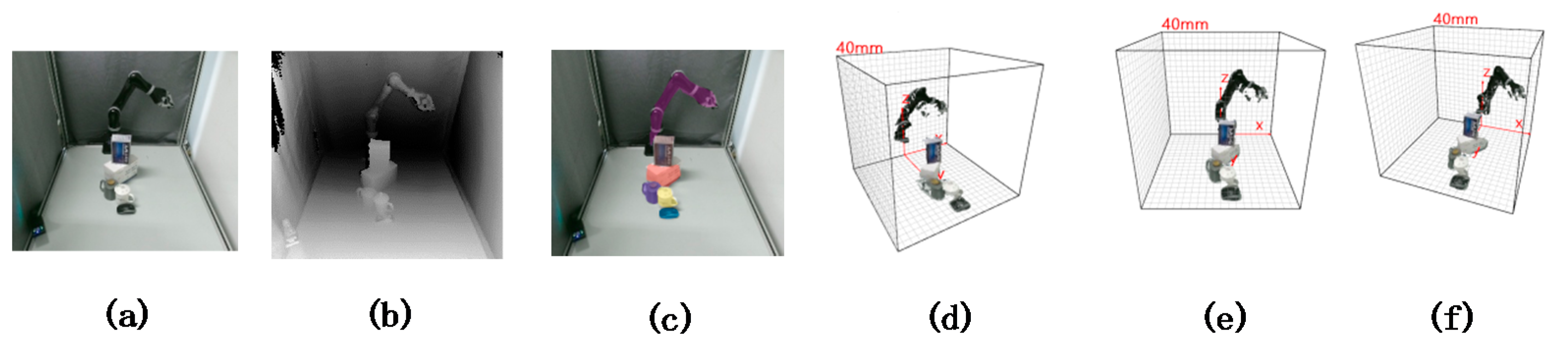
- We use a single depth camera for real-time collection of visual information, and use the powerful real-time segmentation capabilities of the YOLACT++ network to extract the real-time collected information [30,31,32]. Only part of the information of the extracted items is reconstructed to ensure the real-time performance of the method.
- We propose a visual information joint coding three-dimensional restoration method (VJTR) based on deep learning [33,34]. This method combines three stages of deep recovery, deep optimization, and deep fusion. Taking advantage of the high accuracy and fast running speed of ResNet-152 network, through joint coding of different types of visual information, the three-dimensional point cloud with optimized depth value corresponding to the two-dimensional image is output in real time [35,36,37,38,39,40]. At the same time, the most critical visual information combination in the process of this method is determined, so as to ensure the accuracy of the reconstruction of the method.
- For the outliers generated in the process of reconstructing the scene, we propose an outlier adjustment method based on cluster center distance constrained (BCC-Drop) to ensure the reconstruction of the space of each object consistency and reconstruction accuracy.
- We propose a framework organization method that can use a single depth camera to quickly and accurately perform 3D reconstruction. It is without any human assistance or calibration, and can automatically organize the reconstructed objects in the 3D space.
- Experimental results show that our method greatly improves the performance of 3D reconstruction and is always better than other mainstream comparison methods. The reconstruction speed reaches real-time and can be used for real-time reconstruction.
2. Materials and Methods
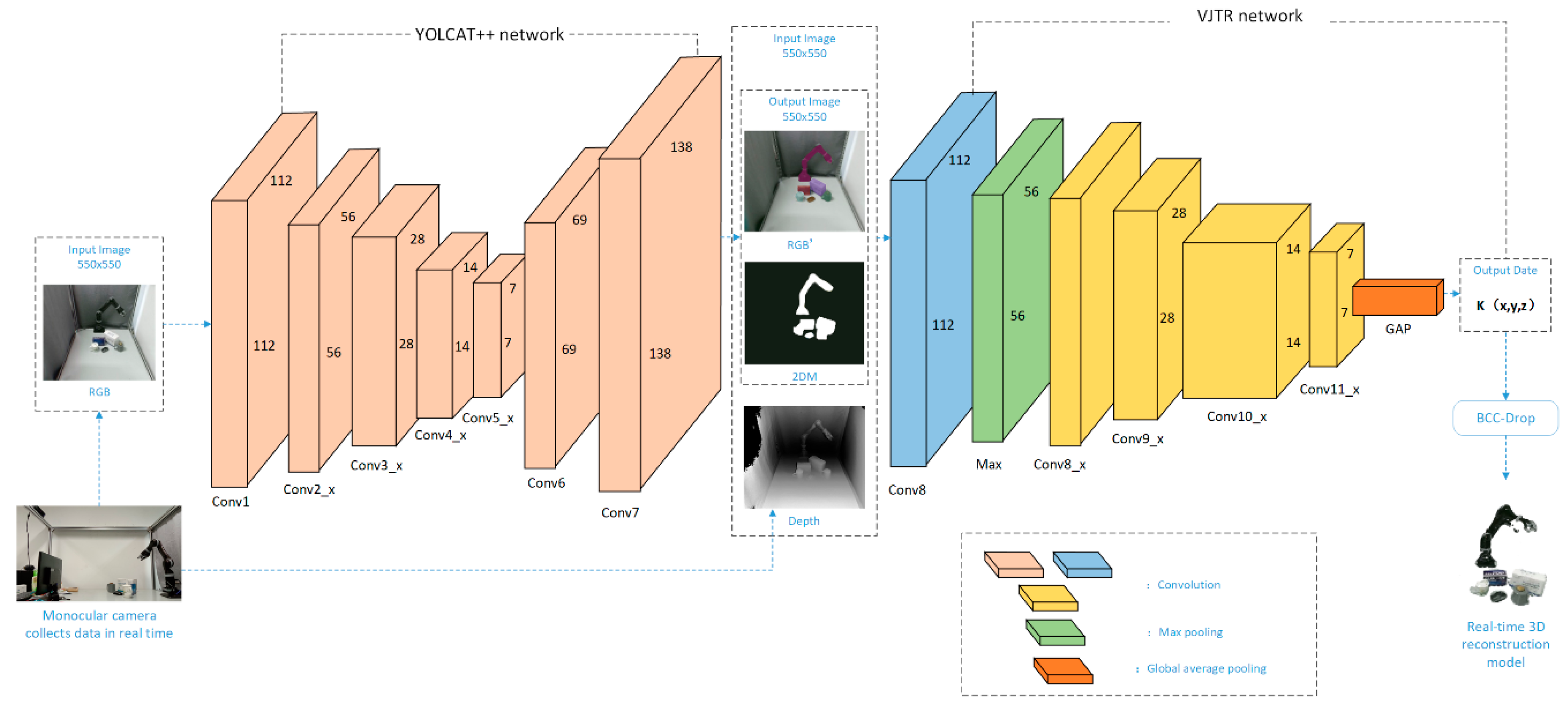
2.1. Framework
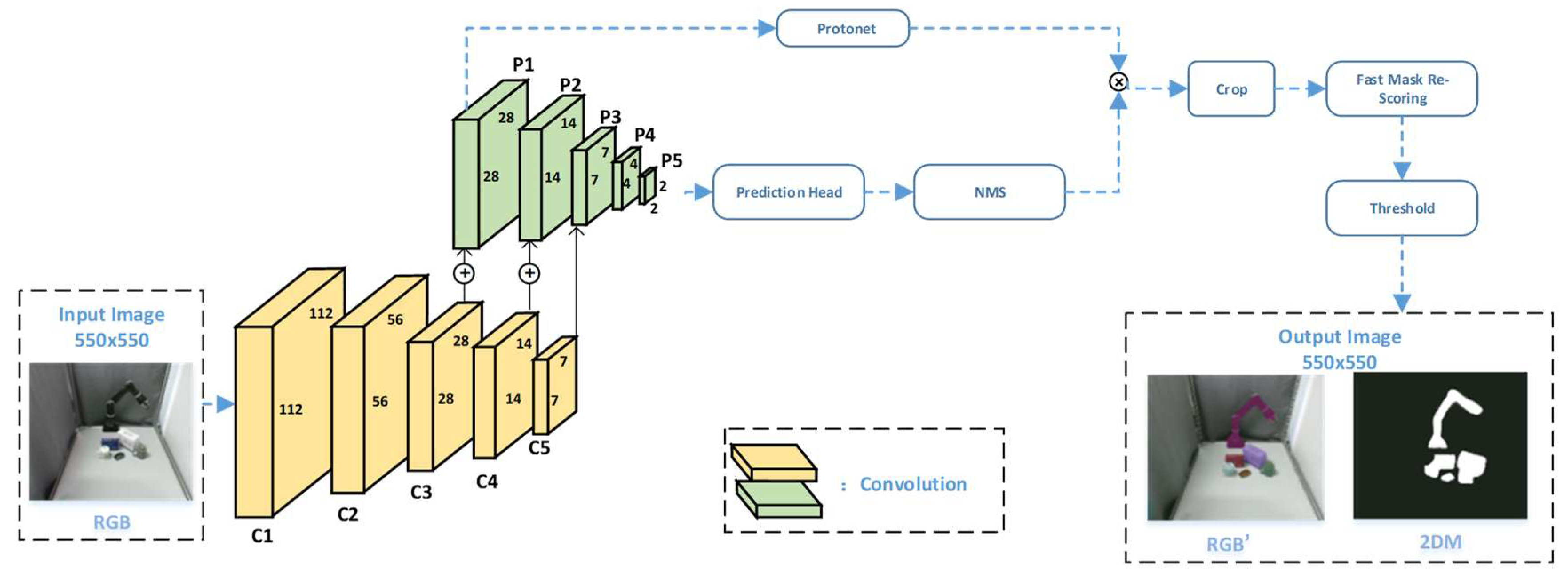
2.2. Visual Information Segmentation and Extraction
2.3. Visual Information Joint Coding Three-Dimensional Restoration Method
2.3.1. Reconstruction of 3D Coordinates from RGB Image and Depth Image
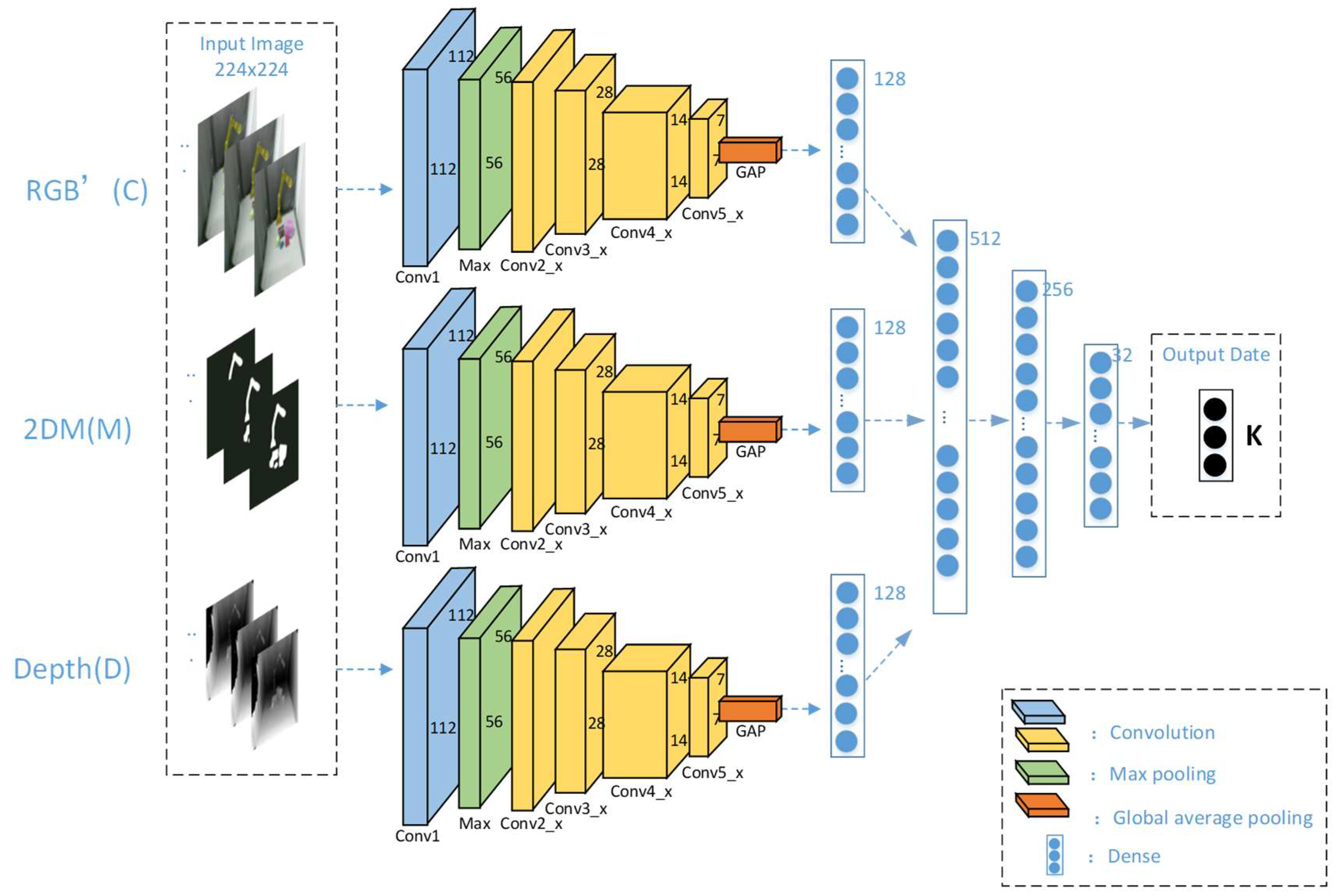
2.3.2. Simultaneous Estimation of Three-Dimensional Values Using ResNet-152 Network
2.4. Reconstruction Error Correction
2.5. Method Summary
| Algorithm 1. The process of the real-time 3D reconstruction method | |
| 1: | The RGB and Depth images of the scene are collected by the monocular camera. |
| 2: | Input RGB to YOLACT++ to obtain the segmented RGB’, 2DM. |
| 3: | Input RGB’, 2DM, Depth to VJTR to get . |
| 4: | Set , then let and . |
| 5: | for Each |
| 6: | Use Formula (10) to calculate the . |
| 7: | for i = 1 to m step do |
| 8: | Use Formula (11) to calculate the . |
| 9: | if () then |
| 10: | . |
| 11: | . |
| 12: | end if |
| 13: | end for |
| 14: | end for |
| 15: | for i = 1 to m step do |
| 16: | if then |
| 17: | Add to . |
| 18: | else |
| 19: | Add to . |
| 20: | end if |
| 21: | end for |
| 22: | for Each |
| 23: | Use Formulas (12)–(14) to normalize its coordinate values. |
| 24: | Add to . |
| 25: | end for |
| 26: | return . |
3. Experiments
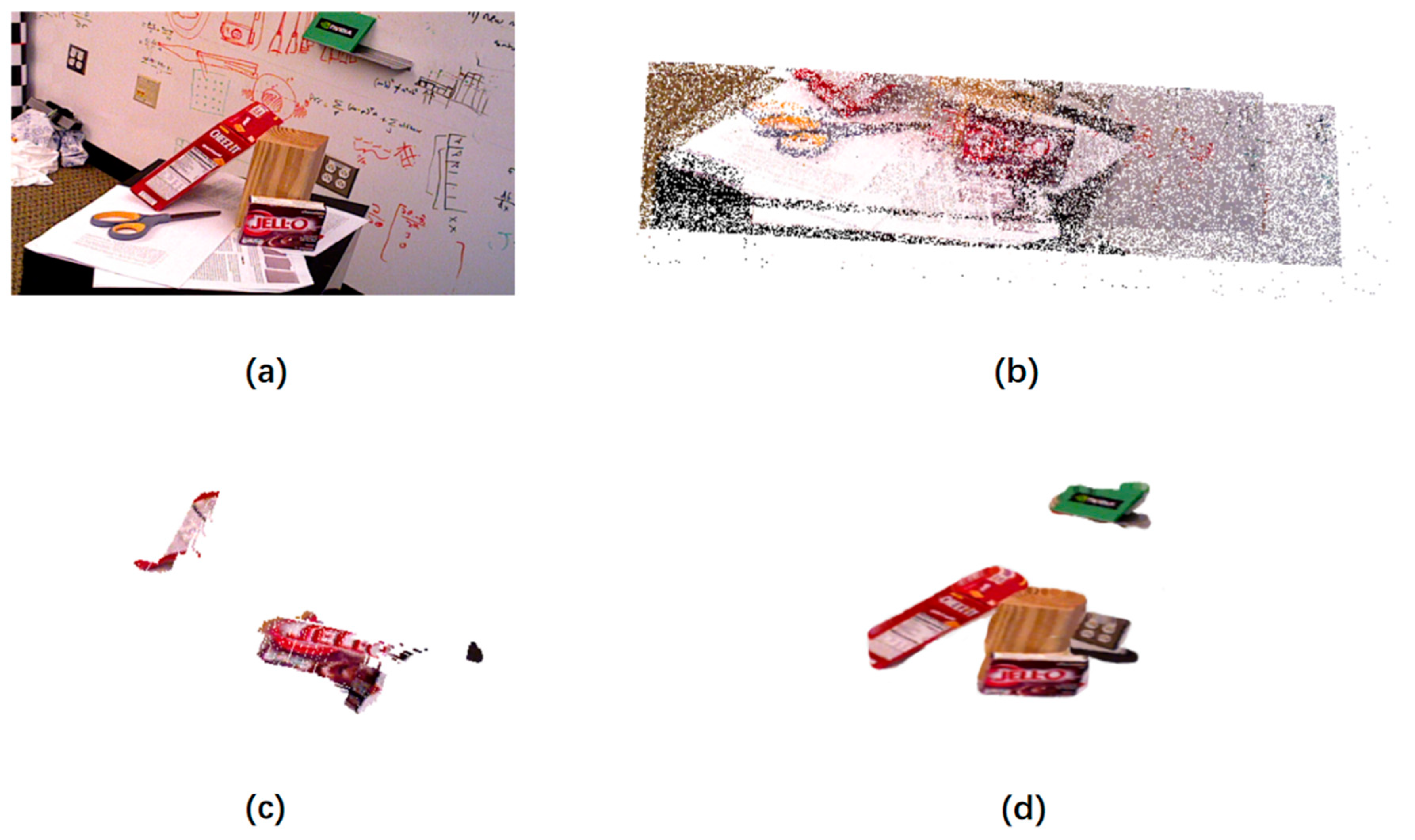
3.1. Experimental Setting
3.2. Implementation and Results of Visual Information Segmentation Extraction
3.3. VJTR Method Realization and Results
3.4. BCC-Drop Strategy Implementation and Results
3.5. Experimental Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yu, C.; Ji, F.; Jing, X.; Liu, M. Dynamic Granularity Matrix Space Based Adaptive Edge Detection Method for Structured Light Stripes. Math. Probl. Eng. 2019, 2019, 1959671. [Google Scholar] [CrossRef]
- Feri, L.E.; Ahn, J.; Lutfillohonov, S.; Kwon, J. A Three-Dimensional Microstructure Reconstruction Framework for Permeable Pavement Analysis Based on 3D-IWGAN with Enhanced Gradient Penalty. Sensors 2021, 21, 3603. [Google Scholar] [CrossRef]
- Li, H.; Wang, R. Method of Real-Time Wellbore Surface Reconstruction Based on Spiral Contour. Energies 2021, 14, 291. [Google Scholar] [CrossRef]
- Storms, W.; Shockley, J.; Raquet, J. Magnetic field navigation in an indoor environment. In Proceedings of the 2010 Ubiquitous Positioning Indoor Navigation and Location Based Service, Kirkkonummi, Finland, 14–15 October 2010; pp. 1–10. [Google Scholar]
- Slavcheva, M.; Baust, M.; Ilic, S. Variational Level Set Evolution for Non-Rigid 3D Reconstruction from a Single Depth Camera. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 2838–2850. [Google Scholar] [CrossRef]
- Fei, C.; Ma, Y.; Jiang, S.; Liu, J.; Sun, B.; Li, Y.; Gu, Y.; Zhao, X.; Fang, J. Real-Time Dynamic 3D Shape Reconstruction with SWIR InGaAs Camera. Sensors 2020, 20, 521. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wen, Q.; Xu, F.; Yong, J. Real-Time 3D Eye Performance Reconstruction for RGBD Cameras. IEEE Trans. Vis. Comput. Graph. 2017, 23, 2586–2598. [Google Scholar] [CrossRef]
- Gu, Z.; Chen, J.; Wu, C. Three-Dimensional Reconstruction of Welding Pool Surface by Binocular Vision. Chin. J. Mech. Eng. 2021, 34, 47. [Google Scholar] [CrossRef]
- Yuan, Z.; Li, Y.; Tang, S.; Li, M.; Guo, R.; Wang, W. A survey on indoor 3D modeling and applications via RGB-D devices. Front. Inf. Technol. Electron. Eng. 2021, 22, 815–826. [Google Scholar] [CrossRef]
- Lu, F.; Peng, H.; Wu, H.; Yang, J.; Yang, X.; Cao, R.; Zhang, L.; Yang, R.; Zhou, B. InstanceFusion: Real-time Instance-level 3D Reconstruction Using a Single RGBD Camera. Comput. Graph. Forum 2020, 39, 433–445. [Google Scholar] [CrossRef]
- Henry, P.; Krainin, M.; Herbst, E.; Ren, X.; Fox, D. RGB-D mapping: Using Kinect-style depth cameras for dense 3D modeling of indoor environments. Int. J. Robot. Res. 2012, 31, 647–663. [Google Scholar] [CrossRef] [Green Version]
- Vogiatzis, G.; Hernández, C. Video-based, real-time multi-view stereo. Image Vis. Comput. 2011, 29, 434–441. [Google Scholar] [CrossRef] [Green Version]
- Engel, J.; Koltun, V.; Cremers, D. Direct Sparse Odometry. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 611–625. [Google Scholar] [CrossRef] [PubMed]
- Stumberg, L.V.; Usenko, V.; Cremers, D. Direct Sparse Visual-Inertial Odometry Using Dynamic Marginalization. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 2510–2517. [Google Scholar]
- Furukawa, Y.; Ponce, J. Accurate, Dense, and Robust Multiview Stereopsis. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 1362–1376. [Google Scholar] [CrossRef] [PubMed]
- Jancosek, M.; Pajdla, T. Multi-view reconstruction preserving weakly-supported surfaces. In Proceedings of the CVPR 2011, Washington, DC, USA, 20–25 June 2011; pp. 3121–3128. [Google Scholar]
- Newcombe, R.A.; Lovegrove, S.J.; Davison, A.J. DTAM: Dense tracking and mapping in real-time. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 2320–2327. [Google Scholar]
- Wu, Z.; Wu, X.; Zhang, X.; Wang, S.; Ju, L. Semantic stereo matching with pyramid cost volumes. In Proceedings of the Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 27–28 October 2019; pp. 7484–7493. [Google Scholar]
- Gu, X.; Fan, Z.; Zhu, S.; Dai, Z.; Tan, F.; Tan, P. Cascade cost volume for high-resolution multi-view stereo and stereo matching. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020; pp. 2495–2504. [Google Scholar]
- Yang, Z.; Gao, F.; Shen, S. Real-time monocular dense mapping on aerial robots using visual-inertial fusion. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 4552–4559. [Google Scholar]
- Schöps, T.; Sattler, T.; Häne, C.; Pollefeys, M. Large-scale outdoor 3D reconstruction on a mobile device. Comput. Vis. Image Underst. 2017, 157, 151–166. [Google Scholar] [CrossRef]
- Azhar, N.; Saad, W.H.M.; Manap, N.A.; Saad, N.M.; Syafeeza, A.R. Silhouette-based approach of 3D image reconstruction for automated image acquisition using robotic arm. IOP Conf. Ser. Mater. Sci. Eng. 2017, 210, 012049. [Google Scholar] [CrossRef] [Green Version]
- Bo, Z.-H.; Zhang, H.; Yong, J.-H.; Gao, H.; Xu, F. DenseAttentionSeg: Segment hands from interacted objects using depth input. Appl. Soft Comput. 2020, 92, 106297. [Google Scholar] [CrossRef] [Green Version]
- Tong, J.; Zhou, J.; Liu, L.; Pan, Z.; Yan, H. Scanning 3D Full Human Bodies Using Kinects. IEEE Trans. Vis. Comput. Graph. 2012, 18, 643–650. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Garcia-Fidalgo, E.; Ortiz, A. Methods for Appearance-Based Loop Closure Detection: Applications to Topological Mapping and Image Mosaicking; Springer: New York, NY, USA, 2018; Volume 122. [Google Scholar]
- Maimone, A.; Fuchs, H. Encumbrance-free telepresence system with real-time 3D capture and display using commodity depth cameras. In Proceedings of the 2011 10th IEEE International Symposium on Mixed and Augmented Reality, Basel, Switzerland, 26–29 October 2011; pp. 137–146. [Google Scholar]
- Alexiadis, D.S.; Zarpalas, D.; Daras, P. Real-Time, Full 3-D Reconstruction of Moving Foreground Objects from Multiple Consumer Depth Cameras. IEEE Trans. Multimed. 2013, 15, 339–358. [Google Scholar] [CrossRef]
- Liu, S.-L.; Guo, H.-X.; Pan, H.; Wang, P.-S.; Tong, X.; Liu, Y. Deep Implicit Moving Least-Squares Functions for 3D Reconstruction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 9–16 November 2021; pp. 1788–1797. [Google Scholar]
- Alexiadis, A. Deep multiphysics: Coupling discrete multiphysics with machine learning to attain self-learning in-silico models replicating human physiology. Artif. Intell. Med. 2019, 98, 27–34. [Google Scholar] [CrossRef] [PubMed]
- Ceron, J.C.A.; Chang, L.; Ochoa-Ruiz, G.; Ali, S. Assessing YOLACT++ for real time and robust instance segmentation of medical instruments in endoscopic procedures. arXiv 2021, arXiv:2103.15997. Available online: https://arxiv.org/abs/2103.15997 (accessed on 28 August 2021).
- Wang, Z.; Xu, Y.; Yu, J.; Xu, G.; Fu, J.; Gu, T. Instance segmentation of point cloud captured by RGB-D sensor based on deep learning. Int. J. Comput. Integr. Manuf. 2021, 1–14. [Google Scholar]
- Bolya, D.; Zhou, C.; Xiao, F.; Lee, Y.J. Yolact++: Better real-time instance segmentation. arXiv 2019, arXiv:1912.06218. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Ngiam, J.; Khosla, A.; Kim, M.; Nam, J.; Lee, H.; Ng, A.Y. Multimodal deep learning. In Proceedings of the ICML, Bellevue, WD, USA, 28 June–2 July 2011. [Google Scholar]
- Jo, H.; Kim, E. New Monte Carlo Localization Using Deep Initialization: A Three-Dimensional LiDAR and a Camera Fusion Approach. IEEE Access 2020, 8, 74485–74496. [Google Scholar] [CrossRef]
- Zhao, C.; Sun, L.; Stolkin, R. A fully end-to-end deep learning approach for real-time simultaneous 3D reconstruction and material recognition. In Proceedings of the 2017 18th International Conference on Advanced Robotics (ICAR), Hong Kong, China, 10–12 July 2017; pp. 75–82. [Google Scholar]
- Lombardi, M.; Savardi, M.; Signoroni, A. Cross-domain assessment of deep learning-based alignment solutions for real-time 3D reconstruction. Comput. Graph. 2021, 99, 54–69. [Google Scholar] [CrossRef]
- Laidlow, T.; Czarnowski, J.; Leutenegger, S. DeepFusion: Real-time dense 3D reconstruction for monocular SLAM using single-view depth and gradient predictions. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 4068–4074. [Google Scholar]
- Kim, M.; Jeng, G.-S.; Pelivanov, I.; O’Donnell, M. Deep-learning image reconstruction for real-time photoacoustic system. IEEE Trans. Med Imaging 2020, 39, 3379–3390. [Google Scholar] [CrossRef] [PubMed]
- Visentini-Scarzanella, M.; Sugiura, T.; Kaneko, T.; Koto, S. Deep monocular 3D reconstruction for assisted navigation in bronchoscopy. Int. J. Comput. Assist. Radiol. Surg. 2017, 12, 1089–1099. [Google Scholar] [CrossRef] [PubMed]
- Dai, J.; Qi, H.; Xiong, Y.; Li, Y.; Zhang, G.; Hu, H.; Wei, Y. Deformable convolutional networks. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 764–773. [Google Scholar]
- Lin, T.-Y.; Goyal, P.; Girshick, R.; He, K.; Dollár, P. Focal loss for dense object detection. In Proceedings of the IEEE international conference on computer vision, Venice, Italy, 22–29 October 2017; pp. 2980–2988. [Google Scholar]
- Rodriguez, A.; Laio, A. Clustering by fast search and find of density peaks. Science 2014, 344, 1492–1496. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Meng, Y.; Zhuang, H. Self-Calibration of Camera-Equipped Robot Manipulators. Int. J. Robot. Res. 2001, 20, 909–921. [Google Scholar] [CrossRef]
- Liu, S.; Qi, L.; Qin, H.; Shi, J.; Jia, J. Path aggregation network for instance segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 8759–8768. [Google Scholar]
- Jiang, M.; Fan, X.; Yan, H. Retinamask: A face mask detector. arXiv 2020, arXiv:2005.03950. Available online: https://arxiv.org/abs/2005.03950 (accessed on 28 August 2021).
- Li, Y.; Qi, H.; Dai, J.; Ji, X.; Wei, Y. Fully convolutional instance-aware semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2359–2367. [Google Scholar]
- He, K.; Gkioxari, G.; Dollár, P.; Girshick, R. Mask r-cnn. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2961–2969. [Google Scholar]
- Huang, Z.; Huang, L.; Gong, Y.; Huang, C.; Wang, X. Mask scoring r-cnn. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 6409–6418. [Google Scholar]


| Network Layer | Kernel Parameter | Repeat | Output |
|---|---|---|---|
| Input | |||
| Block1 | 3 | ||
| Block2 | 8 | ||
| Block3 | 36 | ||
| Block4 | 3 | ||
| Number | Method | Average Precision | FPS | Time (ms) |
|---|---|---|---|---|
| 1 | PA-Net [45] | 36.6 | 4.7 | 212.8 |
| 2 | RetinaMask [46] | 34.7 | 6.0 | 166.7 |
| 3 | FCIS [47] | 29.5 | 6.6 | 151.5 |
| 4 | Mask R-CNN [48] | 35.7 | 8.6 | 116.3 |
| 5 | Mask Scoring R-CNN [49] | 38.3 | 8.6 | 116.3 |
| 6 | YOLACT++ | 34.1 | 33.5 | 29.9 |
| Number | Neural Networks Category | Enter | Average Error (m) | Maximum Error (m) | Parameter Size (MB) | Time (s) |
|---|---|---|---|---|---|---|
| 1 | VGG-16 | C + D + M | 0.041 | 0.098 | 46.20 | 0.159 |
| 2 | C + D | 0.056 | 0.113 | 39.96 | 0.176 | |
| 3 | D + M | 0.040 | 0.079 | 21.71 | 0.169 | |
| 4 | D | 0.030 | 0.101 | 20.04 | 0.159 | |
| 5 | InceptionNet-V3 | C + D + M | 0.049 | 0.094 | 27.77 | 0.151 |
| 6 | C + D | 0.051 | 0.104 | 22.63 | 0.13 | |
| 7 | D + M | 0.026 | 0.063 | 21.63 | 0.129 | |
| 8 | D | 0.031 | 0.096 | 20.04 | 0.125 | |
| 9 | ResNet-152 | C + D + M | 0.037 | 0.085 | 13.47 | 0.121 |
| 10 | C + D | 0.044 | 0.068 | 12.61 | 0.115 | |
| 11 | D + M | 0.017 | 0.052 | 8.79 | 0.115 | |
| 12 | D | 0.041 | 0.070 | 6.52 | 0.096 |
| Object | Point | Precision | Time (ms) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| m | (%) | (%) | TYOLACT++ | VJTR | TBCC-Drop | ||||
| Bottle | 684 | 137 | 8.62 mm | 6.43 mm | 12.29 | 9.16 | 30.12 | 2.32 | 1.14 |
| Blue barrel | 440 | 88 | 9.77 mm | 5.69 mm | 9.71 | 5.65 | 30.01 | 1.35 | 0.44 |
| Brown box | 2680 | 536 | 11.13 mm | 6.94 mm | 9.78 | 6.10 | 30.33 | 5.26 | 2.21 |
| Blue cans | 260 | 52 | 3.58 mm | 2.04 mm | 8.44 | 4.81 | 30.06 | 1.22 | 0.23 |
| Red bowl | 468 | 94 | 9.48 mm | 5.76 mm | 10.75 | 6.53 | 30.03 | 1.48 | 0.51 |
| Mean | / | / | 8.52 mm | 5.37 mm | 10.19 | 6.45 | 30.11 | 2.32 | 0.90 |
| Algorithm | Err (%) | Running Time (ms) | Detection Speed (fps) |
|---|---|---|---|
| EKF-SLAM | 18.41 | 80.11 | 12 |
| ORB | 10.34 | 251.32 | 3 |
| OURS | 6.71 | 33.64 | 29 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, Q.; Chang, L.; Qiang, B.; Zhang, S.; Xie, W.; Yang, X.; Sun, Y.; Yang, M. Real-Time 3D Reconstruction Method Based on Monocular Vision. Sensors 2021, 21, 5909. https://doi.org/10.3390/s21175909
Jia Q, Chang L, Qiang B, Zhang S, Xie W, Yang X, Sun Y, Yang M. Real-Time 3D Reconstruction Method Based on Monocular Vision. Sensors. 2021; 21(17):5909. https://doi.org/10.3390/s21175909
Chicago/Turabian StyleJia, Qingyu, Liang Chang, Baohua Qiang, Shihao Zhang, Wu Xie, Xianyi Yang, Yangchang Sun, and Minghao Yang. 2021. "Real-Time 3D Reconstruction Method Based on Monocular Vision" Sensors 21, no. 17: 5909. https://doi.org/10.3390/s21175909
APA StyleJia, Q., Chang, L., Qiang, B., Zhang, S., Xie, W., Yang, X., Sun, Y., & Yang, M. (2021). Real-Time 3D Reconstruction Method Based on Monocular Vision. Sensors, 21(17), 5909. https://doi.org/10.3390/s21175909






