Opportunistic Rain Rate Estimation from Measurements of Satellite Downlink Attenuation: A Survey
Abstract
1. Introduction
2. Review of Satellite Radio Links
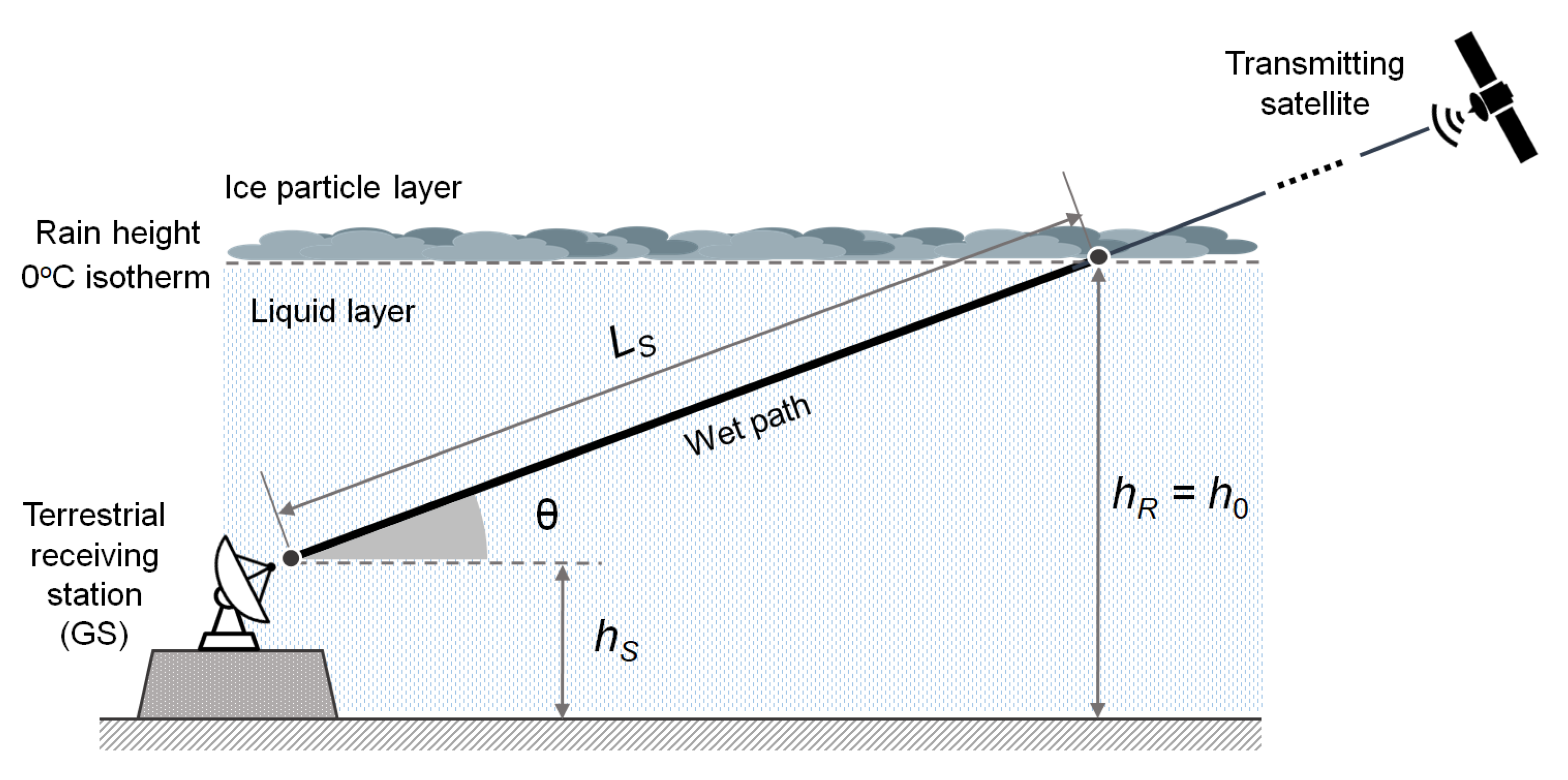
2.1. A Simple Geometrical Model of the Satellite Link through the Troposphere
2.2. Satellite Link Budget
3. Satellite Downlink Impairments
3.1. Attenuation Factors Affecting Signal Level without Rain (in Addition to Free Space Loss)
3.1.1. Effect of Ionosphere and Troposphere
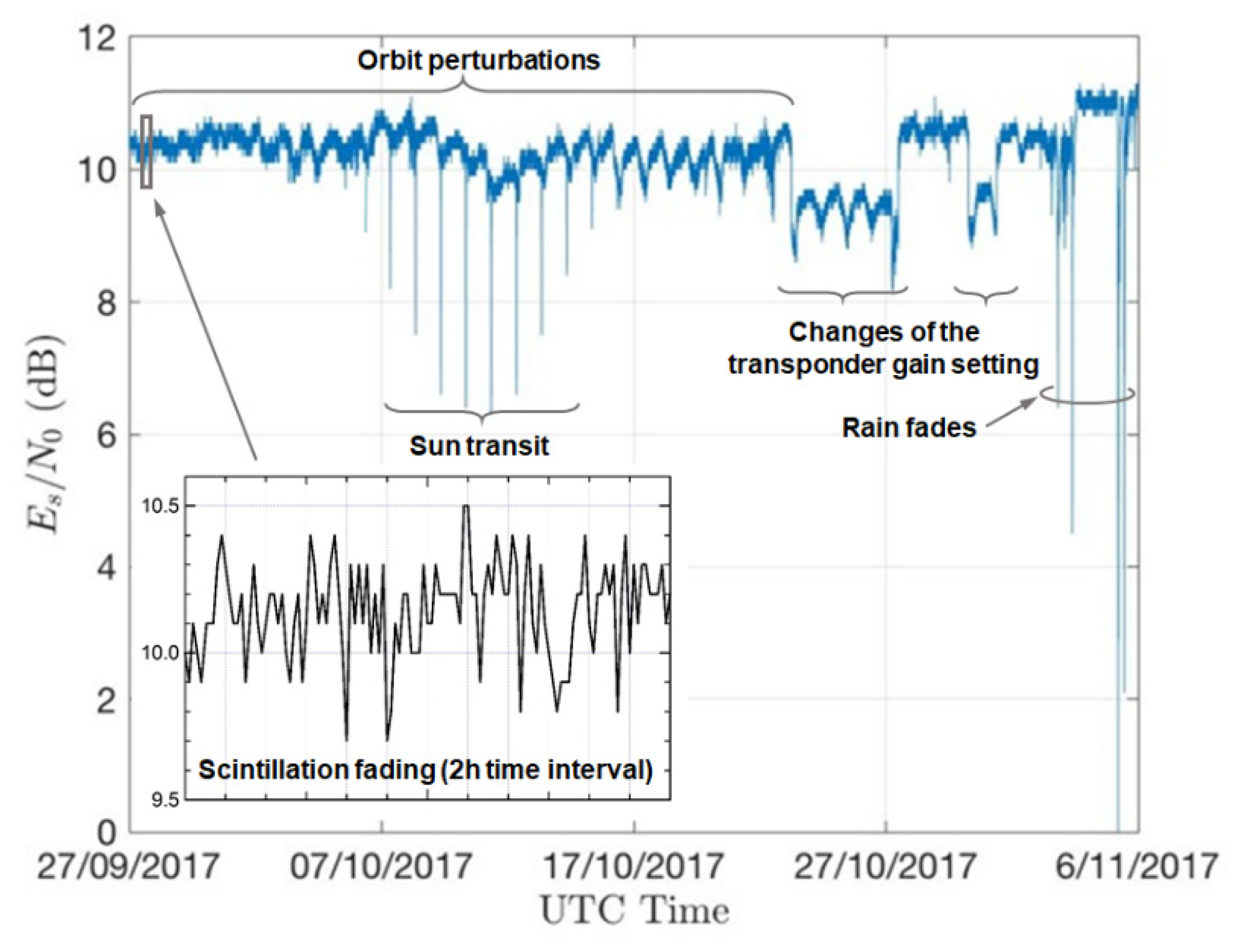
3.1.2. Antenna Mispointing and Orbit Perturbations
3.1.3. Sun Blinding
3.1.4. Operator-Induced Power Variations
3.2. Extra Attenuation Due to Rain
3.2.1. Specific Attenuation Model for the LL
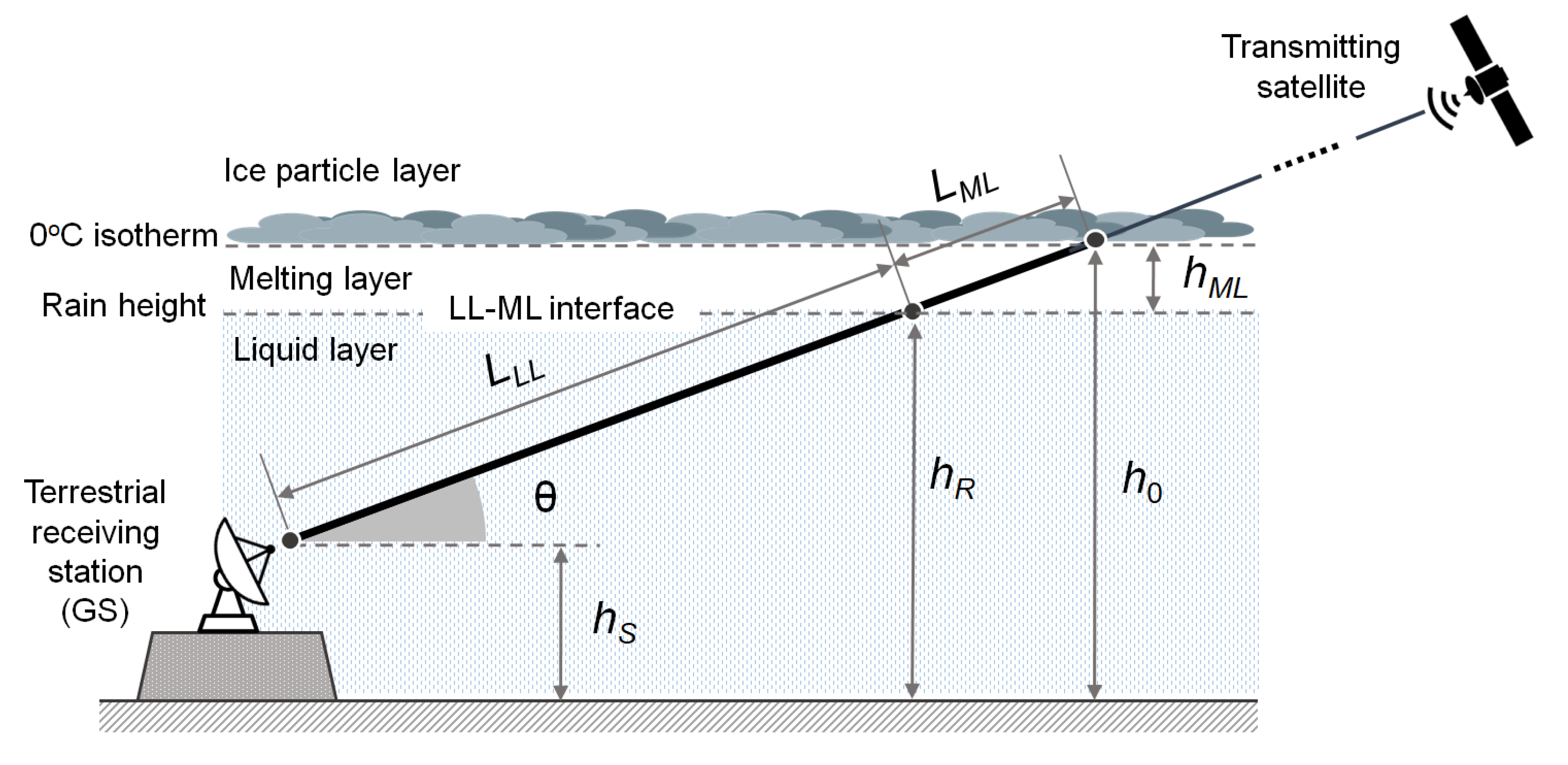
3.2.2. Specific Attenuation Model for the ML
4. Basic Methods for Estimating the Rainfall Rate from Rain Attenuation
4.1. Basic Methods for Measuring Rain Attenuation
4.1.1. Beacon Power Measurement
4.1.2. SNR or ESNDR Measurement on a Wideband Signal
4.2. Mapping of Rain Attenuation onto Rainfall Rate and Related Issues
4.2.1. General Procedure for Mapping
4.2.2. Melting Layer Effects
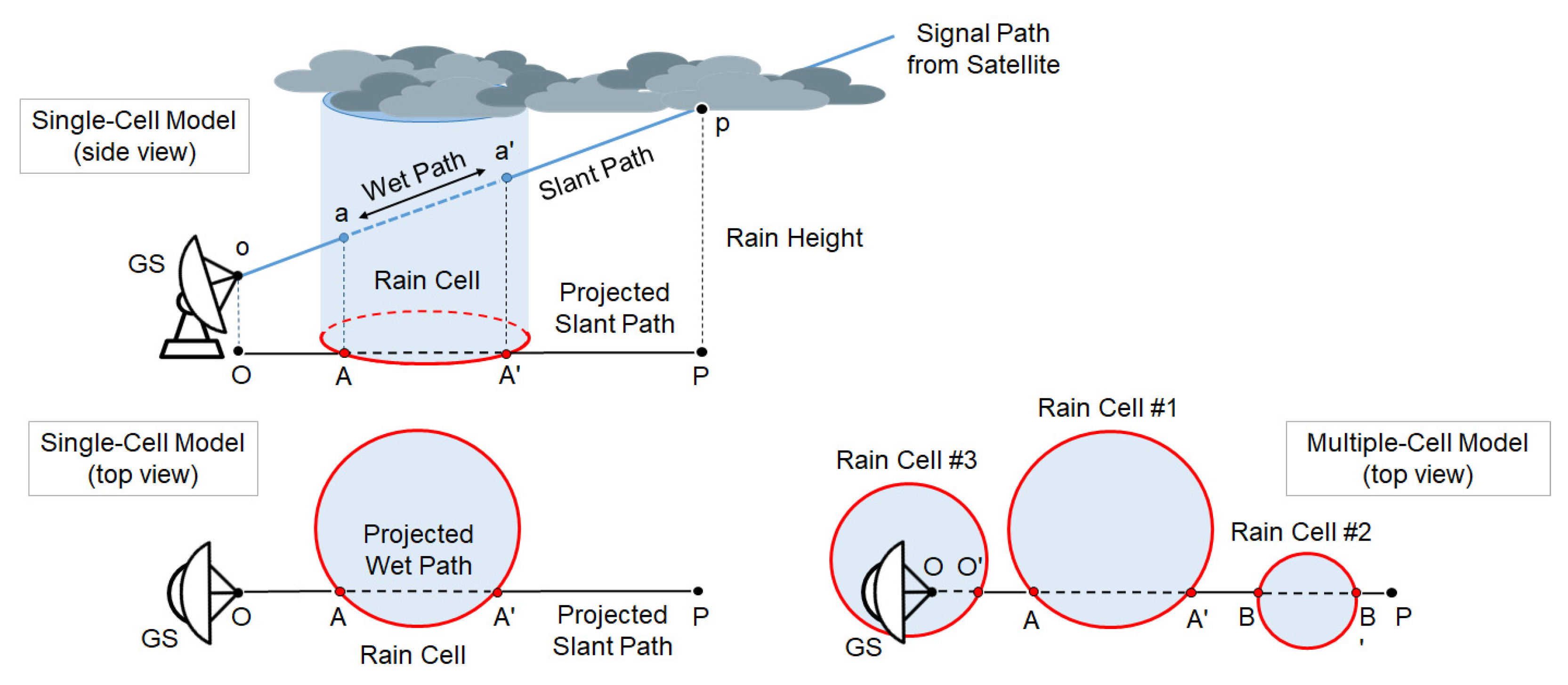
4.2.3. Non-Uniformity of the Rain and Geometrical Issues
- The diameter of a single (cylindrically-shaped) rain cell;
- The average length of the intercept of the projected slant path with the randomly positioned circles representing the ground projection of multiple rain cells;
- A calibration coefficient which takes into account the non-uniform distribution of rain inside the cell.
5. Survey of Rainfall Rate Estimation Techniques
- (i)
- Satellite orbit and downlink frequency band (Section 5.1);
- (ii)
- Physical quantity to measure, generically termed as the “strength” of the received signal, and to be processed for estimating the RR and the type of receiver (Section 5.2);
- (iii)
- Type of processing (Section 5.3) for the following:
- The detection of a rain event, together with the relevant start and end epochs;
- Identifying the “baseline” signal strength in the absence of rain (“clear-sky”) to be used for evaluating the signal strength reduction during rain events;
- Obtaining the estimate of RR from the measurement of signal strength reduction;
- (i)
- Ancillary information (geometric, climatic and meteorological) required by the RR estimation algorithm and how to collect it (Section 5.4);
- (ii)
- Techniques for recognizing and tackling sudden strength variations of the signal strength, not due to rain (Section 5.5).
5.1. Type of Satellites
5.1.1. Satellite Orbits and Frequency Bands
5.1.2. Tomographic Approaches and Other Techniques for the Reconstruction of the Precipitation Fields
5.2. Measurement of Signal Level at the Receiver and Related Hardware Issues
5.2.1. Beacon-Based Approach
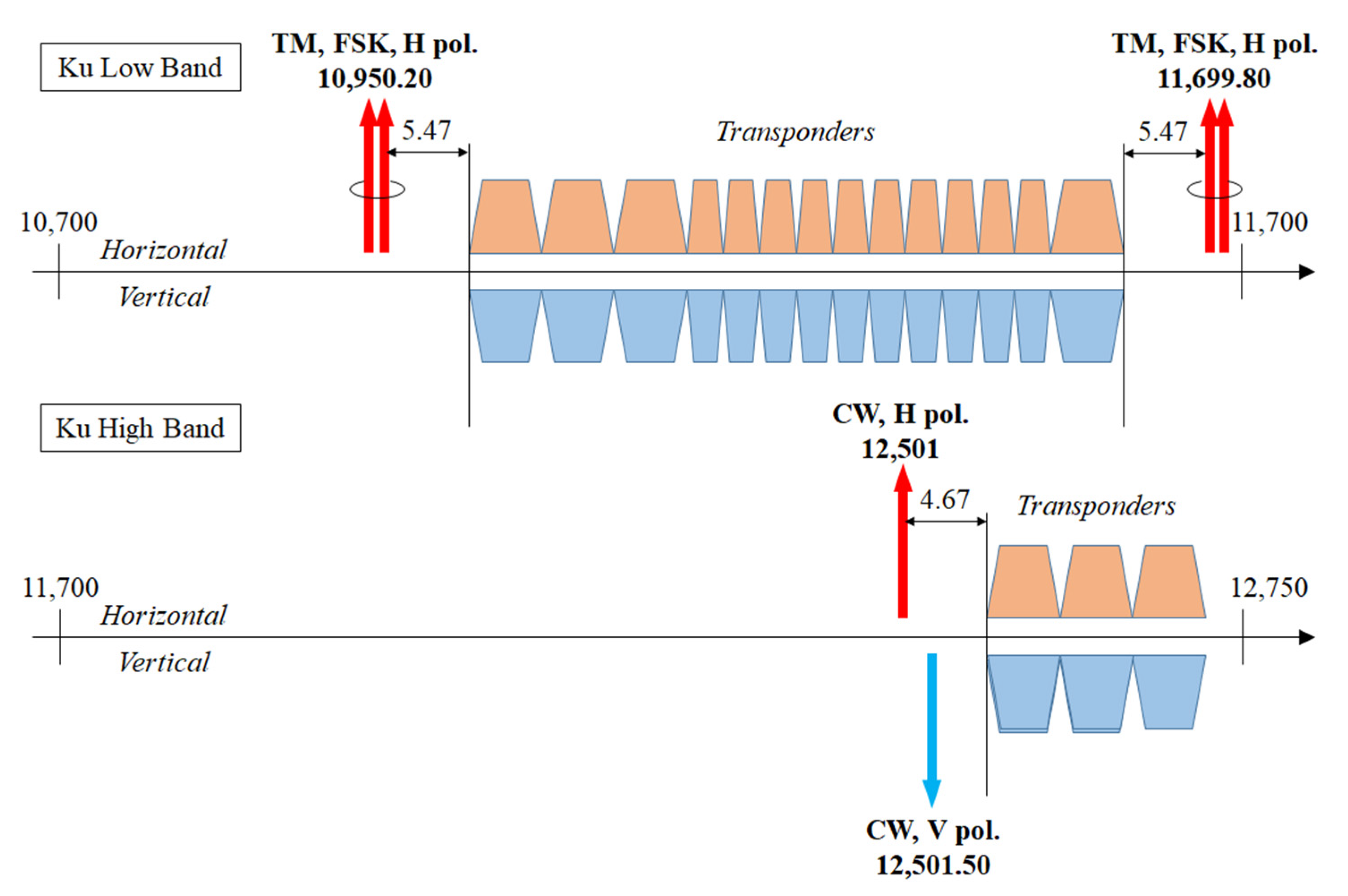
5.2.2. COTS-Receiver-Based Approach—Ku Band
5.2.3. COTS-Receiver-Based Approach—Ka Band
5.3. Processing Issues
5.3.1. Identification of the Rainy Periods
5.3.2. Identification of the Dry Baseline during Dry and Rainy Periods
5.3.3. Rainfall Rate Estimation and Comparison with Rain Gauges
5.3.4. Latency Issues
5.4. Ancillary Information Required by the RR Estimation Algorithm
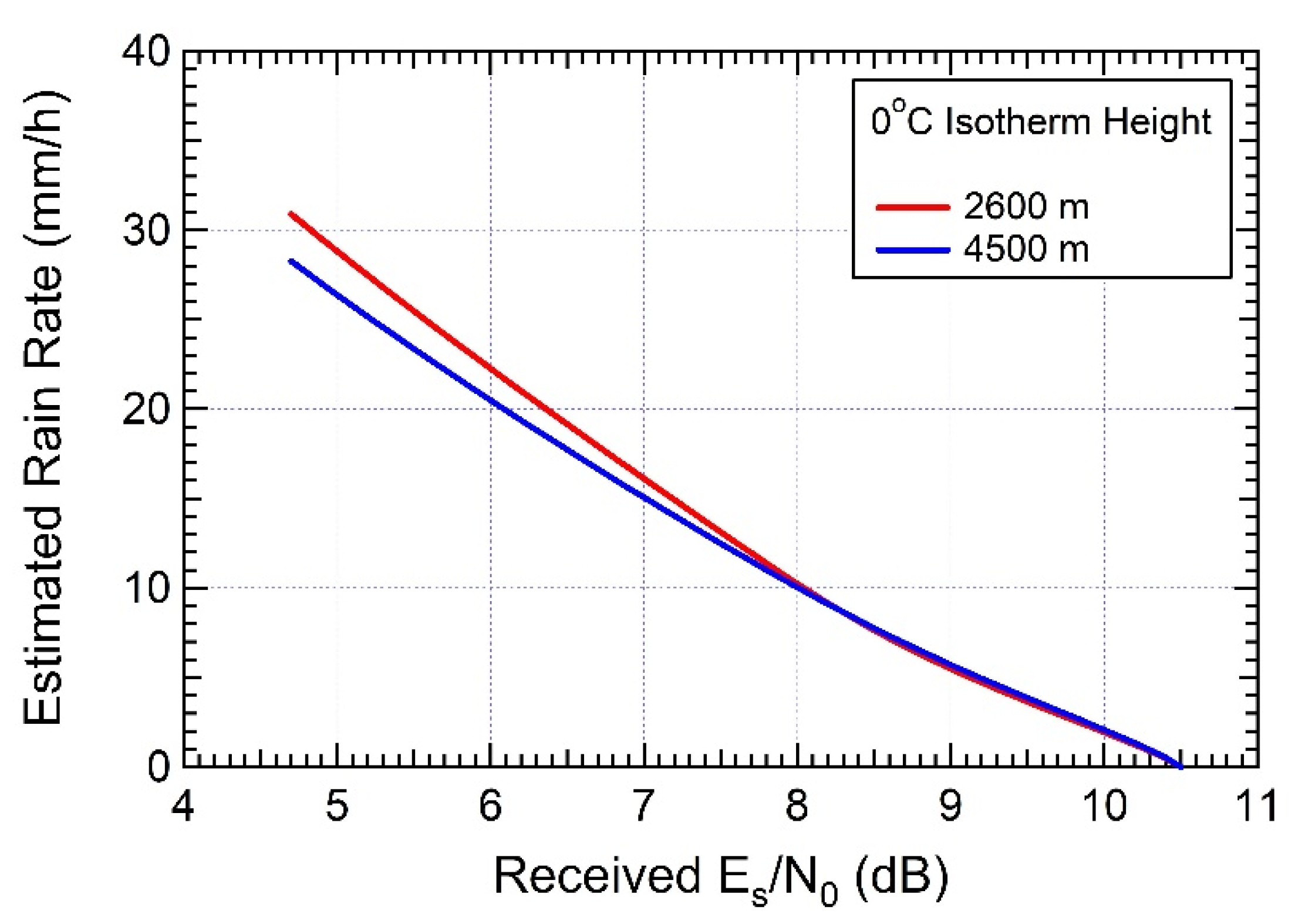
5.4.1. Rain Height vs. 0 °C isotherm Height
5.4.2. Impact of the Melting Layer
5.5. Sudden Variations of Signal Level Due to Causes Different from Rain
5.5.1. Sun Blinding
5.5.2. Operator Corrections
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Barthès, L.; Mallet, C. Rainfall measurement from the opportunistic use of an Earth–space link in the Ku band. Atmos. Meas. Tech. 2013, 6, 2181–2193. [Google Scholar] [CrossRef]
- Messer, H.; Sendik, O. A New Approach to Precipitation Monitoring: A critical survey of existing technologies and challenges. IEEE Signal. Process. Mag. 2015, 32, 110–122. [Google Scholar] [CrossRef]
- Giannetti, F.; Reggiannini, R.; Moretti, M.; Adirosi, E.; Baldini, L.; Facheris, L.; Antonini, A.; Melani, S.; Bacci, G.; Petrolino, A.; et al. Real-Time Rain Rate Evaluation via Satellite Downlink Signal Attenuation Measurement. Sensors 2017, 17, 1864. [Google Scholar] [CrossRef]
- Arslan, C.H.; Aydin, K.; Urbina, J.; Dyrud, L. Satellite-Link Attenuation Measurement Technique for Estimating Rainfall Accumulation. IEEE Trans. Geosci. Remote Sens. 2017, 56, 681–693. [Google Scholar] [CrossRef]
- Gharanjik, A.; Shankar, M.R.B.; Zimmer, F.; Ottersten, B. Centralized Rainfall Estimation Using Carrier to Noise of Satellite Communication Links. IEEE J. Sel. Areas Commun. 2018, 36, 1065–1073. [Google Scholar] [CrossRef]
- Colli, M.; Cassola, F.; Martina, F.; Trovatore, E.; Delucchi, A.; Maggiolo, S.; Caviglia, D.D. Rainfall Fields Monitoring Based on Satellite Microwave Down-Links and Traditional Techniques in the City of Genoa. IEEE Trans. Geosci. Remote Sens. 2020, 58, 6266–6280. [Google Scholar] [CrossRef]
- Adirosi, E.; Antonini, A.; Bacci, G.; Caparrini, F.; Facheris, L.; Giannetti, F.; Mazza, A.; Moretti, M.; Petrolino, A.; Reggiannini, R.; et al. NEFOCAST Project for Real-Time Precipitation Estimation from Ku Satellite Links: Preliminary Results of the Validation Field Campaign. In Proceedings of the 2018 2nd URSI Atlantic Radio Science Meeting (AT-RASC), Gran Canaria, Spain, 28 May–1 June 2018; pp. 1–4. [Google Scholar]
- Giannetti, F.; Moretti, M.; Reggiannini, R.; Vaccaro, A. The NEFOCAST System for Detection and Estimation of Rainfall Fields by the Opportunistic Use of Broadcast Satellite Signals. IEEE Aerosp. Electron. Syst. Mag. 2019, 34, 16–27. [Google Scholar] [CrossRef]
- Christofilakis, V.; Tatsis, G.; Chronopoulos, S.K.; Sakkas, A.; Skrivanos, A.G.; Peppas, K.P.; Nistazakis, H.E.; Baldoumas, G.; Kostarakis, P. Earth-to-Earth Microwave Rain Attenuation Measurements: A Survey On the Recent Literature. Symmetry 2020, 12, 1440. [Google Scholar] [CrossRef]
- Zheng, S.; Han, C.; Huo, J.; Cai, W.; Zhang, Y.; Li, P.; Zhang, G.; Ji, B.; Zhou, J. Research on Rainfall Monitoring Based on E-Band Millimeter Wave Link in East China. Sensors 2021, 21, 1670. [Google Scholar] [CrossRef] [PubMed]
- Cherkassky, D.; Ostrometzky, J.; Messer, H. Precipitation Classification Using Measurements From Commercial Microwave Links. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2350–2356. [Google Scholar] [CrossRef]
- Giuli, D.; Toccafondi, A.; Gentili, G.B.; Freni, A. Tomographic reconstruction of rainfall fields through microwave attenuation measurements. J. Appl. Meteorol. 1991, 9, 1323–1340. [Google Scholar] [CrossRef]
- Mishra, K.V.; Bhavani Shankar, M.R.; Ottersten, B. Deep Rainrate Estimation from Highly Attenuated Downlink Signals of Ground-Based Communications Satellite Terminals. In Proceedings of the ICASSP 2020-2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP, Barcelona, Spain, 4–8 May 2020; pp. 9021–9025. [Google Scholar]
- Ramachandran, V.; Kumar, V. Rain attenuation measurement on Ku-band satellite TV downlink in small island countries. Electron. Lett. 2004, 40, 49–50. [Google Scholar] [CrossRef]
- Freeman, R.L. Radio System Design for Telecommunications, 3rd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2007. [Google Scholar]
- D’Amico, M.; Manzoni, A.; Solazzi, G.L. Use of Operational Microwave Link Measurements for the Tomographic Reconstruction of 2-D Maps of Accumulated Rainfall. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1827–1831. [Google Scholar] [CrossRef]
- Shen, X.; Huang, D.D.; Song, B.; Vincent, C.; Togneri, R. 3-D Tomographic Reconstruction of Rain Field Using Microwave Signals From LEO Satellites: Principle and Simulation Results. IEEE Trans. Geosci. Remote Sens. 2019, 57, 5434–5446. [Google Scholar] [CrossRef]
- Cakaj, S. Rain Attenuation Impact on Performance of Satellite Ground Stations for Low Earth Orbiting (LEO) Satellites in Europe. Int. J. Commun. Netw. Syst. Sci. 2009, 02, 480–485. [Google Scholar] [CrossRef][Green Version]
- The European Table of Frquency Allocations and Application in the Frequency Range 8.3 kHz to 3000 GHz, ERC Report 25. Available online: https://efis.cept.org/reports/ReportDownloader?reportid=1 (accessed on 28 August 2021).
- ETSI TR 103 263 V1.2.1 (2016-02). Available online: https://www.etsi.org/deliver/etsi_tr/103200_103299/103263/01.02.01_60/tr_103263v010201p.pdf (accessed on 28 August 2021).
- Recommendation ITU-R BO.1776-1 (01/2012): Maximum power flux-density for the broadcasting-satellite service in the band 21.4-22.0 GHz in Regions 1 and 3. Available online: https://www.itu.int/dms_pubrec/itu-r/rec/bo/R-REC-BO.1776-1-201201-I!!PDF-E.pdf (accessed on 28 August 2021).
- Status of Telecommunication in W-band and Possible Applications: Satellite Broadband Connection and Networks of Mobile Phones. Available online: http://www.ares-consortium.org/It/wp-content/uploads/2016/03/2_Presentation_TOR.pdf (accessed on 3 June 2021).
- Paulson, K.; Al-Mreri, A. A rain height model to predict fading due to wet snow on terrestrial links. Radio Sci. 2011, 46, 4010. [Google Scholar] [CrossRef]
- Digital Video Broadcasting (DVB); Second Generation Framing Structure, Channel Coding and Modulation Systems for Broad-Casting, Interactive Services, News Gathering and Other Broadband Satellite Applications (DVB-S2), ETSI EN 302 307 V1.2.1 (2009-08). Available online: https://www.etsi.org/deliver/etsi_en/302300_302399/302307/01.02.01_60/en_302307v010201p.pdf (accessed on 28 August 2021).
- Singh, M.S.J.; Hassan, S.I.S.; Ain, M.F.; Igarashi, K.; Tanaka, K.; Iida, M. Analysis of Tropospheric Scintillation Intensity on Earth to Space in Malaysia. Am. J. Appl. Sci. 2006, 3, 2029–2032. [Google Scholar] [CrossRef]
- Crane, R.K.; Blood, D.W. Handbook For The Estimation Of Microwave Propagation Effects–Link Calculation For Earth-Space Paths; NASA Goddard Space Flight Center: Greenbelt, MD, USA, 1979.
- Recommendation ITU-R P.840-5 (02/2012): Attenuation Due To Clouds And Fog. Available online: https://www.itu.int/dms_pubrec/itu-r/rec/p/R-REC-P.840-5-201202-S!!PDF-E.pdf (accessed on 28 August 2021).
- Recommendation ITU-R P.679-4, 2005: Propagation Data Required for the Design of Broadcasting-Satellite Systems. Available online: http://www.srrc.org.cn/spreadmodel/PDFile/R-REC-P.679-4-201507-I!!PDF-E.pdf (accessed on 28 August 2021).
- Fortescue, P.W.; Stark, W.J.P. Spacecraft Systems Engineering; Wiley: Chichester, UK, 2011. [Google Scholar]
- Maral, G.; Bousquet, M. Satellite Communication Systems, 5th ed.; Wiley: Hoboken, NJ, USA, 2002. [Google Scholar]
- Borissov, S.; Wu, Y.; Mortari, D. East–West GEO Satellite Station-Keeping with Degraded Thruster Response. Aerospace 2015, 2, 581–601. [Google Scholar] [CrossRef]
- Matrosov, S. Assessment of Radar Signal Attenuation Caused by the Melting Hydrometeor Layer. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1039–1047. [Google Scholar] [CrossRef]
- Matrosov, S.Y.; Clark, K.A.; Kingsmill, D. A Polarimetric Radar Approach to Identify Rain, Melting-Layer, and Snow Regions for Applying Corrections to Vertical Profiles of Reflectivity. J. Appl. Meteorol. Clim. 2007, 46, 154–166. [Google Scholar] [CrossRef]
- Dissanayake, A.W.; McEwan, N.J. Radar and attenuation properties of rain and bright band. In Proceedings of the International Conference on Antennas and Propagation, London, UK, 28–30 November; pp. 125–129.
- Olsen, R.L.; Rogers, D.V.; Hodge, D.B. The aRbrelation in the calculation of rain attenuation. IRE Trans. Antennas Propag. 1978, 26, 318–329. [Google Scholar] [CrossRef]
- Recommendation ITU-R P.838-3, 2005: Specific Attenuation Model for Rain For Use in Prediction Methods. Available online: https://www.itu.int/dms_pubrec/itu-r/rec/p/R-REC-P.838-3-200503-I!!PDF-E.pdf (accessed on 28 August 2021).
- Adirosi, E.; Baldini, L.; Roberto, N.; Vulpiani, G.; Russo, F. Using disdrometer measured raindrop size distributions to establish weather radar algorithms. AIP Conf. Proc. 2015, 1648, 190007. [Google Scholar]
- Adirosi, E.; Baldini, L.; Lombardo, F.; Russo, F.; Napolitano, F.; Volpi, E.; Tokay, A. Comparison of different fittings of drop spectra for rainfall retrievals. Adv. Water Resour. 2015, 83, 55–67. [Google Scholar] [CrossRef]
- Arslan, C.H.; Aydin, K.; Urbina, J.; Dyrud, L.P. Rainfall measurements using satellite downlink attenuation. In Proceedings of the 2014 IEEE Geoscience and Remote Sensing Symposium, Quebec City, QC, Canada, 13–18 July 2014; pp. 4111–4114. [Google Scholar] [CrossRef]
- Xian, M.; Liu, X.; Gao, T. An Improvement to Precipitation Inversion Model Using Oblique Earth-Space Link Based on the Melting Layer Attenuation. IEEE Trans. Geosci. Remote Sens. 2021, 59, 6451–6465. [Google Scholar] [CrossRef]
- Available online: https://www.rec.ac.in/upload/SCS_M1_ECE-compressed.pdf (accessed on 25 May 2021).
- Essential Characteristics for a Eutelsat W Earthstation Having the Minimum Required Performance for Eurovision; EBU Tech 3288; European Broadcasting Union: Geneva, Switzerland, April 1999.
- Available online: https://www.satsig.net/eut2beac.htm (accessed on 25 May 2021).
- Available online: http://frequencyplansatellites.altervista.org/Eutelsat/Eutelsat_10A.pdf (accessed on 25 May 2021).
- Available online: http://frequencyplansatellites.altervista.org/Beacon-Telemetry_Europe-Africa-MiddleEast/Eutelsat_10A.html (accessed on 25 May 2021).
- Amaya, C.; Nguyen, T. Propagation measurements in Ottawa with the Ka-band beacon of the ANIK F2 satellite. In Proceedings of the 2010 14th International Symposium on Antenna Technology and Applied Electromagnetics & the American Electromagnetics Conference, Ottawa, ON, Canada, 5–8 July 2010; pp. 1–4. [Google Scholar] [CrossRef]
- Kikkert, C.J. The design of a Ka band satellite beacon receiver. In Proceedings of the 2007 6th International Conference on Information, Communications & Signal. Processing, Singapore, 10–13 December 2007. [Google Scholar] [CrossRef]
- Kobeissi, A.; Bellotti, F.; Berta, R.; De Gloria, A. Raspberry Pi 3 Performance Characterization in an Artificial Vision Automotive Application. In Lecture Notes in Electrical Engineering; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 2019; pp. 1–8. [Google Scholar]
- Colli, M.; Stagnaro, M.; Caridi, A.; Lanza, L.G.; Randazzo, A.; Pastorino, M.; Caviglia, D.D.; Delucchi, A. A Field Assessment of a Rain Estimation System Based on Satellite-to-Earth Microwave Links. IEEE Trans. Geosci. Remote Sens. 2019, 57, 2864–2875. [Google Scholar] [CrossRef]
- Giro, R.A.; Luini, L.; Riva, C.G. Rainfall Estimation from Tropospheric Attenuation Affecting Satellite Links. Information 2019, 11, 11. [Google Scholar] [CrossRef]
- Bahri, R.; Yarmohammadi, H.; Keshavarzi, M.; Moradi, G. Typical Ka band satellite beacon receiver design for propagation experimentation. In Proceedings of the 7’th International Symposium on Telecommunications (IST’2014), Tehran, Iran, 9–11 September; pp. 145–149.
- Recommendation ITU-R P.839-4: Rain Height Model for Prediction Methods. 2013. Available online: https://www.itu.int/dms_pubrec/itu-r/rec/p/R-REC-P.839-4-201309-I!!PDF-E.pdf (accessed on 28 August 2021).
- Bryant, G.H.; Adimula, I.; Riva, C.; Brussaard, G. Rain attenuation statistics from rain cell diameters and heights. Int. J. Satell. Commun. 2001, 19, 263–283. [Google Scholar] [CrossRef]
- Csurgai-Horvath, L.; Bito, J. Rain Intensity Estimation Using Satellite Beacon Signal Measurements A Dual Frequency Study. In Proceedings of the 2018 International Symposium on Networks, Computers and Communications (ISNCC), Rome, Italy, 19–21 June 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Csurgai-Horváth, L. Small Scale Rain Field Sensing and Tomographic Reconstruction with Passive Geostationary Satellite Receivers. Remote Sens. 2020, 12, 4161. [Google Scholar] [CrossRef]
- Mercier, F.; Barthes, L.; Mallet, C. Estimation of Finescale Rainfall Fields Using Broadcast TV Satellite Links and a 4DVAR Assimilation Method. J. Atmos. Ocean. Technol. 2015, 32, 1709–1728. [Google Scholar] [CrossRef]
- Arcidiacono, A.; Finocchiaro, D.; Collard, F.; Scalise, S.; Blasco, F.L.; De Gaudenzi, R.; Cioni, S.; Alagha, N.; Andrenacci, M. From S-band mobile interactive multimedia to fixed satellite interactive multimedia: Making satellite interactivity affordable at Ku-band and Ka-band. Int. J. Satell. Commun. Netw. 2016, 34, 575–601. [Google Scholar] [CrossRef]
- Collard, F.; Recchia, A.; Antip, N.; Arcidiacono, A.; Finocchiaro, D.; Pulvirenti, O. Performance Analysis of an Enhanced Spread Spectrum Aloha System. In Lecture Notes of the Institute for Computer Sciences, Social Informatics and Telecommunications Engineering; Springer: Berlin/Heidelberg, Germany, 2013; pp. 26–34. [Google Scholar]
- Recommendation ITU-R PN.837-1 (08/1994): Characteristics of Precipitation for Propagation Modelling. Available online: https://www.itu.int/dms_pubrec/itu-r/rec/p/R-REC-P.837-1-199408-S!!PDF-E.pdf (accessed on 28 August 2021).
- Lolli, S.; D’Adderio, L.P.; Campbell, J.R.; Sicard, M.; Welton, E.J.; Binci, A.; Rea, A.; Tokay, A.; Comerón, A.; Barragan, R.; et al. Vertically Resolved Precipitation Intensity Retrieved through a Synergy between the Ground-Based NASA MPLNET Lidar Network Measurements, Surface Disdrometer Datasets and an Analytical Model Solution. Remote Sens. 2018, 10, 1102. [Google Scholar] [CrossRef]
- Ojo, J.S. Rain Height Statistics Based on 0 °C Isotherm Height Using TRMM Precipitation Data for Earth-Space Satellite Links in Nigeria. ISRN Atmos. Sci. 2014, 2014, 1–5. [Google Scholar] [CrossRef]
- Mondal, N.C.; Sarkar, S.K. Rain height in relation to 0 °C isotherm height for satellite communication over the Indian Subcontinent. Theor. Appl. Clim. 2003, 76, 89–104. [Google Scholar] [CrossRef]
- Mandeep, J. 0 °C isotherm height for satellite communication in Malaysia. Adv. Space Res. 2009, 43, 984–989. [Google Scholar] [CrossRef]
- Badron, K.; Ismail, A.F.; Din, J.; Tharek, A. Rain induced attenuation studies for V-band satellite communication in tropical region. J. Atmos. Solar Terr. Phys. 2011, 73, 601–610. [Google Scholar] [CrossRef]
- Sudarshana, K.P.S.; Samarasinghe, A.T.L.K. Rain rate and rain attenuation estimation for Ku band satellite communications over Sri Lanka. In Proceedings of the 2011 6th International Conference on Industrial and Information Systems, Kandy, Sri Lanka, 16–19 August 2011; pp. 1–6. [Google Scholar]
- Emiliani, L.; Agudelo, J.C.; Gutierrez, E.; Restrepo, J.; Fradique-Mendez, C. Development of rain-attenuation and rain-rate maps for satellite system design in the Ku and Ka bands in Colombia. IEEE Antennas Propag. Mag. 2004, 46, 54–68. [Google Scholar] [CrossRef]
- Tijani, A.; Yusuf, S.D.; Ibrahim, U.; Loko, A.Z.; Mundi, A.A. Evaluation of real time rain-rate on downlink satellite signal at-tenuation in Abuja, Nigeria. EDUCATUM J. Sci. Math. Technol. 2020, 1, 29–38. [Google Scholar] [CrossRef]
- Rienecker, M.M.; Suarez, M.J.; Gelaro, R.; Todling, R.; Bacmeister, J.; Liu, E.; Bosilovich, M.G.; Schubert, S.D.; Takacs, L.; Kim, G.-K.; et al. MERRA: NASA’s Modern-era retrospective analysis for research and applications. J. Clim. 2011, 24, 3624–3648. [Google Scholar] [CrossRef]
- Mugnai, C.; Sermi, F.; Cuccoli, F.; Facheris, L. Rainfall estimation with a commercial tool for satellite internet in KA band: Model evolution and results. In Proceedings of the2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 890–893. [Google Scholar] [CrossRef]
- Baldini, L.; Gorgucci, E. Identification of the Melting Layer through Dual-Polarization Radar Measurements at Vertical Incidence. J. Atmos. Ocean. Technol. 2006, 23, 829–839. [Google Scholar] [CrossRef]
- Saggese, F.; Giannetti, F.; Lottici, V. A Novel Approach to Rainfall Rate Estimation based on Fusing Measurements from Terrestrial Microwave and Satellite Links. In Proceedings of the 2020 XXXIIIrd General Assembly and Scientific Symposium of the International Union of Radio Science, Rome, Italy, 29 August–5 September 2020; pp. 1–4. [Google Scholar]


| Band | Frequency (GHz) | Service | Direction | Ref. |
|---|---|---|---|---|
| Ku | 10.70–12.75 | Space-to-Earth, Fixed-Satellite: Broadcasting-satellite service | downlink | [19] |
| Ka | 17.30–20.20 | Space-to-Earth, Fixed-Satellite: Broadband satellite service | downlink | [20] |
| Ka | 21.40–22.00 | Space-to-Earth, Fixed-Satellite: Broadcasting-satellite service | downlink | [21] |
| Q/V | 37.50–43.50 | Space-to-Earth, Fixed-Satellite: Broadband satellite service | downlink | [22] |
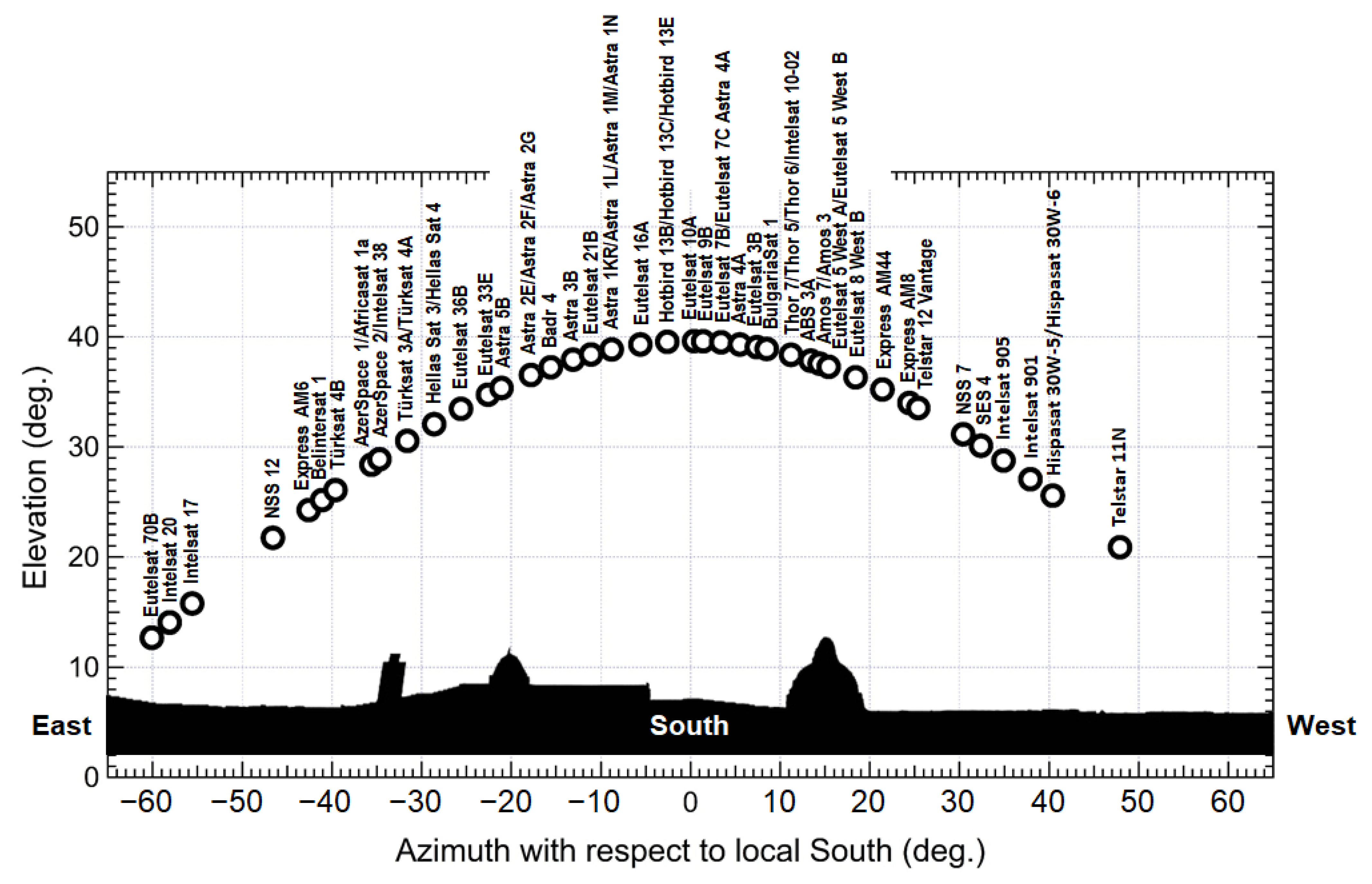
| Geostationary Satellite | Long (°) | Azimuth w.r.t. Local South (°) | Elevation above Horizon (°) | Beam | EIRP (dBW) | Reference |
|---|---|---|---|---|---|---|
| Eutelsat 70B | 70.5 | −60.0853 | 12.6724 | Wide | 44 | LyngSat. Available online: https://www.lyngsat.com (accessed on 28 August 2021). |
| Intelsat 20 | 68.5 | −58.0853 | 14.0569 | Europe and Africa | 44.8 | LyngSat. Available online: https://www.lyngsat.com (accessed on 28 August 2021). |
| Intelsat 17 | 66.0 | −55.5853 | 15.7709 | Europe and Mid-East | 47.6 | Digisat. Available online: https://www.digisat.org (accessed on 28 August 2021). |
| NSS 12 | 57.0 | −46.5853 | 21.7379 | Middle East | 46 | LyngSat. Available online: https://www.lyngsat.com (accessed on 28 August 2021). |
| Express AM6 | 53.0 | −42.5853 | 24.2543 | Fixed 2 | 47 | LyngSat. Available online: https://www.lyngsat.com (accessed on 28 August 2021). |
| Belintersat 1 | 51.5 | −41.0853 | 25.1708 | Europe | 51 | Belintersat. Available online: https://belintersat.com (accessed on 28 August 2021). |
| Türksat 4B | 50.0 | −39.5853 | 26.0710 | West | 54 | SatStar. Available online: http://www.satstar.net (accessed on 28 August 2021). |
| AzerSpace 1/Africasat 1a | 46.0 | −35.5853 | 28.3825 | Europe | 46 | SatStar. Available online: http://www.satstar.net (accessed on 28 August 2021). |
| AzerSpace 2/Intelsat 38 | 45.1 | −34.6853 | 28.8831 | Europe | 51.6 | LyngSat. Available online: https://www.lyngsat.com (accessed on 28 August 2021). |
| Türksat 3A/Türksat 4A | 42.0 | −31.5853 | 30.5469 | West | 52 | LyngSat. Available online: https://www.lyngsat.com (accessed on 28 August 2021). |
| Hellas Sat 3/Hellas Sat 4 | 39.0 | −28.5853 | 32.0591 | Europe FSS | 52 | SatStar. Available online: http://www.satstar.net (accessed on 28 August 2021). |
| Eutelsat 36B | 36.0 | −25.5853 | 33.4642 | Eurasia | 48 | LyngSat. Available online: https://www.lyngsat.com (accessed on 28 August 2021). |
| Eutelsat 33E | 33.0 | −22.5853 | 34.7513 | Wide | 50 | SatStar. Available online: http://www.satstar.net (accessed on 28 August 2021). |
| Astra 5B | 31.5 | −21.0853 | 35.3471 | High power | 52 | LyngSat. Available online: https://www.lyngsat.com (accessed on 28 August 2021). |
| Astra 2E/Astra 2F/Astra 2G | 28.2 | −17.7853 | 36.5375 | Europe | 50 | LyngSat. Available online: https://www.lyngsat.com (accessed on 28 August 2021). |
| Badr 4 | 26.0 | −15.5853 | 37.2336 | BSS | 47 | Arabsat. Available online: https://www.arabsat.com (accessed on 28 August 2021). |
| Astra 3B | 23.5 | −13.0853 | 37.9242 | Europe | 51 | LyngSat. Available online: https://www.lyngsat.com (accessed on 28 August 2021). |
| Eutelsat 21B | 21.5 | −11.0853 | 38.3962 | Western | 46 | LyngSat. Available online: https://www.lyngsat.com (accessed on 28 August 2021). |
| Astra 1KR/Astra 1L/Astra 1M/Astra 1N | 19.2 | −8.7853 | 38.8473 | Europe | 51 | LyngSat. Available online: https://www.lyngsat.com (accessed on 28 August 2021). |
| Eutelsat 16A | 16.0 | −5.5853 | 39.3062 | Europe B | 50 | LyngSat. Available online: https://www.lyngsat.com (accessed on 28 August 2021). |
| Hotbird 13B/Hotbird 13C/Hotbird 13E | 13.0 | −2.5853 | 39.5528 | Wide | 53 | LyngSat. Available online: https://www.lyngsat.com (accessed on 28 August 2021). |
| Eutelsat 10A | 10.0 | 0.4147 | 39.6185 | Wide | 48 | LyngSat. Available online: https://www.lyngsat.com (accessed on 28 August 2021). |
| Eutelsat 9B | 9.0 | 1.4147 | 39.6000 | Wide | 51 | LyngSat. Available online: https://www.lyngsat.com (accessed on 28 August 2021). |
| Eutelsat 7B/Eutelsat 7C | 7.0 | 3.4147 | 39.5026 | Europe A | 49 | Eutelsat. Available online: https://www.eutelsat.com (accessed on 28 August 2021). |
| Astra 4A | 4.9 | 5.5147 | 39.3140 | Europe BSS | 50 | LyngSat. Available online: https://www.lyngsat.com (accessed on 28 August 2021). |
| Eutelsat 3B | 3.0 | 7.4147 | 39.0683 | Europe | 49 | LyngSat. Available online: https://www.lyngsat.com (accessed on 28 August 2021). |
| BulgariaSat 1 | 1.9 | 8.5147 | 38.8938 | Europe | 50 | LyngSat. Available online: https://www.lyngsat.com (accessed on 28 August 2021). |
| Thor 7/Thor 5/Thor 6/Intelsat 10-02 | −0.8 | 11.2147 | 38.3679 | Spot 1 | 53.2 | LyngSat. Available online: https://www.lyngsat.com (accessed on 28 August 2021). |
| ABS 3A | −3.0 | 13.4147 | 37.8395 | Europe | 50 | ABS. Available online: https://absatellite.com (accessed on 28 August 2021). |
| Amos 7/Amos 3 | −4.0 | 14.4147 | 37.5706 | Pan European | 53 | Spacecom. Available online: https://www.amos-spacecom.com (accessed on 28 August 2021). |
| Eutelsat 5 West A (incl. 1.3°)/Eutelsat 5 West B | −5.0 | 15.4147 | 37.2842 | Super | 53 | LyngSat. Available online: https://www.lyngsat.com (accessed on 28 August 2021). |
| Eutelsat 8 West B | −8.0 | 18.4147 | 36.3237 | Europe | 54 | SatStar. Available online: http://www.satstar.net (accessed on 28 August 2021). |
| Express AM44 | −11.0 | 21.4147 | 35.2191 | S1 | 51 | LyngSat. Available online: https://www.lyngsat.com (accessed on 28 August 2021). |
| Express AM8 | −14.0 | 24.4147 | 33.9811 | Fixed 1 | 51 | LyngSat. Available online: https://www.lyngsat.com (accessed on 28 August 2021). |
| Telstar 12 Vantage | −15.0 | 25.4147 | 33.5407 | Europe and Middle East | 51 | SatStar. Available online: http://www.satstar.net (accessed on 28 August 2021). |
| NSS 7 (incl. 4.9°) | −20.0 | 30.4147 | 31.1490 | Europe and Middle East | 49 | SatStar. Available online: http://www.satstar.net (accessed on 28 August 2021). |
| SES 4 | −22.0 | 32.4147 | 30.1113 | Europe and Middle East | 49 | LyngSat. Available online: https://www.lyngsat.com (accessed on 28 August 2021). |
| Intelsat 905 (incl. 2.0°) | −24.5 | 34.9147 | 28.7563 | Spot 1 | 52.6 | LyngSat. Available online: https://www.lyngsat.com (accessed on 28 August 2021). |
| Intelsat 901 | −27.5 | 37.9147 | 27.0528 | Spot 2 | 45 | SatStar. Available online: http://www.satstar.net (accessed on 28 August 2021). |
| Hispasat 30W-5/Hispasat 30W-6 | −30.0 | 40.4147 | 25.5753 | Europe | 54 | LyngSat. Available online: https://www.lyngsat.com (accessed on 28 August 2021). |
| Telstar 11N | −37.5 | 47.9147 | 20.8807 | Europe | 52 | SatStar. Available online: http://www.satstar.net (accessed on 28 August 2021). |
| Receiving location | Pisa, Italy (10.4147° E, 43.7117° N) |
| Satellite name; orbital slot; inclination | Eutelsat 10A; 10° East; 0.072° |
| Satellite EIRP | 48 dBW |
| Frequency; polarization | 11.345 GHz; LVP |
| Protocol; modulation; FEC rate | DVB-S2; QPSK; 4/5 |
| Required ESNDR for QEF performance | 4.68 dB |
| Figure of noise of the receiver | 0.2 dB @ 290 K |
| Noise temperature of the receiver, | 13.7 K |
| Atmospheric attenuation, | 0.09 dB |
| Mean thermodynamic temperature of troposphere, | 275 K |
| Noise temperature of the CBMR, | 2.78 K |
| Noise spillover temperature, | 10 K |
| Receiving antenna diameter; gain (60% efficiency) | 80 cm; 37.34 dBi |
| Typical received ESNDR in clear-sky conditions | 10.5 dB |
| Link margin | 5.82 dB |
| 40° |
| (a) | |||
| a.1 | Beacon frequency | 20 GHz (Ka Band) | |
| a.2 | Beacon EIRP | 30 dBW | |
| a.3 | 17 Hz | ||
| a.4 | 210 dB | ||
| a.5 | 1.0 dB | ||
| a.6 | 275 K | ||
| a.7 | 2.78 K | ||
| a.8 | 10 K | ||
| a.9 | 100 K | ||
| a.10 | 40 dBi | ||
| (b) | |||
| Clear-sky, = 0 dB | |||
| b.1 | −111.00 dBm | Equation (1) | |
| b.2 | −164.35 dBm | Equations (2)–(4) | |
| b.3 | 53.35 dB | (b.1), (b.2) | |
| b.4 | −111.00 dBm | (b.1), (b.2) | |
| b.5 | 53.35 dB | (b.4), (b.2) | |
| Rain, = 44 dB | |||
| b.6 | −155.00 dBm | Equation (1) | |
| b.7 | −160.44 dBm | Equations (2)–(4) | |
| b.8 | 5.44 dB | (b.6), (b.7) | |
| b.9 | −153.91 dBm | (b.6), (b.7) | |
| b.10 | 6.53 dB | (b.9), (b.7) | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Giannetti, F.; Reggiannini, R. Opportunistic Rain Rate Estimation from Measurements of Satellite Downlink Attenuation: A Survey. Sensors 2021, 21, 5872. https://doi.org/10.3390/s21175872
Giannetti F, Reggiannini R. Opportunistic Rain Rate Estimation from Measurements of Satellite Downlink Attenuation: A Survey. Sensors. 2021; 21(17):5872. https://doi.org/10.3390/s21175872
Chicago/Turabian StyleGiannetti, Filippo, and Ruggero Reggiannini. 2021. "Opportunistic Rain Rate Estimation from Measurements of Satellite Downlink Attenuation: A Survey" Sensors 21, no. 17: 5872. https://doi.org/10.3390/s21175872
APA StyleGiannetti, F., & Reggiannini, R. (2021). Opportunistic Rain Rate Estimation from Measurements of Satellite Downlink Attenuation: A Survey. Sensors, 21(17), 5872. https://doi.org/10.3390/s21175872







