A Novel Approach to Global Positioning System Accuracy Assessment, Verified on LiDAR Alignment of One Million Kilometers at a Continent Scale, as a Foundation for Autonomous DRIVING Safety Analysis
Abstract
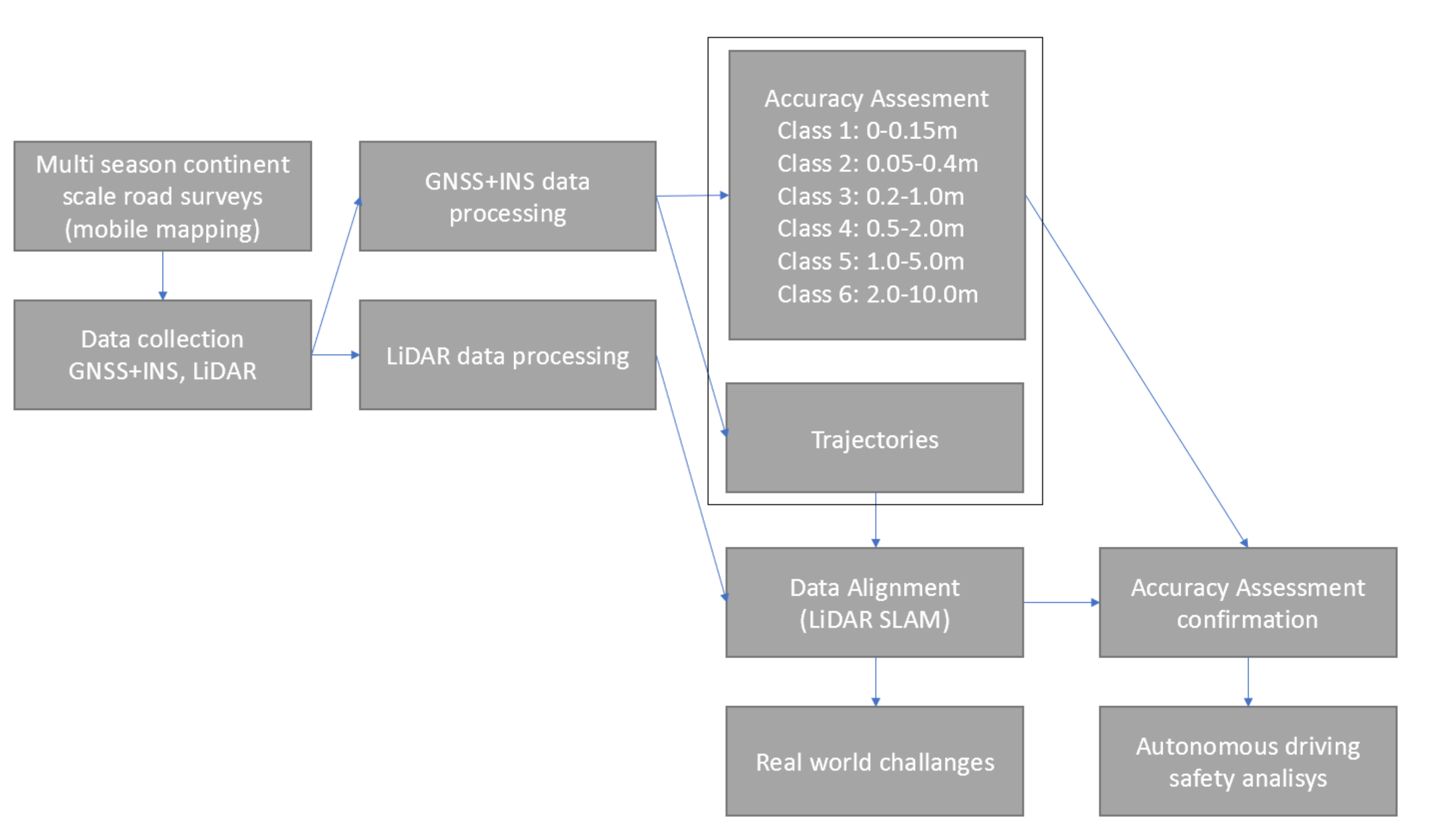
:1. Introduction
- Mobile mapping system minimal setup;
- Global positioning data processing;
- LiDAR data processing;
- Alignment algorithm;
- Accuracy assessment confirmation;
- Autonomous driving safety analysis.
2. State of the Art
2.1. Large-Scale Data Sets
2.2. Long-Term Data Sets
2.3. Large-Scale Surveying and Mapping
3. Experimental Verification of the Methodology
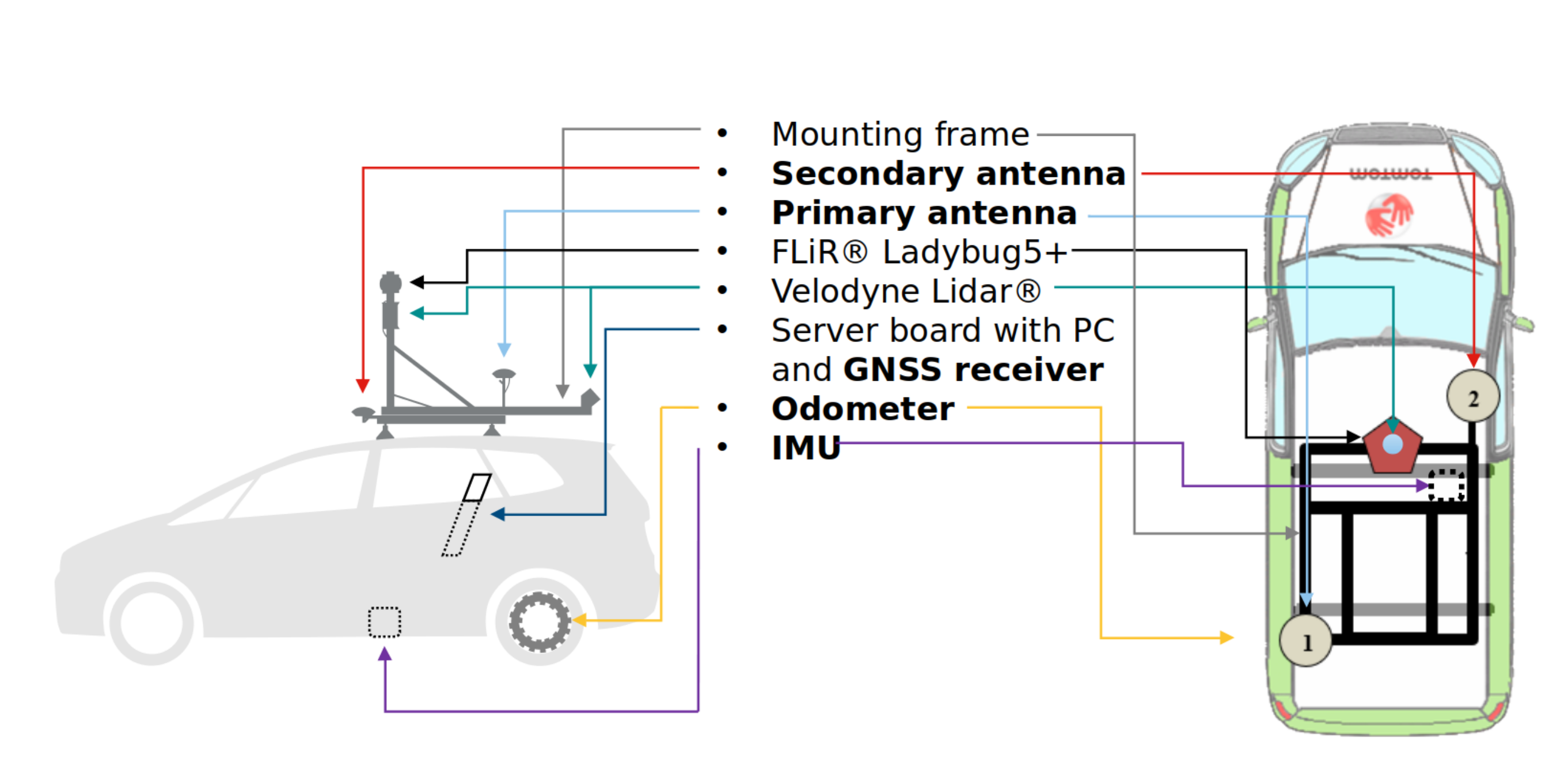
3.1. Mobile Mapping System Minimal Setup
3.2. GNSS + INS Data Processing
3.3. Lidar Data Processing
3.4. Alignment Algorithm
- Semantic point-to-point (Section 3.4.1).
- Semantic point-to-projection (Section 3.4.2).
- Motion model and GNSS + INS as relative poses constraints (Section 3.4.3).
3.4.1. Semantic Point-to-Point Observation Equation
3.4.2. Semantic Point-to-Projection Observation Equation
3.4.3. Relative Pose Observation Equation
3.5. GNSS + INS Accuracy Assessment
4. Real-World Challenges
5. Experimental Validation
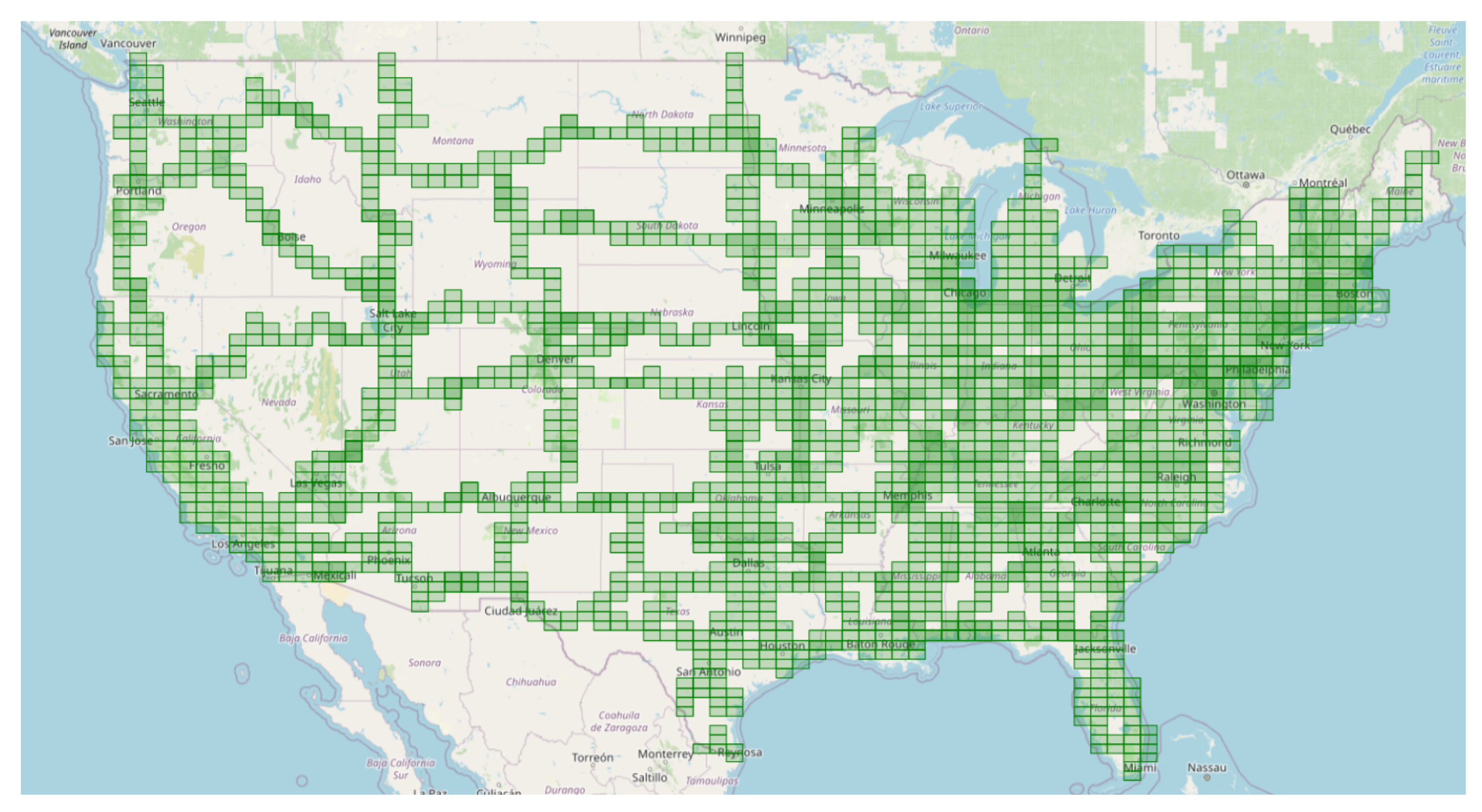
5.1. Scope of Data Set
5.2. Results
6. Impact of GNSS + INS Positioning on Safety
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| LiDAR | Light Detection and Ranging |
| GPS | Global Positioning System |
| GNSS + INS | Global Navigation Satellite System + Inertial Navigation System |
| SLAM | Simultaneous Localization and Mapping |
| RANSAC | Random Sample Consensus |
References
- Reid, T.G.; Houts, S.E.; Cammarata, R.; Mills, G.; Agarwal, S.; Vora, A.; Pandey, G. Localization Requirements for Autonomous Vehicles. SAE Int. J. Connect. Autom. Veh. 2019, 2, 173–190. [Google Scholar] [CrossRef] [Green Version]
- Im, J.H.; Im, S.H.; Jee, G.I. Extended Line Map-Based Precise Vehicle Localization Using 3D LIDAR. Sensors 2018, 18, 3179. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Badue, C.; Guidolini, R.; Carneiro, R.V.; Azevedo, P.; Cardoso, V.B.; Forechi, A.; Jesus, L.; Berriel, R.; Paixão, T.M.; Mutz, F.; et al. Self-driving cars: A survey. Expert Syst. Appl. 2021, 165, 113816. [Google Scholar] [CrossRef]
- Leonard, J.; Durrant-Whyte, H. Simultaneous map building and localization for an autonomous mobile robot. In Proceedings of the IROS ’91:IEEE/RSJ International Workshop on Intelligent Robots and Systems ’91, Osaka, Japan, 3–5 November 1991; Volume 3, pp. 1442–1447. [Google Scholar]
- Skrzypczyński, P. Simultaneous localization and mapping: A feature-based probabilistic approach. Int. J. Appl. Math. Comput. Sci. 2009, 19, 575–588. [Google Scholar] [CrossRef] [Green Version]
- Agarwal, P.; Burgard, W.; Stachniss, C. Survey of Geodetic Mapping Methods: Geodetic Approaches to Mapping and the Relationship to Graph-Based SLAM. Robot. Autom. Mag. IEEE 2014, 21, 63–80. [Google Scholar] [CrossRef]
- Bosse, M.; Zlot, R. Continuous 3D scan-matching with a spinning 2D laser. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 4312–4319. [Google Scholar]
- Nuchter, A.; Lingemann, K.; Hertzberg, J.; Surmann, H. 6D SLAM with approximate data association. In Proceedings of the 12th International Conference on Advanced Robotics, Seattle, WA, USA, 18–20 July 2005; pp. 242–249. [Google Scholar] [CrossRef] [Green Version]
- Silver, D.; Ferguson, D.; Morris, A.; Thayer, S. Topological exploration of subterranean environments. J. Field Robot. 2006, 23, 395–415. [Google Scholar] [CrossRef]
- Kaul, L.; Zlot, R.; Bosse, M. Continuous-Time Three-Dimensional Mapping for Micro Aerial Vehicles with a Passively Actuated Rotating Laser Scanner. J. Field Robot. 2016, 33, 103–132. [Google Scholar] [CrossRef]
- Zlot, R.; Bosse, M. Efficient Large-scale Three-dimensional Mobile Mapping for Underground Mines. J. Field Robot. 2014, 31, 758–779. [Google Scholar] [CrossRef]
- Du, S.; Lauterbach, H.A.; Li, X.; Demisse, G.G.; Borrmann, D.; Nuchter, A. Curvefusion—A Method for Combining Estimated Trajectories with Applications to SLAM and Time-Calibration. Sensors 2020, 20, 6918. [Google Scholar] [CrossRef] [PubMed]
- Bosse, M.; Zlot, R.; Flick, P. Zebedee: Design of a Spring-Mounted 3-D Range Sensor with Application to Mobile Mapping. IEEE Trans. Robot. 2012, 28, 1104–1119. [Google Scholar] [CrossRef]
- Rau, J.Y.; Su, B.W.; Hsiao, K.W.; Jhan, J.P. Systematic calibration for a backpacked spherical photogrammetry imaging system. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, XLI-B1, 695–702. [Google Scholar] [CrossRef] [Green Version]
- Toschi, I.; Rodríguez-Gonzálvez, P.; Remondino, F.; Minto, S.; Orlandini, S.; Fuller, A. Accuracy evaluation of a mobile mapping System with advanced statistical methods. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, XL-5/W4, 245–253. [Google Scholar] [CrossRef] [Green Version]
- Brede, B.; Lau, A.; Bartholomeus, H.M.; Kooistra, L. Comparing RIEGL RiCOPTER UAV LiDAR Derived Canopy Height and DBH with Terrestrial LiDAR. Sensors 2017, 17, 2371. [Google Scholar] [CrossRef]
- Reisdorf, P.; Pfeifer, T.; Breßler, J.; Bauer, S.; Weissig, P.; Lange, S.; Wanielik, G.; Protzel, P. The Problem of Comparable GNSS Results—An Approach for a Uniform Dataset with Low-Cost and Reference Data. In Proceedings of the Fifth International Conference on Advances in Vehicular Systems, Technologies and Applications, Barcelona, Spain, 13–17 November 2016; Ullmann, M., El-Khatib, K., Eds.; 2016; Volume 5, p. 8. [Google Scholar]
- Jeong, J.; Cho, Y.; Shin, Y.S.; Roh, H.; Kim, A. Complex urban dataset with multi-level sensors from highly diverse urban environments. Int. J. Robot. Res. 2019, 36, 0278364919843996. [Google Scholar] [CrossRef] [Green Version]
- Zhu, A.Z.; Thakur, D.; Özaslan, T.; Pfrommer, B.; Kumar, V.; Daniilidis, K. The Multi Vehicle Stereo Event Camera Dataset: An Event Camera Dataset for 3D Perception. CoRR 2018, 3, 2032–2039. [Google Scholar]
- Oettershagen, P.; Stastny, T.; Mantel, T.; Melzer, A.; Rudin, K.; Gohl, P.; Agamennoni, G.; Alexis, K.; Siegwart, R. Long-Endurance Sensing and Mapping using a Hand-Launchable Solar-Powered UAV. In Field and Service Robotics: Results of the 10th International Conference; Wettergreen, D.S., Barfoot, T.D., Eds.; Springer: Berlin, Germany, 2016; Volume 113, pp. 441–454. [Google Scholar] [CrossRef]
- Maddern, W.; Pascoe, G.; Linegar, C.; Newman, P. 1 Year, 1000 km: The Oxford RobotCar Dataset. Int. J. Robot. Res. 2017, 36, 3–15. [Google Scholar] [CrossRef]
- Maddern, W.; Pascoe, G.; Gadd, M.; Barnes, D.; Yeomans, B.; Newman, P. Real-time Kinematic Ground Truth for the Oxford RobotCar Dataset. arXiv 2020, arXiv:2002.10152. [Google Scholar]
- Blanco, J.L.; Moreno, F.A.; Gonzalez-Jimenez, J. The Málaga Urban Dataset: High-rate Stereo and Lidars in a realistic urban scenario. Int. J. Robot. Res. 2014, 33, 207–214. [Google Scholar] [CrossRef] [Green Version]
- Geiger, A.; Lenz, P.; Urtasun, R. Are we ready for Autonomous Driving? The KITTI Vision Benchmark Suite. In Proceedings of the Conference on Computer Vision and Pattern Recognition (CVPR), Providence, RI, USA, 16–21 June 2012. [Google Scholar]
- Choi, Y.; Kim, N.; Hwang, S.; Park, K.; Yoon, J.S.; An, K.; Kweon, I.S. KAIST Multi-Spectral Day/Night Data Set for Autonomous and Assisted Driving. IEEE Trans. Intell. Transp. Syst. 2018, 19, 934–948. [Google Scholar] [CrossRef]
- Miller, M.; Chung, S.J.; Hutchinson, S. The Visual–Inertial Canoe Dataset. Int. J. Robot. Res. 2018, 37, 13–20. [Google Scholar] [CrossRef]
- Carlevaris-Bianco, N.; Ushani, A.K.; Eustice, R.M. University of Michigan North Campus long-term vision and lidar dataset. Int. J. Robot. Res. 2015, 35, 1023–1035. [Google Scholar] [CrossRef]
- Kesten, R.; Usman, M.; Houston, J.; Pandya, T.; Nadhamuni, K.; Ferreira, A.; Yuan, M.; Low, B.; Jain, A.; Ondruska, P.; et al. Lyft Level 5 Perception Dataset 2020. 2019. Available online: https://level5.lyft.com/dataset/ (accessed on 15 August 2021).
- Hotine, M. Geodetic Coordinate Systems. In Differential Geodesy; Zund, J., Ed.; Springer: Berlin/Heidelberg, Germany, 1991; pp. 65–89. [Google Scholar]
- Gerdan, G.P.; Deakin, R.E. Transforming Cartesian Coordinates X, Y, Z to Geographical Coordinates φ, λ, h. Aust. Surv. 1999, 44, 55–63. [Google Scholar] [CrossRef]
- Pujol, J. Hamilton, Rodrigues, Gauss, Quaternions, and Rotations: A Historical Reassessment. Commun. Math. Anal. 2012, 13, 1–14. [Google Scholar]
- Grassia, F.S. Practical Parameterization of Rotations Using the Exponential Map. J. Graph. Tools 1998, 3, 29–48. [Google Scholar] [CrossRef]
- Joldeş, M.; Muller, J.M. Algorithms for manipulating quaternions in floating-point arithmetic. In Proceedings of the ARITH-2020—IEEE 27th Symposium on Computer Arithmetic, Portland, OR, USA, 7–10 June 2020; pp. 1–8. [Google Scholar] [CrossRef]
- Dai, J.S. Euler–Rodrigues formula variations, quaternion conjugation and intrinsic connections. Mech. Mach. Theory 2015, 92, 144–152. [Google Scholar] [CrossRef]
- Liang, K.K. Efficient conversion from rotating matrix to rotation axis and angle by extending Rodrigues’ formula. arXiv 2018, arXiv:cs.CG/1810.02999. [Google Scholar]
- Terzakis, G.; Lourakis, M.; Ait-Boudaoud, D. Modified Rodrigues Parameters: An Efficient Representation of Orientation in 3D Vision and Graphics. J. Math. Imaging Vis. 2018, 60, 422–442. [Google Scholar] [CrossRef] [Green Version]
- Özkaldı, S.; Gündoğan, H. Cayley Formula, Euler Parameters and Rotations in 3-Dimensional Lorentzian Space. Adv. Appl. Clifford Algebr. 2010, 20, 367–377. [Google Scholar] [CrossRef]
- Diebel, J. Representing attitude: Euler angles, unit quaternions, and rotation vectors. Matrix 2006, 58, 1–35. [Google Scholar]
- Blanco, J.L. A Tutorial on SE(3) Transformation Parameterizations and On-Manifold Optimization; Technical Report; University of Malaga: Malaga, Spain, 2010. [Google Scholar]
- Gao, X.; Zhang, T.; Liu, Y.; Yan, Q. 14 Lectures on Visual SLAM: From Theory to Practice; Technical Report; Publishing House of Electronics Industry: Beijing, China, 2017. [Google Scholar]
- Gallego, G.; Yezzi, A. A Compact Formula for the Derivative of a 3-D Rotation in Exponential Coordinates. J. Math. Imaging Vis. 2014, 51, 378–384. [Google Scholar] [CrossRef] [Green Version]
- Solà, J.; Deray, J.; Atchuthan, D. A micro Lie theory for state estimation in robotics. arXiv 2020, arXiv:cs.RO/1812.01537. [Google Scholar]
- NovAtel. 2021. Available online: https://novatel.com/products/waypoint-post-processing-software (accessed on 15 August 2021).
- NovAtel. 2021. Available online: https://novatel.com/an-introduction-to-gnss/chapter-5-resolving-errors/gnss-data-post-processing (accessed on 15 August 2021).
- Fischler, M.A.; Bolles, R.C. Random Sample Consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Rusu, R.B.; Cousins, S. 3D is here: Point Cloud Library (PCL). In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Shanghai, China, 9–13 May 2011. [Google Scholar]
- Crook, P.A.; Hayes, G. Learning in a State of Confusion: Perceptual Aliasing in Grid World Navigation. In Proceedings of the Towards Intelligent Mobile Robots 2003 (Timr 2003), 4th British Conference on (Mobile) Robotics, Bristol, UK, 28–29 August 2003. [Google Scholar]
- Thomas, H.; Deschaud, J.; Marcotegui, B.; Goulette, F.; Gall, Y.L. Semantic Classification of 3D Point Clouds with Multiscale Spherical Neighborhoods. In Proceedings of the 2018 International Conference on 3D Vision, Verona, Italy, 5–8 September 2018. [Google Scholar]
- Hackel, T.; Wegner, J.D.; Schindler, K. Contour Detection in Unstructured 3D Point Clouds. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 1610–1618. [Google Scholar] [CrossRef]
- Bedkowski, J. GPU Computing in Robotics. 2021. Available online: https://github.com/JanuszBedkowski/gpu_computing_in_robotics (accessed on 15 August 2021).
- Kraus, K.; Harley, I.A.; Kyle, S. Photogrammetry: Geometry from Images and Laser Scans; De Gruyter: Berlin, Germany; Boston, MA, USA, 2011. [Google Scholar] [CrossRef]
- Gruen, A.; Akca, D. Least squares 3D surface and curve matching. ISPRS J. Photogramm. Remote Sens. 2005, 59, 151–174. [Google Scholar] [CrossRef] [Green Version]
- Mikhail, E.M.; Ackermann, F.E. Observations and least squares. In Observations and Least Squares; University Press of America: Washington, DC, USA, 1982. [Google Scholar]
- Aitken, A. On Least Squares and Linear Combination of Observations. Proc. R. Soc. Edinb. 1934, 55, 42–48. [Google Scholar] [CrossRef]
- Higham, N. Cholesky factorization. Wiley Interdiscip. Rev. Comput. Stat. 2009, 1, 251–254. [Google Scholar] [CrossRef]
- Besl, P.J.; McKay, N.D. A method for registration of 3-D shapes. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 239–256. [Google Scholar] [CrossRef]
- Ranade, S.; Yu, X.; Kakkar, S.; Miraldo, P.; Ramalingam, S. Can generalised relative pose estimation solve sparse 3D registration? arXiv 2019, arXiv:cs.CV/1906.05888. [Google Scholar]
- Zhang, J.; Singh, S. LOAM: Lidar Odometry and Mapping in Real-time. In Proceedings of the Robotics: Science and Systems Conference, University of California, Berkeley, CA, USA, 12–14 July 2014. [Google Scholar]
- Shan, T.; Englot, B. LeGO-LOAM: Lightweight and Ground-Optimized Lidar Odometry and Mapping on Variable Terrain. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 4758–4765. [Google Scholar] [CrossRef]
- Kümmerle, R.; Grisetti, G.; Strasdat, H.; Konolige, K.; Burgard, W. G2o: A general framework for graph optimization. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 3607–3613. [Google Scholar] [CrossRef]
- Sturm, J.; Engelhard, N.; Endres, F.; Burgard, W.; Cremers, D. A benchmark for the evaluation of RGB-D SLAM systems. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura-Algarve, Portugal, 7–12 October 2012; pp. 573–580. [Google Scholar] [CrossRef] [Green Version]
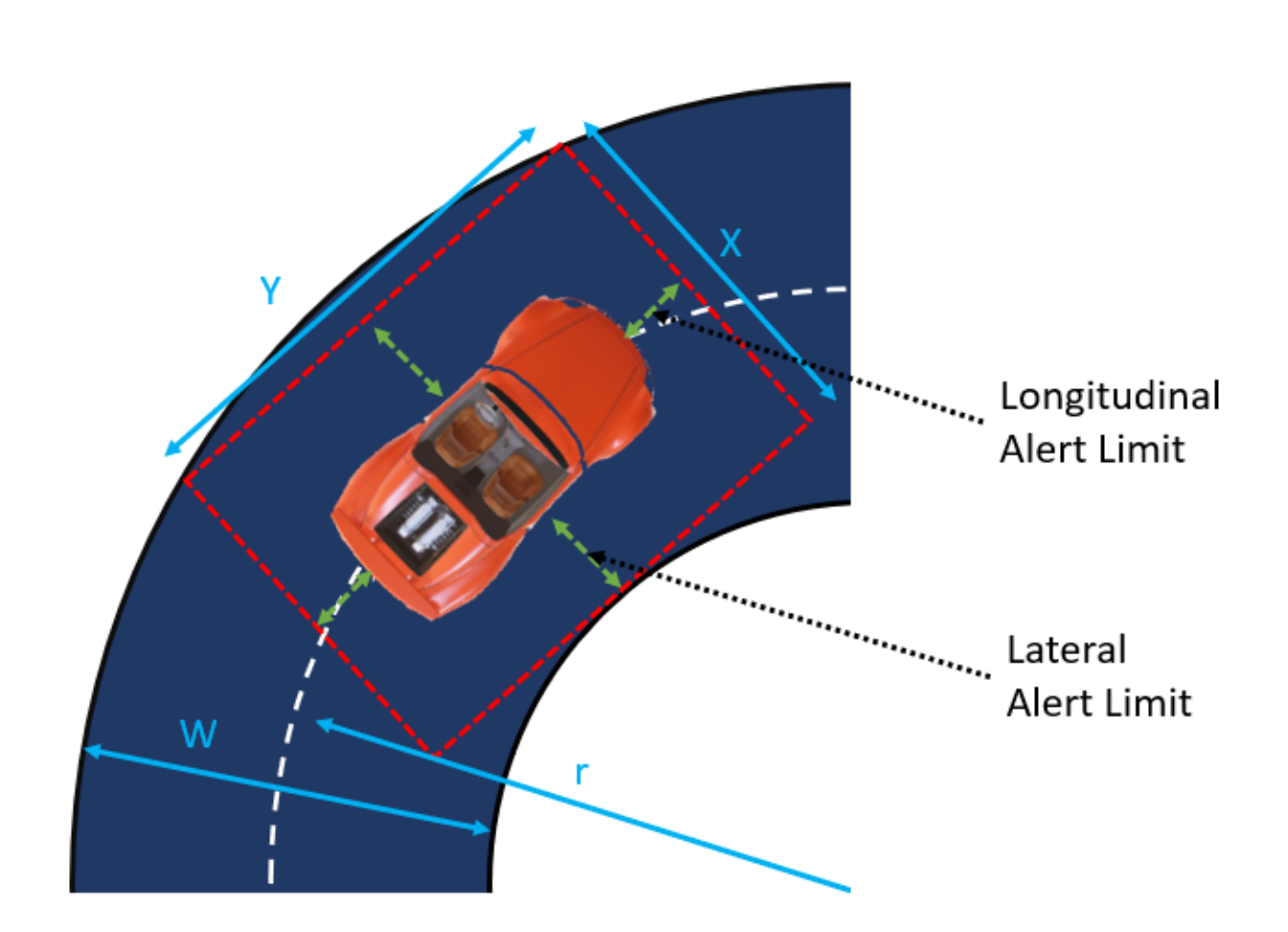










| Vehicle Type | Lateral Alert Limit [m] | Longitudinal Alert Limit [m] |
|---|---|---|
| Mid-Size | 0.72 | 1.40 |
| 6-Wheel Pickup | 0.40 | 1.40 |
| NovAtel Quality | Distance [km] | % of Total | 3D Accuracy (m) |
|---|---|---|---|
| 1 | 710,958 | 61.29 | 0.0–0.15 |
| 2 | 378,453 | 32.63 | 0.05–0.4 |
| 3 | 49,335 | 4.25 | 0.2–1.0 |
| 4 | 14,132 | 1.22 | 0.5–2.0 |
| 5 | 715 | 0.06 | 1.0–5.0 |
| 6 | 59 | 0.01 | 2.0–10.0 |
| Quality | 3D Accuracy (m) | % 3D Diff | % 2D Diff | % Altitude Diff |
|---|---|---|---|---|
| 1 | 0.0–0.15 | 52.5 | 84.0 | 65.6 |
| 2 | 0.05–0.4 | 81.7 | 93.7 | 88.3 |
| 3 | 0.2–1.0 | 91.7 | 97.8 | 94.5 |
| 4 | 0.5–2.0 | 96.1 | 99.0 | 97.3 |
| 5 | 1.0–5.0 | 88.6 | 97.8 | 91.6 |
| 6 | 2.0–10.0 | 98.4 | 99.5 | 99.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bedkowski, J.; Nowak, H.; Kubiak, B.; Studzinski, W.; Janeczek, M.; Karas, S.; Kopaczewski, A.; Makosiej, P.; Koszuk, J.; Pec, M.; et al. A Novel Approach to Global Positioning System Accuracy Assessment, Verified on LiDAR Alignment of One Million Kilometers at a Continent Scale, as a Foundation for Autonomous DRIVING Safety Analysis. Sensors 2021, 21, 5691. https://doi.org/10.3390/s21175691
Bedkowski J, Nowak H, Kubiak B, Studzinski W, Janeczek M, Karas S, Kopaczewski A, Makosiej P, Koszuk J, Pec M, et al. A Novel Approach to Global Positioning System Accuracy Assessment, Verified on LiDAR Alignment of One Million Kilometers at a Continent Scale, as a Foundation for Autonomous DRIVING Safety Analysis. Sensors. 2021; 21(17):5691. https://doi.org/10.3390/s21175691
Chicago/Turabian StyleBedkowski, Janusz, Hubert Nowak, Blazej Kubiak, Witold Studzinski, Maciej Janeczek, Szymon Karas, Adam Kopaczewski, Przemyslaw Makosiej, Jaroslaw Koszuk, Michal Pec, and et al. 2021. "A Novel Approach to Global Positioning System Accuracy Assessment, Verified on LiDAR Alignment of One Million Kilometers at a Continent Scale, as a Foundation for Autonomous DRIVING Safety Analysis" Sensors 21, no. 17: 5691. https://doi.org/10.3390/s21175691
APA StyleBedkowski, J., Nowak, H., Kubiak, B., Studzinski, W., Janeczek, M., Karas, S., Kopaczewski, A., Makosiej, P., Koszuk, J., Pec, M., & Miksa, K. (2021). A Novel Approach to Global Positioning System Accuracy Assessment, Verified on LiDAR Alignment of One Million Kilometers at a Continent Scale, as a Foundation for Autonomous DRIVING Safety Analysis. Sensors, 21(17), 5691. https://doi.org/10.3390/s21175691





