Wireless Signal Propagation Prediction Based on Computer Vision Sensing Technology for Forestry Security Monitoring
Abstract
:1. Introduction
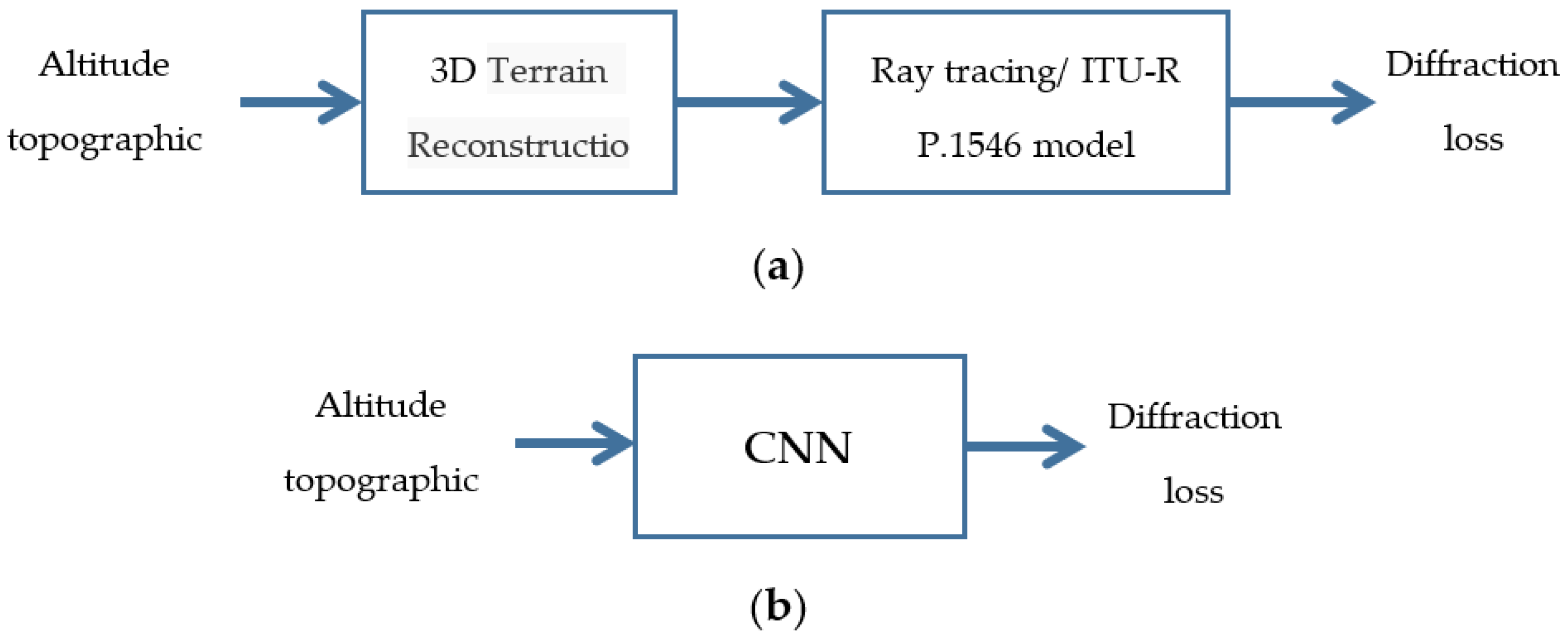
- Our proposed schemes directly process the maps with terrain information by Convolutional Neural Network (CNN) to obtain large-scale propagation/diffraction loss or shadow fading parameters. A framework including data set generation, network structure, training, and metrics evaluation has been constructed to research into the combination of CV and terrain-related radio propagation.
- A direct link is established by a CNN between topographic map to propagation/diffraction loss for a pair of transmitter and receiver on the map. Furthermore, the pathloss between a transmitter and multiple receivers can be predicted in one batch by taking advantage of the multiple parallel outputs defined for the CNN, which greatly enhances the computation efficiency and lays the foundation for extending the scheme to predict the pathloss from a transmitter to a coverage area in a very fast way.
- The quantitative relation is found between the terrain fluctuation pattern to correlation distance of shadow fading through a CNN model that can process a map of a coverage area, and the results would help configure radio access networks, e.g., to optimize handover performance.
2. Diffraction Loss Prediction Based on CNN
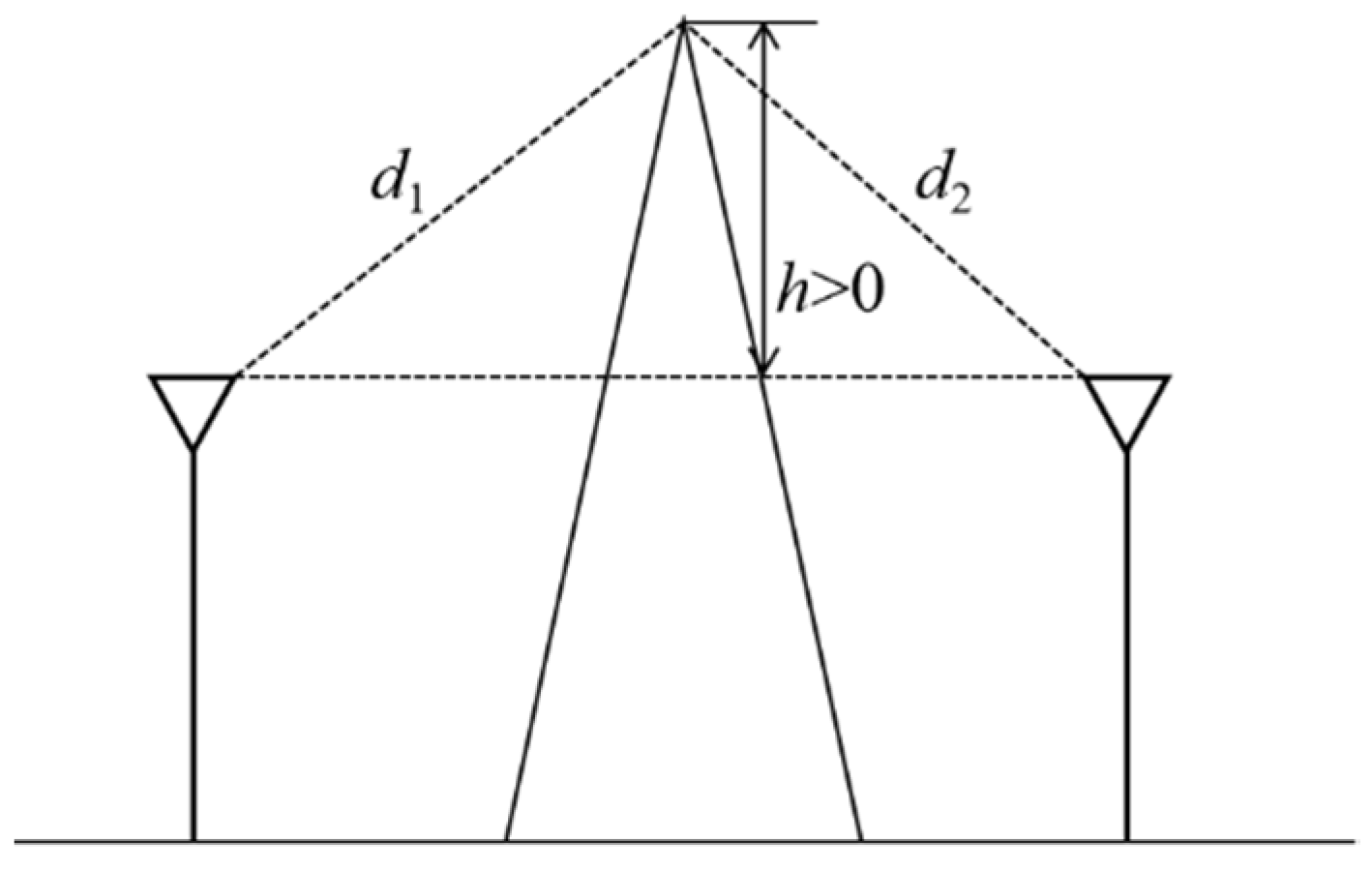
2.1. Prediction Method
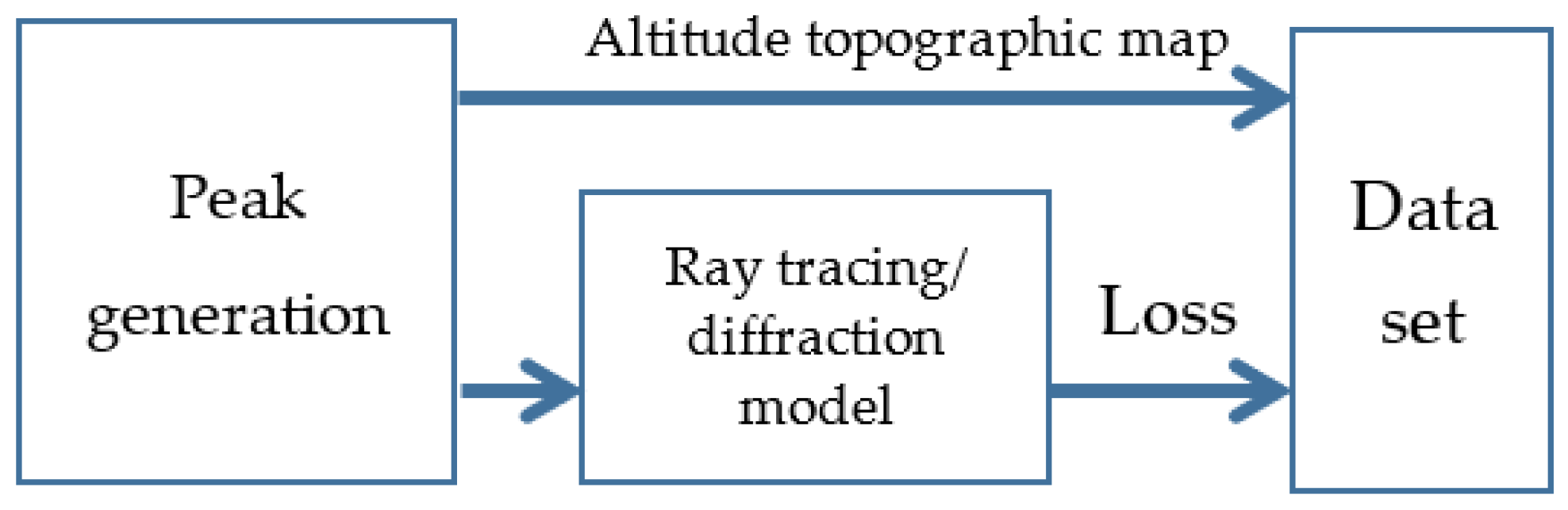
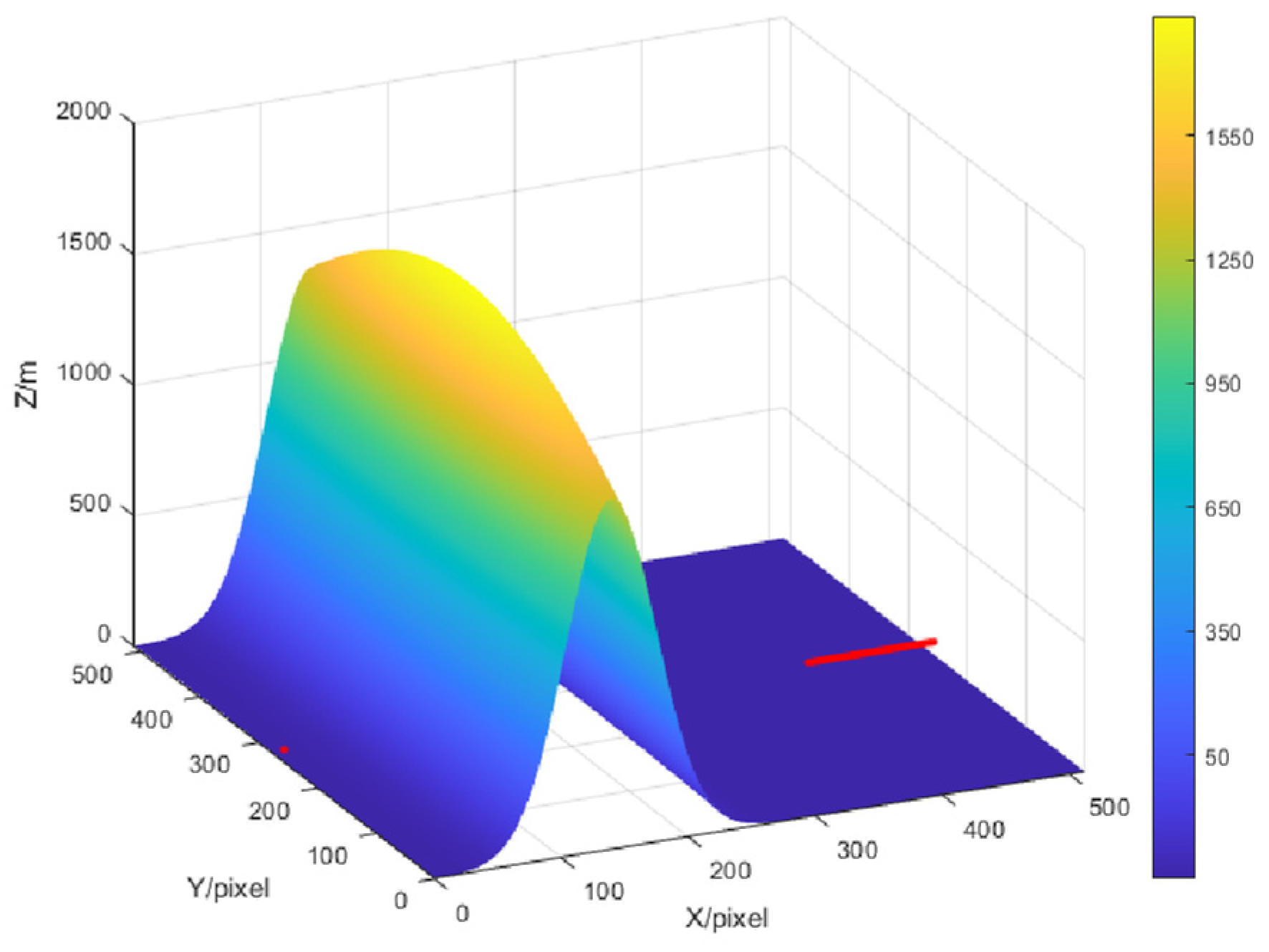
2.2. Data Set Generation
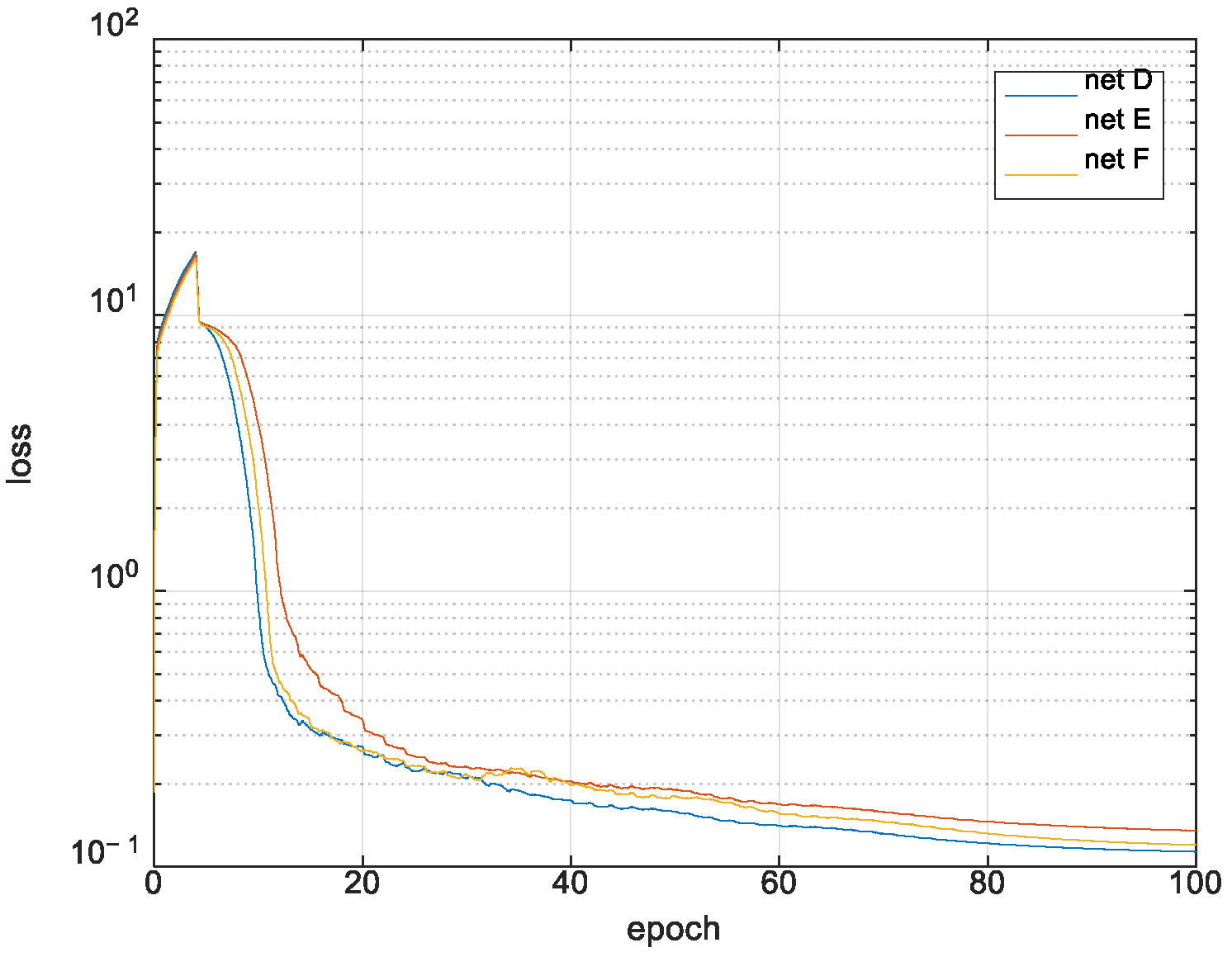
2.3. CNN Structure and Performance Metrics
3. Correlation Distance Prediction Based on CNN for Shadow Fading
3.1. Prediction Method
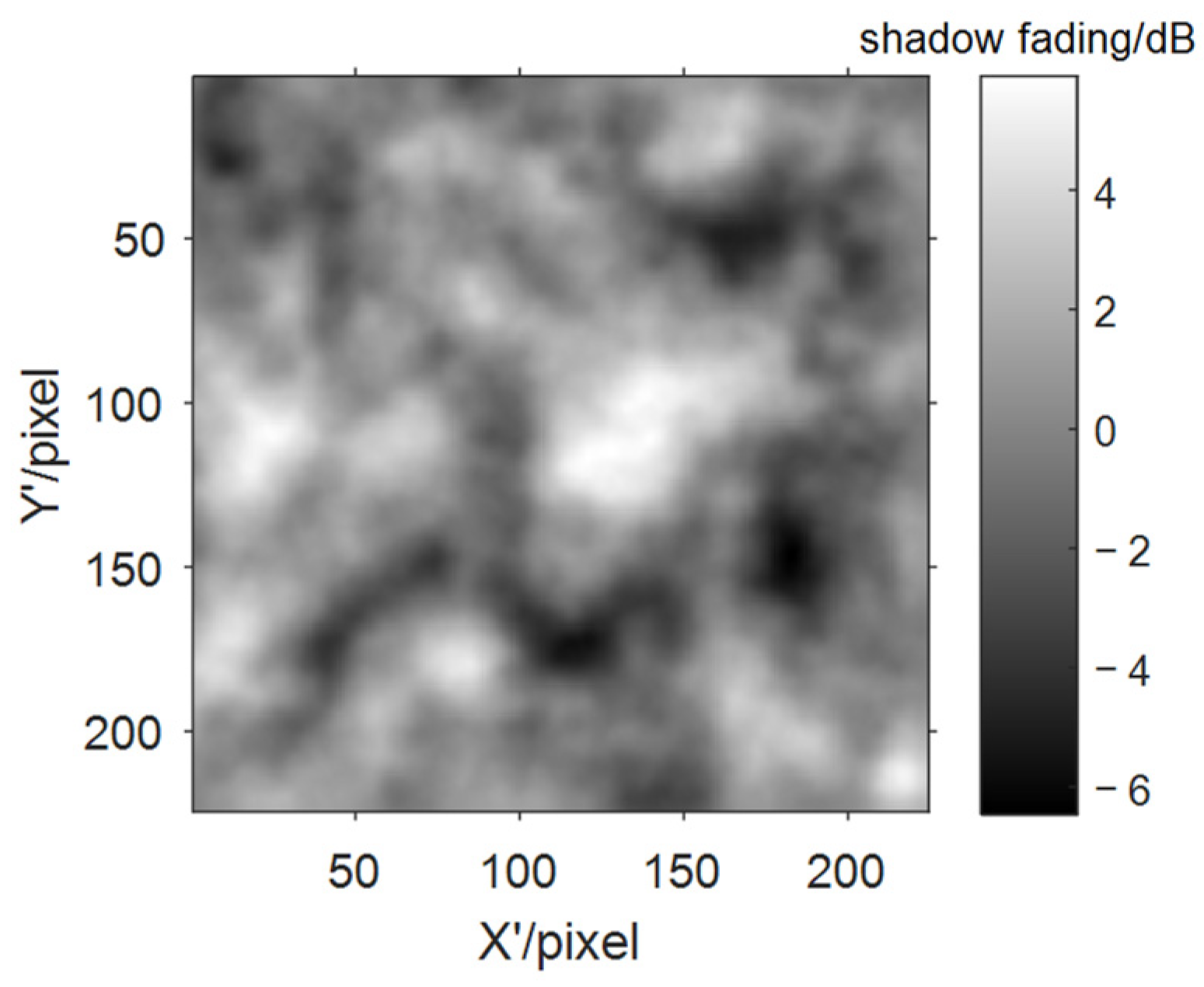
3.2. Data Set Generation
3.3. CNN Structure and Performance Metrics
4. Simulation Results
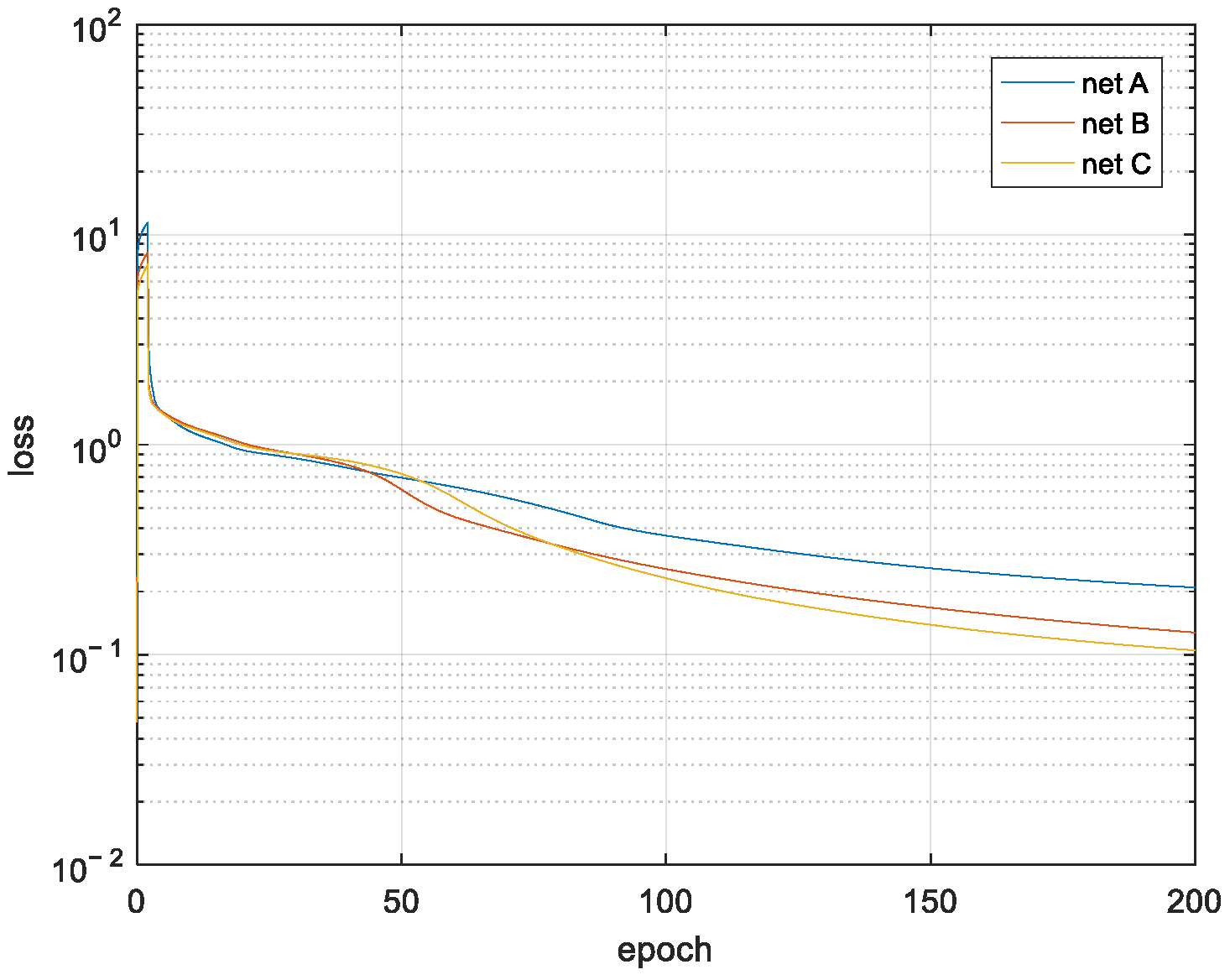
4.1. Results of Diffraction Loss Prediction
4.2. Results of Shadow Fading Correlation Distance Extraction
5. Future Work
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ribero, M.; Heath, R.W.; Vikalo, H.; Chizhik, D.; Valenzuela, R.A. Deep learning propagation models over irregular terrain. In Proceedings of the ICASSP 2019–2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019. [Google Scholar]
- Kuno, N.; Takatori, Y. Prediction Method by Deep-Learning for Path Loss Characteristics in an Open-Square Environment. In Proceedings of the 2018 International Symposium on Antennas and Propagation (ISAP), Busan, Korea, 23–26 October 2018; pp. 1–2. [Google Scholar]
- Qiu, J.; Du, L.; Zhang, D.; Su, S.; Tian, Z. Nei-TTE: Intelligent Traffic Time Estimation Based on Fine-grained Time Derivation of Road Segments for Smart City. IEEE Trans. Ind. Inf. 2020, 16, 2659–2666. [Google Scholar] [CrossRef]
- Taygur, M.M.; Eibert, T.F. A Ray-Tracing Algorithm Based on the Computation of (Exact) Ray Paths with Bidirectional Ray-Tracing. IEEE Trans. Antennas Propag. 2020, 68, 6277–6286. [Google Scholar] [CrossRef]
- Ng, K.H.; Tameh, E.K.; Nix, A.R. A New Heuristic Geometrical Approach for Finding Non-Coplanar Multiple Edge Diffraction Ray Paths. IEEE Trans. Antennas Propag. 2006, 54, 2669–2672. [Google Scholar] [CrossRef]
- Luo, C.; Tan, Z.; Min, G.; Gan, J.; Shi, W.; Tian, Z. A Novel Web Attack Detection System for Internet of Things via Ensemble Classification. IEEE Trans. Ind. Inf. 2021, 17, 5810–5818. [Google Scholar] [CrossRef]
- Qiu, J.; Tian, Z.; Du, C.; Zuo, Q.; Su, S.; Fang, B. A Survey on Access Control in the Age of Internet of Things. IEEE Internet Things J. 2020, 7, 4682–4696. [Google Scholar] [CrossRef]
- Xu, D.; Tian, Z.; Lai, R.; Kong, X.; Tan, Z.; Shi, W. Deep Learning Based Emotional Analysis of Microblog Texts. Inf. Fusion 2020, 64, 1–11. [Google Scholar] [CrossRef]
- Al-Da Bbagh, R.K.; Al-Aboody, N.A.; Al-Raweshidy, H.S. A simplified path loss model for investigating diffraction and specular reflection impact on millimetre wave propagation. In Proceedings of the 2017 8th International Conference on the Network of the Future (NOF), London, UK, 22–24 November 2017. [Google Scholar]
- Kawabata, W.; Nishimura, T.; Ohgane, T.; Ogawa, Y. A study on large-scale signal detection using gaussian belief propagation in overloaded interleave division multiple access. In Proceedings of the 2019 22nd International Symposium on Wireless Personal Multimedia Communications (WPMC), Lisbon, Portugal, 24–27 November 2019. [Google Scholar]
- Ogou, K.; Iwai, H.; Sasaoka, H. Accuracy improvement of distance estimation based on received signal strength by active propagation control. In Proceedings of the 2018 IEEE International Workshop on Electromagnetics: Applications and Student Innovation Competition (iWEM), Nagoya, Japan, 29–31 August 2018. [Google Scholar]
- Wang, Y.; Tian, Z.; Sun, Y.; Du, X.; Guizani, N. LocJury: An IBN-based Location Privacy Preserving Scheme for IoCV. IEEE Trans. Intell. Transp. Syst. 2020, 22, 5028–5037. [Google Scholar] [CrossRef]
- Ma, Y. A Geometry-Based Non-Stationary MIMO Channel Model for Vehicular Communications. China Commun. 2018, 15, 30–38. [Google Scholar] [CrossRef]
- Politanskyi, R.; Klymash, M. Application of artificial intelligence in cognitive radio for planning distribution of frequency channels. In Proceedings of the International Conference on Advanced Information and Communications Technologies, Lviv, Ukraine, 2–6 July 2019. [Google Scholar]
- Qiu, J.; Chai, Y.H.; Tian, Z.H.; Du, X.; Guizani, M. Automatic Concept Extraction Based on Semantic Graphs from Big Data in Smart City. IEEE Trans. Comput. Soc. Syst. 2020, 7, 225–233. [Google Scholar] [CrossRef]
- Liao, R.F.; Wen, H.; Wu, J.; Song, H.; Pan, F.; Dong, L. The Rayleigh Fading Channel Prediction via Deep Learning. Wirel. Commun. Mob. Comput. 2018, 2018, 1–11. [Google Scholar] [CrossRef]
- Ding, T.; Hirose, A. Fading Channel Prediction Based on Combination of Complex-Valued Neural Networks and Chirp Z-Transform. IEEE Trans. Neural Netw. Learn. Syst. 2014, 25, 1686–1695. [Google Scholar] [CrossRef]
- Wei, J.; Schotten, H.D. Neural Network-Based Fading Channel Prediction: A Comprehensive Overview. IEEE Access 2019, 7, 118112–118124. [Google Scholar] [CrossRef]
- Tian, Y.; Pan, G.; Alouini, M.S. Applying Deep-Learning-Based Computer Vision to Wireless Communications: Methodologies, Opportunities, and Challenges. IEEE Open J. Commun. Soc. 2021, 2, 132–143. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, J.; Sun, J.; Adebisi, B.; Gacanin, H.; Gui, G.; Adachi, F. CV-3DCNN: Complex-Valued Deep Learning for CSI Prediction in FDD Massive MIMO Systems. IEEE Wirel. Commun. Lett. 2021, 10, 266–270. [Google Scholar] [CrossRef]
- Chen, X.; Wei, Z.; Zhang, X.; Sang, L. A beamforming method based on image tracking and positioning in the LOS scenario. In Proceedings of the 2017 IEEE 17th International Conference on Communication Technology (ICCT), Chengdu, China, 27–30 October 2017. [Google Scholar]
- Zang, B.; Ding, L.; Feng, Z.; Zhu, M.; Lei, T.; Xing, M.; Zhou, X. CNN-LRP: Understanding Convolutional Neural Networks Performance for Target Recognition in SAR Images. Sensors 2021, 21, 4536. [Google Scholar] [CrossRef] [PubMed]
- Wang, A.; Wang, M.; Wu, H.; Jiang, K.; Iwahori, Y. A Novel LiDAR Data Classification Algorithm Combined CapsNet with ResNet. Sensors 2020, 20, 1151. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Seyedsalehi, S.; Pourahmadi, V.; Sheikhzadeh, H.; Foumani, A.H. Propagation Channel Modeling by Deep learning Techniques. arXiv 2019, arXiv:1908.06767. [Google Scholar]
- Deng, G.; Li, J.; Li, W.; Wang, H. SLAM: Depth image information for mapping and inertial navigation system for localization. In Proceedings of the Intelligent Robot Systems, Tokyo, Japan, 20–24 July 2016. [Google Scholar]
- Rappaport, T.S. Wireless Communications: Principles and Practice, 2nd ed.; Prentice Hall PTR: Hoboken, NJ, USA, 2002. [Google Scholar]
- Method for Point-to-Area Predictions for Terrestrial Services in the Frequency Range 30 MHz to 4000 MHz. Available online: http://www.itu.int/rec/R-REC-P.1546/en (accessed on 20 August 2021).
- Neskovic, A.; Neskovic, N.; Paunovic, D. Improvements of ITU-R field strength prediction method for land mobile services. In Proceedings of the Electrotechnical Conference 2002, MELECON 2002, 11th Mediterranean, Bratislava, Slovakia, 4–7 July 2001; IEEE: Cairo, Egypt, 2002. [Google Scholar]
- Badola, A.; Nair, V.P.; Lal, R.P. An analysis of regularization methods in deep neural networks. In Proceedings of the 2020 IEEE 17th India Council International Conference (INDICON), Delhi, India, 10–13 December 2020; pp. 1–6. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Rumelhart, D.; Hinton, G.; Williams, R. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
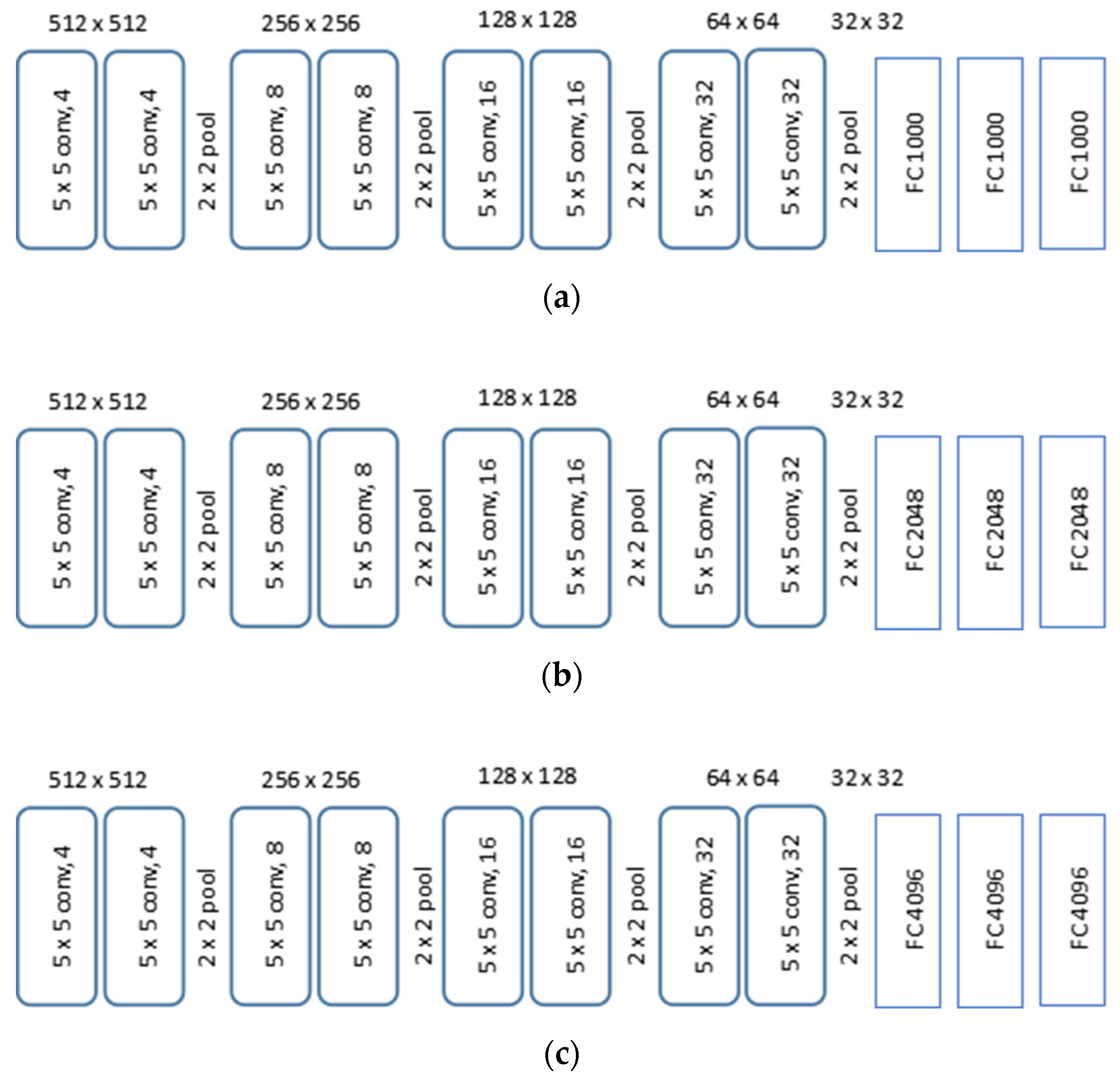
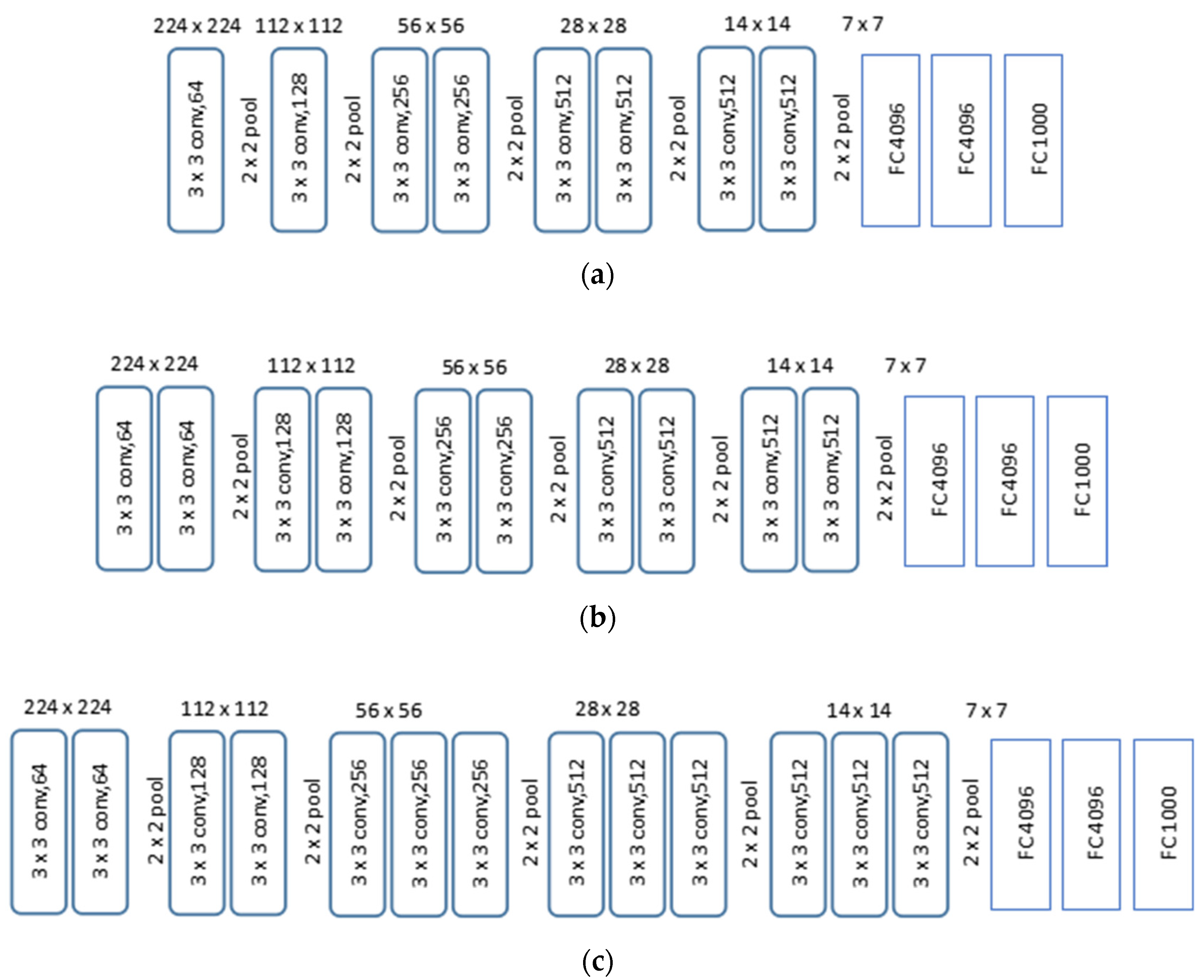
| Hyperparameters | Net A, B and C | Net D, E and F |
|---|---|---|
| batch size | 1 | 16 |
| initial learning rate | 0.00001 | 0.0001 |
| epoch | 200 | 100 |
| learning rate decay | exponential decay | |
| optimizer | Adam | |
| activation | ReLu | |
| Net A | Net B | Net C | ||
|---|---|---|---|---|
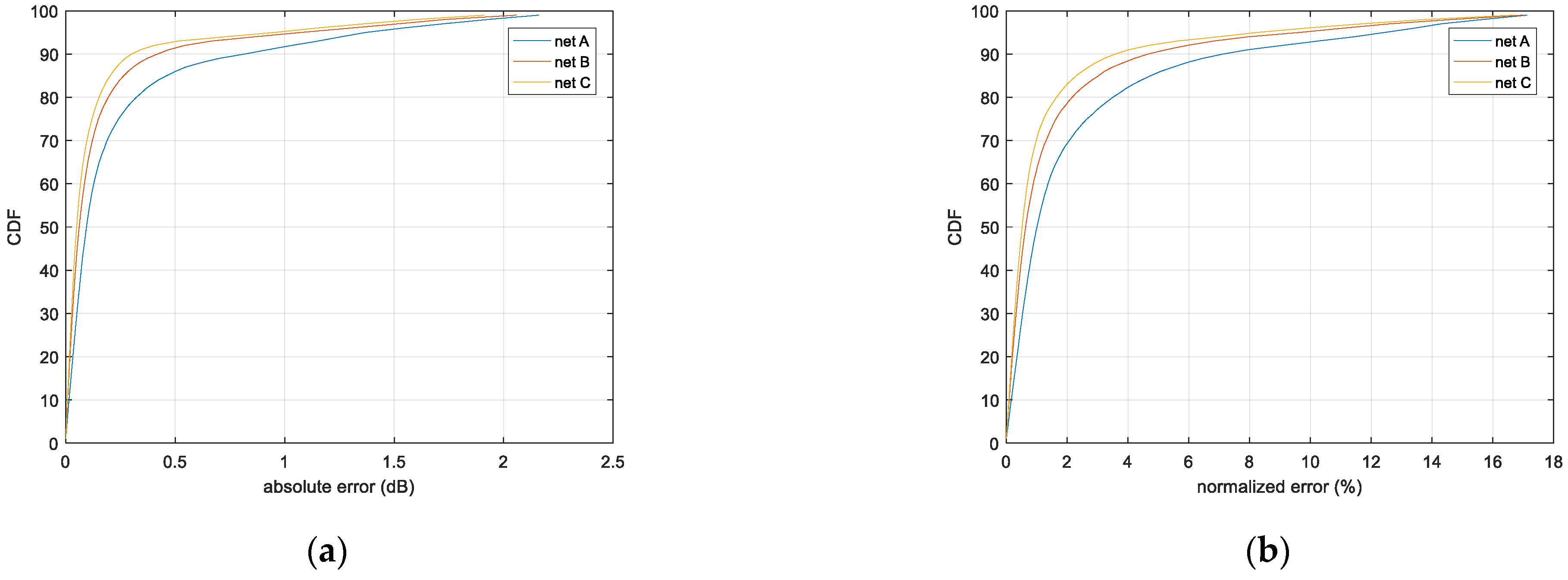
| absolute error (dB) | 50% | 0.095 | 0.061 | 0.050 |
| 90% | 0.816 | 0.418 | 0.300 | |
| 95% | 1.370 | 1.074 | 0.953 | |
| normalized error (%) | 50% | 1.006 | 0.632 | 0.518 |
| 90% | 7.120 | 4.655 | 3.577 | |
| 95% | 12.434 | 9.634 | 8.238 | |
| processing time (ms) | per image | 6.28 | 6.41 | 6.65 |
| per point | 0.0628 | 0.0641 | 0.0665 | |
| Net D | Net E | Net F | ||
|---|---|---|---|---|
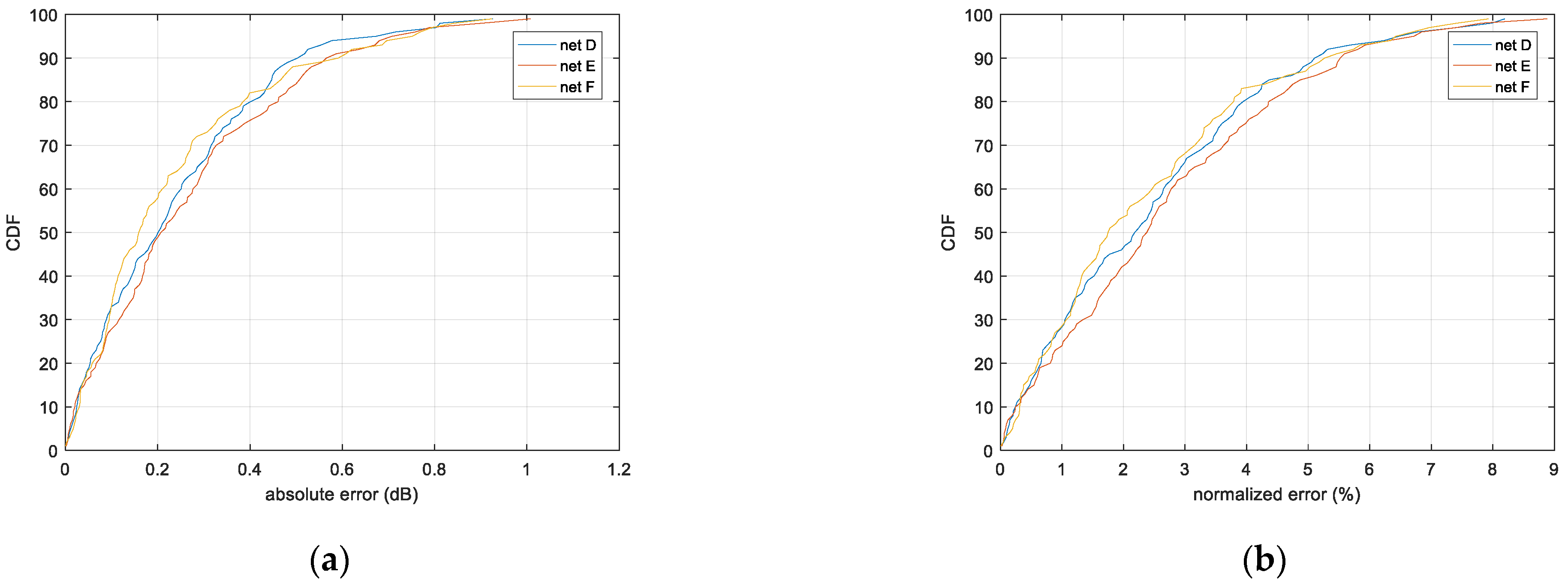
| absolute error (dB) | 50% | 0.210 | 0.207 | 0.159 |
| 90% | 0.503 | 0.565 | 0.591 | |
| 95% | 0.673 | 0.708 | 0.752 | |
| normalized error (%) | 50% | 2.181 | 2.377 | 1.747 |
| 90% | 5.103 | 5.521 | 5.267 | |
| 95% | 6.472 | 6.716 | 6.423 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, J.; Xing, Z.; Xiang, T.; Zhang, X.; Zhou, Y.; Xi, C.; Lu, H. Wireless Signal Propagation Prediction Based on Computer Vision Sensing Technology for Forestry Security Monitoring. Sensors 2021, 21, 5688. https://doi.org/10.3390/s21175688
He J, Xing Z, Xiang T, Zhang X, Zhou Y, Xi C, Lu H. Wireless Signal Propagation Prediction Based on Computer Vision Sensing Technology for Forestry Security Monitoring. Sensors. 2021; 21(17):5688. https://doi.org/10.3390/s21175688
Chicago/Turabian StyleHe, Jialuan, Zirui Xing, Tianqi Xiang, Xin Zhang, Yinghai Zhou, Chuanyu Xi, and Hai Lu. 2021. "Wireless Signal Propagation Prediction Based on Computer Vision Sensing Technology for Forestry Security Monitoring" Sensors 21, no. 17: 5688. https://doi.org/10.3390/s21175688
APA StyleHe, J., Xing, Z., Xiang, T., Zhang, X., Zhou, Y., Xi, C., & Lu, H. (2021). Wireless Signal Propagation Prediction Based on Computer Vision Sensing Technology for Forestry Security Monitoring. Sensors, 21(17), 5688. https://doi.org/10.3390/s21175688






