Stochastic Identification of Guided Wave Propagation under Ambient Temperature via Non-Stationary Time Series Models
Abstract
:1. Introduction
- Investigation of the stochastic and non-stationary nature of guided wave propagation under ambient temperature variation;
- Mathematical modeling of the uncertainty in guided wave propagation due to ambient temperature variation;
- Investigation on the time-varying modal characteristics (natural frequencies and damping ratios) under the influence of ambient temperature as the guided wave propagates through the structure.
- (a)
- Investigation of the stochastic nature of guided wave propagation in an aluminum plate under ambient temperature variation by means of experimental investigation and high-fidelity physics-based finite element modeling.
- (b)
- Introduction of a data-based stochastic time-varying identification framework via RML parameter estimation for tracking the dynamics of non-stationary guided wave signals.
- (c)
- Investigation of the model-based and experimental modeling and quantification of uncertainty in guided wave propagation due to ambient temperature variation with the help of the RML-TAR time series models.
- (d)
- Extraction and assessment of the RML-based time-dependent modal properties, i.e., natural frequencies and damping ratios of the system under the influence of ambient temperature variation as guided waves propagate on the structure.
2. Non-Stationary Guided Wave Signal Representation
3. Non-Stationary TAR Model Identification
3.1. Model Parameter Estimation
3.2. Model Structure Selection
3.3. Modal Characteristics
4. Data Generation
4.1. The Laboratory Experimental Set-Up
4.2. Finite Element Modeling
5. Results and Discussion
5.1. Stochasticity in Guided Wave Propagation
5.1.1. Experimental Guided Wave Signal Analysis
5.1.2. Simulated Guided Wave Signal Analysis
5.2. Non-Parametric Analysis: Experimental Signal
5.3. Parametric RML-TAR Modeling under Ambient Temperature Variation
6. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ACF | Auto-correlation function |
| AIC | Akaike information criteria |
| AR | Autoregressive |
| ARMA | Autoregressive moving average |
| ARMAX | Autoregressive moving average with exogenous excitation |
| BIC | Bayesian information criterion |
| CCF | Cross-correlation function |
| EOC | Environmental and operational conditions |
| EPOT | Electric potential |
| FEM | Finite element model |
| FRF | Frequency response function |
| iid | identically independently distributed |
| MA | Moving average |
| MMSE | Minimum mean square error |
| LSCWA | Least squares cross-wavelet analysis |
| LSWA | Least squares wavelet analysis |
| OLS | Ordinary least squares |
| PEM | Prediction error method |
| PSD | Power spectral density |
| PZT | Lead zirconate titanate |
| RML | Recursive maximum likelihood |
| RSS | Residual sum of squares |
| SEM | Spectral element method |
| SHM | Structural health monitoring |
| SPP | Samples per parameter |
| SSS | Signal sum of squares |
| STFT | Short term Fourier transform |
| TAR | Time-varying autoregressive |
| TARMA | Time-varying autoregressive moving average |
| ToF | Time of Flight |
| WLS | Weighted least squares |
| XWT | Cross-wavelet transform |
Appendix A. Material Properties and Equations
| Materials | Property Name | Values |
|---|---|---|
| Piezo-electric: PZT-5A | Density () | 7750 kg/m |
| Young’s modulus (GPa) | ||
| Poisson ratio | ||
| Piezo-elctric charge constant (m/V) | ||
| Dielectric constant | ||
| Aluminum | Density () (kg/m) | 2700 |
| Young’s modulus (E GPa) | ||
| Poisson ratio | ||
| Adhesive | Density () (kg/m) | 1100 |
| Young’s modulus (E GPa) | ||
| Poisson ratio |
References
- Farrar, C.R.; Worden, K. An introduction to Structural Health Monitoring. R. Soc. Philos. Trans. Math. Phys. Eng. Sci. 2007, 365, 303–315. [Google Scholar] [CrossRef] [PubMed]
- Doebling, S.W.; Farrar, C.R.; Prime, M.B. A summary review of vibration-based damage identification methods. Shock Vib. Dig. 1998, 30, 91–105. [Google Scholar] [CrossRef] [Green Version]
- Kopsaftopoulos, F.; Chang, F.K. A dynamic data-driven stochastic state-awareness framework for the next generation of bio-inspired fly-by-feel aerospace vehicles. In Handbook of Dynamic Data Driven Applications Systems; Blasch, E., Ravela, S., Aved, A., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 697–721. [Google Scholar]
- Royer, D.; Dieulesaint, E. Elastic Waves in Solids I: Free and Guided Propagation; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1999; pp. 311–315. [Google Scholar]
- Graff, K.F. Wave Motion in Elastic Solids; Dover Publications Inc.: New York, NY, USA, 1991. [Google Scholar]
- Rose, J.L. Ultrasonic Guided Waves in Solid Media; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Kundu, T. Mechanics of Elastic Waves and Ultrasonic Nondestructive Evaluation; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Giurgiutiu, V. Structural Health Monitoring: With Piezoelectric Wafer Active Sensors; Academic Press: Oxford, UK, 2008. [Google Scholar]
- Zhao, J.; Gao, H.D.; Chang, G.F.; Ayhan, B.; Yan, F.; Kwan, C.; Rose, J.L. Active health monitoring of an aircraft wing with embedded piezoelectric sensor/actuator network: I. Defect detection, localization and growth monitoring. Smart Mater. Struct. 2007, 16, 1208–1217. [Google Scholar] [CrossRef]
- Giurgiutiu, V. Flutter prediction for flight/wind-tunnel flutter test under atmospheric turbulence excitation. J. Intell. Mater. Syst. Struct. 2005, 16, 291–305. [Google Scholar] [CrossRef]
- Ihn, J.; Chang, F.K. Detection and monitoring of hidden fatigue crack growth using a built-in piezoelectric sensor/actuator network, Part I: Diagnostics. Smart Mater. Struct. 2004, 13, 609–620. [Google Scholar] [CrossRef]
- Ihn, J.; Chang, F.K. Detection and monitoring of hidden fatigue crack growth using a built-in piezoelectric sensor/actuator network, Part II: Validation through riveted joints and repair patches. Smart Mater. Struct. 2004, 13, 621–630. [Google Scholar] [CrossRef]
- Ihn, J.; Chang, F.K. Pitch-catch active sensing methods in structural health monitoring for aircraft structures. Struct. Health Monit. 2008, 7, 5–19. [Google Scholar] [CrossRef]
- Giurgiutiu, V. Piezoelectric Wafer Active Sensors for Structural Health Monitoring of Composite Structures Using Tuned Guided Waves. J. Eng. Mater. Technol. 2011, 133, 041012. [Google Scholar] [CrossRef]
- Kopsaftopoulos, F.; Nardari, R.; Li, Y.H.; Chang, F.K. A stochastic global identification framework for aerospace structures operating under varying flight states. Mech. Syst. Signal Process. 2018, 98, 425–447. [Google Scholar] [CrossRef]
- Spiridonakos, M.; Fassois, S. Non-stationary random vibration modelling and analysis via functional series time-dependent ARMA (FS-TARMA) models—A critical survey. Mech. Syst. Signal Process. 2014, 47, 175–224. [Google Scholar] [CrossRef]
- Zhang, Q.W. Statistical damage identification for bridges using ambient vibration data. Comput. Struct. 2007, 85, 476–485. [Google Scholar] [CrossRef]
- Roy, S.; Lonkar, K.; Janapati, V.; Chang, F.K. A novel physics-based temperature compensation model for structural health monitoring using ultrasonic guided waves. Struct. Health Monit. 2014, 13, 321–342. [Google Scholar] [CrossRef]
- Roy, S.; Ladpli, P.; Chang, F.K. Load monitoring and compensation strategies for guided-waves based structural health monitoring using piezoelectric transducers. J. Sound Vib. 2015, 351, 206–220. [Google Scholar] [CrossRef]
- Croxford, A.J.; Moll, J.; Wilcox, P.D.; Michaels, J.E. Efficient temperature compensation strategies for guided wave structural health monitoring. Ultrasonics 2010, 50, 517–528. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Harley, J.B.; Bergés, M.; Greve, D.W.; Oppenheim, I.J. Robust ultrasonic damage detection under complex environmental conditions using singular value decomposition. Ultrasonics 2015, 58, 75–86. [Google Scholar] [CrossRef] [PubMed]
- Mujica, L.E.; Gharibnezhad, F.; Rodellar, J.; Todd, M. Considering temperature effect on robust principal component analysis orthogonal distance as a damage detector. Struct. Health Monit. 2020, 19, 781–795. [Google Scholar] [CrossRef] [Green Version]
- Cross, E.; Manson, G.; Worden, K.; Pierce, S. Features for damage detection with insensitivity to environmental and operational variations. Proc. R. Soc. A Math. Phys. Eng. Sci. 2012, 468, 4098–4122. [Google Scholar] [CrossRef]
- El Mountassir, M.; Yaacoubi, S.; Mourot, G.; Maquin, D. Sparse estimation based monitoring method for damage detection and localization: A case of study. Mech. Syst. Signal Process. 2018, 112, 61–76. [Google Scholar] [CrossRef]
- Qiu, L.; Fang, F.; Yuan, S.; Boller, C.; Ren, Y. An enhanced dynamic Gaussian mixture model–based damage monitoring method of aircraft structures under environmental and operational conditions. Struct. Health Monit. 2019, 18, 524–545. [Google Scholar] [CrossRef]
- Fendzi, C.; Rebillat, M.; Mechbal, N.; Guskov, M.; Coffignal, G. A data-driven temperature compensation approach for Structural Health Monitoring using Lamb waves. Struct. Health Monit. 2016, 15, 525–540. [Google Scholar] [CrossRef] [Green Version]
- Ren, Y.; Qiu, L.; Yuan, S.; Fang, F. Gaussian mixture model-based path-synthesis accumulation imaging of guided wave for damage monitoring of aircraft composite structures under temperature variation. Struct. Health Monit. 2019, 18, 284–302. [Google Scholar] [CrossRef]
- Croxford, A.; Wilcox, P.; Drinkwater, B.; Konstantinidis, G. Strategies for guided-wave structural health monitoring. Proc. R. Soc. A Math. Phys. Eng. Sci. 2007, 463, 2961–2981. [Google Scholar] [CrossRef]
- Konstantinidis, G.; Wilcox, P.D.; Drinkwater, B.W. An investigation into the temperature stability of a guided wave structural health monitoring system using permanently attached sensors. IEEE Sens. J. 2007, 7, 905–912. [Google Scholar] [CrossRef]
- Clarke, T.; Cawley, P.; Wilcox, P.D.; Croxford, A.J. Evaluation of the damage detection capability of a sparse-array guided-wave SHM system applied to a complex structure under varying thermal conditions. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2009, 56, 2666–2678. [Google Scholar] [CrossRef]
- Putkis, O.; Croxford, A.J. Continuous baseline growth and monitoring for guided wave SHM. Smart Mater. Struct. 2013, 22, 055029. [Google Scholar] [CrossRef]
- Herdovics, B.; Cegla, F. Compensation of phase response changes in ultrasonic transducers caused by temperature variations. Struct. Health Monit. 2019, 18, 508–523. [Google Scholar] [CrossRef] [Green Version]
- Mariani, S.; Heinlein, S.; Cawley, P. Compensation for temperature-dependent phase and velocity of guided wave signals in baseline subtraction for structural health monitoring. Struct. Health Monit. 2020, 19, 26–47. [Google Scholar] [CrossRef]
- Andrews, J.P.; Palazotto, A.N.; DeSimio, M.P.; Olson, S.E. Lamb wave propagation in varying isothermal environments. Struct. Health Monit. 2008, 7, 265–270. [Google Scholar] [CrossRef]
- Ostachowicz, W.; Kudela, P. Wave propagation numerical models in damage detection based on the time domain spectral element method. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2010; Volume 10, p. 012068. [Google Scholar]
- Hayashi, S.; Aso, H.; Watanabe, K.; Nara, H.; Rose, M.T.; Ohwada, S.; Yamaguchi, T. Sequence of IGF-I, IGF-II, and HGF expression in regenerating skeletal muscle. Histochem. Cell Biol. 2000, 122, 427–434. [Google Scholar] [CrossRef] [PubMed]
- Lanza di Scalea, F.; Salamone, S. Temperature effects in ultrasonic Lamb wave structural health monitoring systems. J. Acoust. Soc. Am. 2008, 124, 161–174. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Raghavan, A.; Cesnik, C.E. Effects of elevated temperature on guided-wave structural health monitoring. J. Intell. Mater. Syst. Struct. 2008, 19, 1383–1398. [Google Scholar] [CrossRef]
- Ha, S.; Lonkar, K.; Mittal, A.; Chang, F.K. Adhesive layer effects on PZT-induced lamb waves at elevated temperatures. Struct. Health Monit. 2010, 9, 247–256. [Google Scholar] [CrossRef]
- Hladky-Hennion, A.C. Finite element analysis of the propagation of acoustic waves in waveguides. J. Sound Vib. 1996, 194, 119–136. [Google Scholar] [CrossRef]
- Ahmed, S.; Kopsaftopoulos, F. Uncertainty quantification of guided waves propagation for active sensing structural health monitoring. In Proceedings of the Vertical Flight Society 75th Annual Forum & Technology Display, Philadelphia, PA, USA, 13–16 May 2019. [Google Scholar]
- Ahmed, S.; Kopsaftopoulos, F. Investigation of broadband high-frequency stochastic actuation for active-sensing SHM under varying temperature. In Proceedings of the International Workshop on Structural Health Monitoring, Stanford, CA, USA, 10–12 September 2019. [Google Scholar]
- Spiridonakos, M.; Fassois, S. An FS-TAR based method for vibration-response-based fault diagnosis in stochastic time-varying structures: Experimental application to a pick-and-place mechanism. Mech. Syst. Signal Process. 2013, 38, 206–222. [Google Scholar] [CrossRef]
- Kopsaftopoulos, F.P.; Fassois, S.D. A functional model based statistical time series method for vibration based damage detection, localization, and magnitude estimation. Mech. Syst. Signal Process. 2013, 39, 143–161. [Google Scholar] [CrossRef]
- Fassois, S.D.; Sakellariou, J.S. Time-series methods for fault detection and identification in vibrating structures. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2007, 365, 411–448. [Google Scholar] [CrossRef]
- Kopsaftopoulos, F.; Fassois, S. Vibration based health monitoring for a lightweight truss structure: Experimental assessment of several statistical time series methods. Mech. Syst. Signal Process. 2010, 24, 1977–1997. [Google Scholar] [CrossRef]
- Bhowmik, B.; Tripura, T.; Hazra, B.; Pakrashi, V. First-order eigen-perturbation techniques for real-time damage detection of vibrating systems: Theory and applications. Appl. Mech. Rev. 2019, 71, 060801. [Google Scholar] [CrossRef]
- Poulimenos, A.; Fassois, S. Parametric time-domain methods for non-stationary random vibration modelling and analysis—A critical survey and comparison. Mech. Syst. Signal Process. 2006, 20, 763–816. [Google Scholar] [CrossRef]
- Kay, S.M. Fundamentals of Statistical Signal Processing; Prentice Hall PTR: Upper Saddle River, NJ, USA, 1993. [Google Scholar]
- Box, G.E.; Jenkins, G.M.; Reinsel, G.C. Time Series Analysis: Forecasting and Control; John Wiley & Sons: Hoboken, NJ, USA, 2011; Volume 734. [Google Scholar]
- Kay, S.M. Modern Spectral Estimation: Theory and Application; Prentice Hall: Upper Saddle River, NJ, USA, 1988. [Google Scholar]
- Hammond, J.; White, P. The analysis of non-stationary signals using time-frequency methods. J. Sound Vib. 1996, 190, 419–447. [Google Scholar] [CrossRef]
- Cohen, L. Time-Frequency Analysis; Prentice Hall: Upper Saddle River, NJ, USA, 1995; Volume 778. [Google Scholar]
- Prokoph, A.; El Bilali, H. Cross-wavelet analysis: A tool for detection of relationships between paleoclimate proxy records. Math. Geosci. 2008, 40, 575–586. [Google Scholar] [CrossRef]
- Ghaderpour, E. Least-squares wavelet and cross-wavelet analyses of VLBI baseline length and temperature time series: Fortaleza–Hartebeesthoek–Westford–Wettzell. Publ. Astron. Soc. Pac. 2020, 133, 014502. [Google Scholar] [CrossRef]
- Ghaderpour, E.; Ince, E.S.; Pagiatakis, S.D. Least-squares cross-wavelet analysis and its applications in geophysical time series. J. Geod. 2018, 92, 1223–1236. [Google Scholar] [CrossRef]
- Petsounis, K.; Fassois, S. Non-stationary functional series TARMA vibration modelling and analysis in a planar manipulator. J. Sound Vib. 2000, 231, 1355–1376. [Google Scholar] [CrossRef]
- Owen, J.; Eccles, B.; Choo, B.; Woodings, M. The application of auto–regressive time series modelling for the time–frequency analysis of civil engineering structures. Eng. Struct. 2001, 23, 521–536. [Google Scholar] [CrossRef]
- Grenier, Y. Parametric time-frequency representations. In Time and Frequency Representation of Signals and Systems; Springer: Vienna, Austria, 1989; pp. 125–175. [Google Scholar]
- Mrad, R.B.; Fassois, S.D.; Levitt, J.A. A polynomial-algebraic method for non-stationary TARMA signal analysis–Part I: The method. Signal Process. 1998, 65, 1–19. [Google Scholar] [CrossRef]
- Conforto, S.; D’alessio, T. Spectral analysis for non-stationary signals from mechanical measurements: A parametric approach. Mech. Syst. Signal Process. 1999, 13, 395–411. [Google Scholar] [CrossRef]
- Sotiriou, D.; Kopsaftopoulos, F.; Fassois, S. An adaptive time-series probabilistic framework for 4-D trajectory conformance monitoring. IEEE Trans. Intell. Transp. Syst. 2016, 17, 1606–1616. [Google Scholar] [CrossRef]
- Draper, N.R.; Smith, H. Applied Regression Analysis; John Wiley & Sons: Hoboken, NJ, USA, 1998; Volume 326. [Google Scholar]
- Kitagawa, G.; Gersch, W. A smoothness priors time-varying AR coefficient modeling of nonstationary covariance time series. IEEE Trans. Autom. Control 1985, 30, 48–56. [Google Scholar] [CrossRef]
- Gersch, W.; Kitagawa, G. A time varying AR coefficient model for modelling and simulating earthquake ground motion. Earthq. Eng. Struct. Dyn. 1985, 13, 243–254. [Google Scholar] [CrossRef]
- Fouskitakis, G.N.; Fassois, S.D. On the estimation of nonstationary functional series TARMA models: An isomorphic matrix algebra based method. J. Dyn. Sys. Meas. Control 2001, 123, 601–610. [Google Scholar] [CrossRef]
- Poulimenos, A.G.; Fassois, S.D. Output-only stochastic identification of a time-varying structure via functional series TARMA models. Mech. Syst. Signal Process. 2009, 23, 1180–1204. [Google Scholar] [CrossRef]
- Lennart, L. System Identification: Theory for the User; PTR Prentice Hall: Upper Saddle River, NJ, USA, 1999; Volume 28. [Google Scholar]
- Akaike, H. Prediction and Entropy; Springer: New York, NY, USA, 1985. [Google Scholar]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Jury, E.I. Theory and Application of the z-Transform Method; Wiley: Hoboken, NJ, USA, 1964. [Google Scholar]
- Sugden, R.; Smith, T.; Jones, R. Cochran’s rule for simple random sampling. J. R. Stat. Soc. Ser. B Stat. Methodol. 2000, 62, 787–793. [Google Scholar] [CrossRef]


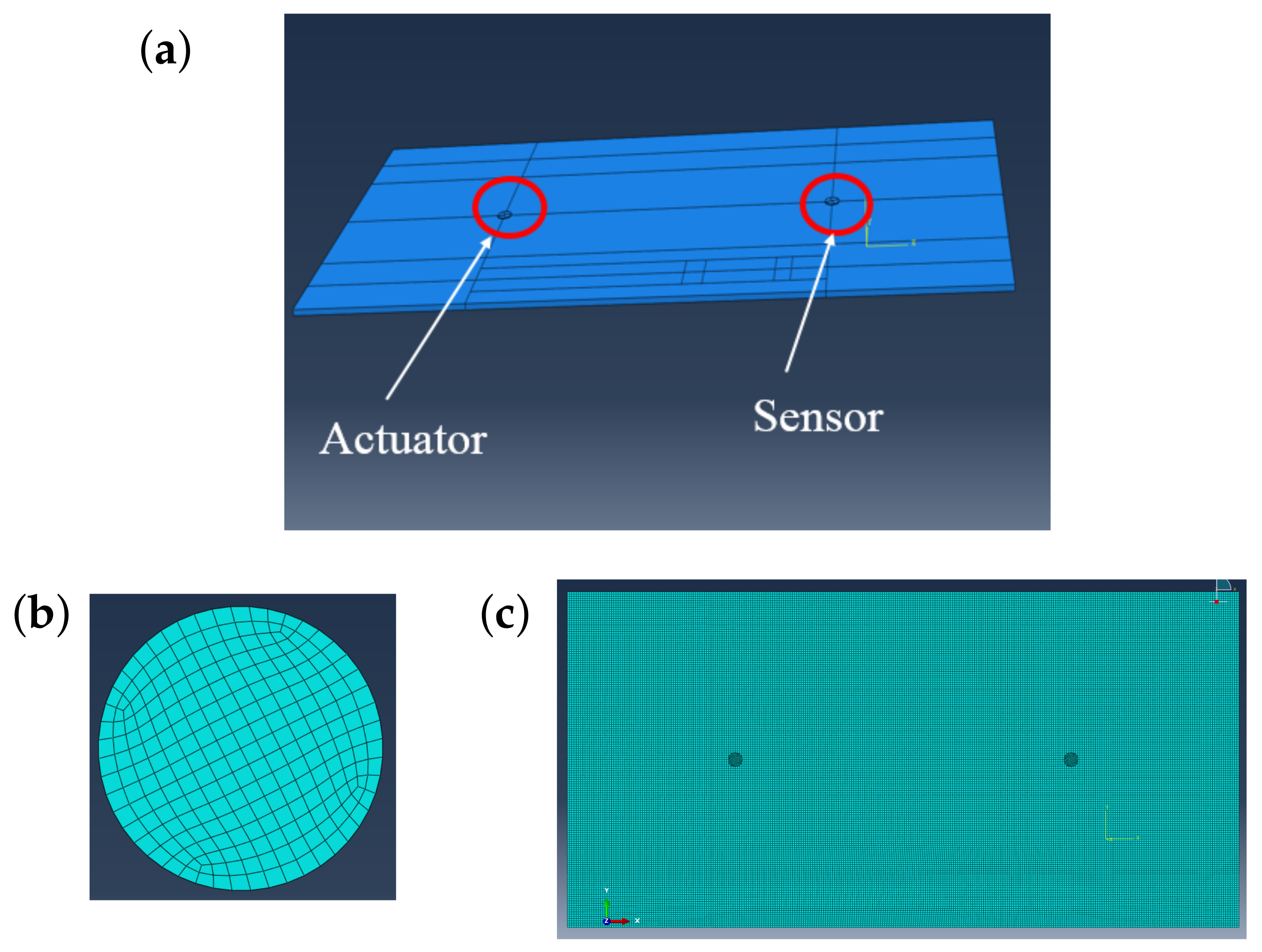


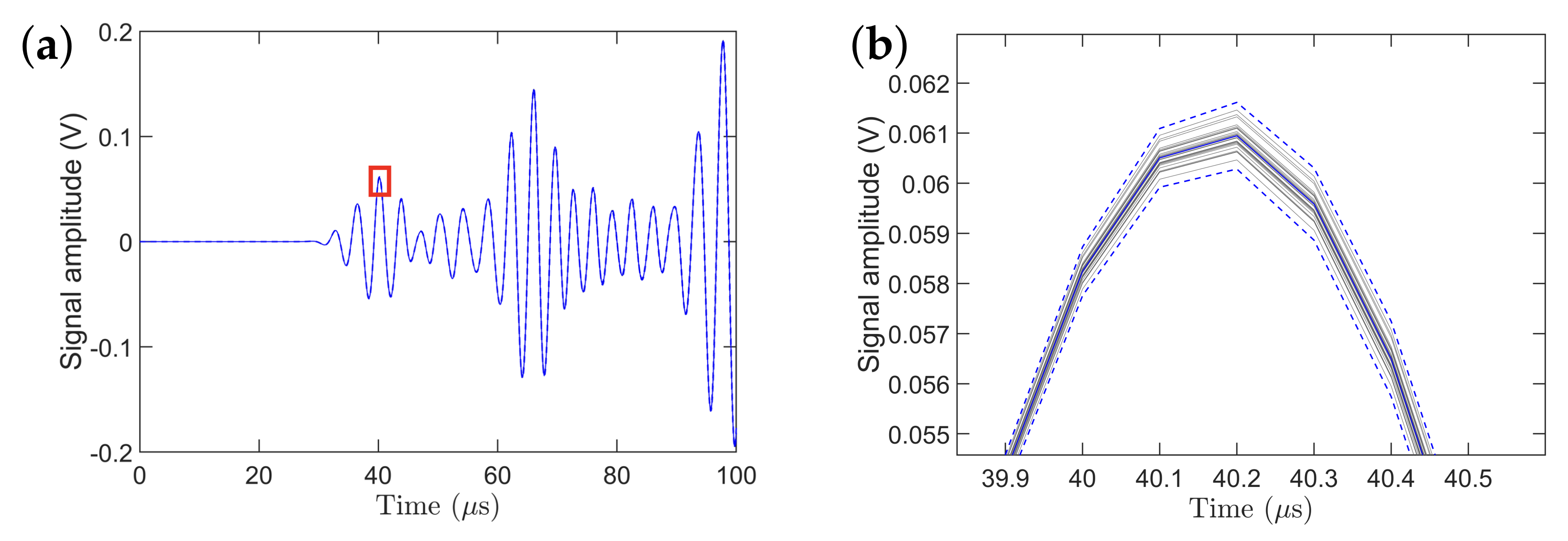
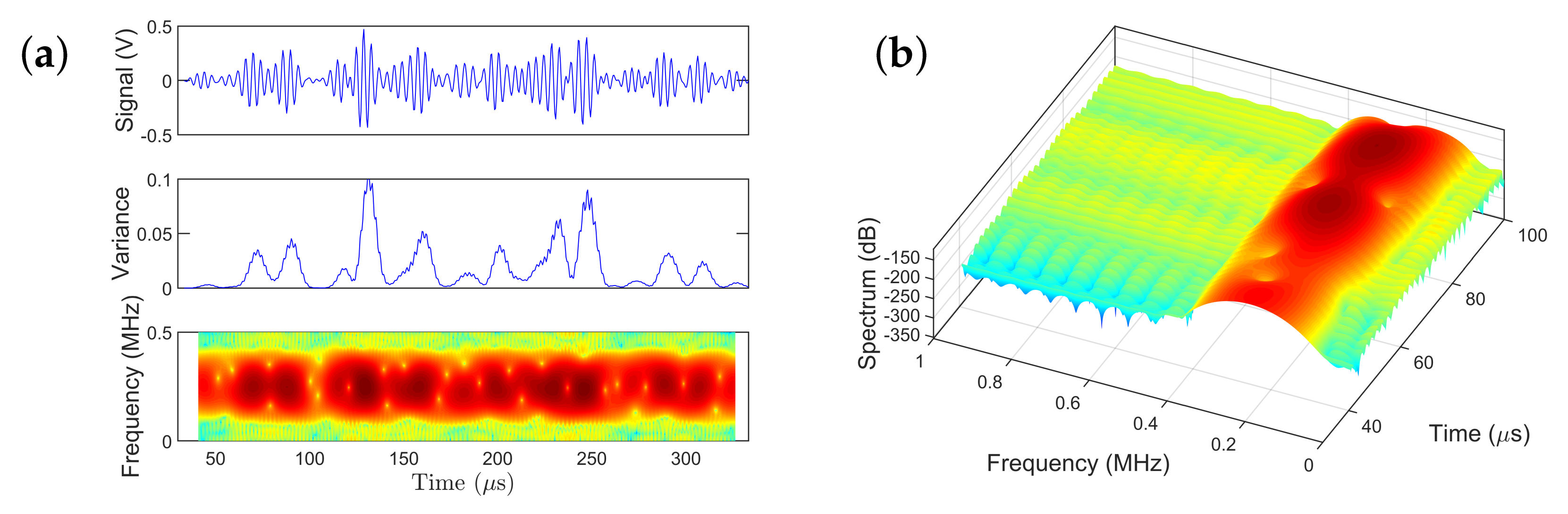
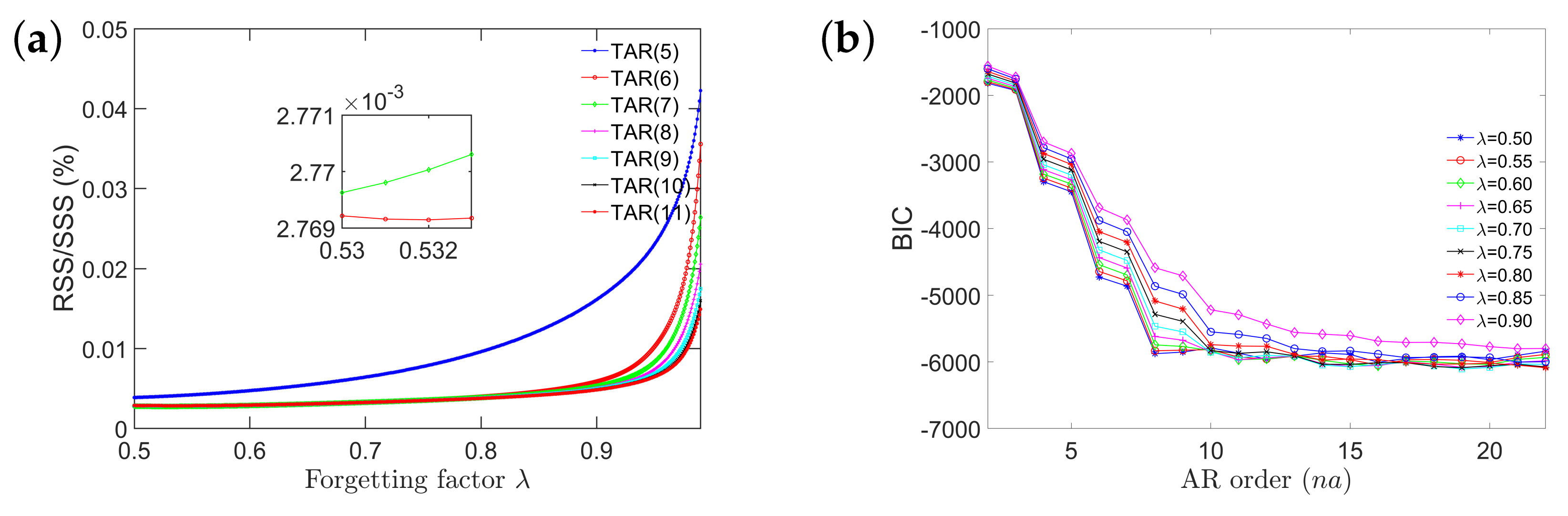

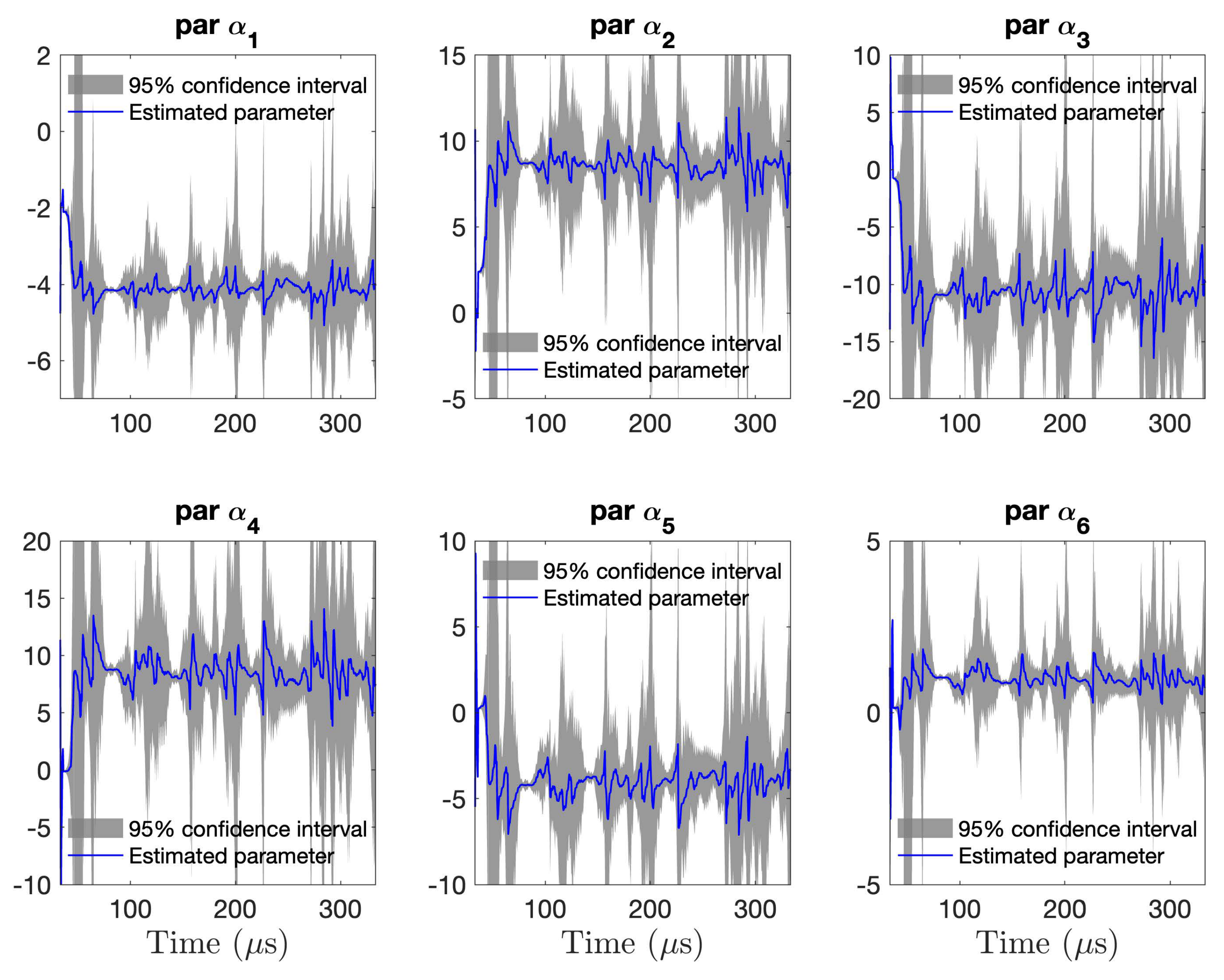




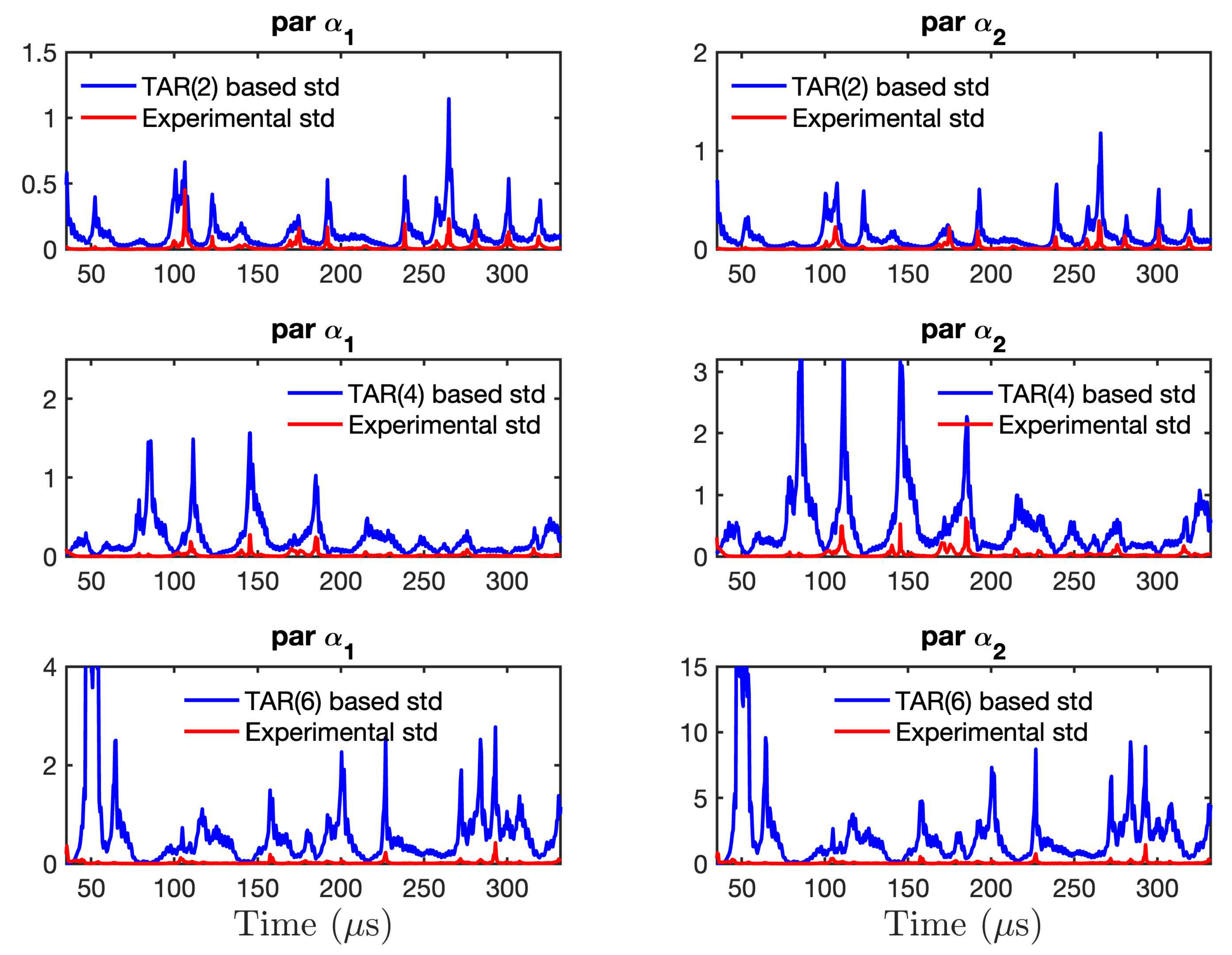
| Object | Dimension |
|---|---|
| Thickness of aluminum plate | mm |
| Thickness of PZT sensor | mm |
| Diameter of PZT sensor | mm |
| Thickness of adhesive | mm |
| Length of aluminum plate | mm |
| Width of aluminum plate | mm |
| (Simulation) | (Simulation) | (Experiment) | (Experiment) | |
|---|---|---|---|---|
| Maximum | ||||
| Minimum | ||||
| Mean | ||||
| Standard deviation |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmed, S.; Kopsaftopoulos, F. Stochastic Identification of Guided Wave Propagation under Ambient Temperature via Non-Stationary Time Series Models. Sensors 2021, 21, 5672. https://doi.org/10.3390/s21165672
Ahmed S, Kopsaftopoulos F. Stochastic Identification of Guided Wave Propagation under Ambient Temperature via Non-Stationary Time Series Models. Sensors. 2021; 21(16):5672. https://doi.org/10.3390/s21165672
Chicago/Turabian StyleAhmed, Shabbir, and Fotis Kopsaftopoulos. 2021. "Stochastic Identification of Guided Wave Propagation under Ambient Temperature via Non-Stationary Time Series Models" Sensors 21, no. 16: 5672. https://doi.org/10.3390/s21165672
APA StyleAhmed, S., & Kopsaftopoulos, F. (2021). Stochastic Identification of Guided Wave Propagation under Ambient Temperature via Non-Stationary Time Series Models. Sensors, 21(16), 5672. https://doi.org/10.3390/s21165672







