Forces: A Motion Capture-Based Ergonomic Method for the Today’s World
Abstract
1. Introduction
2. Materials and Methods
2.1. Motion Capture System
2.2. Human Model, Worker Anthropometry, and Percentiles
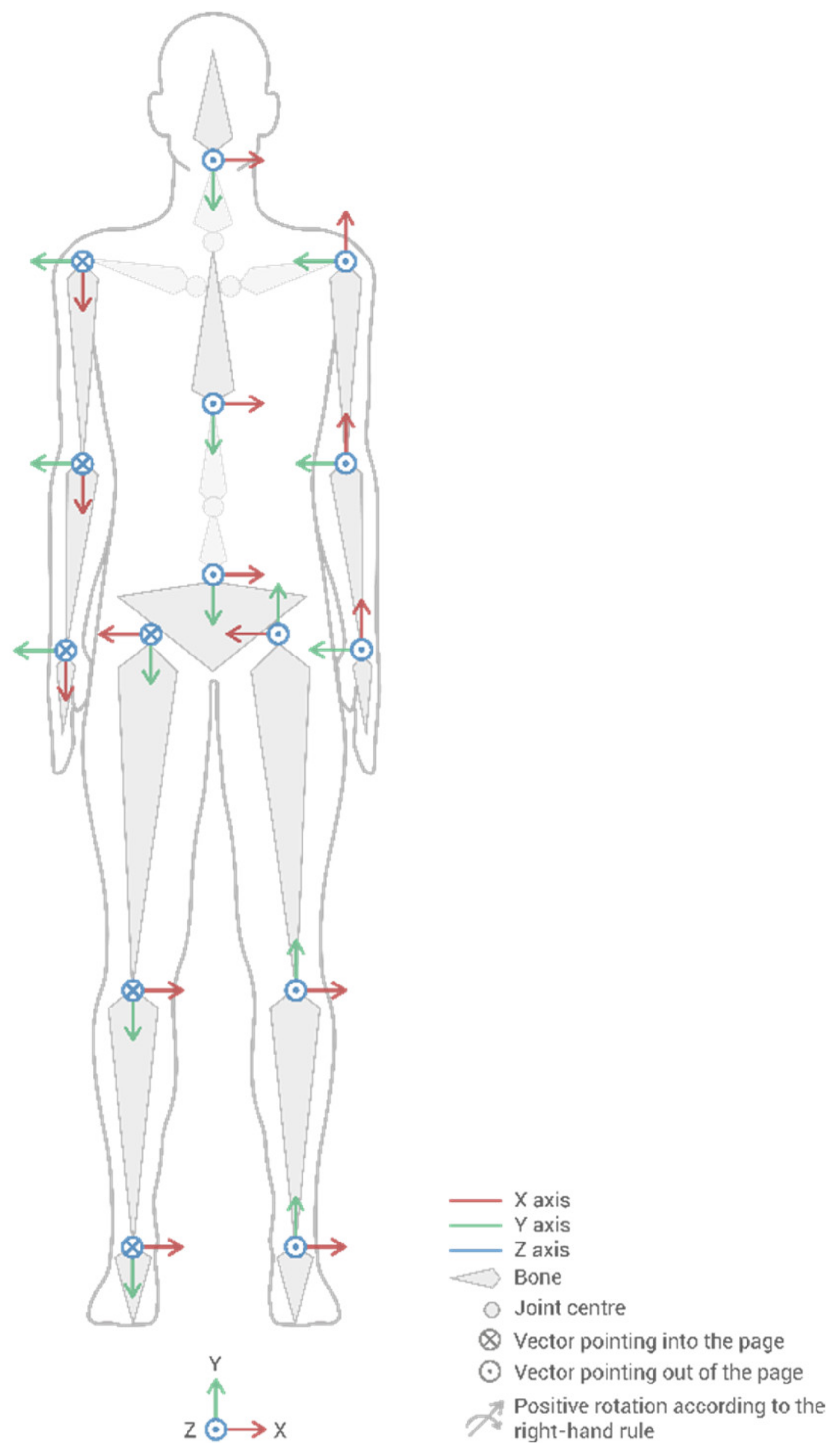
2.3. Kinematics: Calculating Rotations, Displacements, Velocities, and Accelerations in Joints
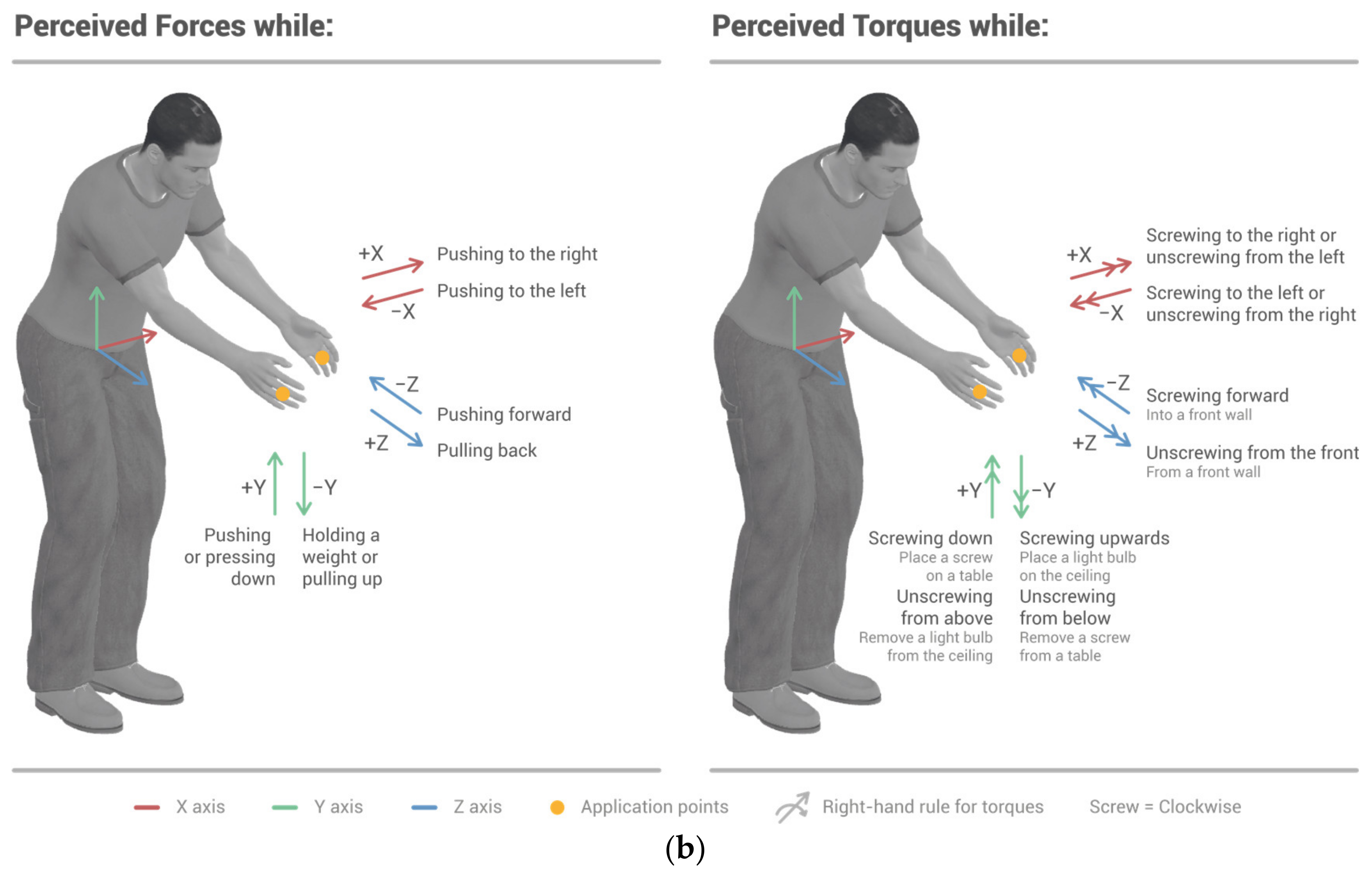
2.4. Kinetics: Calculation of Forces and Torques in Joints
2.5. Risk Calculation Process
- Initial and final frame: This is the range of considered frames to calculate the Forces method. If not specified, the entire range of captured frames is considered.
- Cycle time: This is the time granted in seconds by the production area to accomplish the work cycle. If not specified, the time of the initial and final frame range is taken.
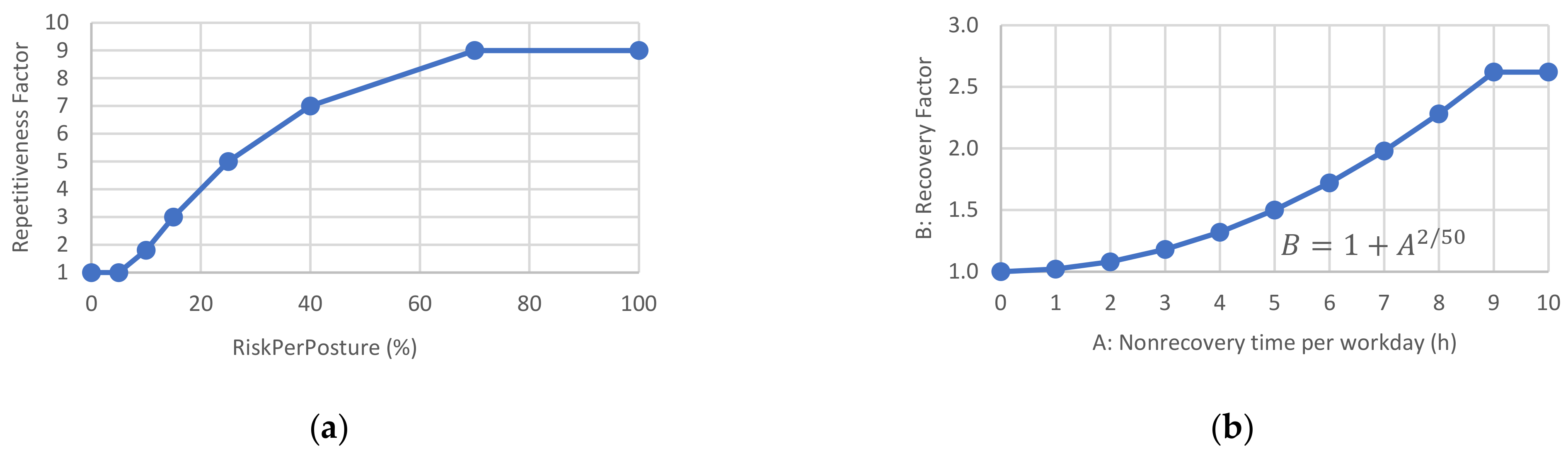
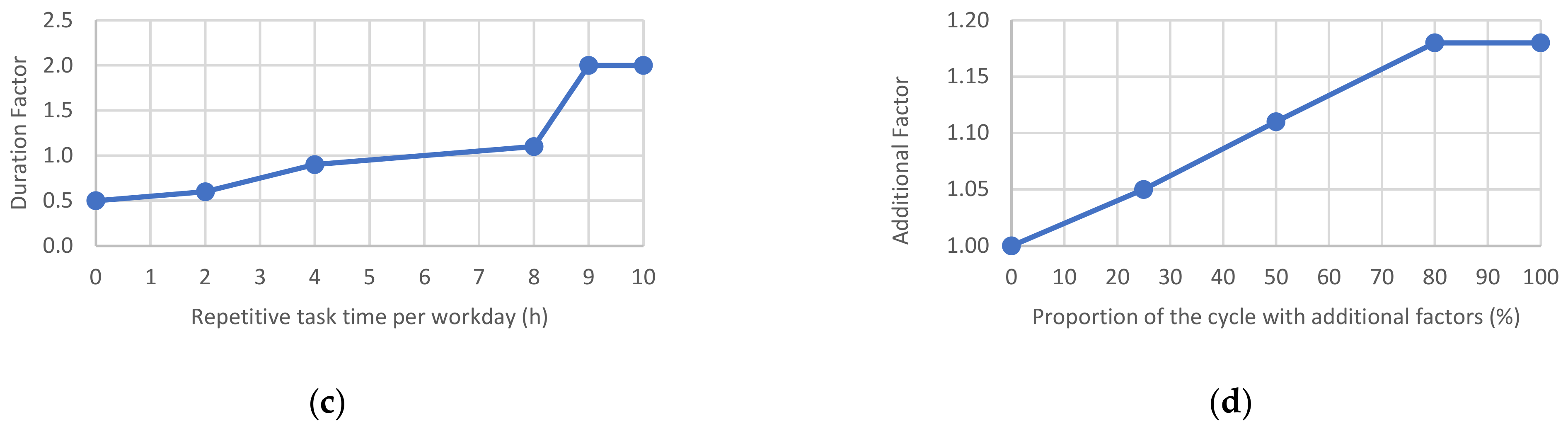
- Nonrecovery time per workday: This is the time in hours without rest (whole number). It is considered 1 h if the worker rests at least 10 min. The final hour of the day is always considered recovered.
- Micro-pauses: This is the risk reduction factor that depends on the number of seconds of rest for each manufacturing cycle. According to Rojas and Ledesma [61], it can be considered 1.0 for a cycle without rest, 0.9 for 1 s every three cycles, 0.8 for 1 s every two cycles, and 0.7 for 1 s each cycle.
- Repetitive task time per workday: The time in hours of the workday (decimal number) with physical activity must be entered for the entire workday of the productive area under study. It can be reduced if a period has nonphysical activity during a certain period of the day. In this manner, it is taken by convention that the risk value resulting from a workstation indicates that the worker remains in the workstation throughout the workday. The implications of this convention are extended in the discussion section (see use case).
- Additional factors: This is the percentage of cycle time with additional factors. The value is established at the evaluator’s discretion to consider other factors cited by the ISO 11228-3 standard. The list of additional factors can be consulted in the Supplementary Materials (first sheet in the Excel workbook Forces_Tables.xlsx). For situations in production plants without highlighting factors, it is advisable to set this value at 20% to penalize the results lightly and be on the safe side.
- Worker preparation: This parameter determines the physical condition of the worker who performs the tasks in the evaluated workstation. This parameter affects the maximum achievable values for the risk calculation, which are established according to the methods in Section 2.6. If the value is 0 (sensitive worker), the maximum thresholds (force and torque) are reduced with a coefficient of 0.9 (reduction of 10%). If the value is 1 (average worker), the maximum efforts are not modified. If the value is 2 (trained worker) or 3 (specially trained worker), the maximum efforts are increased with a coefficient of 1.1 or 1.2, respectively. Therefore, this factor can significantly affect the resulting risks. Thus, a value of 1 is recommended unless the prevention service intends to determine whether the risks are still acceptable for a sensitive worker (value 0) or whether the preparation level of the workers is verified or accredited (a value of 2 or 3).
2.5.1. Biomechanical Risk Per Posture
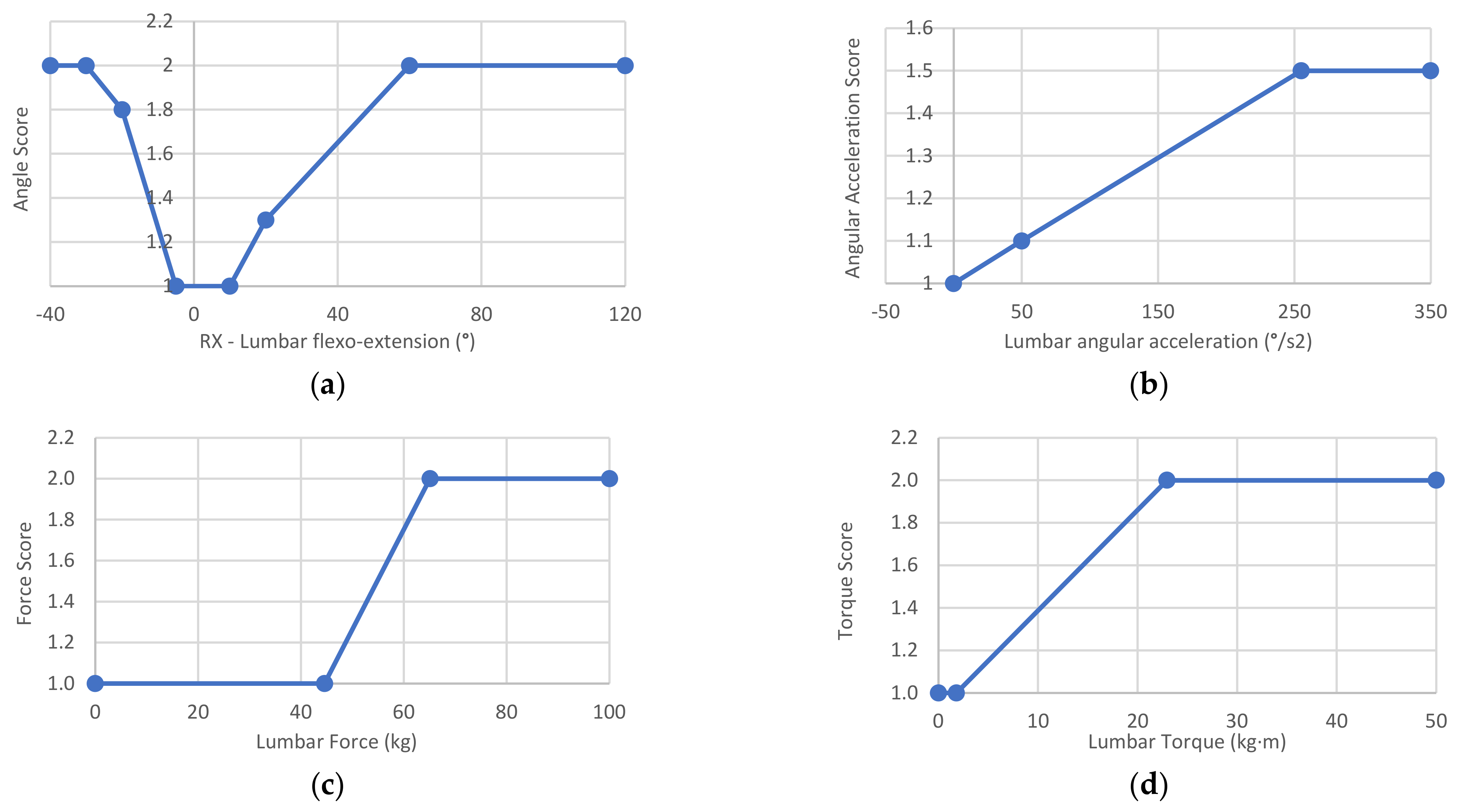
- The AngleScore was established to range from 1 to 2 depending on the joint rotations under study; therefore, it can increase the risk by up to 100%. In the case of the lumbar spine, the rotations are flexion-extension (Rx of the pelvis, see the human model in Figure 2), rotation (Ry), and lateralization (Rz). These angles are entered in the corresponding graph in Figure 5a for the lumbar flexion-extension angle. As a result, three scores between 1 and 2 are obtained, one per angle, and the highest score is then introduced in Equation (4). The supplementary material reveals that the shoulder joint is different from the rest due to its wide range of motion. In this case, a double-entry table is used, with the angles of elevation and anteroposterior rotation. The AngleScore graphs are inspired by the tables of the main postural loading methods: ISO 11226, REBA [10,11], RULA [12], and OWAS [13]. However, unlike these methods, Forces interpolates between the different points and does not score the angle in steps.
- The AngularAccelerationScore was established to range from 1 to 1.5 depending on the angular acceleration of the joint under study; therefore, it can increase the risk by 50%. When the body segment undergoes acceleration or deceleration, the musculoskeletal structures of the involved joint recruit the muscles, tendons, and ligaments necessary to achieve that acceleration and deceleration, which increases the risk on the joint. Therefore, the musculoskeletal requirements on a joint are increased not through speed but change. Thus, each joint has an AngularAccelerationScore graph, such as the one in Figure 5b for the lumbar spine, which comes from the experimentation described in Section 2.6. In this graph, the module of the relative angular acceleration is introduced to obtain the score entered in Equation (4).
- The ForceScore was established to range from 1 to 2 depending on the module of the force supported by the joint under study; therefore, it can increase the total risk by up to 100%. The graphs defined for each joint must be used to obtain this parameter, which comes from the experimentation described in Section 2.6. Figure 5c displays the example for the lumbar spine for a male model of P50. An internal force in the lumbar spine greater than 65.1 kg (maximum value calculated in the experiment in Section 2.6) corresponds to a ForceScore value of 2, and a value less than 44.6 kg (force caused by the body’s weight standing) corresponds to a ForceScore value of 1 (minimum value). Intermediate force values are calculated by interpolation, and the resulting value is entered in Equation (4). In this manner, unlike the previous parameters, the ForceScore depends on the anthropometric characteristics of the human model. Therefore, the maximum thresholds have a version for the male or female model and P5, P50, and P95 percentiles. In addition, as mentioned above, the worker preparation factor also influences the thresholds. All this can be observed in the supplementary material, where a drop-down menu allows the percentile and worker preparation level to be selected to view their influence on the graphs. In this manner, in practice, the thresholds for a worker are calculated automatically by interpolation using the height and values included in the supplementary material tables.
- The TorqueScore was established to range from 1 to 2.5 depending on the module of the torque supported by the joint; therefore, it can increase the total risk by up to 150%. The interpretation, use, and calculation of the TorqueScore factor coincide with the explanation of the ForceScore factor. Figure 5d indicates how to estimate the TorqueScore for the lumbar joint example.
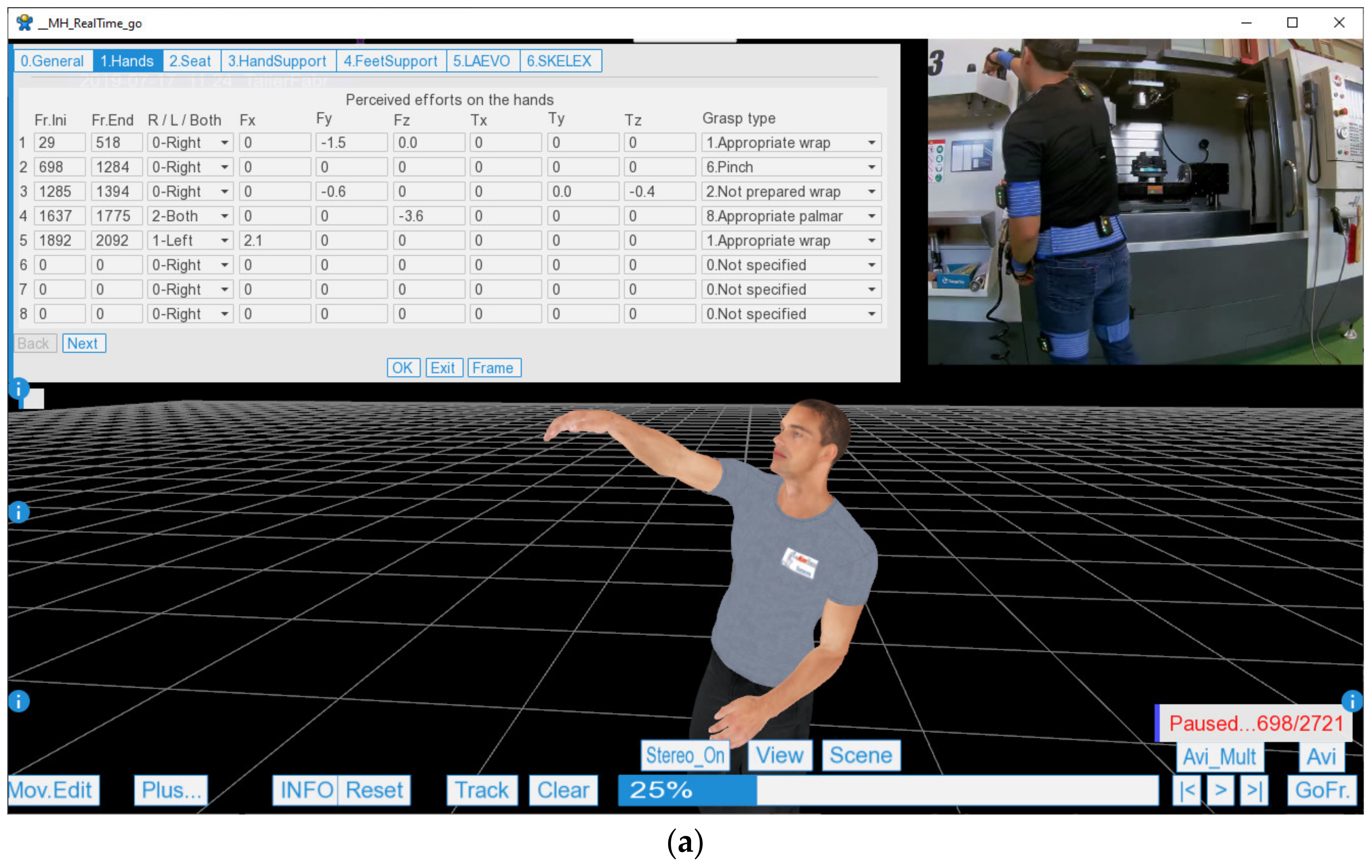
- The GripScore only affects the wrist joint and ranges from 1 to 2; therefore, it can increase the total risk by up to 100%. As described, the grasp type for each action is entered by a drop-down menu using the form in Figure 3. Then, Table 3 is used to obtain the GripScore, which is inspired by ISO 11228-3 (OCRA) [8].
2.5.2. Total Risk per Minute
2.5.3. Final Risk Assessment
2.6. Experimentation to Obtain the Maximum Risk Database
3. Results
- Force Max and Torque Max: module of the force and torque corresponding to the 99th percentile of the set of values resulting from capturing the first type of exercise;
- Force Min and Torque Min: average of the module of the force and torque resulting from a static capture in the standing position (i.e., the second type of exercise);
- Angular Speed Max: module of the angular velocity corresponding to the 99th percentile of the set of values resulting from capturing the first type of exercise;
- Angular Speed Min: average angular speed during slow gesture capture (i.e., the third type of exercise).
4. Discussion
4.1. Value Compared with the Existing Methods
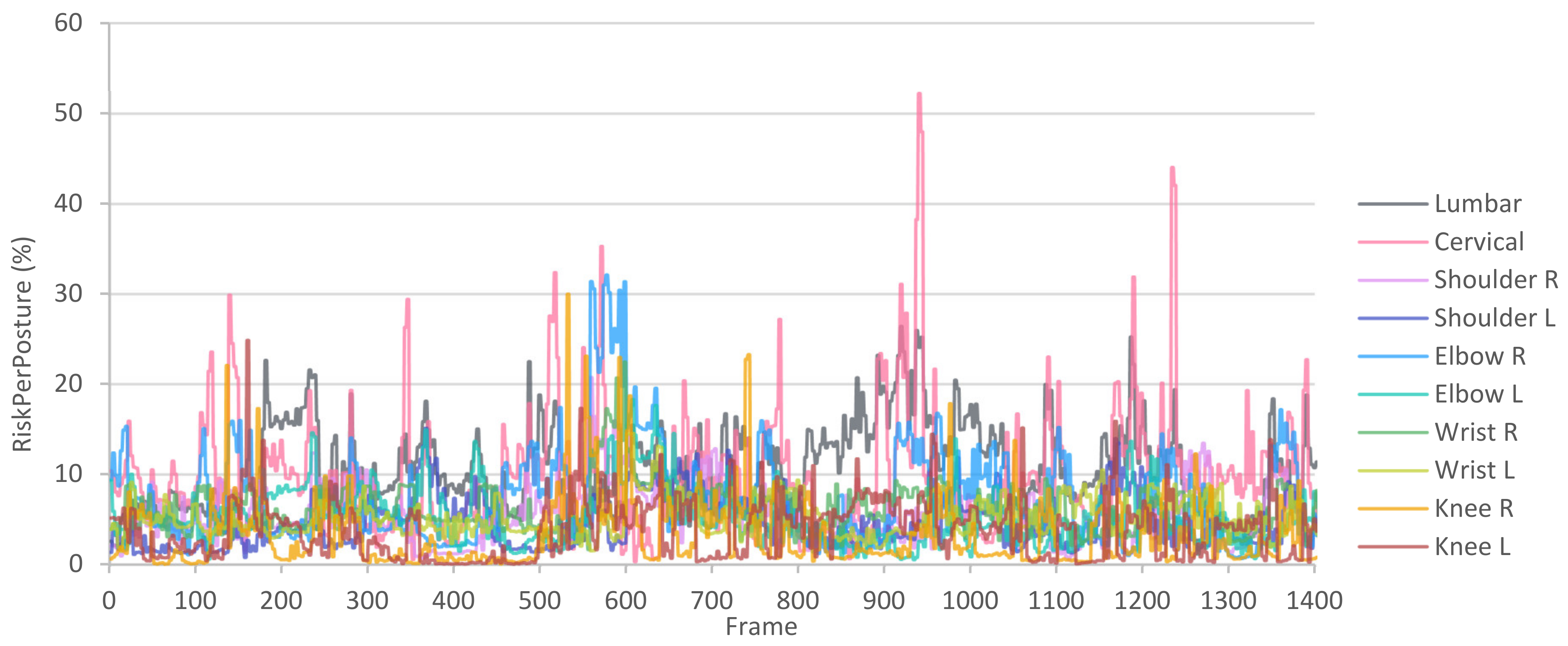
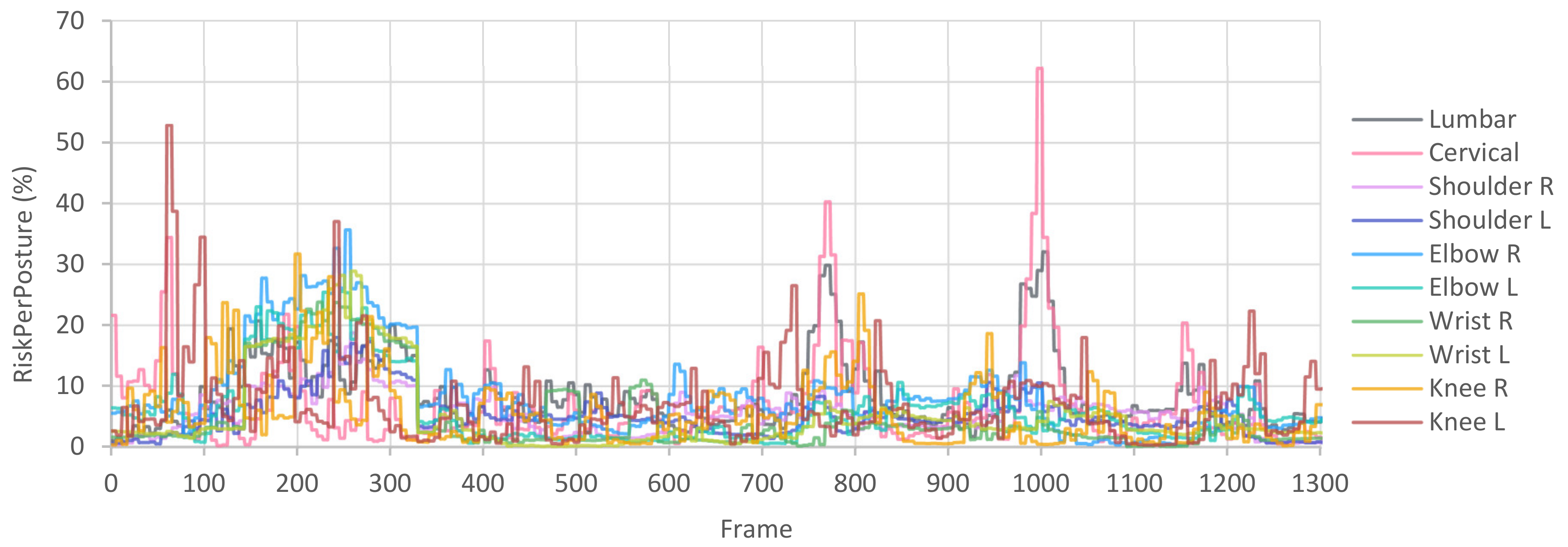
4.2. Manufacturing Industry Use Case
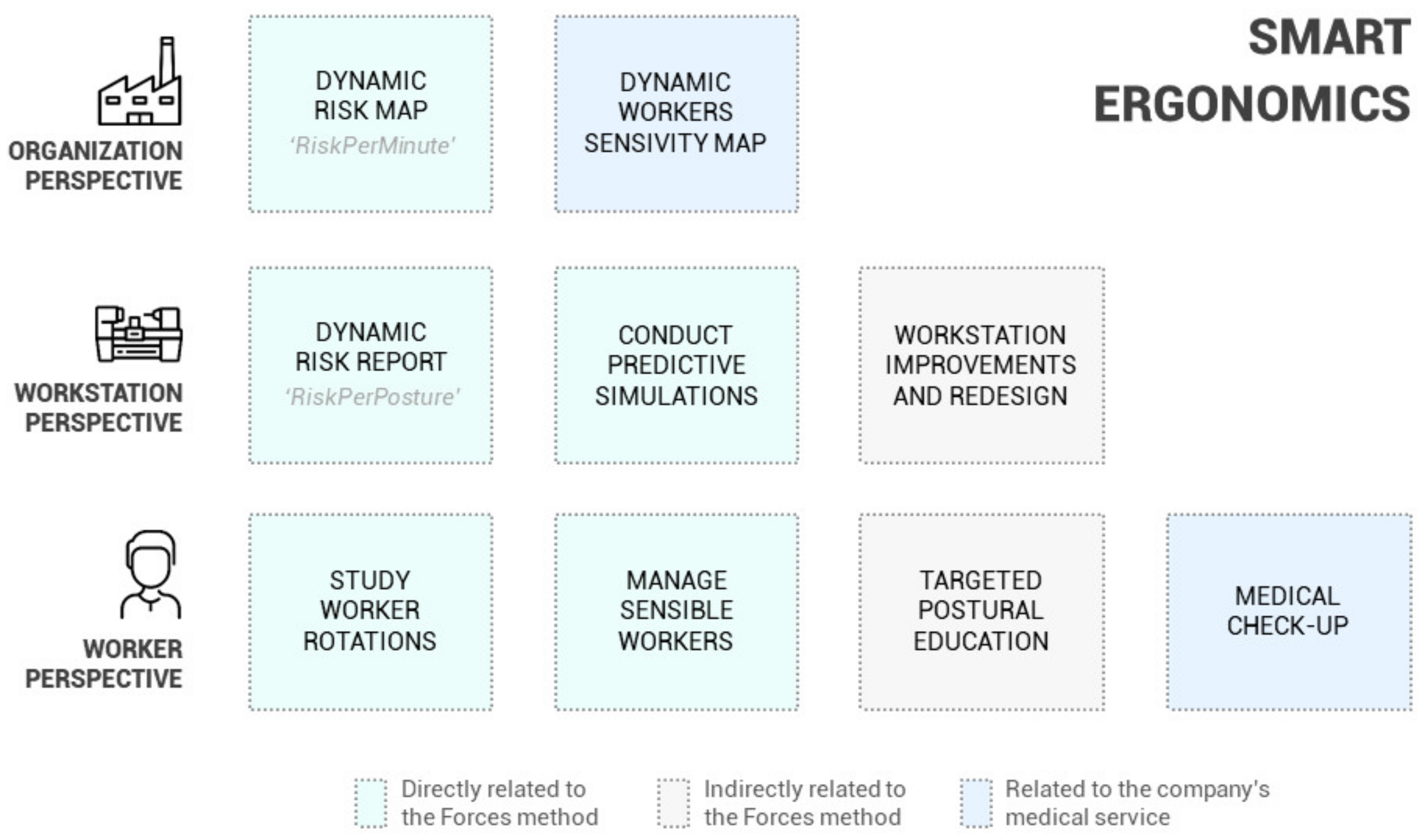
4.3. Smart or 4.0 Ergonomics
4.4. Limitations and Future Work
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- De Kok, J.; Vroonhof, P.; Snijders, J.; Roullis, G.; Clarke, M.; Peereboom, K.; van Dorst, P.; Isusi, I.; Munar, L.; Curtarelli, M. Work-Related Musculoskeletal Disorders: Prevalence, Costs and Demographics in the EU; European Agency for Safety and Health at Work: Bilbao, Spain, 2019. [Google Scholar]
- Da Costa, B.R.; Vieira, E.R. Risk Factors for Work-related Musculoskeletal Disorders: A Systematic Review of Recent Longitudinal Studies. Am. J. Ind. Med. 2010, 53, 285–323. [Google Scholar] [CrossRef]
- Khan, M. Industrial Ergonomics; PHI Learning Pvt. Ltd.: New Delhi, India, 2010. [Google Scholar]
- Karwowski, W. Handbook of Standards and Guidelines in Ergonomics and Human Factors; Routledge: Boca Raton, FL, USA, 2005. [Google Scholar]
- Karlheinz, S.; Michaela, K.; Max, B.; Andrea, S.; Ralph, B. Prevention of MSD by Means of Ergonomic Risk Assessment (Tools) in all Phases of the Vehicle Development Process. Work 2012, 41, 4409–4412. [Google Scholar] [CrossRef]
- Mossa, G.; Boenzi, F.; Digiesi, S.; Mummolo, G.; Romano, V. Productivity and Ergonomic Risk in Human Based Production Systems: A Job-Rotation Scheduling Model. Int. J. Prod. Econ. 2016, 171, 471–477. [Google Scholar] [CrossRef]
- Niskanen, T.; Naumanen, P.; Hirvonen, M.L. An Evaluation of EU Legislation Concerning Risk Assessment and Preventive Measures in Occupational Safety and Health. Appl. Ergon. 2012, 43, 829–842. [Google Scholar] [CrossRef] [PubMed]
- Colombini, D. An Observational Method for Classifying Exposure to Repetitive Movements of the Upper Limbs. Ergonomics 1998, 41, 1261–1289. [Google Scholar] [CrossRef]
- Health Division of Biomedical, Behavioral Science. Work Practices Guide for Manual Lifting; U.S. Department of Health and Human Services, Public Health Service, Centers: Washington, DC, USA, 1981. [Google Scholar]
- Hignett, S.; McAtamney, L. Rapid Entire Body Assessment (REBA). Appl. Ergon. 2000, 31, 201–205. [Google Scholar] [CrossRef]
- Hita-Gutiérrez, M.; Gómez-Galán, M.; Díaz-Pérez, M.; Callejón-Ferre, Á. An Overview of REBA Method Applications in the World. Int. J. Environ. Res. Public Health 2020, 17, 2635. [Google Scholar] [CrossRef]
- McAtamney, L.; Corlett, E.N. RULA: A Survey Method for the Investigation of Work-Related Upper Limb Disorders. Appl. Ergon. 1993, 24, 91–99. [Google Scholar] [CrossRef]
- Scott, G.B.; Lambe, N.R. Working Practices in a Perchery System, using the OVAKO Working Posture Analysing System (OWAS). Appl. Ergon. 1996, 27, 281–284. [Google Scholar] [CrossRef]
- Schaub, K.; Caragnano, G.; Britzke, B.; Bruder, R. The European Assembly Worksheet. Theor. Issues Ergon. Sci. 2013, 14, 616–639. [Google Scholar] [CrossRef]
- Chander, D.S.; Cavatorta, M.P. An Observational Method for Postural Ergonomic Risk Assessment (PERA). Int. J. Ind. Ergon. 2017, 57, 32–41. [Google Scholar] [CrossRef]
- Andreas, G.J.; Johanssons, E. Observational Methods for Assessing Ergonomic Risks for Work-Related Musculoskeletal Disorders. A Scoping Review. Rev. Cienc. Salud 2018, 16, 8–38. [Google Scholar]
- Xu, L.D.; Xu, E.L.; Li, L. Industry 4.0: State of the Art and Future Trends. Int. J. Prod. Res. 2018, 56, 2941–2962. [Google Scholar] [CrossRef]
- Perera, C.; Zaslavsky, A.; Christen, P.; Georgakopoulos, D. Context Aware Computing for the Internet of Things: A Survey. IEEE Commun. Surv. Tutor. 2014, 16, 414–454. [Google Scholar] [CrossRef]
- Liao, Y.; de Freitas Rocha Loures, E.; Deschamps, F. Industrial Internet of Things: A Systematic Literature Review and Insights. IEEE Internet Things J. 2018, 5, 4515–4525. [Google Scholar] [CrossRef]
- Diego-Mas, J.; Alcaide-Marzal, J.; Poveda-Bautista, R. Errors using Observational Methods for Ergonomics Assessment in Real Practice. Hum. Factors 2017, 59, 1173–1187. [Google Scholar] [CrossRef] [PubMed]
- Diego-Mas, J.; Poveda-Bautista, R.; Garzon-Leal, D. Influences on the use of Observational Methods by Practitioners when Identifying Risk Factors in Physical Work. Ergonomics 2015, 58, 1660–1670. [Google Scholar] [CrossRef] [PubMed]
- Kadir, B.A.; Broberg, O.; da Conceicao, C.S. Current Research and Future Perspectives on Human Factors and Ergonomics in Industry 4.0. Comput. Ind. Eng. 2019, 137, 106004. [Google Scholar] [CrossRef]
- Reiman, A.; Kaivo-oja, J.; Parviainen, E.; Takala, E.; Lauraeus, T. Human Factors and Ergonomics in Manufacturing in the Industry 4.0 context–A Scoping Review. Technol. Soc. 2021, 65, 101572. [Google Scholar] [CrossRef]
- Gášová, M.; Gašo, M.; Štefánik, A. Advanced Industrial Tools of Ergonomics Based on Industry 4.0 Concept. Procedia Eng. 2017, 192, 219–224. [Google Scholar] [CrossRef]
- Lanzotti, A.; Vanacore, A.; Tarallo, A.; Nathan-Roberts, D.; Coccorese, D.; Minopoli, V.; Carbone, F.; d’Angelo, R.; Grasso, C.; Di Gironimo, G. Interactive Tools for Safety 4.0: Virtual Ergonomics and Serious Games in Real Working Contexts. Ergonomics 2020, 63, 324–333. [Google Scholar] [CrossRef]
- Felekoglu, B.; Ozmehmet Tasan, S. Interactive Ergonomic Risk Mapping: A Practical Approach for Visual Management of Workplace Ergonomics. Int. J. Occup. Saf. Ergon. 2020, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Zare, M.; Biau, S.; Croq, M.; Roquelaure, Y. Development of a Biomechanical Method for Ergonomic Evaluation: Comparison with Observational Methods. Int. J. Soc. Manag. Econ. Bus. Eng. 2014, 8, 223–227. [Google Scholar]
- Boros, D.P.; Hercegfi, K. Digital Human Modelling in Research and Development–A State of the Art Comparison of Software. In Proceedings of the International Conference on Human Systems Engineering and Design: Future Trends and Applications, Munich, Germany, 16–18 September 2019; pp. 543–548. [Google Scholar]
- Caputo, F.; Greco, A.; Egidio, D.; Notaro, I.; Spada, S. Imu-Based Motion Capture Wearable System for Ergonomic Assessment in Industrial Environment. In Proceedings of the International Conference on Applied Human Factors and Ergonomics, Washington, DC, USA, 24–28 July 2019; pp. 215–225. [Google Scholar]
- Peppoloni, L.; Filippeschi, A.; Ruffaldi, E.; Avizzano, C. A Novel Wearable System for the Online Assessment of Risk for Biomechanical Load in Repetitive Efforts. Int. J. Ind. Ergon. 2016, 52, 1–11. [Google Scholar] [CrossRef]
- Cloete, T.; Scheffer, C. Benchmarking of a Full-Body Inertial Motion Capture System for Clinical Gait Analysis. In Proceedings of the 30th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Vancouver, BC, Canada, 20–25 August 2008; pp. 4579–4582. [Google Scholar]
- Mooney, R.; Corley, G.; Godfrey, A.; Quinlan, L.R.; Ó′Laighin, G. Inertial Sensor Technology for Elite Swimming Performance Analysis: A Systematic Review. Sensors 2015, 16, 18. [Google Scholar] [CrossRef] [PubMed]
- Cooper, G.; Sheret, I.; McMillian, L.; Siliverdis, K.; Sha, N.; Hodgins, D.; Kenney, L.; Howard, D. Inertial Sensor-Based Knee Flexion/Extension Angle Estimation. J. Biomech. 2009, 42, 2678–2685. [Google Scholar] [CrossRef] [PubMed]
- Marin, J.; Blanco, T.; Marin, J.J. Octopus: A Design Methodology for Motion Capture Wearables. Sensors 2017, 17, 1875. [Google Scholar] [CrossRef] [PubMed]
- Marín, J.; Blanco, T.; de la Torre, J.; Marín, J.J. Gait Analysis in a Box: A System Based on Magnetometer-Free IMUs or Clusters of Optical Markers with Automatic Event Detection. Sensors 2020, 20, 3338. [Google Scholar] [CrossRef]
- Robert-Lachaine, X.; Mecheri, H.; Larue, C.; Plamondon, A. Validation of Inertial Measurement Units with an Optoelectronic System for Whole-Body Motion Analysis. Med. Biol. Eng. Comput. 2017, 55, 609–619. [Google Scholar] [CrossRef]
- Ligorio, G.; Bergamini, E.; Truppa, L.; Guaitolini, M.; Raggi, M.; Mannini, A.; Sabatini, A.M.; Vannozzi, G.; Garofalo, P. A Wearable Magnetometer-Free Motion Capture System: Innovative Solutions for Real-World Applications. IEEE Sens. J. 2020, 20, 8844–8857. [Google Scholar] [CrossRef]
- Vignais, N.; Miezal, M.; Bleser, G.; Mura, K.; Gorecky, D.; Marin, F. Innovative System for Real-Time Ergonomic Feedback in Industrial Manufacturing. Appl. Ergon. 2013, 44, 566–574. [Google Scholar] [CrossRef]
- ViveLab Ergo. Available online: https://www.vivelab.cloud/ (accessed on 21 June 2021).
- Nawo Live. Available online: https://www.xsens.com/nawolive (accessed on 21 June 2021).
- ScaleFit. Available online: https://www.scalefit.de/ (accessed on 21 June 2021).
- Blanco, T. Metodologías de diseño como plataforma para la x-disciplinaridad en proyectos tecnológicos: Surfing disciplines. PhD. Thesis, Universitat Politècnica de València, Valencia, Spain, 2016. [Google Scholar]
- Boné, M.J. Método de evaluación ergonómica de tareas repetitivas, basado en simulación dinámica de esfuerzos con modelos humanos. PhD. Thesis, Universidad de Zaragoza, Zaragoza, Spain, 2016. [Google Scholar]
- Blanco, T.; Berbegal, A.; Blasco, R.; Casas, R. Xassess: Crossdisciplinary Framework in User-Centred Design of Assistive Products. J. Eng. Des. 2016, 27, 636–664. [Google Scholar] [CrossRef]
- Pedersen, K.; Emblemsvåg, J.; Bailey, R.; Allen, J.K.; Mistree, F. Validating Design Methods and Research: The Validation Square. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Virtual Conference, 17–19 August 2020; pp. 379–390. [Google Scholar]
- Takala, E.; Pehkonen, I.; Forsman, M.; Hansson, G.; Mathiassen, S.E.; Neumann, W.P.; Sjøgaard, G.; Veiersted, K.B.; Westgaard, R.H.; Winkel, J. Systematic Evaluation of Observational Methods Assessing Biomechanical Exposures at Work. Scand. J. Work Environ. Health 2010, 36, 3–24. [Google Scholar] [CrossRef]
- Marin, J.; Marin, J.J.; Blanco, T.; de la Torre, J.; Salcedo, I.; Martitegui, E. Is My Patient Improving? Individualized Gait Analysis in Rehabilitation. Appl. Sci. 2020, 10, 8558. [Google Scholar] [CrossRef]
- X-io Technologies. Next Generation IMU (NGIMU). Available online: http://x-io.co.uk/ngimu/ (accessed on 21 June 2021).
- Baker, R. Gait Analysis Methods in Rehabilitation. J. Neuroeng. Rehabil. 2006, 3, 4. [Google Scholar] [CrossRef]
- Haratian, R.; Twycross-Lewis, R.; Timotijevic, T.; Phillips, C. Toward Flexibility in Sensor Placement for Motion Capture Systems: A Signal Processing Approach. IEEE Sens. J. 2014, 14, 701–709. [Google Scholar] [CrossRef]
- Bonnet, S.; Bassompierre, C.; Godin, C.; Lesecq, S.; Barraud, A. Calibration Methods for Inertial and Magnetic Sensors. Sens. Actuators A Phys. 2009, 156, 302–311. [Google Scholar] [CrossRef]
- Palermo, E.; Rossi, S.; Marini, F.; Patanè, F.; Cappa, P. Experimental Evaluation of Accuracy and Repeatability of a Novel Body-to-Sensor Calibration Procedure for Inertial Sensor-Based Gait Analysis. Measurement 2014, 52, 145–155. [Google Scholar] [CrossRef]
- Vargas-Valencia, L.S.; Elias, A.; Rocon, E.; Bastos-Filho, T.; Frizera, A. An IMU-to-Body Alignment Method Applied to Human Gait Analysis. Sensors 2016, 16, 2090. [Google Scholar] [CrossRef] [PubMed]
- Huston, R. Principles of Biomechanics; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- Petrescu, F.I.; Petrescu, R.V. Direct and Inverse Kinematics to the Anthropomorphic Robots. Engevista 2016, 18, 109–124. [Google Scholar] [CrossRef][Green Version]
- Nielsen, J.; Roth, B. On the Kinematic Analysis of Robotic Mechanisms. Int. J. Robot. Res. 1999, 18, 1147–1160. [Google Scholar] [CrossRef]
- Robert, T.; Chèze, L.; Dumas, R.; Verriest, J. Joint Forces and Moments Calculation for a 3D Whole Body Model during Complex Movement. In Proceedings of the International Symposium on the 3-D Analysis of Human Movement, Valenciannes, France, 28–30 June 2006; pp. 1–4. [Google Scholar]
- Logar, G.; Munih, M. Estimation of Joint Forces and Moments for the in-Run and Take-Off in Ski Jumping Based on Measurements with Wearable Inertial Sensors. Sensors 2015, 15, 11258–11276. [Google Scholar] [CrossRef] [PubMed]
- Karatsidis, A.; Bellusci, G.; Schepers, H.M.; De Zee, M.; Andersen, M.S.; Veltink, P.H. Estimation of Ground Reaction Forces and Moments during Gait using Only Inertial Motion Capture. Sensors 2017, 17, 75. [Google Scholar] [CrossRef]
- Miyajima, S.; Tanaka, T.; Imamura, Y.; Kusaka, T. Lumbar Joint Torque Estimation Based on Simplified Motion Measurement using Multiple Inertial Sensors. In Proceedings of the 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Milan, Italy, 25–29 August 2019; pp. 6716–6719. [Google Scholar]
- Rojas, A.; Ledesma, J. NTP 629 Movimientos Repetitivos: Métodos De Evaluación. Método OCRA: Actualización; Instituto Nacional de Seguridad e Higiene en el Trabajo (INSHT): Madrid, Spain, 2003. [Google Scholar]
- Polášek, P.; Bureš, M.; Šimon, M. Comparison of Digital Tools for Ergonomics in Practice. Procedia Eng. 2015, 100, 1277–1285. [Google Scholar] [CrossRef]
- Backstrand, G.; Hogberg, D.; De Vin, L.J.; Case, K.; Piamonte, P. Ergonomics Analysis in a Virtual Environment. Int. J. Manuf. Res. 2007, 2, 198–208. [Google Scholar] [CrossRef]
- Hägg, G.M. Corporate Initiatives in Ergonomics—An Introduction. Appl. Ergon. 2003, 34, 3–15. [Google Scholar] [CrossRef]
- Abdul-Tharim, A.; Jaffar, N.; Lop, N.; Mohd-Kamar, I. Ergonomic Risk Controls in Construction Industry—A Literature Review. Procedia Eng. 2011, 20, 80–88. [Google Scholar] [CrossRef][Green Version]
- Soer, R.; Brouwer, S.; Geertzen, J.H.; van der Schans, C.P.; Groothoff, J.W.; Reneman, M.F. Decline of Functional Capacity in Healthy Aging Workers. Arch. Phys. Med. Rehabil. 2012, 93, 2326–2332. [Google Scholar] [CrossRef]
- Chughtai, T. Factors Associated with Performance on Short-Form Functional Capacity Evaluation in Workers’ Compensation Claimants. Master’s Thesis, University of Alberta, Alberta, Canada, 2017. [Google Scholar]
- Kirin, S.; Dragčević, Z.; Firšt Rogale, S. Workplace Redesign in the Computer-Aided Technological Sewing Process. Tekst. J. Text. Cloth. Technol. 2014, 63, 14–26. [Google Scholar]
- Lindskog, E.; Berglund, J.; Vallhagen, J.; Johansson, B. Visualization Support for Virtual Redesign of Manufacturing Systems. Procedia CIRP 2013, 7, 419–424. [Google Scholar] [CrossRef][Green Version]
- Padula, R.S.; Comper, M.L.C.; Sparer, E.H.; Dennerlein, J.T. Job Rotation Designed to Prevent Musculoskeletal Disorders and Control Risk in Manufacturing Industries: A Systematic Review. Appl. Ergon. 2017, 58, 386–397. [Google Scholar] [CrossRef] [PubMed]
- Occupational Safety and Health Administration. Ergonomics Program Management Guidelines for Meatpacking Plants; Department of Labor: Washington, DC, USA, 1990. [Google Scholar]
- Comper, M.L.C.; Padula, R.S. The Effectiveness of Job Rotation to Prevent Work-Related Musculoskeletal Disorders: Protocol of a Cluster Randomized Clinical Trial. BMC Musculoskelet. Disord. 2014, 15, 1–6. [Google Scholar] [CrossRef]
- ErgoPlus. Ergonomics Plus Step-by-Step Guide to Job Rotation. Available online: https://ergo-plus.com/job-rotation/ (accessed on 1 June 2021).
- Sutarto, A.P.; Wahab, M.N.A.; Zin, N.M. Heart Rate Variability (HRV) Biofeedback: A New Training Approach for Operator’s Performance Enhancement. J. Ind. Eng. Manag. 2010, 3, 176–198. [Google Scholar] [CrossRef]
- Naranjo, J.E.; Sanchez, D.G.; Robalino-Lopez, A.; Robalino-Lopez, P.; Alarcon-Ortiz, A.; Garcia, M.V. A Scoping Review on Virtual Reality-Based Industrial Training. Appl. Sci. 2020, 10, 8224. [Google Scholar] [CrossRef]
- Lebleu, J.; Gosseye, T.; Detrembleur, C.; Mahaudens, P.; Cartiaux, O.; Penta, M. Lower Limb Kinematics using Inertial Sensors during Locomotion: Accuracy and Reproducibility of Joint Angle Calculations with Different Sensor-to-Segment Calibrations. Sensors 2020, 20, 715. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.K.; Jeon, T.H. IMU-Based but Magnetometer-Free Joint Angle Estimation of Constrained Links. In Proceedings of the 2018 IEEE Sensors, New Delhi, India, 28–30 October 2018; pp. 1–4. [Google Scholar]
- Laidig, D.; Schauer, T.; Seel, T. Exploiting Kinematic Constraints to Compensate Magnetic Disturbances when Calculating Joint Angles of Approximate Hinge Joints from Orientation Estimates of Inertial Sensors. In Proceedings of the 2017 International Conference on Rehabilitation Robotics (ICORR), London, UK, 17–20 July 2017; pp. 971–976. [Google Scholar]
- Cardarelli, S.; di Florio, P.; Mengarelli, A.; Tigrini, A.; Fioretti, S.; Verdini, F. Magnetometer-Free Sensor Fusion Applied to Pedestrian Tracking: A Feasibility Study. In Proceedings of the 2019 IEEE 23rd International Symposium on Consumer Technologies (ISCT), Ancona, Italy, 19–21 June 2019; pp. 238–242. [Google Scholar]
- Visi, F.; Georgiou, T.; Holland, S.; Pinzone, O.; Donaldson, G.; Tetley, J. Assessing the Accuracy of an Algorithm for the Estimation of Spatial Gait Parameters using Inertial Measurement Units: Application to Healthy Subject and Hemiparetic Stroke Survivor. In Proceedings of the 4th International Conference on Movement Computing, London, UK, 28–30 June 2017; pp. 1–7. [Google Scholar]



| Male Height (cm) | Male Weight (kg) | Female Height (cm) | Female Weight (kg) | |
|---|---|---|---|---|
| P05 | 164.9 | 66.21 | 151.8 | 49.44 |
| P50 | 175.9 | 80.50 | 161.8 | 59.85 |
| P95 | 186.9 | 96.41 | 172.4 | 72.43 |
| %W M | %WF | %CGM | %CGF | T M.P05 | T M.P50 | T M.P95 | T F.P05 | T F.P50 | T F.P95 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Pelvis | 12.42 | 16.72 | 50.0 | 50.0 | [0.065, 0.105, 0.105] | [0.091, 0.148, 0.148] | [0.122, 0.199, 0.190] | [0.052, 0.083, 0.086] | [0.075, 0.120, 0.123] | [0.106, 0.169, 0.174] |
| Lumbar | 13.60 | 11.02 | 50.0 | 50.0 | [0.065, 0.105, 0.105] | [0.091, 0.148, 0.015] | [0.122, 0.199, 0.199] | [0.031, 0.050, 0.051] | [0.045, 0.072, 0.074] | [0.064, 0.102, 0.104] |
| Thorax | 23.19 | 15.55 | 49.7 | 49.7 | [0.052, 0.075, 0.075] | [0.073, 0.106, 0.106] | [0.098, 0.142, 0.142] | [0.021, 0.031, 0.031] | [0.030, 0.044, 0.044] | [0.042, 0.062, 0.062] |
| Head | 8.39 | 9.13 | 30.0 | 30.0 | [0.027, 0.014, 0.027] | [0.038, 0.019, 0.038] | [0.051, 0.026, 0.051] | [0.017, 0.009, 0.017] | [0.025, 0.013, 0.025] | [0.035, 0.018, 0.035] |
| Arm | 2.77 | 2.85 | 38.0 | 37.9 | [0.002, 0.019, 0.019] | [0.003, 0.027, 0.027] | [0.004, 0.036, 0.036] | [0.001, 0.012, 0.012] | [0.002, 0.017, 0.017] | [0.003, 0.024, 0.024] |
| Forearm | 1.73 | 1.71 | 49.5 | 49.6 | [0.001, 0.014, 0.014] | [0.001, 0.020, 0.020] | [0.001, 0.027, 0.027] | [0.001, 0.009, 0.009] | [0.001, 0.013, 0.013] | [0.001, 0.018, 0.018] |
| Hand | 0.65 | 0.69 | 80.0 | 80.0 | [0.001, 0.001, 0.003] | [0.001, 0.001, 0.004] | [0.001, 0.001, 0.005] | [0.001, 0.001, 0.001] | [0.001, 0.001, 0.002] | [0.001, 0.001, 0.003] |
| Thigh | 10.49 | 12.57 | 53.2 | 53.0 | [0.069, 0.017, 0.069] | [0.097, 0.024, 0.097] | [0.130, 0.032, 0.130] | [0.049, 0.013, 0.049] | [0.071, 0.018, 0.071] | [0.100, 0.025, 0.100] |
| Shin | 4.28 | 4.53 | 49.8 | 49.4 | [0.006, 0.001, 0.006] | [0.008, 0.001, 0.008] | [0.011, 0.001, 0.011] | [0.003, 0.001, 0.003] | [0.005, 0.001, 0.005] | [0.007, 0.001, 0.007] |
| Foot | 1.28 | 1.44 | 50.0 | 50.0 | [0.005, 0.005, 0.001] | [0.007, 0.007, 0.001] | [0.009, 0.009, 0.001] | [0.003, 0.003, 0.001] | [0.004, 0.005, 0.001] | [0.006, 0.007, 0.001] |
| Grasp Type | GripScore |
|---|---|
| 0. Not specified | 1.0 |
| 1. Appropriate wrap | 1.3 |
| 2. Unprepared wrap | 1.8 |
| 3. Appropriate hook | 1.3 |
| 4. Reasonably appropriate hook | 1.6 |
| 5. Unprepared hook | 1.9 |
| 6. Pinch | 1.3 |
| 7. Precision pinch | 1.6 |
| 8. Appropriate open hand | 1.7 |
| 9. Unprepared open hand | 2.0 |
| Angle Score | Angular Acceleration Score | Force Score | Torque Score | Grip Score | Maximum Factors Per Posture | |
|---|---|---|---|---|---|---|
| Lumbar | 2.0 | 1.5 | 2.0 | 2.5 | 1.0 | 14 |
| Cervical | 2.0 | 1.5 | 2.0 | 2.5 | 1.0 | 14 |
| Shoulder | 2.0 | 1.5 | 2.0 | 2.5 | 1.0 | 14 |
| Elbow | 2.0 | 1.5 | 2.0 | 2.5 | 1.0 | 14 |
| Wrist | 1.6 | 1.5 | 2.0 | 2.5 | 2.0 | 23 |
| Knee | 2.0 | 1.5 | 2.0 | 2.5 | 1.0 | 14 |
| RiskPerMinute (%) | RiskLevel | Valuation | Interpretation |
|---|---|---|---|
| ≤10 | ≤1 | No risk | Acceptable |
| >10 ≤ 15 | >1 ≤ 2 | Low risk | |
| >15 ≤ 25 | >2 ≤ 3 | Medium risk | |
| >25 ≤ 40 | >3 ≤ 4 | High risk | Conditional |
| >40 ≤ 70 | >4 ≤ 5 | Very high risk | Unacceptable |
| >70 | >5 | Severe risk |
| Variable | P (%) | Lumbar | Cervical | Shoulder R | Shoulder L | Elbow R | Elbow L | Wrist R | Wrist L | Knee R | Knee L |
|---|---|---|---|---|---|---|---|---|---|---|---|
| M. Force Max. (kg) | P50 | 65.1 (0.8) | 8.8 (0.0) | 13.6 (0.1) | 13.6 (0.1) | 11.6 (0.0) | 11.6 (0.0) | 10.6 (0.1) | 10.6 (0.1) | 81.1 (6.7) | 80.2 (10.2) |
| P05 | 56.4 (0.3) | 7.2 (0.0) | 13.0 (0.1) | 13.0 (0.1) | 11.4 (0.1) | 11.4 (0.0) | 10.5 (0.1) | 10.5 (0.1) | 68.0 (5.7) | 67.0 (8.6) | |
| P95 | 75.3 (1.4) | 10.5 (0.0) | 14.3 (0.1) | 14.3 (0.1) | 11.9 (0.0) | 11.9 (0.0) | 10.7 (0.1) | 10.7 (0.1) | 95.8 (7.4) | 95.0 (11.7) | |
| M. Force Min. (kg) | P50 | 44.6 (0.0) | 6.8 (0.0) | 4.2 (0.0) | 4.2 (0.0) | 1.9 (0.0) | 1.9 (0.0) | 0.5 (0.0) | 0.5 (0.0) | 36.4 (0.3) | 37.5 (0.5) |
| F. Force Max. (kg) | P50 | 46.9 (0.2) | 7.1 (0.0) | 12.7 (0.1) | 12.7 (0.1) | 11.2 (0.1) | 11.2 (0.0) | 10.5 (0.1) | 10.5 (0.1) | 60.8 (5.7) | 60.0 (7.9) |
| P05 | 42.0 (0.2) | 5.9 (0.0) | 12.3 (0.1) | 12.3 (0.1) | 11.0 (0.1) | 11.0 (0.1) | 10.4 (0.1) | 10.4 (0.1) | 51.5 (5.1) | 50.8 (6.8) | |
| P95 | 53.0 (0.3) | 8.6 (0.0) | 13.3 (0.1) | 13.3 (0.1) | 11.5 (0.1) | 11.5 (0.0) | 10.5 (0.1) | 10.5 (0.1) | 72.2 (6.5) | 71.3 (9.4) | |
| F. Force Min. (kg) | P50 | 27.7 (0.0) | 5.5 (0.0) | 3.1 (0.0) | 3.1 (0.0) | 1.4 (0.0) | 1.4 (0.0) | 0.4 (0.0) | 0.4 (0.0) | 26.8 (0.2) | 27.6 (0.4) |
| M. Torque Max. (kg∙m) | P50 | 22.95 (2.79) | 0.90 (0.07) | 5.86 (0.09) | 5.85 (0.09) | 3.21 (0.07) | 3.20 (0.09) | 0.83 (0.00) | 0.83 (0.00) | 23.72 (7.31) | 28.95 (11.1) |
| P05 | 18.90 (2.14) | 0.66 (0.05) | 5.39 (0.08) | 5.39 (0.08) | 2.98 (0.07) | 2.97 (0.08) | 0.81 (0.00) | 0.81 (0.00) | 18.32 (5.33) | 22.36 (9.01) | |
| P95 | 27.94 (3.47) | 1.18 (0.1) | 6.37 (0.11) | 6.36 (0.09) | 3.46 (0.08) | 3.44 (0.09) | 0.85 (0.00) | 0.85 (0.00) | 30.16 (9.86) | 36.96 (13.87) | |
| M. Torque Min. (kg∙m) | P50 | 1.81 (0.12) | 0.15 (0.00) | 0.47 (0.02) | 0.50 (0.04) | 0.33 (0.00) | 0.33 (0.00) | 0.04 (0.00) | 0.04 (0.00) | 3.63 (0.51) | 3.84 (0.57) |
| F. Torque Max. (kg∙m) | P50 | 15.92 (1.79) | 0.62 (0.05) | 5.14 (0.07) | 5.16 (0.08) | 2.81 (0.07) | 2.81 (0.08) | 0.7 (0.00) | 0.7 (0.00) | 16.03 (4.73) | 19.3 (8.21) |
| P05 | 13.49 (1.50) | 0.45 (0.03) | 4.76 (0.06) | 4.78 (0.07) | 2.62 (0.06) | 2.62 (0.07) | 0.68 (0.00) | 0.68 (0.00) | 12.27 (3.38) | 14.78 (6.53) | |
| P95 | 19.09 (2.18) | 0.84 (0.07) | 5.58 (0.09) | 5.59 (0.08) | 3.03 (0.07) | 3.02 (0.08) | 0.72 (0.00) | 0.72 (0.00) | 20.67 (6.34) | 25.54 (9.81) | |
| F. Torque Min. (kg∙m) | P50 | 1.08 (0.07) | 0.11 (0.00) | 0.33 (0.01) | 0.35 (0.03) | 0.23 (0.00) | 0.23 (0.00) | 0.03 (0.00) | 0.03 (0.00) | 2.26 (0.33) | 2.39 (0.35) |
| AngSpeed Max. (°/s) | - | 51.0 (6.1) | 222.7 (39.4) | 240.2 (43.9) | 254.5 (40.3) | 219.3 (22.3) | 247.7 (21.4) | 217.1 (51.2) | 230.5 (48.9) | 133.7 (21.5) | 132.9 (25.2) |
| AngSpeed Min. (°/s) | - | 10.0 (1.3) | 40.9 (4.8) | 41.6 (3.8) | 41.3 (4.5) | 64.0 (4.4) | 64.5 (6.7) | 66.2 (3.8) | 67.7 (4.6) | 40.4 (6.7) | 40.2 (6.5) |
| Male | Female | |||||||
|---|---|---|---|---|---|---|---|---|
| Joints | Min. (kg) | Max. (kg) | CoefP05 | CoefP95 | Min. (kg) | Max. (kg) | CoefP05 | CoefP95 |
| Lumbar | 44.6 | 65.1 | 0.87 | 1.16 | 27.7 | 46.9 | 0.90 | 1.13 |
| Cervical | 6.8 | 8.8 | 0.82 | 1.20 | 5.5 | 7.1 | 0.83 | 1.21 |
| Shoulders | 4.2 | 13.6 | 0.96 | 1.05 | 3.1 | 12.7 | 0.96 | 1.04 |
| Elbows | 1.9 | 11.6 | 0.98 | 1.02 | 1.4 | 11.2 | 0.98 | 1.02 |
| Wrists | 0.5 | 10.6 | 0.99 | 1.01 | 0.4 | 10.5 | 0.99 | 1.01 |
| Knees | 36.9 | 80.6 | 0.83 | 1.18 | 27.2 | 60.4 | 0.84 | 1.18 |
| Male | Female | |||||||
|---|---|---|---|---|---|---|---|---|
| Joints | Min. (kg∙m) | Max. (kg∙m) | CoefP05 | CoefP95 | Min. (kg∙m) | Max. (kg∙m) | CoefP05 | CoefP95 |
| Lumbar | 1.81 | 22.95 | 0.82 | 1.22 | 1.08 | 15.92 | 0.85 | 1.20 |
| Cervical | 0.15 | 0.90 | 0.73 | 1.32 | 0.11 | 0.62 | 0.72 | 1.35 |
| Shoulders | 0.49 | 5.85 | 0.92 | 1.09 | 0.34 | 5.15 | 0.93 | 1.09 |
| Elbows | 0.33 | 3.20 | 0.93 | 1.08 | 0.23 | 2.81 | 0.93 | 1.08 |
| Wrists | 0.04 | 0.83 | 0.97 | 1.03 | 0.03 | 0.70 | 0.97 | 1.03 |
| Knees | 3.73 | 26.34 | 0.86 | 1.41 | 2.32 | 17.66 | 0.84 | 1.44 |
| AngularSpeed (°/s) | AngularAcceleration (°/s2) | |||
|---|---|---|---|---|
| Joints | Slow | Maximum | Slow | Maximum |
| Lumbar | 10 | 51 | 50 | 255 |
| Cervical | 41 | 223 | 205 | 1115 |
| Shoulder | 53 | 247 | 265 | 1235 |
| Elbow | 54 | 233 | 270 | 1165 |
| Wrist | 66 | 224 | 330 | 1120 |
| Knee | 40 | 133 | 200 | 665 |
| Lumbar | Cervical | Shoulder R | Elbow R | Wrist R | Knee R | Shoulder L | Elbow L | Wrist L | Knee L | |
|---|---|---|---|---|---|---|---|---|---|---|
| P003_Medium | 22.9% | 22.6% | 8.8% | 16.2% | 15.4% | 20.5% | 9.1% | 26.9% | 14.2% | 14.7% |
| Weight | Lumbar | Cervical | Shoulder R | Elbow R | Wrist R | Knee R | Shoulder L | Elbow L | Wrist L | Knee L | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| P003_Medium | 42.8% | 22.9% | 22.6% | 8.8% | 16.2% | 15.4% | 20.5% | 9.1% | 26.9% | 14.2% | 14.7% |
| P003_Low | 28.6% | 34.2% | 24.1% | 8.6% | 21.7% | 14.9% | 19.6% | 8.6% | 27.3% | 12.4% | 24.7% |
| P003_Top | 28.6% | 21.8% | 20.7% | 14.1% | 24.0% | 16.3% | 15.2% | 12.8% | 29.7% | 13.1% | 18.2% |
| P003_COMBI | 25.8% | 22.5% | 10.3% | 20.0% | 15.5% | 18.7% | 10.0% | 27.8% | 13.4% | 18.6% | |
| Weight | Lumbar | Cervical | Shoulder R | Elbow R | Wrist R | Knee R | Shoulder L | Elbow L | Wrist L | Knee L | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| P001 | 20.0% | 6.8% | 25.4% | 4.6% | 11.4% | 5.0% | 4.5% | 4.2% | 10.3% | 7.3% | 4.7% |
| P002 | 20.0% | 18.2% | 16.7% | 7.9% | 15.7% | 5.9% | 5.3% | 11.7% | 18.7% | 8.1% | 4.3% |
| P003_COMBI | 20.0% | 25.8% | 22.5% | 10.3% | 20.0% | 15.5% | 18.7% | 10.0% | 27.8% | 13.4% | 18.6% |
| P004 | 20.0% | 13.6% | 44.4% | 22.4% | 40.8% | 36.4% | 17.2% | 24.4% | 35.7% | 37.4% | 6.1% |
| P005 | 20.0% | 30.4% | 12.6% | 7.9% | 8.9% | 4.9% | 0.0% | 9.4% | 10.8% | 8.4% | 0.4% |
| Rotation | 19.0% | 24.3% | 10.6% | 19.4% | 13.5% | 9.1% | 11.9% | 20.7% | 14.9% | 6.8% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marín, J.; Marín, J.J. Forces: A Motion Capture-Based Ergonomic Method for the Today’s World. Sensors 2021, 21, 5139. https://doi.org/10.3390/s21155139
Marín J, Marín JJ. Forces: A Motion Capture-Based Ergonomic Method for the Today’s World. Sensors. 2021; 21(15):5139. https://doi.org/10.3390/s21155139
Chicago/Turabian StyleMarín, Javier, and José J. Marín. 2021. "Forces: A Motion Capture-Based Ergonomic Method for the Today’s World" Sensors 21, no. 15: 5139. https://doi.org/10.3390/s21155139
APA StyleMarín, J., & Marín, J. J. (2021). Forces: A Motion Capture-Based Ergonomic Method for the Today’s World. Sensors, 21(15), 5139. https://doi.org/10.3390/s21155139






