A Novel Sensor Foil to Measure Ski Deflections: Development and Validation of a Curvature Model
Abstract
1. Introduction
1.1. Ski Deflection in Alpine Skiing
1.2. Status Quo and Limitations of Research in Measuring Ski Deflection
1.3. Novel Prototype for Ski Deflection Detection
1.4. Goals and Research Questions
2. Materials and Methods
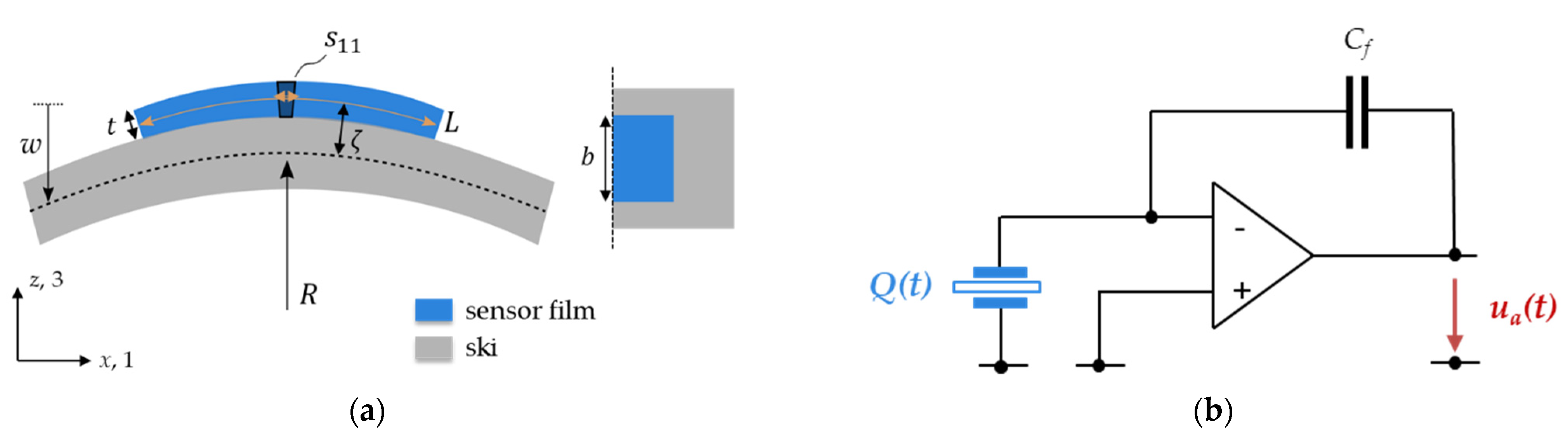
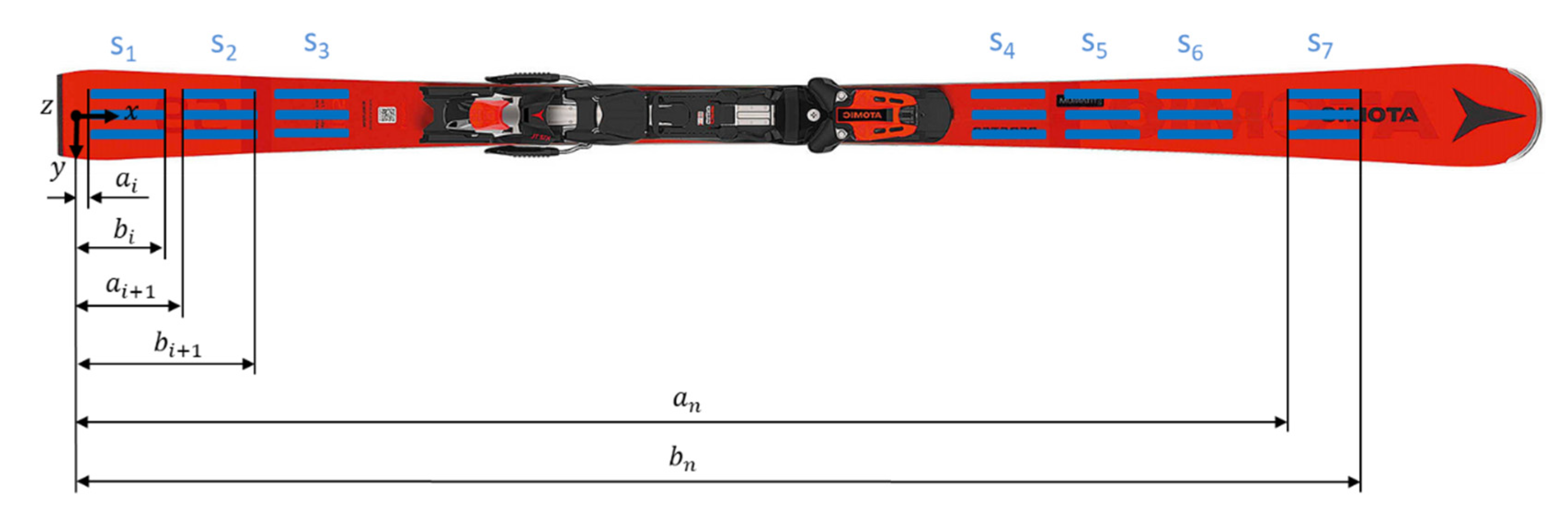
2.1. Development of the Ski Demonstrator
2.2. Development of the Empirical Curvature Model
2.3. Reliability and Validity Assesment
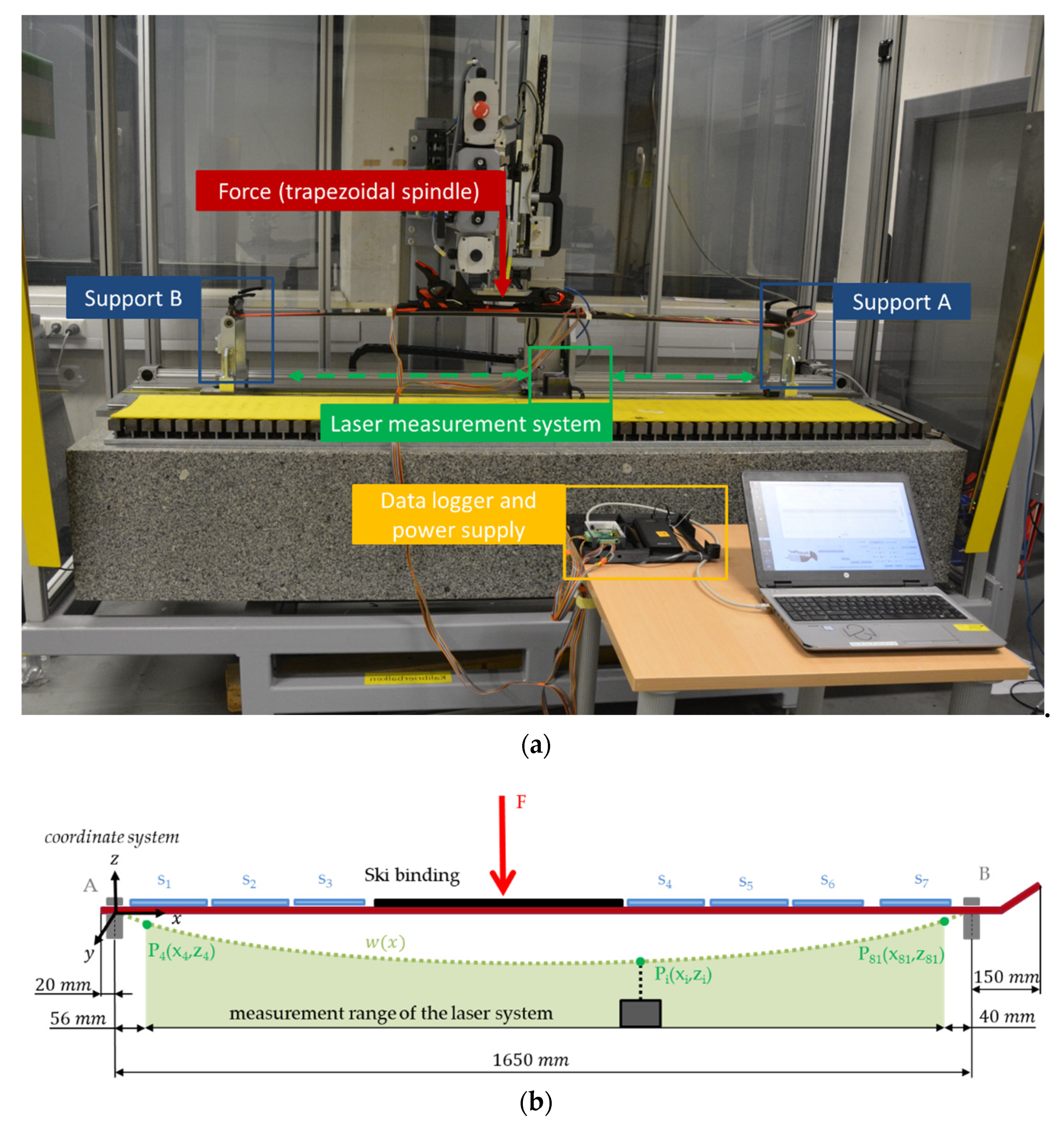
2.3.1. Experimental Setup
2.3.2. Data Processing–Laser Measurement System
2.3.3. Data Processing—PyzoFlex® Sensor System
2.4. Statistical Analysis
3. Results
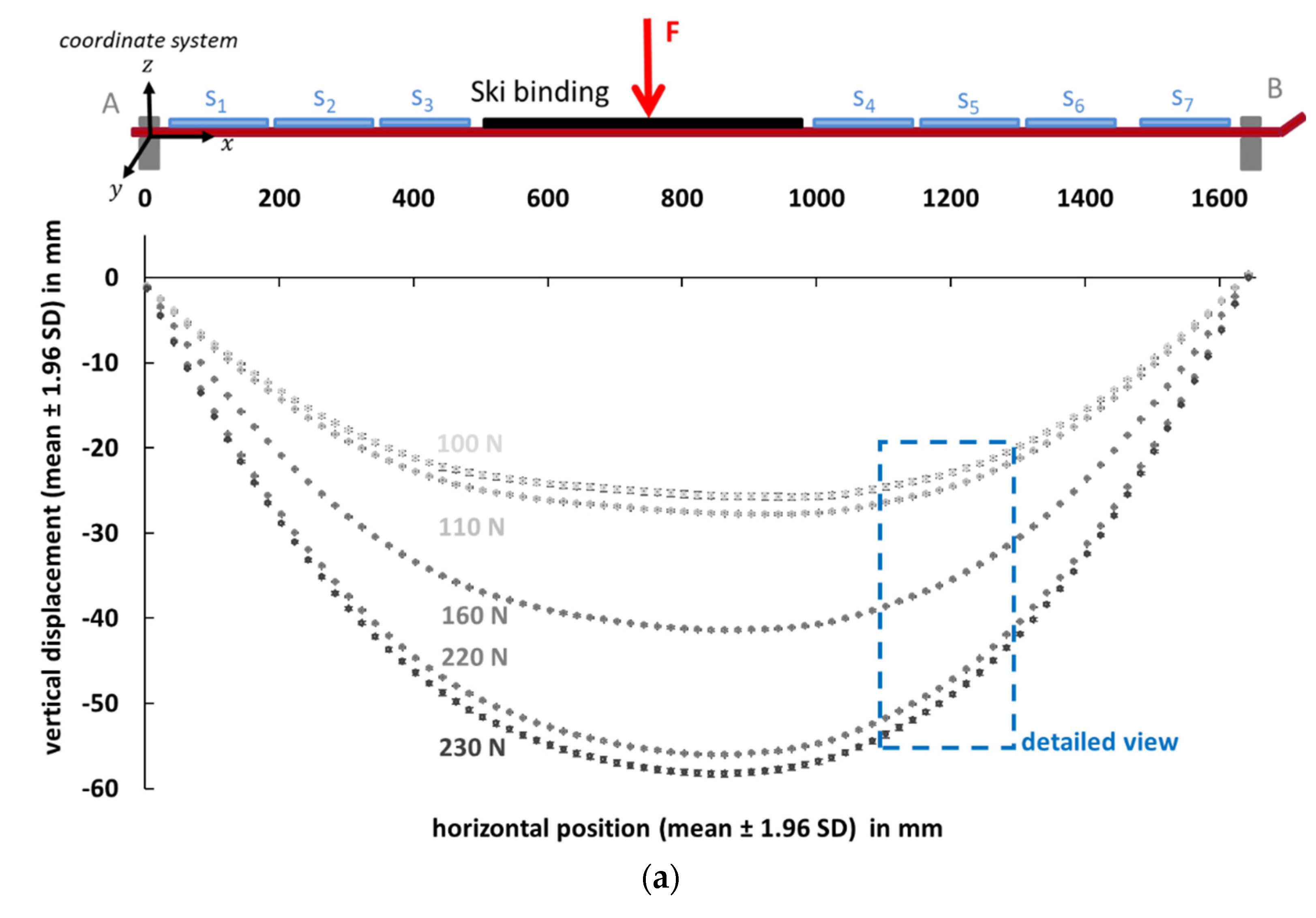
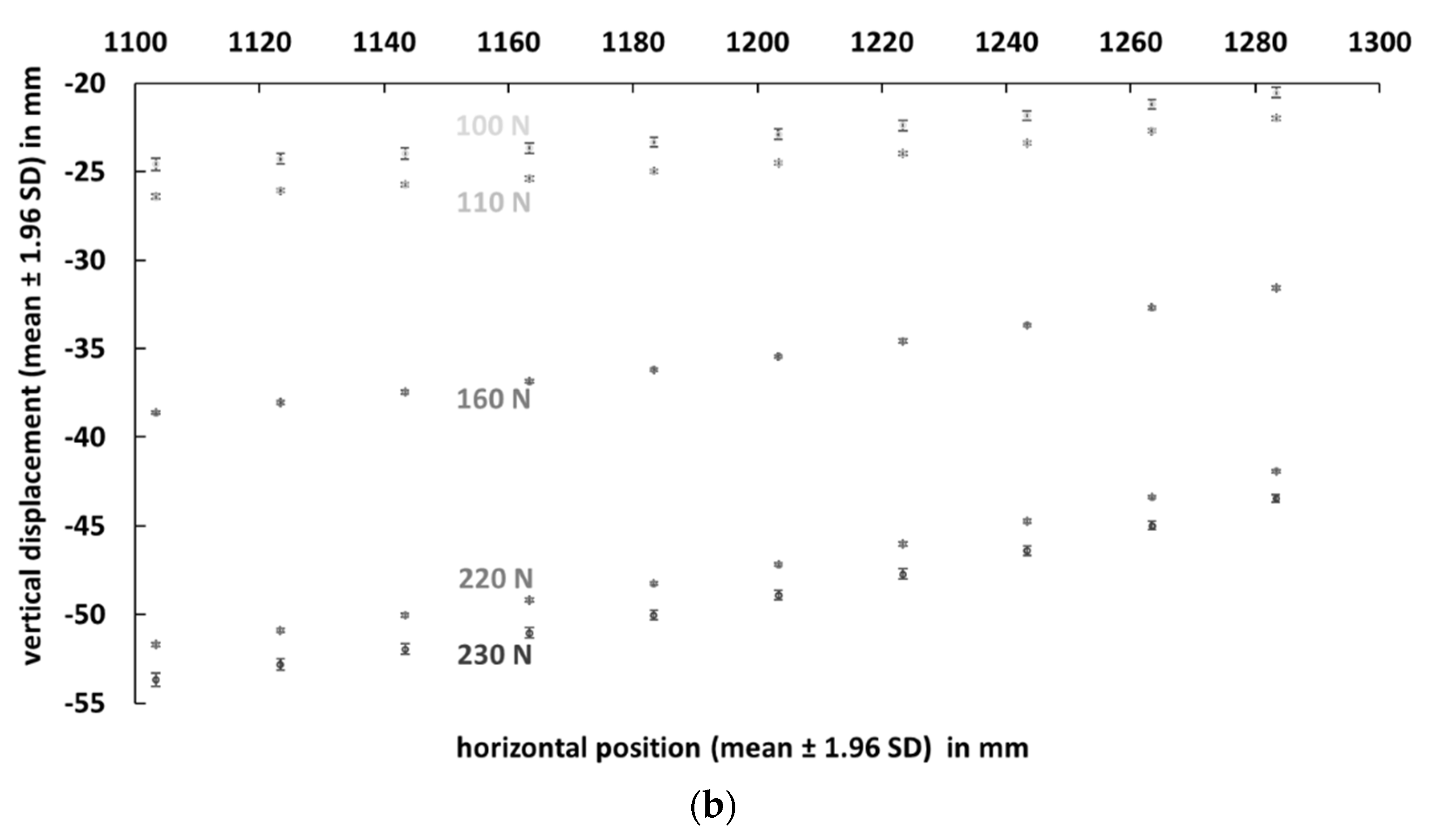
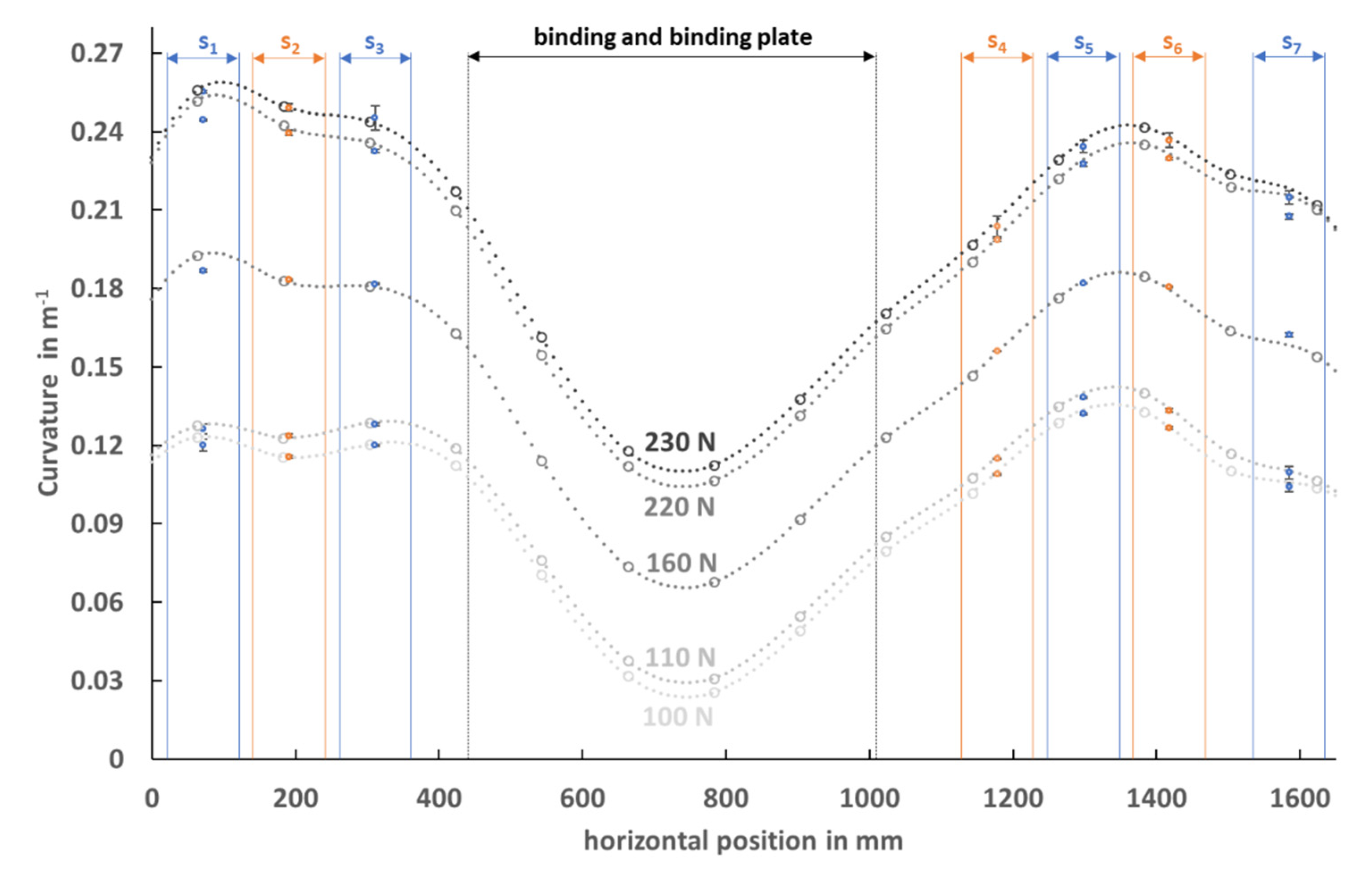
3.1. Descriptive Report
3.2. Instrument Reliability and Accuracy
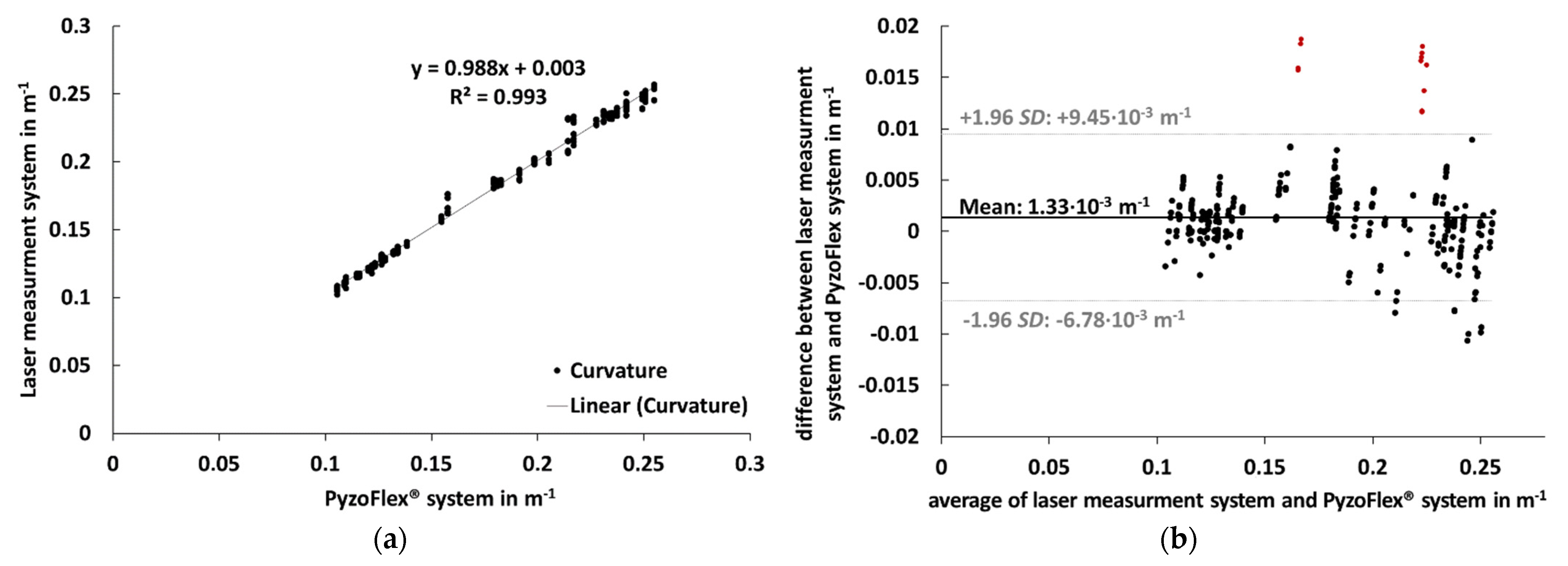
3.3. Criterion Validity
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lieu, D.K.; Mote, C.D. Mechanics of the turning snow ski. In Skiing Trauma and Safety: Fifth International Symposium; Johnson, R.J., Mote, C.D., Eds.; ASTM International: Philadelphia, PA, USA, 1985; Volume 1, pp. 117–140. [Google Scholar]
- Renshaw, A.A.; Mote, C., Jr. A model for the turning snow ski. Int. J. Mech. Sci. 1989, 31, 721–736. [Google Scholar] [CrossRef]
- Reid, R.C.; Haugen, P.; Gilgien, M.; Kipp, R.W.; Smith, G.A. Alpine Ski Motion Characteristics in Slalom. Front. Sports Act. Living 2020, 2, 25. [Google Scholar] [CrossRef] [PubMed]
- Brown, C.A.; Outwater, J.O. On the skiability of snow. In Skiing Trauma and Safety: Seventh International Symposium; Johnson, R.J., Mote, C.D., Binet, M.H., Eds.; ASTM International: Philadelphia, PA, USA, 1989; Volume 1, pp. 329–336. [Google Scholar]
- Kagawa, H.; Yoneyama, T.; Tatsuno, D.; Scott, N.; Osada, K. Development of a measuring system on ski deflection and contacting snow pressure in turns. In Science and Skiing IV; Müller, E., Lindinger, S., Stöggl, T., Eds.; Meyer & Meyer Sport: Aachen, Germany, 2009; Volume 1, pp. 281–291. [Google Scholar]
- Nachbauer, W.; Rainer, F.; Schindelwig, K. Effects of ski stiffness on ski performance. In Proceedings of the Engineering of Sport 5, Winfield, IL, USA, 13–16 September 2004; pp. 472–478. [Google Scholar]
- Rainer, F.; Nachbauer, W.; Schindelwig, K.; Kaps, P. On the measurement of the stiffness of skis. In Science and Skiing III; Müller, E., Bacharach, D., Klika, R., Eds.; Meyer & Meyer Sport: Aachen, Germany, 2005; Volume 1, pp. 136–147. [Google Scholar]
- Deak, A.; Jorgensen, J.; Vagners, J. The engineering characteristics of snow skis—part 1: Static bending and torsional characteristics. J. Eng. Ind. 1975, 97, 131–137. [Google Scholar] [CrossRef]
- Lüthi, A.; Federolf, P.; Fauve, M.; Rhyner, H. Effect of bindings and plates on ski mechanical properties and carving performance. In The Engineering of Sport 6; Hubbard, M., Metha, R.D., Pallis, J.M., Eds.; Springer: Winfield, IL, USA, 2006; Volume 1, pp. 299–304. [Google Scholar]
- De Gobbi, M.; Petrone, N. Structural behaviour of slalom skis in bending and torsion (P269). Eng. Sport 7 2008, 2, 643–652. [Google Scholar]
- Truong, J.; Brousseau, C.; Desbiens, A.L. A Method for Measuring the Bending and Torsional Stiffness Distributions of Alpine Skis. Procedia Eng. 2016, 147, 394–400. [Google Scholar] [CrossRef][Green Version]
- Clifton, P.; Subic, A.; Mouritz, A. Snowboard stiffness prediction model for any composite sandwich construction. Procedia Eng. 2010, 2, 3163–3169. [Google Scholar] [CrossRef][Green Version]
- International Organization for Standardization. Alpine skis—Determination of the Elastic Properties. (ISO Standard No. 5902:2013). 2013. Available online: https://www.iso.org/standard/60844.html (accessed on 15 July 2016).
- Adelsberger, R.; Aufdenblatten, S.; Gilgien, M.; Tröster, G. On bending characteristics of skis in use. Procedia Eng. 2014, 72, 362–367. [Google Scholar] [CrossRef]
- Yoneyama, T.; Kitade, M.; Osada, K. Investigation on the ski-snow interaction in a carved turn based on the actual measurement. Procedia Eng. 2010, 2, 2901–2906. [Google Scholar] [CrossRef]
- Tatsuno, D.; Yoneyama, T.; Kagawa, H.; Scott, N.; Osada, K. Measurement of ski deflection and ski-snow contacting pressure in an actual ski turn on the snow surface. In Science and Skiing IV; Müller, E., Lindinger, S., Stöggl, T., Eds.; Meyer & Meyer Sport: Aachen, Germany, 2009; Volume 1, pp. 505–515. [Google Scholar]
- Yoneyama, T.; Scott, N.; Kagawa, H.; Osada, K. Ski deflection measurement during skiing and estimation of ski direction and edge angle. Sports Eng. 2008, 11, 3–13. [Google Scholar] [CrossRef]
- Schindelwig, K.; Hellberg, F.; Nachbauer, W.; Schretter, H. Measuring dynamic ski behavior with strain gauges. In Proceedings of the ISBS—Conference (XXIV Symposium on Biomechanics in Sports), Salzburg, Austria, 14–18 July 2006; p. 1. [Google Scholar]
- Fauve, M.; Auer, M.; Lüthi, A.; Rhyner, H.; Meier, J. Measurement of dynamical ski behavior during alpine skiing. In Science and Skiing IV; Müller, E., Lindinger, S., Stöggl, T., Eds.; Mayer & Mayer Sport: Aachen, Germany, 2009; Volume 1, pp. 195–206. [Google Scholar]
- Kos, A.; Umek, A. Smart sport equipment: SmartSki prototype for biofeedback applications in skiing. Pers. Ubiquitous Comput. 2018, 22, 535–544. [Google Scholar] [CrossRef]
- Rendl, C.; Greindl, P.; Haller, M.; Zirkl, M.; Stadlober, B.; Hartmann, P. PyzoFlex: Printed piezoelectric pressure sensing foil. In Proceedings of the 25th Annual ACM Symposium on User Interface Software and Technology, Cambridge, MA, USA, 7–10 October 2012; pp. 509–518. [Google Scholar]
- Stadlober, B.; Zirkl, M.; Irimia-Vladu, M. Route towards sustainable smart sensors: Ferroelectric polyvinylidene fluoride-based materials and their integration in flexible electronics. Chem. Soc. Rev. 2019, 48, 1787–1825. [Google Scholar] [CrossRef] [PubMed]
- Furukawa, T.; Wen, J.; Suzuki, K.; Takashina, Y.; Date, M. Piezoelectricity and pyroelectricity in vinylidene fluoride/trifluoroethylene copolymers. J. Appl. Phys. 1984, 56, 829–834. [Google Scholar] [CrossRef]
- Schäffner, P.; Zirkl, M.; Schider, G.; Groten, J.; Belegratis, M.R.; Knoll, P.; Stadlober, B. Microstructured single-layer electrodes embedded in P (VDF-TrFE) for flexible and self-powered direction-sensitive strain sensors. Smart Mater. Struct. 2020, 29, 085040. [Google Scholar] [CrossRef]
- Runge, C. Über empirische Funktionen und die Interpolation zwischen äquidistanten Ordinaten. Z. Math. Phys. 1901, 46, 20. [Google Scholar]
- Koo, T.K.; Li, M.Y. A guideline of selecting and reporting intraclass correlation coefficients for reliability research. J. Chiropr. Med. 2016, 15, 155–163. [Google Scholar] [CrossRef] [PubMed]
- Hopkins, W.G. Spreadsheets for Analysis of Validity and Reliability. Sportscience 2017, 21, 36–44. [Google Scholar]
- Bland, J.M.; Altman, D.G. Measuring agreement in method comparison studies. Stat. Methods Med. Res. 1999, 8, 135–160. [Google Scholar] [CrossRef] [PubMed]
- Omote, K.; Ohigashi, H.; Koga, K. Temperature dependence of elastic, dielectric, and piezoelectric properties of “single crystalline” films of vinylidene fluoride trifluoroethylene copolymer. J. Appl. Phys. 1997, 81, 2760–2769. [Google Scholar] [CrossRef]

| p (t-Test) | CIM (%, 95% CI) | CV (%, 95% CI) | ICC 3.1 (95% CI) | ||
|---|---|---|---|---|---|
| 100 N | Repetition 1 vs. 2 | n.s. | 0.50 (−0.08–1.07) | 1.08 (0.86–1.47) | 0.982 (0.962–0.991) |
| Repetition 2 vs. 3 | n.s. | 0.39 (0.05–0.73) | 0.63 (0.51–0.86) | 0.994 (0.987–0.997) | |
| 160 N | Repetition 1 vs. 2 | <0.01 | −0.46 (−0.70–0.23) | 0.44 (0.35–0.60) | 0.995 (0.990–0.998) |
| Repetition 2 vs. 3 | n.s. | −0.26 (−0.80–0.27) | 1.01 (0.81–1.37) | 0.977 (0.952–0.989) | |
| 230 N | Repetition 1 vs. 2 | n.s. | 0.32 (−0.45–1.09) | 1.45 (1.16–1.97) | 0.961 (0.920–0.982) |
| Repetition 2 vs. 3 | <0.001 | −1.41 (−1.86–0.95) | 0.86 (0.69–1.17) | 0.983 (0.966–0.992) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thorwartl, C.; Kröll, J.; Tschepp, A.; Schäffner, P.; Holzer, H.; Stöggl, T. A Novel Sensor Foil to Measure Ski Deflections: Development and Validation of a Curvature Model. Sensors 2021, 21, 4848. https://doi.org/10.3390/s21144848
Thorwartl C, Kröll J, Tschepp A, Schäffner P, Holzer H, Stöggl T. A Novel Sensor Foil to Measure Ski Deflections: Development and Validation of a Curvature Model. Sensors. 2021; 21(14):4848. https://doi.org/10.3390/s21144848
Chicago/Turabian StyleThorwartl, Christoph, Josef Kröll, Andreas Tschepp, Philipp Schäffner, Helmut Holzer, and Thomas Stöggl. 2021. "A Novel Sensor Foil to Measure Ski Deflections: Development and Validation of a Curvature Model" Sensors 21, no. 14: 4848. https://doi.org/10.3390/s21144848
APA StyleThorwartl, C., Kröll, J., Tschepp, A., Schäffner, P., Holzer, H., & Stöggl, T. (2021). A Novel Sensor Foil to Measure Ski Deflections: Development and Validation of a Curvature Model. Sensors, 21(14), 4848. https://doi.org/10.3390/s21144848








