Lane Following Method Based on Improved DDPG Algorithm
Abstract
:1. Introduction
2. Algorithm Architecture
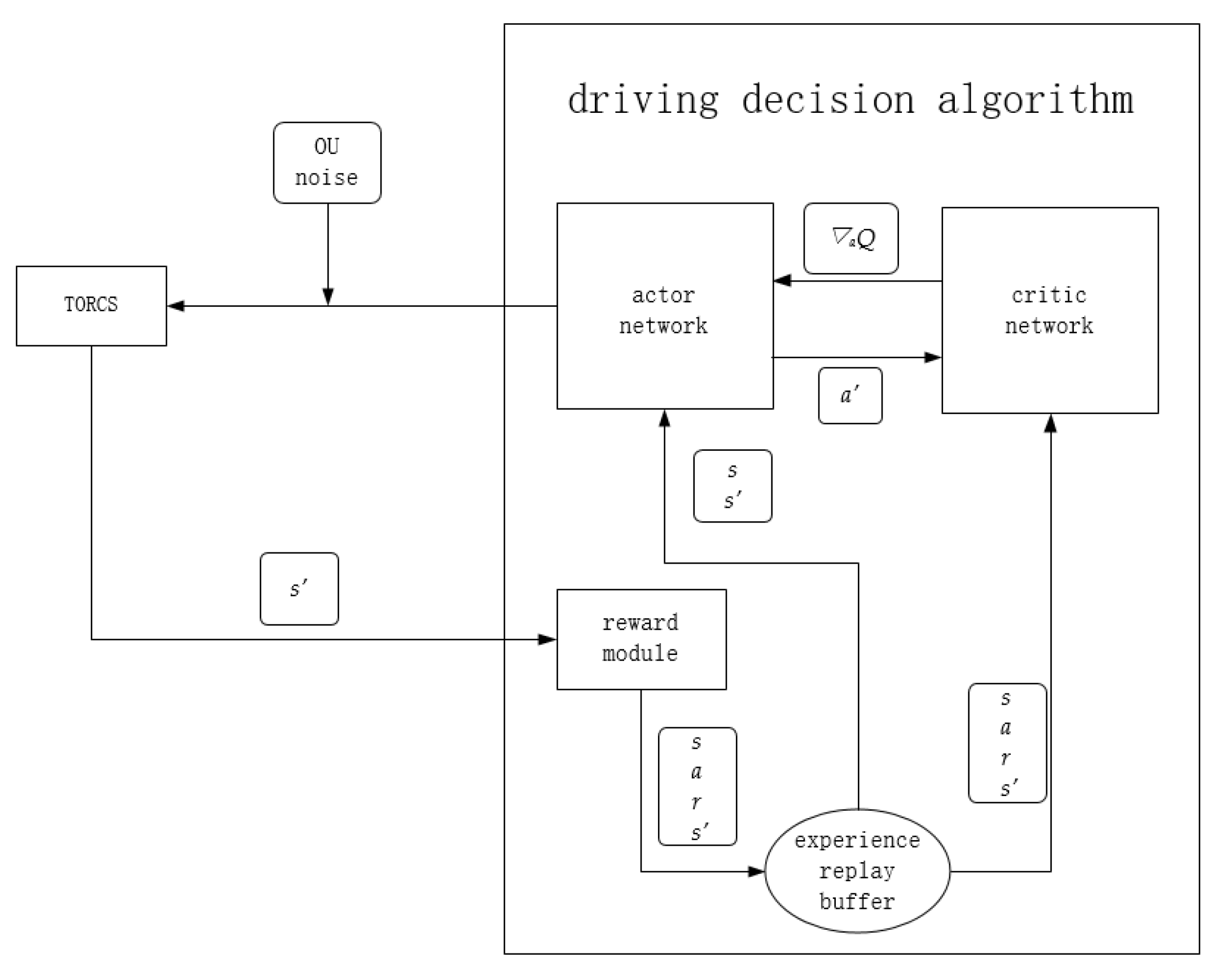
2.1. Lane Following Algorithm Framework
- A set of action values is generated by the actor network, namely steering, throttle, and braking values, and random noise is added and input into the TORCS simulation software;
- TORCS input the next state s’ into the reward function module according to the action, and store it into the experience pool together with the current state s, reward value r, and action value a;
- Sample a certain number of samples from the experience replay buffer, each sample contains s, a, r, s’. Then respectively pass s, s’ to the actor network, and s, a, r, s’ to the critic network for an iterative update;
- For the actor network, it accepts s and s’, then outputs a to TORCS together with random noise. Meanwhile, it outputs the next action a’ to the critic network. After that, accepts the gradient of the state action value Q(s, a) to a’ to update the network.
- For the critic network, it accepts s’, a’ to calculate Q(s’, a’). Next, it combines Q(s’, a’) with r to calculate a label for the iterative update of the network. At the same time, s and a are input into the critic network, and the mean square error between the output and the label is used as the loss function to update the network iteratively. Finally, calculate the gradient of the Q value to a’ under s and return that to the actor network for an iterative update.
2.2. Input Data Selection
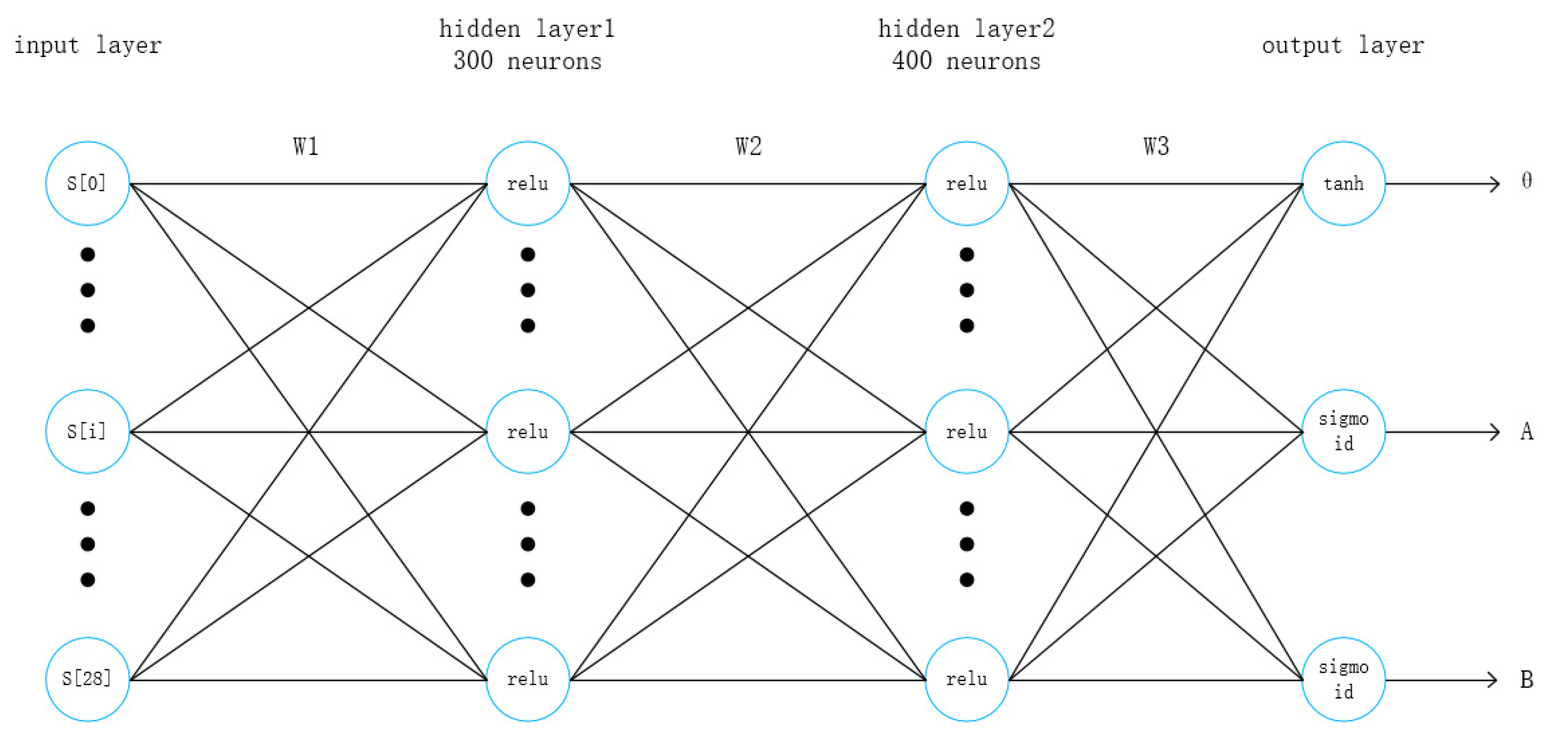
2.3. Network Structure
2.3.1. Actor Network Structure
2.3.2. Critic Network Structure
3. Lane Following Strategy
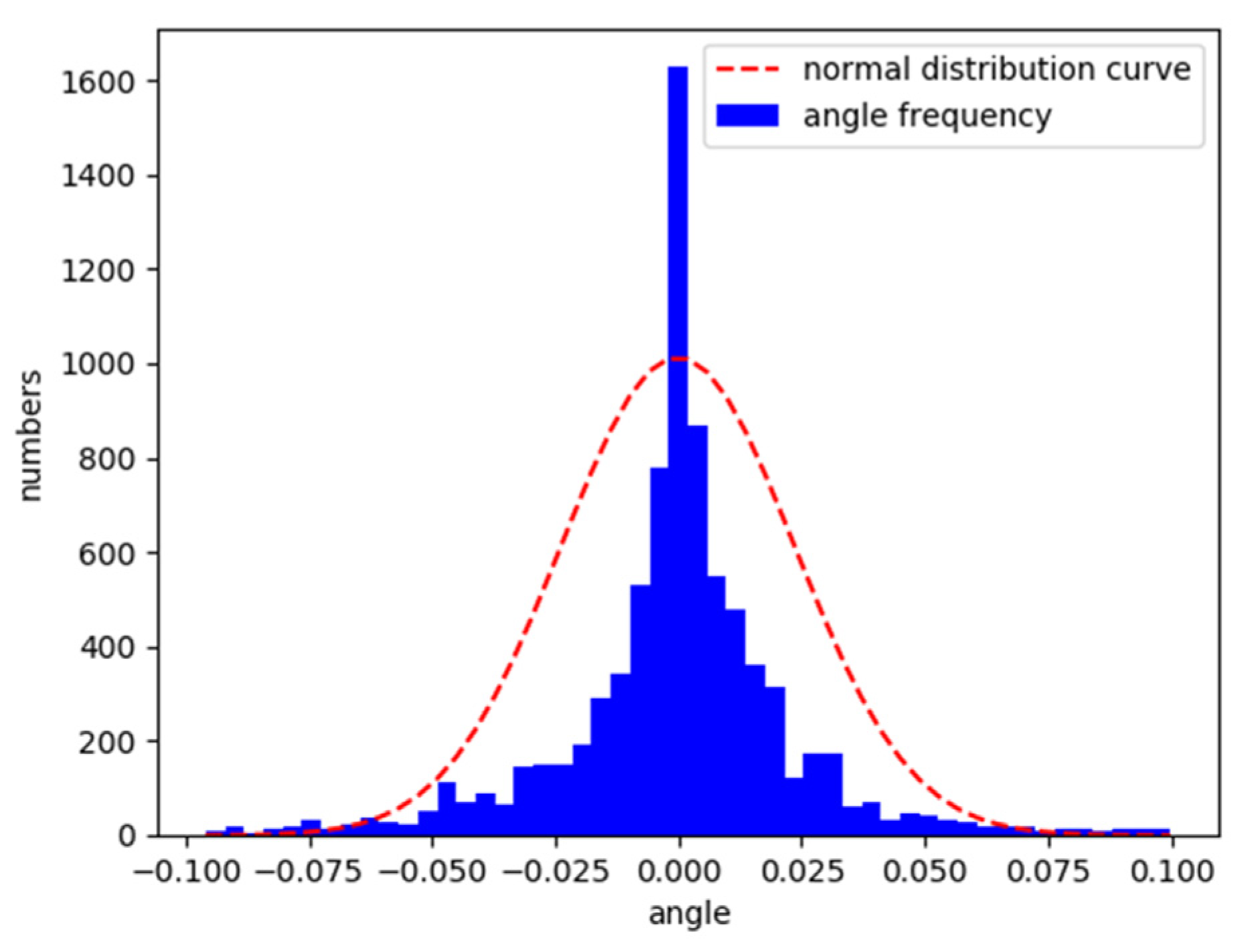
3.1. Reward Function
3.2. Exploration Strategy
3.3. Double Critic Networks and Priority Experience Replay of DDPG Algorithm
| Algorithm 1: DCPER-DDPG |
| Randomly initialize the actor network and critic networks and |
| Initialize the weights of the target networks ,, Initialize the replay buffer R, Set the maximum storage capacity of the buffer S Initialize state S0, batch_size = K Initialize maximum priority D, priority parameters α, β for episode = 1,…, M do: Initialize random noise εt for t = 0,…, T do: Select actions based on the actor network and add random noise and get the next state given by the environment st+1, reward rt Store (st, at, rt, st+1) into replay buffer R, and set the maximum priority if t > S: for j = 1, K do: Sample transition according to priority:(sj, aj, rj, sj+1) Calculate the optimization goal of the critic network: Calculate the corresponding importance sampling weight Wj and TD error δj According to the absolute value of TD error |δj| update the priority of transition end for Update the two critic networks separately by minimizing the loss function: if t mod policy_update_frequency == 0: Use policy gradient to update the actor network: Use update rate γ to update the weight of the target network , and end if end if end for end for |
4. Experiment
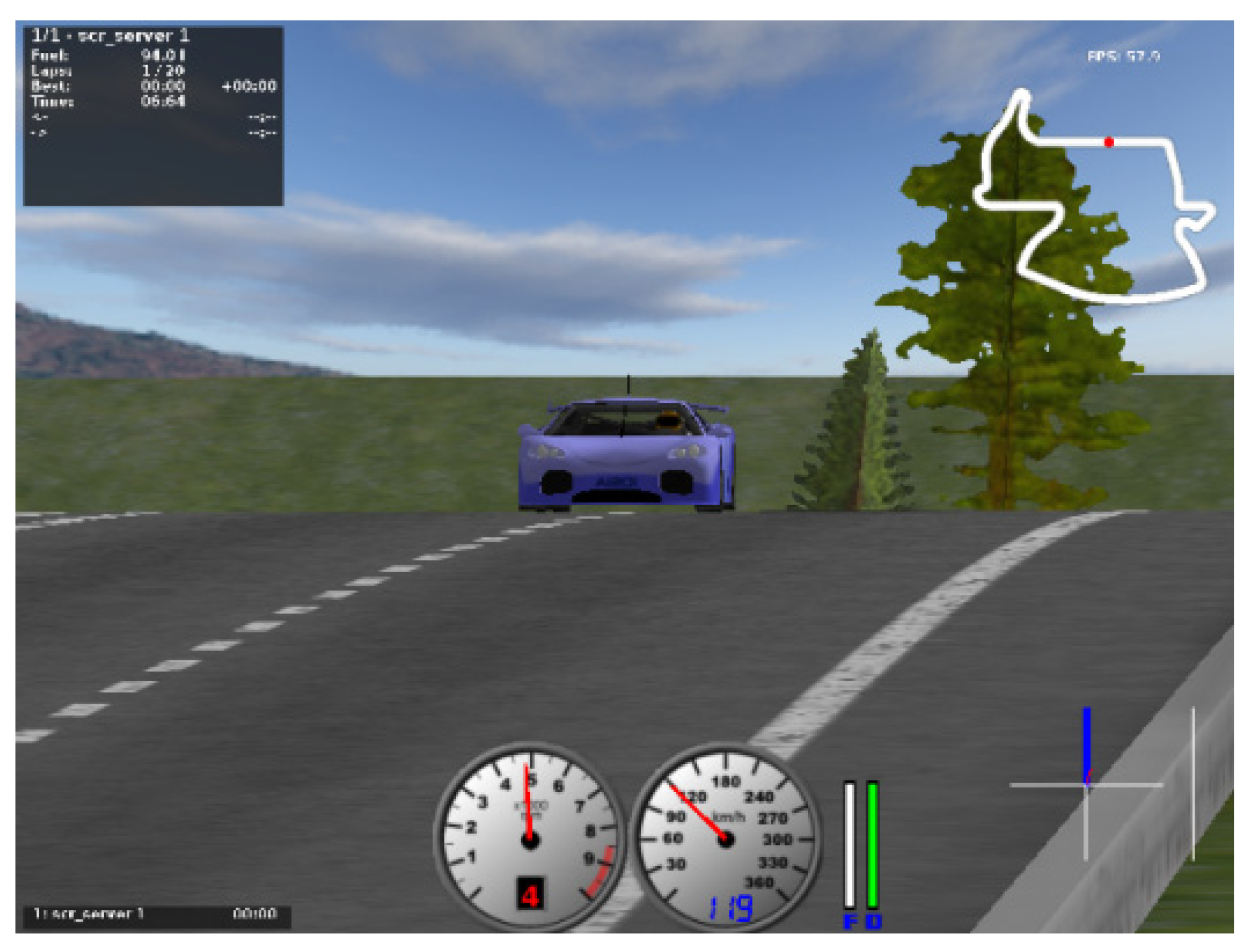
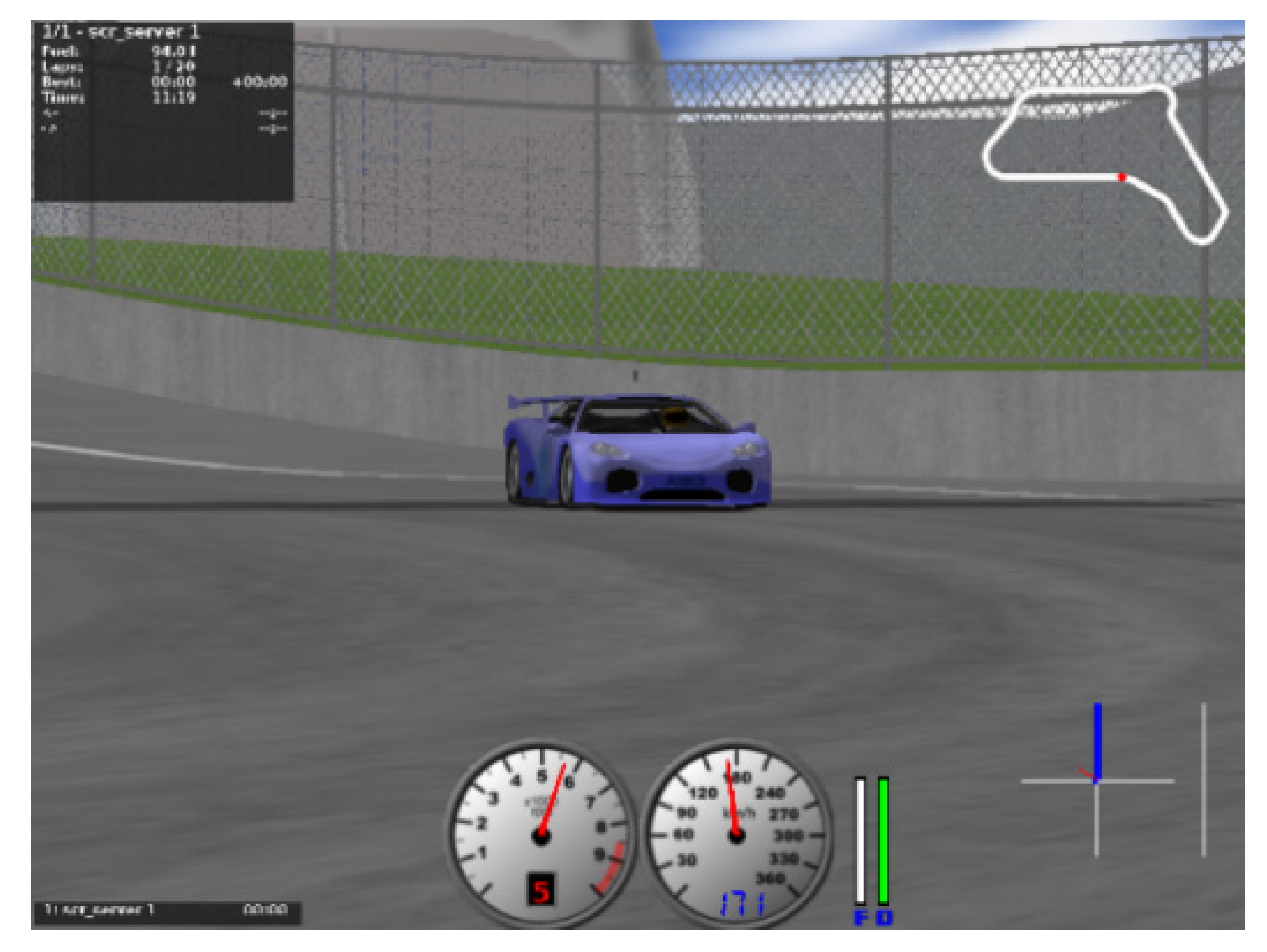
4.1. Simulation Environment
4.2. Termination Condition Setting
- (1)
- The vehicle stalls. If the longitudinal speed of the target vehicle is always less than 5 km/h in 100 time steps, it will end the current episode and start a new episode.
- (2)
- The vehicle drives off the track. If the vehicle runs off the track, it will automatically end the current episode and restart a new episode.
- (3)
- The vehicle travels in reverse. If the vehicle’s forward direction reverses, a new episode is started.
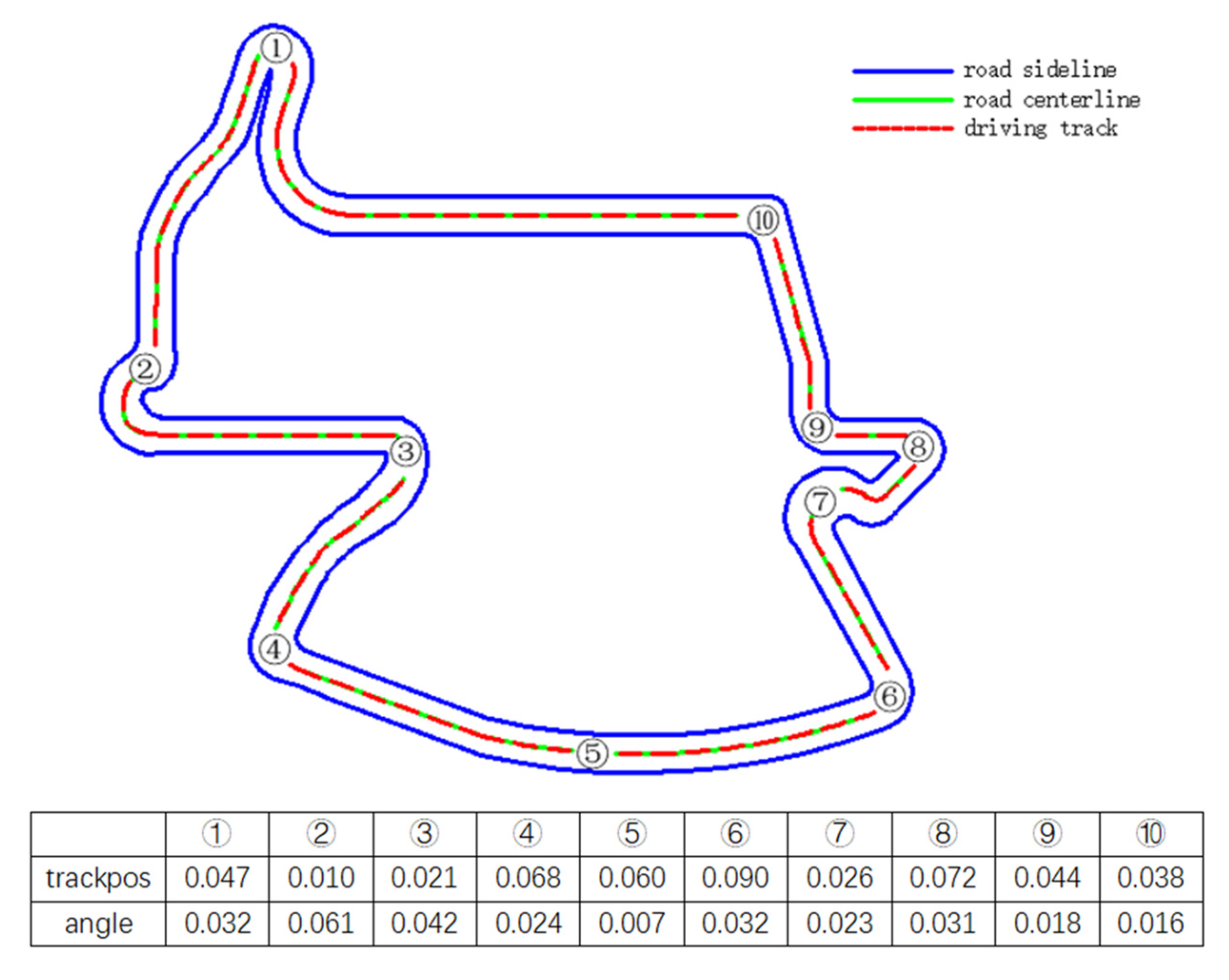
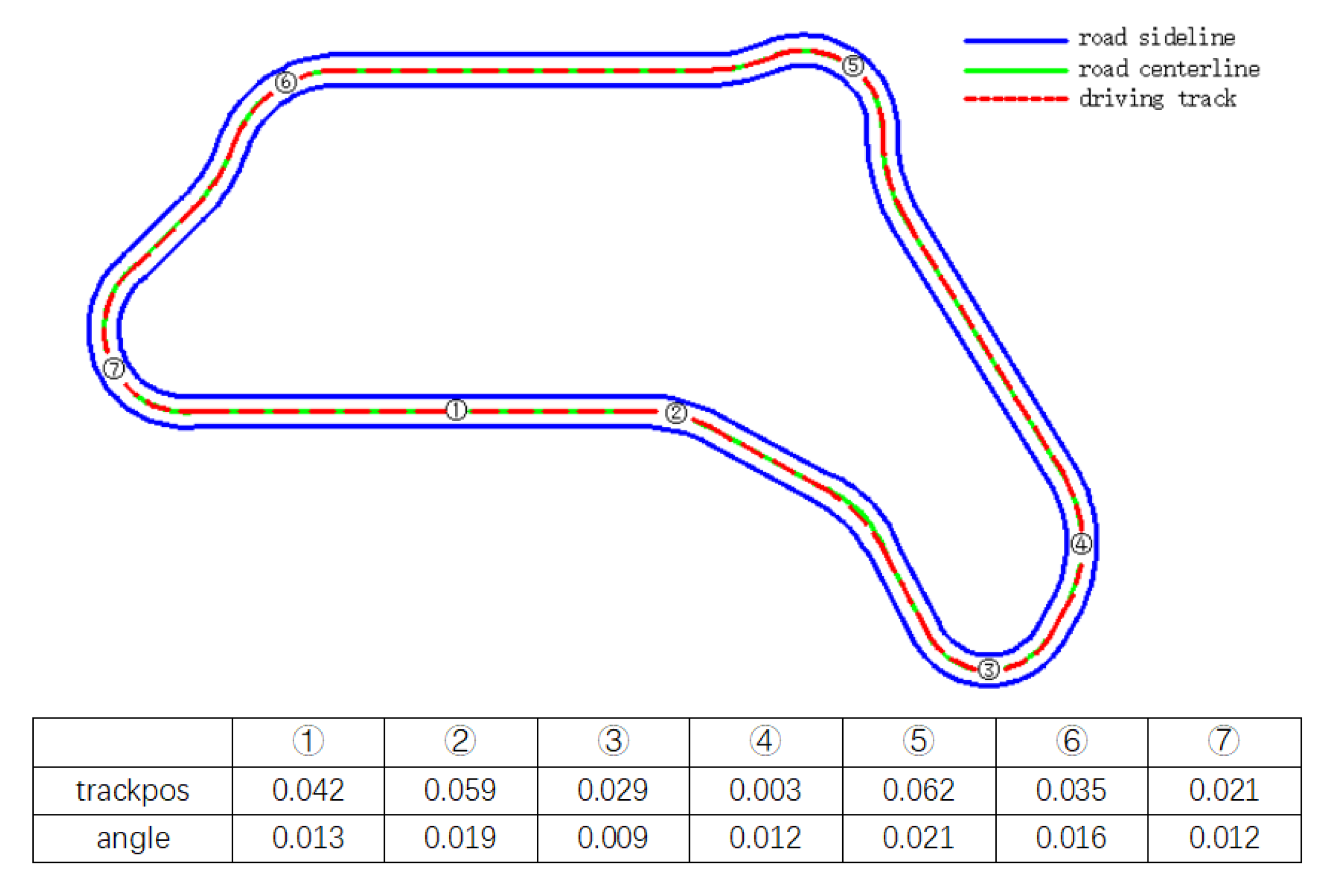
4.3. Scene Selection
4.4. Training Parameter Settings
5. Result Analysis
5.1. Training Average Reward
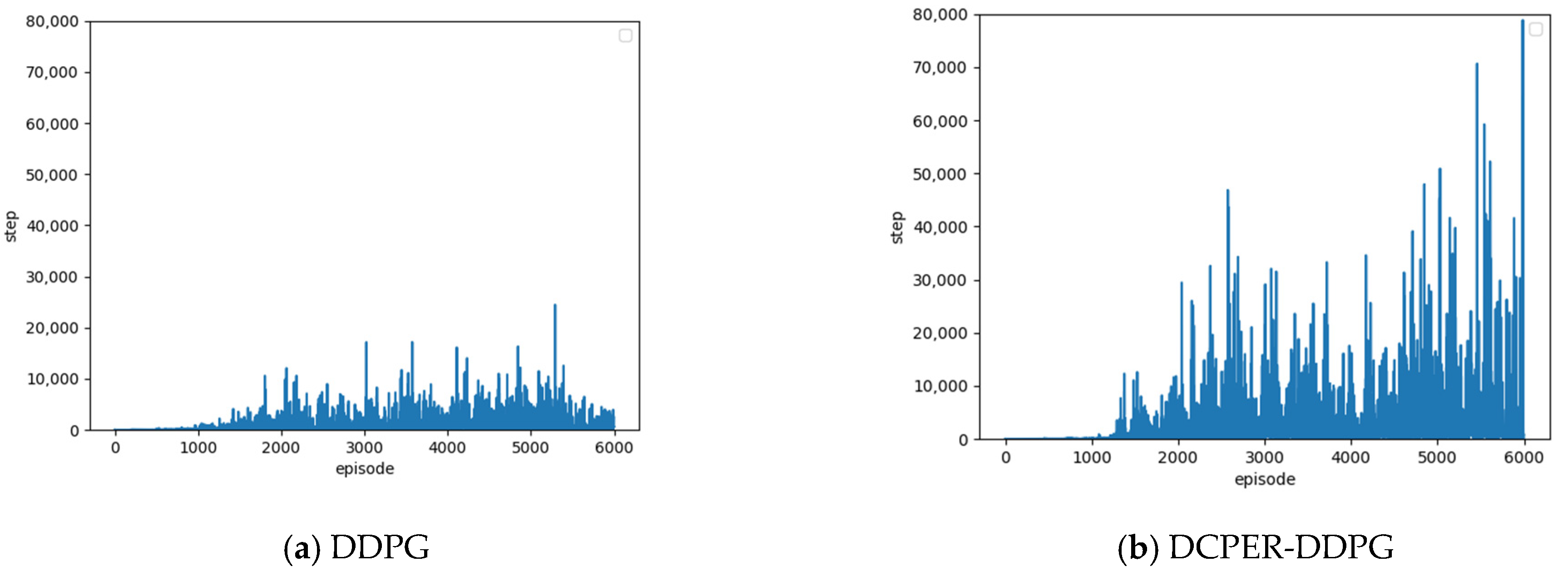
5.2. Number of Steps Completed in One Episode
5.3. Analysis of Comparative Results
5.4. Vehicle Characteristics under the Control of Deep Reinforcement Learning Model
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Lee, M.; Han, K.Y.; Yu, J.; Lee, Y.-S. A new lane following method based on deep learning for automated vehicles using surround view images. J. Ambient Intell. Humaniz. Comput. 2019, 1–14. [Google Scholar] [CrossRef]
- Kővári, B.; Hegedüs, F.; Bécsi, T. Design of a Reinforcement Learning-Based Lane Keeping Planning Agent for Automated Vehicles. Appl. Sci. 2020, 10, 7171. [Google Scholar] [CrossRef]
- Chen, Y.; Ju, Z.; Yang, C. Combining Reinforcement Learning and Rule-based Method to Manipulate Objects in Clutter. In Proceedings of the 2020 International Joint Conference on Neural Networks (IJCNN), Glasgow, UK, 19–24 July 2020; pp. 1–6. [Google Scholar]
- Huang, Z.; Zhang, J.; Tian, R.; Zhang, Y. End-to-end autonomous driving decision based on deep reinforcement learning. In Proceedings of the 2019 5th International Conference on Control, Automation and Robotics (ICCAR), Beijing, China, 19–22 April 2019; pp. 658–662. [Google Scholar]
- Chen, J.; Li, S.E.; Tomizuka, M. Interpretable End-to-End Urban Autonomous Driving with Latent Deep Reinforcement Learning. IEEE Trans. Intell. Transp. Syst. 2021, 1–11. [Google Scholar] [CrossRef]
- Luo, M.; Tong, Y.; Liu, J. Orthogonal Policy Gradient and Autonomous Driving Application. In Proceedings of the 2018 IEEE 9th International Conference on Software Engineering and Service Science (ICSESS), Beijing, China, 23–25 November 2018; pp. 1–4. [Google Scholar]
- Liu, M.; Zhao, F.; Yin, J.; Niu, J.; Liu, Y. Reinforcement-Tracking: An Effective Trajectory Tracking and Navigation Method for Autonomous Urban Driving. IEEE Trans. Intell. Transp. Syst. 2021, 1–17. [Google Scholar] [CrossRef]
- Guo, Y.; Gao, Q.; Pan, F. Trained Model Reuse of Autonomous-Driving in Pygame with Deep Reinforcement Learning. In Proceedings of the 2020 39th Chinese Control Conference (CCC), Shenyang, China, 27–29 July 2020; pp. 5660–5664. [Google Scholar]
- Yu, G.; Sethi, I.K. Road-following with continuous learning. In Proceedings of the Intelligent Vehicles’ 95. Symposium, Detroit, MI, USA, 25–26 September 1995; pp. 412–417. [Google Scholar]
- Wang, P.; Chan, C.-Y.; de La Fortelle, A. A reinforcement learning based approach for automated lane change maneuvers. In Proceedings of the 2018 IEEE Intelligent Vehicles Symposium (IV), Changshu, China, 26–30 June 2018; pp. 1379–1384. [Google Scholar]
- Dai, X.; Li, C.K.; Rad, A.B. An Approach to Tune Fuzzy Controllers Based on Reinforcement Learning for Autonomous Vehicle Control. IEEE Trans. Intell. Transp. Syst. 2005, 6, 285–293. [Google Scholar] [CrossRef]
- Desjardins, C.; Chaib-draa, B. Cooperative Adaptive Cruise Control: A Reinforcement Learning Approach. IEEE Trans. Intell. Transp. Syst. 2011, 12, 1248–1260. [Google Scholar] [CrossRef]
- Huang, Z.; Xu, X.; He, H.; Tan, J.; Sun, Z. Parameterized Batch Reinforcement Learning for Longitudinal Control of Autonomous Land Vehicles. IEEE Trans. Syst. Man Cybern. Syst. 2019, 49, 730–741. [Google Scholar] [CrossRef]
- Chae, H.; Kang, C.M.; Kim, B.; Kim, J.; Chung, C.C.; Choi, J.W. Autonomous braking system via deep reinforcement learning. In Proceedings of the 2017 IEEE 20th International Conference on Intelligent Transportation Systems (ITSC), Yokohama, Japan, 16–19 October 2017; pp. 1–6. [Google Scholar]
- Kuderer, M.; Gulati, S.; Burgard, W. Learning driving styles for autonomous vehicles from demonstration. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 2641–2646. [Google Scholar]
- Ly, A.O.; Akhloufi, M. Learning to Drive by Imitation: An Overview of Deep Behavior Cloning Methods. IEEE Trans. Intell. Veh. 2021, 6, 195–209. [Google Scholar] [CrossRef]
- Xia, W.; Li, H.; Li, B. A control strategy of autonomous vehicles based on deep reinforcement learning. In Proceedings of the 2016 9th International Symposium on Computational Intelligence and Design (ISCID), Hangzhou, China, 10–11 December 2016; pp. 198–201. [Google Scholar]
- Sallab, A.E.; Abdou, M.; Perot, E.; Yogamani, S. End-to-end deep reinforcement learning for lane keeping assist. arXiv 2016, arXiv:1612.04340. [Google Scholar]
- Wu, J.; He, H.; Peng, J.; Li, Y.; Li, Z. Continuous reinforcement learning of energy management with deep Q network for a power split hybrid electric bus. Appl. Energy 2018, 222, 799–811. [Google Scholar] [CrossRef]
- Sogabe, T.; Malla, D.B.; Takayama, S.; Shin, S.; Sakamoto, K.; Yamaguchi, K.; Singh, T.P.; Sogabe, M.; Hirata, T.; Okada, Y. Smart grid optimization by deep reinforcement learning over discrete and continuous action space. In Proceedings of the 2018 IEEE 7th World Conference on Photovoltaic Energy Conversion (WCPEC) (A Joint Conference of 45th IEEE PVSC, 28th PVSEC & 34th EU PVSEC), Waikoloa, HI, USA, 10–15 June 2018; pp. 3794–3796. [Google Scholar]
- Aslani, M.; Seipel, S.; Mesgari, M.S.; Wiering, M. Traffic signal optimization through discrete and continuous reinforcement learning with robustness analysis in downtown Tehran. Adv. Eng. Inform. 2018, 38, 639–655. [Google Scholar] [CrossRef]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv 2015, arXiv:1509.02971. [Google Scholar]
- Konda, V.R.; Tsitsiklis, J.N. Actor-critic algorithms. In Proceedings of the Advances in Neural Information Processing Systems, Denver, CO, USA, 29 November 1999; pp. 1008–1014. [Google Scholar]
- Silver, D.; Lever, G.; Heess, N.; Degris, T.; Wierstra, D.; Riedmiller, M. Deterministic policy gradient algorithms. In Proceedings of the International Conference on Machine Learning, Beijing, China, 7 January 2014; pp. 387–395. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Graves, A.; Antonoglou, I.; Wierstra, D.; Riedmiller, M. Playing atari with deep reinforcement learning. arXiv 2013, arXiv:1312.5602. [Google Scholar]
- Fujimoto, S.; Hoof, H.; Meger, D. Addressing function approximation error in actor-critic methods. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 3 July 2018; pp. 1587–1596. [Google Scholar]
- Schaul, T.; Quan, J.; Antonoglou, I.; Silver, D. Prioritized experience replay. arXiv 2015, arXiv:1511.05952. [Google Scholar]
- Ashraf, N.M.; Mostafa, R.R.; Sakr, R.H.; Rashad, M. Optimizing hyperparameters of deep reinforcement learning for autonomous driving based on whale optimization algorithm. PLoS ONE 2021, 16, e0252754. [Google Scholar] [CrossRef] [PubMed]
- Loiacono, D.; Cardamone, L.; Lanzi, P.L. Simulated car racing championship: Competition software manual. arXiv 2013, arXiv:1304.1672. [Google Scholar]
- Jeerige, A.; Bein, D.; Verma, A. Comparison of deep reinforcement learning approaches for intelligent game playing. In Proceedings of the 2019 IEEE 9th Annual Computing and Communication Workshop and Conference (CCWC), Las Vegas, NV, USA, 7–9 January 2019; pp. 366–371. [Google Scholar]
- Gulde, R.; Tuscher, M.; Csiszar, A.; Riedel, O.; Verl, A. Deep Reinforcement Learning using Cyclical Learning Rates. In Proceedings of the 2020 Third International Conference on Artificial Intelligence for Industries (AI4I), Irvine, CA, USA, 21–23 September 2020; pp. 32–35. [Google Scholar]
- Ghadirzadeh, A.; Chen, X.; Yin, W.; Yi, Z.; Bjorkman, M.; Kragic, D. Human-Centered Collaborative Robots With Deep Reinforcement Learning. IEEE Robot. Autom. Lett. 2021, 6, 566–571. [Google Scholar] [CrossRef]
- Kuchibhotla, V.; Harshitha, P.; Goyal, S. An N-step Look Ahead Algorithm Using Mixed (On and Off) Policy Reinforcement Learning. In Proceedings of the 2020 3rd International Conference on Intelligent Sustainable Systems (ICISS), Thoothukudi, India, 3–5 December 2020; pp. 677–681. [Google Scholar]



| Name | Range (Unit) | Description |
|---|---|---|
| speedX | (−∞, +∞) (km/h) | Vehicle speed along the longitudinal axis of the vehicle (the direction of driving) |
| speedY | (−∞, +∞) (km/h) | Vehicle speed along the transverse axis of the vehicle |
| angle | [−π, +π] (rad) | The angle between the direction of the vehicle and the direction of the road axis |
| trackpos | (−∞, +∞) | The distance between the car and the road axis, this value is normalized by the width of the road, 0 means the car is on the central axis, and greater than 1 or less than −1 means the car runs off the road |
| track | (0, 200) (m) | A vector of 19 rangefinder sensors, each sensor returns the distance between the vehicle and the edge of the road within 200 m |
| ζ | μ | σ | |
|---|---|---|---|
| Steer | 0.60 | 0.00 | 0.30 |
| Throttle | 1.00 | 0.50 | 0.10 |
| Brake | 1.00 | −0.10 | 0.05 |
| Parameter | Value |
|---|---|
| Buffer size | 100,000 |
| Batch size | 32 |
| Discount factor | 0.99 |
| Soft update factor | 0.001 |
| Actor network learning rate | 0.0001 |
| Critic network learning rate | 0.001 |
| Max steps | 100,000 |
| Delayed policy update frequency | 2 |
| DDPG | DCPER-DDPG | |
|---|---|---|
| Reward | 75.38 | 85.82 |
| Speed (km/h) | 97.15 | 100.86 |
| Angle (rad) | 0.00042 | 0.00030 |
| Trackpos | 0.037 | 0.019 |
| DDPG | DCPER-DDPG | |
|---|---|---|
| Reward | 87.69 | 101.98 |
| Speed (km/h) | 127.62 | 140.58 |
| Angle (rad) | 0.0029 | 0.00054 |
| Trackpos | 0.13 | 0.09 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, R.; Lv, H.; Zhang, S.; Zhang, D.; Zhang, H. Lane Following Method Based on Improved DDPG Algorithm. Sensors 2021, 21, 4827. https://doi.org/10.3390/s21144827
He R, Lv H, Zhang S, Zhang D, Zhang H. Lane Following Method Based on Improved DDPG Algorithm. Sensors. 2021; 21(14):4827. https://doi.org/10.3390/s21144827
Chicago/Turabian StyleHe, Rui, Haipeng Lv, Sumin Zhang, Dong Zhang, and Hang Zhang. 2021. "Lane Following Method Based on Improved DDPG Algorithm" Sensors 21, no. 14: 4827. https://doi.org/10.3390/s21144827
APA StyleHe, R., Lv, H., Zhang, S., Zhang, D., & Zhang, H. (2021). Lane Following Method Based on Improved DDPG Algorithm. Sensors, 21(14), 4827. https://doi.org/10.3390/s21144827





