TMA from Cosines of Conical Angles Acquired by a Towed Array
Abstract
:1. Introduction
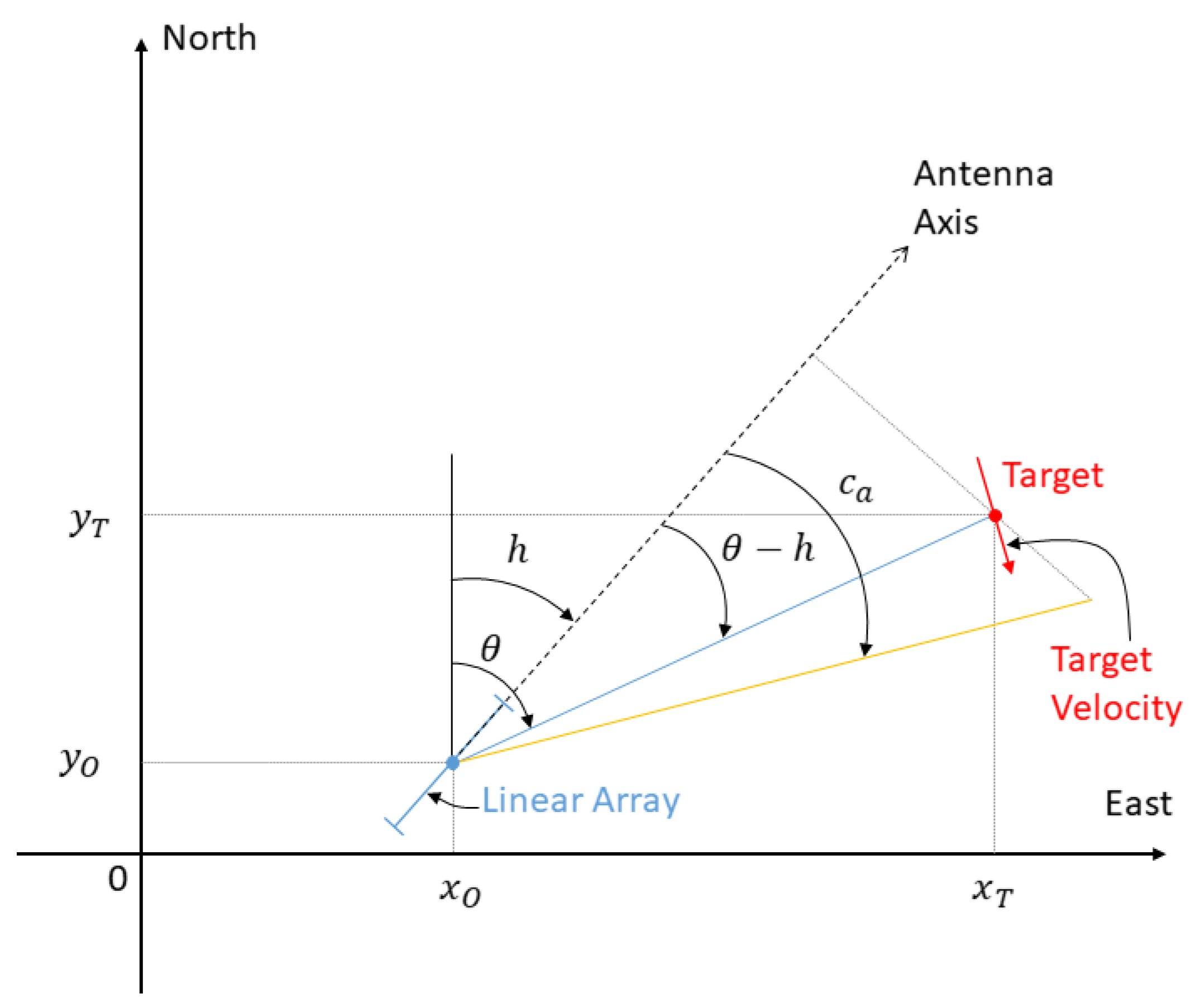
2. Notation and Problem Formulation
- indicates the direction of the path of the sound emitted by the source: if the path is toward the surface, , otherwise ,
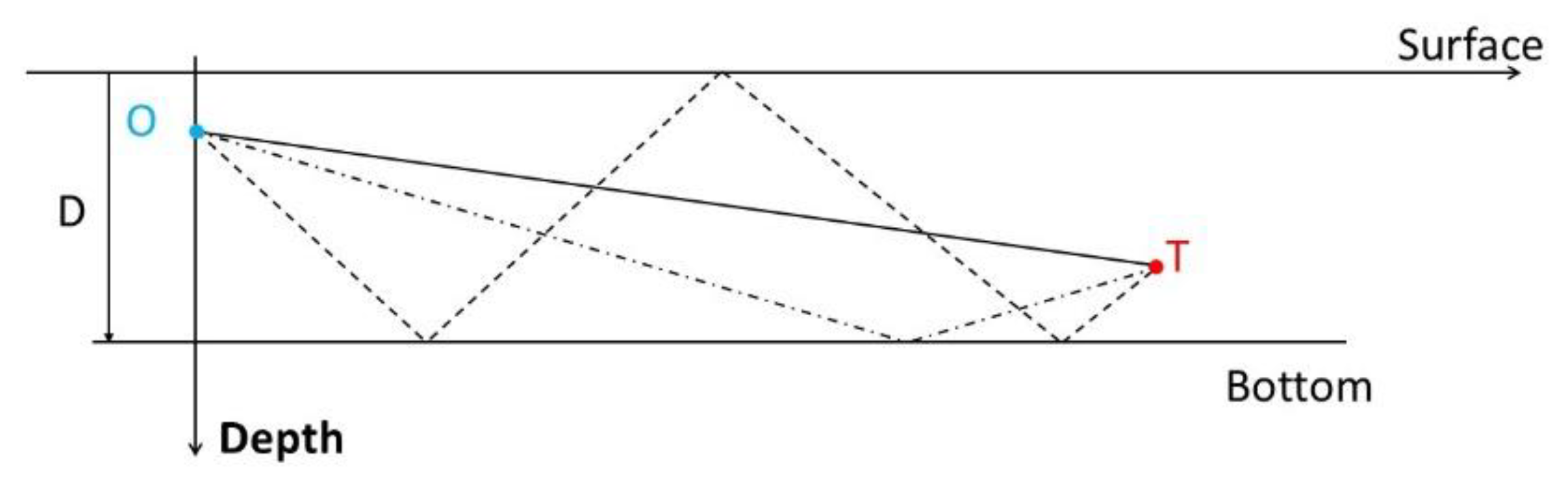
- is the number of bottom reflections, and
- is the number of surface reflections.
- Only one ray is detected by the array during the scenario; in this case, we have at each time t a measurement , given the path along which the wave propagates.
- Two rays (traveling on two different paths) arrive at the sensor’s antenna. In this case, the available measurement at time t is a couple of measurements, say , given the two paths along which the wave propagates.
- If not, what are the ghost targets (those which could be detected at the same set of measurements )?
- How do we make observable or with which new information?
- Is the vector observable from the set of couples ?
3. TMA from One Ray
3.1. Observability Analysis
- 1.
- If the target is broadside to the antenna, then the set of ghost targets is composed of virtual sources broadside to the antenna.
- 2.
- If the target is endfire to the antenna, the set of ghost targets is composed of virtual sources endfire to the antenna.
- 3.
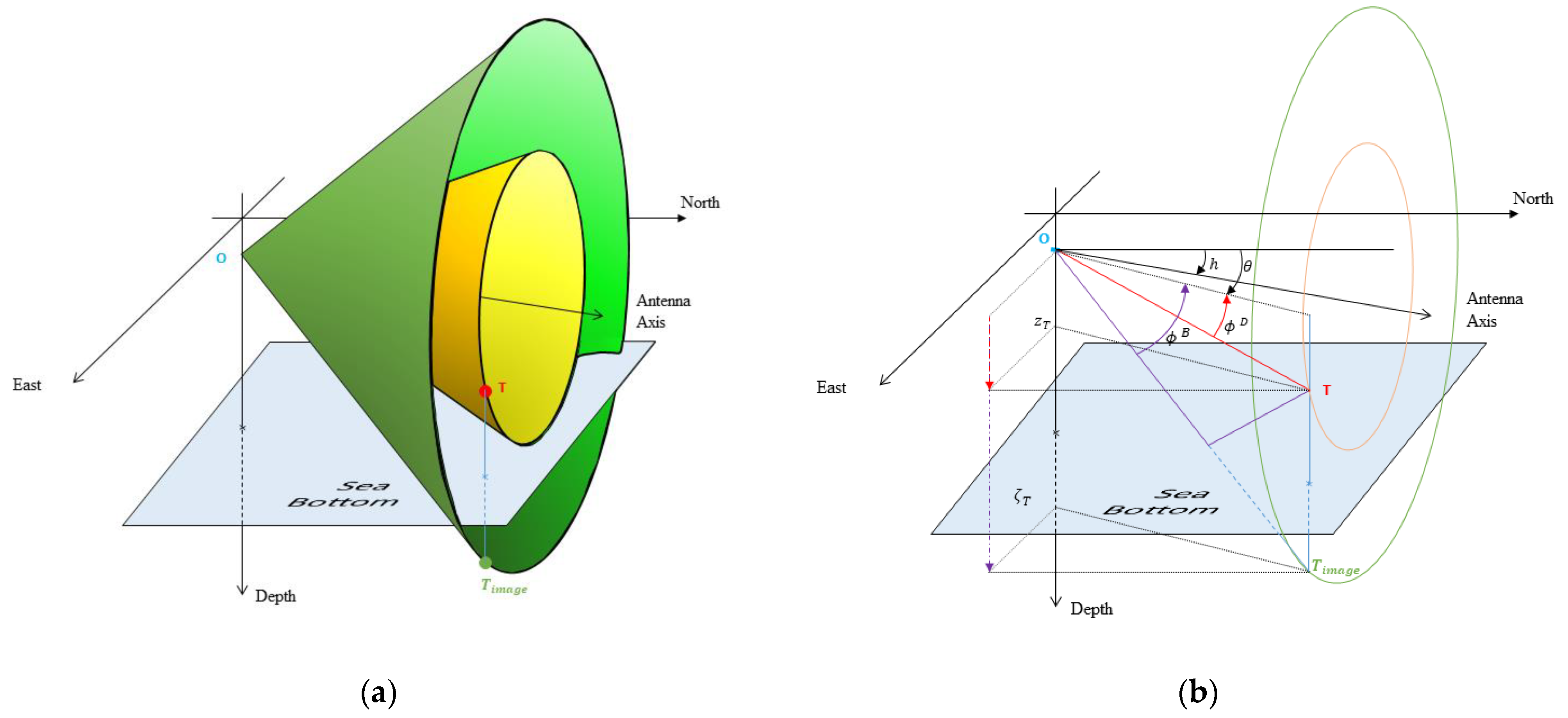
- If the target has the same heading as the array (but is not endfire to it), then the set of ghost targets is composed of virtual targets with the same heading as the antenna. More precisely, the ghost image of each ghost target is moving on a cylinder whose axis is the antenna axis, and whose radius is a positive scalar . The relative ghost target velocity is equal to times the target’s velocity. The initial distance between the ghost image and the center of the antenna is equal to times the initial distance between the target-image and the center of the antenna.
- 4.
- In any other case, for a chosen image-depth , the set of ghost targets is composed of virtual targets whose motion relative to the array is defined by or , where is the 2D axial symmetry around the line of the array, and is a positive scalar. The scalar is equal to if . If (which can happen with a direct path only), can have any positive value.
- 1.
- When the source and the observer are at the same depth, and the path is direct, Theorem 1 recovers the conclusions given in [26].
- 2.
- The cases (1), (2) and (3) of Theorem 1 are “rare events”, since the events of dealing with a source in endfire, broadside or having the same heading as the antenna during the scenario occur with a probability equal to 0.However,when the target has a trajectory close to one of these special cases, the estimates will have a poor behavior.
- 3.
- For case (4), when the detected ray is not a direct path, for example, when the ray is bottom-reflected, a hypothesis about the source is sufficient to obtain one solution, corresponding to a ghost target. Indeed, if we suppose that the depth of the target is (whereas the true value is ), then we have , whose biggest value , and the minimum value is , where is the largest depth of a submarine vehicle. Typically, in deep water, m. A reasonable choice of could be 400 m. We can then have a range of : . For instance, when the depths of the antenna and the target are, respectively, 200 and 100 m, we have . In this way, we bound the set of ghost targets, and we can expect that the bias induced by a wrong choice of is very low.
- 4.
- For case (4) again, with a direct path, if the target is not at the same depth as the antenna, . Because is a positive number, has the same sign as : if , then , and ; if , then , and . In both cases, the range is too wide to be useful.If the target and the antenna are at the same depth,can take any positive value.
3.2. Estimation of the Trajectory
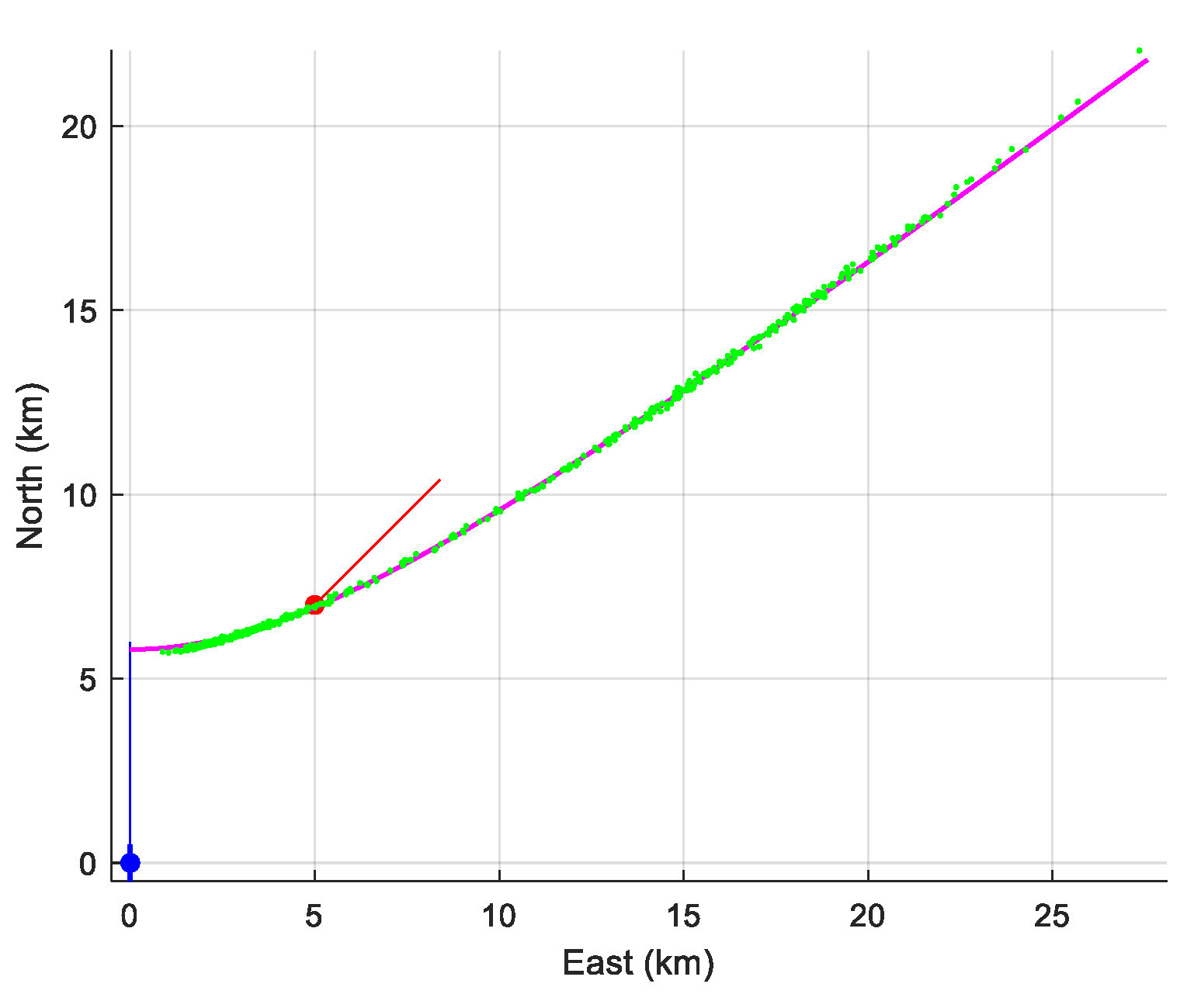
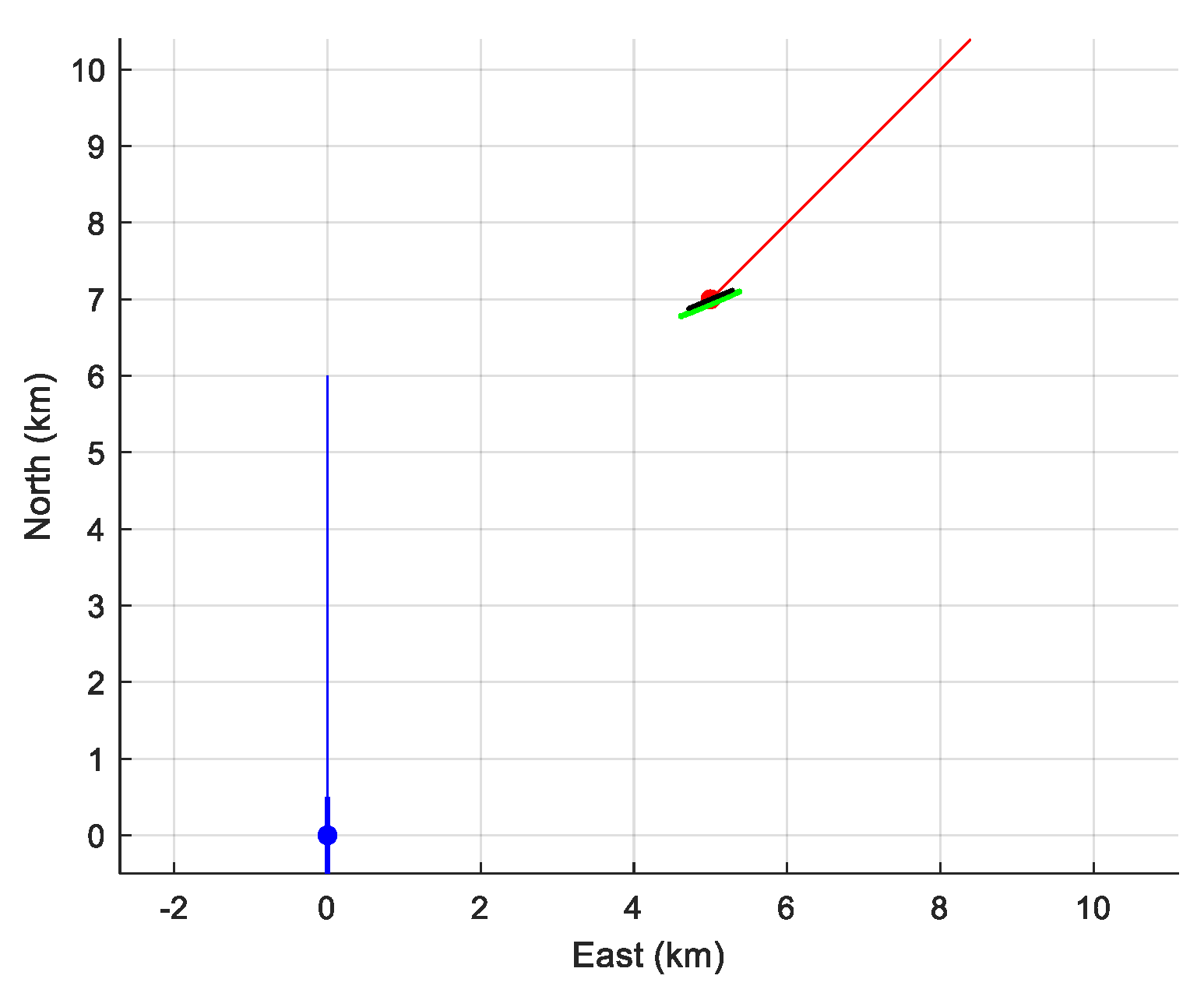
- The measurements are collected every 4 s (s). The scenario lasts 20 min.
- The sea bottom depth is 4000 m. The detected ray is a bottom-reflected ray.
- The assumed target depth is m (whereas the true one is 100 m).
- First, the measurements have been corrupted with an additive Gaussian noise whose standard deviation is .
4. TMA with One Ray When the Array Maneuvers
4.1. Observability Analysis
4.2. Estimation
4.2.1. Estimation of
4.2.2. Estimation of Reduced When the Depth of the Target Is Fixed
4.2.3. Estimation of the Reduced State Vector by the Conventional BOTMA
5. TMA from the Direct Path and the Bottom-Reflected Path
5.1. Observability
- 1.
- If the target is broadside to the array, then the set of ghost targets is uncountable: it is composed of all the (virtual) targets at broadside to the array.
- 2.
- If the target is endfire to the antenna, the set of ghost targets is composed of virtual sources at endfire to the antenna.
- 3.
- If the route of the antenna and the route of the target are parallel, then the set of ghost targets is uncountable: at each depth , there are two ghost targets moving on a cylinder whose axis is the antenna axis, and the radius is a positive scalar . The relative ghost target velocity is equal to times the target’s velocity. The initial distance between the ghost image and the center of the antenna is equal to times the initial distance between the ghost image and the center of the antenna.
- 4.
- If the route of the antenna and the route of the target are not parallel, then there are three ghost targets whose motion relative to the antenna is ,, and , where is the matrix of the axial symmetry around the line of the antenna, and . If the depth of the antenna is equal to the depth of the source, then there is one single ghost target given by .
- when the target’s depth is larger than the array’s depth, there is a ghost whose depth is smaller than the array’s depth, and vice versa.
- , which is a positive coefficient, is equal to , or 1.
5.2. Estimation of the Trajectory
5.2.1. Estimability
- First scenario
- 2.
- Second scenario
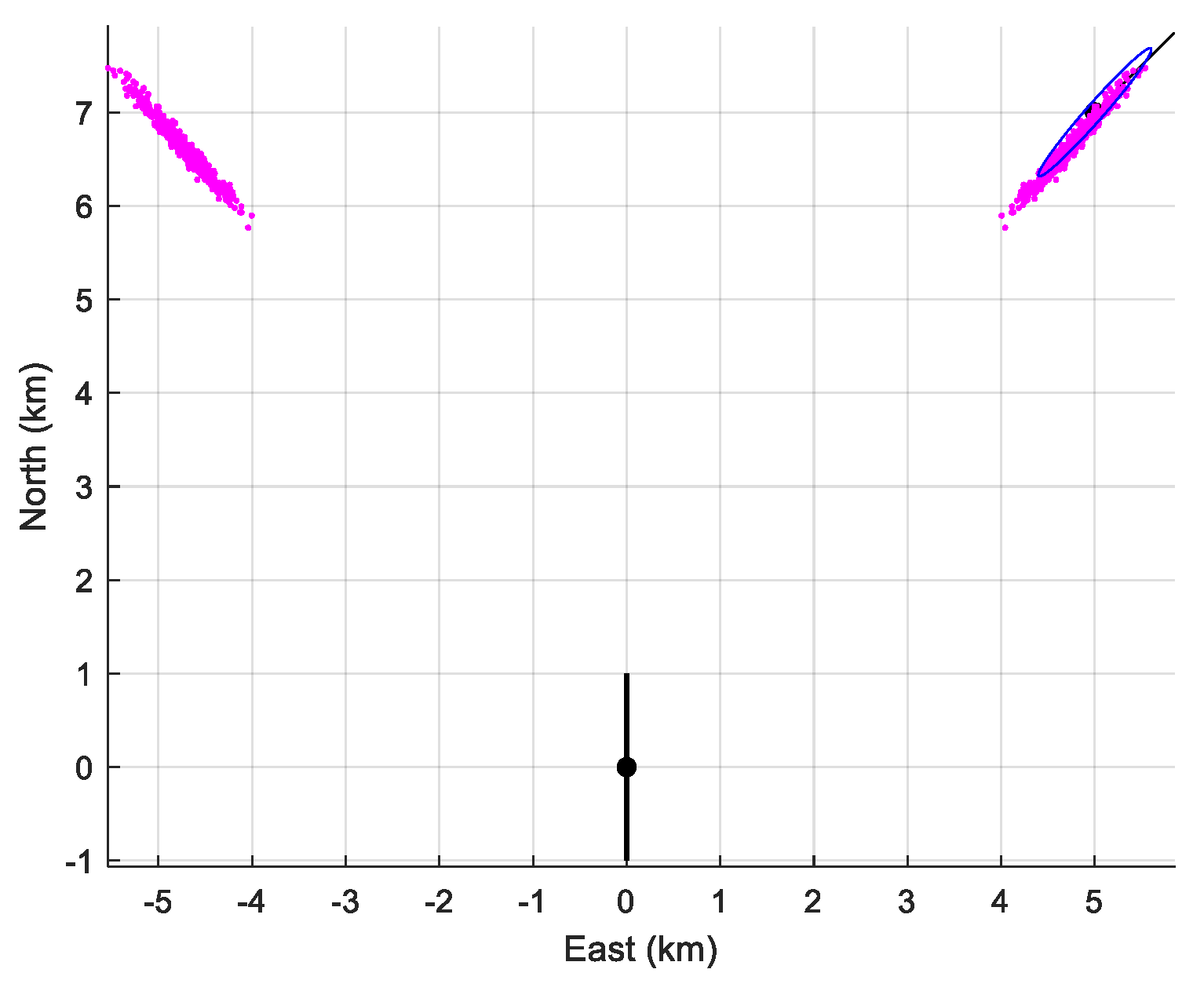
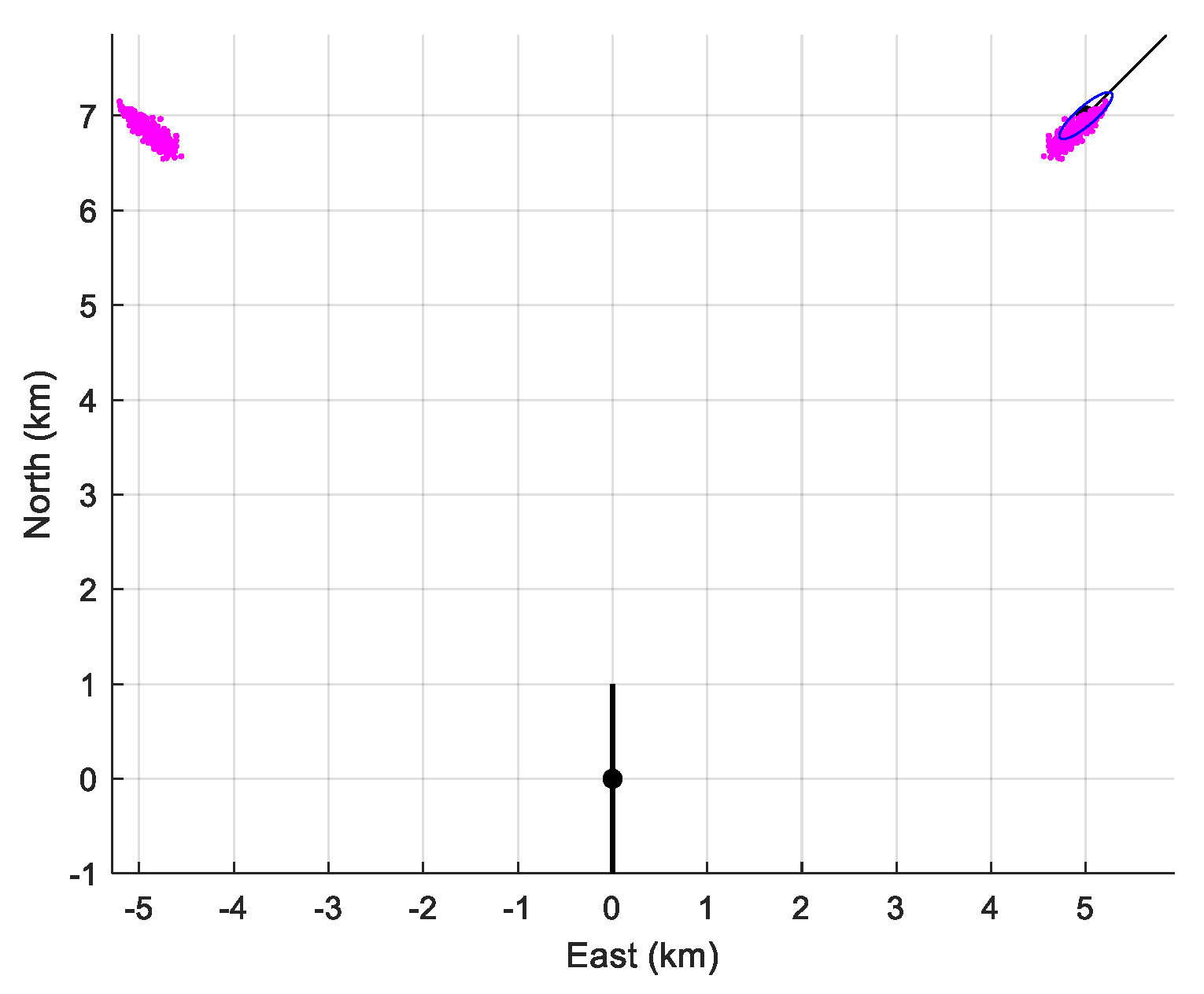
5.2.2. Monte Carlo simulations
- First scenario
- 2.
- Second scenario: Bottom depth m.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Appendix A
- the target is broadside to the antenna,
- the target is endfire to the antenna,
- the target has the same heading as the array (but is not endfire to it),
- the other cases.
References
- Nardone, S.; Lindgren, A.; Gong, K. Fundamental properties and performance of conventional bearings-only target motion analysis. IEEE Trans. Autom. Control 1984, 29, 775–787. [Google Scholar] [CrossRef]
- Song, T.L.; Um, T.Y. Practical guidance for homing missiles with bearings-only measurements. IEEE Trans. Aerosp. Electron. Syst. 1996, 32, 434–443. [Google Scholar] [CrossRef]
- Clavard, J.; Pillon, D.; Pignol, A.-C.; Jauffret, C. Target Motion Analysis of a Source in a Constant Turn from a Nonmaneuvering Observer. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 1760–1780. [Google Scholar] [CrossRef]
- Farina, A. Target tracking with bearingsOnly measurements. Signal. Process 1999, 78, 61–78. [Google Scholar] [CrossRef]
- Jauffret, C.; Pillon, D.; Pignol, A.-C. Bearings-Only Maneuvering Target Motion Analysis from a Nonmaneuvering Platform. IEEE Trans. Aerosp. Electron. Syst. 2010, 46, 1934–1949. [Google Scholar] [CrossRef]
- Zhang, Y.; Lan, J.; Mallick, M.; Li, X.R. Bearings-Only Filtering Using Uncorrelated Conversion Based Filters. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 882–896. [Google Scholar] [CrossRef]
- Aidala, V.; Hammel, S. Utilization of modified polar coordinates for bearings-only tracking. IEEE Trans. Autom. Control 1983, 28, 283–294. [Google Scholar] [CrossRef] [Green Version]
- Arulampalam, S.; Clark, M.; Vinter, R. Performance of the shifted Rayleigh filter in single-sensor bearings-only tracking. In Proceedings of the 2007 10th International Conference on Information Fusion, Quebec, QC, Canada, 9–12 July 2007; pp. 1–6. [Google Scholar]
- Laneuville, D.; Jauffret, C. Recursive Bearings-Only TMA via Unscented Kalman Filter: Cartesian vs. Modified Polar Coordinates. In Proceedings of the 2008 IEEE Aerospace Conference, Big Sky, MT, USA, 1–8 March 2008; pp. 1–11. [Google Scholar]
- Arulampalam, M.S.; Ristic, B.; Gordon, N.; Mansell, T. Bearings-Only Tracking of Maneuvring Targets Using Particle Filters. Eurasip J. App. Sig. Process. 2004, 15, 2351–2365. [Google Scholar]
- Zhang, Y.J.; Xu, G.Z. Bearings-Only Target Motion Analysis via Instrumental Variable Estimation. IEEE Trans. Signal. Process. 2010, 58, 5523–5533. [Google Scholar] [CrossRef]
- Doğançay, K. On the efficiency of a bearings-only instrumental variable estimator for target motion analysis. Signal. Process. 2005, 85, 481–490. [Google Scholar] [CrossRef]
- Chan, Y.T.; Rea, T.A. Bearings-only tracking using data fusion and instrumental variables. In Proceedings of the Proceedings of the Third International Conference on Information Fusion, Paris, France, 10–13 July 2000. [Google Scholar]
- Kirubarajan, T.; Bar-Shalom, Y.; Lerro, D. Bearings-only tracking of maneuvering targets using a batch-recursive estimator. IEEE Trans. Aerosp. Electron. Syst. 2001, 37, 770–780. [Google Scholar] [CrossRef]
- Jauffret, C.D.; Pillon, D. Observability in Passive Target Motion Analysis. IEEE Trans. Aerosp. Electro. Syst. 1996, AES-32, 1290–1300. [Google Scholar] [CrossRef]
- Le Cadre, J.; Jauffret, C. Discrete-time observability and estimability analysis for bearings-only target motion analysis. IEEE Trans. Aerosp. Electron. Syst. 1997, 33, 178–201. [Google Scholar] [CrossRef]
- Nardone, S.C.; Aidala, V.J. Observability Criteria for Bearings-Only Target Motion Analysis. IEEE Trans. Aerosp. Electron. Syst. 1981, AES-17, 162–166. [Google Scholar] [CrossRef]
- Urick, R.J. Principles of Underwater Sound; McGraw-Hill: New York, NY, USA, 1983. [Google Scholar]
- Van Trees, H.L. Optimum Array Processing: Part IV of Detection, Estimation, and Modulation Theory; Wiley Interscience: New York, NY, USA, 2002. [Google Scholar]
- Abraham, D.A. Underwater Acoustic Signal Processing: Modeling, Detection, and Estimation; Modern Acoustic and Signal Processing; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Gong, K.F. Multipath Target Motion Analysis: Properties and Implication of the Multipath Process; in Technical Report 6687; NUSC: Newport, RI, USA, 1982. [Google Scholar]
- Blanc-Benon, P.; Jauffret, C. Target Motion Analysis from Bearing and Time-delay Measurements: The Use of Multipath. IEEE Trans. Aerosp. Electron. Syst. 1997, AES-33, 813–824. [Google Scholar] [CrossRef]
- Oh, R.; Song, T.L.; Choi, J.W. Batch Processing through Particle Swarm Optimization for Target Motion Analysis with Bottom Bounce Underwater Acoustic Signals. Sensors 2020, 20, 1234. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Steven, S.M. Fundamentals if Statistical Signal Processing—Estimation Theory; Prentice Hall: Englehood Cliffs, NJ, USA, 1993. [Google Scholar]
- Jauffret, C. Observability and fisher information matrix in nonlinear regression. IEEE Trans. Aerosp. Electron. Syst. 2007, 43, 756–759. [Google Scholar] [CrossRef]
- Pignol, A.-C.; Jauffret, C.; Pillon, D. A statistical fusion for a leg-by-leg bearings-only TMA without observer maneuver. In Proceedings of the 13th International Conference on Information Fusion, Edinburgh, UK, 26–29 July 2010; Volume 6, pp. 1–8. [Google Scholar] [CrossRef]
- Bar-Shalom, Y.; Rong Li, X.; Kirubarajan, T. Estimation and Tracking: Principles, Techniques and Software; Artech House: Boston, MA, USA, 1993. [Google Scholar]
- Payan, J.; Lebon, A.; Perez, A.-C.; Jauffret, C.; Laneuville, D. Passive Target Motion Analysis by Fusion of Linear Arrays and Sonobuoys in a Cluttered Environment. IEEE Trans. Aerosp. Electron. Syst. 2021, 1. [Google Scholar] [CrossRef]
- Le Cadre, J.-P.; Gauvrit, H. Optimization of the observer motion for bearings-only target motion analysis. In Proceedings of the 1st Australian Data Fusion Symposium, Adelaide, SA, Australia, 21–22 November 1996; pp. 190–195. [Google Scholar]
- Fawcett, J. Effect of course maneuvers on bearings-only range estimation. IEEE Trans. Acoust. Speech, Signal. Process 1988, 36, 1193–1199. [Google Scholar] [CrossRef]
- Passerieux, J.M.; Van Cappel, D. Optimal observer maneuver for bearings-only tracking. IEEE Trans. Aerosp. Electron. Syst. 1998, 34, 777–788. [Google Scholar] [CrossRef]



| Bias | |||
|---|---|---|---|
| 5000 m | −3525 | 6962 | 13,356 |
| 7000 m | −2367 | 4052 | 5599 |
| 2.83 m/s | −1.37 | 1.81 | 4.35 |
| 2.83 m/s | 0.53 | 1.62 | 2.75 |
| Bias | |||
|---|---|---|---|
| 5000 m | 60.40 | 138.67 | 133.56 |
| 7000 m | 88.20 | 58.42 | 55.99 |
| 2.83 m/s | 0.043 | 0.044 | 0.044 |
| 2.83 m/s | 0.037 | 0.028 | 0.028 |
| Bias | |||
|---|---|---|---|
| 5000 m | −44.77 | 854.72 | 868.12 |
| 7000 m | −68.16 | 1162.1 | 1173.60 |
| 100 m | 7.14 | 558.55 | 545.99 |
| 2.83 m/s | 0.092 | 1.67 | 1.65 |
| 2.83 m/s | 0.194 | 2.72 | 2.68 |
| Bias | |||
|---|---|---|---|
| 5000 m | 65.40 | 655.61 | 606.41 |
| 7000 m | 93.05 | 831.75 | 762.56 |
| 2.83 m/s | 0.034 | 1.71 | 1.58 |
| 2.83 m/s | 0.063 | 2.76 | 2.52 |
| Bias | |||
|---|---|---|---|
| 5000 m | 401.12 | 281.85 | 281.17 |
| 7000 m | 557.24 | 330.87 | 319.37 |
| 2.83 m/s | 0.13 | 1.58 | 1.78 |
| 2.83 m/s | 0.12 | 1.81 | 2.02 |
| Bias | |||
|---|---|---|---|
| 5000 m | 306.81 | 219.28 | 130.08 |
| 7000 m | 432.46 | 276.61 | 115.26 |
| 2.83 m/s | 0.18 | 0.74 | 0.80 |
| 2.83 m/s | 0.18 | 0.66 | 0.71 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lebon, A.; Perez, A.-C.; Jauffret, C.; Laneuville, D. TMA from Cosines of Conical Angles Acquired by a Towed Array. Sensors 2021, 21, 4797. https://doi.org/10.3390/s21144797
Lebon A, Perez A-C, Jauffret C, Laneuville D. TMA from Cosines of Conical Angles Acquired by a Towed Array. Sensors. 2021; 21(14):4797. https://doi.org/10.3390/s21144797
Chicago/Turabian StyleLebon, Antoine, Annie-Claude Perez, Claude Jauffret, and Dann Laneuville. 2021. "TMA from Cosines of Conical Angles Acquired by a Towed Array" Sensors 21, no. 14: 4797. https://doi.org/10.3390/s21144797
APA StyleLebon, A., Perez, A.-C., Jauffret, C., & Laneuville, D. (2021). TMA from Cosines of Conical Angles Acquired by a Towed Array. Sensors, 21(14), 4797. https://doi.org/10.3390/s21144797





