A Statistical Method for Exploratory Data Analysis Based on 2D and 3D Area under Curve Diagrams: Parkinson’s Disease Investigation
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Data
2.2. Signal Preprocessing
- The 50, 100, 150, and 200 Hz notch filters removed the power line interference.
- The 60–240 Hz fourth-order Butterworth bandpass filter was applied to EMG in the forward and reverse directions.
- The envelope of the signal was decimated; the decimation factor was 4.
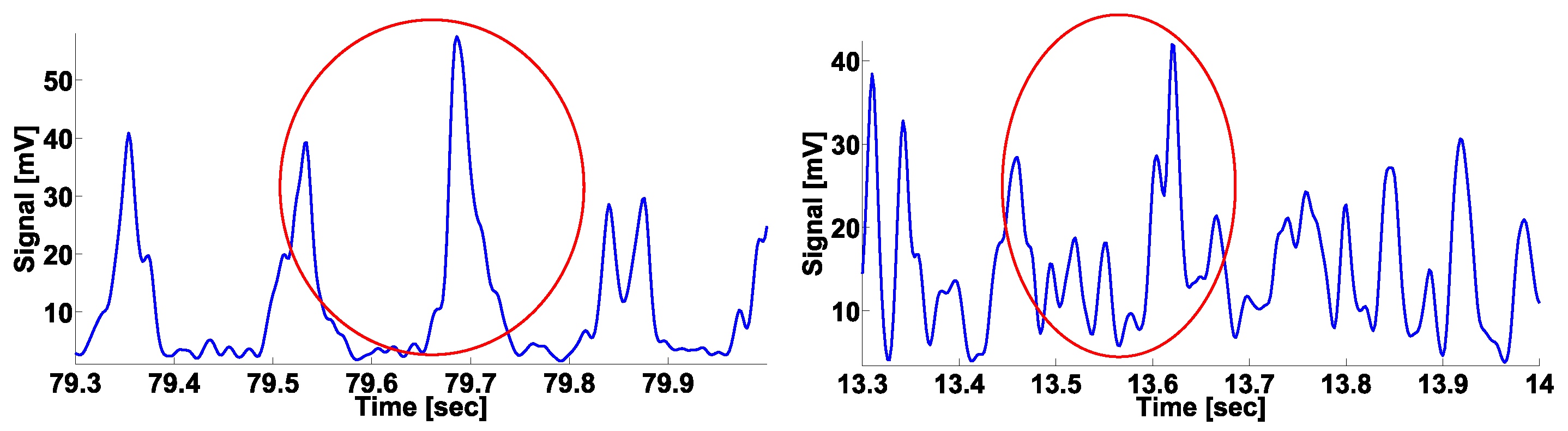
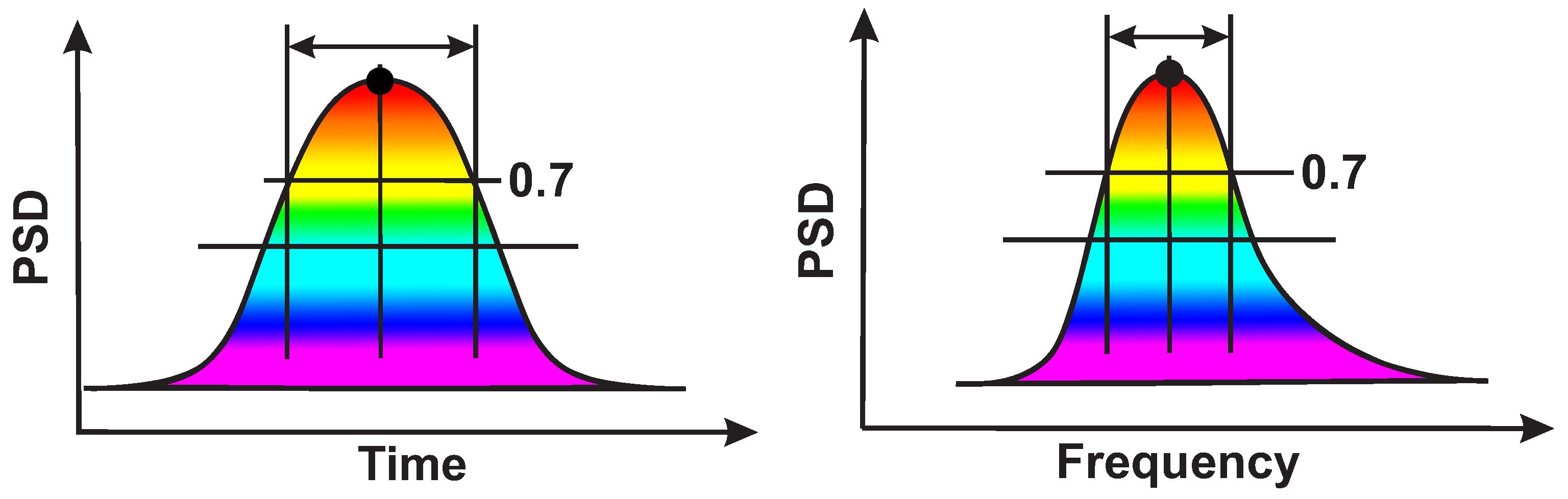
2.3. Calculation of Local Maxima in the Wavelet Spectrogram
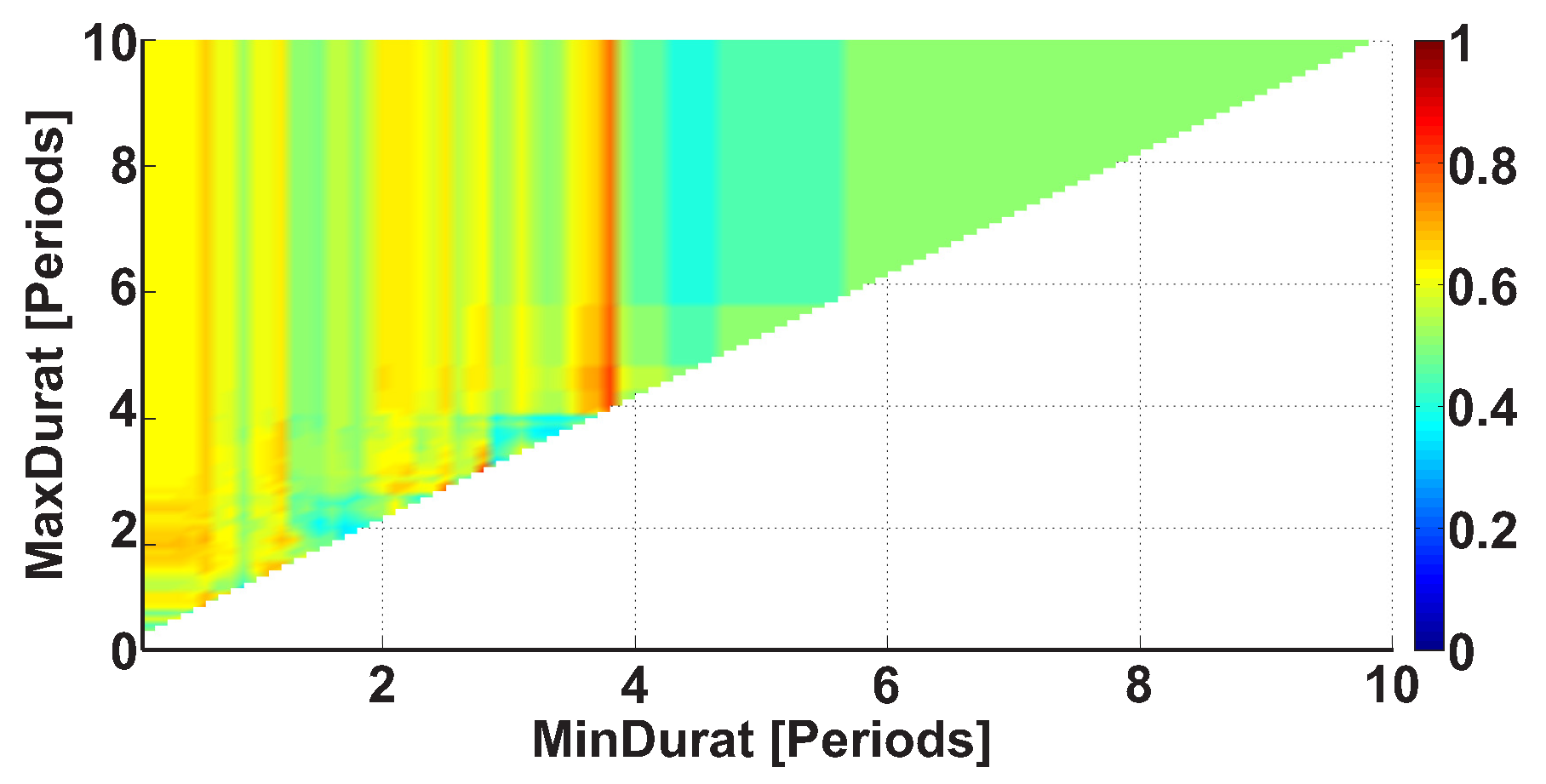
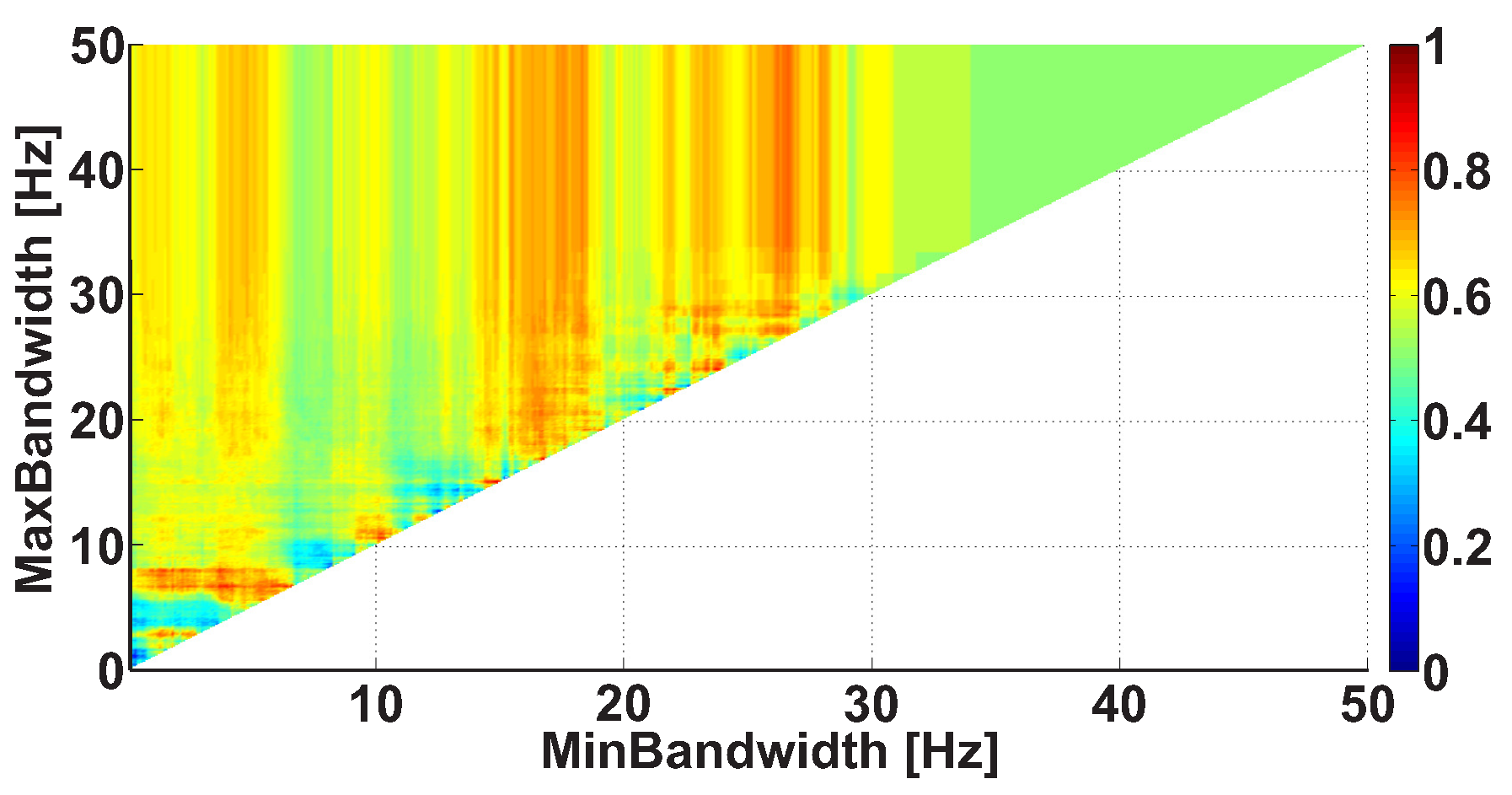
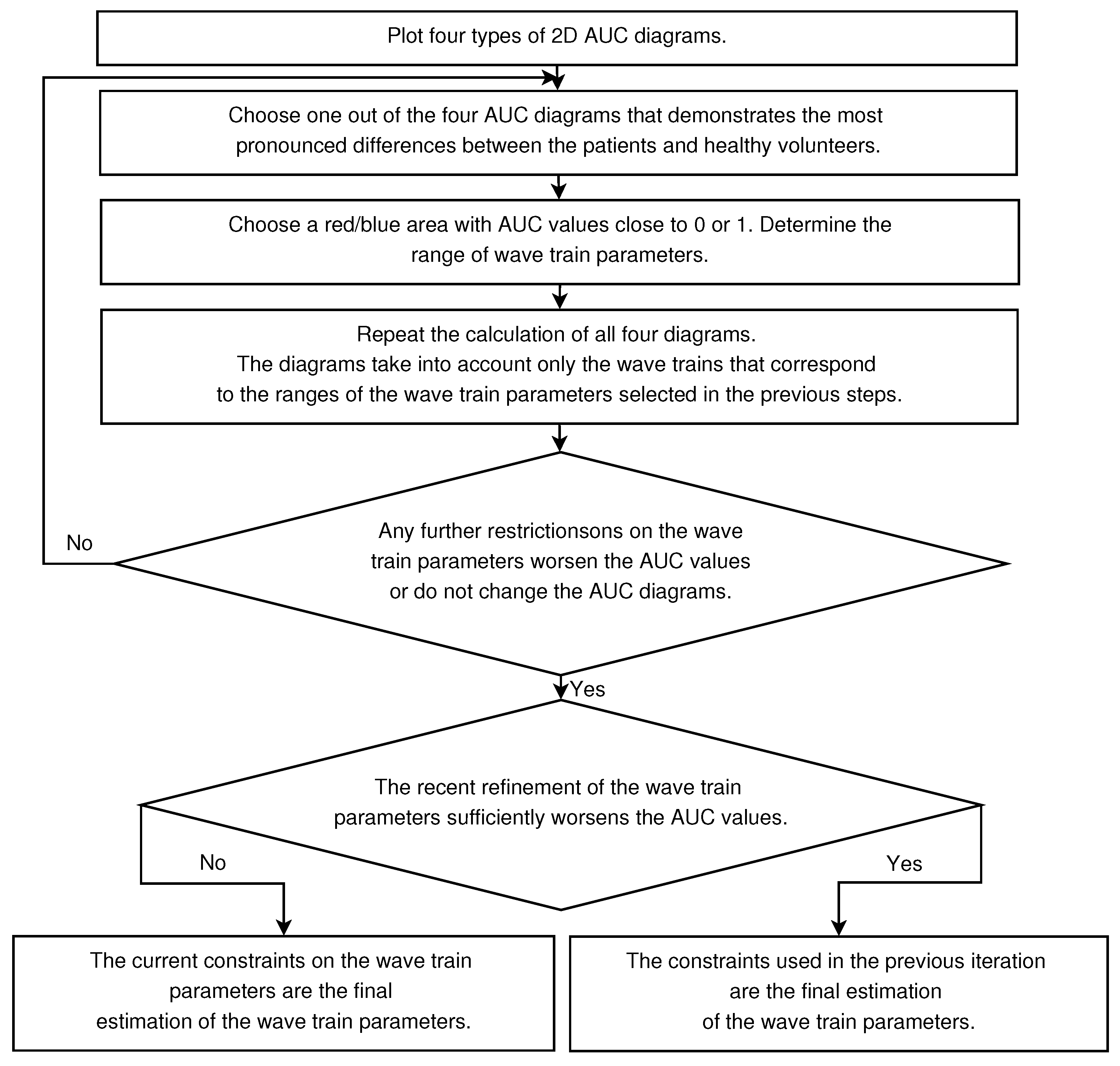
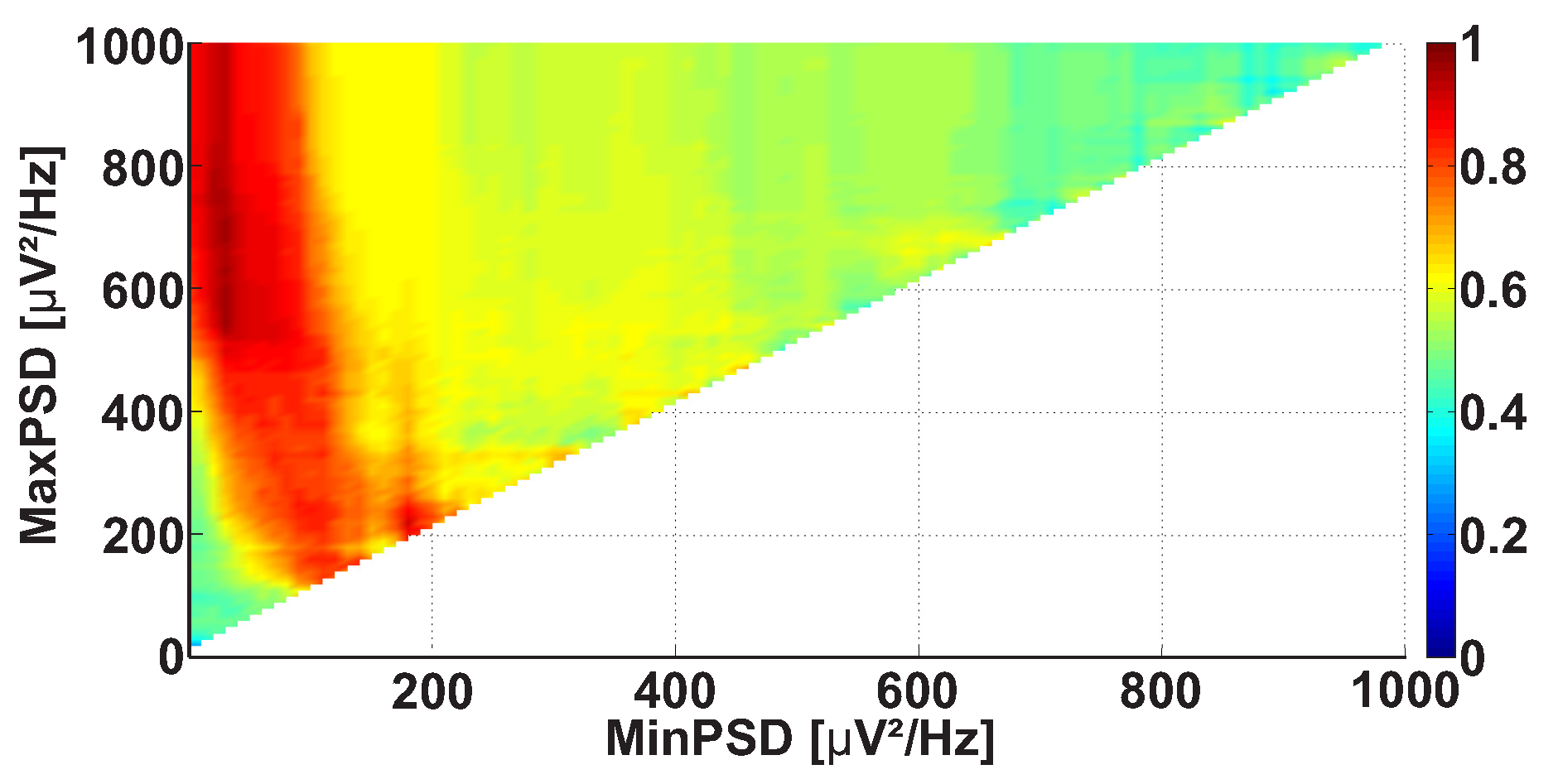
2.4. 2D AUC Diagrams
- Any further restrictions on the parameters of the wave trains do not change the AUC diagrams. This means that the further refinement of the wave train parameters makes no sense.
- The refinement of the wave train parameters worsens the AUC values sufficiently in the AUC diagrams. This means that the investigated ranges of the wave train parameters became too narrowed; the number of wave trains considered in the AUC diagrams is too small. Theoretically speaking, in this case the refinement of the wave train parameters could be continued. However, the available dataset is not sufficient for this. The investigation of the wave train parameters could be continued if the number of subjects and/or the duration of EMG records are sufficiently increased.
2.5. 3D AUC Diagrams
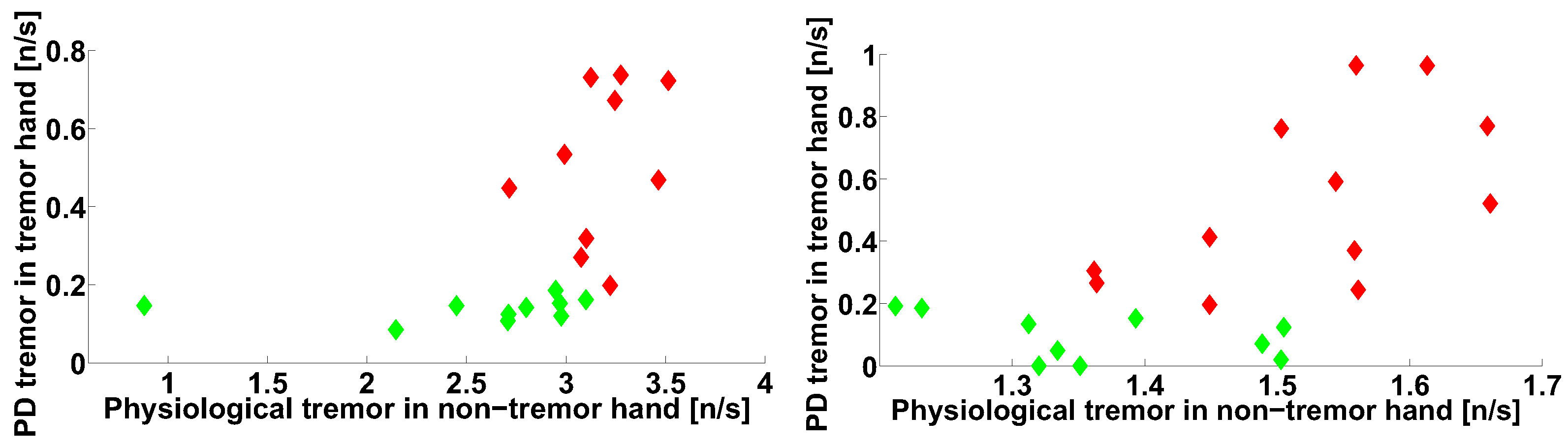
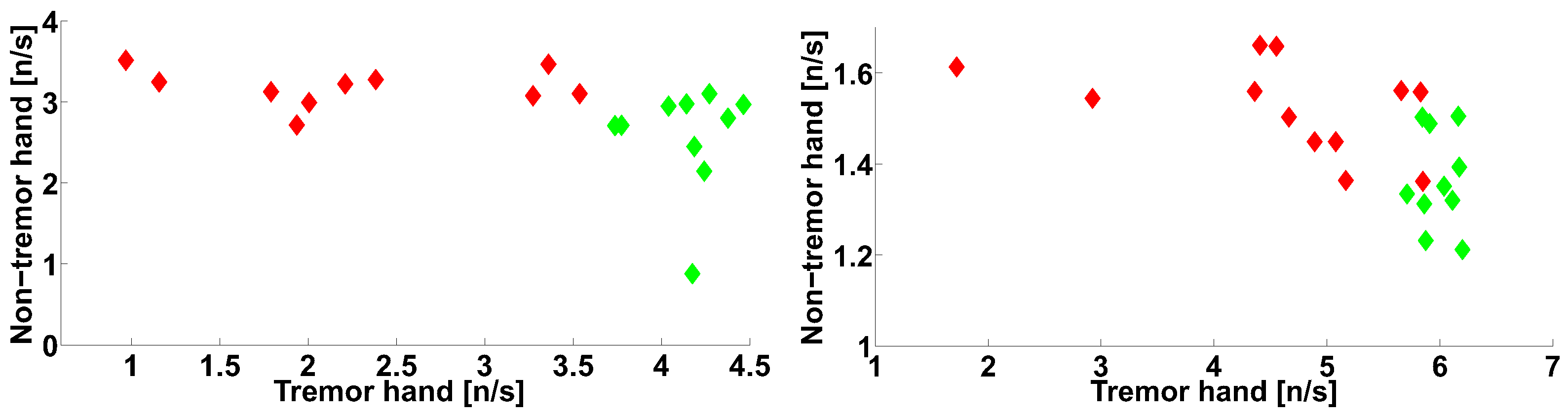
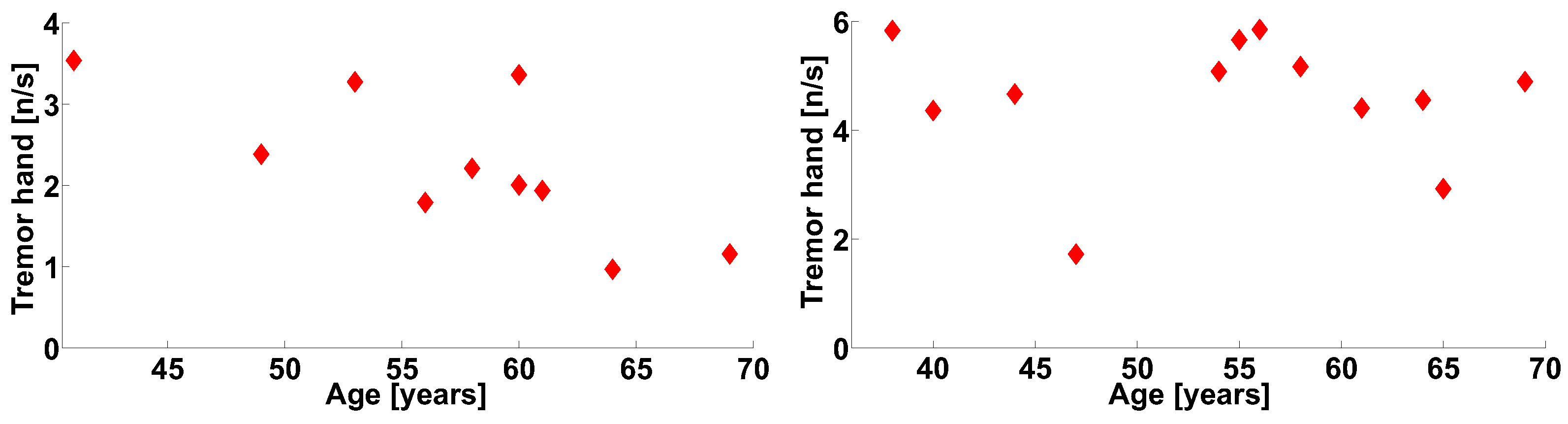
3. Group Data Analysis
4. Discussion
5. Conclusions
6. Patents
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Andreeva, Y.; Khutorskaya, O. EMGs spectral analysis method for the objective diagnosis of different clinical forms of Parkinson’s disease. J. Electromyogr. Clin. Neurophysiol. 1996, 36, 187–192. [Google Scholar]
- Khutorskaya, O.E. Method for Early and Differential Electromyographic Diagnosis of the Main Symptoms of Parkinson’s Disease. Russian Federation Patent Application No. 2626557, 28 July 2017. [Google Scholar]
- Lukhanina, E.; Kapoustina, M.; Karaban, I. A quantitative surface electromyogram analysis for diagnosis and therapy control in Parkinson’s disease. Park. Relat. Disord. 2000, 6, 77–86. [Google Scholar] [CrossRef]
- Fattorini, L.; Felici, F.; Filligoi, G.; Traballesi, M.; Farina, D. Influence of high motor unit synchronization levels on non-linear and spectral variables of the surface EMG. J. Neurosci. Methods 2005, 143, 133–139. [Google Scholar] [CrossRef] [PubMed]
- Robichaud, J.A.; Pfann, K.D.; Vaillancourt, D.E.; Comella, C.L.; Corcos, D.M. Force control and disease severity in Parkinson’s disease. Mov. Disord. 2005, 20, 441–450. [Google Scholar] [CrossRef] [PubMed]
- Yang, W.; Yang, D.; Liu, Y.; Liu, H. EMG pattern recognition using convolutional neural network with different scale signal/spectra input. Int. J. Humanoid Robot. 2019, 16, 1950013. [Google Scholar] [CrossRef]
- Sung, P.S.; Zurcher, U.; Kaufman, M. Comparison of spectral and entropic measures for surface electromyography time series: A pilot study. J. Rehabil. Res. Dev. 2007, 44, 599–609. [Google Scholar] [CrossRef] [PubMed]
- Rissanen, S.; Kankaanpää, M.; Tarvainen, M.P.; Nuutinen, J.; Tarkka, I.M.; Airaksinen, O.; Karjalainen, P.A. Analysis of surface EMG signal morphology in Parkinson’s disease. Physiol. Meas. 2007, 28, 1507. [Google Scholar] [CrossRef]
- Pfann, K.D.; Buchman, A.S.; Comella, C.L.; Corcos, D.M. Control of movement distance in Parkinson’s disease. Mov. Disord. 2001, 16, 1048–1065. [Google Scholar] [CrossRef]
- Zeng, Y.; Yang, J.; Peng, C.; Yin, Y. Evolving Gaussian process autoregression based learning of human motion intent using improved energy kernel method of EMG. IEEE Trans. Biomed. Eng. 2019, 66, 2556–2565. [Google Scholar] [CrossRef]
- Al-Timemy, A.H.; Bugmann, G.; Escudero, J.; Outram, N. Classification of finger movements for the dexterous hand prosthesis control with surface electromyography. IEEE J. Biomed. Health Inform. 2013, 17, 608–618. [Google Scholar] [CrossRef]
- Xiong, D.; Zhang, D.; Zhao, X.; Zhao, Y. Deep learning for EMG-based human-machine interaction: A review. IEEE/CAA J. Autom. Sin. 2021, 8, 512–533. [Google Scholar] [CrossRef]
- Parajuli, N.; Sreenivasan, N.; Bifulco, P.; Cesarelli, M.; Savino, S.; Niola, V.; Esposito, D.; Hamilton, T.J.; Naik, G.R.; Gunawardana, U.; et al. Real-time EMG based pattern recognition control for hand prostheses: A review on existing methods, challenges and future implementation. Sensors 2019, 19, 4596. [Google Scholar] [CrossRef] [Green Version]
- Reaz, M.B.I.; Hussain, M.S.; Mohd-Yasin, F. Techniques of EMG signal analysis: Detection, processing, classification and applications. Biol. Proced. Online 2006, 8, 11–35. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dogan, S.; Tuncer, T. A novel statistical decimal pattern-based surface electromyogram signal classification method using tunable q-factor wavelet transform. Soft Comput. 2021, 25, 1085–1098. [Google Scholar] [CrossRef]
- Subba, R.; Bhoi, A.K. Feature Extraction and Classification Between Control and Parkinson’s Using EMG Signal. In Cognitive Informatics and Soft Computing; Springer: Berlin/Heidelberg, Germany, 2020; pp. 45–52. [Google Scholar]
- Meigal, A.; Rissanen, S.; Tarvainen, M.; Airaksinen, O.; Kankaanpää, M.; Karjalainen, P. Non-linear EMG parameters for differential and early diagnostics of Parkinson’s disease Front. Neurol 2013, 4, 135. [Google Scholar]
- Namazi, H. Decoding of hand gestures by fractal analysis of electromyography (EMG) signal. Fractals 2019, 27, 1950022. [Google Scholar] [CrossRef]
- Ivanova, E.; Fedin, P.; Brutyan, A.; Ivanova-Smolenskaya, I.; Illarioshkin, S. Analysis of tremor activity of antagonist muscles in essential tremor and Parkinson’s diseases. Nevrol. Zhurnal 2014, 19, 11–18. [Google Scholar] [CrossRef]
- Webber, C.; Marwan, N. Recurrence Quantification Analysis–Theory and Best Practices; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Farina, D.; Fattorini, L.; Felici, F.; Filligoi, G. Nonlinear surface EMG analysis to detect changes of motor unit conduction velocity and synchronization. J. Appl. Physiol. 2002, 93, 1753–1763. [Google Scholar] [CrossRef]
- Buongiorno, D.; Cascarano, G.D.; De Feudis, I.; Brunetti, A.; Carnimeo, L.; Dimauro, G.; Bevilacqua, V. Deep learning for processing electromyographic signals: A taxonomy-based survey. Neurocomputing 2020, 452, 549–565. [Google Scholar] [CrossRef]
- Rim, B.; Sung, N.J.; Min, S.; Hong, M. Deep learning in physiological signal data: A survey. Sensors 2020, 20, 969. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mahmud, M.; Kaiser, M.S.; Hussain, A.; Vassanelli, S. Applications of deep learning and reinforcement learning to biological data. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 2063–2079. [Google Scholar] [CrossRef] [Green Version]
- Mahmud, M.; Kaiser, M.S.; McGinnity, T.M.; Hussain, A. Deep learning in mining biological data. Cogn. Comput. 2021, 13, 1–33. [Google Scholar] [CrossRef] [PubMed]
- Phinyomark, A.; Limsakul, C.; Phukpattaranont, P. Application of wavelet analysis in EMG feature extraction for pattern classification. Meas. Sci. Rev. 2011, 11, 45–52. [Google Scholar] [CrossRef]
- Englehart, K.; Hudgin, B.; Parker, P.A. A wavelet-based continuous classification scheme for multifunction myoelectric control. IEEE Trans. Biomed. Eng. 2001, 48, 302–311. [Google Scholar] [CrossRef] [PubMed]
- De Michele, G.; Sello, S.; Carboncini, M.C.; Rossi, B.; Strambi, S.K. Cross-correlation time-frequency analysis for multiple EMG signals in Parkinson’s disease: A wavelet approach. Med. Eng. Phys. 2003, 25, 361–369. [Google Scholar] [CrossRef]
- Valls-Solé, J.; Valldeoriola, F. Neurophysiological correlate of clinical signs in Parkinson’s disease. Clin. Neurophysiol. 2002, 113, 792–805. [Google Scholar] [CrossRef]
- Hallett, M.; Shahani, B.T.; Young, R.R. EMG analysis of stereotyped voluntary movements in man. J. Neurol. Neurosurg. Psychiatry 1975, 38, 1154–1162. [Google Scholar] [CrossRef] [Green Version]
- Flament, D.; Vaillancourt, D.; Kempf, T.; Shannon, K.; Corcos, D. EMG remains fractionated in Parkinson’s disease, despite practice-related improvements in performance. Clin. Neurophysiol. 2003, 114, 2385–2396. [Google Scholar] [CrossRef]
- Robichaud, J.A.; Pfann, K.D.; Comella, C.L.; Corcos, D.M. Effect of medication on EMG patterns in individuals with Parkinson’s disease. Mov. Disord. 2002, 17, 950–960. [Google Scholar] [CrossRef] [Green Version]
- Robichaud, J.A.; Pfann, K.D.; Comella, C.L.; Brandabur, M.; Corcos, D.M. Greater impairment of extension movements as compared to flexion movements in Parkinson’s disease. Exp. Brain Res. 2004, 156, 240–254. [Google Scholar]
- Meigal, A.I.; Rissanen, S.; Tarvainen, M.; Karjalainen, P.; Iudina-Vassel, I.; Airaksinen, O.; Kankaanpää, M. Novel parameters of surface EMG in patients with Parkinson’s disease and healthy young and old controls. J. Electromyogr. Kinesiol. 2009, 19, e206–e213. [Google Scholar] [CrossRef] [PubMed]
- Rissanen, S.M.; Kankaanpää, M.; Meigal, A.; Tarvainen, M.P.; Nuutinen, J.; Tarkka, I.M.; Airaksinen, O.; Karjalainen, P.A. Surface EMG and acceleration signals in Parkinson’s disease: Feature extraction and cluster analysis. Med. Biol. Eng. Comput. 2008, 46, 849–858. [Google Scholar] [CrossRef] [PubMed]
- Oktay, A.B.; Kocer, A. Differential diagnosis of Parkinson and essential tremor with convolutional LSTM networks. Biomed. Signal Process. Control 2020, 56, 101683. [Google Scholar] [CrossRef]
- Kim, H.B.; Lee, W.W.; Kim, A.; Lee, H.J.; Park, H.Y.; Jeon, H.S.; Kim, S.K.; Jeon, B.; Park, K.S. Wrist sensor-based tremor severity quantification in Parkinson’s disease using convolutional neural network. Comput. Biol. Med. 2018, 95, 140–146. [Google Scholar] [CrossRef]
- Ivanova, E.; Fedin, P.; Brutyan, A.; Ivanova-Smolenskaya, I.; Illarioshkin, S. Clinical and electrophysiological analysis of tremor in patients with essential tremor and Parkinson’s disease. Nevrol. Zhurnal 2013, 5, 21–26. Available online: https://cyberleninka.ru/article/n/kliniko-elektrofiziologicheskiy-analiz-drozhatelnogo-giperkineza-pri-essentsialnom-tremore-i-bolezni-parkinsona/viewer (accessed on 7 July 2021).
- Illarioshkin, S.N.; Ivanova-Smolenskaya, I.A. Trembling Hyperkinesis; Atmosfera: Moscow, Russia, 2011; (In Russian). Available online: https://www.ozon.ru/product/drozhatelnye-giperkinezy-rukovodstvo-dlya-vrachey-162350391/ (accessed on 7 July 2021).
- Shaffer, J.P. Multiple hypothesis testing: A review. Annu. Rev. Psychol. 1995, 46, 561–584. [Google Scholar] [CrossRef]
- Schnitzler, A.; Timmermann, L.; Gross, J. Physiological and pathological oscillatory networks in the human motor system. J. Physiol. Paris 2006, 99, 3–7. [Google Scholar] [CrossRef]
- Deiber, M.P.; Pollak, P.; Passingham, R.; Landais, P.; Gervason, C.; Cinotti, L.; Friston, K.; Frackowiak, R.; Mauguière, F.; Benabid, A.L. Thalamic stimulation and suppression of parkinsonian tremor: Evidence of a cerebellar deactivation using positron emission tomography. Brain 1993, 116, 267–279. [Google Scholar] [CrossRef]
- Elias, W.J.; Shah, B.B. Tremor. JAMA 2014, 311, 948–954. [Google Scholar] [CrossRef]
- Helmich, R.C.; Janssen, M.J.; Oyen, W.J.; Bloem, B.R.; Toni, I. Pallidal dysfunction drives a cerebellothalamic circuit into Parkinson tremor. Ann. Neurol. 2011, 69, 269–281. [Google Scholar] [CrossRef]
- Poewe, W. The natural history of Parkinson’s disease. J. Neurol. 2006, 253, vii2–vii6. [Google Scholar] [CrossRef]
- Woytowicz, E.J.; Westlake, K.P.; Whitall, J.; Sainburg, R.L. Handedness results from complementary hemispheric dominance, not global hemispheric dominance: Evidence from mechanically coupled bilateral movements. J. Neurophysiol. 2018, 120, 729–740. [Google Scholar] [CrossRef]
- Woytowicz, E.J.; Sainburg, R.L.; Westlake, K.P.; Whitall, J. Competition for limited neural resources in older adults leads to greater asymmetry of bilateral movements than in young adults. J. Neurophysiol. 2020, 123, 1295–1304. [Google Scholar] [CrossRef] [PubMed]
- Sainburg, R.L. Evidence for a dynamic-dominance hypothesis of handedness. Exp. Brain Res. 2002, 142, 241–258. [Google Scholar] [CrossRef] [PubMed]
- Sainburg, R.L. Handedness: Differential specializations for control of trajectory and position. Exerc. Sport Sci. Rev. 2005, 33, 206–213. [Google Scholar] [CrossRef] [PubMed]
- Sainburg, R.L. Convergent models of handedness and brain lateralization. Front. Psychol. 2014, 5, 1092. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pigeot, I. Basic concepts of multiple tests—A survey. Stat. Pap. 2000, 41, 3–36. [Google Scholar] [CrossRef]
- Nichols, T.E. Multiple testing corrections, nonparametric methods, and random field theory. Neuroimage 2012, 62, 811–815. [Google Scholar] [CrossRef] [Green Version]
- Austin, S.R.; Dialsingh, I.; Altman, N. Multiple hypothesis testing: A review. J. Indian Soc. Agric. Stat. 2014, 68, 303–314. [Google Scholar]
- Petersson, K.M.; Nichols, T.E.; Poline, J.B.; Holmes, A.P. Statistical limitations in functional neuroimaging II. Signal detection and statistical inference. Philos. Trans. R. Soc. Lond. B Biol. Sci. 1999, 354, 1261–1281. [Google Scholar] [CrossRef] [Green Version]
- Brett, M.; Penny, W.; Kiebel, S. Chapter 44-Introduction to random field theory. In Human Brain Function, 2nd ed.; Frackowiak, R.S., Friston, K.J., Frith, C.D., Dolan, R.J., Price, C.J., Zeki, S., Ashburner, J.T., Penny, W.D., Eds.; Academic Press: Burlington, MA, USA, 2004; pp. 867–879. [Google Scholar]
- Rohani, F. Nonparametric Random Fields with Applications in Functional Imaging. Ph.D. Thesis, McGill University, Montréal, QC, Canada, 2009. [Google Scholar]
- Worsley, K.J.; Wolforth, M.; Evans, A.C. Scale space searches for a periodic signal in fMRI data with spatially varying hemodynamic response. In Proceedings of BrainMap; Citeseer: Princeton, NJ, USA, 1997; Volume 96, Available online: https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.34.7019&rep=rep1&type=pdf (accessed on 7 July 2021).
- Sushkova, O.S.; Morozov, A.A.; Gabova, A.V. Data mining in EEG wave trains in early stages of Parkinson’s disease. In Advances in Soft Computing; MICAI 2016. Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2017; Volume 10062, pp. 403–412. [Google Scholar]
- Sushkova, O.S.; Morozov, A.A.; Gabova, A.V.; Karabanov, A.V. Application of brain electrical activity burst analysis method for detection of EEG characteristics in the early stage of Parkinson’s disease. S.S. Korsakov J. Neurol. Psychiatry 2018, 118, 45–48. [Google Scholar] [CrossRef] [PubMed]
- Sushkova, O.S.; Morozov, A.A.; Gabova, A.V. Investigation of specificity of Parkinson’s disease features obtained using the method of cerebral cortex electrical activity analysis based on wave trains. In Proceedings of the 2017 13th International Conference on Signal-Image Technology & Internet-Based Systems (SITIS), Jaipur, India, 4–7 December 2017; pp. 168–172. [Google Scholar]
- Sushkova, O.S.; Morozov, A.A.; Gabova, A.V.; Karabanov, A.V. An investigation of the specificity of features of early stages of Parkinson’s disease obtained using the method of cortex electrical activity analysis based on wave trains. J. Phys. Conf. Ser. 2018, 1096, 012078. [Google Scholar] [CrossRef] [Green Version]
- Sushkova, O.S.; Morozov, A.A.; Gabova, A.V.; Karabanov, A.V. Investigation of surface EMG and acceleration signals of limbs’ tremor in Parkinson’s disease patients using the method of electrical activity analysis based on wave trains. In Advances in Artificial Intelligence; Simari, G., Eduardo, F., Gutierrez, S.F., Melquiades, J.R., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 253–264. [Google Scholar]
- Sushkova, O.S.; Morozov, A.A.; Gabova, A.V.; Karabanov, A.V.; Chigaleychik, L.A. Investigation of the 0.5–4 Hz low-frequency range in the wave train electrical activity of muscles in patients with Parkinson’s disease and essential tremor. Radioelectron. Nanosyst. Inf. Technol. 2019, 11, 225–236. [Google Scholar] [CrossRef]
- Sushkova, O.; Morozov, A.; Gabova, A.; Karabanov, A. Investigation of the multiple comparisons problem in the analysis of the wave train electrical activity of muscles in Parkinson’s disease patients. J. Phys. Conf. Ser. 2019, 1368, 052004. Available online: https://iopscience.iop.org/article/10.1088/1742-6596/1368/5/052004/meta (accessed on 7 July 2021). [CrossRef]
- Sushkova, O.; Morozov, A.; Gabova, A.; Karabanov, A. Investigation of the Multiple Comparisons Problem in the Wave Train Electrical Activity Analysis in Parkinson’s Disease Patients. Basic Clin. Pharmacol. Toxicol. 2019, 124, 24–25. [Google Scholar] [CrossRef]
- Sushkova, O.; Gabova, A.; Karabanov, A.; Kershner, I.; Obukhov, K.Y.; Obukhov, Y.V. Time–frequency analysis of simultaneous measurements of electroencephalograms, electromyograms, and mechanical tremor under Parkinson disease. J. Commun. Technol. Electron. 2015, 60, 1109–1116. [Google Scholar] [CrossRef]
- Obukhov, Y.V.; Gabova, A.; Zaljalova, Z.; Illarioshkin, S.; Karabanov, A.; Korolev, M.; Kuznetsova, G.; Morozov, A.; Nigmatullina, R.; Obukhov, K.; et al. Electroencephalograms features of the early stage Parkinson’s disease. Pattern Recognit. Image Anal. 2014, 24, 593–604. [Google Scholar] [CrossRef]
- Sushkova, O.S.; Morozov, A.A.; Gabova, A.V.; Karabanov, A.V.; Chigaleychik, L.A. An investigation of accelerometer signals in the 0.5–4 Hz range in Parkinson’s disease and essential tremor patients. In Proceedings of International Conference on Frontiers in Computing and Systems; Springer: Berlin/Heidelberg, Germany, 2021; pp. 455–462. [Google Scholar]
- Sushkova, O.; Morozov, A.; Gabova, A.; Karabanov, A. Development of a method for early and differential diagnosis of Parkinson’s disease and essential tremor based on analysis of wave train electrical activity of muscles. In Proceedings of the 2020 International Conference on Information Technology and Nanotechnology (ITNT), Samara, Russia, 26–29 May 2020; pp. 1–5. [Google Scholar]
- Sushkova, O.S.; Morozov, A.A.; Kershner, I.A.; Petrova, N.G.; Gabova, A.V.; Chigaleychik, L.A.; Karabanov, A.V. Investigation of distribution laws of the phase difference of the envelopes of electromyograms of antagonist muscles in Parkinson’s disease and essential tremor patients. RENSIT 2020, 12, 415–428. [Google Scholar] [CrossRef]
- Sushkova, O.S.; Morozov, A.A.; Gabova, A.V. A method of analysis of EEG wave trains in early stages of Parkinson’s disease. In Proceedings of the International Conference on Bioinformatics and Systems Biology (BSB-2016), Allahabad, India, 4–6 March 2016; pp. 1–4. [Google Scholar]
- Sushkova, O.S.; Morozov, A.A.; Gabova, A.V. Development of a method of analysis of EEG wave packets in early stages of Parkinson’s disease. In Proceedings of the International Conference Information Technology and Nanotechnology ITNT 2016, Samara, Russia, 17–19 May 2016; CEUR: Samara, Russia, 2016; pp. 681–690. [Google Scholar]
- Sushkova, O.S.; Morozov, A.A.; Gabova, A.V. EEG beta wave trains are not the second harmonic of mu wave trains in Parkinson’s disease patients. In Proceedings of the International conference Information Technology and Nanotechnology ITNT 2017, Samara, Russia, 25–25 April 2017; CEUR: Samara, Russia, 2017; Volume 1901, pp. 226–234. [Google Scholar]
- Sushkova, O.S.; Morozov, A.A. GitHub Repository. Wave Train Analysis of EMG Signals. AUC Diagrams. 2021. Available online: https://github.com/OlgaSushkova/Wave-Train-Analysis (accessed on 7 July 2021).
- Sushkova, O.S.; Morozov, A.A.; Gabova, A.V.; Karabanov, A.V. Method for Differential Diagnosing of Essential Tremor and Early and First Stages of Parkinson’s Disease Using Wave Train Activity Analysis of Muscles. Russian Federation Patent Application No. 2741233, 22 January 2021. [Google Scholar]
Short Biography of Authors
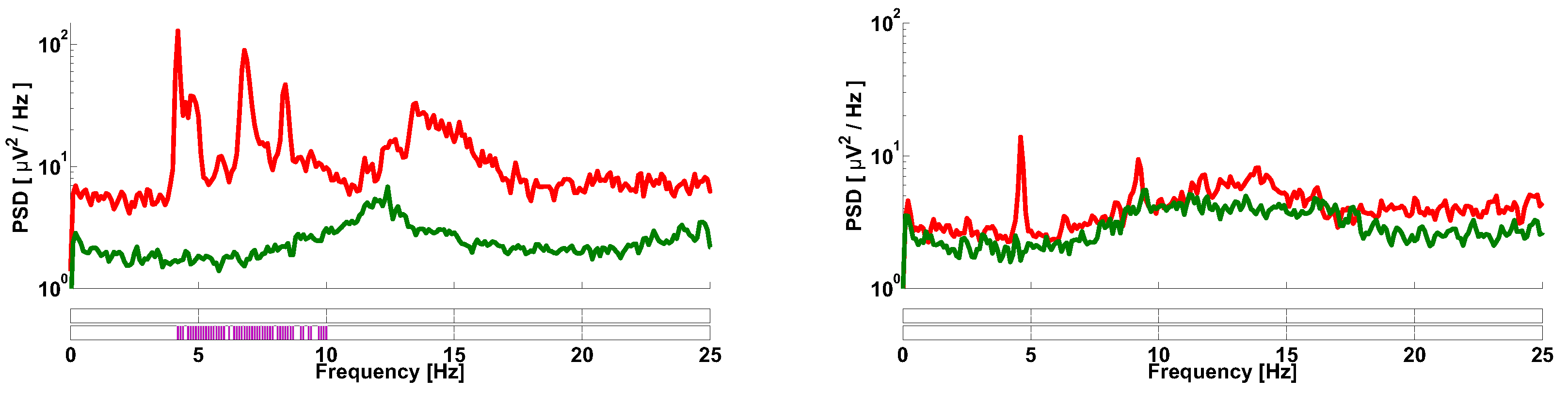
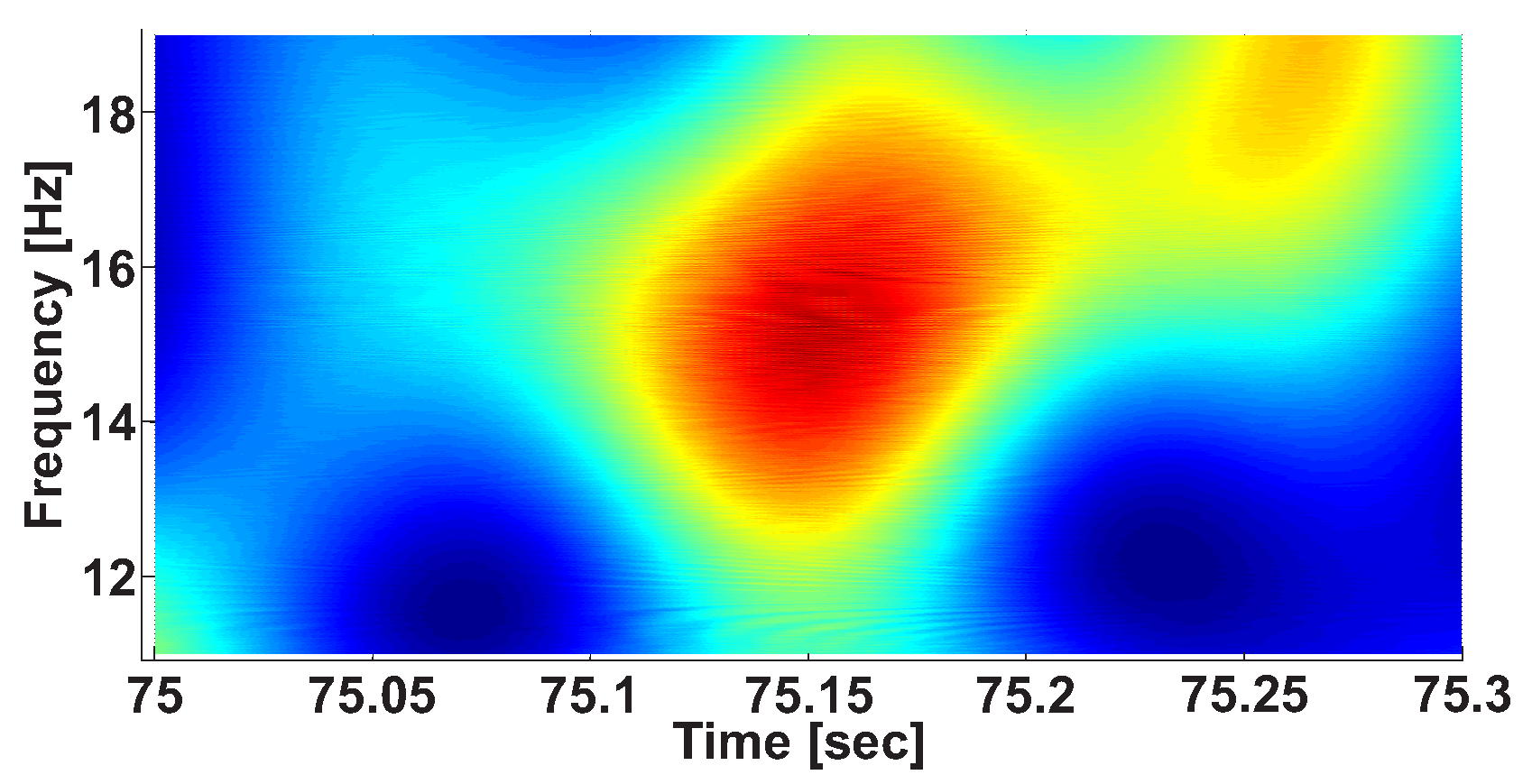
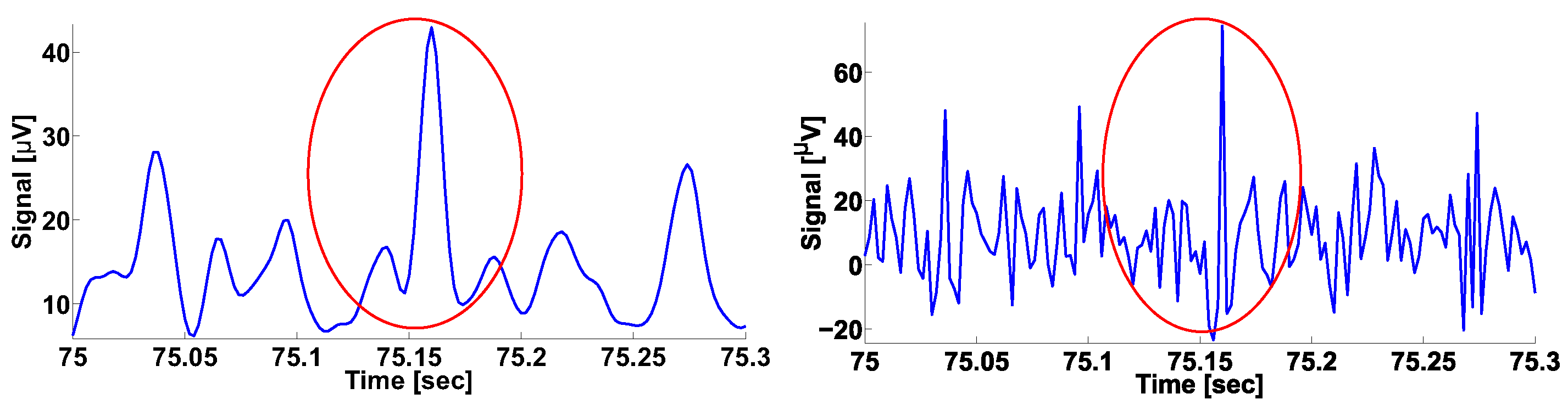
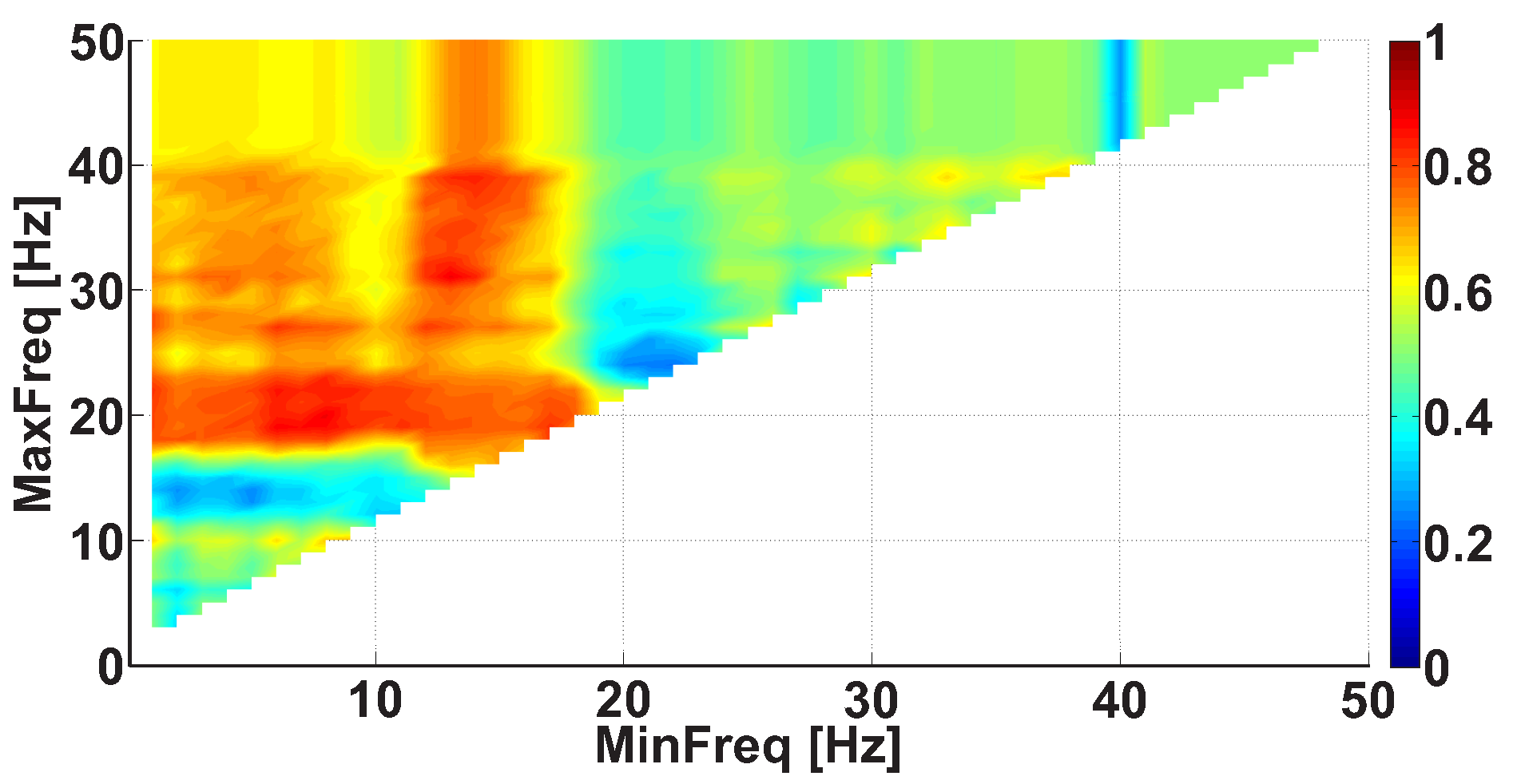
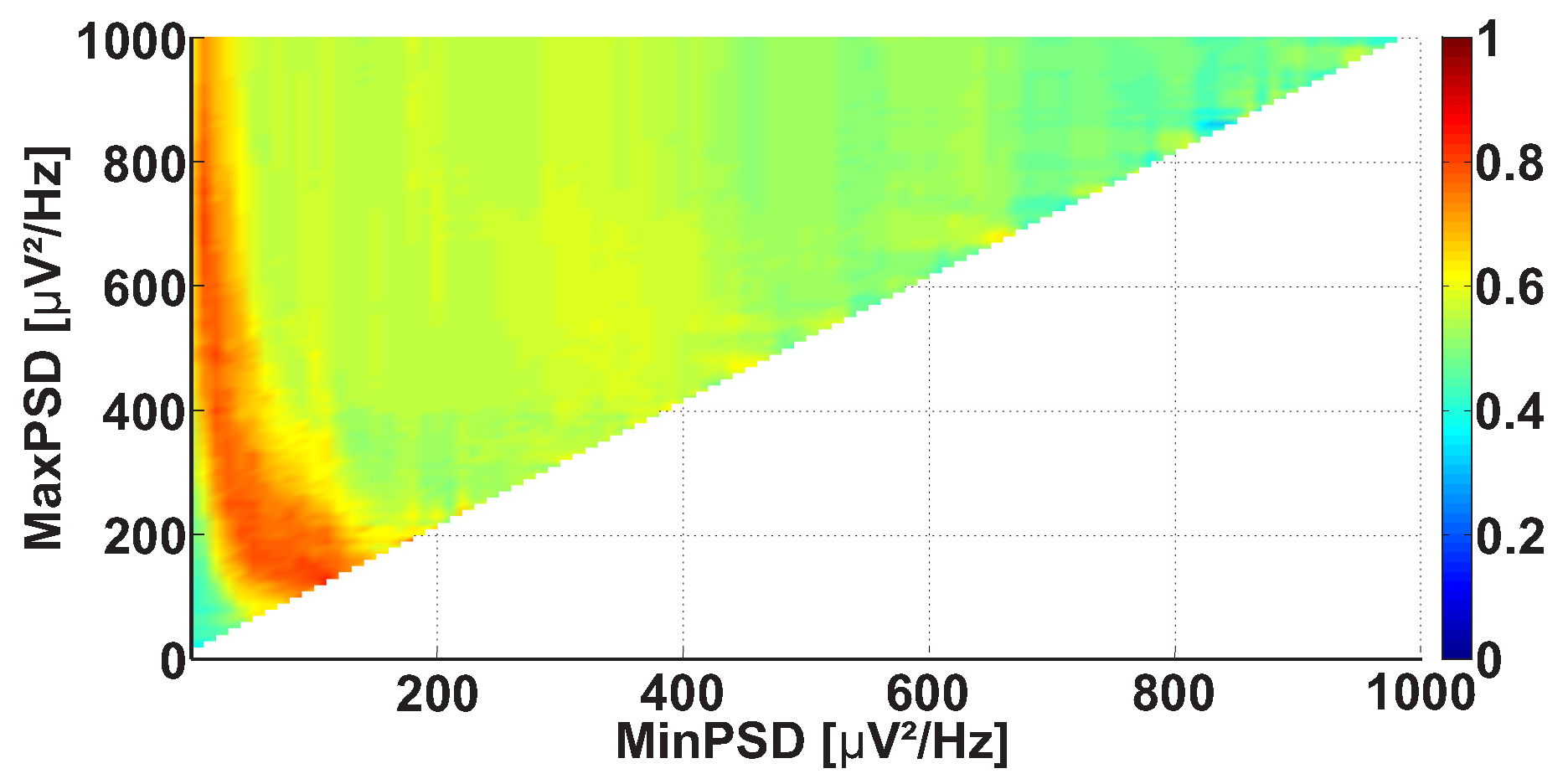
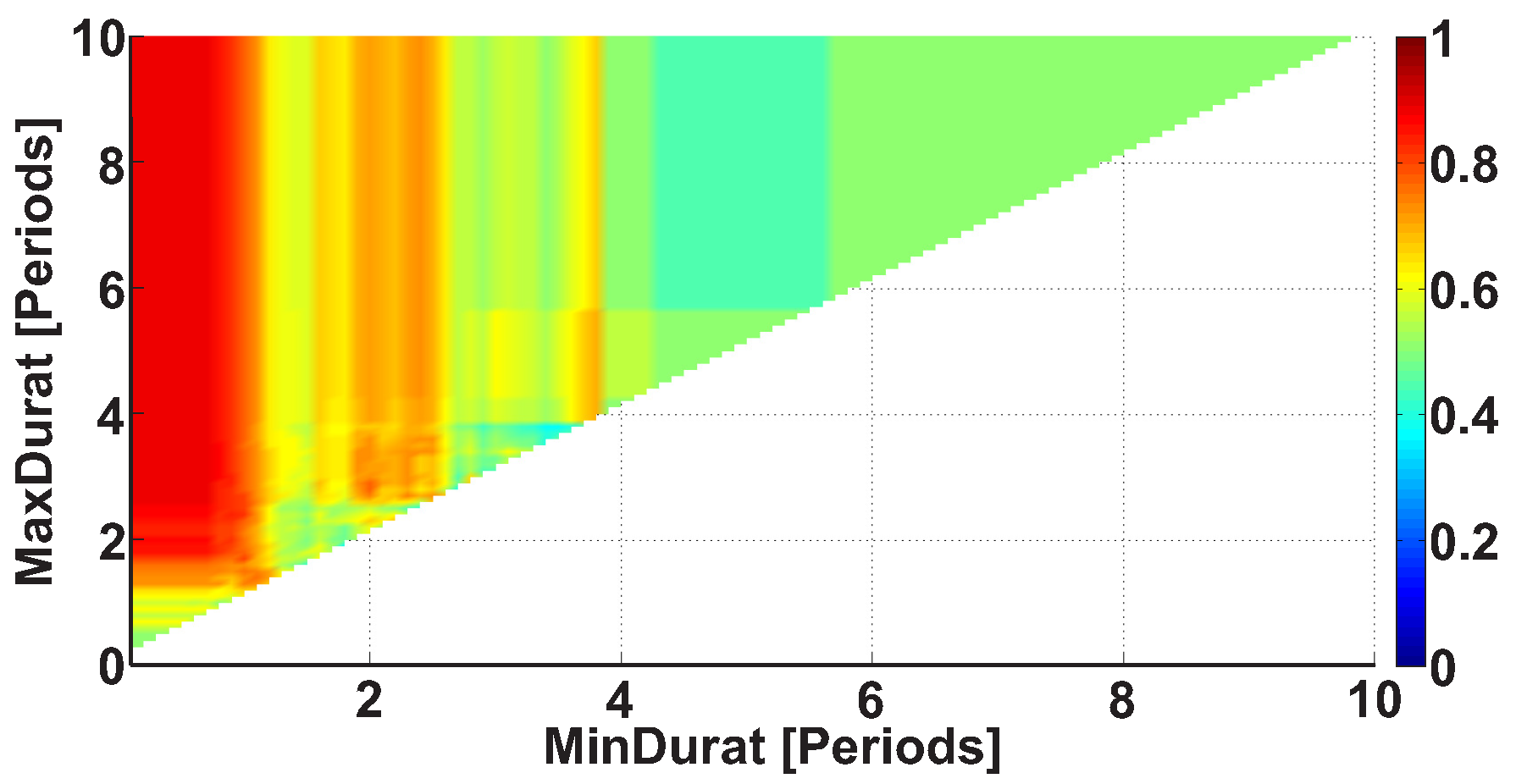
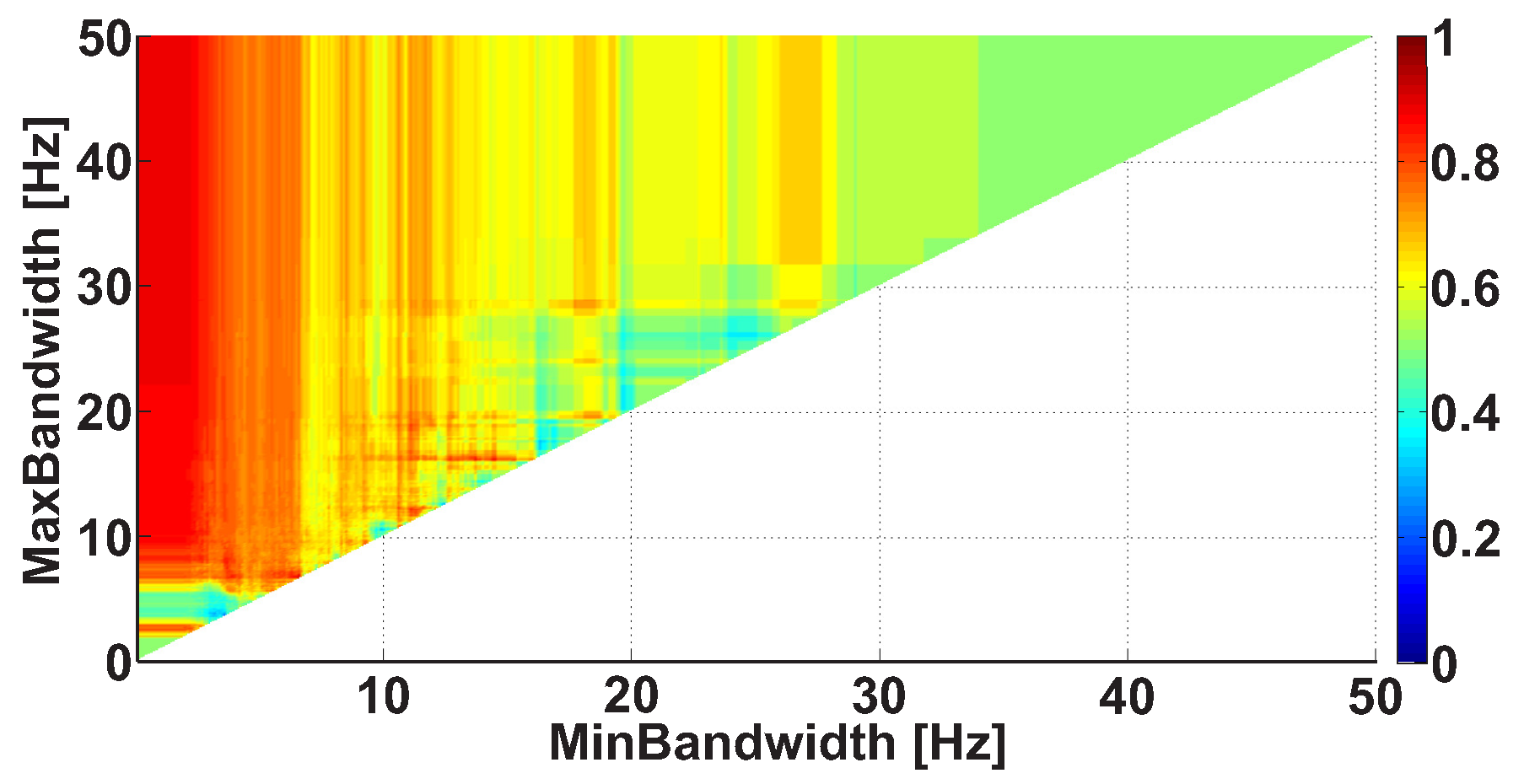
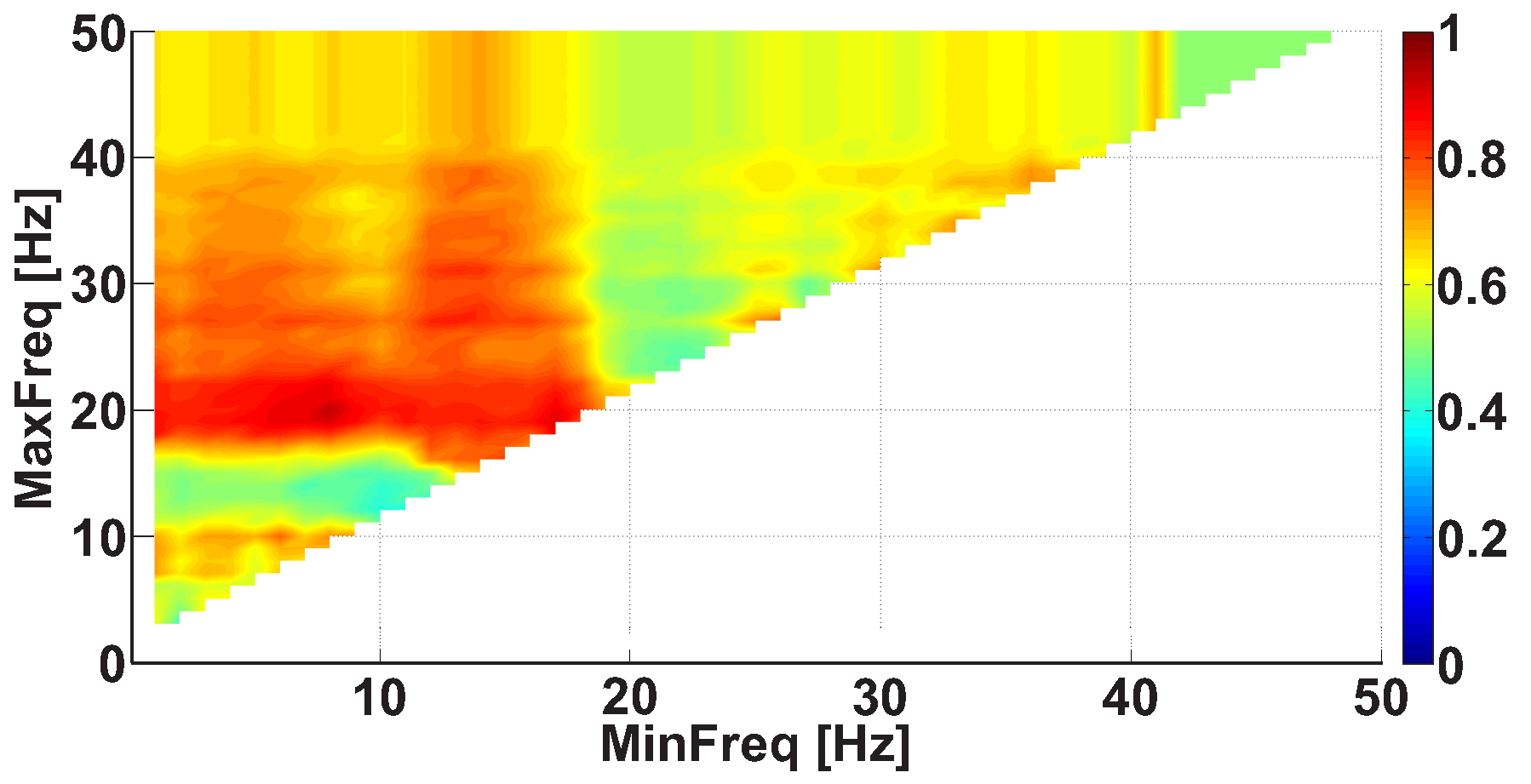
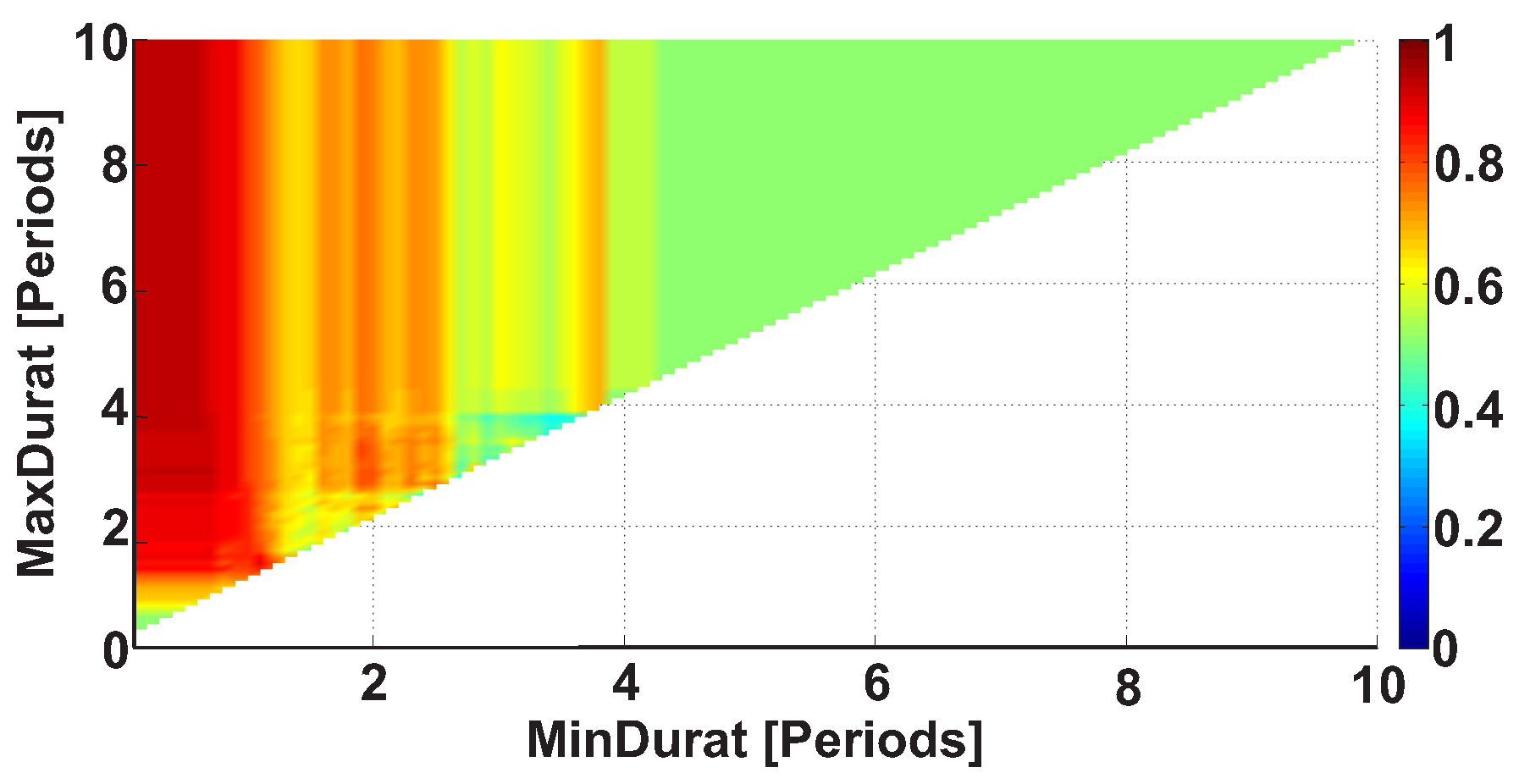
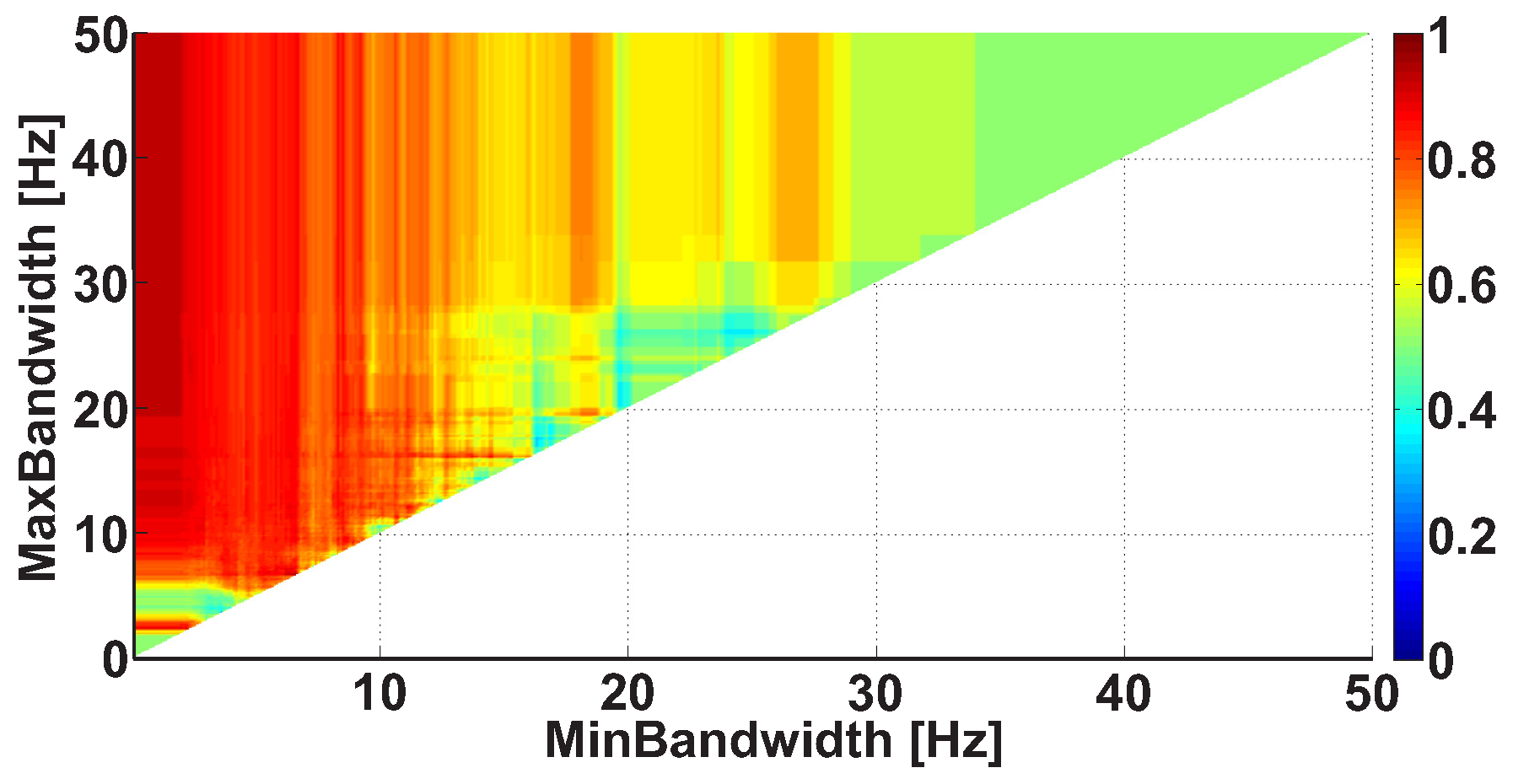
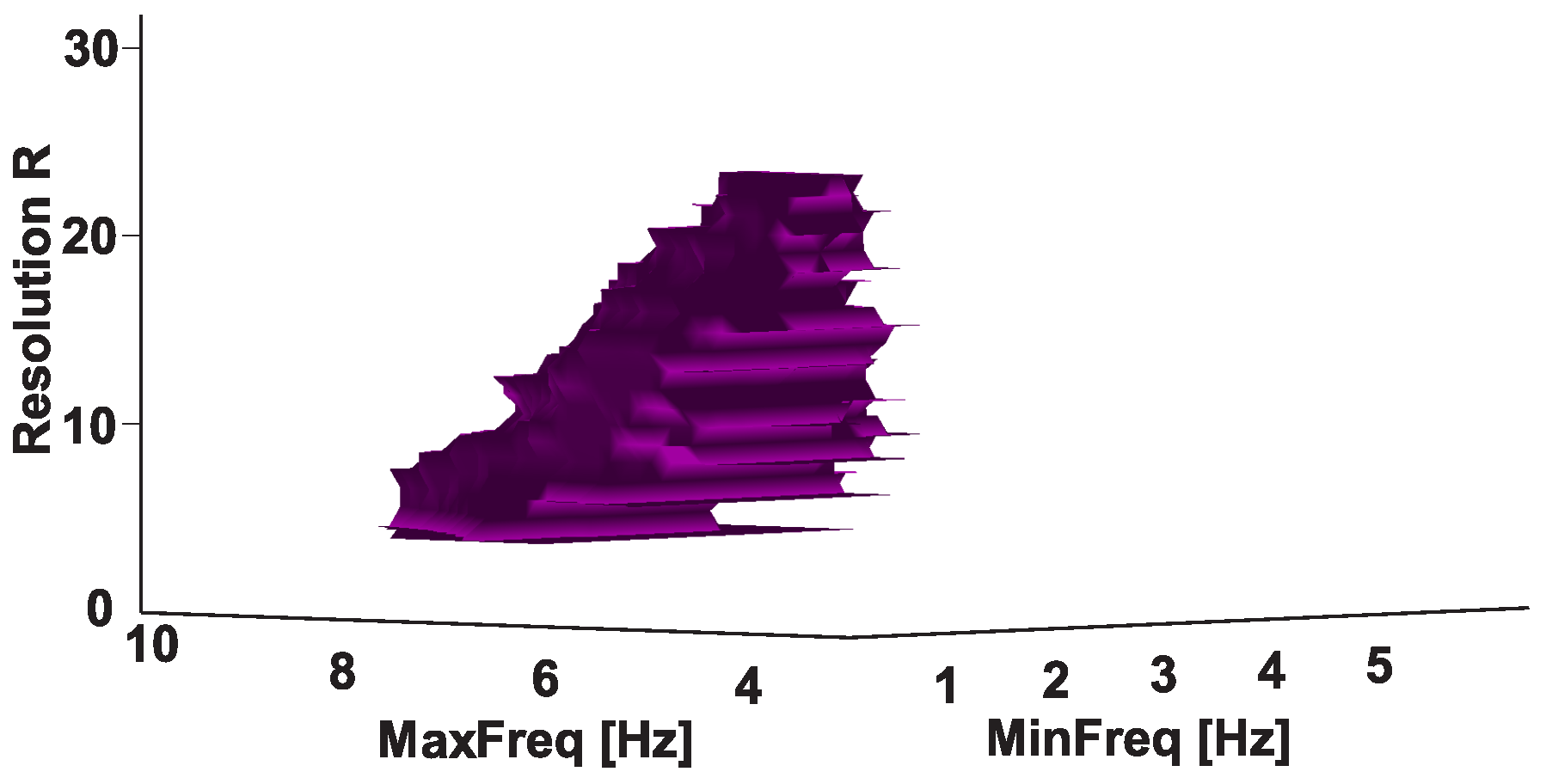
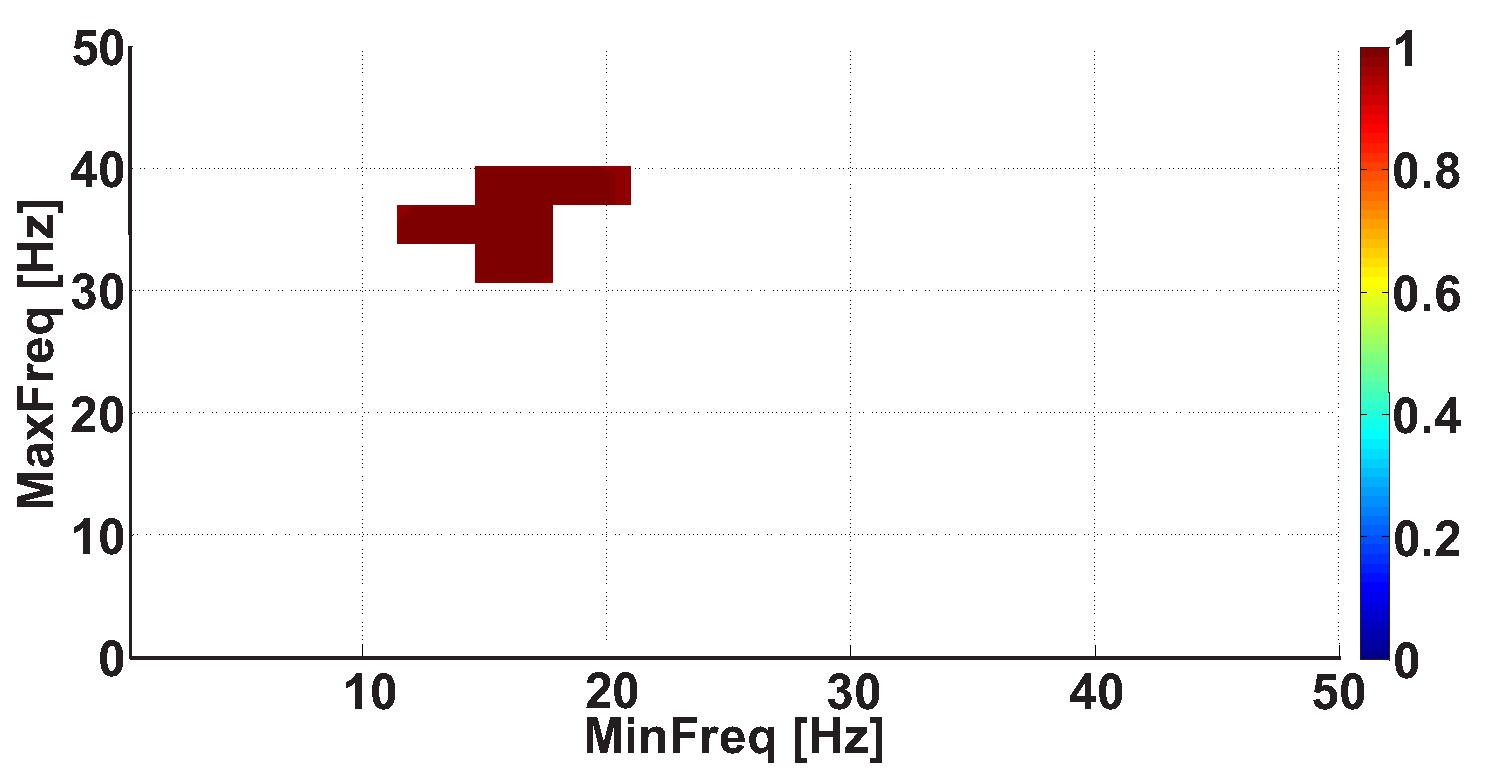
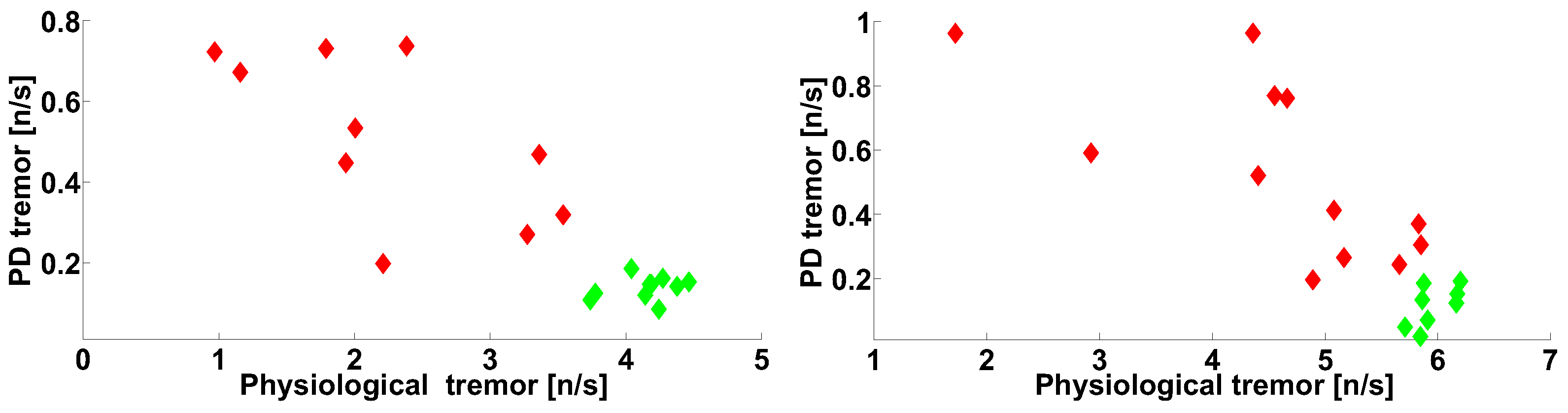
| Investigated Regularity | Frequency, Hz | PSD, V Hz | Duration, Periods | Bandwidth, Hz | AUC | p |
|---|---|---|---|---|---|---|
| A red area. The right non-tremor arm in the left-hand-tremor PD patients. | 8–20 | ≥30 | 0.5–4 | 1–28 | 0.93 | 0.0011 |
| A red area. The left non-tremor arm in the right-hand-tremor PD patients. | 2–9 | any | 0.8–2.3 | any | 0.87 | 0.0033 |
| A blue area. The left tremor arm in the left-hand-tremor PD patients. | 1–50 | any | ≥1 | ≥3 | 0 | ≤0.001 |
| A blue area. The right tremor arm in the right-hand-tremor PD patients. | 6–33 | any | ≥0.5 | ≥3.5 | 0.02 | ≤0.001 |
| A red area. The left tremor arm in the left-hand-tremor PD patients. | 3–7 | ≥11 | ≥1.5 | any | 1 | ≤0.001 |
| A red area. The right tremor arm in the right-hand-tremor PD patients. | 4–8 | ≥103 | ≥1.3 | any | 1 | ≤0.0001 |
| Investigated Regularity | Frequency, Hz | PSD, V Hz | Duration, Periods | Bandwidth, Hz | AUC | p |
|---|---|---|---|---|---|---|
| A red area. The right non-tremor arm in the left-hand-tremor PD patients. | 5–13 | 0–50 | any | 3.1–3.8 | 0.92 | 0.0017 |
| A red area. The left non-tremor arm in the right-hand-tremor PD patients. | 2–16 | any | 1.4–2.1 | any | 0.8 | 0.0161 |
| A blue area. The left tremor arm in the left-hand-tremor PD patients. | 1–39 | any | ≥0.5 | ≥2.5 | 0 | ≤0.001 |
| A blue area. The right tremor arm in the right-hand-tremor PD patients. | 24–34 | any | any | any | 0.07 | ≤0.001 |
| A red area. The left tremor arm in the left-hand-tremor PD patients. | 4–7 | ≥4 | ≥1.2 | any | 1 | ≤0.001 |
| A red area. The right tremor arm in the right-hand-tremor PD patients. | 2–8 | ≥2 | ≥2.3 | any | 0.85 | 0.0037 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sushkova, O.S.; Morozov, A.A.; Gabova, A.V.; Karabanov, A.V.; Illarioshkin, S.N. A Statistical Method for Exploratory Data Analysis Based on 2D and 3D Area under Curve Diagrams: Parkinson’s Disease Investigation. Sensors 2021, 21, 4700. https://doi.org/10.3390/s21144700
Sushkova OS, Morozov AA, Gabova AV, Karabanov AV, Illarioshkin SN. A Statistical Method for Exploratory Data Analysis Based on 2D and 3D Area under Curve Diagrams: Parkinson’s Disease Investigation. Sensors. 2021; 21(14):4700. https://doi.org/10.3390/s21144700
Chicago/Turabian StyleSushkova, Olga Sergeevna, Alexei Alexandrovich Morozov, Alexandra Vasilievna Gabova, Alexei Vyacheslavovich Karabanov, and Sergey Nikolaevich Illarioshkin. 2021. "A Statistical Method for Exploratory Data Analysis Based on 2D and 3D Area under Curve Diagrams: Parkinson’s Disease Investigation" Sensors 21, no. 14: 4700. https://doi.org/10.3390/s21144700
APA StyleSushkova, O. S., Morozov, A. A., Gabova, A. V., Karabanov, A. V., & Illarioshkin, S. N. (2021). A Statistical Method for Exploratory Data Analysis Based on 2D and 3D Area under Curve Diagrams: Parkinson’s Disease Investigation. Sensors, 21(14), 4700. https://doi.org/10.3390/s21144700







