Research on Self-Balancing System of Autonomous Vehicles Based on Queuing Theory
Abstract
:1. Introduction
- (1)
- Define a traffic system with self-balancing of autonomous vehicles;
- (2)
- Based on the queuing theory, a road network model with self-balancing characteristics is established;
- (3)
- The balance strategy reduces the waiting time of the system;
- (4)
- While increasing service efficiency, the service intensity of the system is reduced;
- (5)
- Improve the operation efficiency of the transportation system.
2. Modeling Basis and Research Methods
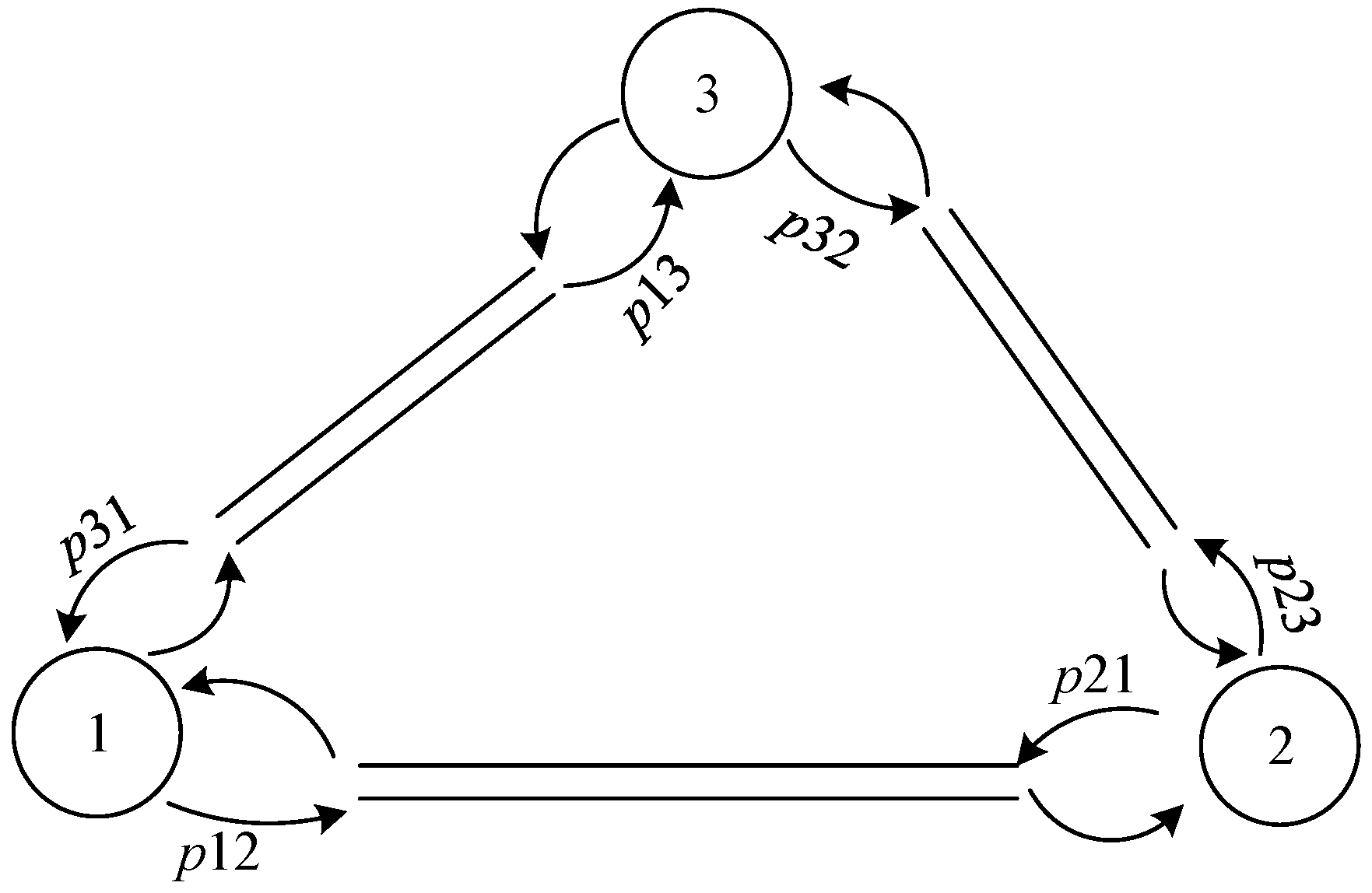
2.1. Queuing Network of Autonomous Vehicles
- (1)
- The service rate of node i is related to its queue length. When there are ni customers in the queue of node i, the service rate is , and the service time of each node is independent and follows a negative exponential distribution;
- (2)
- Node i receives Poisson flow with a rate of ;
- (3)
- Passengers transfer to node j with probability after completion of service at node i, and the transfer probability has Markov characteristics;
- (4)
- The network is closed, with a fixed number of passengers K.
2.2. Probability Distribution in Steady State
2.3. State Parameter Determination
- (1)
- Queue length of node i:
- (2)
- The probability of node i being idle is:
- (3)
- The average queue length of node i:
3. Self-Balancing System for Fully Autonomous Vehicles
3.1. Self-Balancing System Framework
3.2. Queue Network Model of Self-Balancing System
3.3. Establishment of Self-Balancing Optimization Model
3.4. Self-Balancing System Performance Index Calculation
4. Experimental Analysis
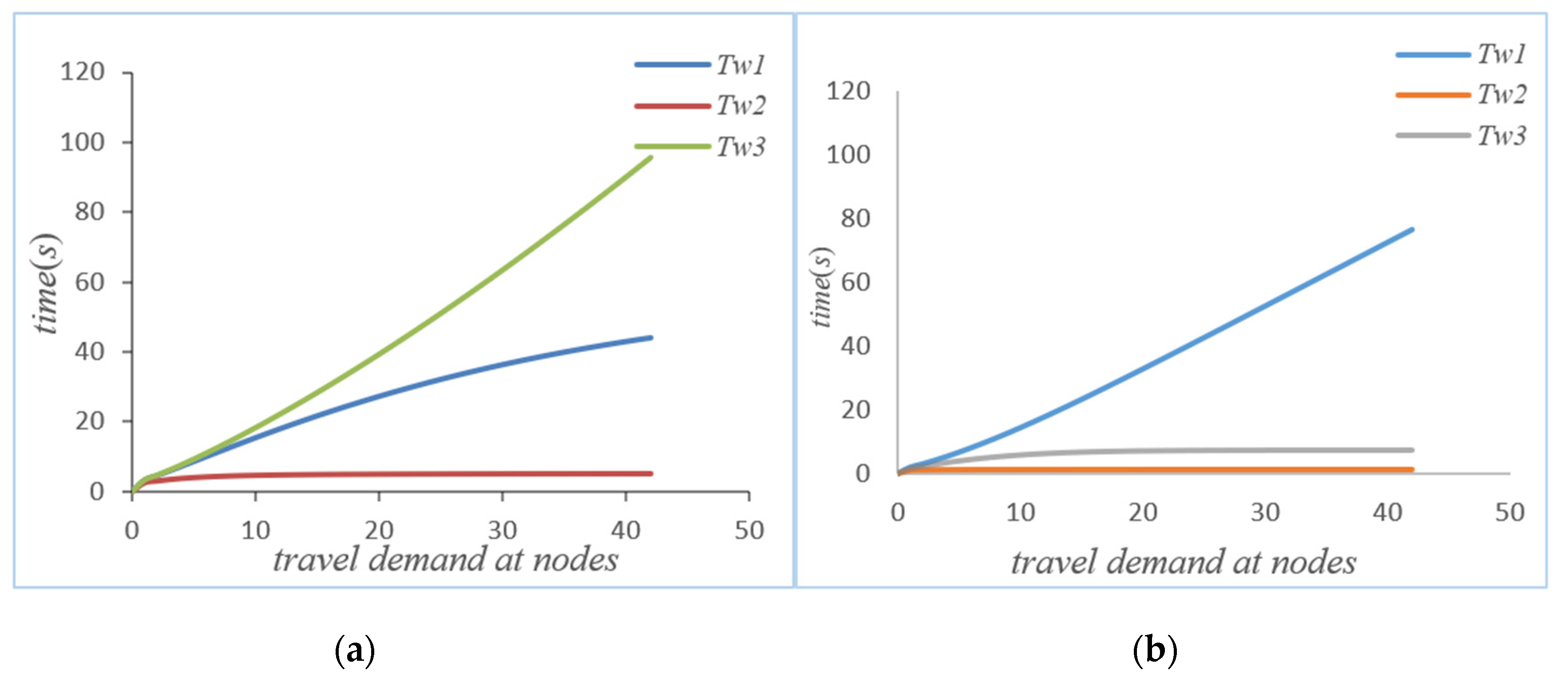
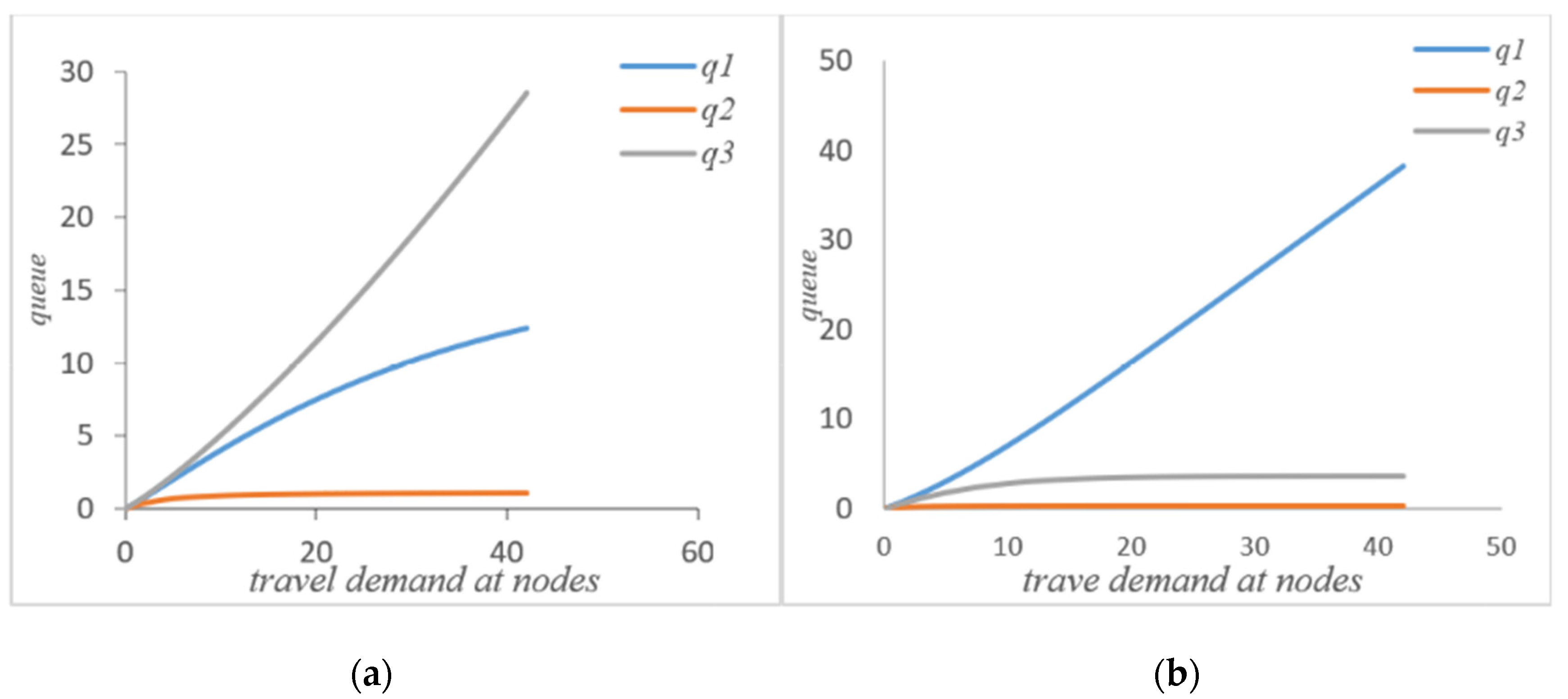
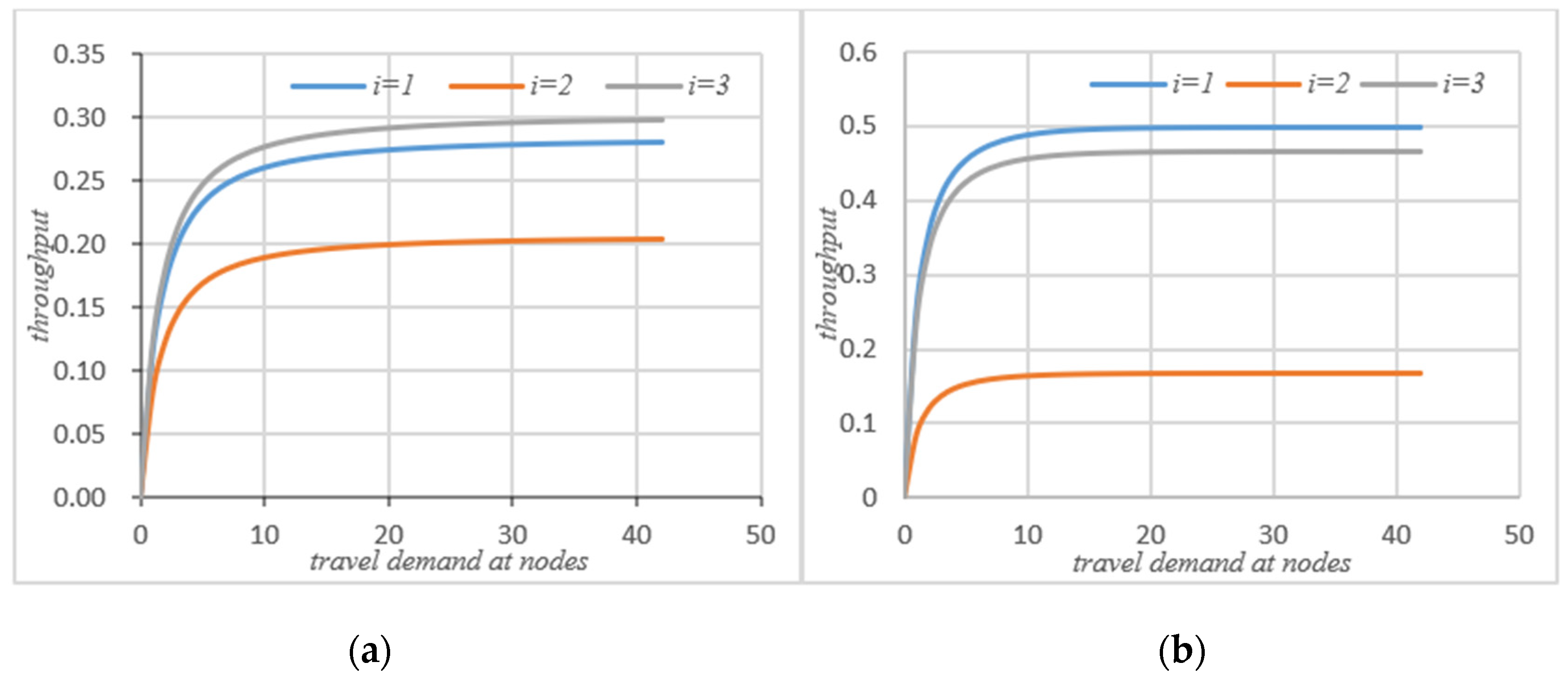
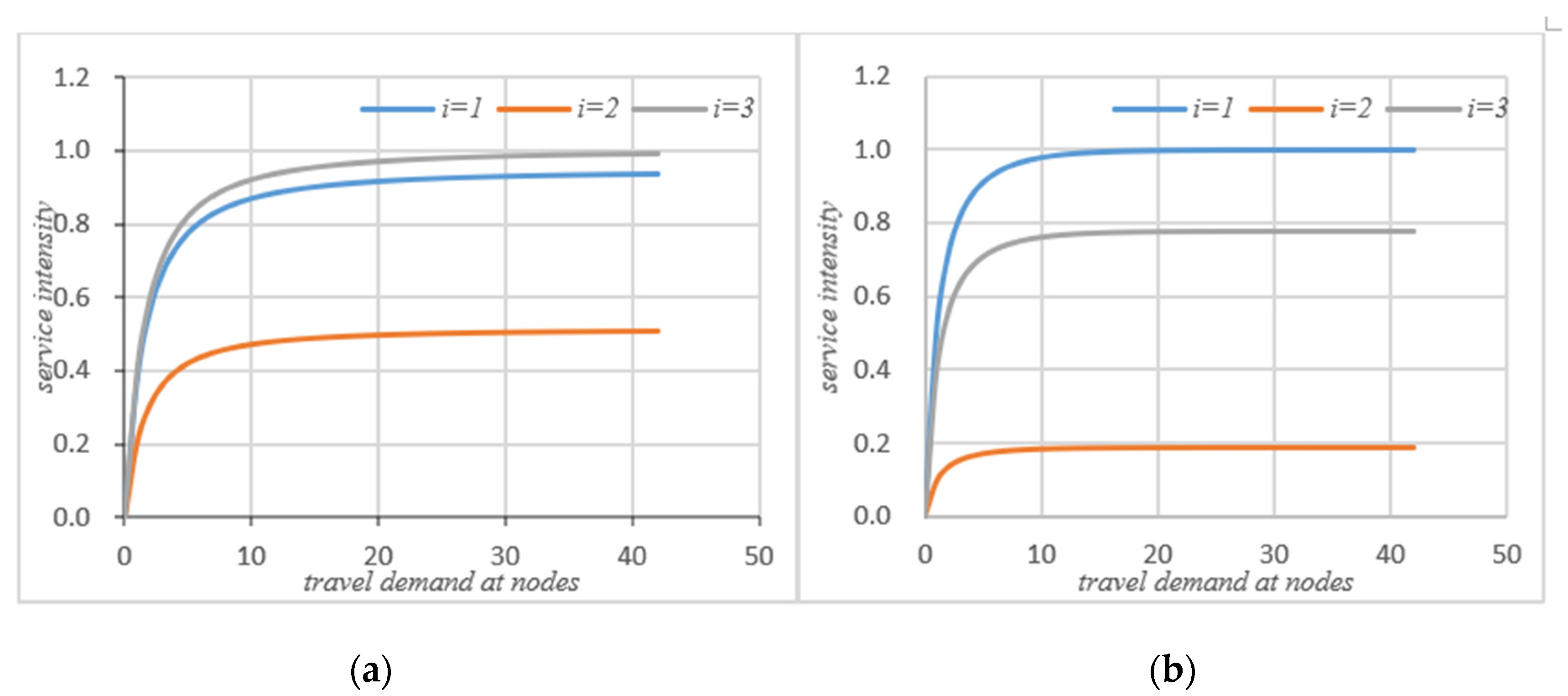
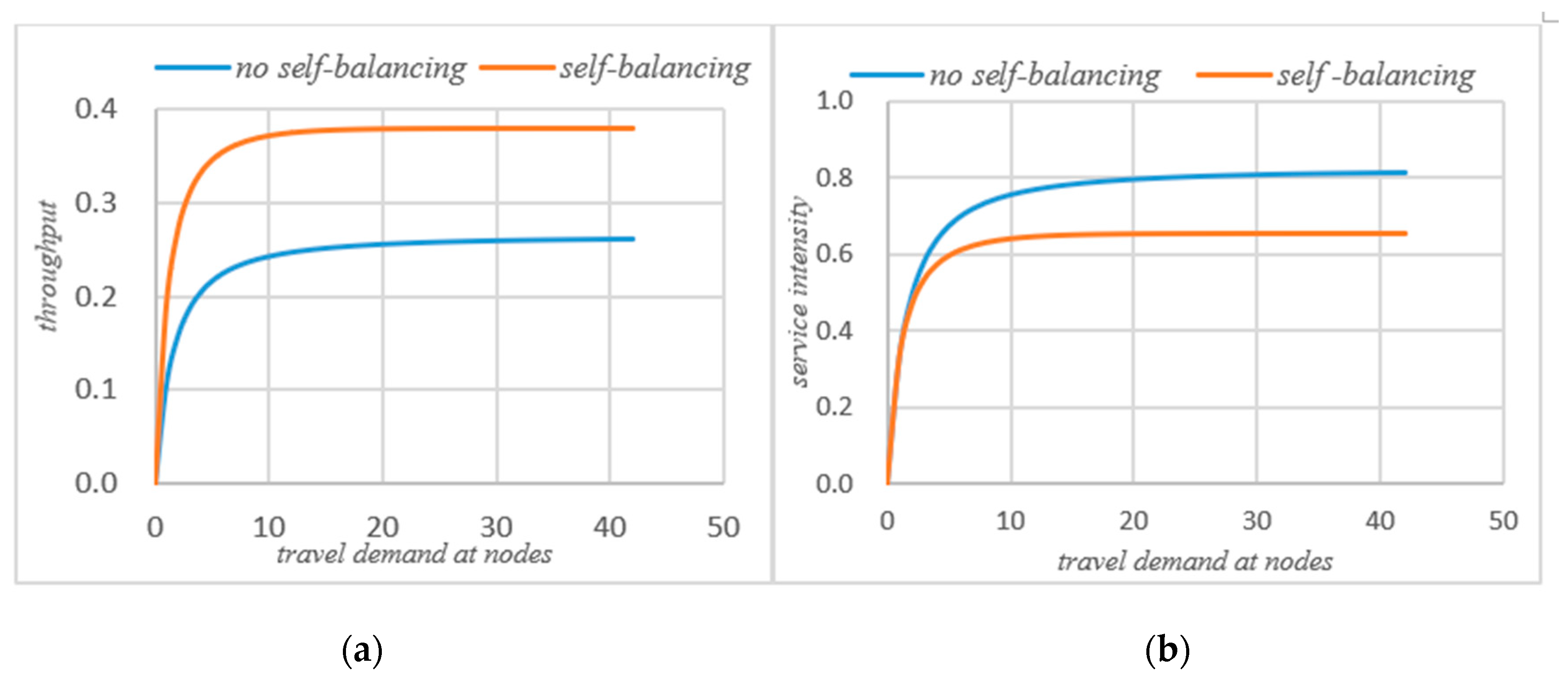
4.1. Comparative Analysis before and after Self-Balancing
4.2. Comparative Analysis before and after System Self-Balancing
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pavone, M.; Smith, S.L.; Frazzoli, E.; Rus, D. Robotic load balancing for mobility-on-demand systems. Int. J. Robot. Res. 2012, 31, 839–854. [Google Scholar] [CrossRef]
- Shoup, D.C. The High Cost of Free-Parking; Planners Press: Chicago, IL, USA, 2005. [Google Scholar]
- George, D.K.; Xia, C.H. Fleet-sizing and service availability for a vehicle rental system via closedqueueing networks. Eur. J. Oper. Res. 2011, 211, 198–207. [Google Scholar] [CrossRef]
- Treleaven, K.; Pavone, M.; Frazzoli, E. Asymptotically optimal algorithms for pickup and delivery problems with application to large-scale transportation systems. IEEE Trans. Autom. Control 2013, 58, 2261–2276. [Google Scholar] [CrossRef] [Green Version]
- Shu, J.; Chou, M.; Liu, O.; Teo, C.P.; Wang, I.-L. Bicycle-Sharing System: Deployment, Utilization and the Value of Redistribution. 2010. Available online: http://bschool.nus.edu/Staff/bizteocp/BS2010 (accessed on 1 January 2019).
- Lin, J.-R.; Yang, T.-H. Strategic design of public bicycle sharing systems with service level constraints. Transp. Res. Part E Logist. Transp. Rev. 2011, 47, 284–294. [Google Scholar] [CrossRef]
- Fricker, C.; Gast, N. Incentives and regulations in bike-sharing systems with stations of finitecapacity. arXiv 2012, arXiv:1201.1178v4. [Google Scholar]
- Fricker, C.; Gast, N.; Mohamed, H. Mean field analysis for inhomogeneous bike sharing systems. In Proceedings of the 23rd International Meeting on Probabilistic, Combinatorial, and Asymptotic Methods for the Analysisof Algorithms (AofA’12), Montreal, QC, Canada, 18–22 June 2012. [Google Scholar]
- Car2go. Ulm, Germnay; Vancouver, BC, Canada; San Diego, CA, USA. 2008. Available online: http://www.car2go.com (accessed on 8 January 2019).
- Autolib’. Paris, France. 2011. Available online: http://www.autolib-paris.fr (accessed on 1 January 2014).
- Bullo, F.; Frazzoli, E.; Pavone, M.; Savla, K.; Smith, S.L. Dynamic vehicle routing for robotic systems. Proc. IEEE 2011, 99, 1482–1504. [Google Scholar] [CrossRef] [Green Version]
- Waserhole, A.; Jost, V. Vehicle Sharing System Pricing Regulation: A Fluid Approximation. 2013. Available online: http://hal.archives-ouvertes.fr/hal-00727041 (accessed on 1 January 2014).
- Serfozo, R. Introduction to Stochastic Networks; Springer: New York, NY, USA, 1999; Volume 44. [Google Scholar]
- Raviv, T.; Tzur, M.; Forma, I.A. Static repositioning in a bike-sharing system: Models and solution approaches. EURO J. Transp. Logist. 2013, 2, 187–229. [Google Scholar] [CrossRef] [Green Version]
- Contardo, C.; Morency, C.; Rousseau, L.-M. Balancing a dynamic public bike-sharing system. In Technical Report 09, CIRRELT; Cirrelt: Montreal, QC, Canada, 2012. [Google Scholar]
- Dong, J.X.; Song, D.P. Container fleet sizing and empty repositioning in liner shipping systems. Transp. Res. Part E 2009, 45, 860–877. [Google Scholar] [CrossRef]
- Sayarshad, H.R.; Marler, T. A new multi-objective optimization formulation for rail-car fleet sizing problems. Oper. Res. 2010, 10, 175–198. [Google Scholar] [CrossRef]
- Sayarshad, H.R.; Tavakkoli-Moghaddam, R. Solving a multi periodic stochastic model of the rail-car fleet sizing by two-stage formulation. Appl. Math. Model. 2010, 34, 1164–1174. [Google Scholar] [CrossRef]
- Muntz, R.R.; Wong, J.W. Asymptotic properties of closed queueing network models. In Proceedings of the 8th Annual Princeton Conference on Information Sciences and Systems, Princeton, NJ, USA, 28–29 March 1974; pp. 348–352. [Google Scholar]
- Bertsekas, D.P.; Gallager, R.G.; Humblet, P. Data Networks; Prentice-Hall International: Englewood Cliffs, NJ, USA, 1992; Volume 2. [Google Scholar]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Wang, J.; Bai, G.; Hu, X. Research on Self-Balancing System of Autonomous Vehicles Based on Queuing Theory. Sensors 2021, 21, 4619. https://doi.org/10.3390/s21134619
Li H, Wang J, Bai G, Hu X. Research on Self-Balancing System of Autonomous Vehicles Based on Queuing Theory. Sensors. 2021; 21(13):4619. https://doi.org/10.3390/s21134619
Chicago/Turabian StyleLi, Huanping, Jian Wang, Guopeng Bai, and Xiaowei Hu. 2021. "Research on Self-Balancing System of Autonomous Vehicles Based on Queuing Theory" Sensors 21, no. 13: 4619. https://doi.org/10.3390/s21134619
APA StyleLi, H., Wang, J., Bai, G., & Hu, X. (2021). Research on Self-Balancing System of Autonomous Vehicles Based on Queuing Theory. Sensors, 21(13), 4619. https://doi.org/10.3390/s21134619





