Overall Profile Measurements of Tiny Parts with Complicated Features with the Cradle-Type Five-Axis System
Abstract
:1. Introduction
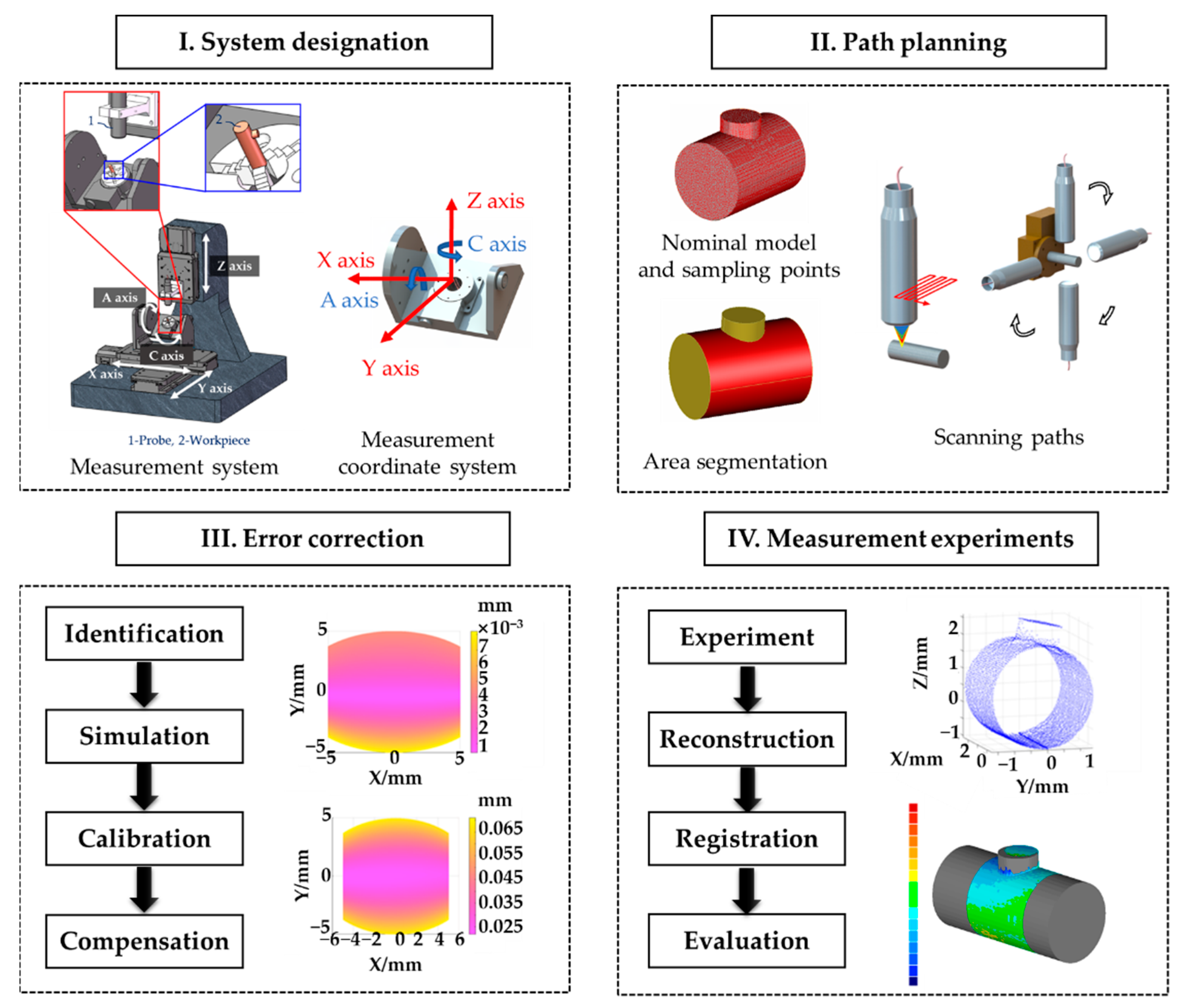
2. Measurement Scheme
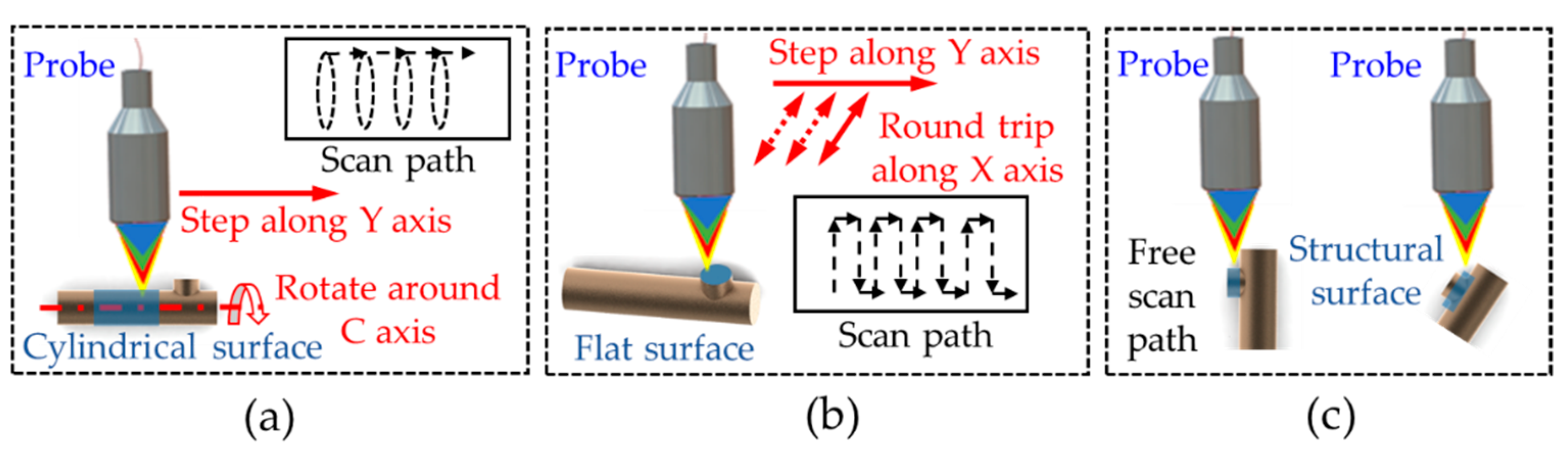
3. Coordinate System Construction and Path Planning
4. Error Correction Theory of the Cradle-Type Measurement System
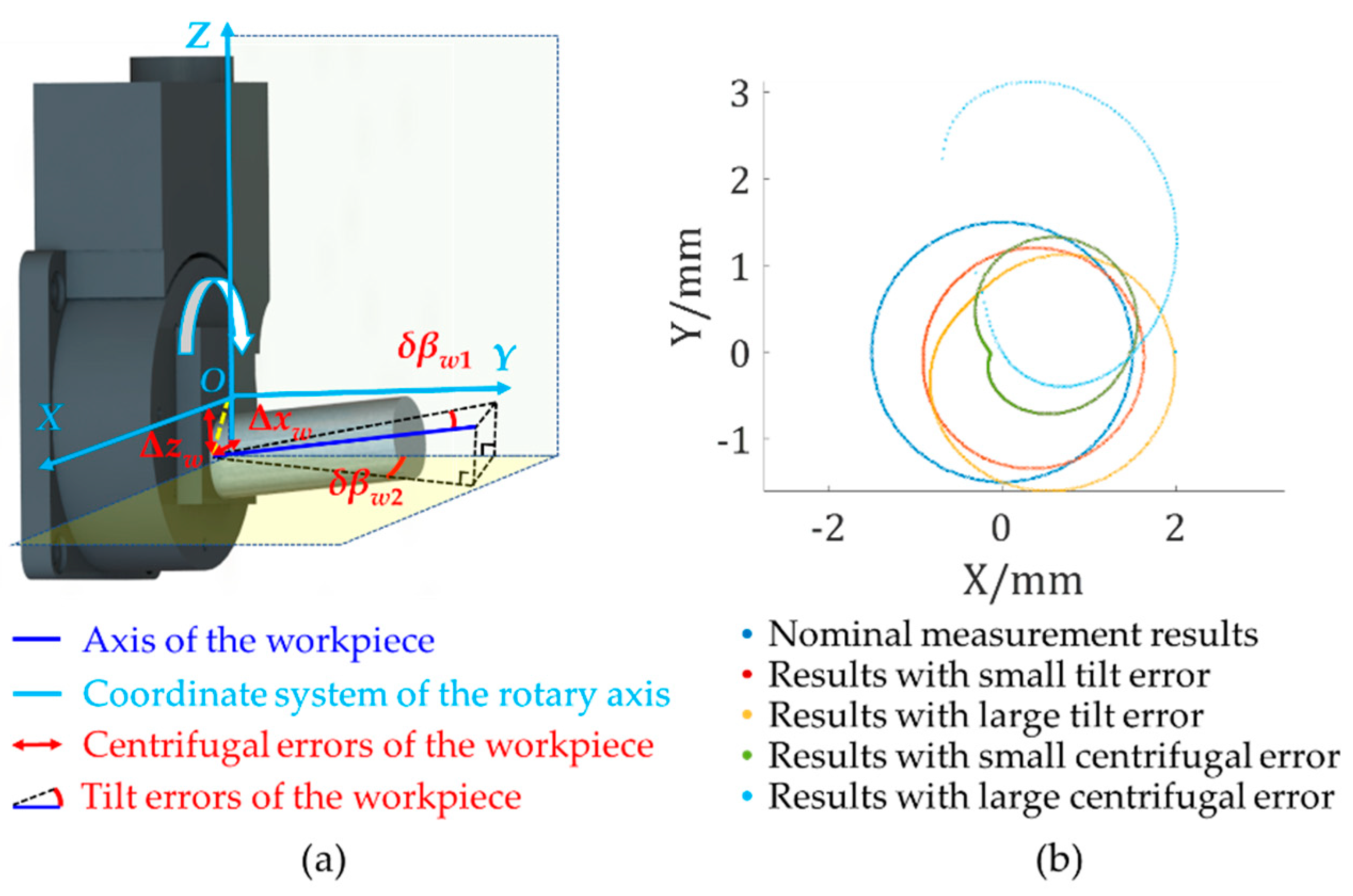
4.1. Error Identification
4.2. Error Calibration and Compensation
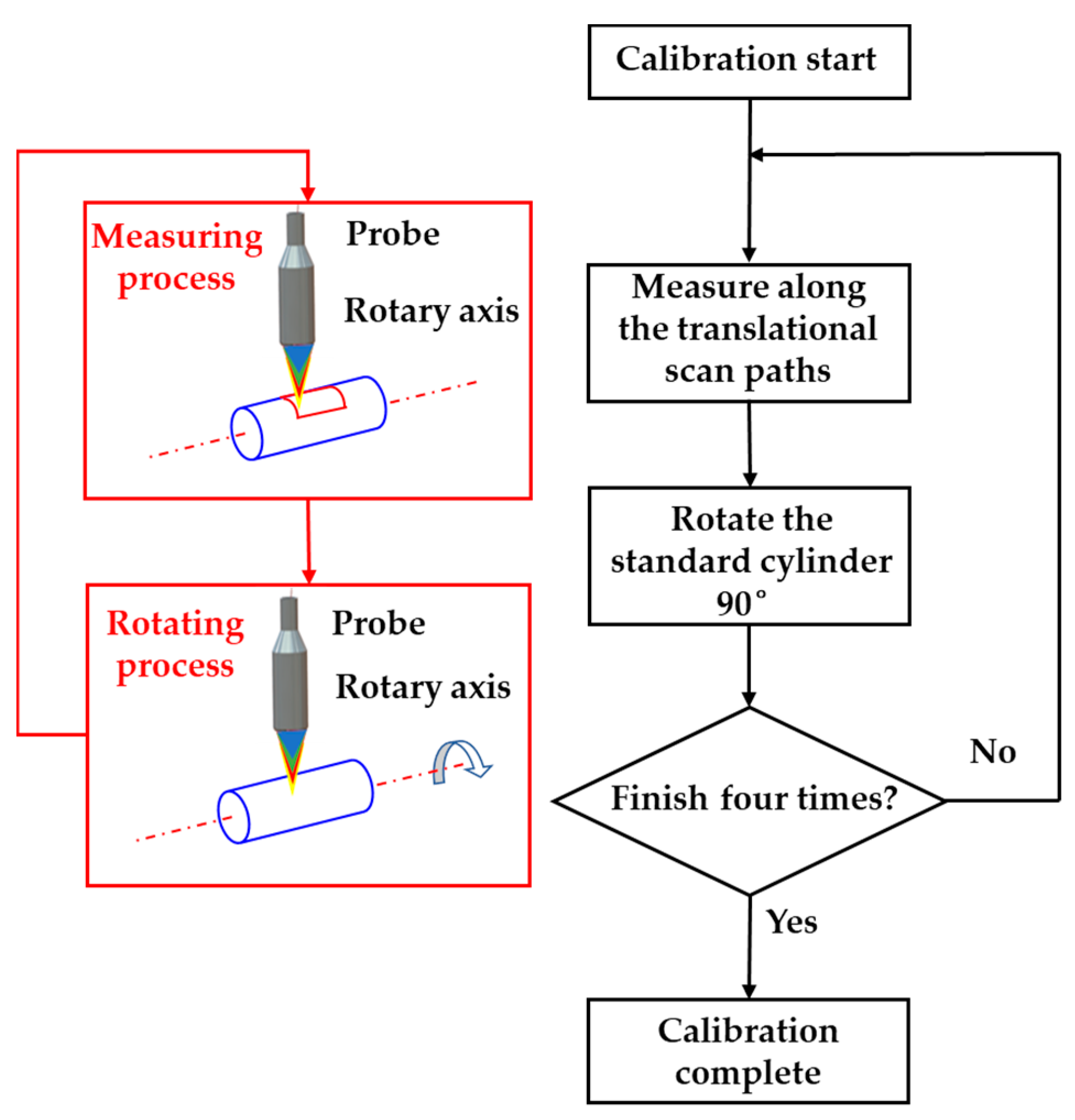
4.2.1. Calibration and Compensation of Static Errors of Rotary Stages
4.2.2. Calibration and Compensation of Clamping Errors
5. Experiments and Results
5.1. System Construction and Error Calibration
5.2. Measurement Results
6. Conclusions
- (1)
- An optical, cradle-type, non-registration point-scanning measurement method was proposed, which does not need the point cloud registration process and adapts to multiple complicated features of different sizes. This measurement system has strong flexibility.
- (2)
- A process to identify major error terms in measurement systems and apply calibration and compensation on them was proposed. The advantages of this process are that it does not rely on any additional high-precision equipment and promotes the system’s accuracy conveniently and efficiently. This method can also be applied to correct error terms in other measurement systems with rotary axes.
- (3)
- A five-axis experiment setup was built and tiny parts were measured in experiments. The measurement accuracy and capability of overall profile measurements were verified by measuring standard workpieces and complicated tiny parts separately. It was proved that in terms of overall profile measurement, this cradle-type five-axis measurement system had more advantages than some commercial instruments. It is worth noting that, measurement accuracy can be further improved if hardware with higher accuracy is used in the future. With the help of a premeasurement by an external measurement device, a fully automatic measurement is the next research goal.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jiang, J.; Luo, T.; Zhang, G.; Dai, Y. Novel tool offset fly cutting straight-groove-type micro-structure arrays. J. Mater. Process. Technol. 2021, 288, 116900. [Google Scholar] [CrossRef]
- Yang, J.; Li, S.; Wang, Z.; Yang, G. Real-time tiny part defect detection system in manufacturing using deep learning. IEEE Access 2019, 7, 89278–89291. [Google Scholar] [CrossRef]
- Sawada, K.; Odaka, S.; Kawai, T.; Hirai, T.; Takeuchi, Y.; Sata, T. Manufacture of diffraction grating on tiny parts by means of ultraprecision milling. Microsyst. Technol. 1999, 5, 157–160. [Google Scholar] [CrossRef]
- Fu, G.; Fu, J.; Xu, Y.; Chen, Z.; Lai, J. Accuracy enhancement of five-axis machine tool based on differential motion matrix: Geometric error modeling, identification and compensation. Int. J. Mach. Tools Manuf. 2015, 89, 170–181. [Google Scholar] [CrossRef]
- Boltryk, J.B.; Martyn, H.; John, W.M.; Antony, N. A comparison of precision optical displacement sensors for the 3D measurement of complex surface profiles. Sens. Actuators A Phys. 2007, 142, 2–11. [Google Scholar] [CrossRef]
- Giovanni, M.; Stefano, P.; Wahyudin, P.S. Four-axis micro measuring systems performance verification. CIRP Ann. Manuf. Technol. 2014, 63, 485–488. [Google Scholar] [CrossRef] [Green Version]
- Soons, J.A.; Theuws, F.C.; Schellekens, P.H. Modeling the errors of multi-axis machines: A general methodology. Precis. Eng. 1992, 14, 5–19. [Google Scholar] [CrossRef] [Green Version]
- Weckenmann, A.; Knauer, M.; Kunzmann, H. The influence of measurement strategy on the uncertainty of CMM-measurements. CIRP Ann. Manuf. Technol. 1998, 47, 451–454. [Google Scholar] [CrossRef]
- Schwenke, H.; Knapp, W.; Haitjema, H.; Weckenmann, A.; Schmitt, R.; Delbressine, F. Geometric error measurement and compensation of machines—An update. CIRP Ann. Manuf. Technol. 2008, 57, 660–675. [Google Scholar] [CrossRef]
- Huang, T.; Hong, Z.Y.; Mei, J.P.; Chetwynd, D.G. Kinematic calibration of the 3-DOF module of a 5-DOF reconfigurable hybrid robot using a double-ball-bar system. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 9–15 October 2006; pp. 508–512. [Google Scholar]
- Li, Q.Z.; Wang, W.; Jiang, Y.F.; Li, H.; Zhang, J.; Jiang, Z. A sensitivity method to analyze the volumetric error of five-axis machine tool. Int. J. Adv. Manuf. Technol. 2018, 98, 1791–1805. [Google Scholar] [CrossRef]
- Chen, S.Y.; Xue, S.; Zhai, D.D.; Tie, G.P. Measurement of freeform optical surfaces: Trade-off between accuracy and dynamic range. Laser Photon Rev. 2020, 14, 1–32. [Google Scholar] [CrossRef]
- Piotr, G.; Adam, G.; Maciej, G. Challenges for modeling of five-axis coordinate measuring systems. Appl. Sci. 2017, 7, 803. [Google Scholar] [CrossRef] [Green Version]
- Henselmans, R.; Cacace, L.A.; Kramer, G.F.Y.; Rosielle, P.C.J.N.; Steinbuch, M. Nanometer level freeform surface measurements with the NANOMEFOS non-contact measurement machine. Proc. SPIE 2009, 742606–742617. [Google Scholar] [CrossRef]
- The LuphoScan 260 HD from Taylor Hobson, Taking Precision Measurement of Optical Surfaces to the Next Level. Available online: https://www.taylor-hobson.com/pressreleases/news/2017/july/luphoscan260hd-launch?news_lang=en (accessed on 8 April 2021).
- ChaBum, L.; Sun-Kyu, L. Multi-degree-of-freedom motion error measurement in an ultraprecision machine using laser encoder—Review. J. Mech. Sci. Technol. 2013, 27, 141–152. [Google Scholar] [CrossRef]
- Miao, L.; Zhu, L.; Fang, C.; Yan, N.; Yang, X.; Zhang, X. Modeling and analysis of system error for highly curved freeform surface measurement by noncontact dual-axis rotary scanning. Sensors 2021, 21, 554. [Google Scholar] [CrossRef] [PubMed]
- S Neox Five Axis: Complete 3D Measurement Solution. Available online: https://www.sensofar.com/metrology/products/sneox-fiveaxis/ (accessed on 8 April 2021).
- Werth StentCheck. Available online: https://www.werth.de/index.php?id=661&L=12 (accessed on 8 April 2021).
- Hu, L.; Chen, Z.G.; Chen, Y.L. Precision measurement method of “cradle-type” five-axis machining center. Int. J. Adv. Manuf. Technol. 2021, 113, 3195–3209. [Google Scholar] [CrossRef]
- Chen, G.D.; Liang, Y.C.; Sun, Y.Z.; Chen, W.Q.; Wang, B. Volumetric error modeling and sensitivity analysis for designing a five-axis ultra-precision machine tool. Int. J. Adv. Manuf. Technol. 2013, 68, 2525–2534. [Google Scholar] [CrossRef]
- Liu, Y.; Wan, M.; Xing, W.J.; Xiao, Q.B.; Zhang, W.H. Generalized actual inverse kinematic model for compensating geometric errors in five-axis machine tools. Int. J. Mech. Sci. 2018, 145, 299–317. [Google Scholar] [CrossRef]
- Fan, K.C.; Wang, Y.H.; Yang, H.W.; Chen, L.M. Techniques of multi-degree-of-freedom measurement on the linear motion errors of precision machines. Adv. Opt. Technol. 2014, 3, 375–386. [Google Scholar] [CrossRef]
- Jeong, J.H.; Khim, G.; Oh, J.S.; Chung, S.C. Method for measuring location errors using a touch trigger probe on four-axis machine tools. Int. J. Adv. Manuf. Technol. 2018, 99, 1003–1012. [Google Scholar] [CrossRef]
- Zhang, Y.; Fu, J.Z.; Chen, Z.C. Simple modeling method for the volumetric error of cradle-type five-axis machine tools. J. Mach. Des. 2012, 29, 76–79. [Google Scholar] [CrossRef]
- Schwenke, H.; Schmitt, R.; Jatzkowski, P.; Warmann, C. On-the-fly calibration of linear and rotary axes of machine tools and CMMs using a tracking interferometer. CIRP Ann. Manuf. Technol. 2009, 58, 477–480. [Google Scholar] [CrossRef]
- Chen, J.C.; Lin, S.W.; He, B.W. Geometric error measurement and identification for rotary table of multi-axis machine tool using double ballbar. Int. J. Mach. Tools Manuf. 2014, 77, 47–55. [Google Scholar] [CrossRef]
- Hong, C.F.; Ibaraki, S. Non-contact R-test with laser displacement sensors for error calibration of five-axis machine tools. Precis. Eng. 2013, 37, 159–171. [Google Scholar] [CrossRef] [Green Version]
- Bjrklund, S.; Bjurstam, P.; Novak, A. Compensation of systematic errors in five-axis high-speed machining. Int. J. Prod. Res. 2002, 40, 3765–3778. [Google Scholar] [CrossRef]
- Ibaraki, S.; Ota, Y. Error calibration for five-axis machine tools by on-the-machine measurement using a touch-trigger probe. Autom. Technol. 2014, 8, 20–27. [Google Scholar] [CrossRef]
- Hong, C.F.; Ibaraki, S.; Matsubara, A. Influence of position-dependent geometric errors of rotary axes on a machining test of cone frustum by five-axis machine tools. Precis. Eng. 2010, 35, 1–11. [Google Scholar] [CrossRef]
- Remus, O.; Feng, H.Y. Configuration analysis of five-axis machine tools using a generic kinematic model. Int. J. Mach. Tools Manuf. 2004, 44, 1235–1243. [Google Scholar] [CrossRef]



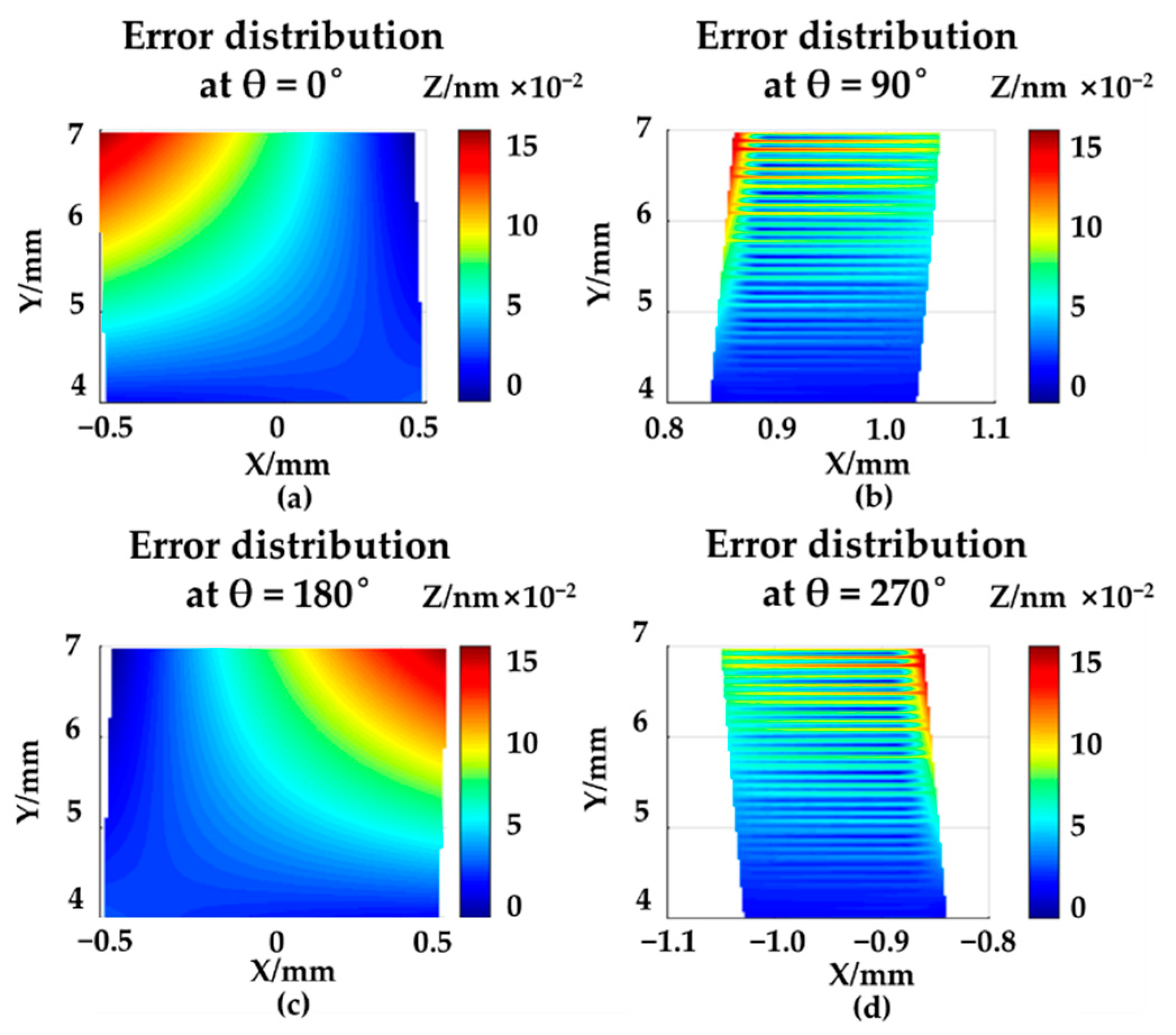
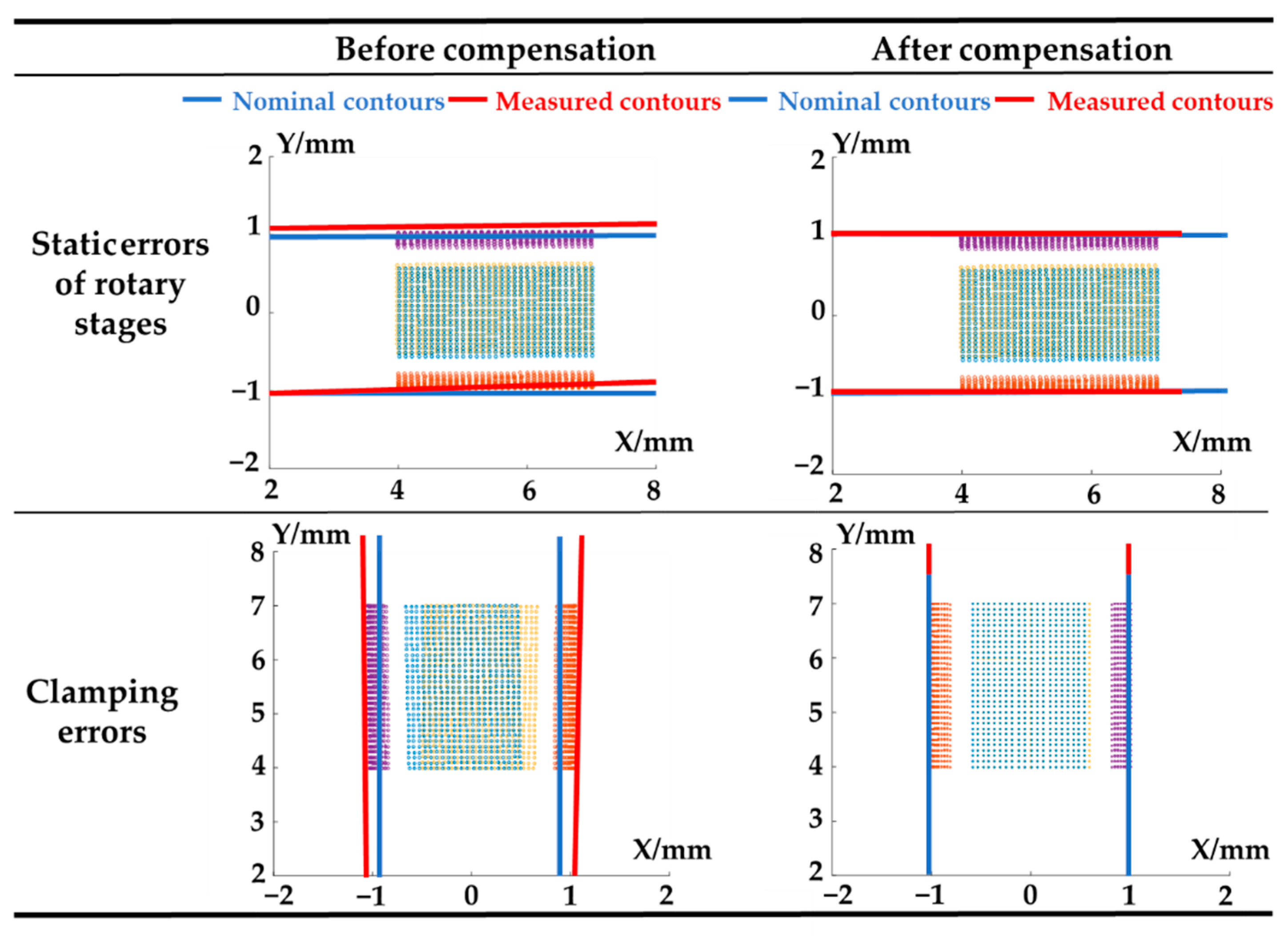


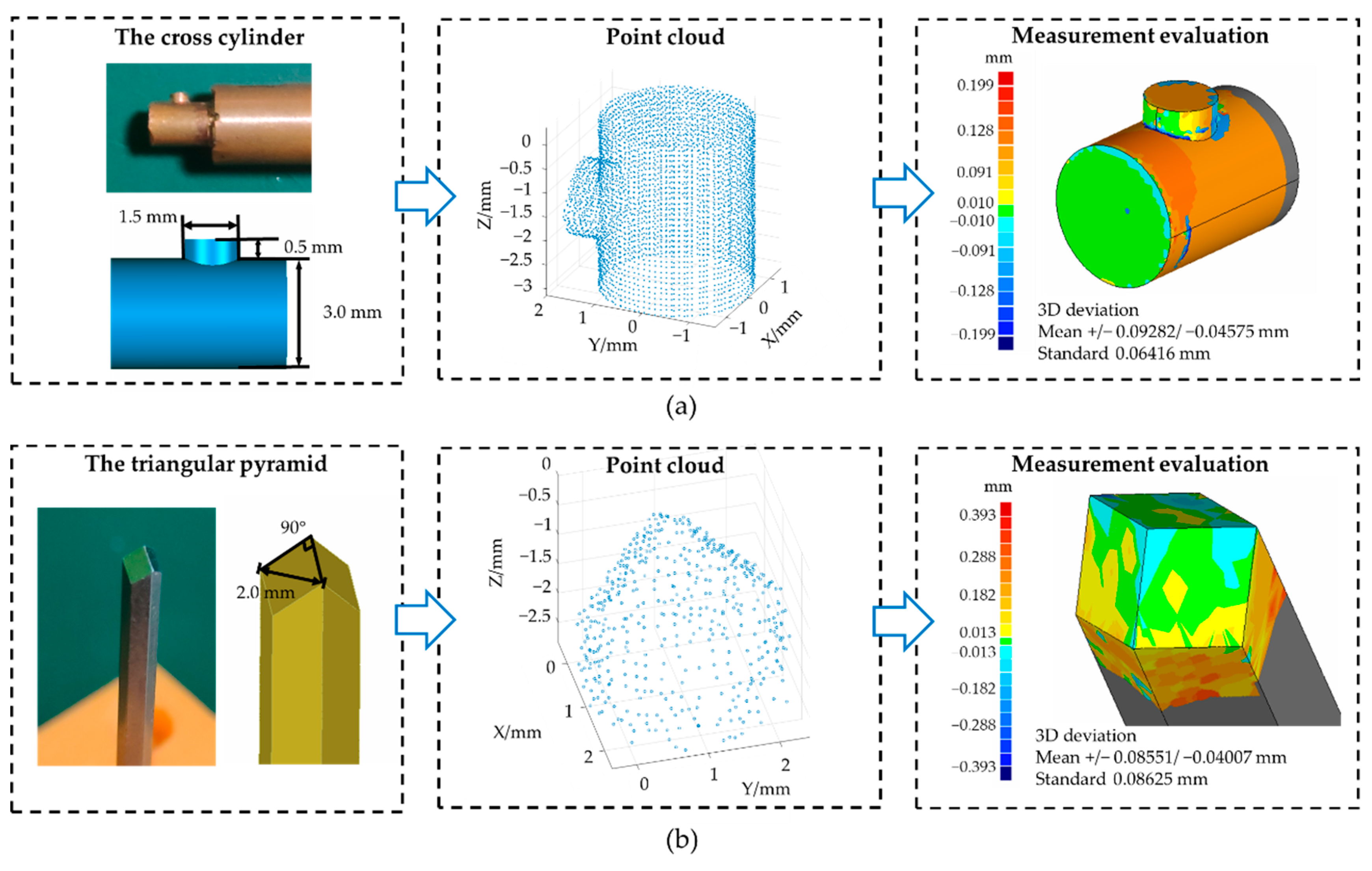
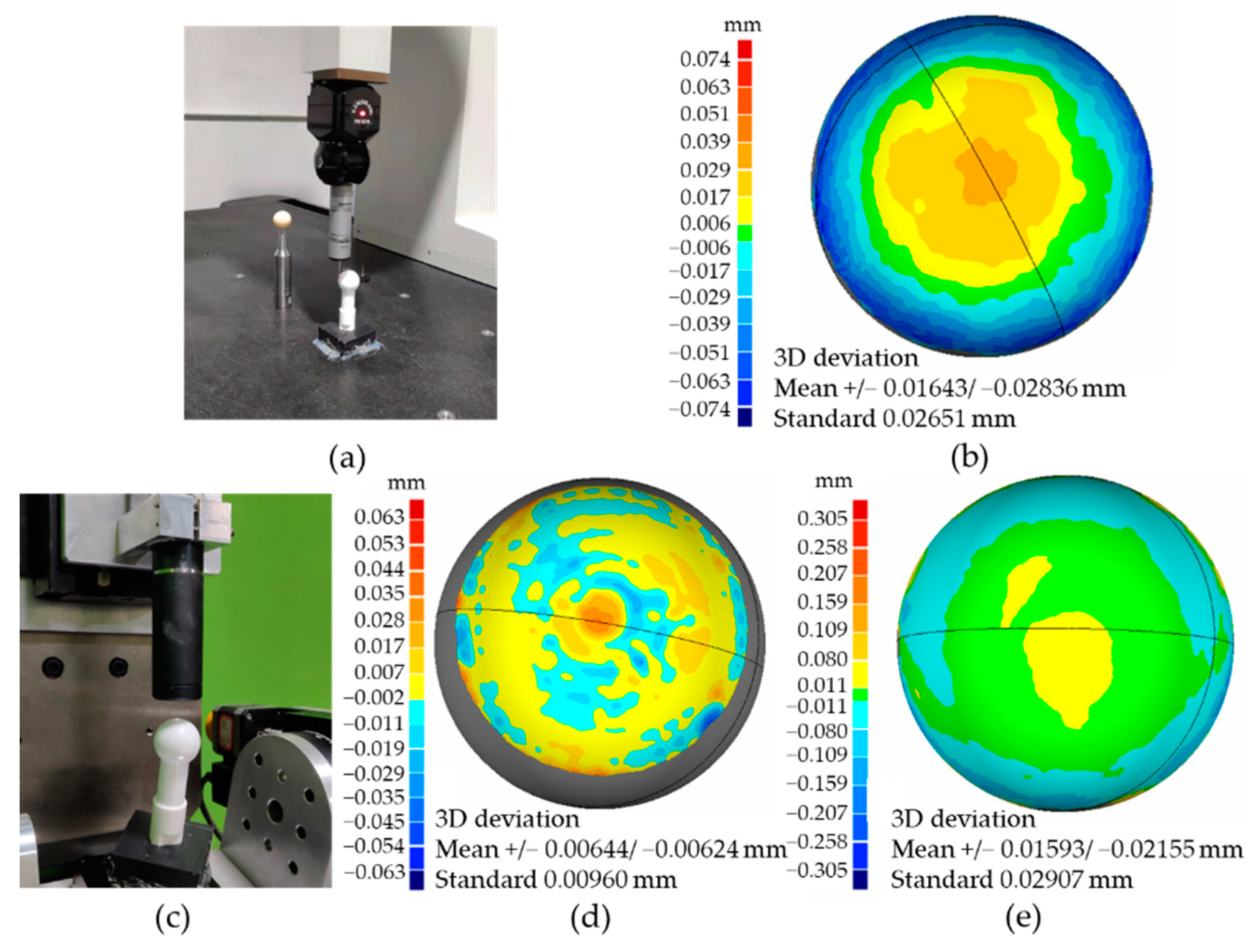
| Error Types | Specific Error Terms | Symbols | Ratios |
|---|---|---|---|
| System errors | Static errors of linear stages | δx, δy, δz | 2.430% |
| Dynamic errors of linear stages | Δd | 0.367% | |
| Static errors of rotary stages | δθ1, δθ2, Δx, Δy, Δz | 73.013% | |
| Dynamic errors of rotary stages | δβ | 0.083% | |
| Clamping errors of workpieces | Tilt errors | δβw1, δβw2 | 17.247% |
| Centrifugal errors | Δxw, Δzw | 6.860% |
| Hardware | Travel/Range | Accuracy | Others |
|---|---|---|---|
| X/Y/Z axes | 200 mm | 1 μm | \ |
| A/C axes | 360° | 0.004° | Surface radius of C-axis stage: 30 mm |
| Probe | 400 μm | 0.1 μm | NA: ±28° |
| Standard cylinder | r: 10 mm | Cylindricity: 14 μm | \ |
| Error Source | Error Terms | Value (° or μm) |
|---|---|---|
| A axis | δθ1, δθ2 | 0.0741, 0.3413 |
| Δx, Δy, Δz | (0.8424, −0.0012, 0.0177) | |
| C axis | δθ1, δθ2 | 0.5035, −0.8466 |
| Δx, Δy, Δz | (0.2906, 0.5074, 0.6875) | |
| Workholding device | δβw1, δβw2 | −5.6936, 2.2561 |
| Δxw, Δzw | (0.0651, −0.2498) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.; Zhu, L.; Miao, L.; Li, C.; Fang, C.; Zhang, X. Overall Profile Measurements of Tiny Parts with Complicated Features with the Cradle-Type Five-Axis System. Sensors 2021, 21, 4609. https://doi.org/10.3390/s21134609
Liu L, Zhu L, Miao L, Li C, Fang C, Zhang X. Overall Profile Measurements of Tiny Parts with Complicated Features with the Cradle-Type Five-Axis System. Sensors. 2021; 21(13):4609. https://doi.org/10.3390/s21134609
Chicago/Turabian StyleLiu, Lei, Linlin Zhu, Li Miao, Chen Li, Changshuai Fang, and Xiaodong Zhang. 2021. "Overall Profile Measurements of Tiny Parts with Complicated Features with the Cradle-Type Five-Axis System" Sensors 21, no. 13: 4609. https://doi.org/10.3390/s21134609
APA StyleLiu, L., Zhu, L., Miao, L., Li, C., Fang, C., & Zhang, X. (2021). Overall Profile Measurements of Tiny Parts with Complicated Features with the Cradle-Type Five-Axis System. Sensors, 21(13), 4609. https://doi.org/10.3390/s21134609







