A Sustainable Early Warning System Using Rolling Forecasts Based on ANN and Golden Ratio Optimization Methods to Accurately Predict Real-Time Water Levels and Flash Flood
Abstract
1. Introduction
1.1. Background
1.2. Literature Review
1.3. Contributions
- Developing a novel rolling forecast model for flash-floods-based ANN technique equipped with an early warning system based on the weather forecast data and real-time measurements of water level in the street drainage system (downtown/Amman). The proposed EFWS in this paper aims to support decision makers by providing them with reliable and accurate information and warning about any possible flood events. Furthermore, the EFWS will provide accurate forecasts with efficient lead-time to reduce any damages due to flash floods.
- This paper develops an ANN using a new optimization method, called the Golden Ratio Optimization Method (GROM) technique, to estimate the water level over one day ahead during flash flood events. The result of the new forecast model (ANN based on GROM) will be compared to the literature, the traditional ANN model.
- This article examines the impact of using different exogenous variables on the ANN forecast and investigate the optimal ANN structure for forecasting the flash flood in Jordan.
- Developing a rolling ANN forecast model to treat the stochasticity of weather forecast data and improve the prediction accuracy of the flash flood in Jordan compared to fixed point forecast models.
1.4. Outline of Paper
2. Methodology
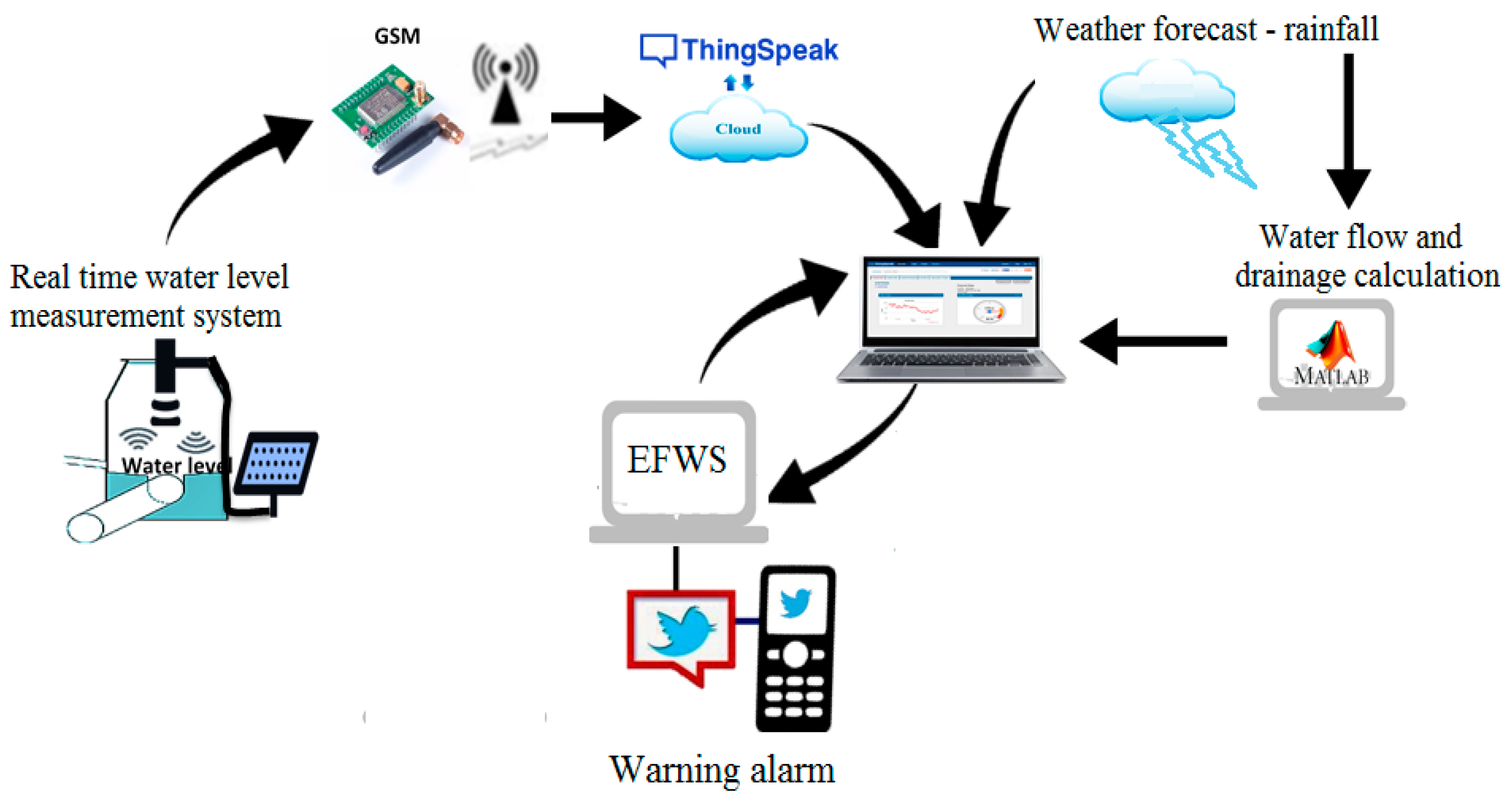
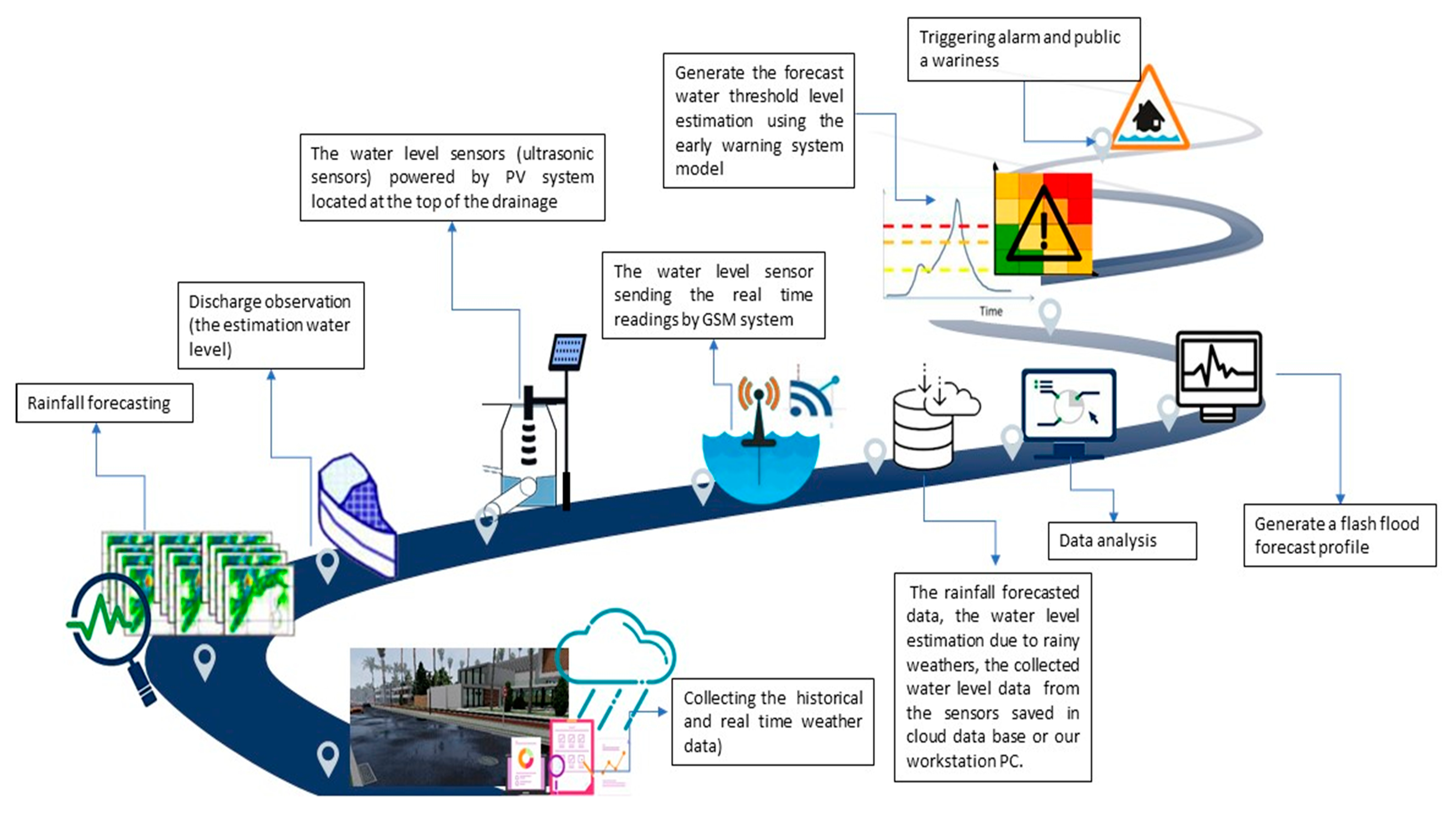
3. EFWS System Modeling and Study Area
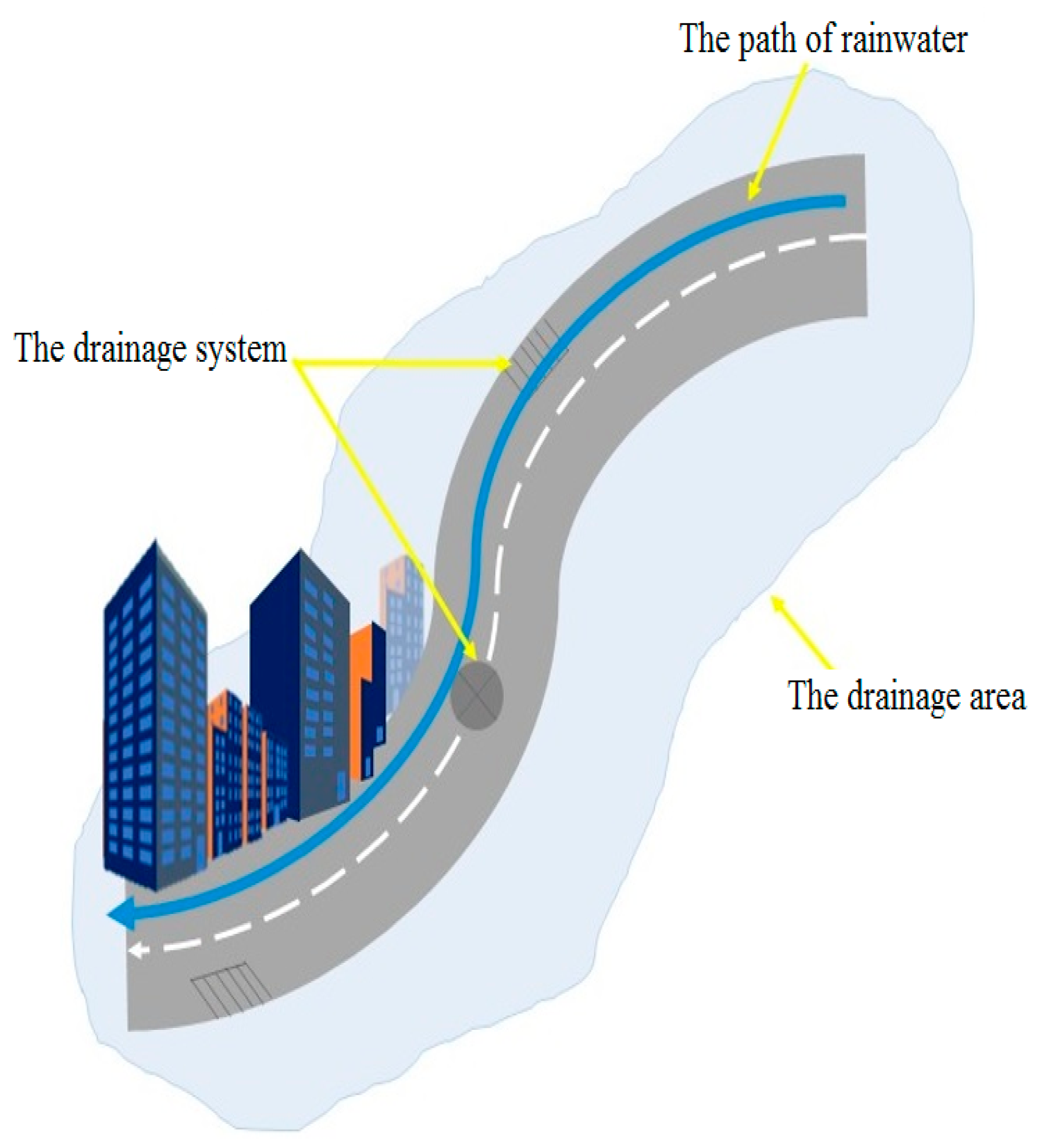
3.1. Study Area and the Water Drainage System
3.2. Real-Time Measurement Model
3.3. Flood Warning System
4. Rolling ANN Forecast Model Optimized by GROM
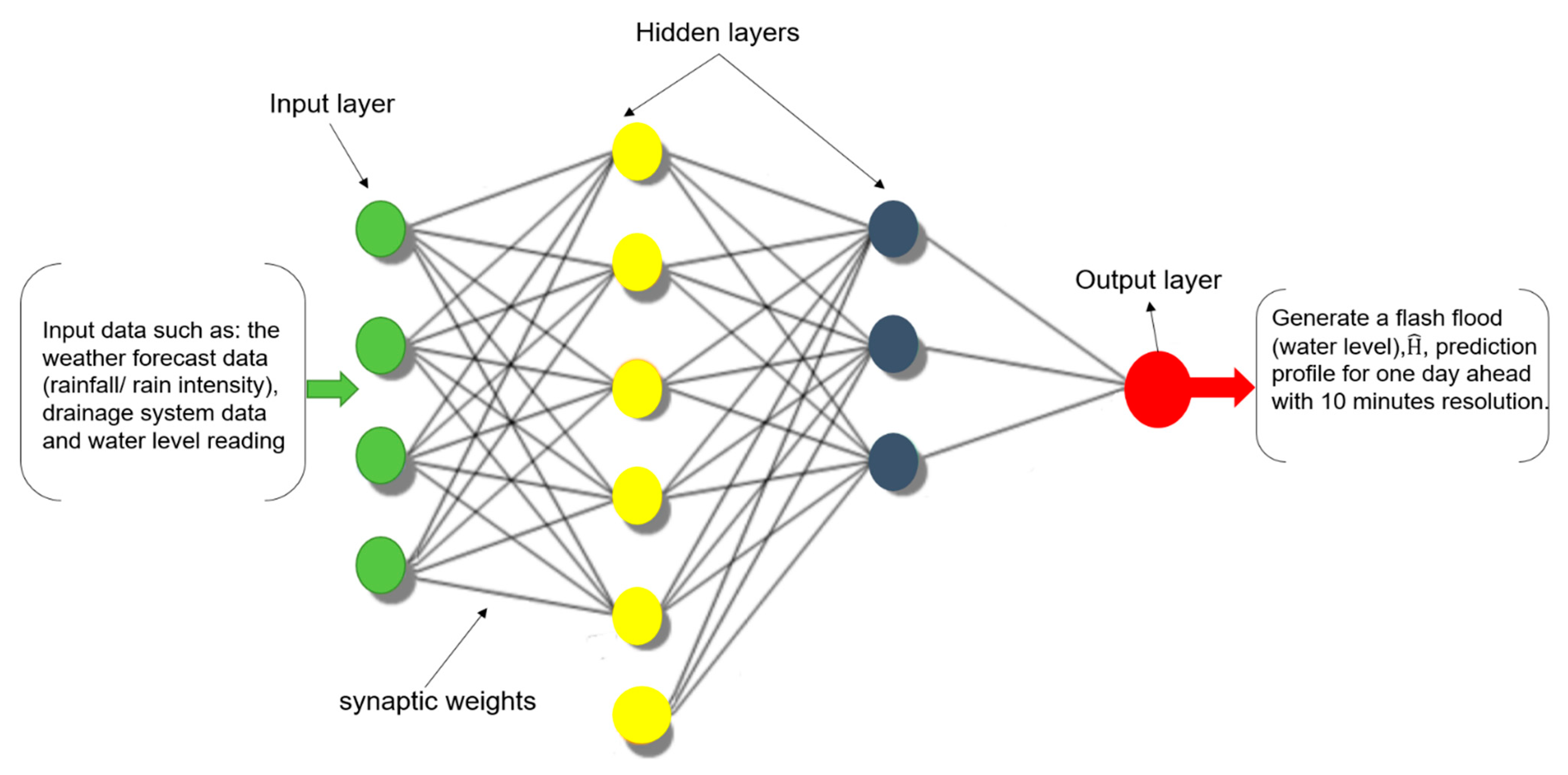
4.1. ANN Forecast Model for ESWS Optimized by GROM
- Traditional ANN model: this proposed model is a feedforward ANN model trained by one of the most common methods called Levenberg-Marquard and the neuron activated by a sigmoid function. This traditional ANN model has been widely used in the literature with stochastic targets [24].
- ANN forecast model optimized by Golden Ratio Optimization Method (GROM) algorithm [33]: the feedforward ANN model will use the GROM algorithm to handle the learning process and achieve the optimal performance in ANN.
4.1.1. Implementation of ANN Models (Traditional and GROM Models)
- Inputs variables: initially, the following variables (adding water level at a time, (t), and real-time measurement for the water level, have been carefully selected as the main input variables, where they are directly connected to calculate the future water level. In order to improve the forecast model performance and select more suitable input variables, the previous time steps from 10 min until one hour, the previous day water level at the same time, previous day data of daily rain intensity and temperature are tested in this work as external variables.
- Output variables: the future water level, over the next day with 10 min time resolution.
- Data processing: weather conditions data has been collected over three years from 2017 to 2019. These data sets are divided into training (60%), validation (10%) and testing data sets (30%). In general, the training set is the largest data set, and it is used to fit the parameters of the model, train the forecast model and find the patterns. The training set needs to be large enough to represent the data characteristics. This data set is mainly used to select the potential models. Then the validation set is used to try and find the best of these by training each of the model parameters in the training set and then testing the errors for forecasts in the validation set. The validation set is used as a final performance check for the trained network before testing the model with around 10% of the training set. The reason for this structure is to avoid a specific good forecast on the training set which turns out to be inaccurate in the test set. In addition, this way aims to avoid “overfitting” by selecting a forecast that is over-trained on the training set. Finally, the testing set is used to provide an unbiased evaluation of the final forecast model and is typically 10% to 30% of the training set.
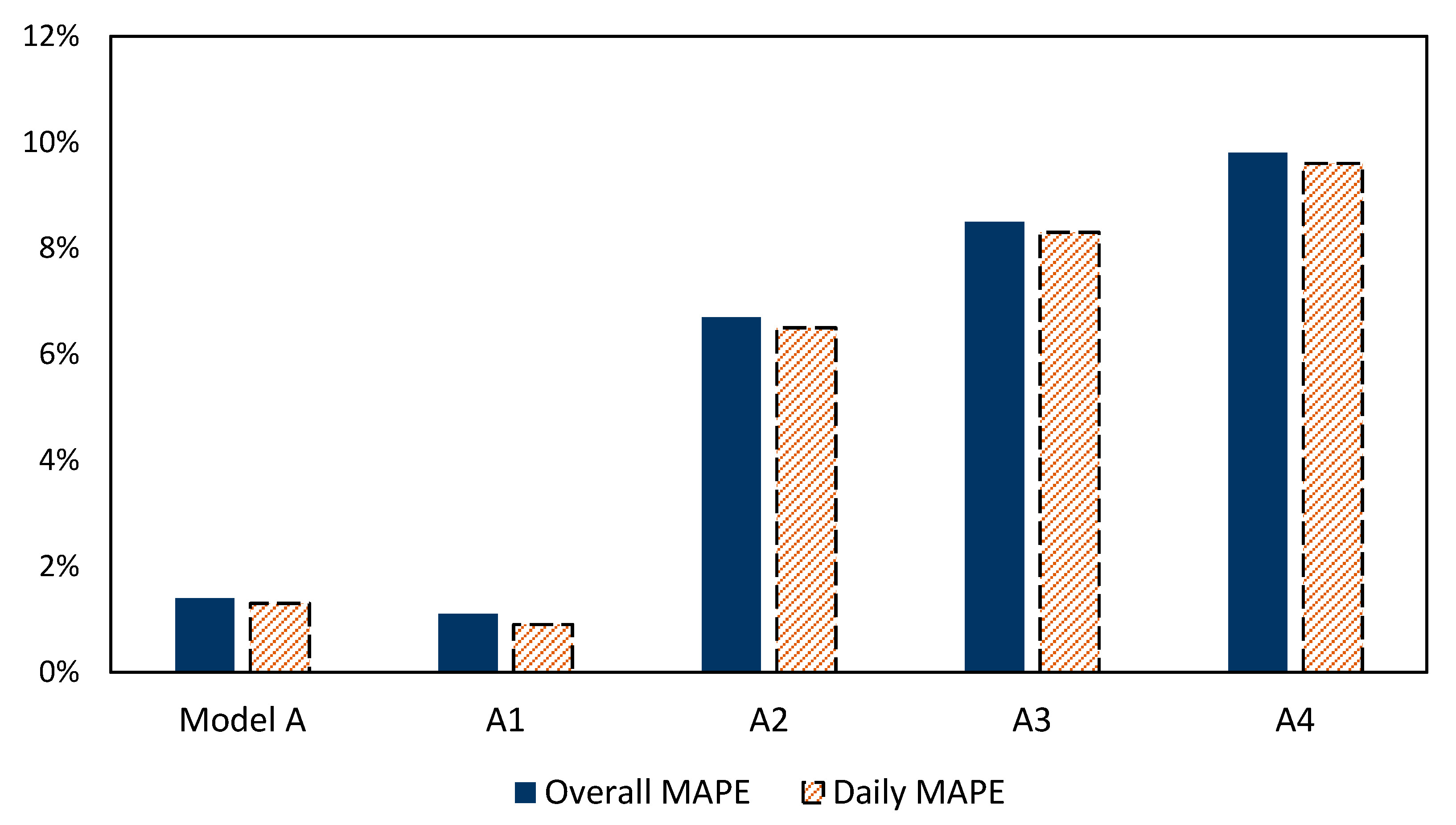
- The number of hidden layers and neurons: to optimally select the number of hidden layers and neurons for the ANN in EFW, different number of hidden layers (1 to 5) and different number of hidden neurons (10 to 50) has been tested.
- Training and learning algorithm: Levenberg-Marquardt and GROM algorithms are used and tested.
- The stopping criteria: in case there are no improvements in the accuracy.
4.1.2. ANN Forecast Model Based on GROM Algorithm
4.2. The Forecast Model Evaluation
- Evaluating different exogenous variables and ANN structure parameters to determine the optimal parameters for the ANN models
- Overall comparisons are presented for the traditional ANN and ANN optimized by GROM.
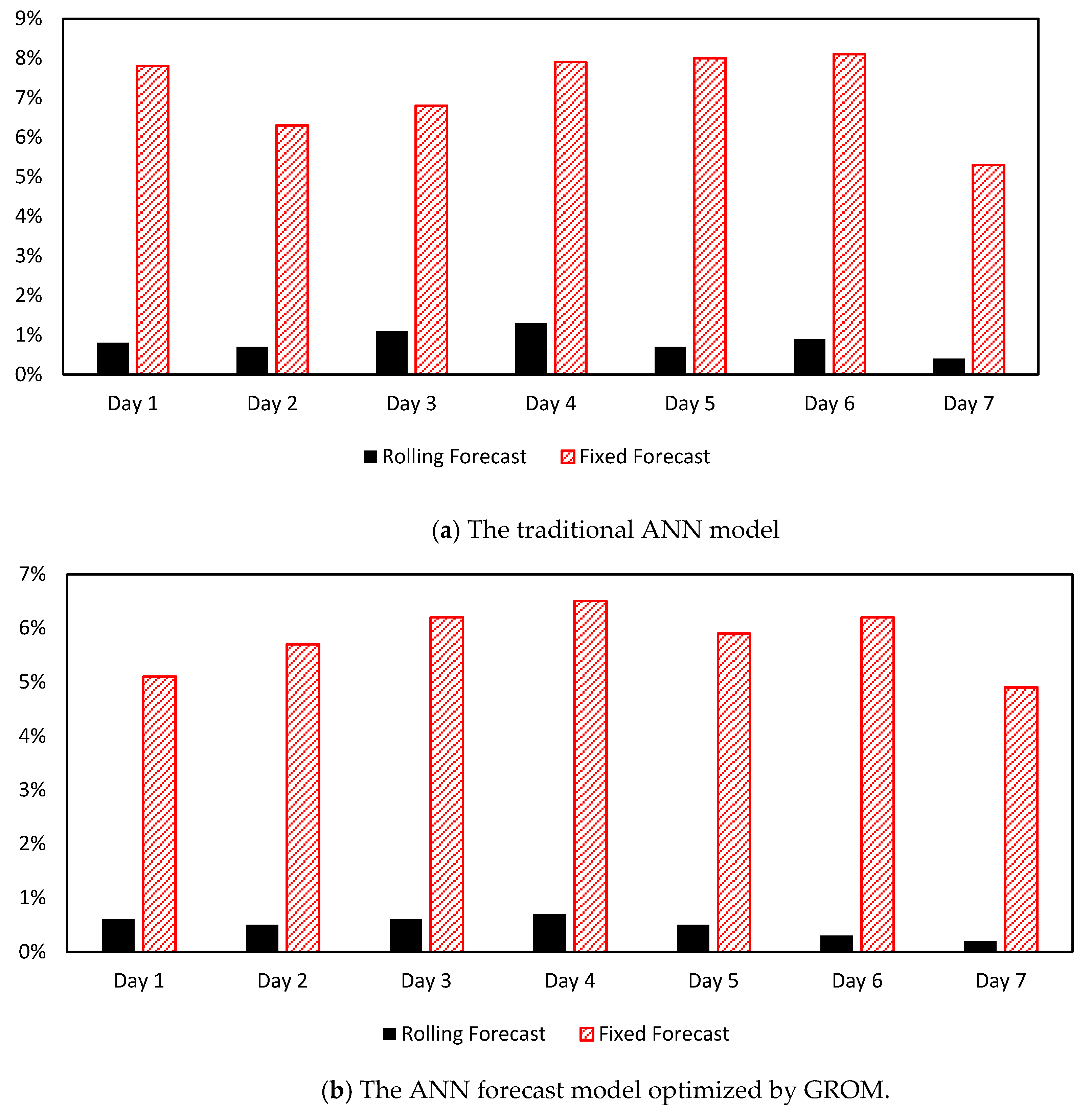
- Evaluating the significance of using the rolling forecasts compared to a fixed model.
5. Results and Discussion
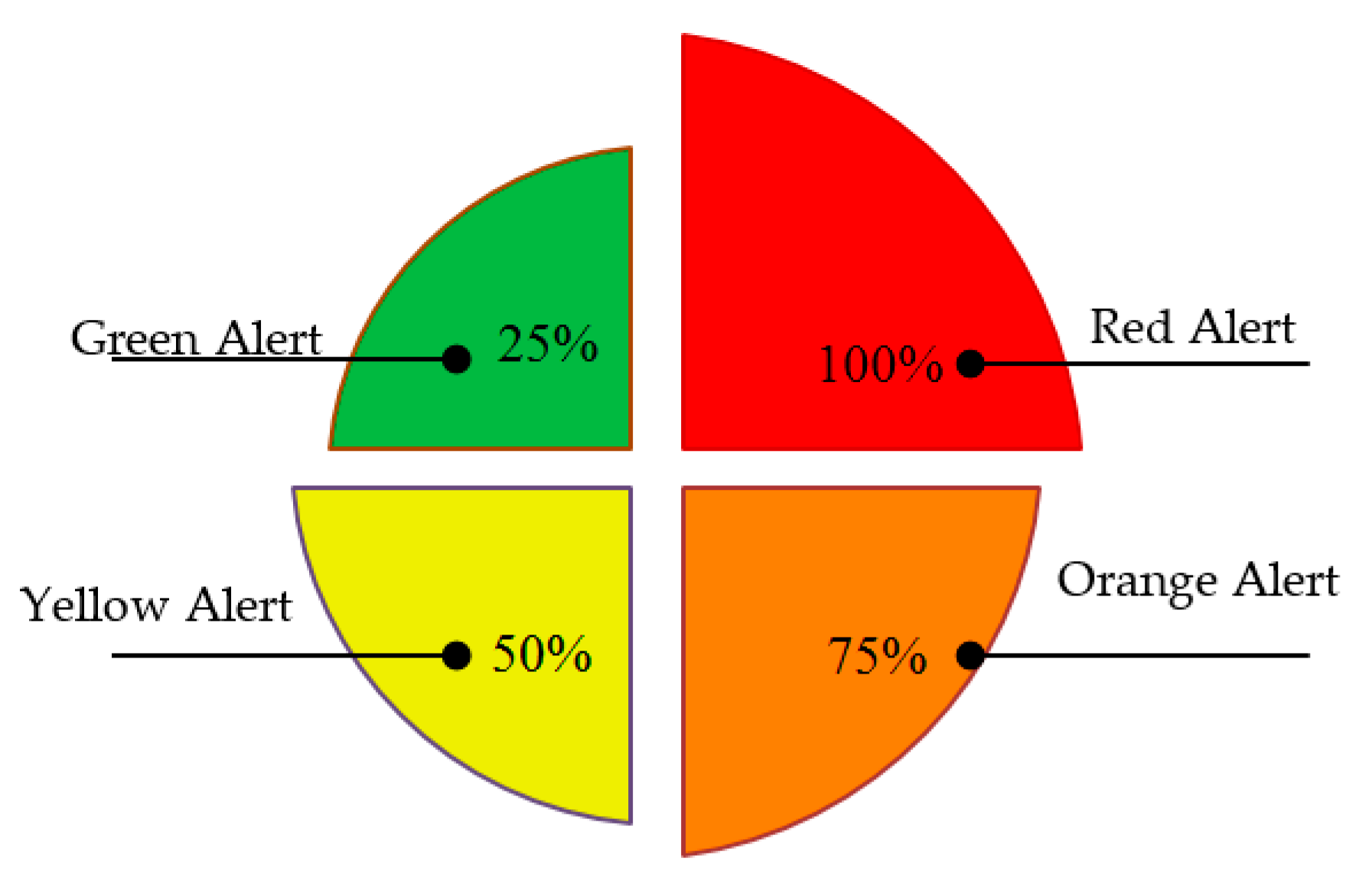
5.1. Risk Knowledge and Flood Warning System
- The EFWS generates daily and hourly reports (excel sheets) and dialog box warning (lights and sound) in the workstation (control center). This data and information will be available for the decision-maker and government to make necessary decisions and actions.
- The EFWS model will send an email notification to selected emails by control center holder such as private and government stockholders and emergency team.
- To increase the awareness of the flash flood risk among communities, the EFWS model will post a warning message on Twitter if the estimated water level in orange or red zones.
5.2. Effect of Exogenous Variables and Model Parameters on Forecast Models
- Input exogenous variables: adding water level at time t, (t), and real-time measurement for the water level,
- Hidden layers: two layers.
- Hidden neurons in each layer: 10 neurons.
- Rolling forecasts.
5.3. Traditional ANN Model and ANN Forecast Model Optimized by GROM
- Input exogenous variables: adding water level at time t, (t), and real-time measurement for the water level, and (the previous time steps from 20 min until one hour)
- Hidden layers: two layers.
- Hidden neurons in each layer: 20 neurons.
5.4. Evaluating the Significance of Using the Rolling Forecasts Compared to a Fixed Model
5.5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mambretti, S.; DeWrachien, D.; Sole, A. Flood-risk assessment and hazard mitigation measures: Case studies and lessons learnt in Italy. WIT Trans. Ecol. Environ. 2013, 118, 17–26. [Google Scholar]
- Dottori, F.; Szewczyk, W.; Ciscar, J.C.; Zhao, F.; Alfieri, L.; Hirabayashi, Y.; Bianchi, A.; Mongelli, I.; Frieler, K.; Betts, R.A.; et al. Increased human and economic losses from river flooding with anthropogenic warming. Nat. Clim. Chang. 2018, 8, 781–786. [Google Scholar] [CrossRef]
- Abdelkarim, A.; Gaber, A.F.D.; Youssef, A.M.; Pradhan, B. Flood Hazard Assessment of the Urban Area of Tabuk City, Kingdom of Saudi Arabia by Integrating Spatial-Based Hydrologic and Hydrodynamic Modeling. Sensors 2019, 19, 1024. [Google Scholar] [CrossRef]
- Costache, R.; Arabameri, A.; Blaschke, T.; Pham, Q.B.; Pham, B.T.; Pandey, M.; Arora, A.; Linh, N.T.T.; Costache, I. Flash-Flood Potential Mapping Using Deep Learning, Alternating Decision Trees and Data Provided by Remote Sensing Sensors. Sensors 2021, 21, 280. [Google Scholar] [CrossRef]
- Louvain, C. Natural Disasters 2018; Centre for Research on the Epidemiology of Disasters CRED: Brussels, Belgium; USAID: Geneva, Switzerland, 2019; p. 8. [Google Scholar]
- Al-Shibli, F.; Maher, W.; Thompson, R. The Need for a Quantitative Analysis of Risk and Reliability for Formulation of Water Budget in Jordan. Jordan J. Earth Environ. Sci. 2017, 8, 77–89. [Google Scholar]
- Abu-Awad, B.; Abu-Hammad, N.; Abu-Hamatteh, S. Urban and Architectural Development in Amman Downtown between Natural Disasters and Great Heritage Lose: Case Study. Int. J. Archit. Urban Dev. 2019, 9, 31–38. [Google Scholar]
- Prime Ministry of Jordan. Amman Downtown Flood Report on 28/2/2019, an Initial Technical Study. Available online: https://petra.gov.jo/upload/Files/%D8%AA%D9%82%D8%B1%D9%8A%D8%B1%20%D9%81%D9%8A%D8%B6%D8%A7%D9%86%20%D9%88%D8%B3%D8%B7%20%D8%B9%D9%85%D8%A7%D9%86%20(1).pdf (accessed on 10 June 2021).
- Al Nawas, B. Over 100 Amman Shops Claim Damage after Recent Flooding. JT (Jordan Times). 2020. Available online: https://www.jordantimes.com/news/local/over-100-amman-shops-claim-damage-after-recent-flooding (accessed on 12 June 2021).
- Farhan, Y.; Anaba, O. Flash Flood Risk Estimation of Wadi Yutum (Southern Jordan) Watershed Using GIS Based Morphometric Analysis and Remote Sensing Techniques. J. Mod. Hydrol. 2016, 6, 79–100. [Google Scholar] [CrossRef]
- Alhasanat, H. Flash Flood Assessment for Wadi Mousa City-Jordan. Procedia Econ. Financ. 2014, 18, 675–683. [Google Scholar] [CrossRef][Green Version]
- Al-Weshah, R.; El-Khoury, F. Flood Analysis and Mitigation for Petra Area in Jordan. J. Water Resour. Plan. Manag. 1999, 125, 170–177. [Google Scholar] [CrossRef][Green Version]
- Ibarreche, J.; Aquino, R.; Edwards, R.M.; Rangel, V.; Pérez, I.; Martínez, M.; Castellanos, E.; Álvarez, E.; Jimenez, S.; Rentería, R.; et al. Flash Flood Early Warning System in Colima, Mexico. Sensors 2020, 20, 5231. [Google Scholar] [CrossRef]
- Alfieri, L.; Thielen, J. A European precipitation index for extreme rain-storm and flash flood early warning. Meteorol. Appl. 2015, 22, 3–13. [Google Scholar] [CrossRef]
- Hoedjes, J.; Kooiman, A.; Maathius, B.; Said, M.; Becht, R.; Limo, A.; Mumo, M.; Nduhiu-Mathenge, J.; Shaka, A.; Su, B. A Conceptual Flash Flood Early Warning System for Africa, Based on Terrestrial Microwave Links and Flash Flood Guidance. ISPRS Int. J. Geo-Inf. 2014, 3, 584–598. [Google Scholar] [CrossRef]
- Cools, J.; Innocenti, D.; O’Brien, S. Lessons from flood early warning systems. Environ. Sci. Policy 2016, 58, 117–122. [Google Scholar] [CrossRef]
- Apollonio, C.; Balacco, G.; Gioia, A.; Iacobellis, V.; Piccinni, A.F. Flood Hazard Assessment of the Fortore River Downstream the Occhito Dam, in Southern Italy. In Constructive Side-Channel Analysis and Secure Design; Springer International Publishing: Berlin/Heidelberg, Germany, 2017; Volume 10405, pp. 201–216. [Google Scholar]
- Gamperl, M.; Singer, J.; Thuro, K. Internet of Things Geosensor Network for Cost-Effective Landslide Early Warning Systems. Sensors 2021, 21, 2609. [Google Scholar] [CrossRef] [PubMed]
- Guesmi, H. Wireless Smart Sensor Networks for Real-Time Warning System of Flash Floods and Torrents in KSA. Int. J. Comput. Appl. 2017, 165, 13–21. [Google Scholar] [CrossRef]
- Hofmann, J.; Schüttrumpf, H. Risk-Based Early Warning System for Pluvial Flash Floods: Approaches and Foundations. Geosciences 2019, 9, 127. [Google Scholar] [CrossRef]
- Chang, N.; Guo, D.-H. (Eds.) Urban Flash Flood Monitoring, Mapping and Forecasting via a Tailored Sensor Network System. In Proceedings of the 2006 IEEE International Conference on Networking, Sensing and Control, Ft. Lauderdale, FL, USA, 23–25 April 2006; pp. 757–761, ISBN 1-4244-0065-1. [Google Scholar]
- Song, Y.; Park, Y.; Lee, J.; Park, M.; Song, Y. Flood Forecasting and Warning System Structures: Procedure and Application to a Small Urban Stream in South Korea. Water 2019, 11, 1571. [Google Scholar] [CrossRef]
- Robinson, Y.; Vimal, S.; Julie, E.; Narayanan, K.; Rho, S. 3-Dimensional Manifold and Machine Learning Based Localization Algorithm for Wireless Sensor Networks. Wirel. Pers. Commun. 2021. [Google Scholar] [CrossRef]
- Rathore, M.; Paul, A.; Rho, S.; Khan, M.; Vimal, S.; Shah, S. Smart traffic control: Identifying driving violations using fog devices with vehicular cameras in smart cities. Sustain. Cities Soc. 2021, 71, 102986. [Google Scholar] [CrossRef]
- Alasali, F.; Nusair, K.; Alhmoud, L.; Zarour, E. Impact of the COVID-19 Pandemic on Electricity Demand and Load Forecasting. Sustainability 2021, 13, 1435. [Google Scholar] [CrossRef]
- Aichouri, I.; Hani, A.; Bougherira, N.; Djabri, L.; Chaffai, H.; Lallahem, S. River flow model using artificial neural networks. Energy Procedia 2015, 74, 1007–1014. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, Q.; Zhang, G.; Nie, Z.; Gui, Z. A hybrid model for annual runoff time series forecasting using Elman neural network with ensemble empirical mode decomposition. Water 2018, 10, 416. [Google Scholar] [CrossRef]
- Rhee, J.H.; Seo, J. Low-Cost Curb Detection and Localization System Using Multiple Ultrasonic Sensors. Sensors 2019, 19, 1389. [Google Scholar] [CrossRef]
- Alasali, F.; Haben, S.; Becerra, V.; Holderbaum, W. Optimal Energy Management and MPC Strategies for Electrified RTG Cranes with Energy Storage System. Energies 2017, 10, 1598. [Google Scholar] [CrossRef]
- Alasali, F.; Haben, S.; Becerra, V.; Holderbaum, W. Day-ahead industrial load forecasting for electric RTG cranes. J. Mod. Power Syst. Clean Energy 2018, 6, 223–234. [Google Scholar] [CrossRef]
- Wei, D.; Wang, J.; Ni, K.; Tang, G. Research and Application of a Novel Hybrid Model Based on a Deep Neural Network Combined with Fuzzy Time Series for Energy Forecasting. Energies 2019, 12, 3588. [Google Scholar] [CrossRef]
- Alasali, F.; Foudeh, H.; Ali, E.M.; Nusair, K.; Holderbaum, W. Forecasting and Modelling the Uncertainty of Low Voltage Network Demand and the Effect of Renewable Energy Sources. Energies 2021, 14, 2151. [Google Scholar] [CrossRef]
- Nusair, K.; Alasali, F. Optimal Power Flow Management System for a Power Network with Stochastic Renewable Energy Resources Using Golden Ratio Optimization Method. Energies 2020, 13, 3671. [Google Scholar] [CrossRef]




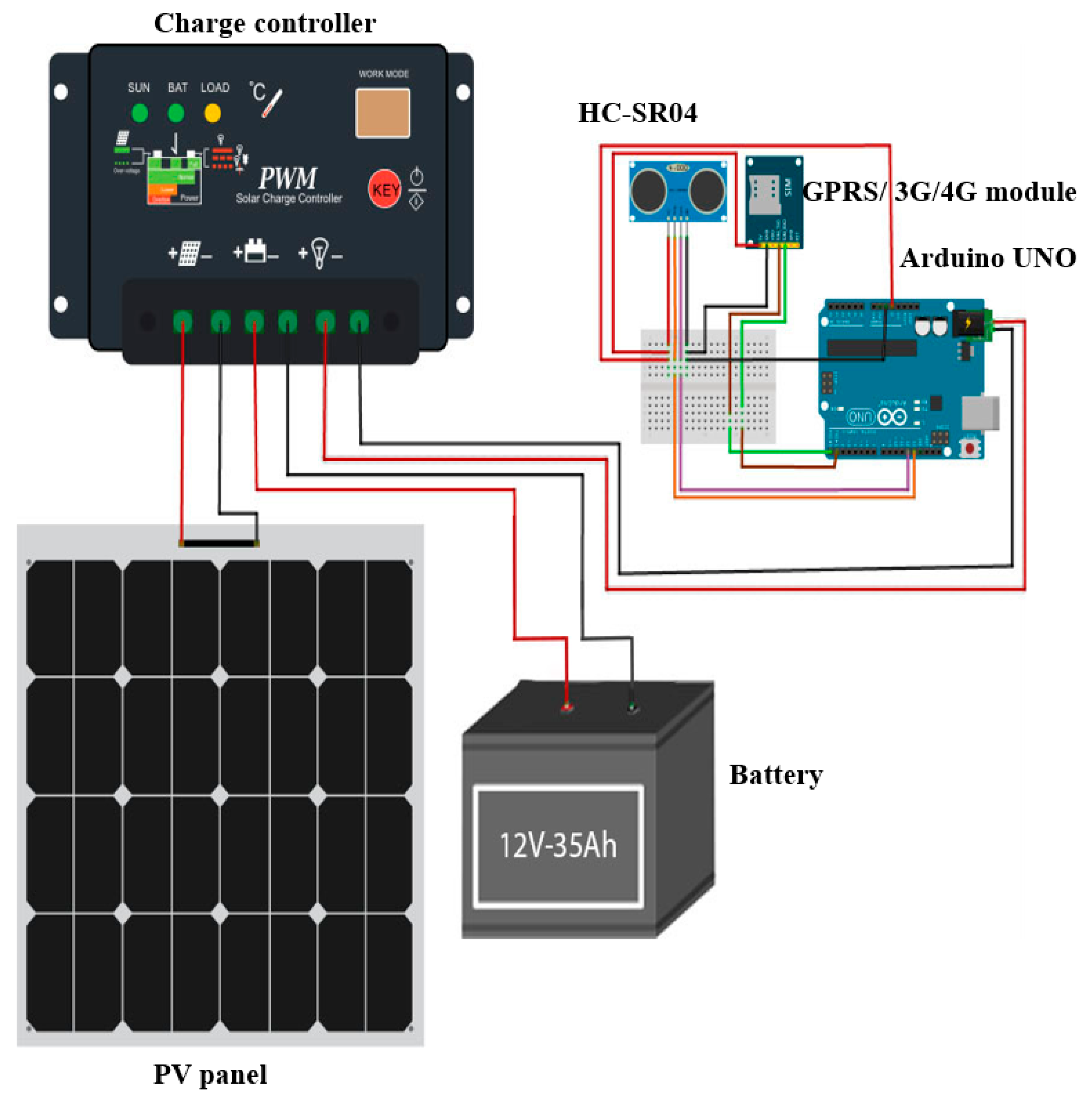
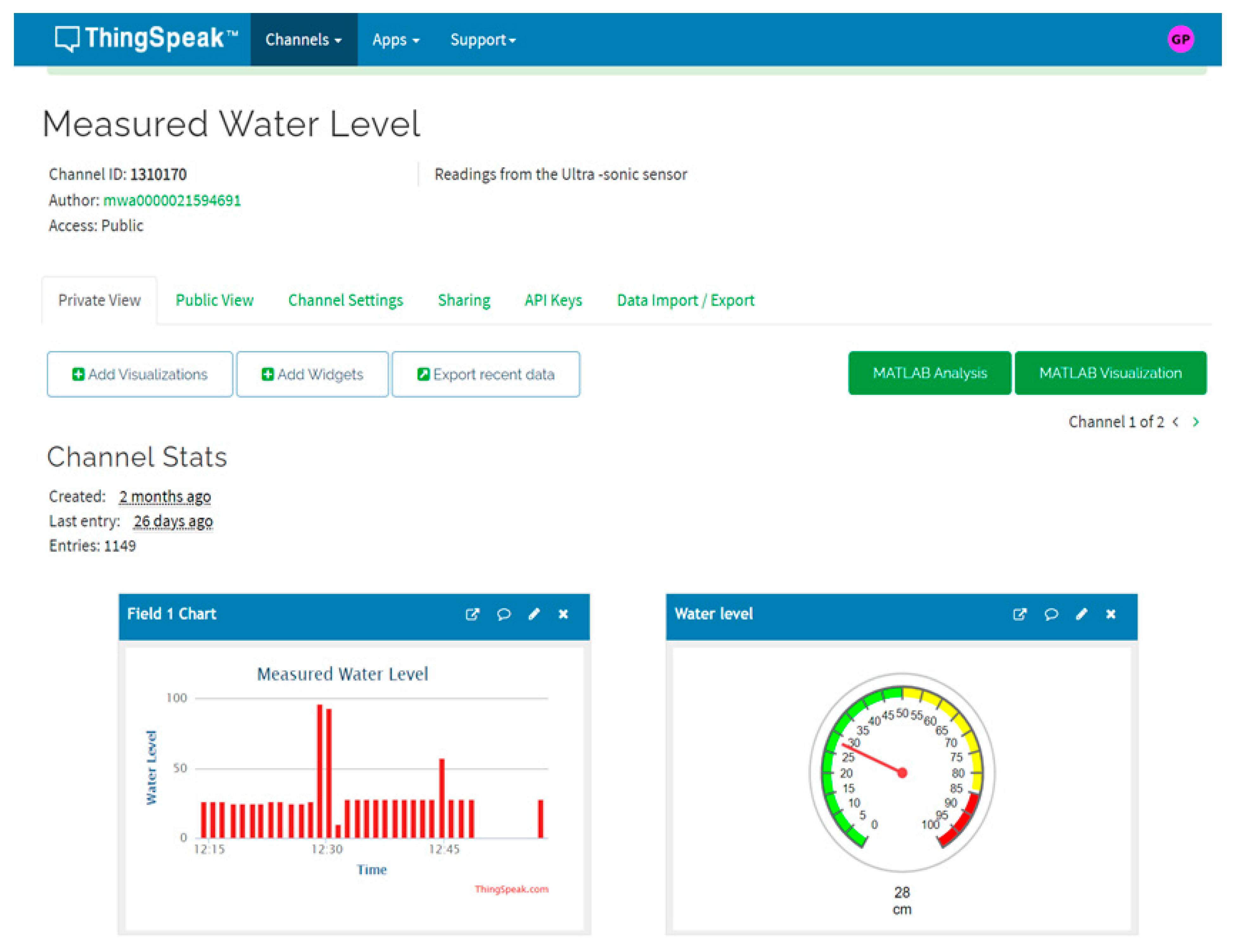

| Equipment | Specifications |
|---|---|
| Arduino microcontroller (ATMega328) | Input: Voltage: 5~12 V, current: 50 mA, Temp range: −40 °C to 80 °C |
| Ultrasonic Sensor (HC-SR04) | Input: Voltage: 3.3~5 V, Distance range: 2 cm–400 cm |
| GPRS/3G/4G module | Input power: Voltage: 5 V, Output: SMS texts |
| Solar panel | O/P: 6 V, Power: 3 W, Current: 300 mA |
| Battery lead acid | Voltage: 6 V, Cpacity: 12 Ah. |
| Step | Description |
|---|---|
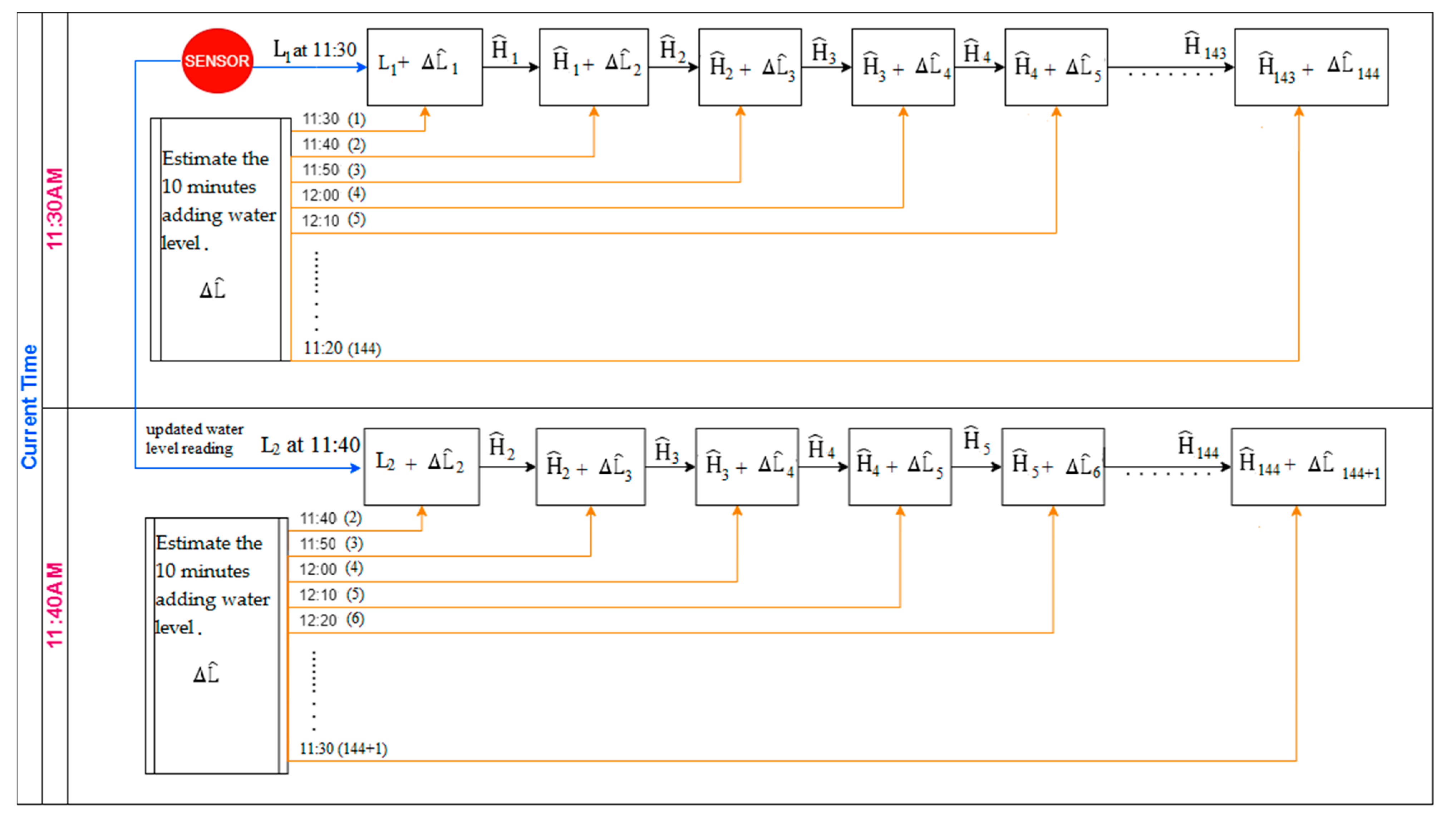
| 1 | Estimate the 10 min adding water level, , for one day ahead using the weather forecast data, the water drainage flow and maximum discharge of the drainage channel data. |
| 2 | Collect the real-time water level measurements at time . |
| 3 | Generate a flash flood (water level) prediction profile), , for one day ahead with 10 min resolution by ANN forecast model. The details of forecast model will be discussed in Section 4.1. |
| 4 | Collect and feed all updated data (water level measurements and forecast error) back to the forecast model to reforecast the water level. |
| Step | Description |
|---|---|
| 1 | Create an initialization population for the learning parameters in the ANN forecast model. |
| 2 | Calculate the mean value of the population. |
| 3 | Calculate the objective function (forecast error), as fitness term, for all and mean populations. To achieve convergence within minimum time, if the fitness value of the mean solution is better than the worst solution, the worst solution will be replaced by the mean solution. |
| 4 | Create a random solution vector in the population to determine the new searching step angle and movement using the golden ratio method. This process aims to move the searching towards the best solution area. |
| 5 | Compare the fitness value of the new random solution and the mean solution. This comparison aims to create a random searching and increase the ability of to search the whole solution of the fitness function and achieve the global solution. |
| 6 | The optimal solution for the ANN parameters will achieve the minimum fitness value. |
| Number of Hidden Layers | Overall MAPE | Mean of the Daily MAPE |
|---|---|---|
| 1 | 3.2% | 3.0% |
| 2 (Model A) | 1.4% | 1.3% |
| 3 | 4.5% | 4.4% |
| 4 | 5.2% | 5.1% |
| 5 | 6.7% | 6.6% |
| Number of Neurons | First Hidden Layer | |||||
|---|---|---|---|---|---|---|
| 10 | 20 | 30 | 40 | 50 | ||
| Second hidden layer | 10 | 1.3% | 1.5% | 2.2% | 2.9% | 3.3% |
| 20 | 1.2% | 1.1% | 2.3% | 2.2% | 3.1% | |
| 30 | 1.6% | 1.9% | 2.5% | 3.4% | 3.4% | |
| 40 | 2.1% | 1.6% | 2.9% | 3.7% | 4.2% | |
| 50 | 2.3% | 1.9% | 2.7% | 3.9% | 4.8% | |
| Description | the water level of previous time steps from 20 min until one hour | the previous day water level at the same time | the previous day data of daily rain intensity | the hourly temperature |
| Unit | cm | cm | mm/hour | °C |
| Correlated Variables | |
|---|---|
| 93.7% | |
| 51.8% | |
| 35.1% | |
| 27.7% |
| Daily MAPE | Overall RMSE | ||
|---|---|---|---|
| Traditional ANN | 1.0% | 0.8% | 17 cm |
| ANN optimized by GROM | 0.6% | 0.5% | 7 cm |
| ANN optimized by MPSO | 0.9% | 0.8% | 14 cm |
| ANN optimized by TLBO | 0.7% | 0.6% | 10 cm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alasali, F.; Tawalbeh, R.; Ghanem, Z.; Mohammad, F.; Alghazzawi, M. A Sustainable Early Warning System Using Rolling Forecasts Based on ANN and Golden Ratio Optimization Methods to Accurately Predict Real-Time Water Levels and Flash Flood. Sensors 2021, 21, 4598. https://doi.org/10.3390/s21134598
Alasali F, Tawalbeh R, Ghanem Z, Mohammad F, Alghazzawi M. A Sustainable Early Warning System Using Rolling Forecasts Based on ANN and Golden Ratio Optimization Methods to Accurately Predict Real-Time Water Levels and Flash Flood. Sensors. 2021; 21(13):4598. https://doi.org/10.3390/s21134598
Chicago/Turabian StyleAlasali, Feras, Rula Tawalbeh, Zahra Ghanem, Fatima Mohammad, and Mohammad Alghazzawi. 2021. "A Sustainable Early Warning System Using Rolling Forecasts Based on ANN and Golden Ratio Optimization Methods to Accurately Predict Real-Time Water Levels and Flash Flood" Sensors 21, no. 13: 4598. https://doi.org/10.3390/s21134598
APA StyleAlasali, F., Tawalbeh, R., Ghanem, Z., Mohammad, F., & Alghazzawi, M. (2021). A Sustainable Early Warning System Using Rolling Forecasts Based on ANN and Golden Ratio Optimization Methods to Accurately Predict Real-Time Water Levels and Flash Flood. Sensors, 21(13), 4598. https://doi.org/10.3390/s21134598







