1. Introduction
Graphs have been widely used to model entities (as vertices) and their relationships (as edges). Community detection and community search over massive networks have been broadly studied [
1,
2,
3,
4]. Given a graph
, community detection is used to cut vertices
V into meaningful subgraphs/communities, and the vertices are similar to each other in the same community and dissimilar in different communities. Different from the detection problem, the prerequisite of a community search requires an additional set of query vertices
q, and the aim is to search for a set of
cohesive subgraphs, each of which should contain all vertices of
q.
As far as the current situation is concerned, most community detection and search methods only focus on the topology of a network. Currently, most of the existing works on community detection and community search only consider the topological structure of a graph. However, with the proliferation of a network along with location such as Twitter, MeetUp, and Foursquare, interest on the topic of community detection/search over a geo-social network has increased [
5,
6,
7,
8,
9]. In such networks, users are usually associated with location data, which is important for making sense of detected communities (e.g., check-ins and hometown). A typical instance of a location-based social network is shown in
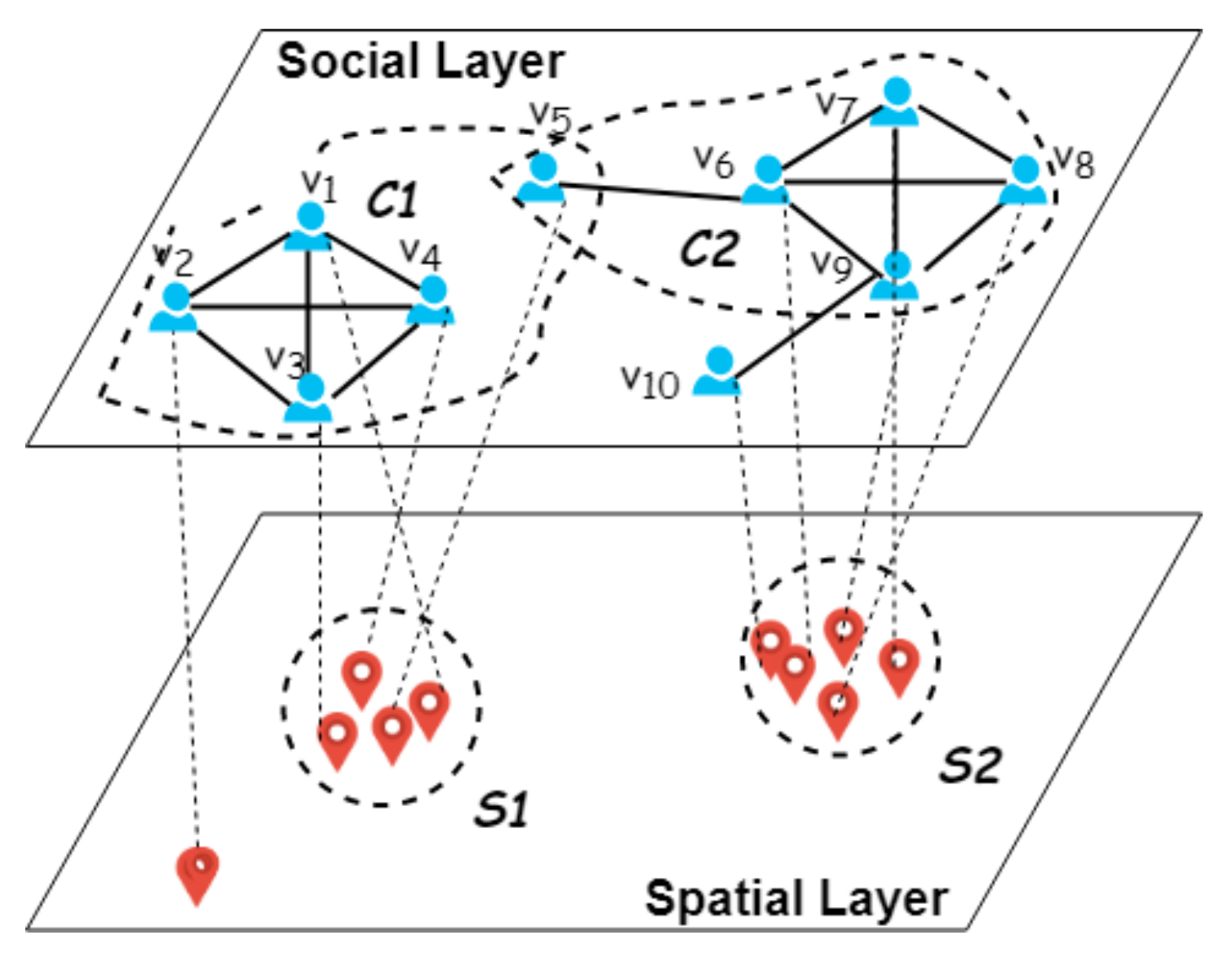
Figure 1. Two communities with strong social connections are
and
. Additionally, two communities with strong spatial relationships are
and
. We use irregular ellipses to represent users’ social relationship and dashed circles to denote users’ physical locations.
Existing Approaches and Limitations. Traditional community detection [
1] or subgraph mining approaches [
10] mainly focus on link analysis regardless of the spatial features. Some recent works [
6,
7,
8,
11] that are based on massive networks associated with physical location information has attracted more and more attention. A spatially oblivious approach to identifying communities is to compute and fuse each pair of vertices’ social distance with its Euclidean distance to define a new geo-social distance (e.g., see [
7,
8]). Alternatively, different from pairwise geo-social distance, some community search work [
6] takes spatial cohesiveness of a community into account, where a community search problem mainly constitutes a query vertices set
q and a spatial covering threshold. The final output of community search problem in [
6] is one community satisfying the following constraints: (1) this community should contain all vertices of
q; (2) it should satisfy specific structural constraints, and (3) all the community members should be in a
minimum covering circle with the smallest diameter. However, the problem of a spatial-aware community search requires the inclusion of all given query vertices of
q, which is inherently different from subgraph mining over location-based social networks.
Compute Geo-Social Groups (GSGs). Given a network with location data, in this paper, we aim to detect all qualified subgraphs, called
geo-social groups (GSGs), where each GSG not only is structurally cohesive but also has strong spatial closeness. This model is more reasonable due to its spatial cohesive definition (see
Figure 2, red circle is our detected group and the green one is from Yao et al. [
8]). Consider the example in
Figure 1: it is obvious that
is far from the other members in community
. On the contrary, community
, as an alternative option, may be more significant for location-based services (LBS), such as event recommendation, social marketing, and geo-social data analysis.
Formally speaking, given a network and parameters , where each vertex v carries location coordinates , a is a set C of vertices such that (1) (structurally cohesive) the subgraph of G induced by C is a structural graph cluster under and and (2) (spatially cohesive) vertices in C are all within a maximum minimum covering circle (MCC) for which the radius is no greater than a distance threshold .
Compute Top-
kGeo-Social Groups (T
kGSGs). Furthermore, we extend the GSG detection problem to significant top-
k geo-social group (T
kGSG) mining. Instead of discovering all location-based group pattern defined in the GSG detection problem, T
kGSG mining is returns
k GSGs
such that (1) all of the
k GSGs satisfy the social constraints; (2) any GSG
satisfying the social constraints joined in
results in a union density reduction (see
Section 5).
Applications. We now discuss the applications of geo-social group detection.
Event recommendation. Online location-based services, such as Meetup (
https://www.meetup.com/ accessed on 4 June 2021), Eventbrite (
https://www.eventbrite.com/ accessed on 4 June 2021) and Meetin (
https://www.meetin.org/ accessed on 4 June 2021), allow social network users to meet each other physically for entertainment or work purposes (e.g., business forum, dinner, and dating). Suppose that Meetup wishes to recommend different events to users. We can first detect potential groups of users that are spatially and socially close and then recommend events in their vicinity. Intuitively, people who have relatively tight social relations are more likely to participate in a nearby event as a group.
Geo-social data analysis. A common data analysis task is to study features about geographic regions. As discussed in [
12], these features are often related to the people located there and their interactions. Another important task is to classify users based on their social connections, tags, geographic locations, and time stamps. GSGD can be employed to provide concrete geo-social context, e.g., by detecting socially dense communities in a geographic area.
Challenges and Our Approaches. In this paper, we address the limitations of previous work as well as propose a novel GSG model that thinks over not only users’ social relationships but also physical distance. To the best of our knowledge, we are the first to formulate and investigate the problem of geo-social group detection and top-k GSGs mining over location-based social networks. There are several challenges to tackle.
First, the GSG detection problem intends to discover a user group within a circle with a radius not larger than . How to extract the smallest enclosing circle of a group efficiently is the first challenge.
Second, it is unclear how to effectively quantify the significance of a set of GSGs, considering that (1) each GSG has a set of vertices as well as an MCC with radius and center, and (2) GSGs may significantly overlap with each other.
Third, it is also challenging to efficiently compute the set of top-k GSGs, considering the large size of real networks as well as the wide variety of radius of MCC.
Contributions. Our contributions are summarized as follows:
We define a geo-social group model, named GSG, and an effective distance measure among users including both social and physical aspects.
We formulate the problem of a significant GSG discovery in large geo-social networks and propose effective techniques to generate the candidate set.
We propose effective pruning techniques to efficiently enumerate the set of all GSG in a network.
We extend the GSG detection to the significant top-k geo-social group (TkGSG) discovery problem. Instead of extracting all qualified GSGs in a network, TkGSG discovers k groups to guarantee the diversity of detection processing while achieving an approximation ratio of .
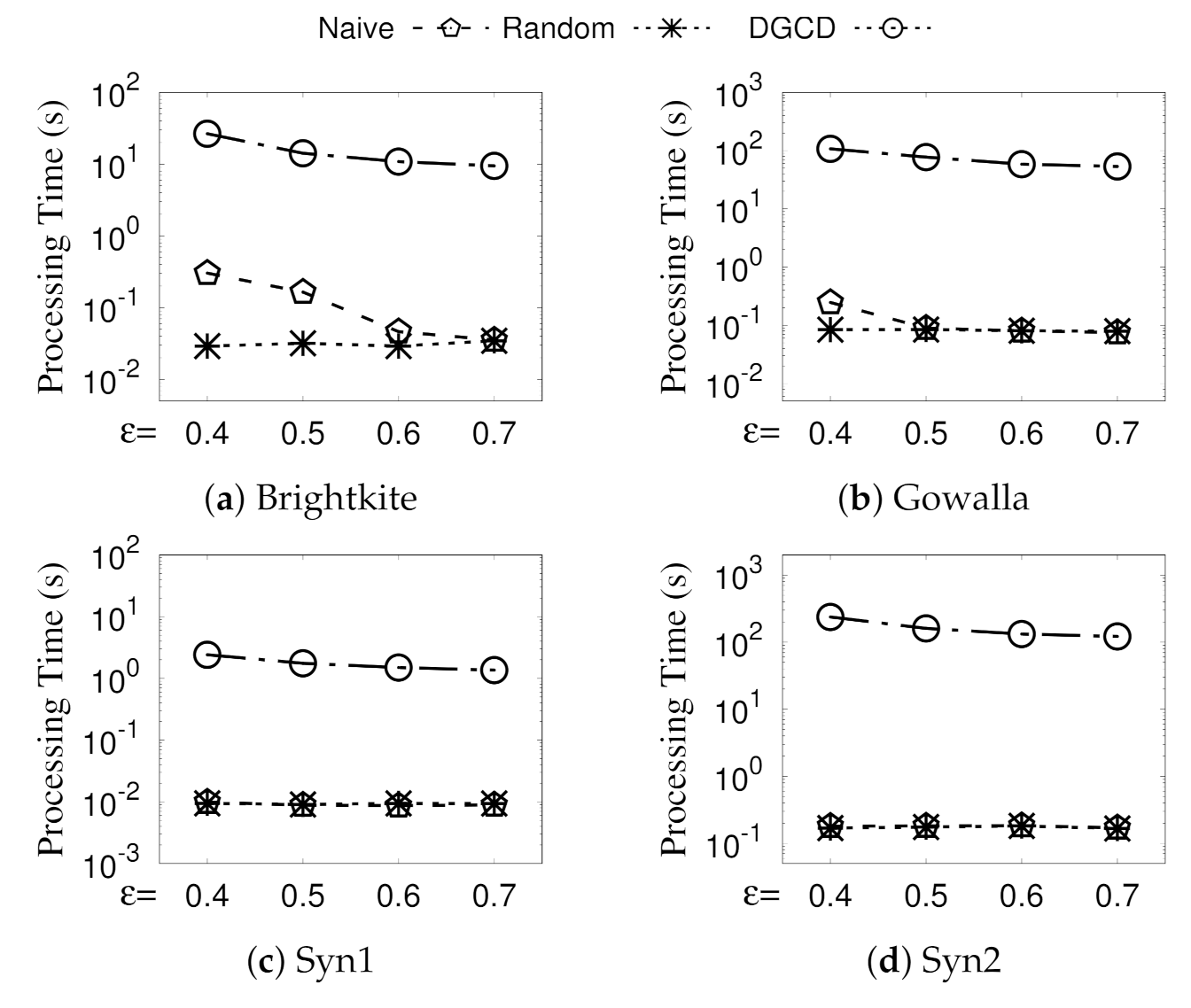
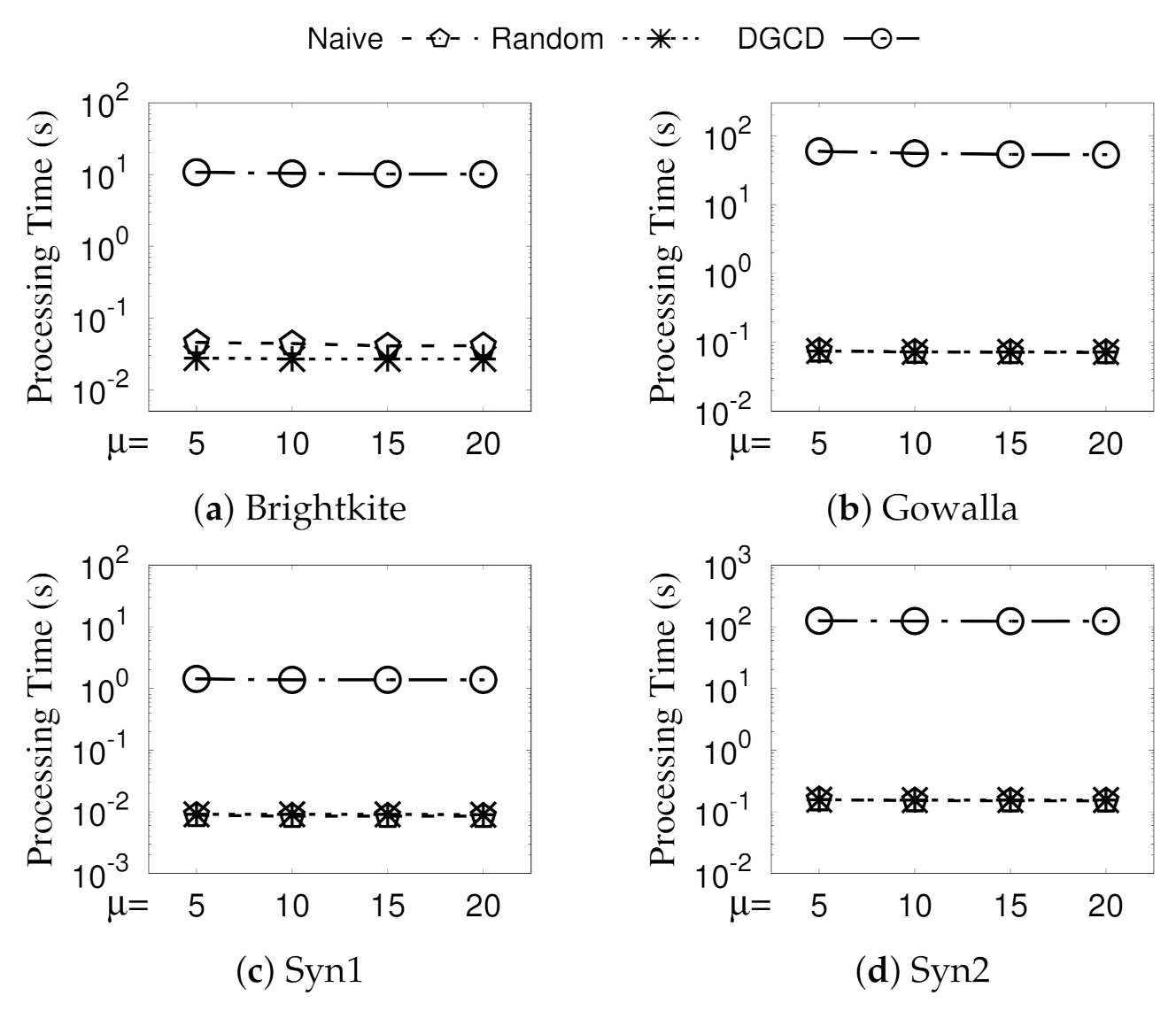
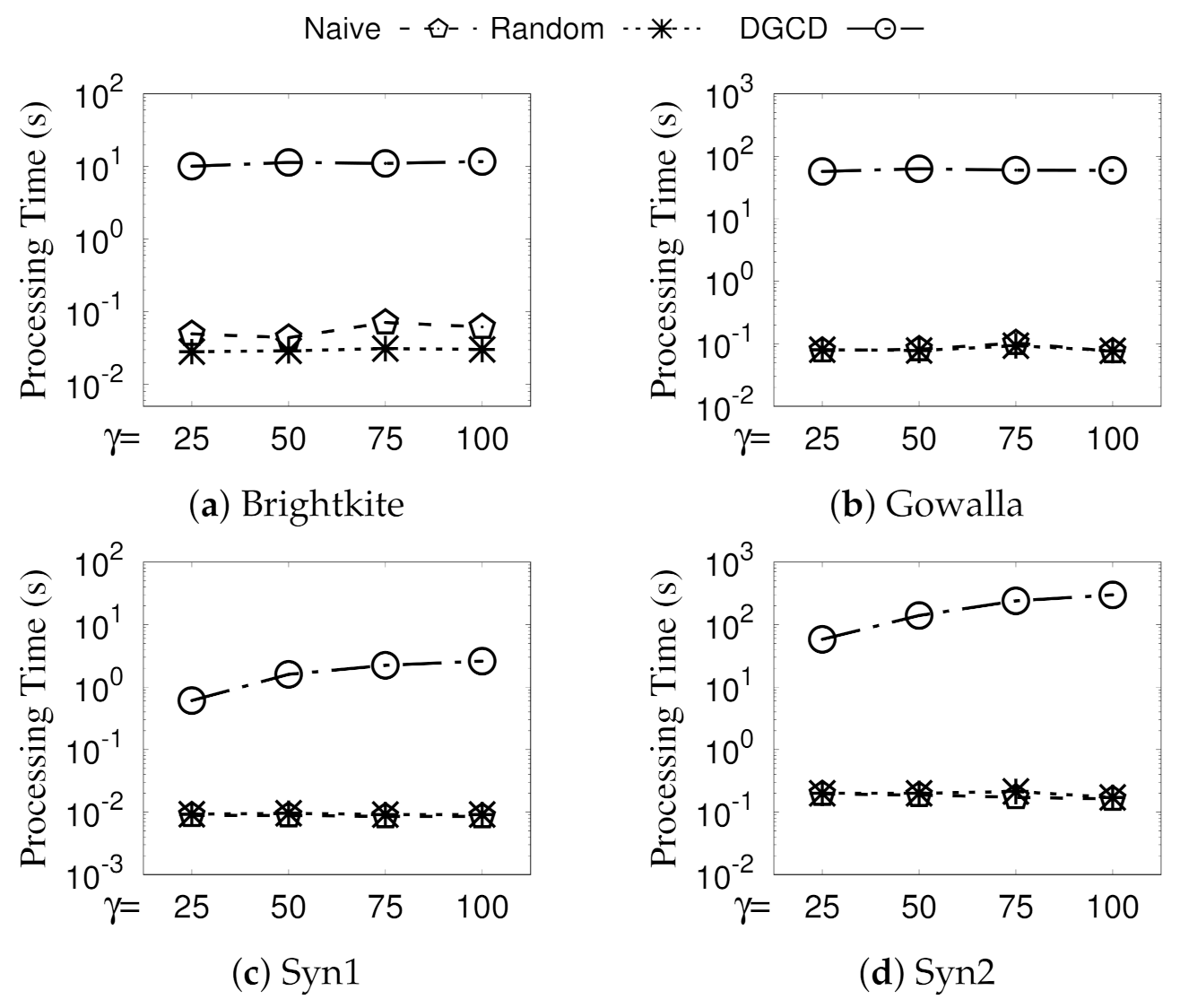
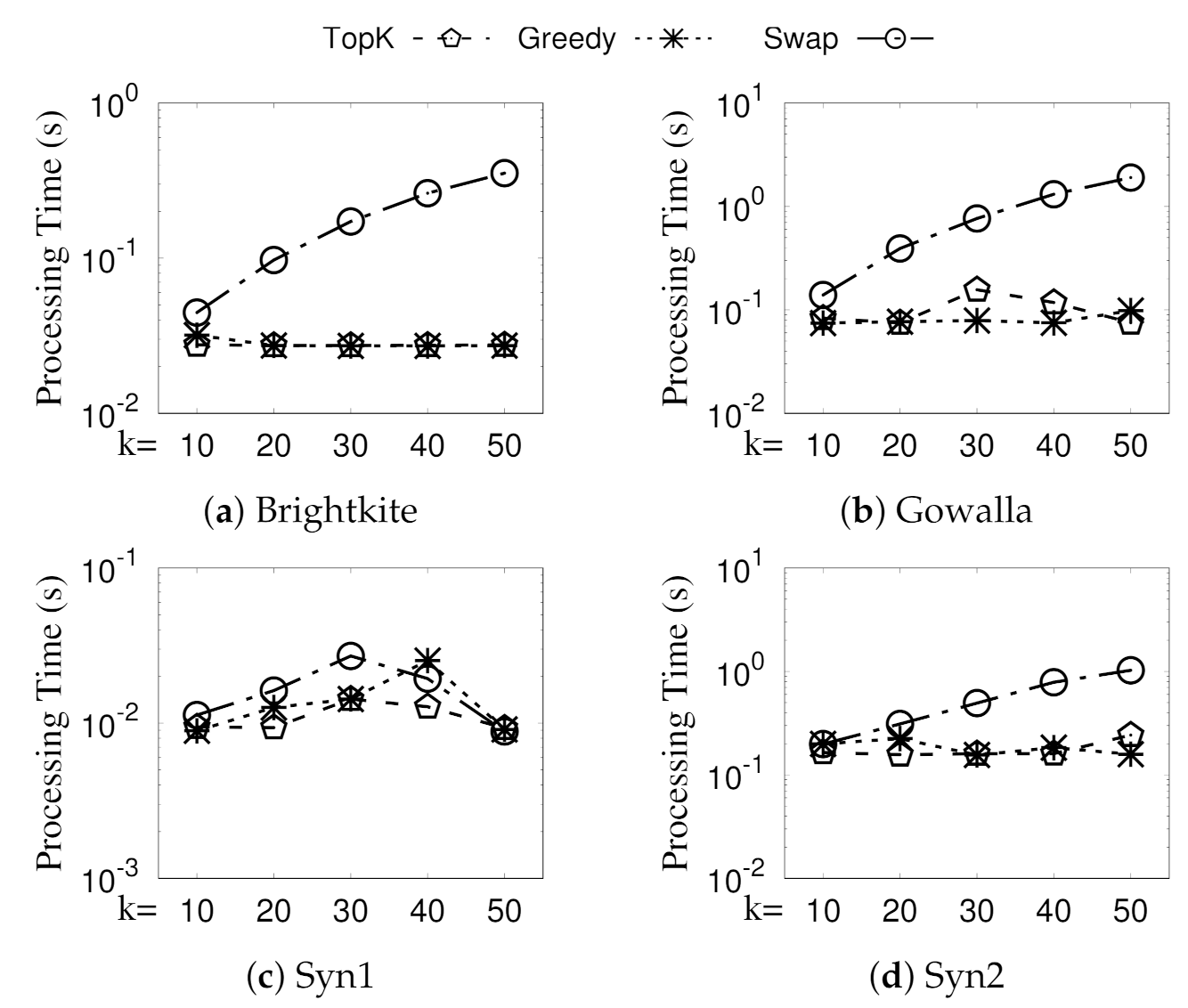
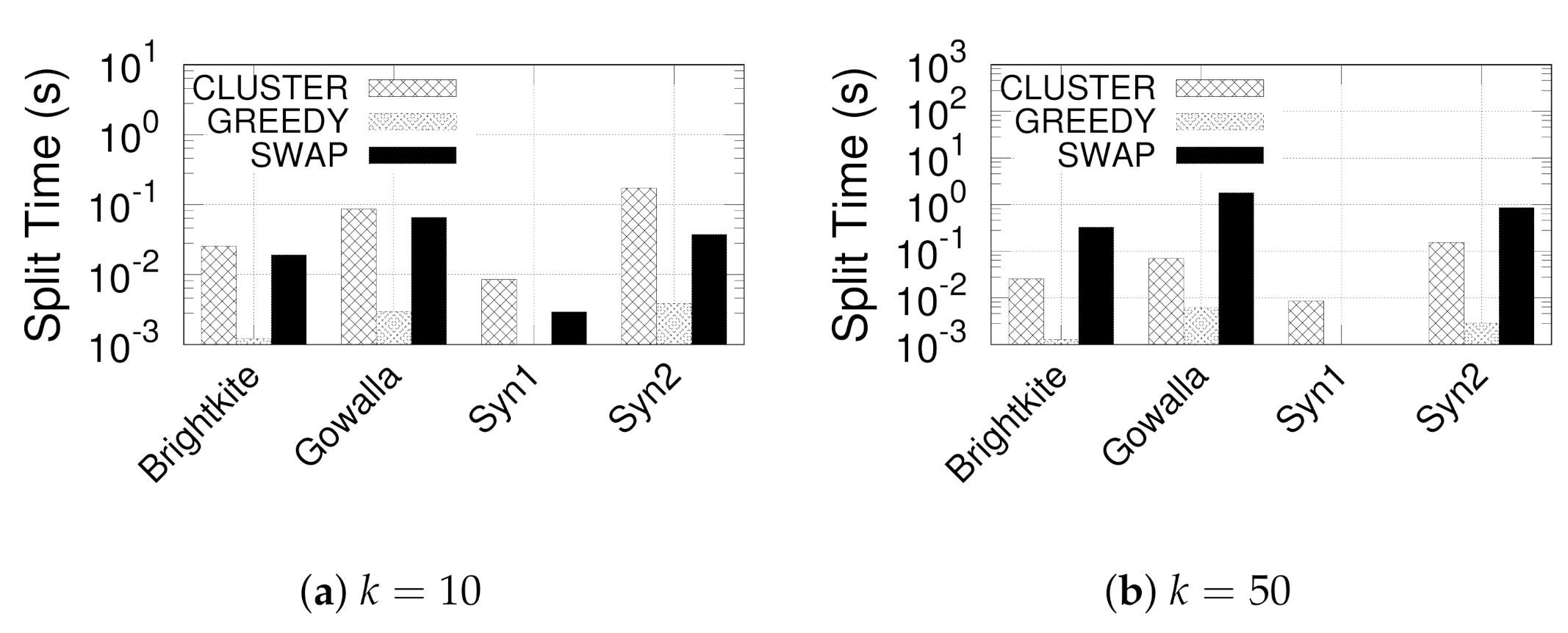
We conduct extensive empirical studies on large real and synthetic location-based social networks in
Section 6. The results show that (i) the formulated community model identifies a set of GSG with both social and spatial cohesiveness guarantee and (ii) our enumerating techniques can can effectively mining all qualified GSGs. Additionally, (iii) our greedy and streaming-like algorithm can achieve high-quality solutions and short run times. Note that the contribution of the significant top-
k geo-social group (T
kGSG) discovery listed above is a new extension compared with our conference version in [
13].
Organization. The remainder of this paper is structured as follows.
Section 2 presents a brief overview of related work;
Section 3 defines the geo-social group model and community detection problem. A novel three-step paradigm and efficient GSGD approaches are proposed in
Section 4. In
Section 5, we present two effective approaches to process the T
kGSG mining problem.
Section 6 reports the experimental results, and
Section 7 provides the conclusion and possible future directions.
3. Problem Definition
In this paper, we concentrate on an unweighted, undirected, and location-based network , where V is the vertex set and E is the set of edges. denotes the number of vertices in G by n, and denotes the number of edges in G by m. Let represent an edge between two vertices u and v; u (resp. v) is considered a neighbor of v (resp. u). Each vertex v in G has a location , where and are its 2D coordinates along the x and y axes. In the rest, for ease of presentation, we simply refer to an unweighted, undirected, and location-based network as a network.
Due to structural graph clustering being adopted for community detection, we refer to the
structural neighborhood (i.e.,
closed neighborhood) of a vertex
u, denoted by
(i.e.,
) as the neighbors of
u. Note that the
open neighborhood [
17] of
u is
. The
degree of vertex
u, denoted by
, is the cardinality of
(i.e.,
). Taking
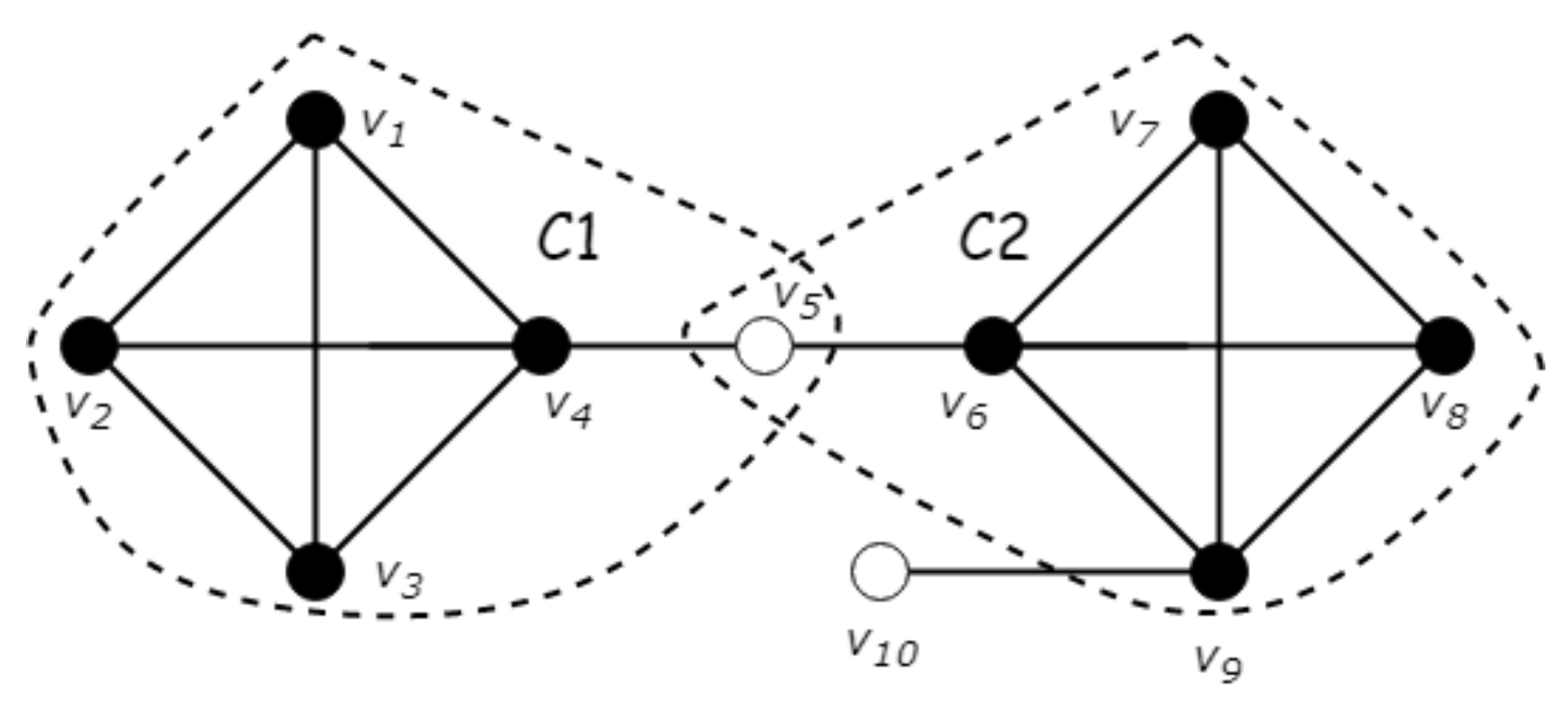
Figure 3 as an example, the
structural neighborhood of vertex
is
, its degree is
, and its
open neighborhood is
. Considering a vertex subset
of a graph
, an induced subgraph of
G by
C, denoted by
, consists of all vertices in
C and all edges for which the two endpoints should be in
C as well (i.e.,
).
Table 1 is a summary of the mathematical notations used throughout this paper.
3.1. Geo-Social Group (GSG)
Considering a location-based social network , in this paper, our goal is to detect all qualified geo-social groups, termed GSGs. Intuitively, a GSG can be regarded as a vertex subset C of V and subgraph has a strong cohesiveness value, showing that the group members are closely connected in social and spatial dimensions.
Structure cohesiveness. As discussed in the related works in
Section 2, several structure cohesiveness measures have been proposed. Thereinto, structural graph clustering [
30] can effectively discover hidden structures in a graph. Therefore, we continue to use it in our community structure.
In 2007, Xu et.al. [
23] first proposed structural graph clustering, in which the clustering criteria are the neighborhoods of the vertices. They developed the concept of
structural similarity between vertices
u and
v, denoted by
, as the number of their common neighbors normalized by the geometric mean of their structural neighborhood sizes. Intuitively, for any two connected vertices, the more common neighbors, the greater the
structural similarity value. The range of
structural similarity value is in
; that is,
. Given a similarity threshold
and the minimum number of neighborhoods
, if
, vertices
u and
v can be considered
structurally similar to each other. When a vertex
u has no less than
neighbors that are structurally similar to it, it is a
core vertex; on the contrary, it is a
non-core vertex.
If a sequence of vertices (parameter ) in G satisfies the following conditions: (1) and ; (2) are core vertices; and (3) for each , we say vertex v is structurally reachable from vertex u.
A structurally connected cluster C is a subset of V with no less than two vertices (i.e., ) such that we have the following : (i) For any two vertices , there exists a vertex such that both vertices and are structurally reachable from u; (ii) Once a core vertex , all vertices that are structurally reachable from u are also part of C.
Example 1. Regarding Figure 3, and ; thus, . Similarly, and . Given and , and . Thus, and are core vertices since . Similarly, it is easy to know that and are non-core vertices. Finally, we obtain two clusters from the graph as shown in Figure 3, and . Spatial cohesiveness. In order to ensure that there is an accessible physical distance among members of the discovered community, a maximum
minimum covering circle (MCC) is adopted in our community criterion that vertices in a structurally connected
cluster are required within an MCC in which the radius is no greater than the given user-defined distance threshold
. Note that the notion of MCC has been broadly adopted to achieve strong spatial closeness for a group of members [
6,
31,
32] in a two-dimensional space. It is defined as follows.
Definition 1 (
Minimum Covering Circle [
6])
. Given a set of vertices C, the Minimum Covering Circle of C is a spatial circle that can cover all of the vertices in C with the smallest diameter, denoted by . In this paper, using the structural graph clusters and MCC spatial compactness measure cooperatively, we formally define our GSG community model as follows.
Definition 2. Given a location-based social network G and three parameters , and , a GSG is an induced subgraphin G that satisfies the following constraints.
Connectivity:is connected;
Structure cohesiveness:is a induced connected subgraph from structural graph clustering, w.r.t. ϵ and μ;
Spatial cohesiveness: The MCC of vertices inhas radius no larger than γ.
Example 2. Given and , we continue to consider Figure 1. From social layer, two existing groups in social layer are = {,,,,} and = {,,,,}. From spatial layer, there are two other communities = {,,,} and = {}. Intuitively, is obviously far away from other users in so a new community = is more meaningful when considering member positions in actual location based service (LBS). Furthermore, even belongs to ; however, it is an outlier for , new geo-spatial group can be . 3.2. Problem Statement
Along with the aforementioned GSG definitions, we begin to formally define the problem of Geo-Social Group Detection (GSGD) in a network in the following statement:
Problem Statement. Given a network and three parameters , and , the problem of GSG detection is to disclose a set of GSG in G.
4. GSG Detection Algorithm
In this section, we first present our new paradigm in
Section 4.1, based on which we then develop our GSGD algorithm that effectively and correctly identifies all GSGs in a massive graph.
4.1. Three-Step Paradigm
Our GSG detection algorithm follows a new three-step paradigm: (i) clustering core vertices, (ii) clustering non-core vertices, and (iii) computing MCC and discarding invalid clusters.
Lemma 1 ([
30]).
Each core vertex in the graph must belong to a unique cluster in a structural graph clustering problem. Lemma 2 ([
30]).
Given the clusters of core vertices in graph G, non-core vertices in G can be directly clustered by assigning each non-core vertex v to any cluster such that there exists a core vertex and . Based on Lemmas 1 and 2, our paradigm first computes the clusters of all core vertices by iterating each vertex in graph and by constructing a connected component with only core vertices, and then, the noncore vertices are added to clusters according to Lemma 2.
The minimum covering circle problem (also known as the smallest enclosing circle problem) is a classic computation geometry problem, and most of the geometric approaches look for points that lie on the boundary of the minimum circle and are based on the following lemmas.
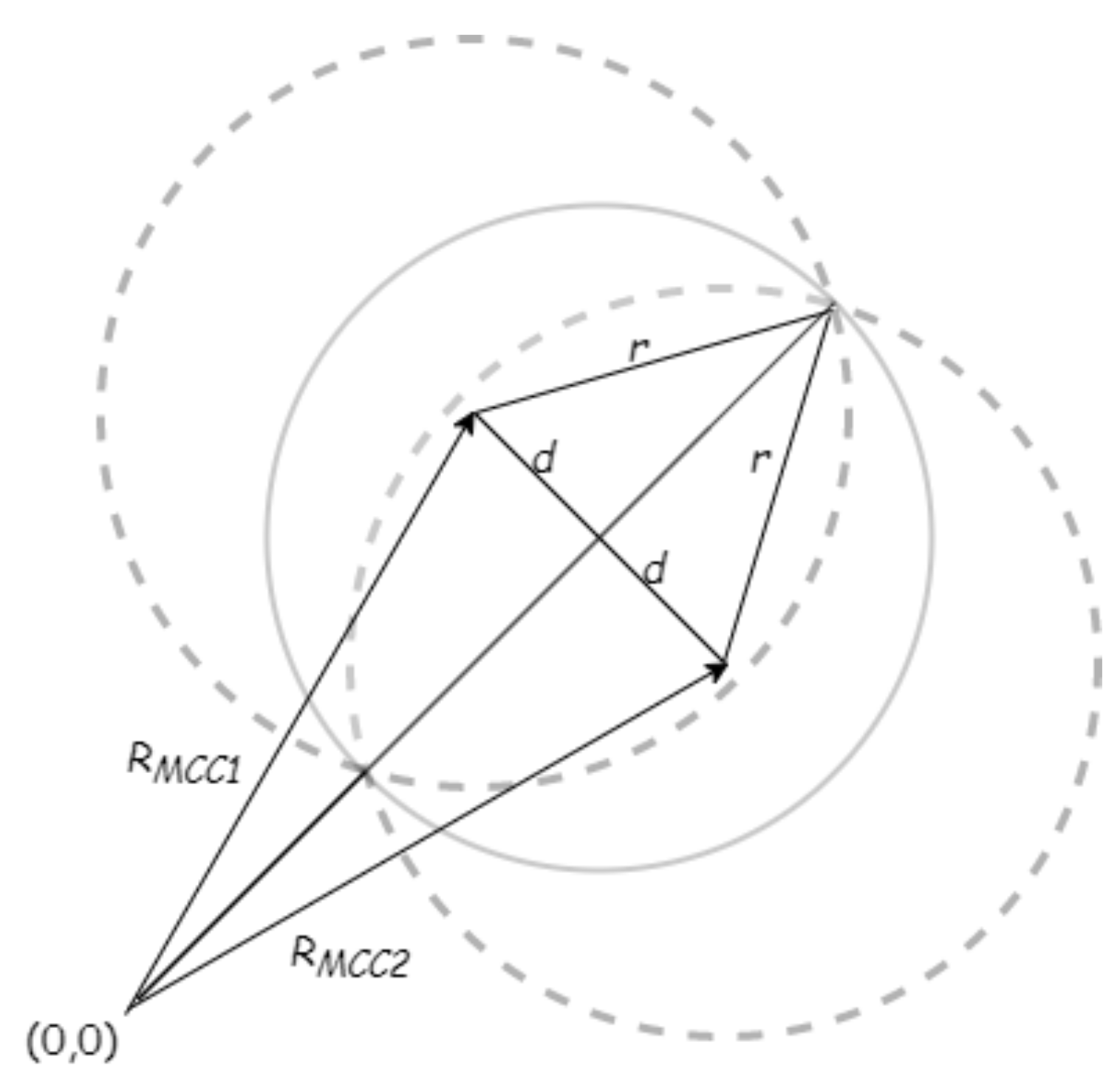
Theorem 1. Given a set of points C, the minimum covering circle (containing all the nodes) is unique.
Proof of Theorem 1. We prove the theorem by contradiction. Assume that
C is a set of points in the 2D plane and that
and
are the centers of two minimum covering circles (MCCs) of set
C. Then, let
r be their shared radius and let
be the distance between their centers. Due to
C being a subset of both circles, it must be a subset of their intersection. However, it is easy to see that their intersection is contained within the circles with center
and radius
, as shown in
Figure 4. Since
r is minimal, as a result,
must be equal to
r; that means
, so the circles are identical. We reach a contradiction, and the theorem holds. □
Lemma 3 ([
32]).
Given a vertex set S (), the minimum covering circle (MCC) of S can be determined by up to three vertices in S, which are on the border of the circle. When MCC is determined by only two vertices, the line segment connecting these two vertices must be a diameter of the MCC circle; otherwise, the triangle consisting of three determined vertices is not obtuse. Following Lemma 3, it is easy to understand that at least two or three vertices lie on the boundary of the MCC circle of the output GSG.
4.2. Our GSGD Approach
Based on the paradigm proposed in
Section 4.1, in this section, we present our GSGD approach to geo-social group detection. The pseudocode of our GSGD is shown in Algorithm 1. We initially iterate each pair of adjacent vertices and calculate the structural similarity between them (Line 1–2). In Algorithm 1, we use a disjoint-set data structure [
33] to incrementally maintain the connected components when clustering core vertices. The data structure maintains a collection
of disjoint dynamic subsets and has two fundamental operations: find-subset and union; find-subset determines which subset a particular element is in, and union joins two subsets into a single subset. Line 3 initializes a disjoint-set data structure for each vertex in
G, and then adding an edge
into connected component is achieved by union(
) (see procedure ClusterCore) (Line 18–19);. Thus,
two vertices u and v are in the same connected component if and only if they are in the same subset in the data structure (i.e., find-subset(
u) = find-subset(
v)). Then, we iteratively scan each vertex
u in
G and determine if
u is a core vertex (Line 3); if so, we unify its neighbors, which are core vertices as well (Line 18–19). The set
of clusters of core vertices can be formed from the abovementioned disjoint-set data structure (Line 7). After that, clustering of non-core vertices is performed by
(Line 8). Lastly, we check each cluster
C in the set
and compute the MCC
of cluster
C (Line 10–11) when
,
C is marked as a qualified GSG (Line 9).
Computing MCC. The pseudocode for computing the MCC for each cluster derived from Algorithm 1 is given in Algorithms 2 and 3. A naive algorithm (see Algorithm 2) with three nested for-loops take polynomial time
. A more efficient randomized incremental method [
34] (see Algorithm 3) is adopted in our paper and runs at an expected linear time
.
Definition 3. (MCC Center). Center is the position that is at the minimum distance from all vertices on or within the circle.
Definition 4. (MCC Radius). Radius r is the radius of the minimum covering circle of a set of points.
| Algorithm 1: GSGD |
![Sensors 21 04551 i001]() |
Example 3. Considering our example in Figure 1 given parameters and . We first determine core nodes by calculating the structural similarity of each pair of connected nodes, e.g., , , and . After that, we iterate each node in the graph and calculate and . Thus, and are two unique core vertices since . In Algorithm 1, non-core vertices (e.g., ) are directly assigned to corresponding core clusters by Lemma 2; that is, vertices belonging to cluster and are in cluster . Next, we traverse clusters and and compute MCC of current cluster through Algorithm 3. We know that is eliminated from and that does not belong to as well. Finally, two valid GSGs are and . | Algorithm 2: MCCNaive(C) |
![Sensors 21 04551 i002]() |
4.3. Optimization Techniques
In this section, we propose optimization techniques to improve the efficiency of GSGD.
(1) Efficiently Compute Structural Similarity between Two Vertices. GSGD (i.e., Algorithm 1) computes when exploring u and when exploring v. These two structurally similar calculations significantly increase computational burden. Therefore, we adopt the cross link technique, which links edge with edge ; then, the structural similarity between u and v only needs to be calculated once. Overall, the size of structural similarity calculations in a graph is expected to be reduced by half. Concerning time complexity, we assume that the adjacent list of each vertex u is ordered by vertex IDs; then, we can utilize a binary search (with time complexity of ) on to search edge when is processed. In total, the time complexity of this cross link is .
(2) Spatial-Structural Neighborhood Pruning Rules. Due to spatial cohesiveness constraints, we consider the physical distance between vertices when computing clustering in Phase-I. Thus, rather than focusing on pure structural neighborhood, we redefine the neighborhood of a vertex u in G by considering the physical distance between u and , as follows.
Definition 5. (Spatial-Structural Neighborhood). The spatial-structural neighborhood of a vertex u, denoted by , is defined as a set of vertices in the structural neighborhood of u, and the distance between them and vertex u is not greater than γ; that is, , where is the spatial distance between u and v.
Intuitively, two vertices u and v cannot be in the same geo-social group if the distance between them is already larger than the spatial threshold according to the definition of GSG.
| Algorithm 3: MCCRandom(C) |
![Sensors 21 04551 i003]() |
5. Top-k Densest GSGs
In this section, we present our basic definitions and formulate the top-k densest GSG search problem. Instead of finding all valid geo-social group defined in the GSG detection, the top-k densest GSGs search returns a set of k GSGs .
Density of a GSG. Intuitively, the larger the size of the GSG and the smaller the radius r of MCC, the more important the GSG. Thus, we define a density of a GSG as . For example, consider Example 3. The GSG has five vertices, and the radius is 20; thus, . Formally, we define the density as follows.
Definition 6. (Density). Given a geo-social group GSG C and its MCC radius r, the density of such a GSG C is defined as .
Definition 7. (Densest GSG). Given a geo-social graph , the densest GSG is a GSG that maximizes the density function, i.e., .
Diversified Density of a Set of GSGs. Given a set
of GSGs, a naive approach to quantifying the score of
is to sum up
for each GSG
C in
. However, this may significantly overestimate the score of
in view of the overlaps that may exist among the GSG. Based on the observations discussed in [
30], the resulting clusters may overlap.
In view of the above, we first define the diversified union density of a set of GSG, denoted as follows.
Definition 8. (Diversified Union Density). The diversified union density of a set of GSGs is defined as .
The rationality of our definition is that, although a vertex u may be covered by many GSG of , we only discount its weight based on the radius of the smallest GSG that covers u. Note that the union discussed in this paper uses the set-based semantics; that is, each element is included into the union result at most once.
5.1. Problem Statement
Armed with the above definitions, we are ready to define our problem of top-k GSG selection as follows.
Problem Statement. Given a geo-social network and parameters , , and k, the problem of the top-k densest GSG selection is to uncover a set of k GSGs for which the diversified union density is the largest among all sets of k GSGs in G.
Hardness Analysis. Assuming that the set of all GSGs in
G has been generated and stored in
, it it still a hard problem to extract the set of top-
k GSGs from
. Intuitively, given
, our problem becomes computing the set of
k GSGs from
that covers the most vertices with the smallest MCC radius, which is an instance of the NP-hard
k-set-coverage problem [
35]. As a result, to exactly compute the set of top-
k GSGs from
, we may need to enumerate all sets of
k GSGs of
, to compute their density, and to finally return the set of
k GSGs with the maximum union density. Moreover, it is worth noting that
can be of exponential size with respect to the size of
G in the worst case.
5.2. A Greedy Approach
According to the hardness of computing the optimal GSG exactly or approximately, we propose a two-phase approach to computing top-k GSGs by (Phase-I) first exhaustively generating the set of all GSGs and (Phase-II) by then selecting the top-k ones from .
Phase-I: Generate All GSGs . As we have demonstrated how to enumerate a qualified MCC under the condition that the radius of GSG’s MCC should be less than a threshold in
Section 4, we can release the above radius condition and regard each cluster as a valid GSG with an MCC which covers all vertices in that GSG.
Based on this revision, the pseudocode generating all GSGs in a graph is shown in Algorithm 4. We compute the structural similarities for all pairs of adjacent vertices (Line 1). In Lines 2–6, we continue to cluster core vertices, and then, Line 7 clusters non-core vertices. After that, MCC can be calculated using Algorithm 3 for each cluster in the graph. Instead of dropping all clusters for which the MCC radius is less than the defined threshold, we keep all generated clusters and its MCC radius in order to select the following top-k GSGs in Phase-II.
Phase-II: Greedily Select Top-kGSGs. As discussed in
Section 5, given
, it is still a hard problem to select the top-
k GSGs from
. The good news is that our density of a set of GSGs (see Definition 8) is monotone and submodular, as proven in the lemma below.
Lemma 4. For any two sets of GSGs, and , such that , we have (Monotone). Moreover, for any GSG , we have (Submodular).
Proof of Lemma 4. Due to only discounting the weight of vertex u based on the size of the smallest GSG that covers u, we use to denote the weight of u in , which is . Note that (1) if and (2) for any .
As every vertex covered by
is also covered by
, we have
as illustrated in
Figure 5, where each ellipse represents the set of vertices that are covered by the GSG or the set of GSGs. Moreover, for each
, we have
since
. Thus,
holds.
| Algorithm 4: Greedy |
![Sensors 21 04551 i004]() |
Now, we prove the submodularity of
. According to the definition, we have
. Note that (1)
for each
and (2) we can partition
C into three parts,
,
, and
, as shown in
Figure 5. Thus, we have
. Now, we compare the three components of
with that of
one by one. First, for every
, we have
, since
. Second, for every
, we consider
in two cases. If
, we have
; otherwise,
, and we have
and
, since
. As a result, we have
. □
Following Lemma 4, a greedy algorithm can be designed to compute a result with an approximation ratio of , as follows. Given an initially empty , we iteratively add into the GSG C that together with result in the largest total density; that is, . The pseudocode of the greedy selection is shown at Lines 14–16 of Algorithm 4. Thus, Algorithm 4 reports the exact top-k GSG when , and the general approximation ratio of Algorithm 4 is proven by the theorem below.
Theorem 2. Given a network G and parameters , let be the optimal top-k GSGs and be the set of k GSGs obtained by Algorithm 4. Then, we have ,
Proof of Theorem 2. This theorem directly follows from Lemma 4 and the results in [
36]. □
5.3. A Swap-Based Approach
Greedy needs to store the set
of all GSGs, which may be, in the worst case, too large to be stored in the main memory. If this is the case, then we can switch our algorithm to a stream-like processing in a similar fashion to the existing works on diversified top-
k search (e.g., [
27]). That is, we maintain a set
of at most
k GSGs during the execution of the algorithm. After obtaining a new GSG
C (e.g., at Line 14 of Algorithm 4), rather than storing it in
, we directly update
by
C. Specifically, if
contains less than
k GSGs, then we insert
C into
. Otherwise, we try to replace one of the GSG in
with
C, as follows. Let
, and let
. Then, we insert
C into
and remove
from
if
, and keep
unchanged otherwise. We denote this algorithm by Swap as shown in Algorithm 5.
| Algorithm 5: Swap |
![Sensors 21 04551 i005]() |
5.4. Optimization Techniques
Efficiently Select Top-kGSGs. In Algorithm 4, given a subset of , we need to select the next GSG C such that is maximized. One naive approach is computing for every GSG , and then selecting the best one. However, this is time-consuming if becomes large. Thus, we develop an upper bound-based pruning as follows.
Note that ; thus, can be regarded as an upper bound of . We first sort all GSGs of in decreasing order with respect to their individual scores, which is also the decreasing order with respect to their upper bounds. Thus, we process GSGs in in decreasing order with respect to upper bounds and terminate them once the upper bound becomes not larger than , where C is the currently best selected one. As a result, we do not need to process the entire list of GSGs in each time.