The 2019–2020 Rise in Lake Victoria Monitored from Space: Exploiting the State-of-the-Art GRACE-FO and the Newly Released ERA-5 Reanalysis Products
Abstract
:1. Introduction
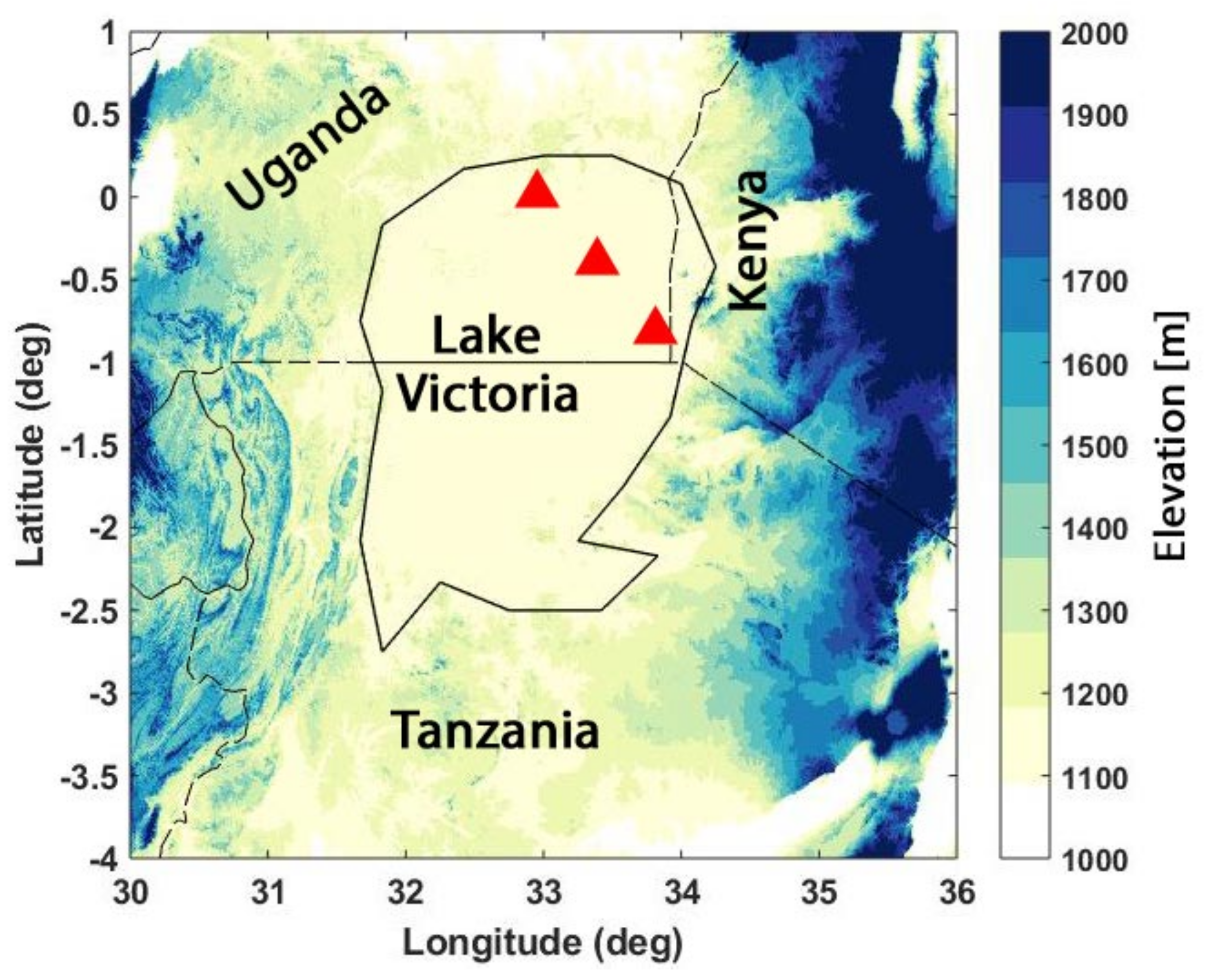
2. Lake Victoria
3. Materials and Methods
3.1. Model and Data
3.1.1. Land Surface Model
3.1.2. Satellite Remote Sensing
GRACE-FO TWS
Satellite Radar Altimetry
3.1.3. Precipitation and Climate Variability Data
3.2. Methods
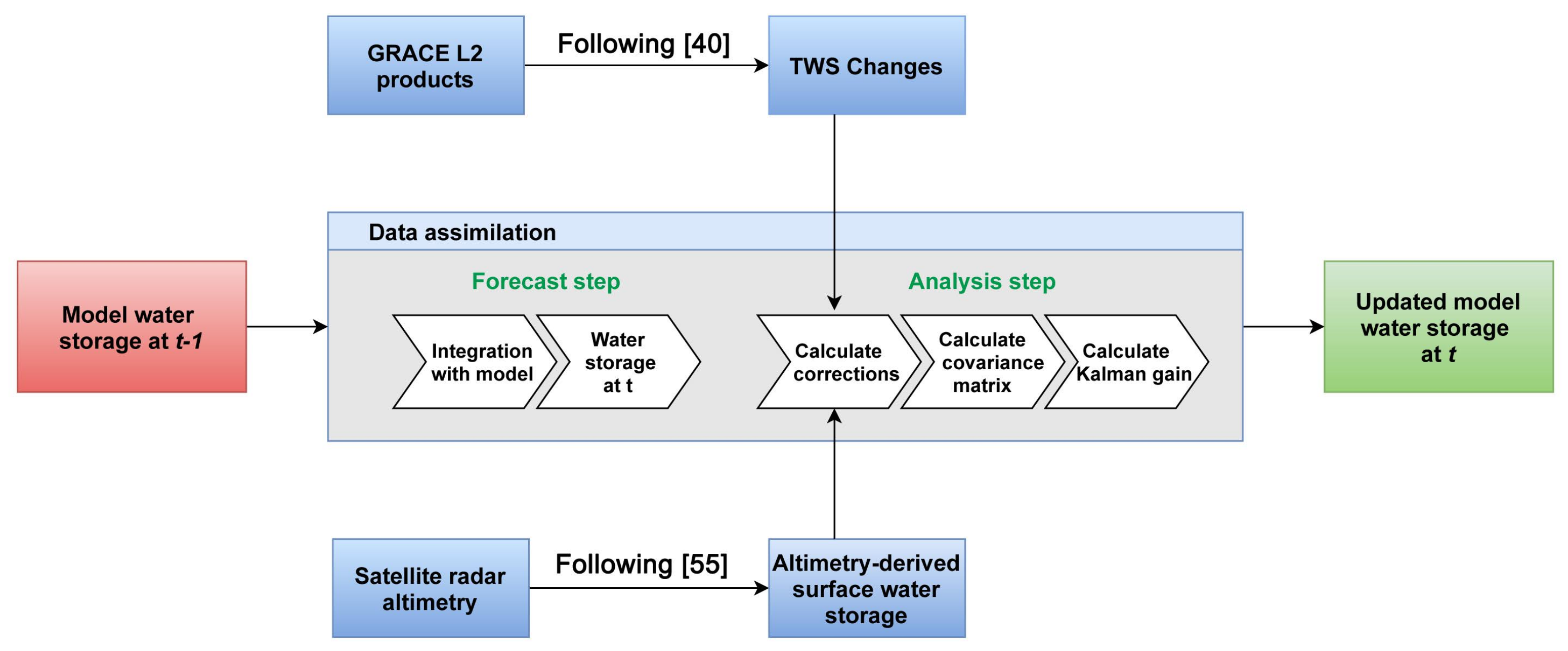
3.2.1. Data Assimilation
3.2.2. Experimental Design
3.2.3. Correlation Analysis
4. Results
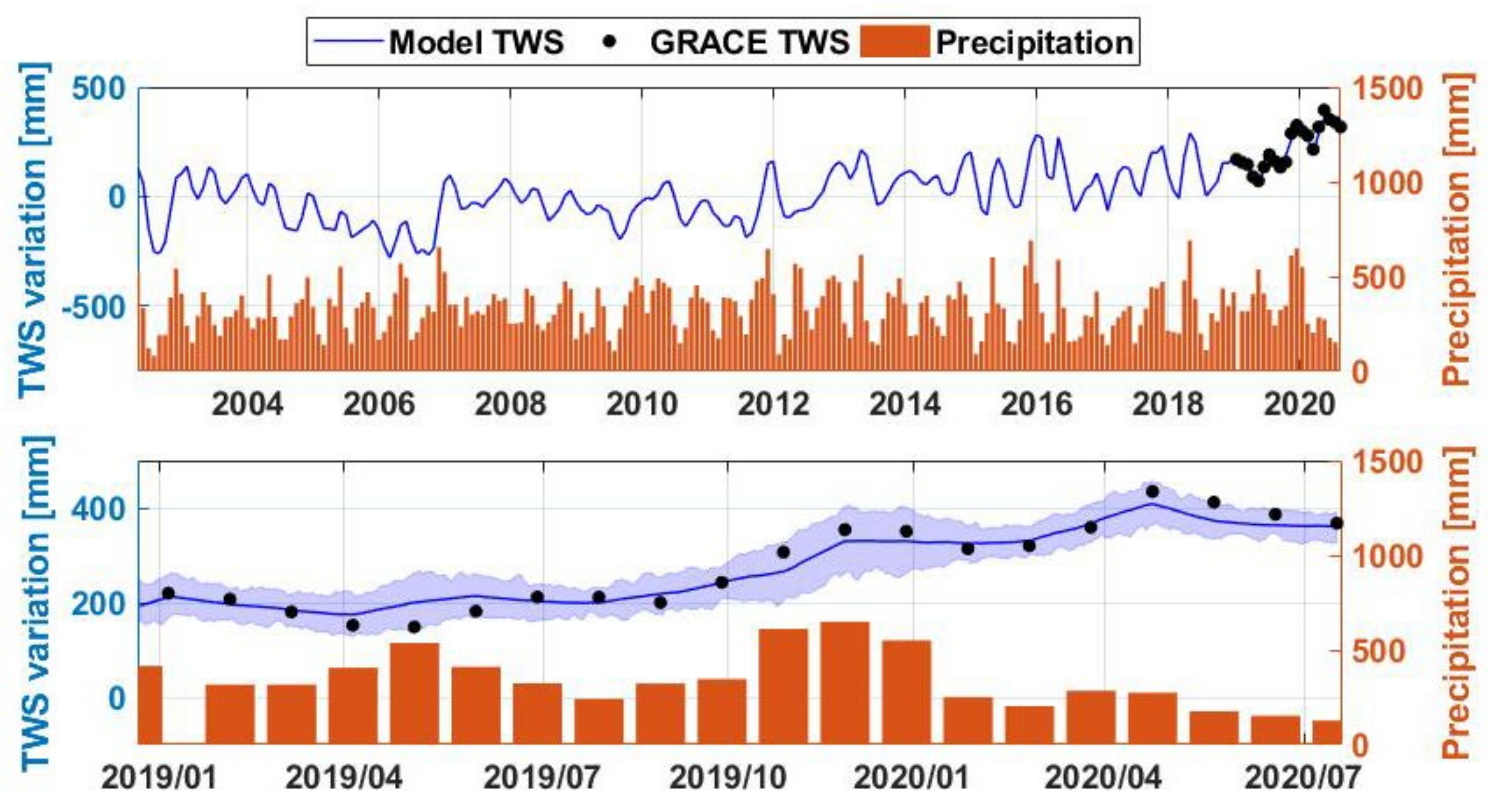
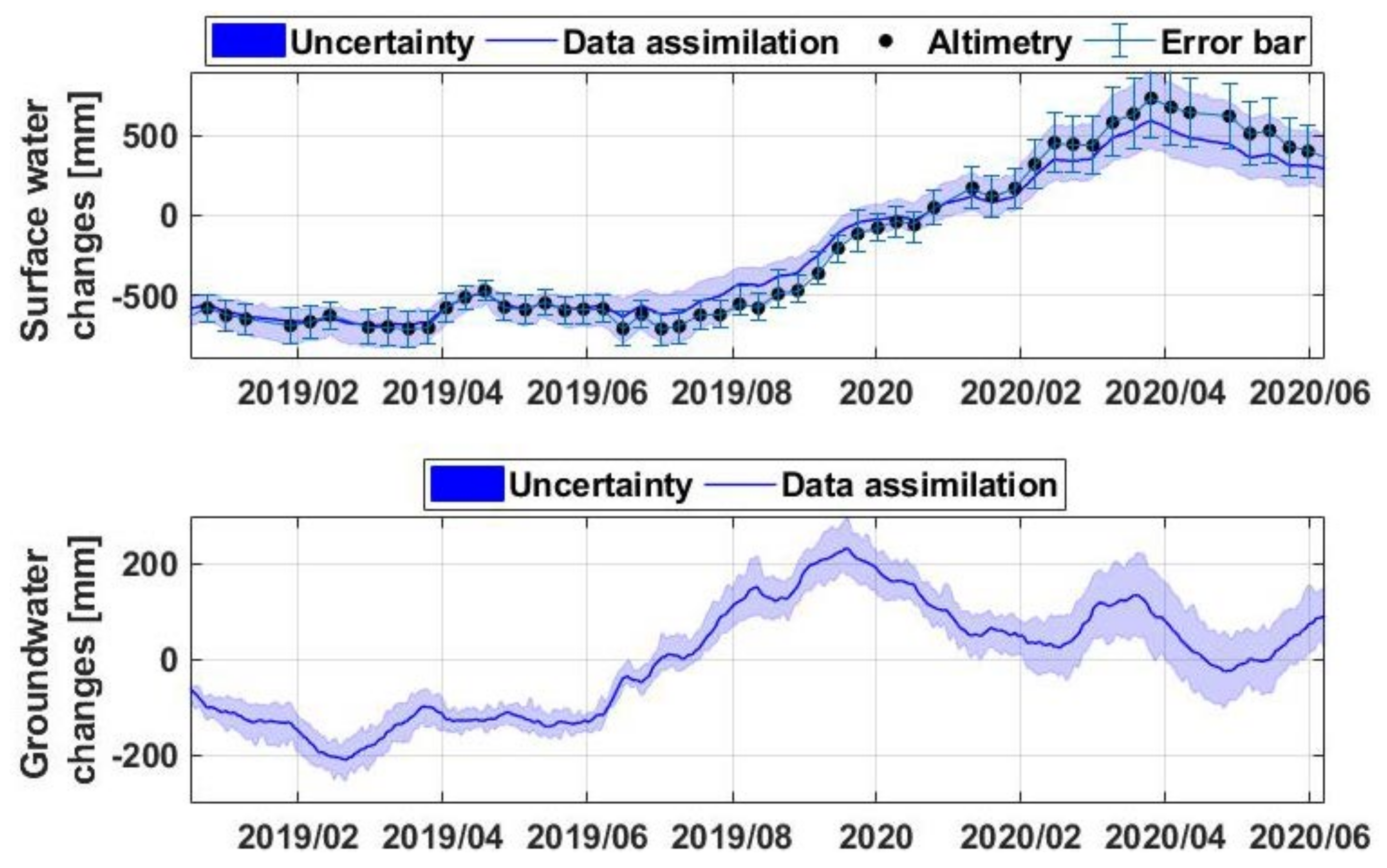
4.1. Assimilation Results
4.2. Hydroclimate Variability
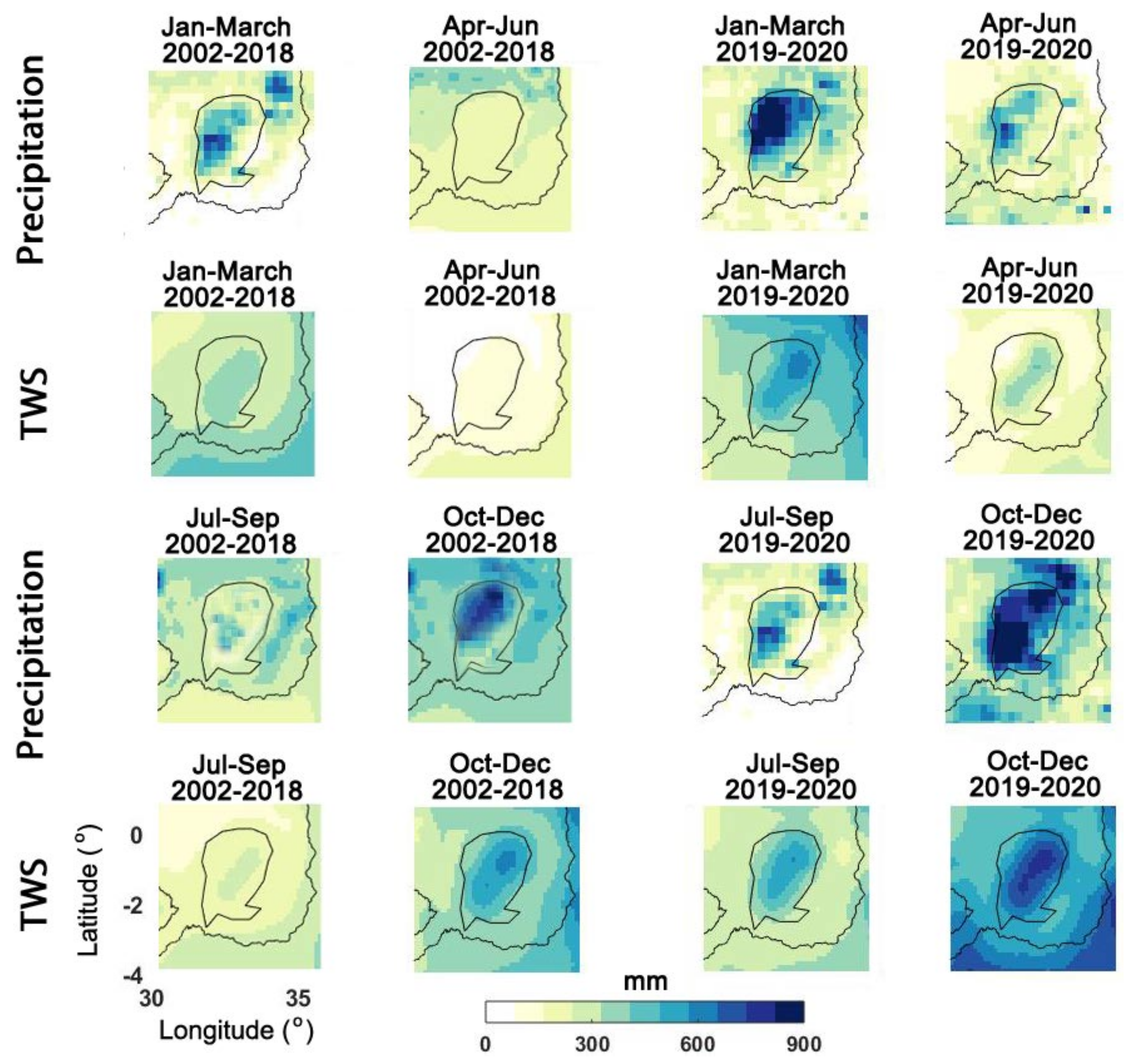
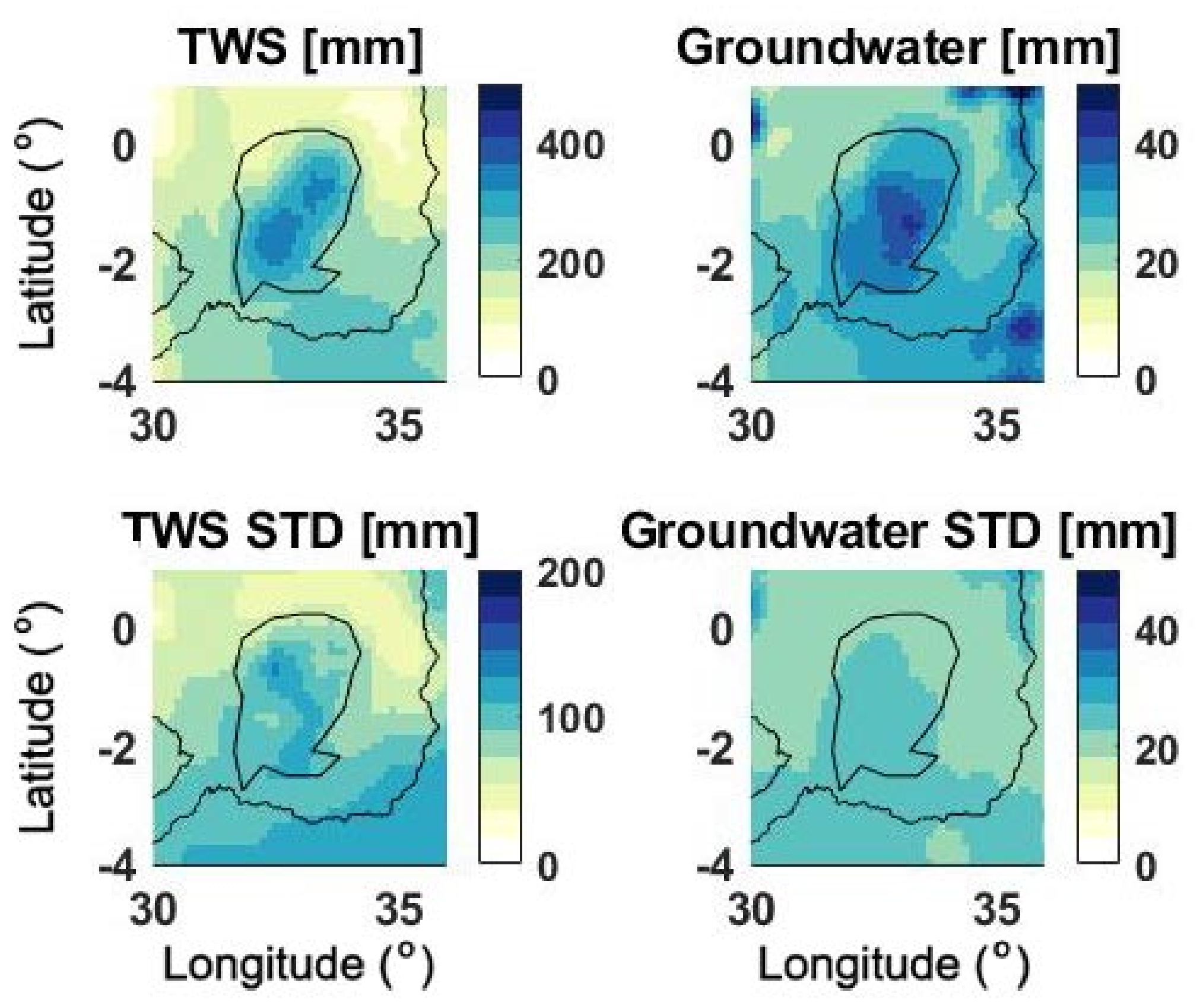
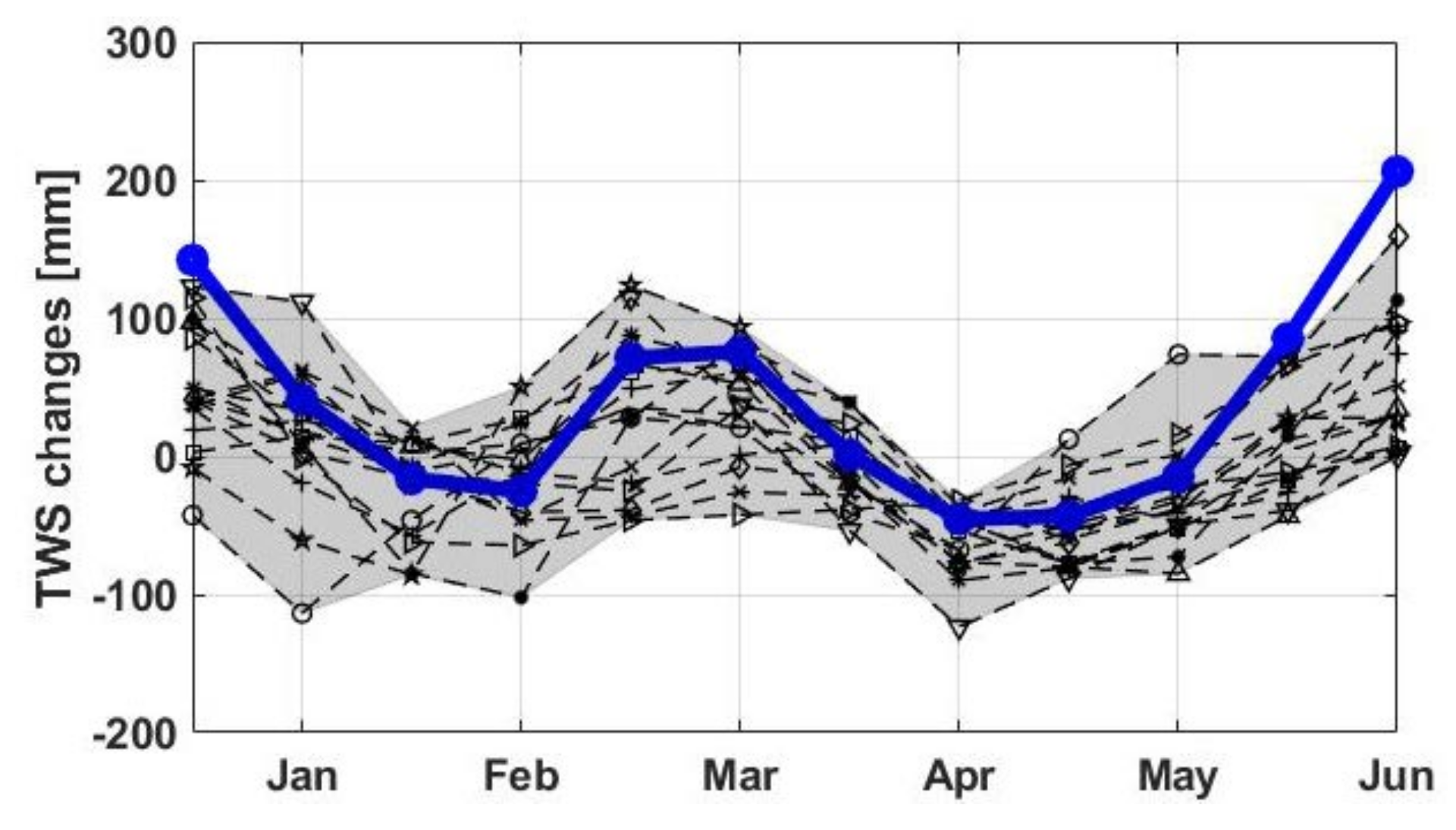
4.3. Water Storage Trend
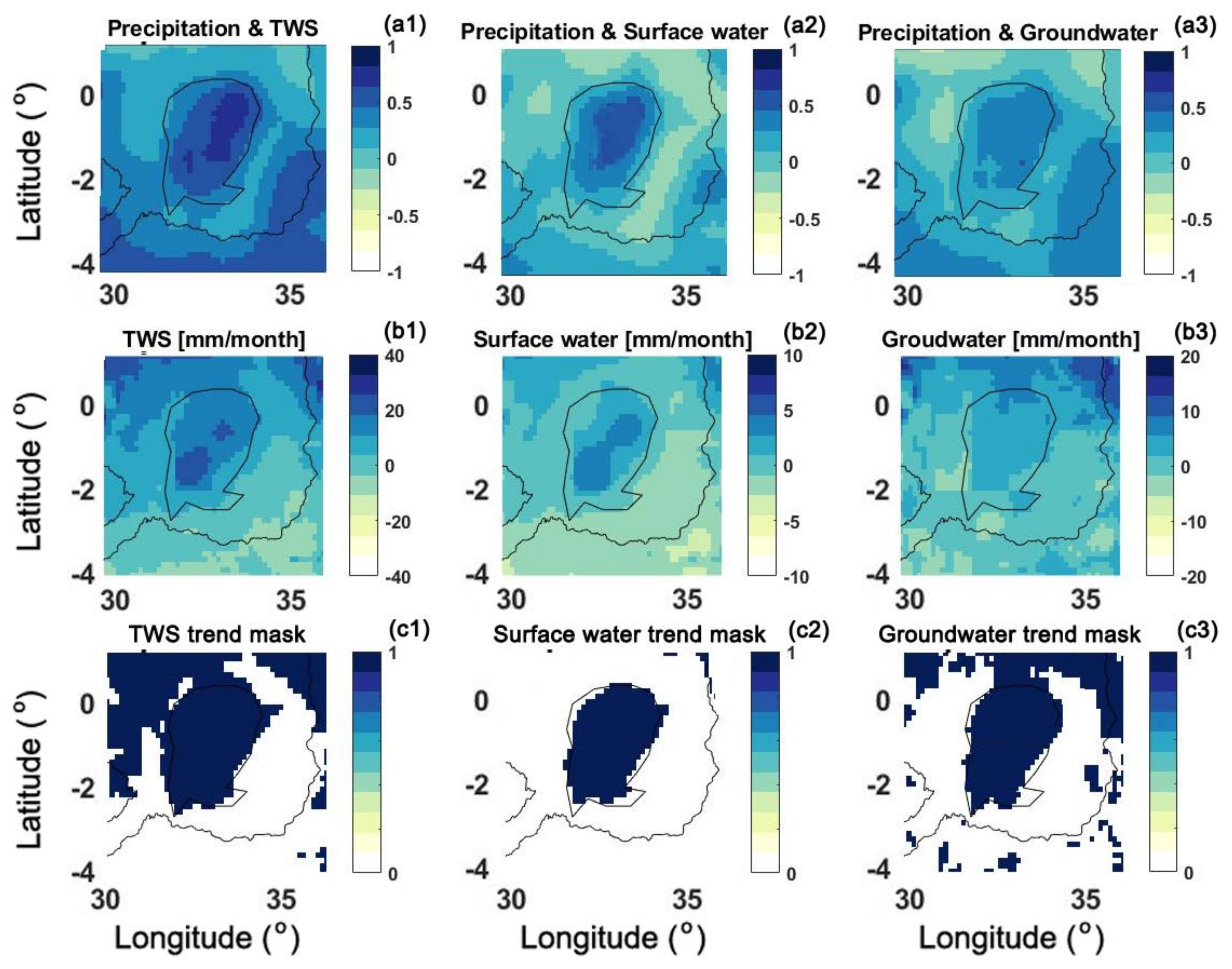
4.4. Principal Component Analysis (PCA)
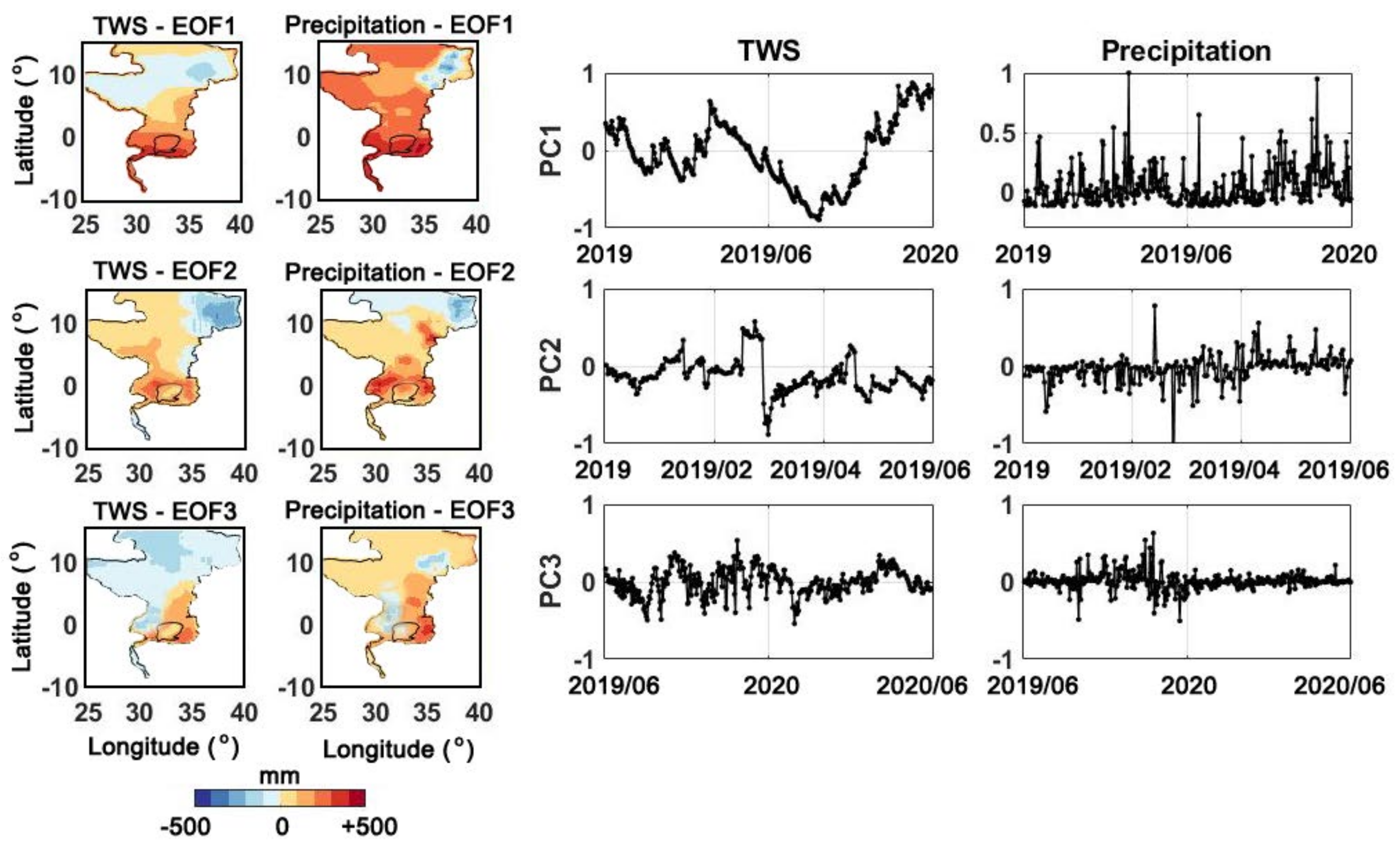
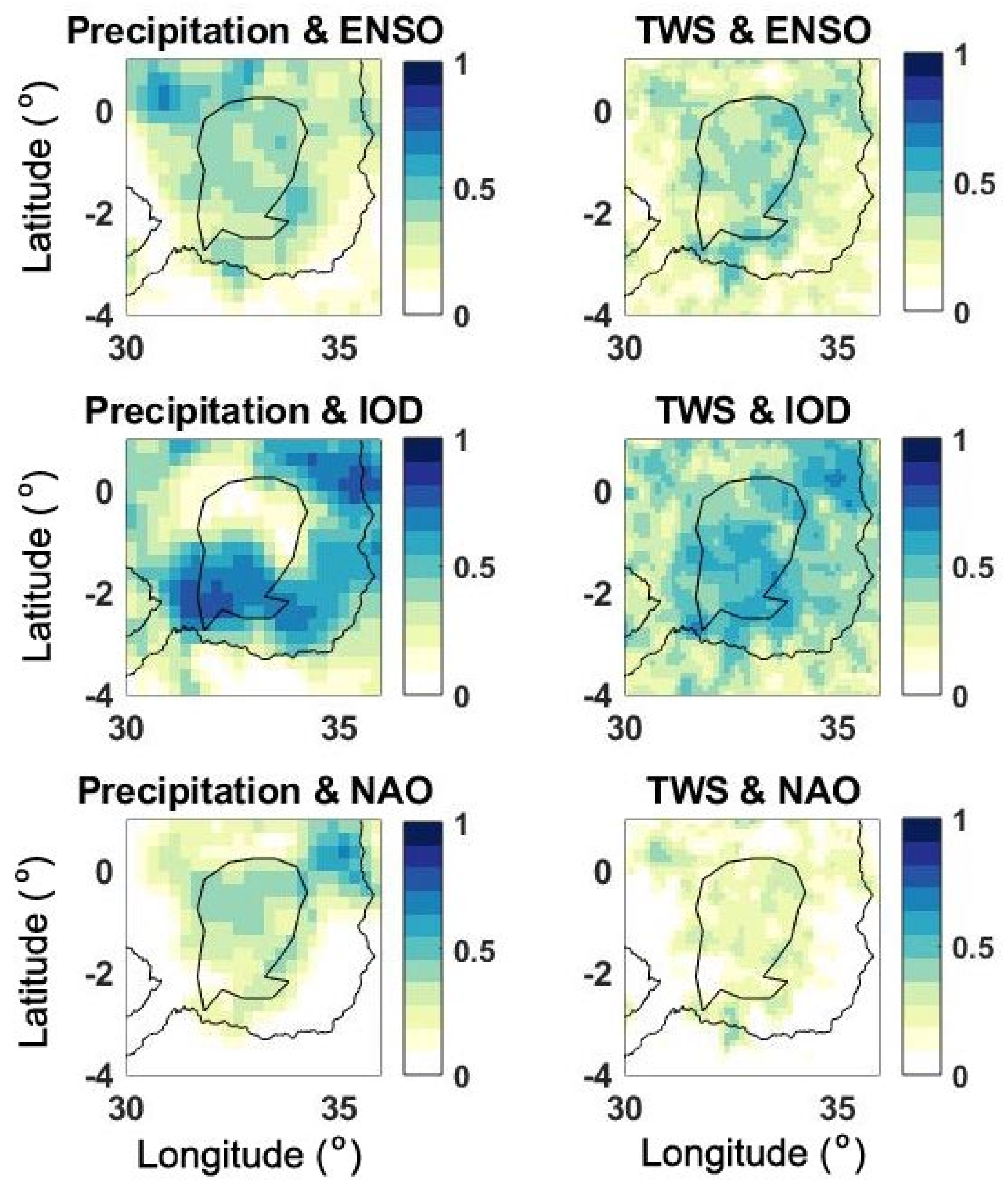
4.5. Climate Impacts
5. Discussion
6. Conclusions
- (i)
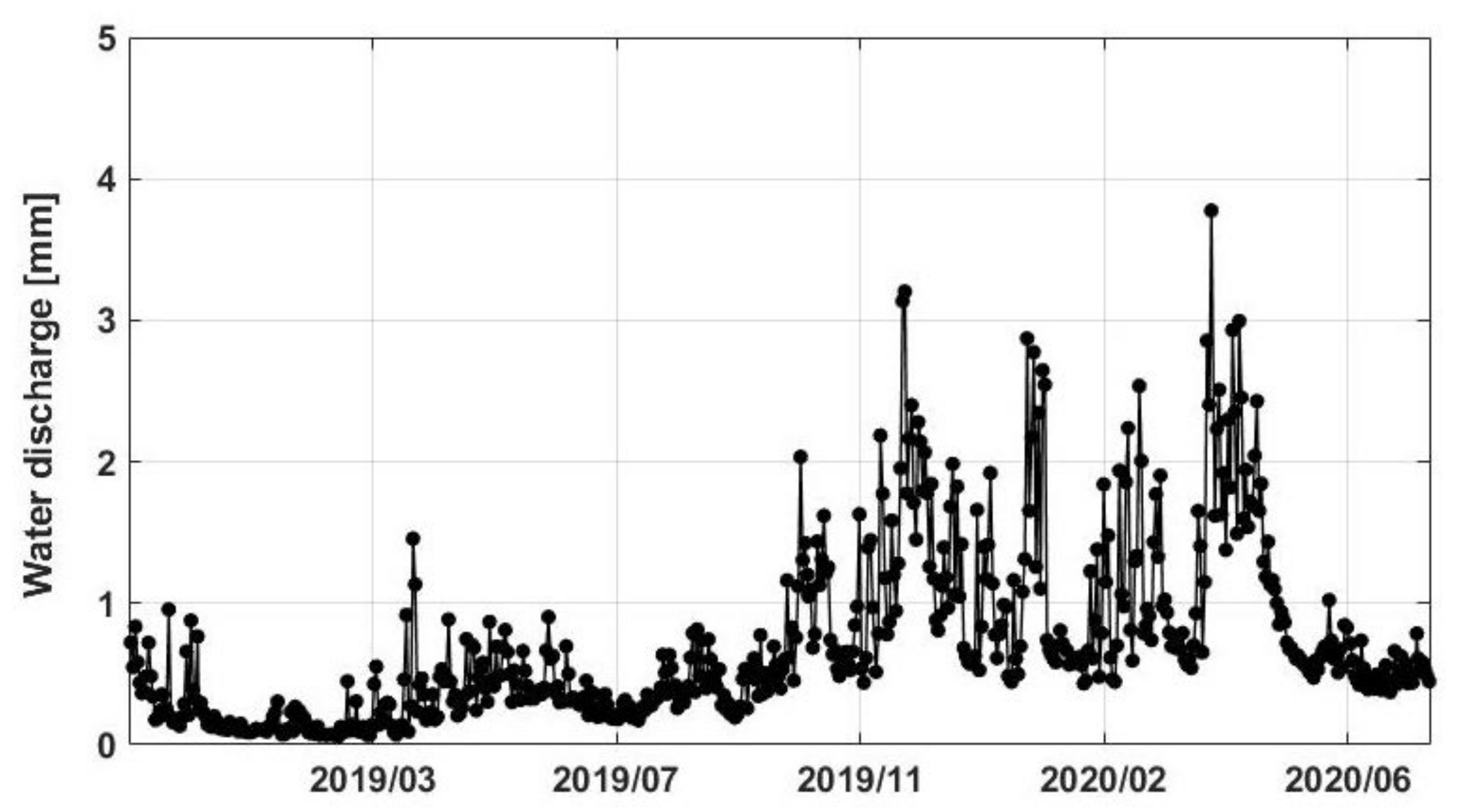
- Recent intense precipitations particularly during 2019 caused an enormous water storage increase over the lake (∼25% TWS increase with respect to the period 2002–2018). Based on altimetry data, Lake Victoria’s water level rose by ∼1.4 m. This, according to the estimated water storage from data assimilation led to approximately 1750 gigatonne volume increase. A positive trend is observed in the past two years in the lakes water storage increase with two major events in April–May 2019 and December 2019–January 2020. Increased precipitation is found to be the main factor for these large positive water storage anomalies.
- (ii)
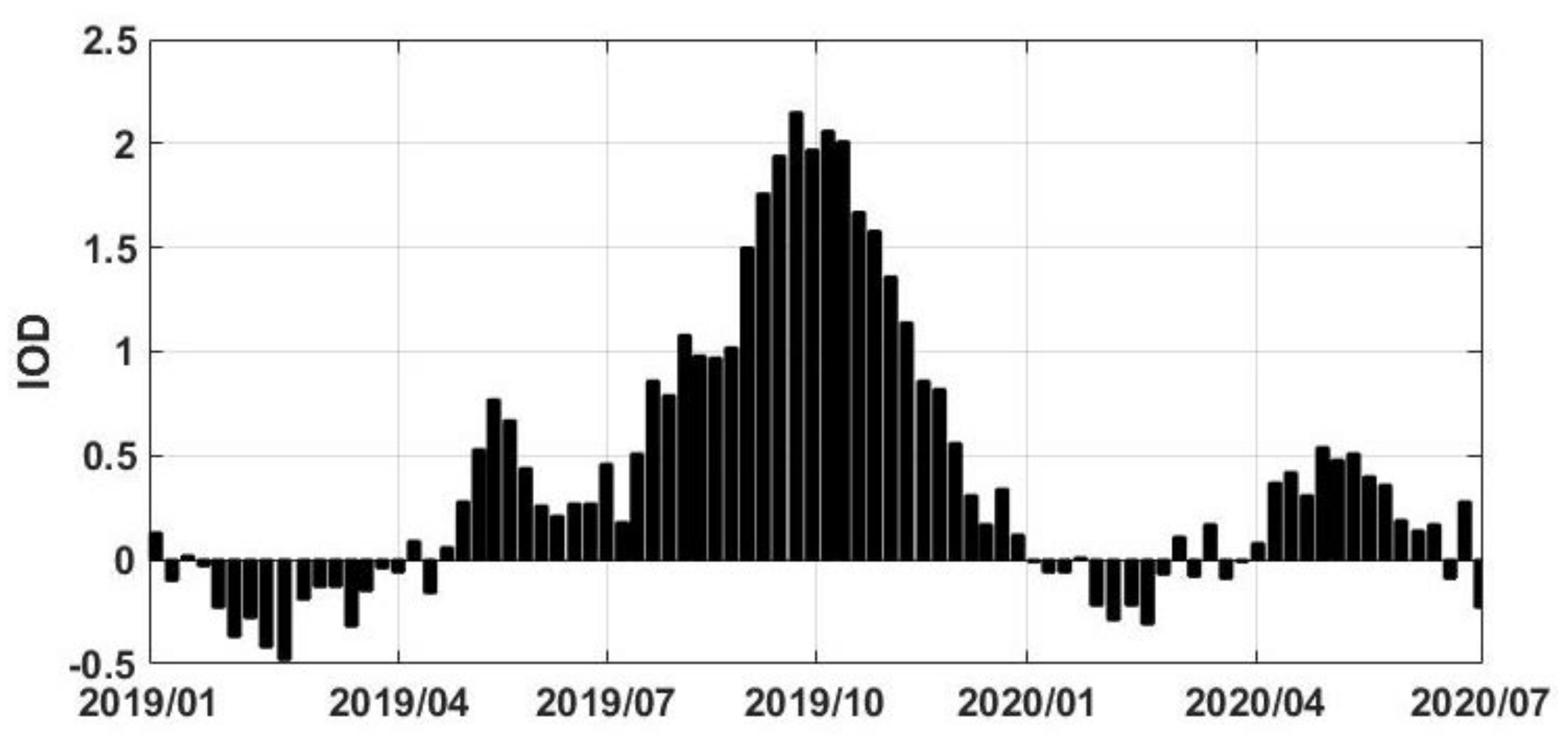
- The overall trend, however, begins a negative pattern from early 2020 as seen by all the time series including TWS change and water level data. The impact of large scale climate variabilities on water changes within the area is also investigated using climate indicators including ENSO, IOD, NAO. Amongst these, IOD is found to be the main player that caused the above-average precipitation due to a strong positive IOD phenomenon mostly in the second half of 2019.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Awange, J.L.; Saleem, A.; Sukhadiya, R.M.; Ouma, Y.O.; Kexiang, H. Physical dynamics of Lake Victoria over the past 34 years (1984–2018): Is the lake dying? Sci. Total Environ. 2019, 658, 199–218. [Google Scholar] [CrossRef]
- Awange, J.L.; Sharifi, M.A.; Ogonda, G.; Wickert, J.; Grafarend, E.; Omulo, M. The Falling Lake Victoria Water Levels: GRACE, TRIMM and CHAMP satellite analysis of the lake Basin. Water Resour. Manag. 2008, 22, 775–796. [Google Scholar] [CrossRef]
- Akurut, M.; Willems, P.; Niwagaba, C.B. Potential Impacts of Climate Change on Precipitation over Lake Victoria, East Africa, in the 21st Century. Water 2014, 6, 2634–2659. [Google Scholar] [CrossRef] [Green Version]
- Awange, J.L. Lake Victoria Monitored from Space; Springer International Publishing: Cham, Switzerland, 2021. [Google Scholar]
- Nicholson, S.E. Historical fluctuations of Lake Victoria and other lakes in the Northern Rift Valley of East Africa. In Environmental Change and Response in East African Lakes; Lehman, J.T., Ed.; Kluwer: Dordrecht, The Netherlands, 1998; pp. 7–35. [Google Scholar]
- Olaka, L.A.; Ogutu, J.O.; Said, M.Y.; Oludhe, C. Projected Climatic and Hydrologic Changes to Lake Victoria Basin Rivers under Three RCP Emission Scenarios for 2015–2100 and Impacts on the Water Sector. Water 2019, 11, 1449. [Google Scholar] [CrossRef] [Green Version]
- Sitoki, L.; Gichuki, J.; Ezekiel, C.; Wanda, F.; Mkumbo, O.C.; Marshall, B.E. The Environment of Lake Victoria (East Africa): Current Status and Historical Changes. Int. Rev. Hydrobiol. 2010, 95, 209–223. [Google Scholar] [CrossRef]
- Awange, J.L.; Anyah, R.; Agola, N.; Forootan, E.; Omondi, P. Potential impacts of climate and environmental change on the stored water of Lake Victoria Basin and economic implications. Water Resour. Res. 2013, 49, 8160–8173. [Google Scholar] [CrossRef] [Green Version]
- Swenson, S.; Wahr, J. Monitoring the water balance of Lake Victoria, East Africa, from space. J. Hydrol. 2009, 370, 163–176. [Google Scholar] [CrossRef]
- Vanderkelen, I.; van Lipzig, N.P.M.; Thiery, W. Modelling the water balance of Lake Victoria (East Africa)—Part 1: Observational analysis. Hydrol. Earth Syst. Sci. 2018, 22, 5509–5525. [Google Scholar] [CrossRef] [Green Version]
- Paul, S. Data Preparation, Hydrodynamic and Contaminant Transport Shallow-Water Simulations of Lake Victoria. Master’s Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2019. [Google Scholar]
- UNEP. Lake Victoria Basin Environment Outlook: Environment and Development; UNEP: Nairobi, Kenya, 2006. [Google Scholar]
- Lettenmaier, D.P.; Alsdorf, D.; Dozier, J.; Huffman, G.J.; Pan, M.; Wood, E.F. Inroads of remote sensing into hydrologic science during the WRR era. Water Resour. Res. 2015, 51, 7309–7342. [Google Scholar] [CrossRef]
- Sheffield, J.; Wood, E.F.; Pan, M.; Beck, H.; Coccia, G.; Serrat-Capdevila, A.; Verbist, K. Satellite remote sensing for water resources management: Potential for supporting sustainable development in data-poor regions. Water Resour. Res. 2018, 54, 9724–9758. [Google Scholar] [CrossRef] [Green Version]
- Anyah, R.O.; Forootan, E.; Awange, J.L.; Khaki, M. Understanding linkages between global climate indices and terrestrial water storage changes over Africa using GRACE products. Sci. Total Environ. 2018, 635, 1405–1416. [Google Scholar] [CrossRef] [Green Version]
- Kizza, M.; Rodhe, A.; Xu, C.Y.; Natle, K.H.; Halldian, S. Temporal rainfall variability in the Lake Victoria Basin in east Africa during the twentieth century. Theor. Appl. Climatol. 2009, 98, 119–135. [Google Scholar] [CrossRef]
- Sichangi, A.W.; Makokha, G.O. Monitoring water depth, surface area and volume changes in Lake Victoria: Integrating the bathymetry map and remote sensing data during 1993–2016. Model. Earth Syst. Environ. 2017, 3, 533–538. [Google Scholar] [CrossRef]
- Khaki, M.; Awange, J. Improved remotely sensed satellite products for studying Lake Victoria’s water storage changes. Sci. Total Environ. 2019, 652, 915–926. [Google Scholar] [CrossRef]
- Phoon, S.Y.; Shamseldin, A.Y.; Vairavamoorthy, K. Assessing Impacts of Climate Change on Lake Victoria Basin, Africa. Available online: https://hdl.handle.net/2134/30346 (accessed on 22 June 2021).
- Kolding, J.; van Zwieten, P.; Marttin, F.; Funge-Smith, S.; Poulain, F. Freshwater small pelagic fish and fisheries in major African lakes and reservoirs in relation to food security and nutrition. In FAO Fisheries and Aquaculture; Technical Paper No. 642; FAO: Rome, Italy, 2019; p. 124. [Google Scholar]
- Khaki, M.; Awange, J. Altimetry-derived surface water data assimilation over the Nile Basin. Sci. Total Environ. 2020, 735, 139008. [Google Scholar] [CrossRef] [PubMed]
- Yin, X.; Nicholson, S.E. The water balance of Lake Victoria. Hydrol. Sci. J. 1998, 43, 789–811. [Google Scholar] [CrossRef]
- Lake Victoria Basin Commission. Special Report on the Declining of Water Levels of Lake Victoria, Arusha, Tanzania. 2006. Available online: https://www.oieau.org/eaudoc/system/files/documents/41/208894/208894_doc.pdf (accessed on 12 December 2020).
- Sewagudde, S. Lake Victoria’s Water Budget and the Potential Effects of Climate Change in the 21st Century. Afr. J. Trop. Hydrobiol. Fish. 2009, 12. [Google Scholar] [CrossRef]
- Mwirigi, P.; Rutagemwa, D.; Gikuma-Njuru, P.; Njuguna, H.; Matovu, A.; Waya, R.; Mwebaza-Ndawula, L.; Ssenfuma-Nsubuga, M.; Kinobe, J.; Abuodha, J.; et al. Lake Victoria Environment Management Project (LVEMP) Water Quality and Ecosystem Status: Lake Victoria Regional Water Quality Synthesis Report. Available online: http://hdl.handle.net/1834/6905 (accessed on 22 June 2021).
- Hecky, R.E.; Mugidde, R.; Ramlal, P.S.; Talbot, M.R.; Kling, G.W. Multiple stressors cause rapid ecosystem change in Lake Victoria. Freshw. Biol. 2010, 55, 19–42. [Google Scholar] [CrossRef] [Green Version]
- Vrugt, J.A.; Braak, C.J.F.; Diks, C.G.H.; Schoups, G. Advancing hydrologic data assimilation using particle Markov chain Monte Carlo simulation: Theory, concepts and applications. Adv. Water Resour. 2013, 51, 457–478. [Google Scholar] [CrossRef]
- Van Dijk, A.I.J.M.; Renzullo, L.J.; Wada, Y.; Tregoning, P. A global water cycle reanalysis (2003–2012) merging satellite gravimetry and altimetry observations with a hydrological multi-model ensemble. Hydrol. Earth. Syst. Sci. 2014, 18, 2955–2973. [Google Scholar] [CrossRef] [Green Version]
- Eicker, A.; Schumacher, M.; Kusche, J.; Döll, P.; Müller-Schmied, H. Calibration/data assimilation approach for integrating GRACE data into the WaterGAP global hydrology model (WGHM) using an ensemble Kalman filter: First results. Surv. Geophys. 2014, 35, 1285–1309. [Google Scholar] [CrossRef]
- Girotto, M.; De Lannoy, G.J.M.; Reichle, R.H.; Rodell, M.; Draper, C.; Bhanja, S.N.; Mukherjee, A. Benefits and pitfalls of GRACE data assimilation: A case study of terrestrial water storage depletion in India. Geophys. Res. Lett. 2017, 44, 4107–4115. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, B.; Rodell, M.; Kumar, S.; Beaudoing, H.K.; Getirana, A.; Zaitchik, B.F.; de Goncalves, L.G.; Cossetin, C.; Bhanja, S.; Mukherjee, A.; et al. Global GRACE data assimilation for groundwater and drought monitoring: Advances and challenges. Water Resour. Res. 2019, 55, 7564–7586. [Google Scholar] [CrossRef] [Green Version]
- Morgan, B.; Awange, J.L.; Saleem, A.; Hu, K. Understanding vegetation variability and their “hotspots” within Lake Victoria Basin (LVB: 2003–2018). Appl. Geogr. 2020, 122, 102238. [Google Scholar] [CrossRef]
- Bugenyi, F.W.B.; Magumba, K.M. The present physicochemical ecology of Lake Victoria, Uganda. In The Limnology, Climatology and Paleoclimatology of East African Lakes; Routledge: London, UK, 1996. [Google Scholar]
- IPCC. Special Report on the Regional Impacts of Climate Change: An Assessment of Vulnerability; Cambridge University Press: Cambridge, UK, 1997; p. 517. [Google Scholar]
- Mpelasoka, F.; Awange, J.L.; Zerihun, A. Influence of coupled ocean-atmosphere phenomena on the Greater Horn of Africa droughts and their implications. Sci. Total Environ. 2018, 610–611, 691–702. [Google Scholar] [CrossRef] [Green Version]
- Van Dijk, A.I.J.M.; Peña-Arancibia, J.L.; Wood, E.F.; Sheffield, J.; Beck, H.E. Global analysis of seasonal streamflow predictability using an ensemble prediction system and observations from 6192 small catchments worldwide. Water Resour. Res. 2013, 49, 2729–2746. [Google Scholar] [CrossRef]
- Mayer-Gürr, T.; Behzadpour, S.; Ellmer, M.; Klinger, B.; Kvas, A.; Strasser, S.; Zehentner, N. ITSG-Grace2018: The new GRACE time series from TU Graz. In Proceedings of the GRACE/GRACE-FO Science Team Meeting 2018, Potsdam, Germany, 9–11 October 2018. [Google Scholar]
- Cheng, M.K.; Tapley, B.D. Variations in the Earth’s oblateness during the past 28 years. J. Geophys. Res. 2004, 109, B09402. [Google Scholar] [CrossRef]
- Swenson, S.; Chambers, D.; Wahr, J. Estimating geocentervariations from a combination of GRACE and ocean model output. J. Geophys. Res. 2008, 113, B08410. [Google Scholar]
- Wahr, J.; Molenaar, M.; Bryan, F. Time variability of the Earth’s gravity field’ Hydrological and oceanic effects and their possible detection using GRACE. J. Geophys. Res. 1998, 103, 30205–30229. [Google Scholar] [CrossRef]
- Khaki, M.; Forootan, E.; Kuhn, M.; Awange, J.; Longuevergne, L.; Wada, Y. Efficient Basin Scale Filtering of GRACE Satellite Products. Remote Sens. Environ. 2018, 204, 76–93. [Google Scholar] [CrossRef] [Green Version]
- Couhert, A.; Cerri, L.; Legeais, J.F.; Ablain, M.; Zelensky, N.P.; Haines, B.J.; Lemoine, F.G.; Bertiger, W.I.; Desai, S.D.; Otten, M. Towards the 1 mm/y stability of the radial orbit error at regional scales. Adv. Space Res. 2015, 55, 2–23. [Google Scholar] [CrossRef]
- Khaki, M.; Forootan, E.; Sharifi, M.A.; Awange, J.; Kuhn, M. Improved gravity anomaly fields from retracked multimission satellite radar altimetry observations over the Persian Gulf and the Caspian Sea. Geophys. J. Int. 2015, 202, 1522–1534. [Google Scholar] [CrossRef] [Green Version]
- Baarda, W. A Testing Procedure for Use in Geodetic Networks. Geodesy 1968, 2, 97. [Google Scholar]
- Frappart, F.; Papa, F.; Famiglietti, J.S.; Prigent, C.; Rossow, W.B.; Seyler, F. Interannual variations of river water storage from a multiple satellite approach: A case study for the Rio Negro River basin. J. Geophys. Res. 2008, 113, D21104. [Google Scholar] [CrossRef] [Green Version]
- Huffman, G.; Bolvin, D.; Braithwaite, D.; Hsu, K.; Joyce, R.; Xie, P. Integrated Multi-satellitE Retrievals for GPM (IMERG), Version 4.4. NASA’s Precipitation Processing Center, 2014. Available online: ftp://arthurhou.pps.eosdis.nasa.gov/gpmdata/ (accessed on 31 March 2015).
- Muñoz Sabater, J. ERA5-Land Hourly Data from 1981 to Present. Available online: https://doi.org/10.24381/cds.e2161bac (accessed on 3 January 2020).
- Zaitchik, B.F.; Rodell, M.; Reichle, R.H. Assimilation of GRACE terrestrial water storage data into a land surface model: Results for the Mississippi River Basin. J. Hydrometeorol. 2008, 9, 535–548. [Google Scholar] [CrossRef]
- Tangdamrongsub, N.; Steele-Dunne, S.C.; Gunter, B.C.; Ditmar, P.G.; Weerts, A.H. Data assimilation of GRACE terrestrial water storage estimates into a regional hydrological model of the Rhine River basin. Hydrol. Earth Syst. Sci. 2015, 19, 2079–2100. [Google Scholar] [CrossRef] [Green Version]
- Getirana, A. Integrating spatial altimetry data into the automatic calibration of hydrological models. J. Hydrol. 2010, 387, 244–255. [Google Scholar] [CrossRef]
- Michailovsky, C.I.; Milzow, C.; Bauer-Gottwein, P. Assimilation of radar altimetry to a routing model of the Brahmaputra River. Water Resour. Res. 2013, 49, 4807–4816. [Google Scholar] [CrossRef]
- Frost, A.J.; Ramchurn, A.; Smith, A. The Bureau’s Operational AWRA Landscape (AWRA-L) Model; Bureau of Meteorology: Melbourne, Australia, 2016.
- Kvas, A.; Behzadpour, S.; Ellmer, M.; Klinger, B.; Strasser, S.; Zehentner, N.; Mayer-Gürr, T. ITSG-Grace2018: Overview and evaluation of a new GRACE-only gravity field time series. J. Geophys. Res. Solid Earth 2019, 124, 9332–9344. [Google Scholar] [CrossRef] [Green Version]
- Mazzoleni, M.; Noh, S.J.; Lee, H.; Liu, Y.; Seo, D.J. Real-time assimilation of streamflow observations into a hydrological routing model: Effects of model structures and updating methods. Hydrol. Sci. J. 2018, 63, 386–407. [Google Scholar] [CrossRef]
- Khaki, M.; Awange, J.; Forootan, E.; Kuhna, M. Understanding the association between climate variability and the Nile’s water level fluctuations and water storage changes during 1992–2016. Sci. Total Environ. 2018, 645, 1509–1521. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Anderson, M.C.; Norman, J.M.; Mecikalski, J.R.; Otkin, J.A.; Kustas, W.P. A climatological study of evapotranspiration and moisture stress across the continental United States based on thermal remote sensing: 1. Model formulation. J. Geophys. Res. 2007, 112, D10117. [Google Scholar] [CrossRef]
- Khaki, M.; Hendricks Franssen, H.J.; Han, S.C. Multi-mission satellite remote sensing data for improving land hydrological models via data assimilation. Sci. Rep. 2020, 10, 18791. [Google Scholar] [CrossRef]
- Oleson, K.; Lawrence, D.M.; Bonan, G.B.; Drewniak, B.; Huang, M.; Koven, C.D.; Levis, S.; Li, F.; Riley, M.J.; Subin, Z.M.; et al. Technical Description of Version 4.5 of the Community Land Model (CLM); Ncar Technical Note NCAR/TN-503+STR; National Center for Atmospheric Research: Boulder, CO, USA, 2013; p. 422. [Google Scholar] [CrossRef]
- Sutanudjaja, E.H.; van Beek, R.; Wanders, N.; Wada, Y.; Bosmans, J.H.C.; Drost, N.; van der Ent, R.J.; de Graaf, I.E.M.; Hoch, J.M.; de Jong, K.; et al. PCR-GLOBWB 2: A 5 arcmin global hydrological and water resources model. Geosci. Model Dev. 2018, 11, 2429–2453. [Google Scholar] [CrossRef] [Green Version]
- Müller, S.H.; Eisner, S.; Franz, D.; Wattenbach, M.; Portmann, F.T.; Flörke, M.; Döll, P. Sensitivity of simulated global-scale freshwater fluxes and storages to input data, hydrological model structure, human water use and calibration. Hydrol. Earth Syst. Sci. 2014, 18, 3511–3538. [Google Scholar] [CrossRef] [Green Version]
- Yilmaz, M.; Crow, W.; Anderson, M.; Hain, C. An objective methodology for merging satellite-and model-based soil moisture products. Water Resour. Res. 2012, 48, 11502. [Google Scholar] [CrossRef]
- GEBCO (Global Ocean & Land Terrain Models) Compilation Group. GEBCO 2020 Grid. 2020. Available online: https://www.gebco.net/data_and_products/gridded_bathymetry_data/ (accessed on 21 March 2020).
- Preisendorfer, R.W. Principal Component Analysis in Meteorology and Oceanography; Elsevier: New York, NY, USA, 1988; p. 425. [Google Scholar] [CrossRef]
- Gocic, M.; Trajkovic, S. Analysis of Changes in Meteorological Variables Using Mann—Kendall and Sen’s Slope Estimator Statistical Tests in Serbia; Elsevier: New York, NY, USA, 2012. [Google Scholar]
- Doi, T.; Behera, S.K.; Yamagata, T. Predictability of the super IOD event in 2019 and its link with El Niño Modoki. Geophys. Res. Lett. 2020, 47, e2019GL086713. [Google Scholar] [CrossRef]
- Hu, K.; Awange, J.L.; Kuhn, M.; Nanteza, J. Assessment of hydro-climate, topographical and geological products to characterise groundwater spatio-temporal variability and areas of potential storage in data deficient regions: Exemplified by Lake Victoria Basin. Sci. Total Environ. 2021, in press. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khaki, M.; Awange, J. The 2019–2020 Rise in Lake Victoria Monitored from Space: Exploiting the State-of-the-Art GRACE-FO and the Newly Released ERA-5 Reanalysis Products. Sensors 2021, 21, 4304. https://doi.org/10.3390/s21134304
Khaki M, Awange J. The 2019–2020 Rise in Lake Victoria Monitored from Space: Exploiting the State-of-the-Art GRACE-FO and the Newly Released ERA-5 Reanalysis Products. Sensors. 2021; 21(13):4304. https://doi.org/10.3390/s21134304
Chicago/Turabian StyleKhaki, Mehdi, and Joseph Awange. 2021. "The 2019–2020 Rise in Lake Victoria Monitored from Space: Exploiting the State-of-the-Art GRACE-FO and the Newly Released ERA-5 Reanalysis Products" Sensors 21, no. 13: 4304. https://doi.org/10.3390/s21134304
APA StyleKhaki, M., & Awange, J. (2021). The 2019–2020 Rise in Lake Victoria Monitored from Space: Exploiting the State-of-the-Art GRACE-FO and the Newly Released ERA-5 Reanalysis Products. Sensors, 21(13), 4304. https://doi.org/10.3390/s21134304







