Development of Magnetic-Based Navigation by Constructing Maps Using Machine Learning for Autonomous Mobile Robots in Real Environments
Abstract
1. Introduction
2. Magnetic Navigation Method
- Updating the location particles given the robot’s movement.
- Computing the likelihood of each particle based on the most current sensor measurement and the observation modelwhere is particle’s likelihood, is the variance of the observations, is the magnetic information on the map, is observation acquired by magnetic sensor.
- Resampling particles according to when necessary.
3. Machine Learning for Generating Magnetic Map
3.1. Gaussian Process Regression (GPR)
3.2. Sparse Gaussian Process Regression (SGPR)
- Compute the vector and matrix and store them in memory.
- Compute the inverse matrix and store it in memory.
- Calculate and store it in memory.
3.2.1. Subset of Data Approximation (SoD)
3.2.2. The Inducing Variables Method
4. Kernel Function for High-Accuracy Localization
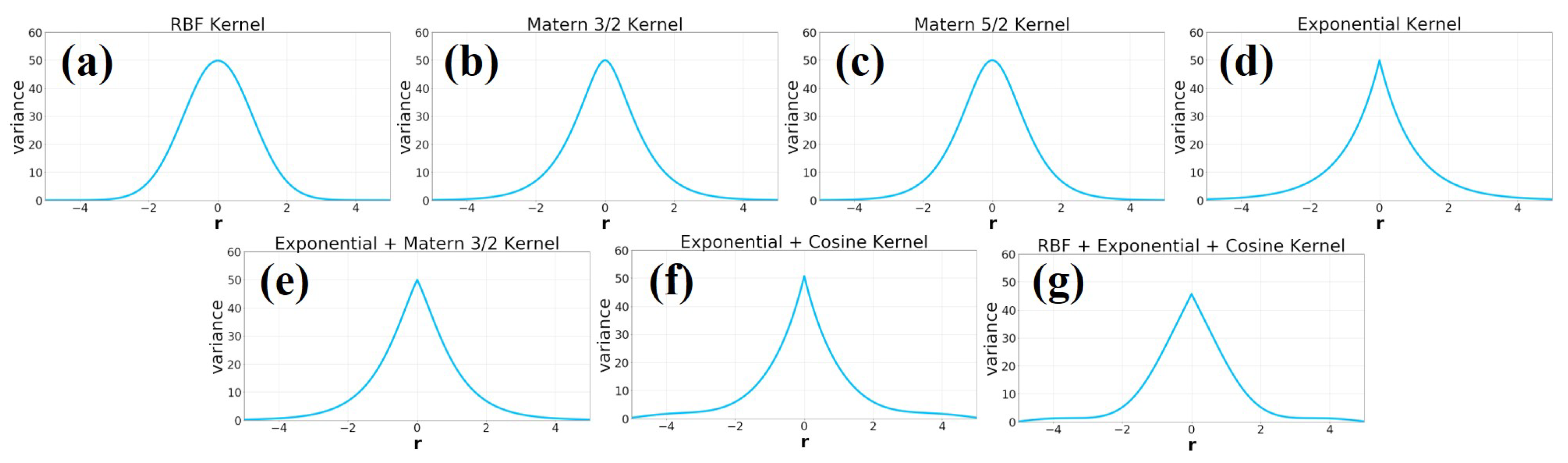
4.1. Kernel Function
- (1)
- Radial Basis Function (RBF) Kernel
- (2)
- Exponential Kernel
- (3)
- Matern 3/2 Kernel
- (4)
- Matern 5/2 Kernel
- (5)
- Exponential + Cosine Kernel
- (6)
- Exponential + Matern 3/2 Kernel
- (7)
- RBF + Exponential + Matern 3/2 Kernelwhere expresses a distance between two vectors (), .
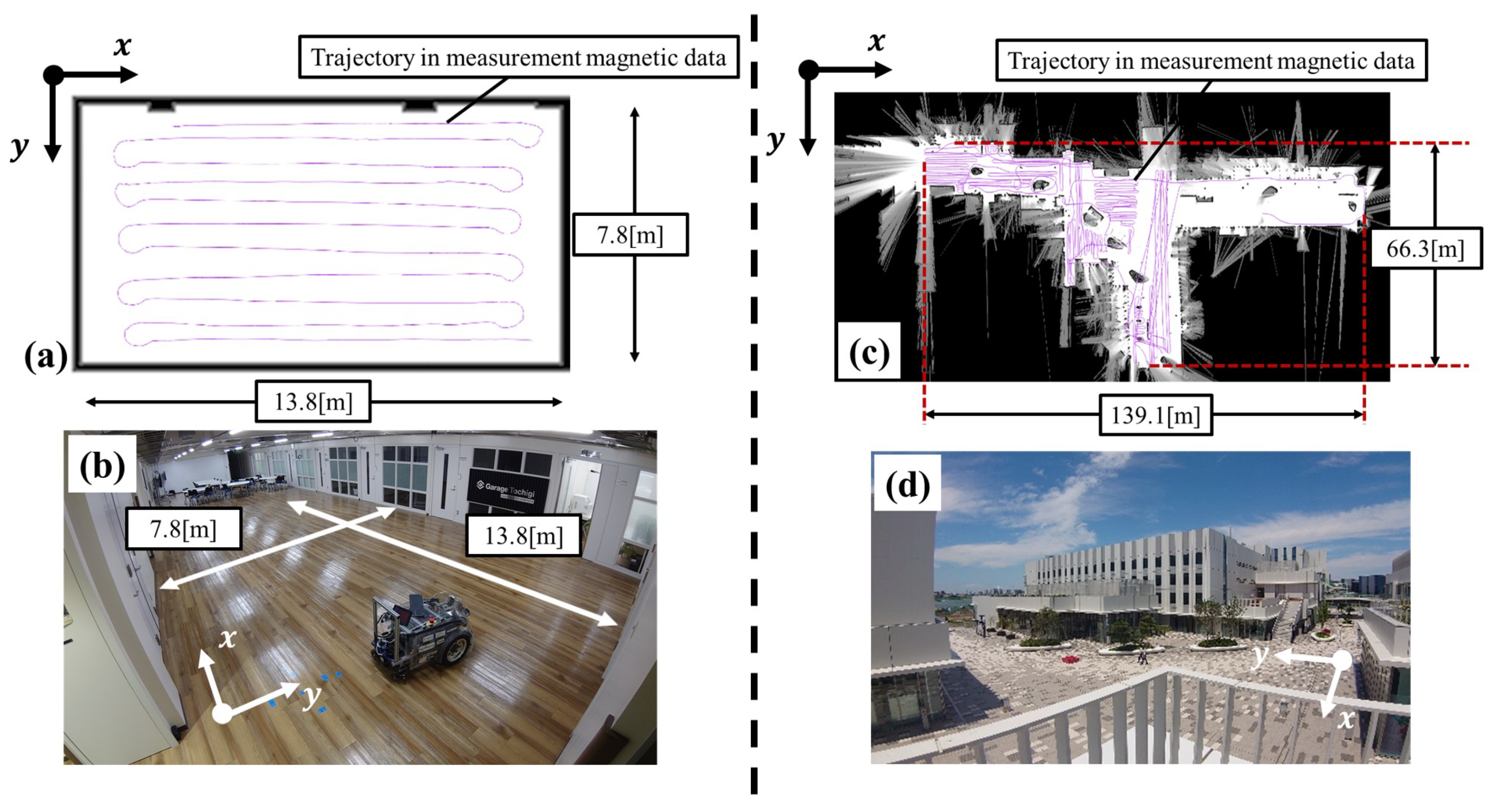
4.2. Experiments and Discussions
- REAL: 5, 10, 20, 30, 40, 50
- HICity: 10, 50, 100, 500, 1K, 2K
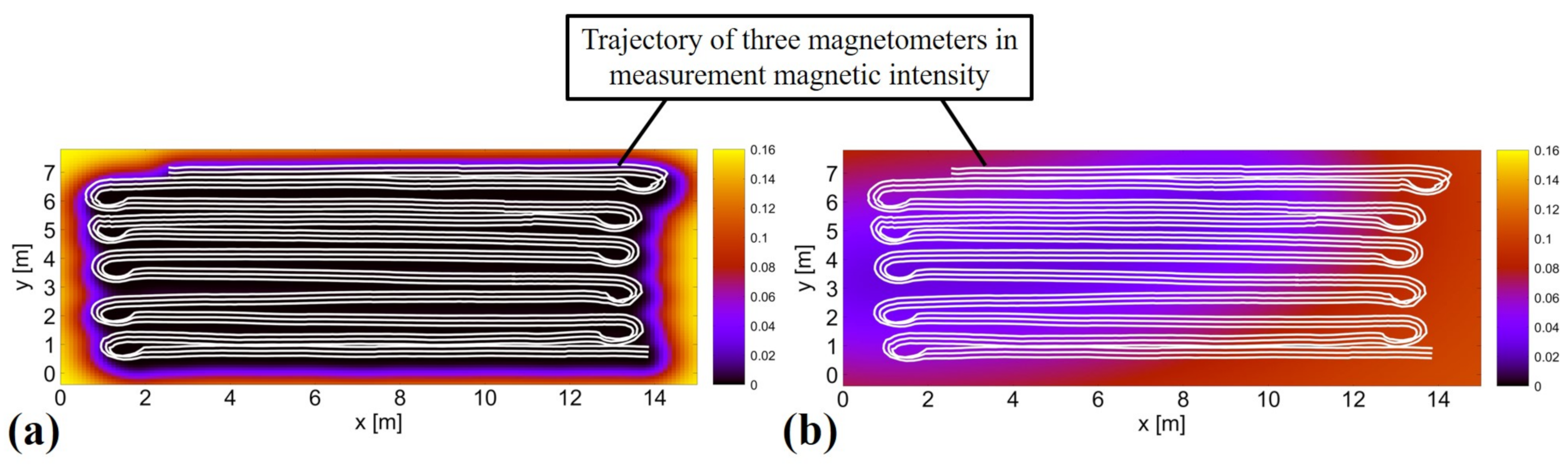
4.2.1. Magnetic Maps
- Exponential kernelThe Exponential kernel generates magnetic maps that are considerably smoother than those generated by the RBF Kernel. Smoother maps have been shown to improve localization accuracy when combined with MCL [34]. However, the maps generated by this kernel seem to be too smooth, which could limit the ability of the localization algorithm to differentiate between nearby points (as both have similar intensities), lowering its potential localization accuracy.
- Matern 3/2 kernelContrary to the exponential kernel, the Matern 3/2 generates maps that accentuate magnetic disturbances (higher peaks and valleys), while still generating smooth maps. As it can be observed, compared to the RBF kernel, several peaks are combined into larger ones.
- Matern 5/2 kernelSimilar to the Matern 3/2 kernel, the Matern 5/2 kernel also generates maps that accentuate magnetic disturbances. However, it does not tend to combine peaks, showing the same patterns as the RBF Kernel. Compared with the RBF kernel and Matern 3/2 kernel, it is hard to assess which would yield higher localization accuracies, hence the requirement to test the actual localization accuracy that can be achieved with them.
- Exponential + Cosine kernelThe Cosine kernel has periodicity in one dimension, but when combined with other kernels, the result does not show such periodicity. The main idea when testing the Exponential + Cosine kernel was to see if the training found some periodicity in the data. As can be seen, when compared with the Exponential kernel, this kernel has no significant differences. This means that no such periodicities were dominant in the data.
- Exponential + Matern 3/2 kernelAs both the Exponential and the Matern 3/2 kernels showed similar maps, we combined them to see if their combination would increase localization accuracy. As expected, the resulting maps are smooth and somewhat in the middle between the exponential and Matern in terms of the height of its peaks and valleys.
- Exponential + Cosine + RBF kernelThe RBF, Exponential, and Cosine kernels were combined to see if the addition of several kernels would improve localization accuracy.
4.2.2. Localization Accuracy Using Different Magnetic Maps
5. SGPR for Generating Large-Scale Magnetic Map
5.1. Mapping
- GPR.
- GPR with clustered data (KM-GPR).
- SGPR.
5.1.1. Memory Consumption
5.1.2. Generating Time
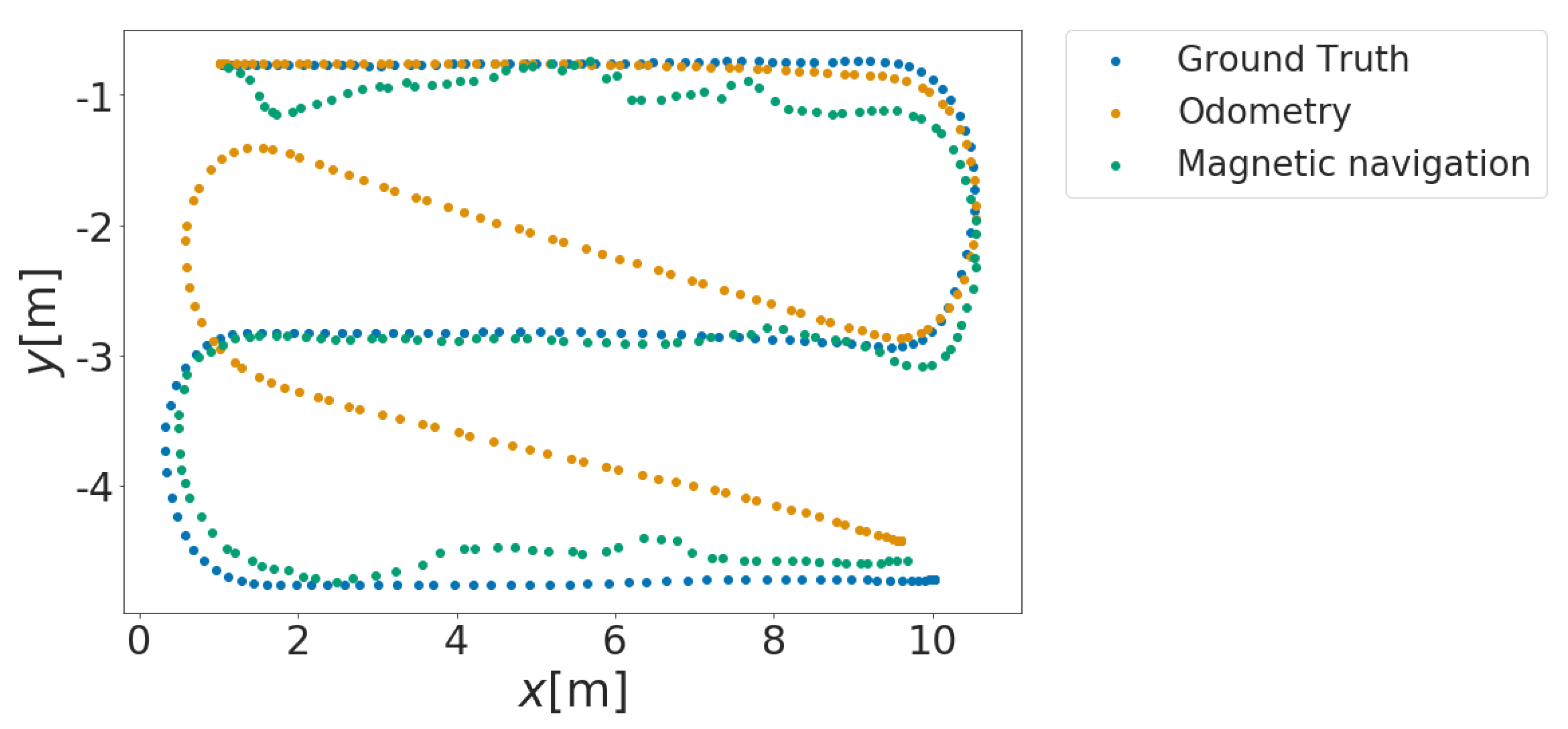
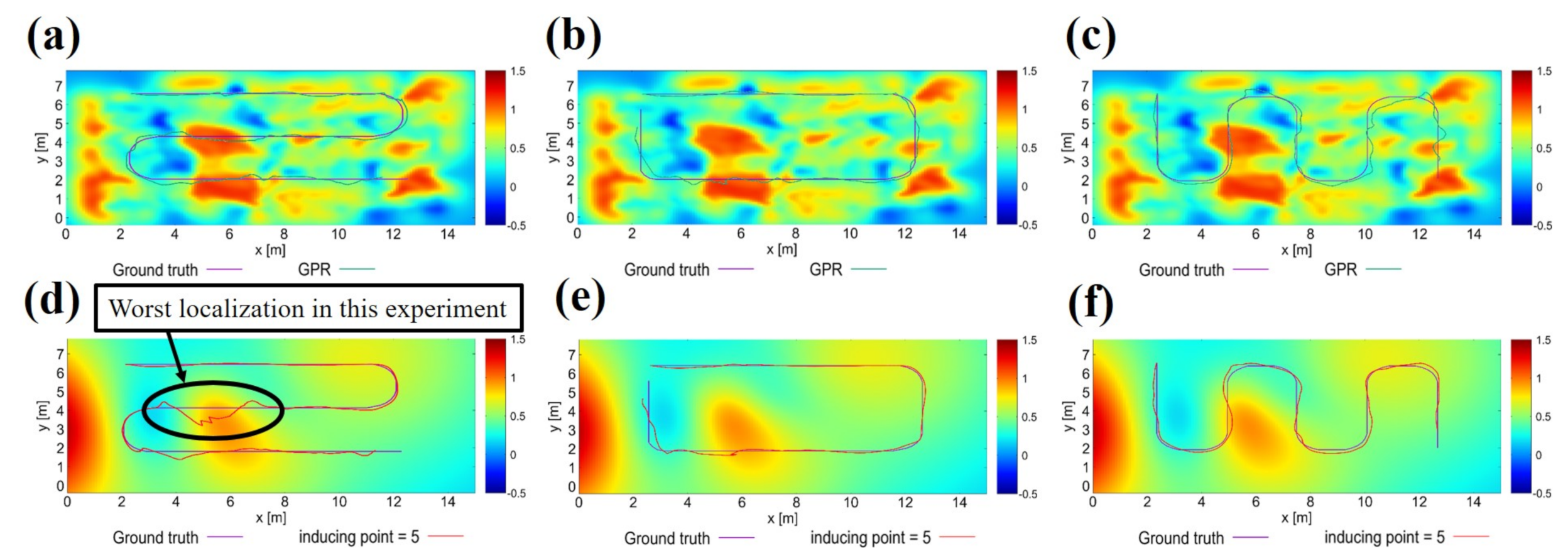
5.2. Effect to Localization
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviation
| i.i.d | independent and identically distributed |
References
- Lu, Y.H.; Juang, J.G. Application of Differential Global Positioning System and Path Planning to Robot Outdoor Patrol. Sens. Mater. 2018, 30, 1643. [Google Scholar] [CrossRef]
- Neloy, A.; Bindu, R.; Alam, S.; Haque, R.; Khan, M.S.; Mishu, N.; Siddique, S. Alpha-N-V2: Shortest Path Finder Automated Delivery Robot with Obstacle Detection and Avoiding System. Vietnam. J. Comput. Sci. 2020, 7, 1–17. [Google Scholar] [CrossRef]
- Sathyamoorthy, A.J.; Patel, U.; Savle, Y.A.; Paul, M.; Manocha, D. COVID-Robot: Monitoring Social Distancing Constraints in Crowded Scenarios. arXiv 2020, arXiv:cs.RO/2008.06585. [Google Scholar]
- Kim, S.S.; Kim, J.; Badu-Baiden, F.; Giroux, M.; Choi, Y. Preference for robot service or human service in hotels? Impacts of the COVID-19 pandemic. Int. J. Hosp. Manag. 2021, 93, 102795. [Google Scholar] [CrossRef]
- Makarenko, A.; Williams, S.; Bourgault, F.; Durrant-Whyte, H. An experiment in integrated exploration. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Lausanne, Switzerland, 30 September–4 October 2002; Volume 1, pp. 534–539. [Google Scholar] [CrossRef]
- Bonadies, S.; Gadsden, S.A. An overview of autonomous crop row navigation strategies for unmanned ground vehicles. Eng. Agric. Environ. Food 2019, 12, 24–31. [Google Scholar] [CrossRef]
- Yang, L.; Noguchi, N. Development of a Wheel-Type Robot Tractor and its Utilization. IFAC Proc. Vol. 2014, 47, 11571–11576. [Google Scholar] [CrossRef]
- Niewola, A.; Podsędkowski, L. PSD—Probabilistic algorithm for mobile robot 6D localization without natural and artificial landmarks based on 2.5D map and a new type of laser scanner in GPS-denied scenarios. Mechatronics 2020, 65, 102308. [Google Scholar] [CrossRef]
- Wang, H.; Lin, Y.; Wang, Z.; Yao, Y.; Zhang, Y.; Wu, L. Validation of a low-cost 2D laser scanner in development of a more-affordable mobile terrestrial proximal sensing system for 3D plant structure phenotyping in indoor environment. Comput. Electron. Agric. 2017, 140, 180–189. [Google Scholar] [CrossRef]
- Andreasson, H.; Treptow, A.; Duckett, T. Localization for Mobile Robots using Panoramic Vision, Local Features and Particle Filter. In Proceedings of the 2005 IEEE International Conference on Robotics and Automation, Barcelona, Spain, 18–22 April 2005; pp. 3348–3353. [Google Scholar] [CrossRef]
- Winterhalter, W.; Fleckenstein, F.; Steder, B.; Spinello, L.; Burgard, W. Accurate indoor localization for RGB-D smartphones and tablets given 2D floor plans. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 3138–3143. [Google Scholar] [CrossRef]
- Ferris, B.; Haehnel, D.; Fox, D. Gaussian processes for signal strength-based location estimation. In Proceedings of the Robotics Science and Systems, Philadelphia, PA, USA, 16–19 August 2006; pp. 1–8. [Google Scholar]
- Miyagusuku, R.; Yamashita, A.; Asama, H. Precise and accurate wireless signal strength mappings using Gaussian processes and path loss models. Robot. Auton. Syst. 2018, 103, 134–150. [Google Scholar] [CrossRef]
- Rahok, S.A.; Shikanai, Y.; Ozaki, K. Trajectory tracking using environmental magnetic field for outdoor autonomous mobile robots. In Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems, Taipei, Taiwan, 18–22 October 2010; pp. 1402–1407. [Google Scholar] [CrossRef]
- Chen, C.; Chen, Y.; Lai, H.; Han, Y.; Liu, K.J.R. High accuracy indoor localization: A WiFi-based approach. In Proceedings of the 2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Shanghai, China, 20–25 March 2016; pp. 6245–6249. [Google Scholar] [CrossRef]
- Shi, Y.; Zhang, W.; Li, F.; Huang, Q. Robust Localization System Fusing Vision and Lidar Under Severe Occlusion. IEEE Access 2020, 8, 62495–62504. [Google Scholar] [CrossRef]
- Solin, A.; Cortes, S.; Rahtu, E.; Kannala, J. PIVO: Probabilistic Inertial-Visual Odometry for Occlusion-Robust Navigation. In Proceedings of the 2018 IEEE Winter Conference on Applications of Computer Vision (WACV), Lake Tahoe, NV, USA, 12–15 March 2018; pp. 616–625. [Google Scholar] [CrossRef]
- Wang, X.; Gao, L.; Mao, S.; Pandey, S. CSI-Based Fingerprinting for Indoor Localization: A Deep Learning Approach. IEEE Trans. Veh. Technol. 2017, 66, 763–776. [Google Scholar] [CrossRef]
- Akai, N.; Ozaki, K. Gaussian processes for magnetic map-based localization in large-scale indoor environments. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 4459–4464. [Google Scholar] [CrossRef]
- Miyagusuku, R.; Arai, Y.; Kakigi, Y.; Takebayashi, T.; Fukushima, A.; Ozaki, K. Toward Autonomous Garbage Collection Robots in Terrains with Different Elevations. J. Robot. Mechatron. 2020, 32, 1164–1172. [Google Scholar] [CrossRef]
- Miyagusuku, R.; Seow, Y.; Yamashita, A.; Asama, H. Fast and robust localization using laser rangefinder and wifi data. In Proceedings of the IEEE International Conference on Multisensor Fusion and Integration for Intelligent Systems, Daegu, Korea, 16–18 November 2017; pp. 111–117. [Google Scholar]
- Ferris, B.; Fox, D.; Lawrence, N.D. WiFi-SLAM Using Gaussian Process Latent Variable Models. IJCAI 2007, 7, 2480–2485. [Google Scholar]
- Kok, M.; Solin, A. Scalable Magnetic Field SLAM in 3D Using Gaussian Process Maps. In Proceedings of the 2018 21st International Conference on Information Fusion (FUSION), Cambridge, UK, 10–13 July 2018; pp. 1353–1360. [Google Scholar] [CrossRef]
- Brunato, M.; Battiti, R. Statistical learning theory for location fingerprinting in wireless LANs. Comput. Netw. 2005, 47, 825–845. [Google Scholar] [CrossRef]
- Du, Y.; Arslan, T. A segmentation-based matching algorithm for magnetic field indoor positioning. In Proceedings of the 2017 International Conference on Localization and GNSS (ICL-GNSS), Nottingham, UK, 27–29 June 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Del Mundo, L.B.; Ansay, R.L.D.; Festin, C.A.M.; Ocampo, R.M. A comparison of wireless fidelity (Wi-Fi) fingerprinting techniques. In Proceedings of the International Conference on Convergence, Seoul, Korea, 28–30 September 2011; pp. 20–25. [Google Scholar]
- Tsunakawa, H.; Takahashi, F.; Shimizu, H.; Shibuya, H.; Matsushima, M. Surface vector mapping of magnetic anomalies over the Moon using Kaguya and Lunar Prospector observations. J. Geophys. Res. Planets 2015, 120, 1160–1185. [Google Scholar] [CrossRef]
- Benjamin, B.; Erinc, G.; Carpin, S. Real-time WiFi localization of heterogeneous robot teams using an online random forest. Auton. Robot. 2015, 39, 155–167. [Google Scholar] [CrossRef]
- Biswas, J.; Veloso, M. WiFi localization and navigation for autonomous indoor mobile robots. In Proceedings of the IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, 3–7 May 2010; pp. 4379–4384. [Google Scholar]
- Gutmann, J.S.; Eade, E.; Fong, P.; Munich, M.E. Vector Field SLAM—Localization by Learning the Spatial Variation of Continuous Signals. IEEE Trans. Robot. 2012, 28, 650–667. [Google Scholar] [CrossRef]
- Schwaighofer, A.; Grigoras, M.; Tresp, V.; Hoffmann, C. GPPS: A Gaussian Process Positioning System for Cellular Networks. Adv. Neural Inf. Process. Syst. 2003, 16, 579–586. [Google Scholar]
- Miyagusuku, R.; Yamashita, A.; Asama, H. Data Information Fusion From Multiple Access Points for WiFi-Based Self-localization. IEEE Robot. Autom. Lett. 2019, 4, 269–276. [Google Scholar] [CrossRef]
- Ito, S.; Endres, F.; Kuderer, M.; Diego Tipaldi, G.; Stachniss, C.; Burgard, W. W-RGB-D: Floor-plan-based indoor global localization using a depth camera and wifi. In Proceedings of the IEEE International Conference on Robotics and Automation, Hong Kong, China, 31 May–7 June 2014; pp. 417–422. [Google Scholar]
- Miyagusuku, R.; Yamashita, A.; Asama, H. Gaussian processes with input-dependent noise variance for wireless signal strength-based localization. In Proceedings of the 2015 IEEE International Symposium on Safety, Security, and Rescue Robotics (SSRR), West Lafayette, IN, USA, 18–20 October 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Yamazaki, K.; Kato, K.; Ono, K.; Saegusa, H.; Tokunaga, K.; Iida, Y.; Yamamoto, S.; Ashiho, K.; Fujiwara, K.; Takahashi, N. Analysis of magnetic disturbance due to buildings. IEEE Trans. Magn. 2003, 39, 3226–3228. [Google Scholar] [CrossRef]
- Kemppainen, A.; Haverinen, J.; Vallivaara, I.; Röning, J. Near-optimal SLAM exploration in Gaussian processes. In Proceedings of the 2010 IEEE Conference on Multisensor Fusion and Integration, Salt Lake City, UT, USA, 5–7 September 2010; pp. 7–13. [Google Scholar] [CrossRef]
- Vallivaara, I.; Haverinen, J.; Kemppainen, A.; Röning, J. Simultaneous localization and mapping using ambient magnetic field. In Proceedings of the 2010 IEEE Conference on Multisensor Fusion and Integration, Salt Lake City, UT, USA, 5–7 September 2010; pp. 14–19. [Google Scholar] [CrossRef]
- Wahlström, N.; Kok, M.; Schön, T.B.; Gustafsson, F. Modeling magnetic fields using Gaussian processes. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; pp. 3522–3526. [Google Scholar] [CrossRef]
- Robertson, P.; Frassl, M.; Angermann, M.; Doniec, M.; Julian, B.J.; Garcia Puyol, M.; Khider, M.; Lichtenstern, M.; Bruno, L. Simultaneous Localization and Mapping for pedestrians using distortions of the local magnetic field intensity in large indoor environments. In Proceedings of the International Conference on Indoor Positioning and Indoor Navigation, Montbeliard, France, 28–31 October 2013; pp. 1–10. [Google Scholar] [CrossRef]
- Miyagusuku, R.; Yamashita, A.; Asama, H. Improving Gaussian Processes based mapping of wireless signals using path loss models. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Daejeon, Korea, 9–14 October 2016; pp. 4610–4615. [Google Scholar]
- Torres-Sospedra, J.; Rambla, D.; Montoliu, R.; Belmonte, O.; Huerta, J. UJIIndoorLoc-Mag: A new database for magnetic field-based localization problems. In Proceedings of the 2015 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Banff, AB, Canada, 13–16 October 2015; pp. 1–10. [Google Scholar] [CrossRef]
- Eisa, S.; Peixoto, J.; Meneses, F.; Moreira, A. Removing useless APs and fingerprints from WiFi indoor positioning radio maps. In Proceedings of the International Conference on Indoor Positioning and Indoor Navigation, Montbeliard, France, 28–31 October 2013; pp. 1–7. [Google Scholar]
- Miyagusuku, R.; Ozaki, K. Distance Invariant Sparse Autoencoder for Wireless Signal Strength Mapping. In Proceedings of the 2021 IEEE/SICE International Symposium on System Integration (SII), Iwaki, Japan, 11–14 January 2021; pp. 29–34. [Google Scholar] [CrossRef]
- Dellaert, F.; Fox, D.; Burgard, W.; Thrun, S. Monte Carlo localization for mobile robots. In Proceedings of the 1999 IEEE International Conference on Robotics and Automation (Cat. No.99CH36288C), Detroit, MI, USA, 10–15 May 1999; Volume 2, pp. 1322–1328. [Google Scholar] [CrossRef]
- Grisetti, G.; Stachniss, C.; Burgard, W. Improved Techniques for Grid Mapping with Rao-Blackwellized Particle Filters. IEEE Trans. Robot. 2007, 23, 34–46. [Google Scholar] [CrossRef]
- Doucet, A.; Freitas, N.; Gordon, N. Sequential Monte-Carlo Methods in Practice; Springer: New York, NY, USA, 2001; Volume 1. [Google Scholar] [CrossRef]
- Rasmussen, C.E. Gaussian Processes in Machine Learning. In ML 2003: Advanced Lectures on Machine Learning; Springer: Berlin/Heidelberg, Germany, 2004; pp. 63–71. [Google Scholar] [CrossRef]
- Bauer, M.; van der Wilk, M.; Rasmussen, C.E. Understanding Probabilistic Sparse Gaussian Process Approximations. arXiv 2017, arXiv:stat.ML/1606.04820. [Google Scholar]
- Snelson, E.; Ghahramani, Z. Sparse Gaussian Processes Using Pseudo-Inputs. 2005. Available online: http://papers.nips.cc/paper/2857-sparse-gaussian-processes-using-pseudo-inputs (accessed on 1 March 2021).
- Takebayashi, T.; Miyagusuku, R.; Ozaki, K. Effect of Kernel Function to Magnetic Map and Evaluation of Localization of Magnetic Navigation. In Proceedings of the 2020 IEEE International Conference on Multisensor Fusion and Integration for Intelligent Systems (MFI), Karlsruhe, Germany, 14–16 September 2020; pp. 381–386. [Google Scholar] [CrossRef]
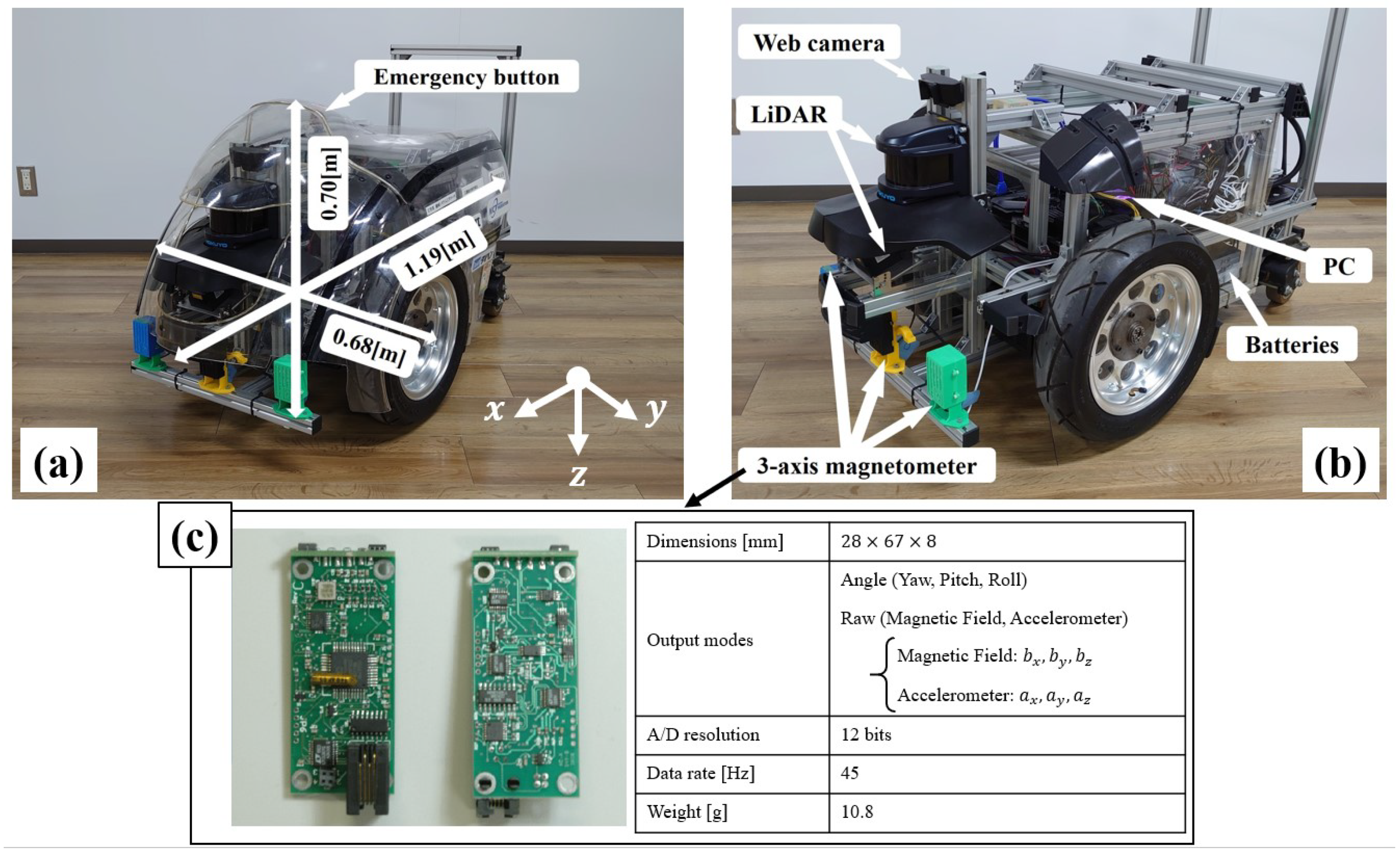
- Kakigi, Y.; Inoue, K.; Hijikata, M.; Ozaki, K. Development of Flexible Cowl Covered Mobile Robot in Consideration with Safety and Design Property. J. Robot. Mech. 2017, 29, 630–638. [Google Scholar] [CrossRef]
- Inoue, K.; Rahok, S.A.; Ozaki, K. Proposal and Consideration of Design Policy for Autonomous Mobile Robots in Real World Robot Challenge. J. Robot. Soc. Jpn. 2012, 30, 234–244. [Google Scholar] [CrossRef][Green Version]
- Hess, W.; Kohler, D.; Rapp, H.; Andor, D. Real-time loop closure in 2D LIDAR SLAM. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 1271–1278. [Google Scholar] [CrossRef]
- Teng, T.; Chen, J.; Zhang, Y.; Low, K.H. Scalable Variational Bayesian Kernel Selection for Sparse Gaussian Process Regression. AAAI 2020, 34, 5997–6004. [Google Scholar] [CrossRef]
- Richardson, R.; Osborne, M.; Howey, D. Gaussian process regression for forecasting battery state of health. J. Power Sources 2017, 357. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Q.; Zhang, L.; Shi, J. Self-Parking management system based on geomagnetic detection and parking lock. IOP Conf. Ser. Mater. Sci. Eng. 2020, 715, 012096. [Google Scholar] [CrossRef]
- Guan, Y.; Li, W.; Tan, J.; Zhu, Y.; Ding, X.; Xiong, Y.; Hou, Q. Research on Geomagnetic Waveform Detection and Vehicle Identification Technology. In Proceedings of the 2021 IEEE 5th Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), Chongqing, China, 12–14 March 2021; Volume 5, pp. 2343–2347. [Google Scholar] [CrossRef]



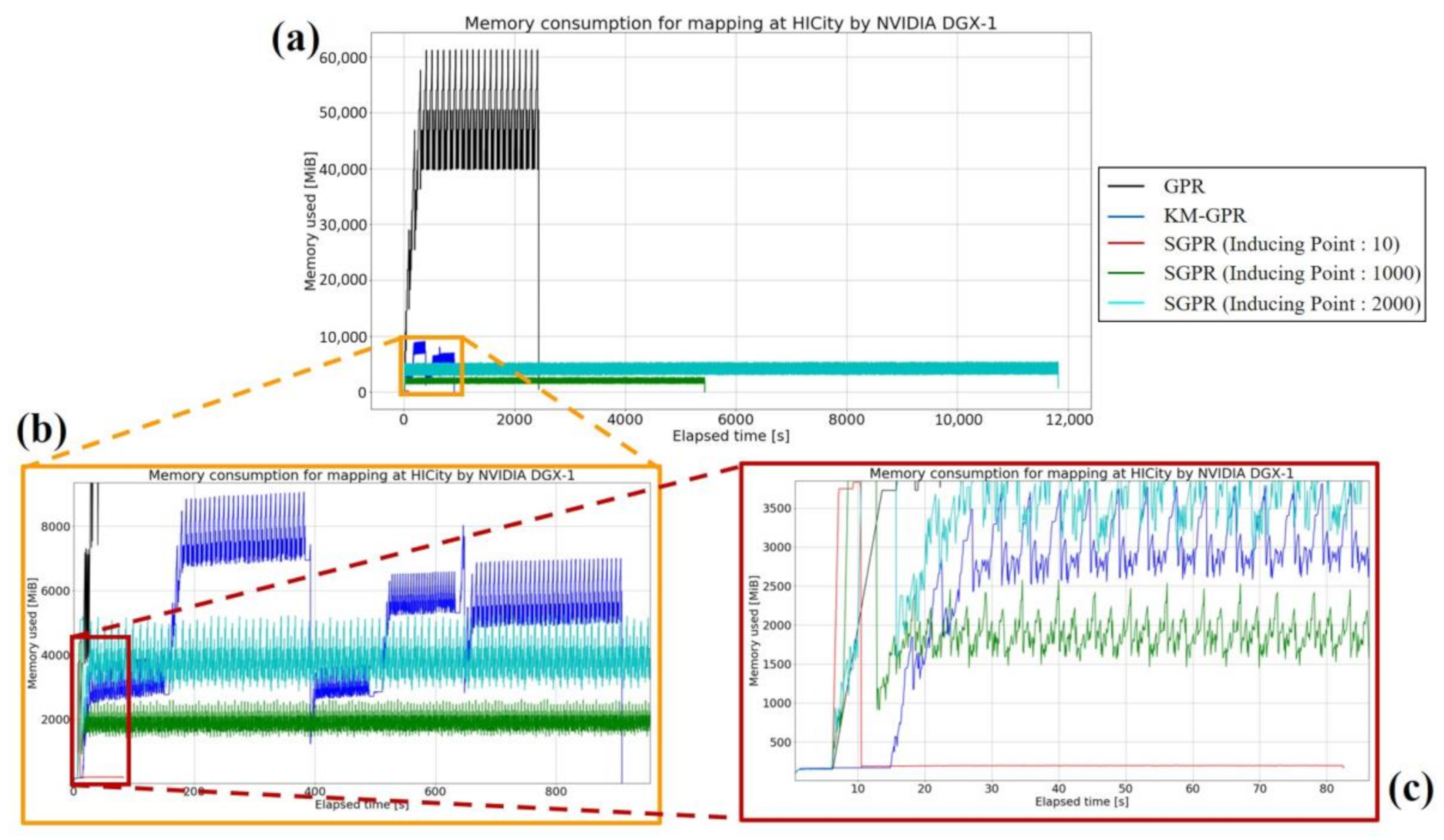
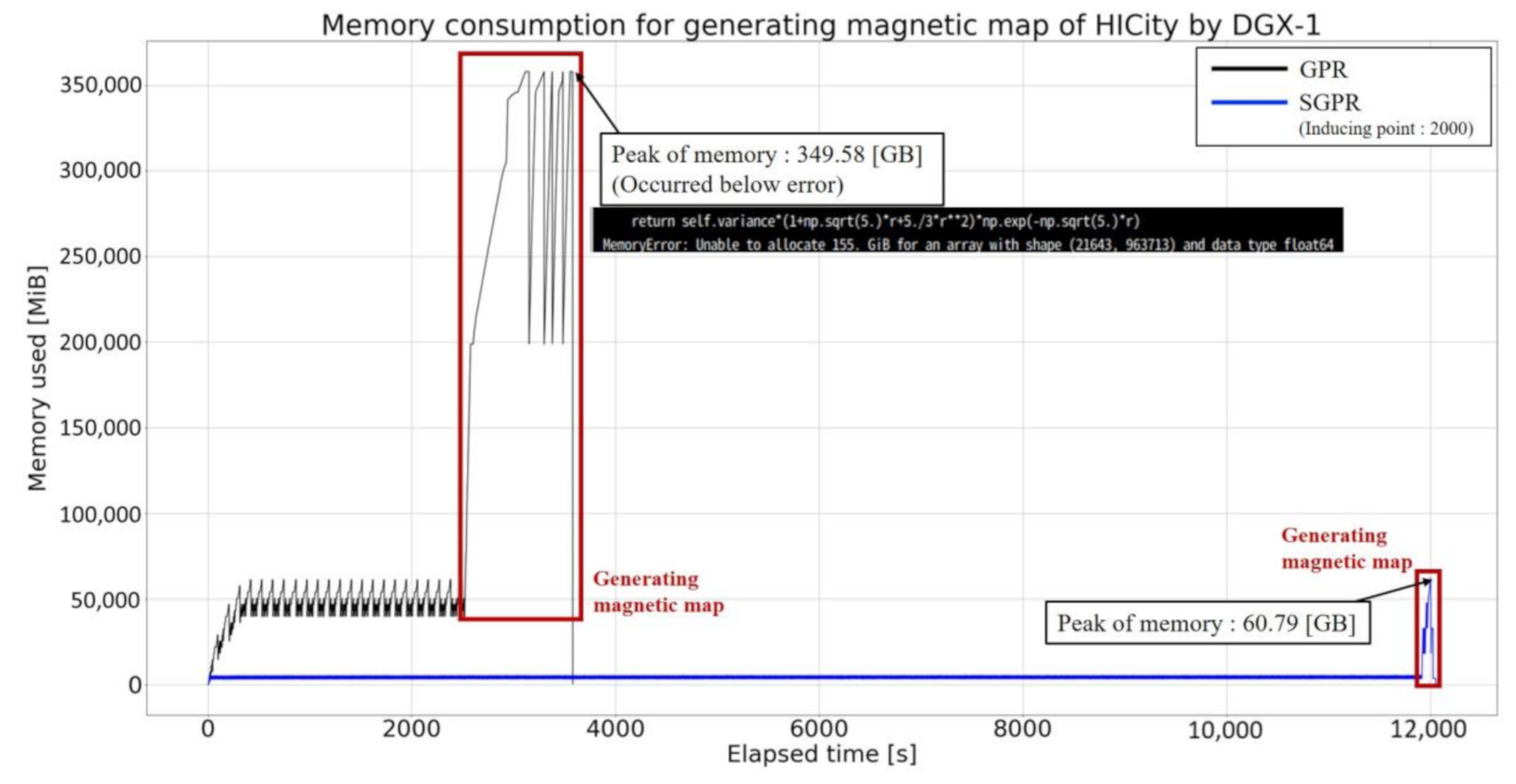
| Path | # Sample | Elapsed Time (mean ± 2std) [s] | Memory Consumption [MiB] | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Full GP | SGPR | Full GP | SGPR | ||||||
| Desktop PC | DGX-1 | Desktop PC | DGX-1 | Desktop PC | DGX-1 | Desktop PC | DGX-1 | ||
| 1 | 540 | 0.26 () | 0.68 () | 1.71 () | 2.11 () | 178.379 | 215.223 | 124.738 | 160.602 |
| 2 | 356 | 0.17 () | 0.45 () | 1.49 () | 2.21 () | 146.918 | 182.457 | 125.832 | 162.594 |
| 3 | 876 | 0.66 () | 1.55 () | 2.15 () | 2.52 () | 247.039 | 294.352 | 124.336 | 161.336 |
| 4 | 859 | 0.65 () | 1.59 () | 1.81 () | 2.36 () | 243.086 | 290.250 | 124.945 | 161.465 |
| 5 | 362 | 0.15 () | 0.38 () | 1.59 () | 2.02 () | 143.902 | 183.395 | 126.637 | 162.480 |
| 6 | 224 | 0.08 () | 0.22 () | 1.27 () | 1.88 () | 130.973 | 169.520 | 125.418 | 161.199 |
| 7 | 211 | 0.09 () | 0.26 () | 1.42 () | 1.69 () | 130.016 | 169.371 | 124.629 | 161.844 |
| 8 | 246 | 0.12 () | 0.24 () | 4.97 () | 2.55 () | 132.621 | 170.117 | 124.910 | 162.012 |
| 9 | 196 | 0.08 () | 0.23 () | 1.71 () | 1.94 () | 129.906 | 168.516 | 125.336 | 161.133 |
| 10 | 223 | 0.08 () | 0.22 () | 5.89 () | 7.81 () | 131.219 | 168.621 | 125.074 | 161.285 |
| 11 | 287 | 0.10 () | 0.26 () | 3.78 () | 6.08 () | 139.516 | 174.492 | 125.156 | 161.816 |
| Desktop PC | NVIDIA DGX-1 1 | |
|---|---|---|
| Processor | Intel Core i7-9700 CPU@3.00 GHz × 8 2 | Dual 20-Core Intel Xeon E5-2698 v4 2.2 GHz |
| RAM | 32 GB (Crucial CT16G4SFD8266 × 2 3) | 512 GB 2,133 MHz DDR4 RDIMM |
| Storage | Samusung SSD 860 EVO MZ-76E500 4 | 4X 1.92 TB SSD RAID 0 |
| OS | Ubuntu 20.04.1 LTS | Ubuntu 18.04.1 LTS |
| Calculation Process | Memory Consumption Order | Computational Order | |
|---|---|---|---|
| GPR | Covariance vector: | ||
| Covariance matrix: | |||
| Inverse matrix of : | |||
| Matrix product: | |||
| SGPR | Covariance matrix: | ||
| Diagonal matrix: | |||
| Matrix: | |||
| Inverse matrix: |
| RBF | Exponential | Matern 3/2 | Matern 5/2 | Exponential + Cosine | Exponential + Matern 3/2 | Exponential + Cosine + RBF | |
|---|---|---|---|---|---|---|---|
| Ave (±2std) [m] | 0.616 () | 0.715 () | 0.578 () | 0.495 () | 0.788 () | 0.693 () | 0.619 () |
| Min [m] | 0.295 | 0.340 | 0.301 | 0.266 | 0.286 | 0.317 | 0.293 |
| Max [m] | 3.07 | 3.18 | 1.96 | 2.13 | 4.09 | 1.86 | 2.32 |
| REAL | Hardware | 5 | 10 | 20 | 30 | 40 | 50 | GPR |
| Desktop PC | 2.61 () | 4.55 () | 7.27 () | 10.9 () | 14.5 () | 17.7 () | 75.0 () | |
| DGX-1 | 18.78 () | 29.30 () | 43.71 () | 58.26 () | 67.36 () | 77.77 () | 127.6 () | |
| HICity | Hardware | 10 | 50 | 100 | 500 | 1K | 2K | GPR |
| Desktop PC | 15.4 () | 78.7 () | 166.4 () | 1197.3 () | 2753.3 () | - | - | |
| DGX-1 | 63.8 () | 228.1 () | 456.7 () | 2670.3 () | 5426.4 () | 11358.1 () | 2315.4 () |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Takebayashi, T.; Miyagusuku, R.; Ozaki, K. Development of Magnetic-Based Navigation by Constructing Maps Using Machine Learning for Autonomous Mobile Robots in Real Environments. Sensors 2021, 21, 3972. https://doi.org/10.3390/s21123972
Takebayashi T, Miyagusuku R, Ozaki K. Development of Magnetic-Based Navigation by Constructing Maps Using Machine Learning for Autonomous Mobile Robots in Real Environments. Sensors. 2021; 21(12):3972. https://doi.org/10.3390/s21123972
Chicago/Turabian StyleTakebayashi, Takumi, Renato Miyagusuku, and Koichi Ozaki. 2021. "Development of Magnetic-Based Navigation by Constructing Maps Using Machine Learning for Autonomous Mobile Robots in Real Environments" Sensors 21, no. 12: 3972. https://doi.org/10.3390/s21123972
APA StyleTakebayashi, T., Miyagusuku, R., & Ozaki, K. (2021). Development of Magnetic-Based Navigation by Constructing Maps Using Machine Learning for Autonomous Mobile Robots in Real Environments. Sensors, 21(12), 3972. https://doi.org/10.3390/s21123972







