Performance Enhancement for Full-Duplex Relaying with Time-Switching-Based SWIPT in Wireless Sensors Networks
Abstract
1. Introduction
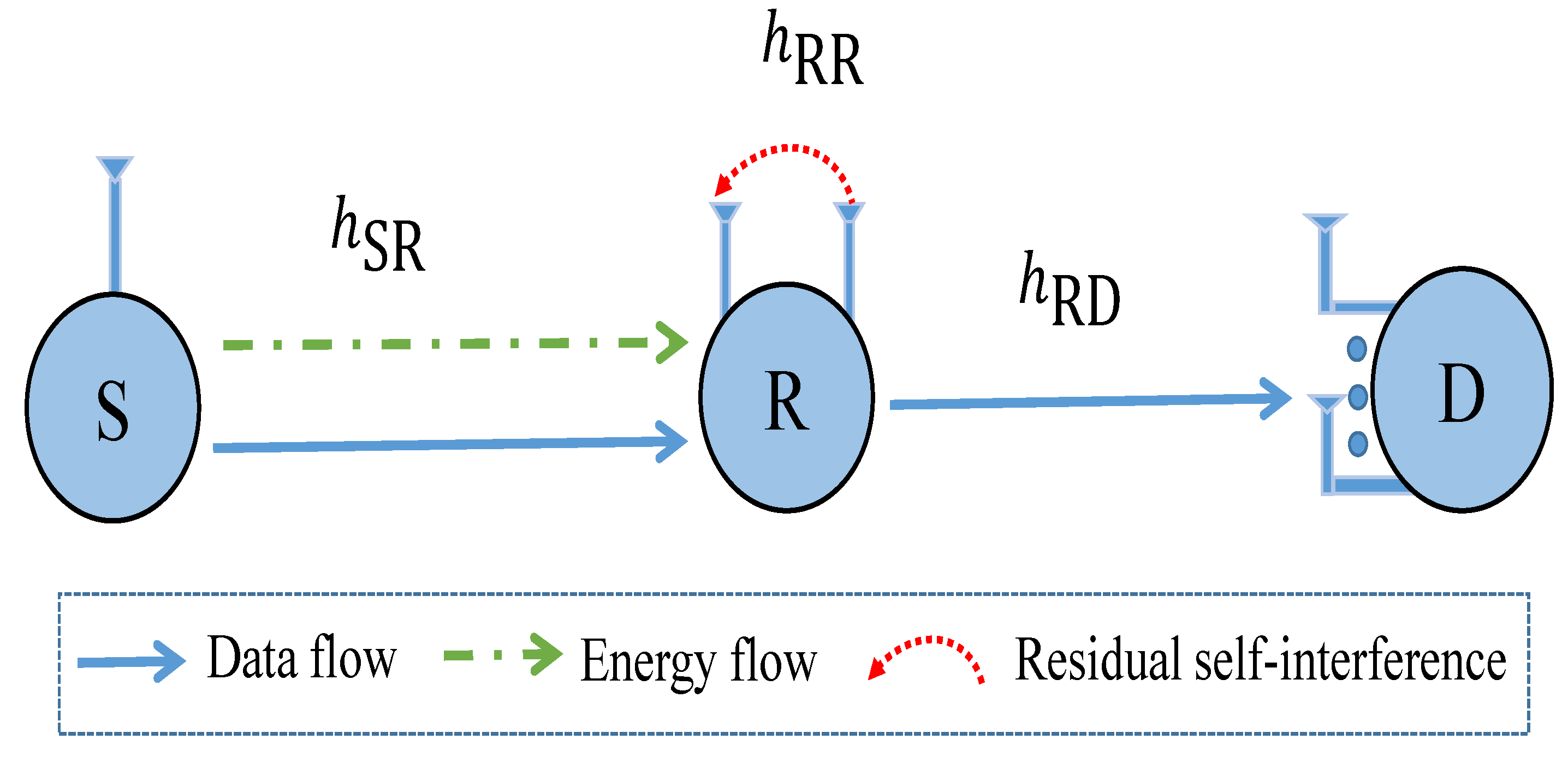
- We propose a SIMO system model in which a two-antenna FD relay node can harvest energy from RF signals of a single-antenna source and then use the harvested energy to transfer information to a multi-antenna destination. Specifically, the destination can adopt SC or MRC to decode the received information.
- Both static TS factor (STSF)- and optimal dynamic TS factor (ODTSF)-based methods are investigated in our work. Especially in ODTSF methods, we derive the exact closed form of optimal dynamic TS factor for maximizing the total throughput obtained at the destination.
- To fully investigate the system performance, we propose four protocols, namely static time-switching factor with selection combining (STSF-SC), static time-switching factor with maximal ratio combing (STSF-MRC), optimal dynamic time-switching factor with selection combining (ODTSF-SC), and optimal dynamic time-switching factor with maximal ratio combing (ODTSF-MRC).
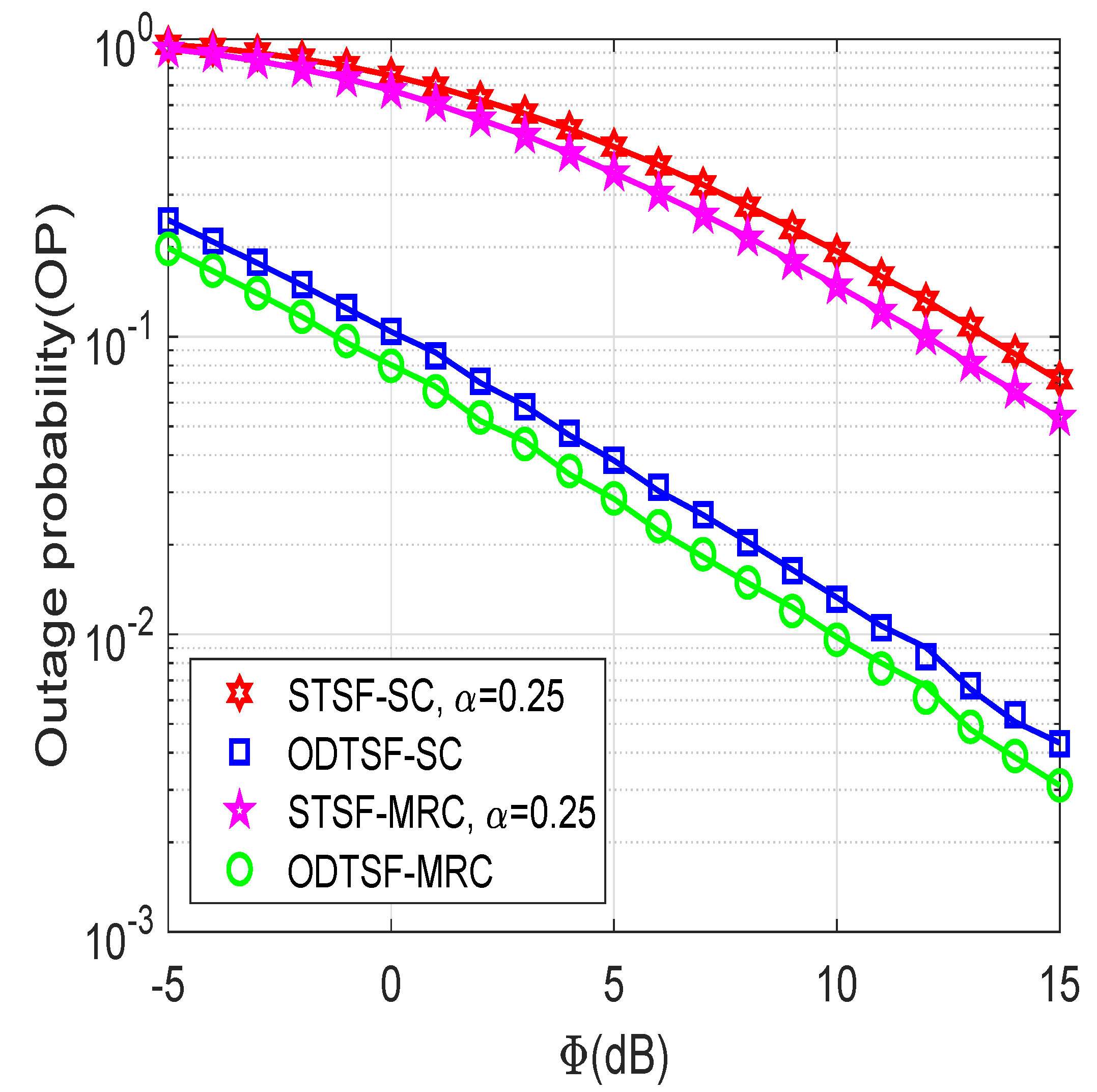
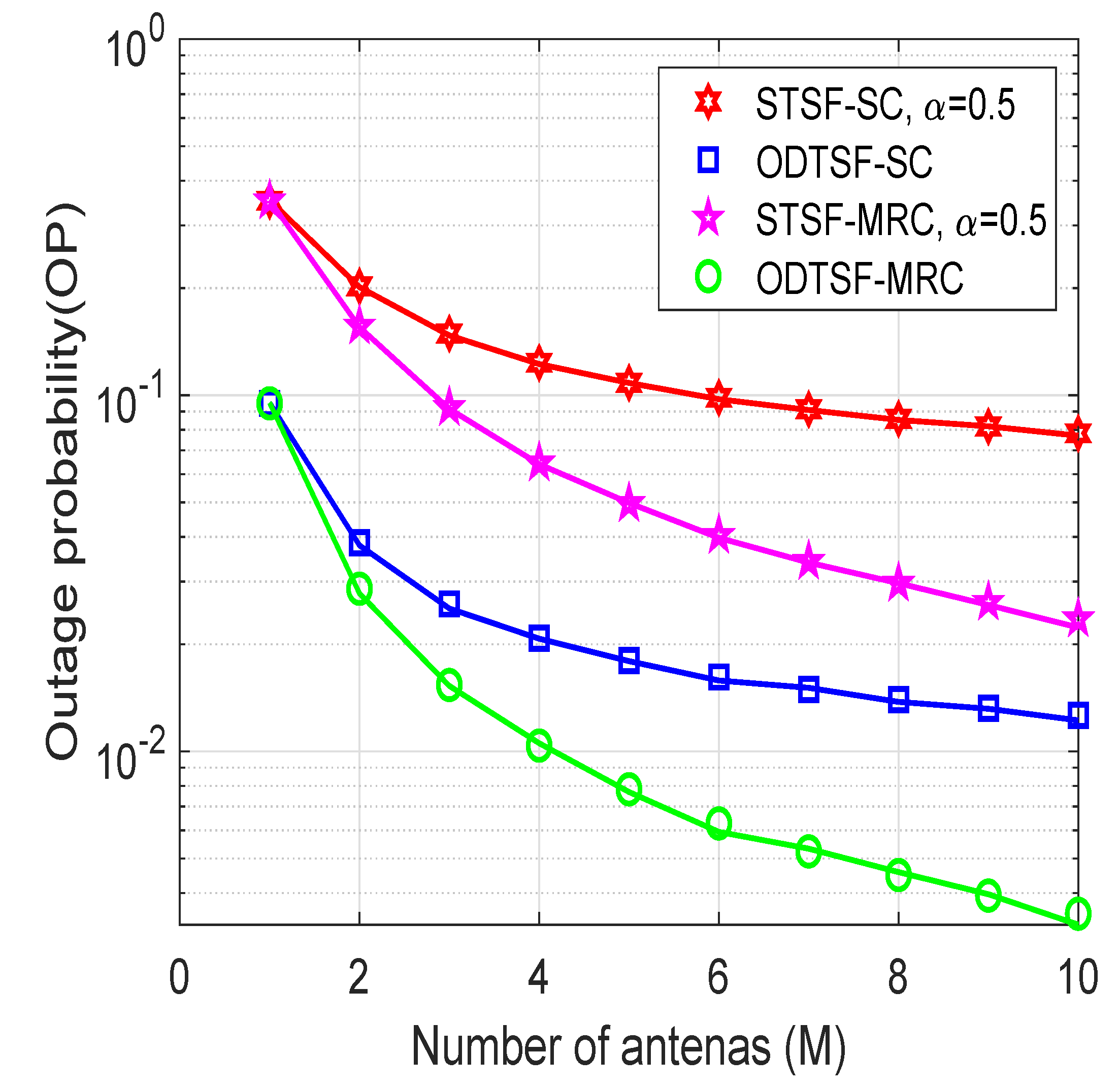
- Monte Carlo simulations are performed to corroborate the effectiveness of our proposed methods. Specifically, the results show that ODTSF-MRC always outperforms other schemes in terms of outage probability.
2. System Model
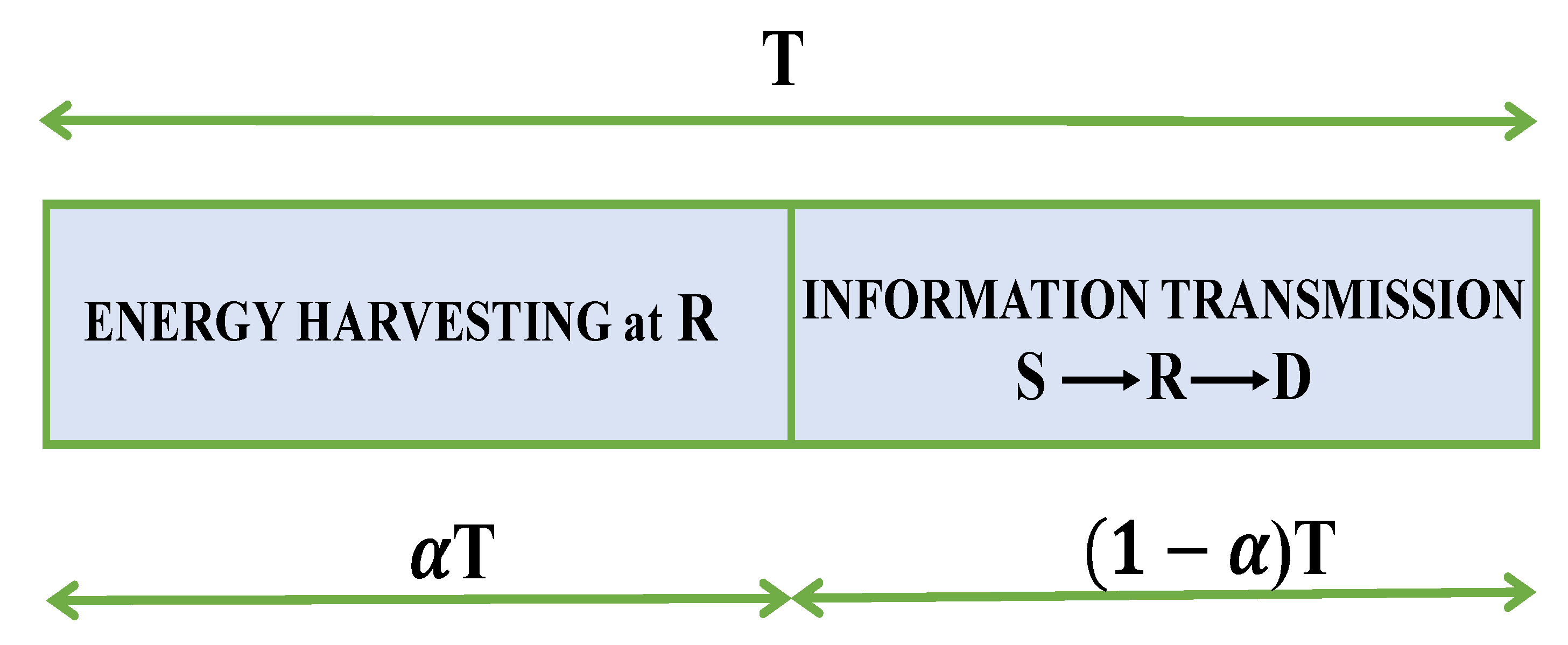
2.1. Energy Harvesting and Information Transmission
2.1.1. Case 1: Selection Combining (SC) Is Adopted at the Destination
2.1.2. Case 2: Maximal Ratio Combining (MRC) Is Adopted at the Destination
3. Outage Probability (OP) Analysis
3.1. Case 1: Static Time-Switching Factor (STSF)
3.1.1. With SC
3.1.2. With MRC
3.2. Case 2: Optimal Dynamic Time-Switching Factor (ODTSF)
3.2.1. With SC
3.2.2. With MRC
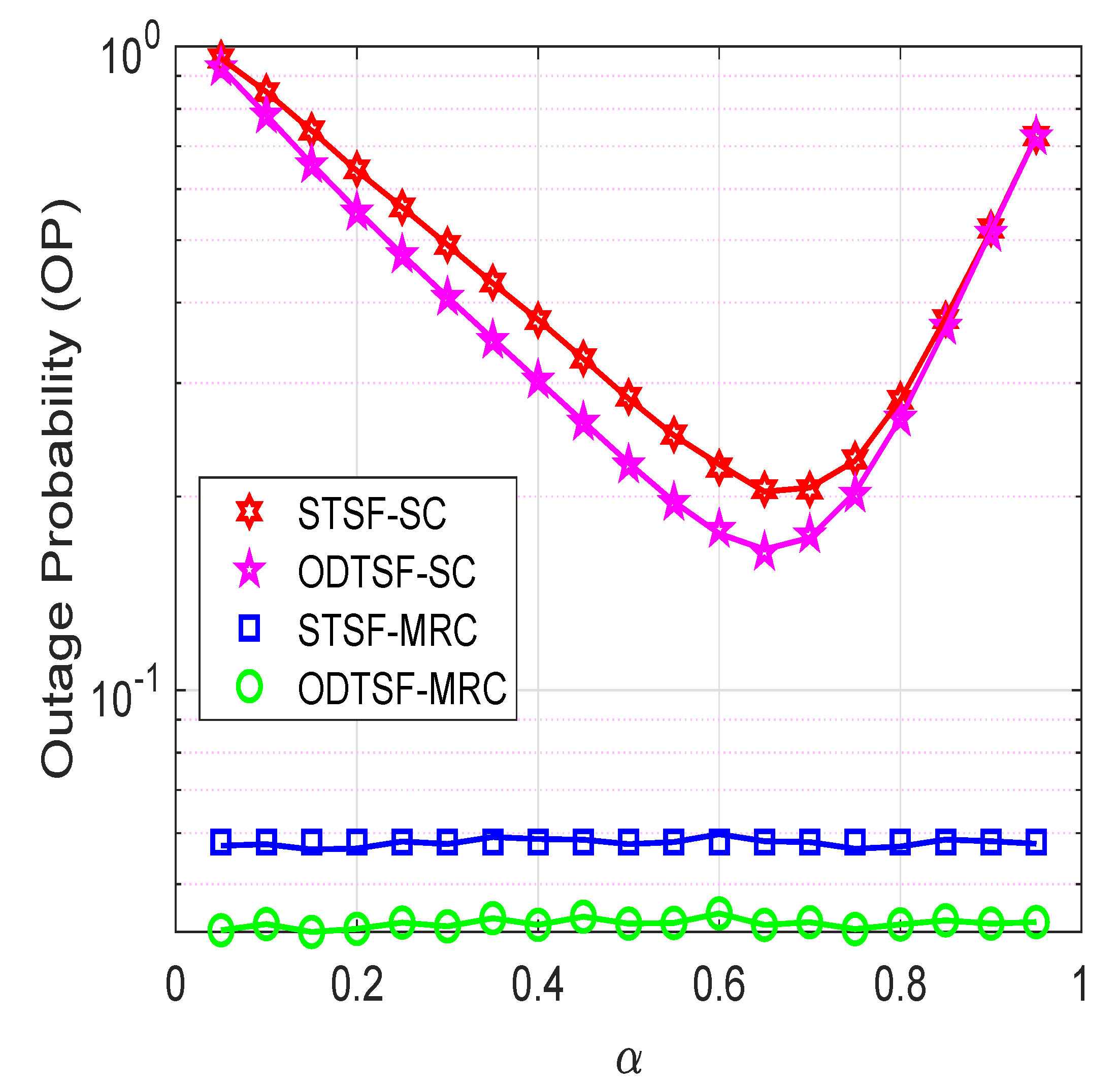
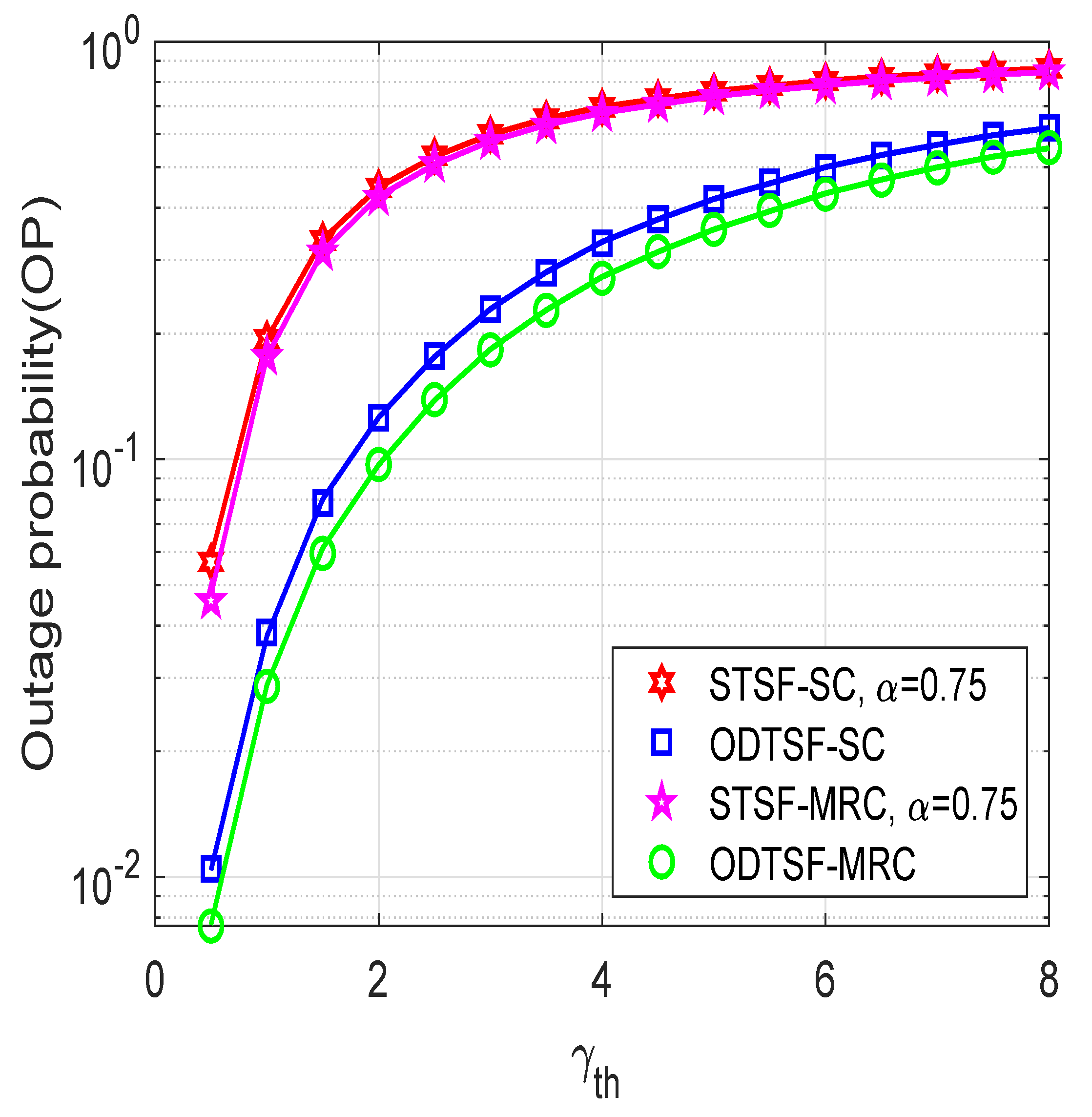
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Baniata, M.; Reda, H.T.; Chilamkurti, N.; Abuadbba, A. Energy-Efficient Hybrid Routing Protocol for IoT Communication Systems in 5G and Beyond. Sensors 2021, 21, 537. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, P.X.; Tran, D.H.; Onireti, O.; Tin, P.T.; Nguyen, S.Q.; Chatzinotas, S.; Poor, H.V. Backscatter-Assisted Data Offloading in OFDMA-based Wireless Powered Mobile Edge Computing for IoT Networks. IEEE Internet Things J. 2021, 9233–9243. [Google Scholar] [CrossRef]
- Nguyen, A.N.; Vo, V.N.; So-In, C.; Ha, D.B. System Performance Analysis for an Energy Harvesting IoT System Using a DF/AF UAV-Enabled Relay with Downlink NOMA under Nakagami-m Fading. Sensors 2021, 21, 285. [Google Scholar] [CrossRef] [PubMed]
- Tran, D.H.; Nguyen, V.D.; Symeon, C.; Vu, X.T.; Bjorn, O. UAV Relay-Assisted Emergency Communications in IoT Networks: Resource Allocation and Trajectory Optimization. arXiv 2020, arXiv:2008.00218. [Google Scholar]
- Holst, A. Number of IoT Connected Devices Worldwide 2019–2030. 2021. Available online: https://www.statista.com/statistics/1183457/iot-connected-devices-worldwide/ (accessed on 1 June 2021).
- Ponnusamy, V.; Jung, L.T.; Ramachandran, T.; Zaman, N. Bio-inspired energy scavenging in wireless ad hoc network. In Proceedings of the 2017 International Conference on Innovations in Electrical Engineering and Computational Technologies (ICIEECT), Karachi, Pakistan, 5–7 April 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Vacca, J.R. Computer and Information Security Handbook; Elsevier Science: Amsterdam, The Netherlands, 2012; Chapter 11. [Google Scholar]
- Hieu, T.D.; Dung, L.T.; Kim, B.S. Stability-aware geographic routing in energy harvesting wireless sensor networks. Sensors 2016, 16, 696. [Google Scholar] [CrossRef]
- Bi, S.; Ho, C.K.; Zhang, R. Wireless powered communication: Opportunities and challenges. IEEE Commun. Mag. 2015, 53, 117–125. [Google Scholar] [CrossRef]
- Niyato, D.; Kim, D.I.; Maso, M.; Han, Z. Wireless powered communication networks: Research directions and technological approaches. IEEE Wirel. Commun. 2017, 24, 88–97. [Google Scholar] [CrossRef]
- Nguyen, T.N.; Tran, M.; Nguyen, T.L.; Ha, D.H.; Voznak, M. Multisource power splitting energy harvesting relaying network in half-duplex system over block Rayleigh fading channel: System performance analysis. Electronics 2019, 8, 67. [Google Scholar] [CrossRef]
- Lee, S.; Zhang, R.; Huang, K. Opportunistic Wireless Energy Harvesting in Cognitive Radio Networks. IEEE Trans. Wirel. Commun. 2013, 12, 4788–4799. [Google Scholar] [CrossRef]
- Maso, M.; Liu, C.; Lee, C.; Quek, T.Q.S.; Cardoso, L.S. Energy-recycling full-duplex radios for next-generation networks. IEEE J. Sel. Areas Commun. 2015, 33, 2948–2962. [Google Scholar] [CrossRef]
- Nguyen, T.N.; Minh, T.H.Q.; Tran, P.T.; Voznak, M.; Duy, T.T.; Nguyen, T.L.; Tin, P.T. Performance enhancement for energy harvesting based two-way relay protocols in wireless ad-hoc networks with partial and full relay selection methods. Ad Netw. 2019, 84, 178–187. [Google Scholar] [CrossRef]
- Hieu, T.D.; Duy, T.T.; Kim, B. Performance Enhancement for Multihop Harvest-to-Transmit WSNs With Path-Selection Methods in Presence of Eavesdroppers and Hardware Noises. IEEE Sens. J. 2018, 18, 5173–5186. [Google Scholar] [CrossRef]
- Kellogg, B.; Parks, A.; Gollakota, S.; Smith, J.R.; Wetherall, D. Wi-Fi backscatter: Internet connectivity for RF-powered devices. In Proceedings of the 2014 ACM Conference on SIGCOMM, Chicago, IL, USA, 17–22 August 2014; pp. 607–618. [Google Scholar]
- Tran Dinh, H.; Duy, T.T.; Choi, S.G. Performance enhancement for harvest-to-transmit cognitive multi-hop networks with best path selection method under presence of eavesdropper. In Proceedings of the 2018 20th International Conference on Advanced Communication Technology (ICACT), Chuncheon, Korea, 11–14 February 2018; pp. 323–328. [Google Scholar]
- Varshney, L.R. Transporting information and energy simultaneously. In Proceedings of the 2008 IEEE International Symposium on Information Theory, Toronto, ON, Canada, 6–11 July 2008; pp. 1612–1616. [Google Scholar] [CrossRef]
- Grover, P.; Sahai, A. Shannon meets Tesla: Wireless information and power transfer. In Proceedings of the 2010 IEEE International Symposium on Information Theory, Austin, TX, USA, 13–18 June 2010; pp. 2363–2367. [Google Scholar] [CrossRef]
- Zhang, R.; Ho, C.K. MIMO Broadcasting for Simultaneous Wireless Information and Power Transfer. IEEE Trans. Wirel. Commun. 2013, 12, 1989–2001. [Google Scholar] [CrossRef]
- Ha, D.H.; Nguyen, T.N.; Tran, M.H.Q.; Li, X.; Tran, P.T.; Voznak, M. Security and Reliability Analysis of a Two-Way Half-Duplex Wireless Relaying Network Using Partial Relay Selection and Hybrid TPSR Energy Harvesting at Relay Nodes. IEEE Access 2020, 8, 187165–187181. [Google Scholar] [CrossRef]
- Nguyen, T.N.; Tran, P.T.; Minh, T.H.Q.; Vozňák, M.; Ševčík, L. Two-way half duplex decode and forward relaying network with hardware impairment over Rician fading channel: System performance analysis. Elektron. Elektrotech. 2018, 24, 74–78. [Google Scholar] [CrossRef]
- Yuan, T.; Liu, M.; Feng, Y. Performance Analysis for SWIPT Cooperative DF Communication Systems with Hybrid Receiver and Non-Linear Energy Harvesting Model. Sensors 2020, 20, 2472. [Google Scholar] [CrossRef]
- Nguyen, T.N.; Tran, P.T.; Voznak, M. Wireless energy harvesting meets receiver diversity: A successful approach for two-way half-duplex relay networks over block Rayleigh fading channel. Comput. Netw. 2020, 172, 107176. [Google Scholar] [CrossRef]
- Zhou, X.; Guo, J.; Durrani, S.; Krikidis, I. Performance of Maximum Ratio Transmission in Ad Hoc Networks With SWIPT. IEEE Wirel. Commun. Lett. 2015, 4, 529–532. [Google Scholar] [CrossRef]
- Psomas, C.; Krikidis, I. Successive Interference Cancellation in Bipolar Ad Hoc Networks with SWIPT. IEEE Wirel. Commun. Lett. 2016, 5, 364–367. [Google Scholar] [CrossRef]
- Park, J.; Clerckx, B.; Song, C.; Wu, Y. An Analysis of the Optimum Node Density for Simultaneous Wireless Information and Power Transfer in Ad Hoc Networks. IEEE Trans. Veh. Technol. 2018, 67, 2713–2726. [Google Scholar] [CrossRef]
- Sharma, S.K.; Bogale, T.E.; Le, L.B.; Chatzinotas, S.; Wang, X.; Ottersten, B. Dynamic Spectrum Sharing in 5G Wireless Networks With Full-Duplex Technology: Recent Advances and Research Challenges. IEEE Commun. Surv. Tutor. 2018, 20, 674–707. [Google Scholar] [CrossRef]
- Huang, H.; Hu, S.; Yang, T.; Yuan, C.W. Full Duplex Non-orthogonal Multiple Access with Layers-based Optimized Mobile Relays Subsets Algorithm in B5G/6G Ubiquitous Networks. IEEE Internet Things J. 2020. [Google Scholar] [CrossRef]
- Nguyen, B.C.; Hoang, T.M.; Tran, P.T.; Nguyen, T.N. Outage probability of NOMA system with wireless power transfer at source and full-duplex relay. AEU Int. J. Electron. Commun. 2020, 116, 152957. [Google Scholar] [CrossRef]
- Ye, H.; Kang, X.; Joung, J.; Liang, Y. Optimization for Full-Duplex Rotary-Wing UAV-Enabled Wireless-Powered IoT Networks. IEEE Trans. Wirel. Commun. 2020, 19, 5057–5072. [Google Scholar] [CrossRef]
- Zhu, L.; Zhang, J.; Xiao, Z.; Cao, X.; Xia, X.G.; Schober, R. Millimeter-Wave Full-Duplex UAV Relay: Joint Positioning, Beamforming, and Power Control. IEEE J. Sel. Areas Commun. 2020, 38, 2057–2073. [Google Scholar] [CrossRef]
- Nguyen, T.N.; Tran, M.; Nguyen, T.L.; Voznak, M. Adaptive relaying protocol for decode and forward full-duplex system over Rician fading channel: System performance analysis. China Commun. 2019, 16, 92–102. [Google Scholar] [CrossRef]
- Ding, Q.; Lian, Y.; Jing, Y. Performance Analysis of Full-Duplex Massive MIMO Systems with Low-Resolution ADCs/DACs Over Rician Fading Channels. IEEE Trans. Veh. Technol. 2020, 69, 7389–7403. [Google Scholar] [CrossRef]
- Nguyen, B.C.; Tran, X.N.; Hoang, T.M. Performance analysis of full-duplex vehicle-to-vehicle relay system over double-rayleigh fading channels. Mob. Netw. Appl. 2020, 25, 363–372. [Google Scholar] [CrossRef]
- Nguyen, B.C.; Hoang, T.M. Performance analysis of vehicle-to-vehicle communication with full-duplex amplify-and-forward relay over double-Rayleigh fading channels. Veh. Commun. 2019, 19, 100166. [Google Scholar] [CrossRef]
- Nguyen, B.C.; Thang, N.N.; Hoang, T.M. Analysis of outage probability and throughput for energy harvesting full-duplex decode-and-forward vehicle-to-vehicle relay system. Wirel. Commun. Mob. Comput. 2020, 2020, 3539450. [Google Scholar] [CrossRef]
- Su, Y.; Jiang, L.; He, C. Decode-and-forward relaying with full-duplex wireless information and power transfer. IET Commun. 2017, 11, 2110–2115. [Google Scholar] [CrossRef]
- Duy, T.T.; Duong, T.Q.; Thanh, T.L.; Bao, V.N.Q. Secrecy performance analysis with relay selection methods under impact of co-channel interference. IET Commun. 2015, 9, 1427–1435. [Google Scholar] [CrossRef]
- Nguyen, T.N.; Tran, P.T.; Vozňák, M. Power splitting-based energy-harvesting protocol for wireless-powered communication networks with a bidirectional relay. Int. J. Commun. Syst. 2018, 31, e3721. [Google Scholar] [CrossRef]
- Jeffrey, A.; Zwillinger, D. Table of Integrals, Series, and Products, 7th ed.; Elsevier: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Ashraf, M.; Jang, J.; Han, J.; Lee, K.G. Capacity Maximizing Adaptive Power Splitting Protocol for Cooperative Energy Harvesting Communication Systems. IEEE Commun. Lett. 2018, 22, 902–905. [Google Scholar] [CrossRef]
- Dinh Tran, H.; Trung Tran, D.; Choi, S.G. Secrecy performance of a generalized partial relay selection protocol in underlay cognitive networks. Int. J. Commun. Syst. 2018, 31, e3806. [Google Scholar] [CrossRef]
- Tran Tin, P.; Nguyen, T.N.; Duy, T.T.; Voznak, M. Secrecy performance enhancement for underlay cognitive radio networks employing cooperative multi-hop transmission with and without presence of hardware impairments. Entropy 2019, 21, 217. [Google Scholar] [CrossRef]
| Symbol | Parameter Name | Fixed Value | Varying Range |
|---|---|---|---|
| SNR threshold of the system | 1 | 0.5 to 8 | |
| Energy harvesting efficiency | 0.8 | none | |
| Time-switching factor | 0.05–0.95 | 0.05 to 0.95 | |
| Distance between source S and relay R | 1 | none | |
| Distance between relay R and destination D | 0.5 | none | |
| Rate parameter of | 1 | none | |
| Rate parameter of | 0.5 | none | |
| Rate parameter of | 5 | none | |
| Transmit-power-to-noise-ratio | 5 dB | −5 to 15 (dB) | |
| M | No. of antennas at the destination | 2; 3 | 1 to 10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tin, P.T.; Nguyen, T.N.; Tran, D.-H.; Voznak, M.; Phan, V.-D.; Chatzinotas, S. Performance Enhancement for Full-Duplex Relaying with Time-Switching-Based SWIPT in Wireless Sensors Networks. Sensors 2021, 21, 3847. https://doi.org/10.3390/s21113847
Tin PT, Nguyen TN, Tran D-H, Voznak M, Phan V-D, Chatzinotas S. Performance Enhancement for Full-Duplex Relaying with Time-Switching-Based SWIPT in Wireless Sensors Networks. Sensors. 2021; 21(11):3847. https://doi.org/10.3390/s21113847
Chicago/Turabian StyleTin, Phu Tran, Tan N. Nguyen, Dinh-Hieu Tran, Miroslav Voznak, Van-Duc Phan, and Symeon Chatzinotas. 2021. "Performance Enhancement for Full-Duplex Relaying with Time-Switching-Based SWIPT in Wireless Sensors Networks" Sensors 21, no. 11: 3847. https://doi.org/10.3390/s21113847
APA StyleTin, P. T., Nguyen, T. N., Tran, D.-H., Voznak, M., Phan, V.-D., & Chatzinotas, S. (2021). Performance Enhancement for Full-Duplex Relaying with Time-Switching-Based SWIPT in Wireless Sensors Networks. Sensors, 21(11), 3847. https://doi.org/10.3390/s21113847







