Feature Extraction Using Sparse Kernel Non-Negative Matrix Factorization for Rolling Element Bearing Diagnosis
Abstract
1. Introduction
2. Kernel Non-Negative Matrix Factorization
2.1. NMF
2.2. Kernel NMF
3. Sparse KNMF and Update Rule
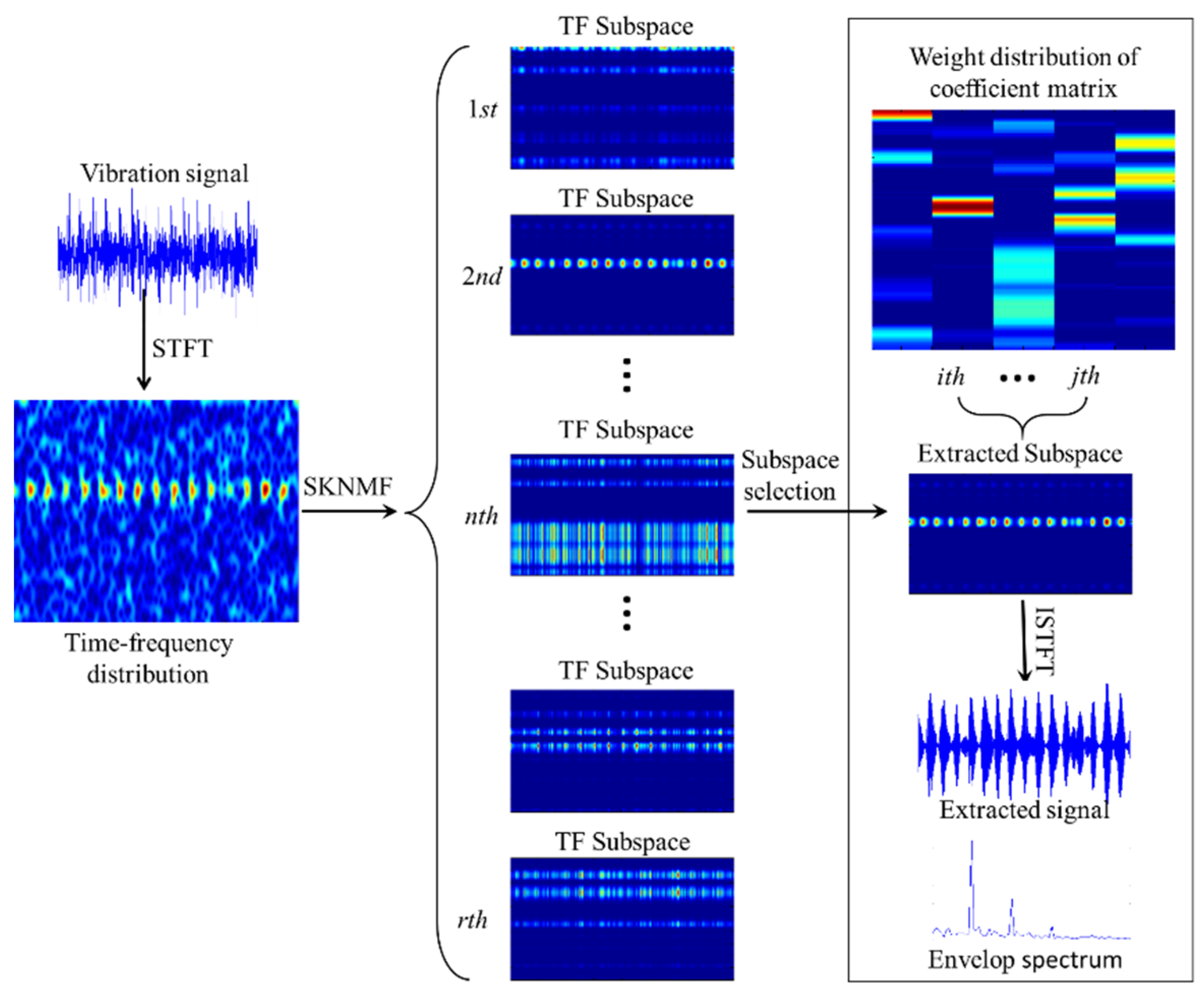
4. Feature Extraction Strategy Based on SKNMF
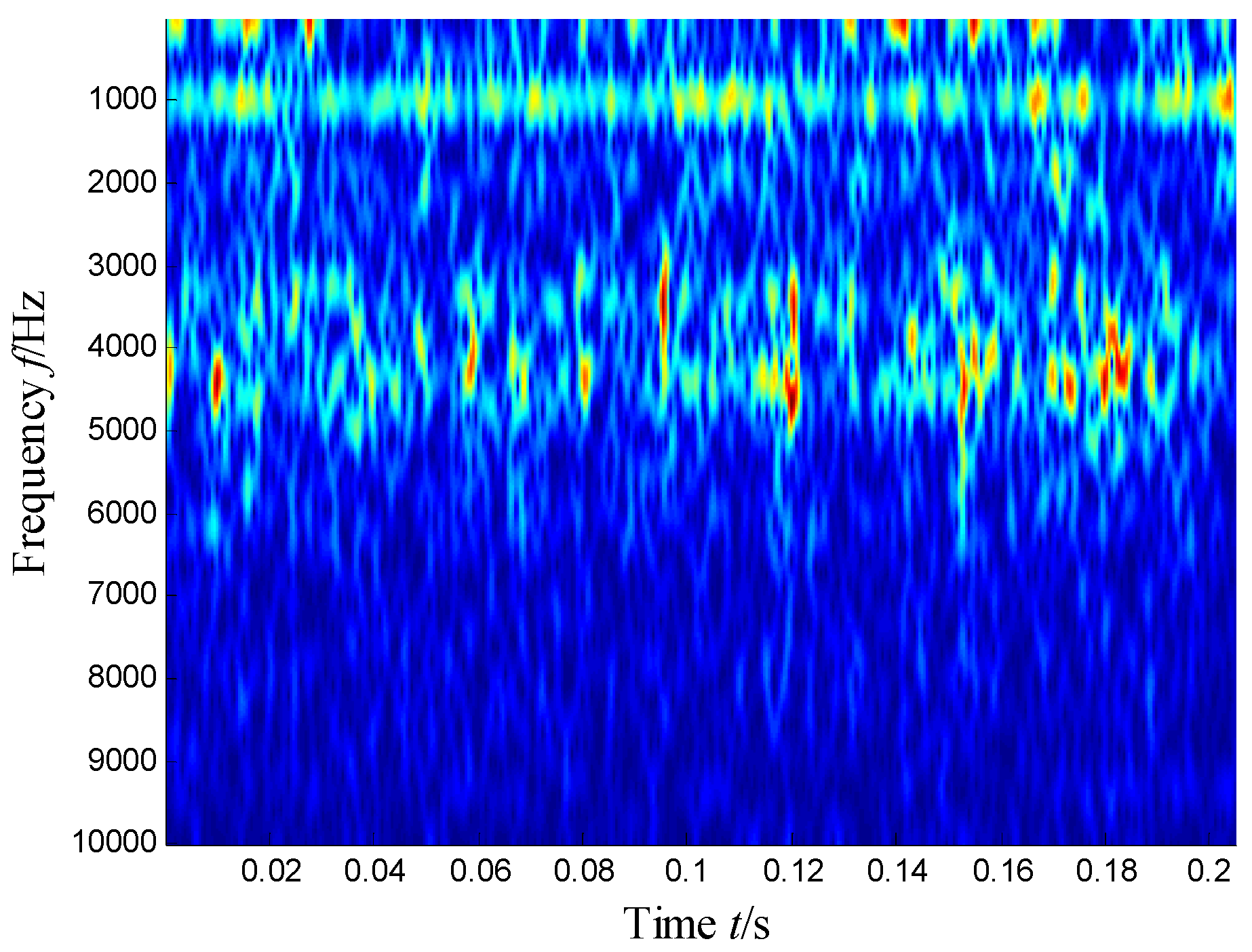
4.1. Time–frequency Distribution Construction
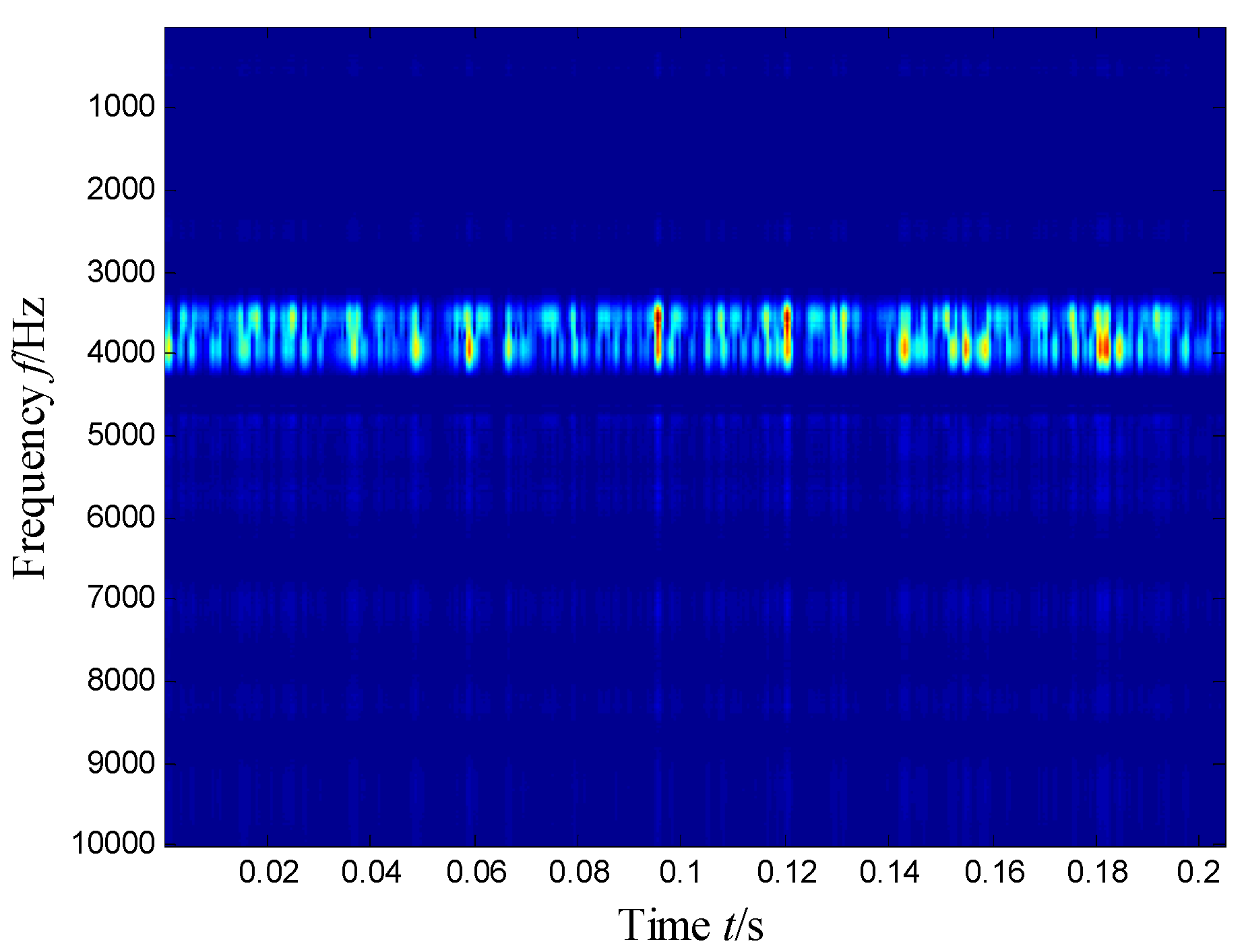
4.2. Subspace Extraction with SKNMF
4.3. Subspace Selection and Waveform Reconstruction
4.4. Envelope Demodulation
5. Experimental Results
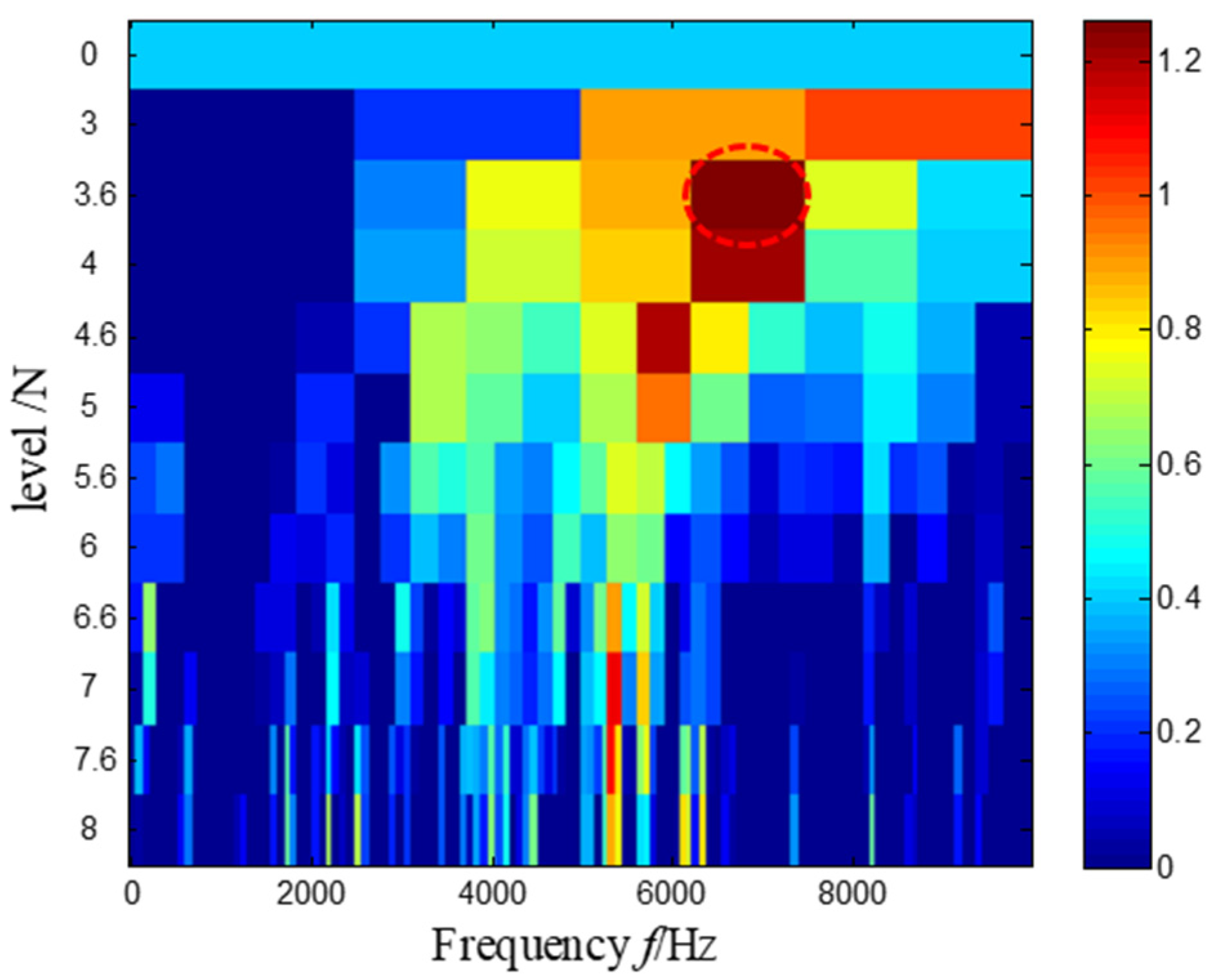
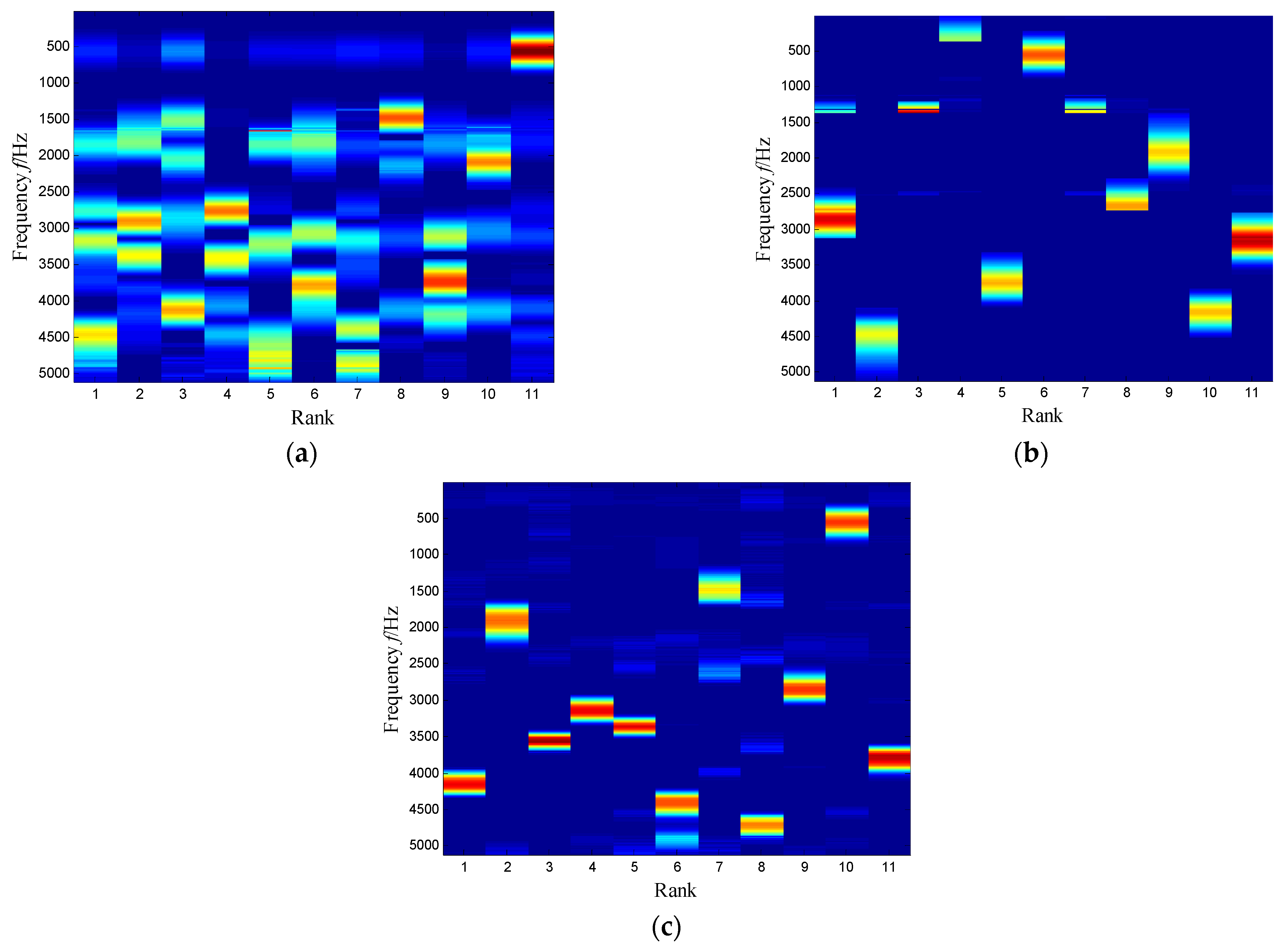
5.1. Comparison Analysis Experiment
5.2. Experimental Verification
5.2.1. Test Rig
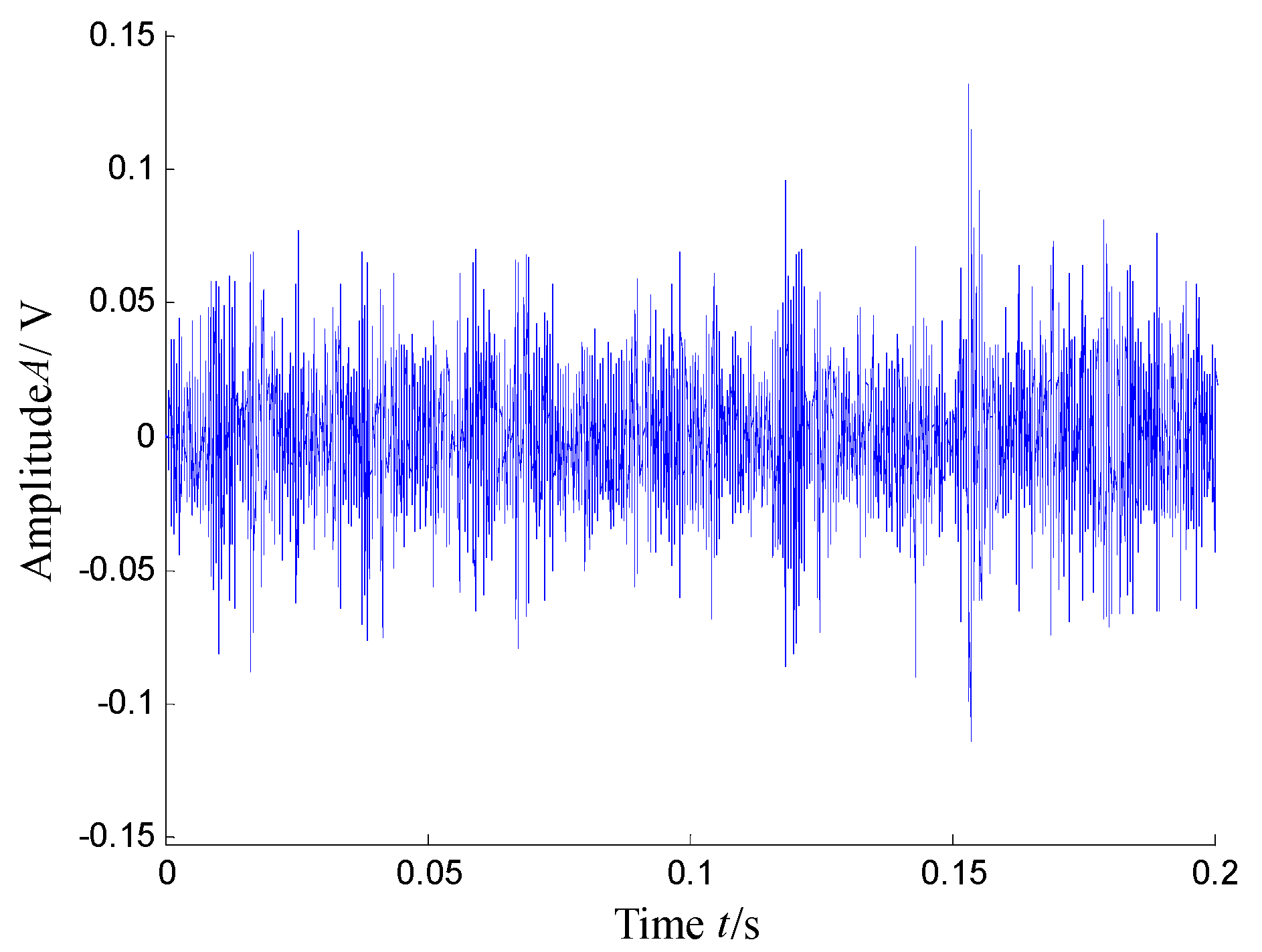
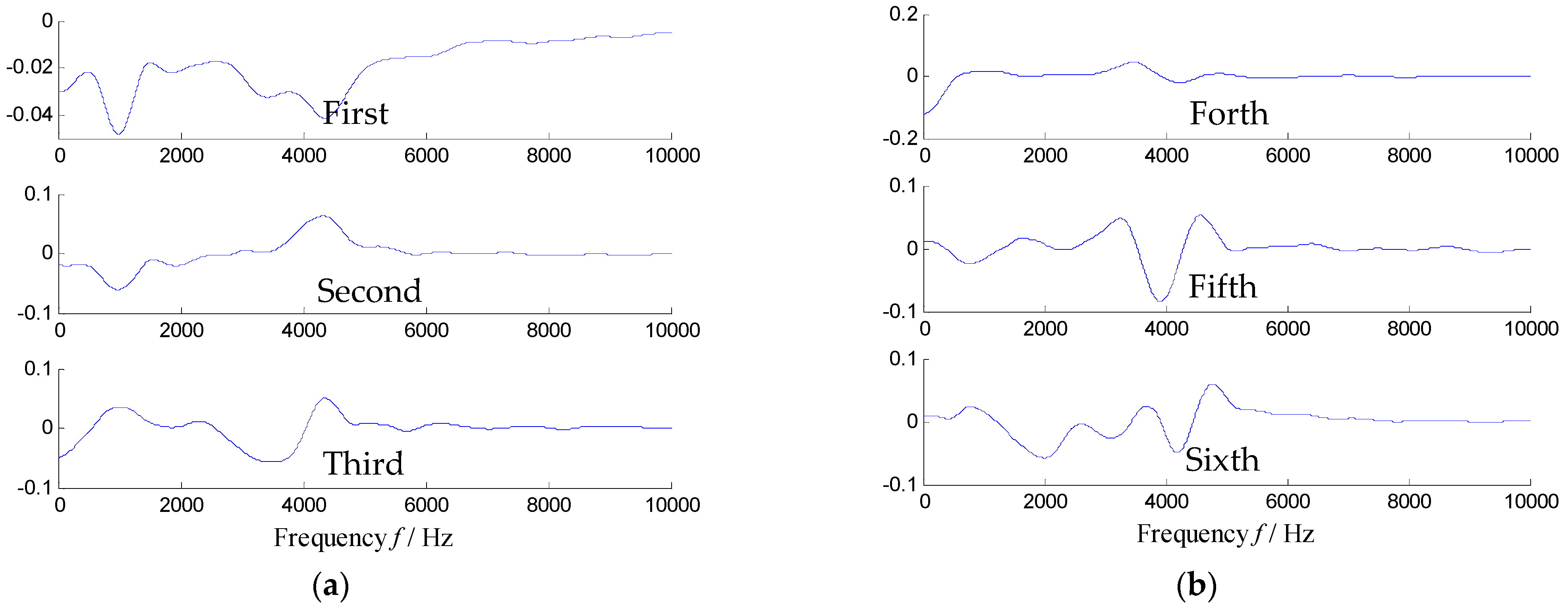
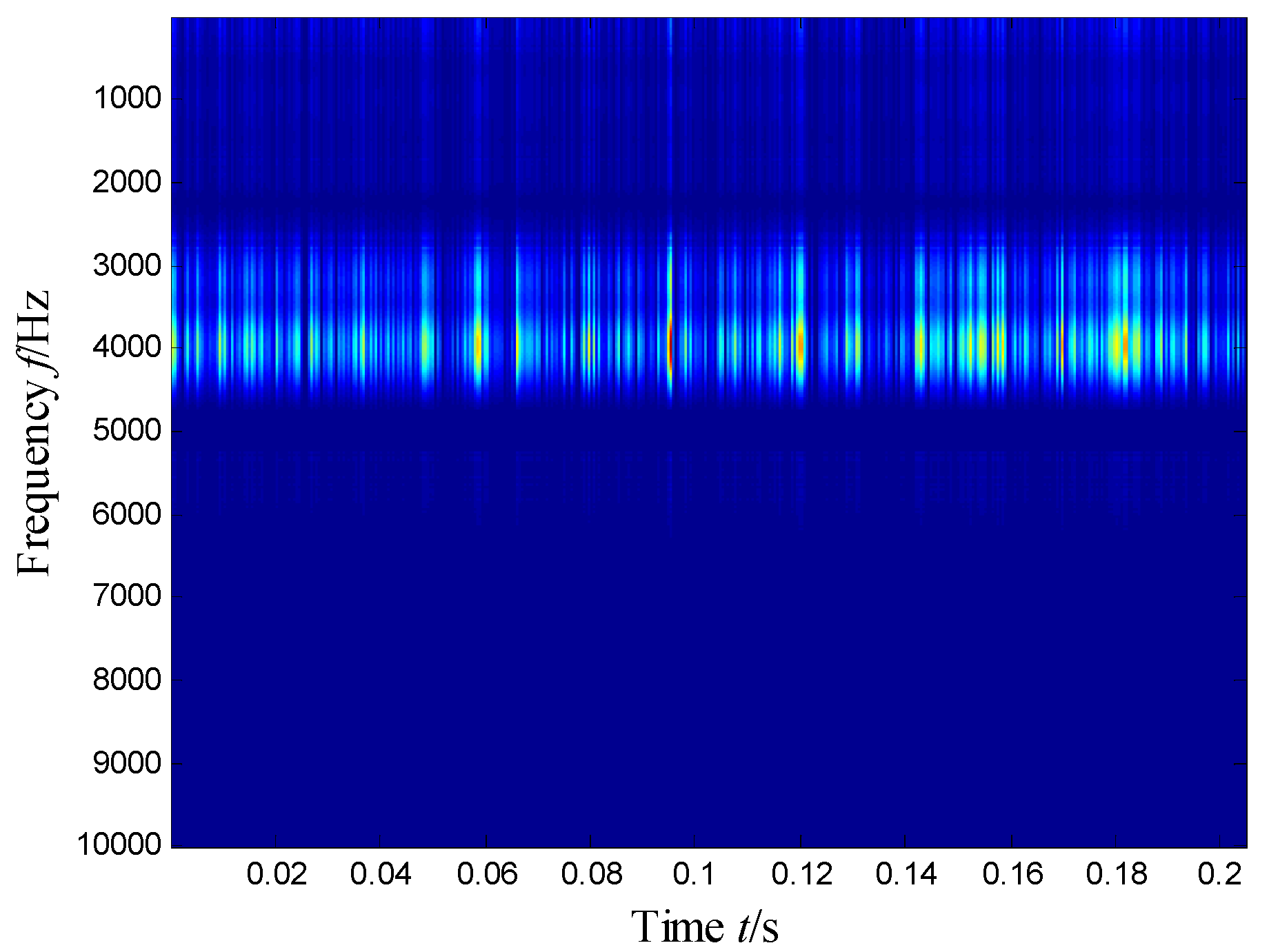
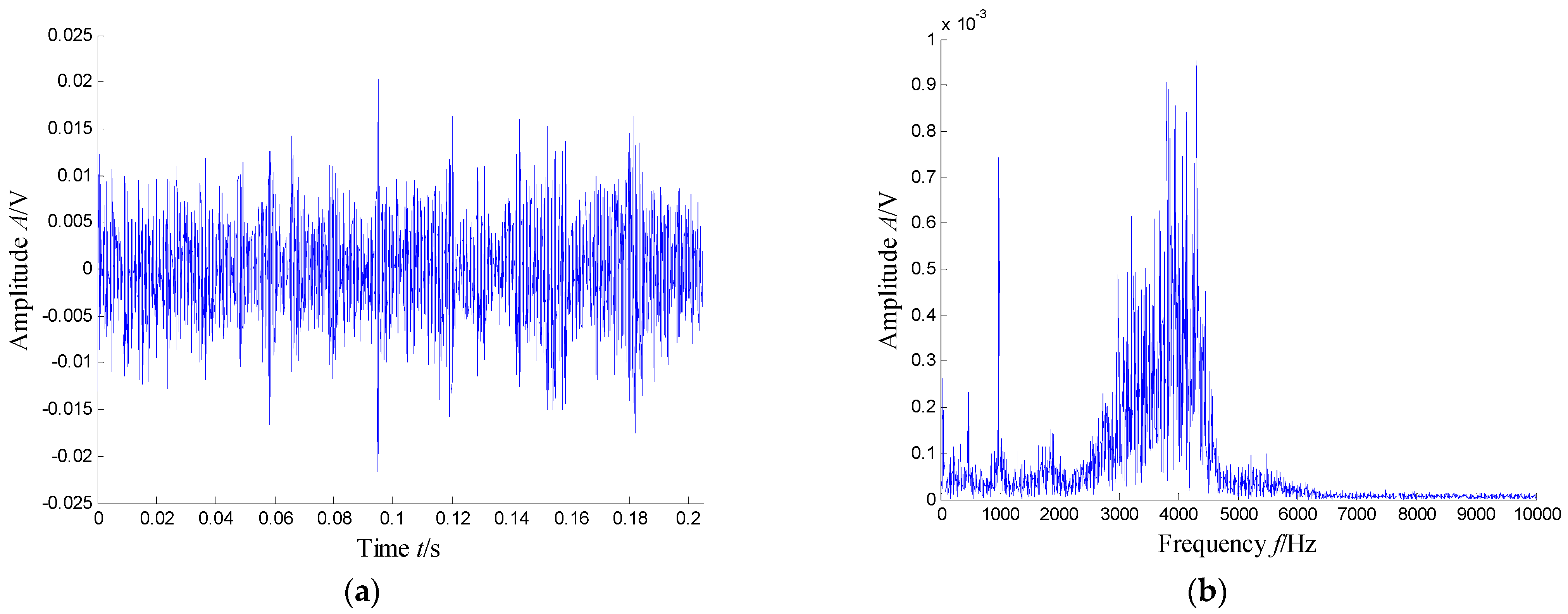
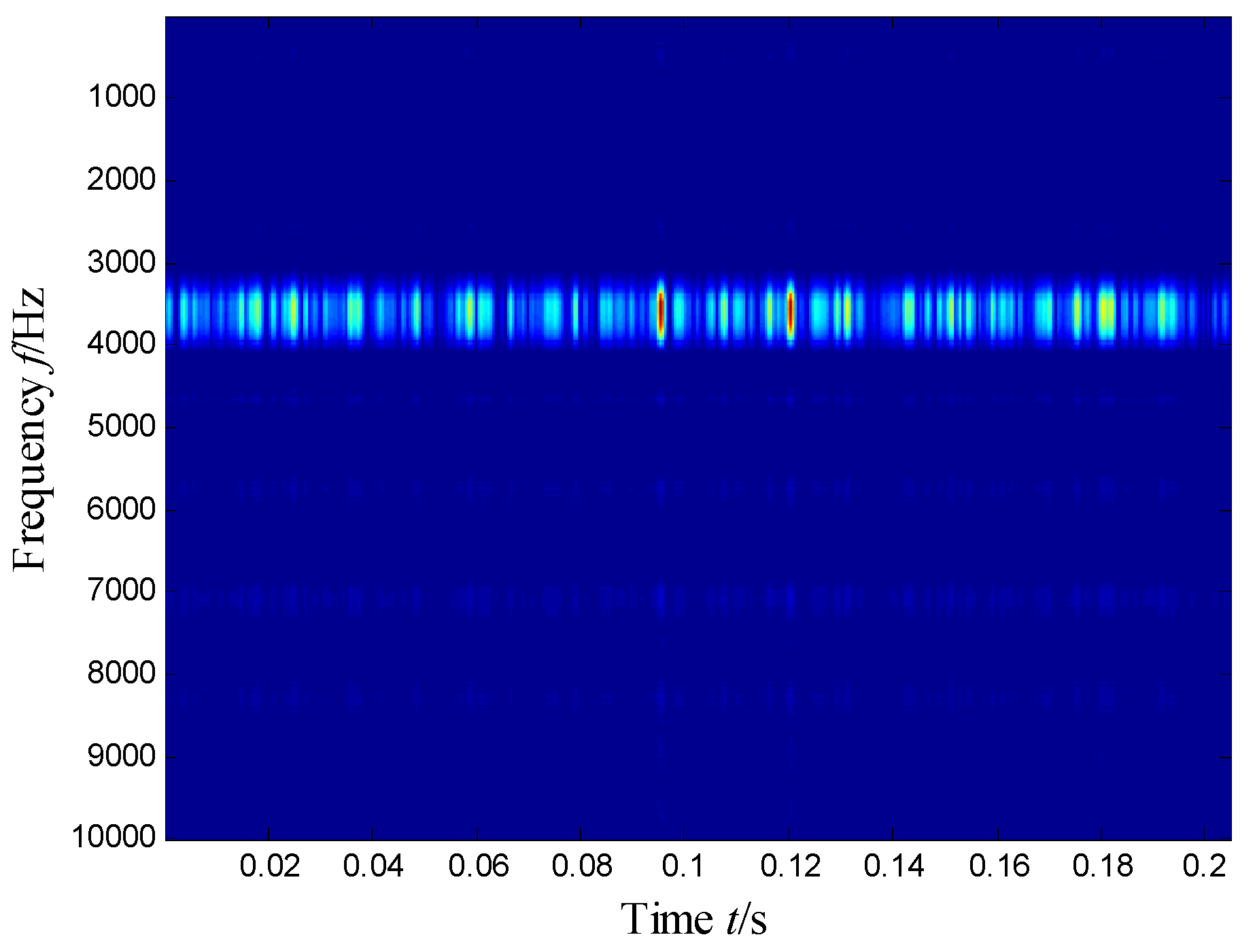
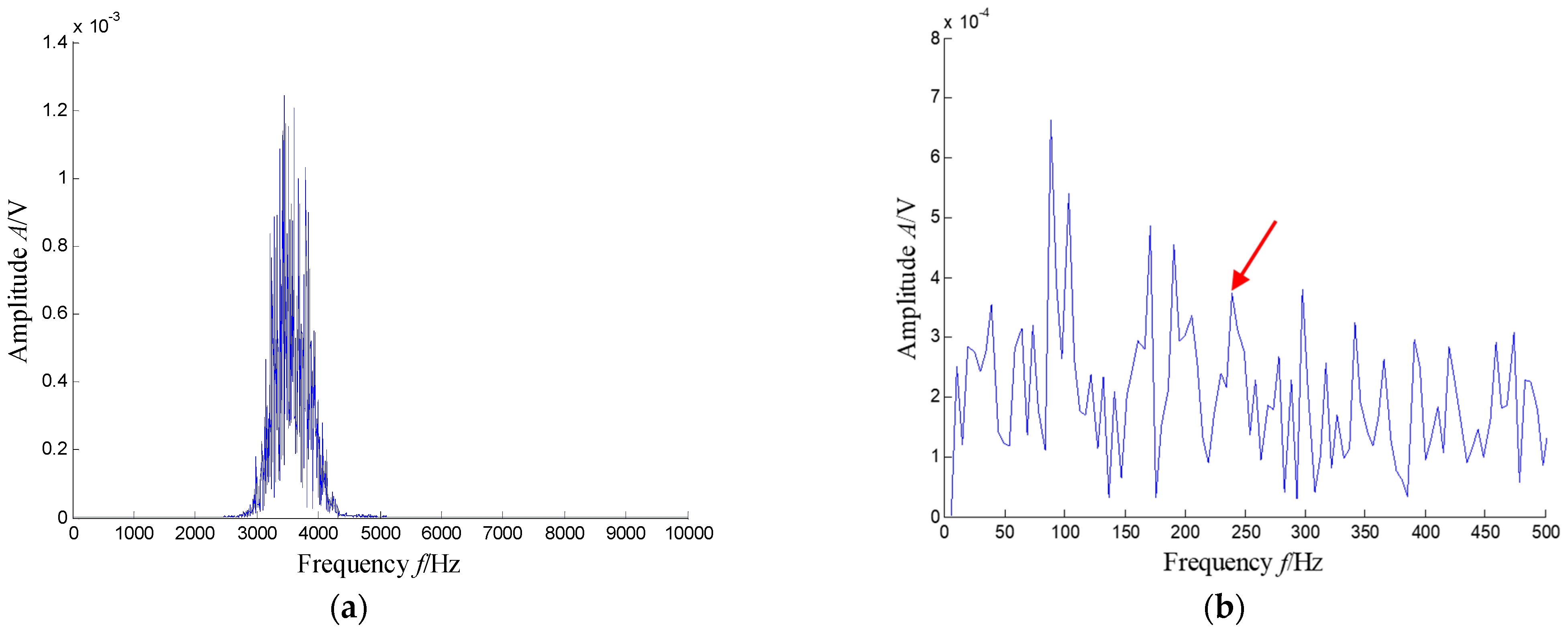
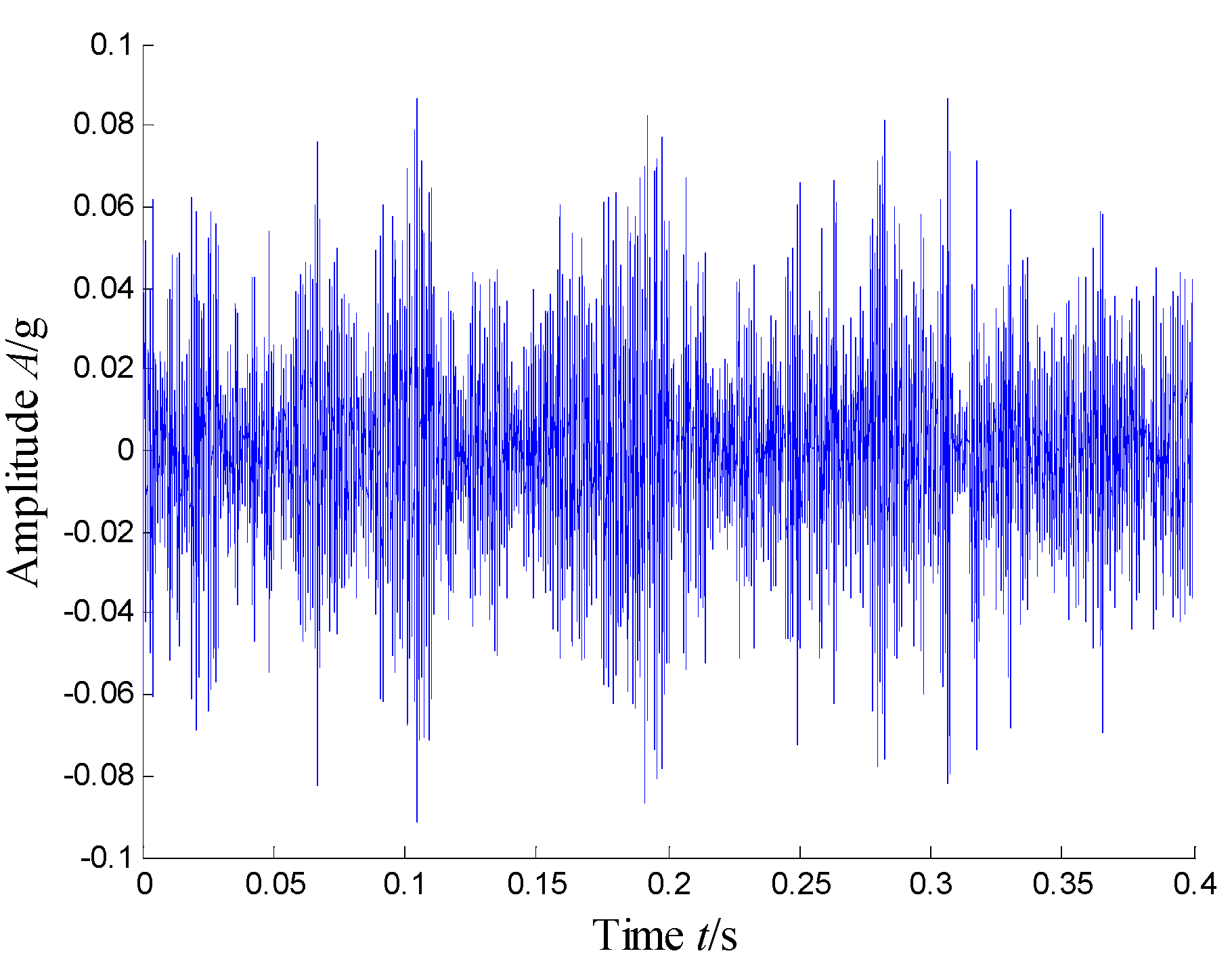
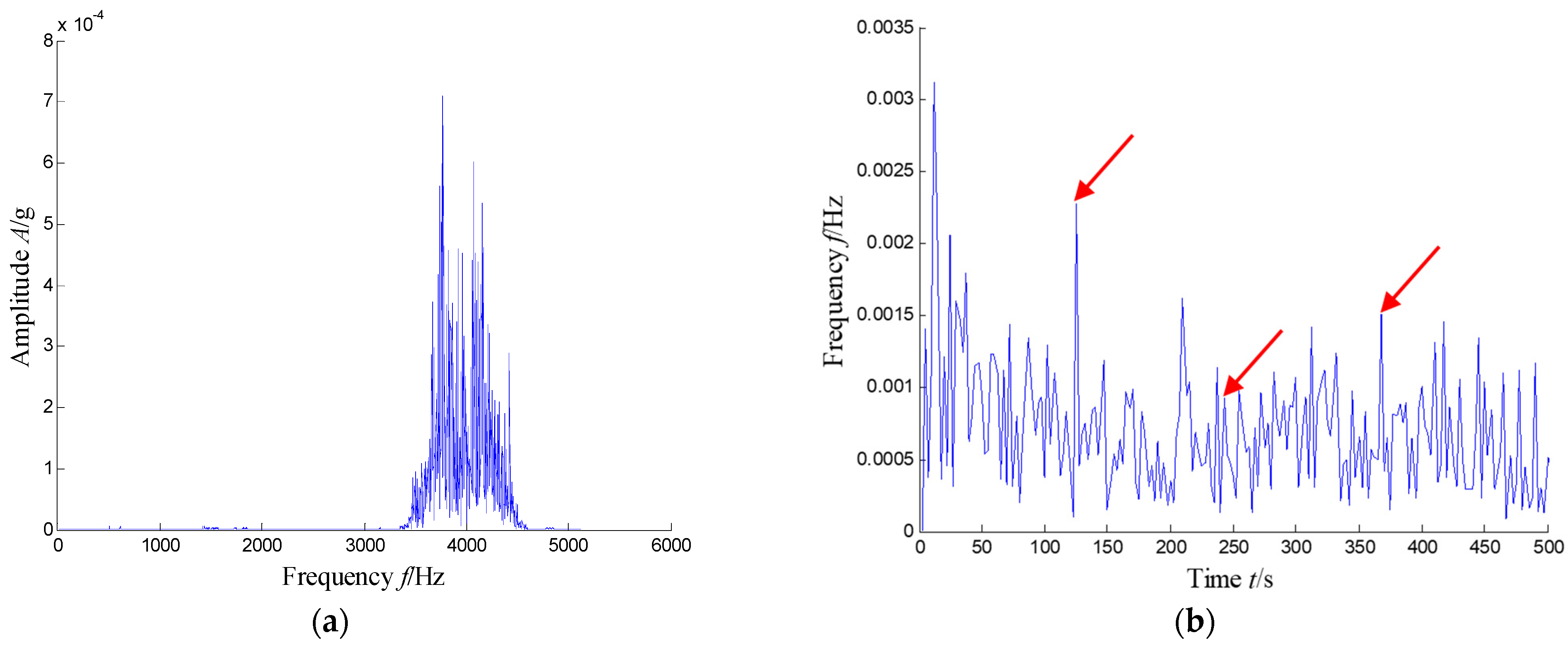
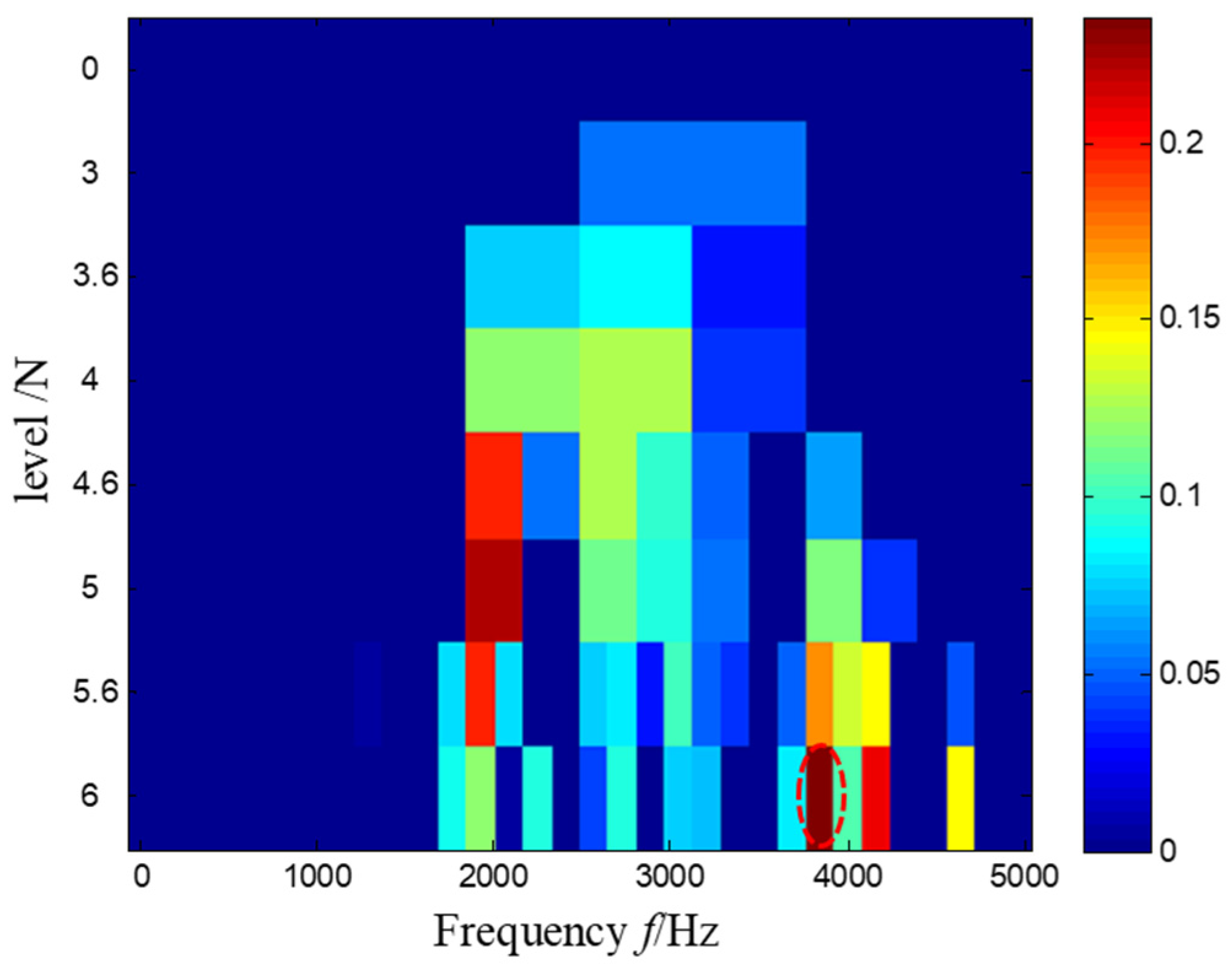
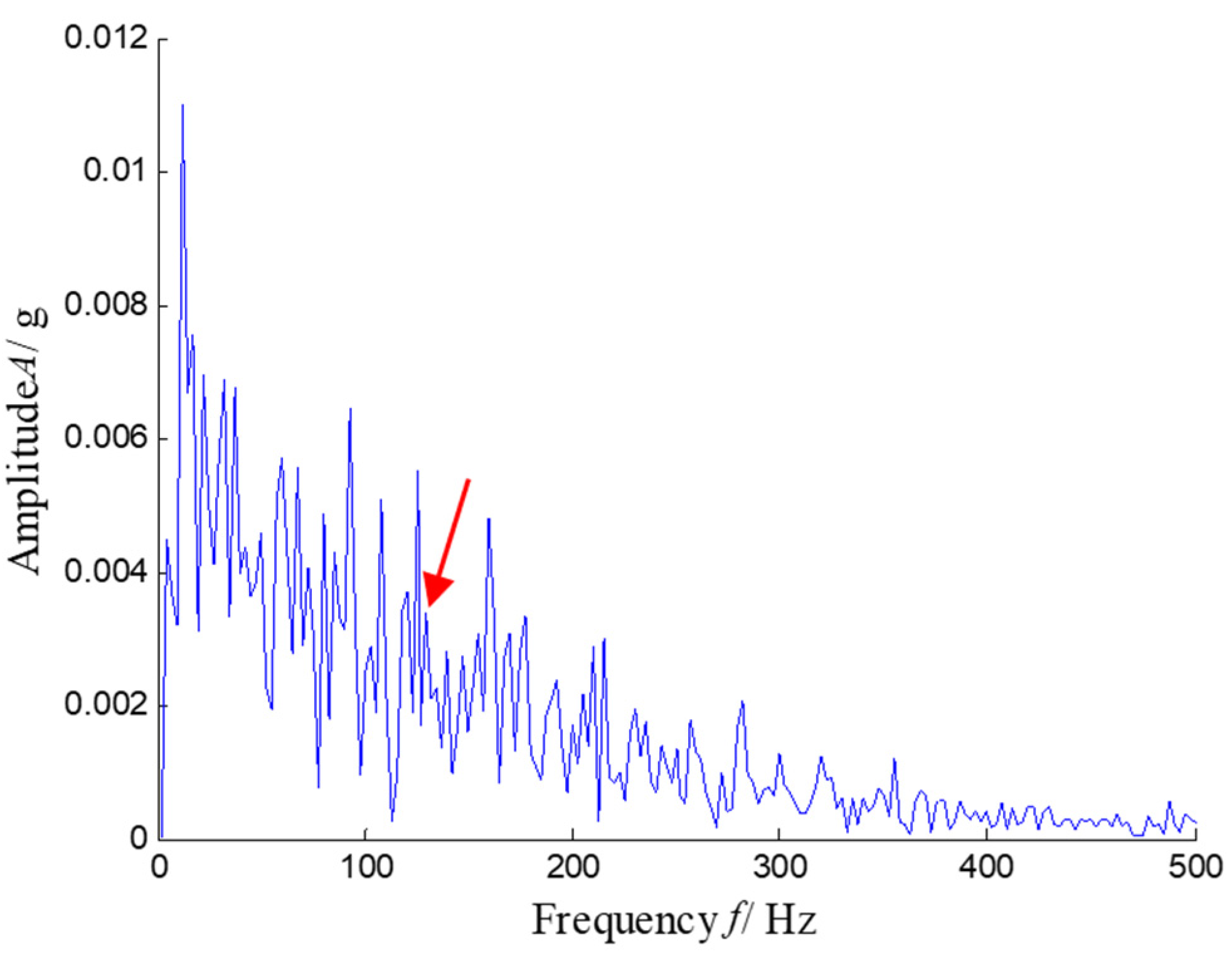
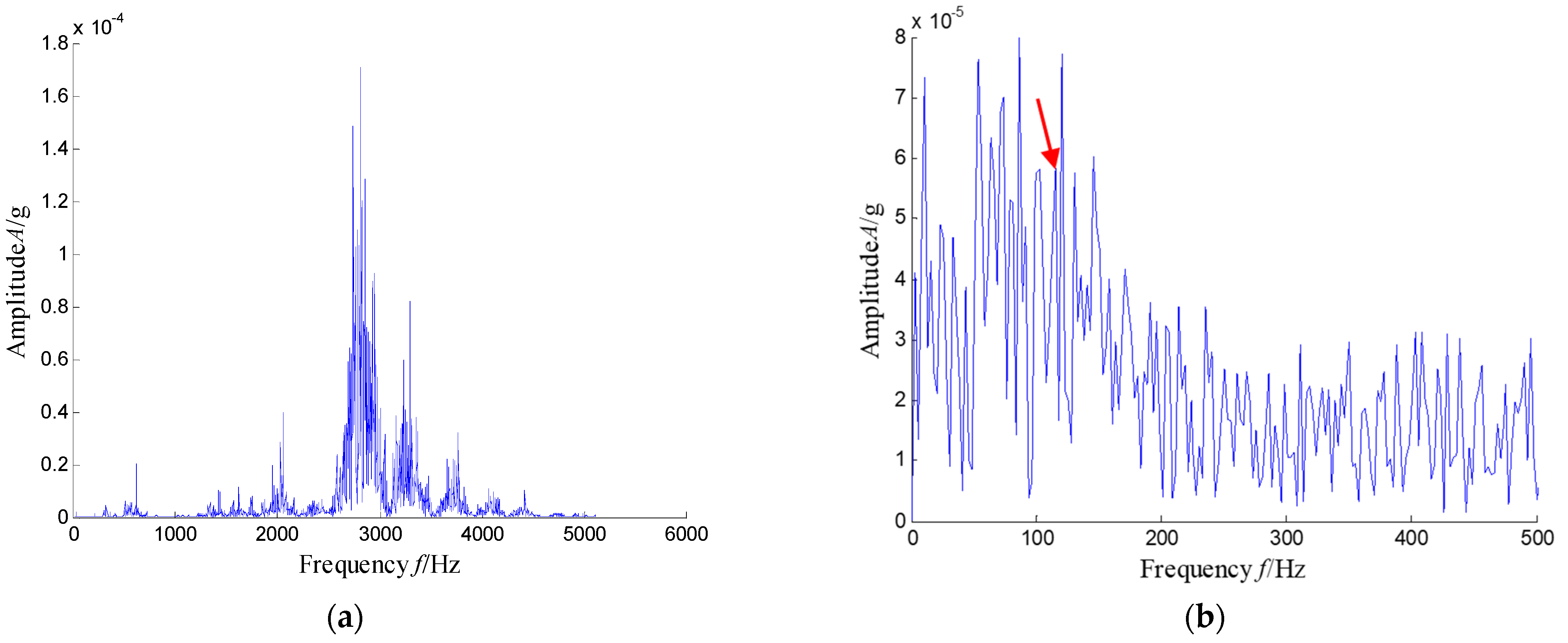
5.2.2. Results and Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Liang, L.; Liu, F.; Li, M.; He, K.; Xu, G. Feature selection for machine fault diagnosis using clustering of non-negation matrix factorization. Meas. J. Int. Meas. Confed. 2016, 94, 295–305. [Google Scholar] [CrossRef]
- Immovilli, F.; Bellini, A.; Rubini, R.; Tassoni, C. Diagnosis of bearing faults in induction machines by vibration or current signals: A critical comparison. IEEE Trans. Ind. Appl. 2010, 46, 1350–1359. [Google Scholar] [CrossRef]
- Rzeszucinski, P.; Orman, M.; Pinto, C.T.; Tkaczyk, A.; Sulowicz, M. Bearing Health Diagnosed with a Mobile Phone: Acoustic Signal Measurements Can be Used to Test for Structural Faults in Motors. IEEE Ind. Appl. Mag. 2018, 24, 17–23. [Google Scholar] [CrossRef]
- Orman, M.; Rzeszucinski, P.; Tkaczyk, A.; Krishnamoorthi, K.; Pinto, C.T.; Sulowicz, M. Bearing fault detection with the use of acoustic signals recorded by a hand-held mobile phone. In Proceedings of the 2015 International Conference on Condition Assessment Techniques Electrical Systems (CATCON), Bangalore, India, 10–12 December 2015; pp. 252–256. [Google Scholar] [CrossRef]
- Frosini, L.; Harlişca, C.; Szabó, L. Induction machine bearing fault detection by means of statistical processing of the stray flux measurement. IEEE Trans. Ind. Electron. 2014, 62, 1846–1854. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, X.; Du, Z.; Yan, R. Kurtosis based weighted sparse model with convex optimization technique for bearing fault diagnosis. Mech. Syst. Signal Process. 2016, 80, 349–376. [Google Scholar] [CrossRef]
- Sheen, Y.T. An envelope analysis based on the resonance modes of the mechanical system for the bearing defect diagnosis. Meas. J. Int. Meas. Confed. 2010, 43, 912–934. [Google Scholar] [CrossRef]
- Zimroz, R.; Bartelmus, W. Application of adaptive filtering for weak impulsive signal recovery for bearings local damage detection in complex mining mechanical systems working under condition of varying load. Trans Tech Publ. 2012, 180, 250–257. [Google Scholar] [CrossRef]
- Barszcz, T.; Randall, R.B. Application of spectral kurtosis for detection of a tooth crack in the planetary gear of a wind turbine. Mech. Syst. Signal Process. 2009, 23, 1352–1365. [Google Scholar] [CrossRef]
- Antoni, J. Fast computation of the kurtogram for the detection of transient faults. Mech. Syst. Signal Process. 2007, 21, 108–124. [Google Scholar] [CrossRef]
- Antoni, J. The spectral kurtosis: A useful tool for characterising non-stationary signals. Mech. Syst. Signal Process. 2006, 20, 282–307. [Google Scholar] [CrossRef]
- Barszcz, T.; Jabłoński, A. A novel method for the optimal band selection for vibration signal demodulation and comparison with the Kurtogram. Mech. Syst. Signal Process. 2011, 25, 431–451. [Google Scholar] [CrossRef]
- Moshrefzadeh, A.; Fasana, A. The Autogram: An effective approach for selecting the optimal demodulation band in rolling element bearings diagnosis. Mech. Syst. Signal Process. 2018, 105, 294–318. [Google Scholar] [CrossRef]
- Tse, P.W.; Wang, D. The sparsogram: A new and effective method for extracting bearing fault features. In Proceedings of the 2011 Prognostics and System Health Managment Conference, Shenzhen, China, 24–25 May 2011. [Google Scholar] [CrossRef]
- Antoni, J. The infogram: Entropic evidence of the signature of repetitive transients. Mech. Syst. Signal Process. 2016, 74, 73–94. [Google Scholar] [CrossRef]
- Cong, F.; Chen, J.; Dong, G.; Zhao, F. Short-time matrix series based singular value decomposition for rolling bearing fault diagnosis. Mech. Syst. Signal Process. 2013, 34, 218–230. [Google Scholar] [CrossRef]
- Li, H.; Liu, T.; Wu, X.; Chen, Q. Research on bearing fault feature extraction based on singular value decomposition and optimized frequency band entropy. Mech. Syst. Signal Process. 2019, 118, 477–502. [Google Scholar] [CrossRef]
- Jiang, H.; Chen, J.; Dong, G.; Liu, T.; Chen, G. Study on Hankel matrix-based SVD and its application in rolling element bearing fault diagnosis. Mech. Syst. Signal Process. 2015, 52–53, 338–359. [Google Scholar] [CrossRef]
- Jiang, Y.; Kan, J.; Zhang, Z.; Cheng, G.; Wen, J. Machine fault diagnosis based on reassigned wavelet scalogram and SVD. Int. J. Adv. Comput. Technol. 2012, 4, 10–21. [Google Scholar] [CrossRef]
- Zhao, M.; Jia, X. A novel strategy for signal denoising using reweighted SVD and its applications to weak fault feature enhancement of rotating machinery. Mech. Syst. Signal Process. 2017, 94, 129–147. [Google Scholar] [CrossRef]
- Wen, H.; Liang, L.; Liu, F. Speech enhancement using nonnegative matrix factorization with overlapping group sparsity constraint. ACM Int. Conf. Proceeding Ser. 2020, 87–91. [Google Scholar] [CrossRef]
- Zhou, Q.; Feng, Z.; Benetos, E. Adaptive noise reduction for sound event detection using subband-weighted NMF. Sensors 2019, 19, 3206. [Google Scholar] [CrossRef]
- Liang, L.; Shan, L.; Liu, F.; Li, M.; Niu, B.; Xu, G. Impulse Feature Extraction of Bearing Faults Based on Convolutive Nonnegative Matrix Factorization. IEEE Access 2020, 8, 88617–88632. [Google Scholar] [CrossRef]
- Liu, H.; Wen, H.; Liang, L.; Wang, J.; Fan, Z.; Hu, J. Impulse Response Extraction for Rolling Bearing Faults Based on Semi-NMF. In Proceedings of the 2019 IEEE 4th Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), Chengdu, China, 20–22 December 2019; pp. 884–887. [Google Scholar] [CrossRef]
- Wodecki, J.; Kruczek, P.; Bartkowiak, A.; Zimroz, R.; Wyłomańska, A. Novel method of informative frequency band selection for vibration signal using Nonnegative Matrix Factorization of spectrogram matrix. Mech. Syst. Signal Process. 2019, 130, 585–596. [Google Scholar] [CrossRef]
- Pan, B.; Lai, J.; Chen, W.S. Nonlinear nonnegative matrix factorization based on Mercer kernel construction. Pattern Recognit. 2011, 44, 2800–2810. [Google Scholar] [CrossRef]
- Kallas, M.; Honeine, P.; Richard, C.; Francis, C.; Amoud, H. Non-negativity constraints on the pre-image for pattern recognition with kernel machines. Pattern Recognit. 2013, 46, 3066–3080. [Google Scholar] [CrossRef]
- Li, Y.; Ngom, A. A new Kernel non-negative matrix factorization and its application in microarray data analysis. In Proceedings of the 2012 IEEE Symposium on Computational Intelligence in Bioinformatics and Computational Biology (CIBCB), San Diego, CA, USA, 9–12 May 2012; pp. 371–378. [Google Scholar] [CrossRef]
- Hoyer, P.O. Non-negative matrix factorization with sparseness constraints. J. Mach. Learn. Res. 2004, 5, 1457–1469. [Google Scholar]
- Pascual-Montano, A.; Carazo, J.M.; Kochi, K.; Lehmann, D.; Pascual-Marqui, R.D. Nonsmooth nonnegative matrix factorization (nsNMF). IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 403–415. [Google Scholar] [CrossRef]
- Pauca, V.P.; Piper, J.; Plemmons, R.J. Nonnegative matrix factorization for spectral data analysis. Linear Algebra Its Appl. 2006, 416, 29–47. [Google Scholar] [CrossRef]
- Kim, H.; Park, H. Sparse non-negative matrix factorizations via alternating non-negativity-constrained least squares for microarray data analysis. Bioinformatics 2007, 23, 1495–1502. [Google Scholar] [CrossRef]
- Hale, E.T.; Yin, W.; Zhang, Y. Fixed-point continuation for 11-minimization: Methodology and convergence. SIAM J. Optim. 2008, 19, 1107–1130. [Google Scholar] [CrossRef]
- Berry, M.W.; Browne, M.; Langville, A.N.; Pauca, V.P.; Plemmons, R.J. Algorithms and applications for approximate nonnegative matrix factorization. Comput. Stat. Data Anal. 2007, 52, 155–173. [Google Scholar] [CrossRef]
- Qiu, H.; Lee, J.; Lin, J.; Yu, G. Wavelet filter-based weak signature detection method and its application on rolling element bearing prognostics. J. Sound Vib. 2006, 289, 1066–1090. [Google Scholar] [CrossRef]









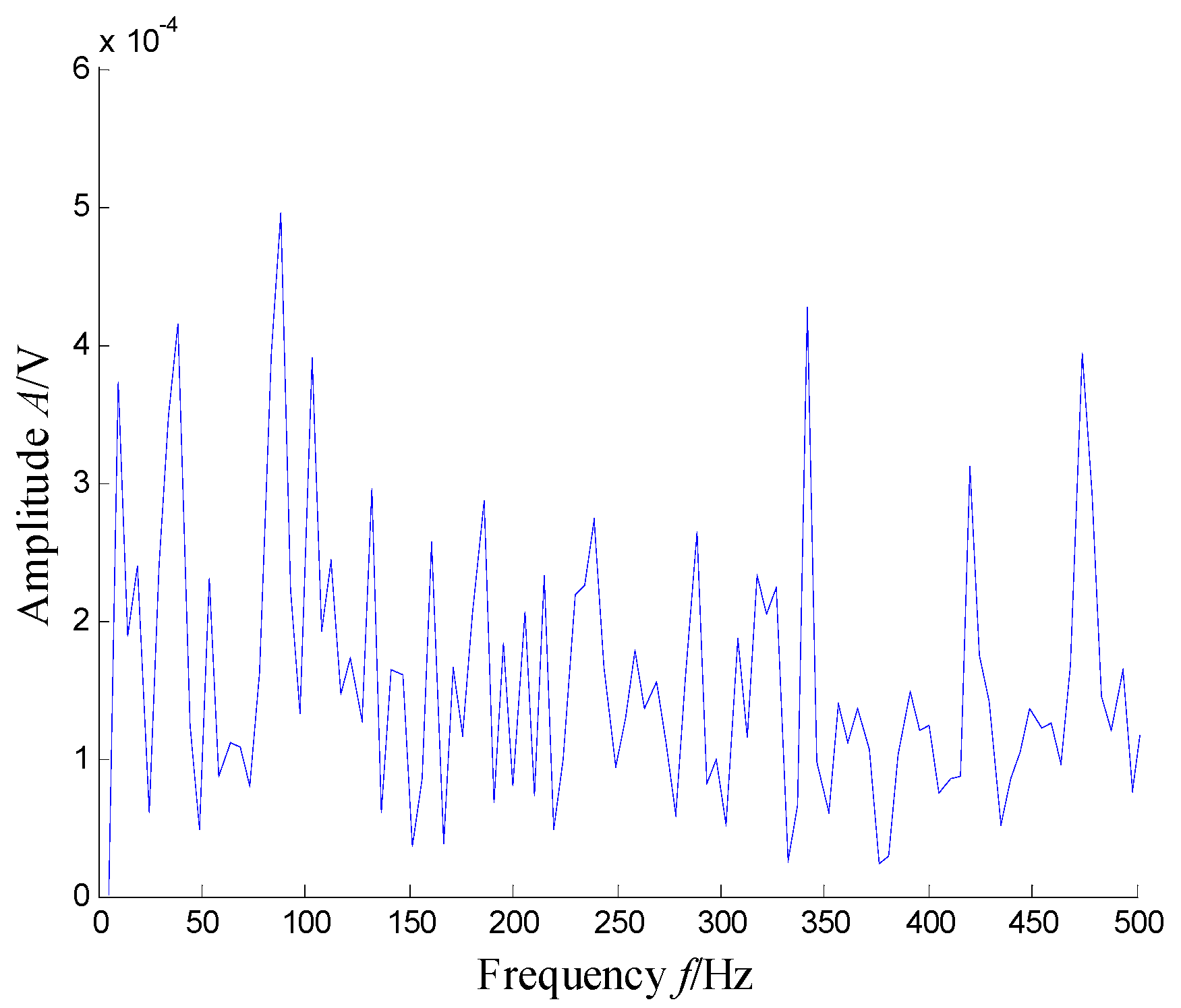
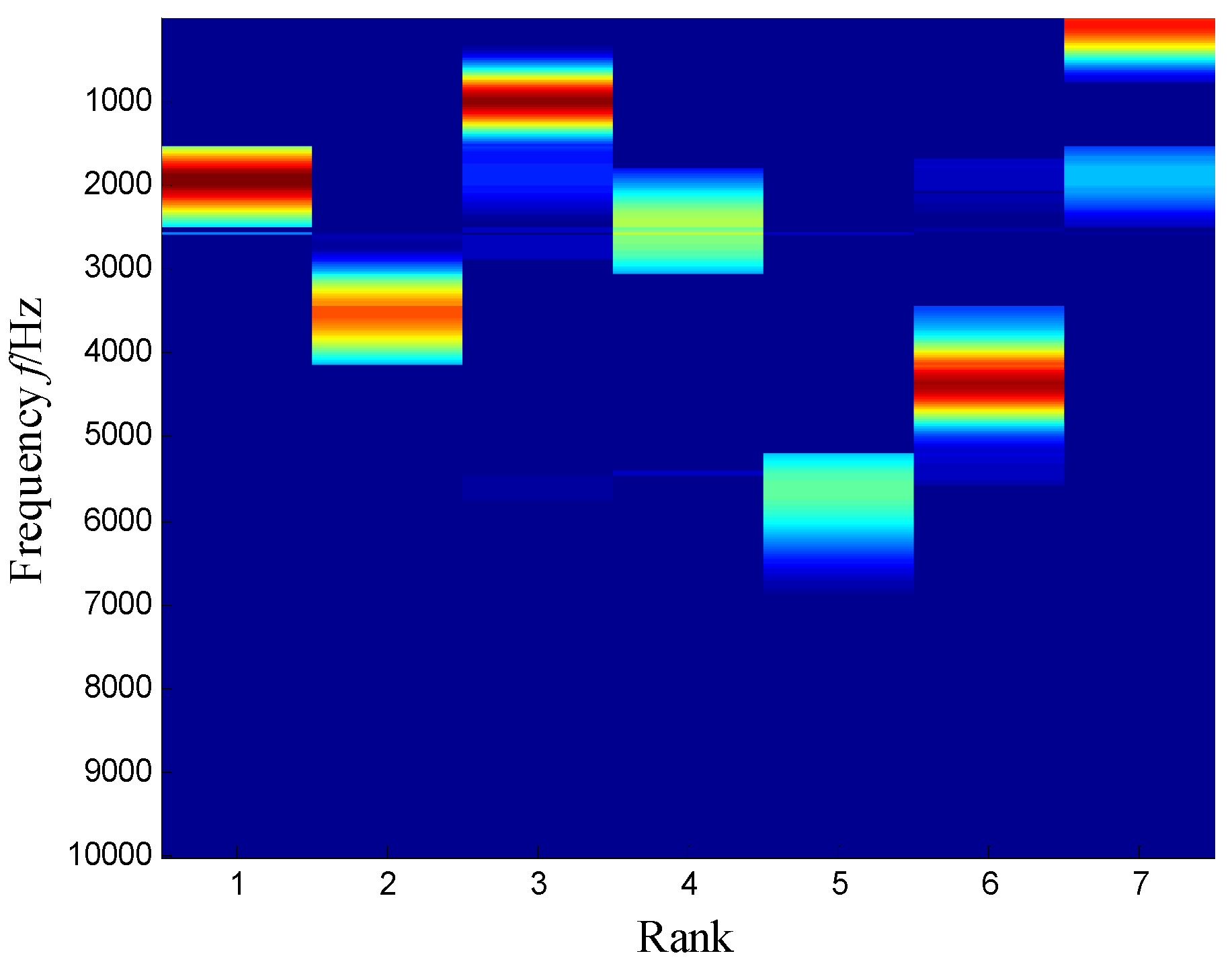
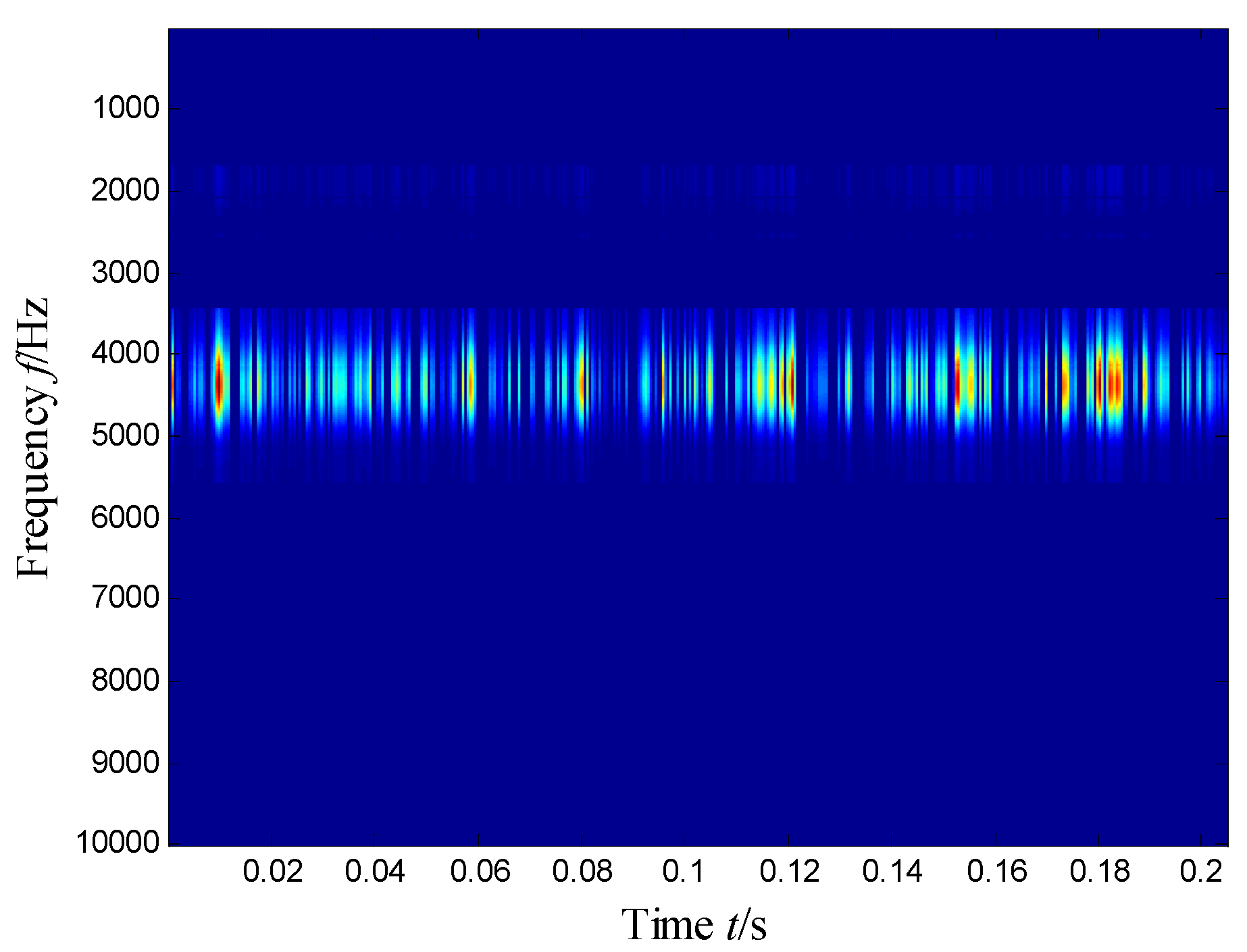


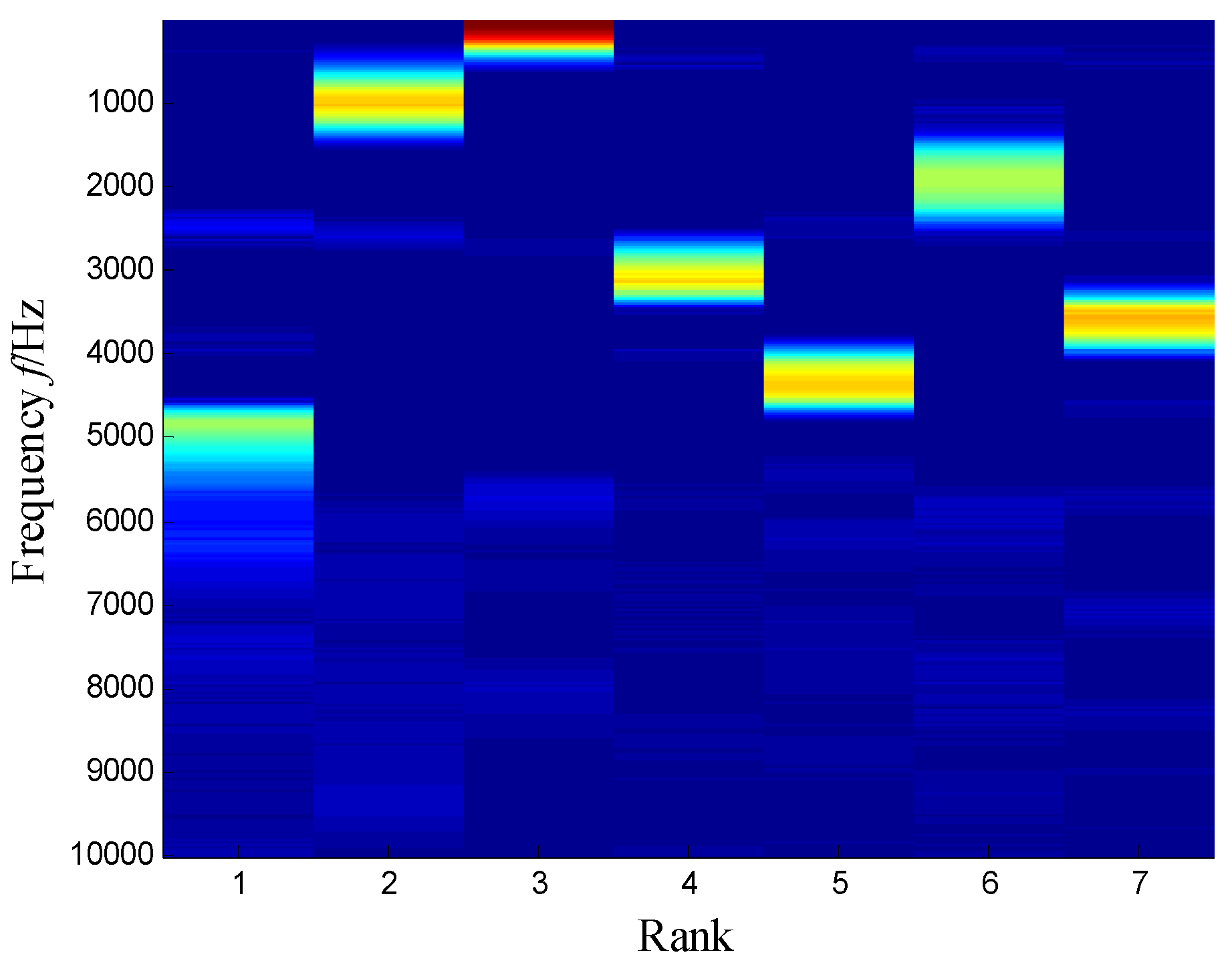





| Sensor Model | Sensitivity | Measurement Range | Broadband Resolution | Frequency Range |
|---|---|---|---|---|
| PCB 352C68 ICP | (±10%) 100 mV/g (10.2 mV/(m/s²)) | ±50 g pk (±491 m/s² pk) | 0.00016 g rms (0.0015 m/s² rms) | (±5%) 0.5 to 10,000 Hz |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, L.; Ding, X.; Liu, F.; Chen, Y.; Wen, H. Feature Extraction Using Sparse Kernel Non-Negative Matrix Factorization for Rolling Element Bearing Diagnosis. Sensors 2021, 21, 3680. https://doi.org/10.3390/s21113680
Liang L, Ding X, Liu F, Chen Y, Wen H. Feature Extraction Using Sparse Kernel Non-Negative Matrix Factorization for Rolling Element Bearing Diagnosis. Sensors. 2021; 21(11):3680. https://doi.org/10.3390/s21113680
Chicago/Turabian StyleLiang, Lin, Xingyun Ding, Fei Liu, Yuanming Chen, and Haobin Wen. 2021. "Feature Extraction Using Sparse Kernel Non-Negative Matrix Factorization for Rolling Element Bearing Diagnosis" Sensors 21, no. 11: 3680. https://doi.org/10.3390/s21113680
APA StyleLiang, L., Ding, X., Liu, F., Chen, Y., & Wen, H. (2021). Feature Extraction Using Sparse Kernel Non-Negative Matrix Factorization for Rolling Element Bearing Diagnosis. Sensors, 21(11), 3680. https://doi.org/10.3390/s21113680






