Rotation Active Sensors Based on Ultrafast Fibre Lasers
Abstract
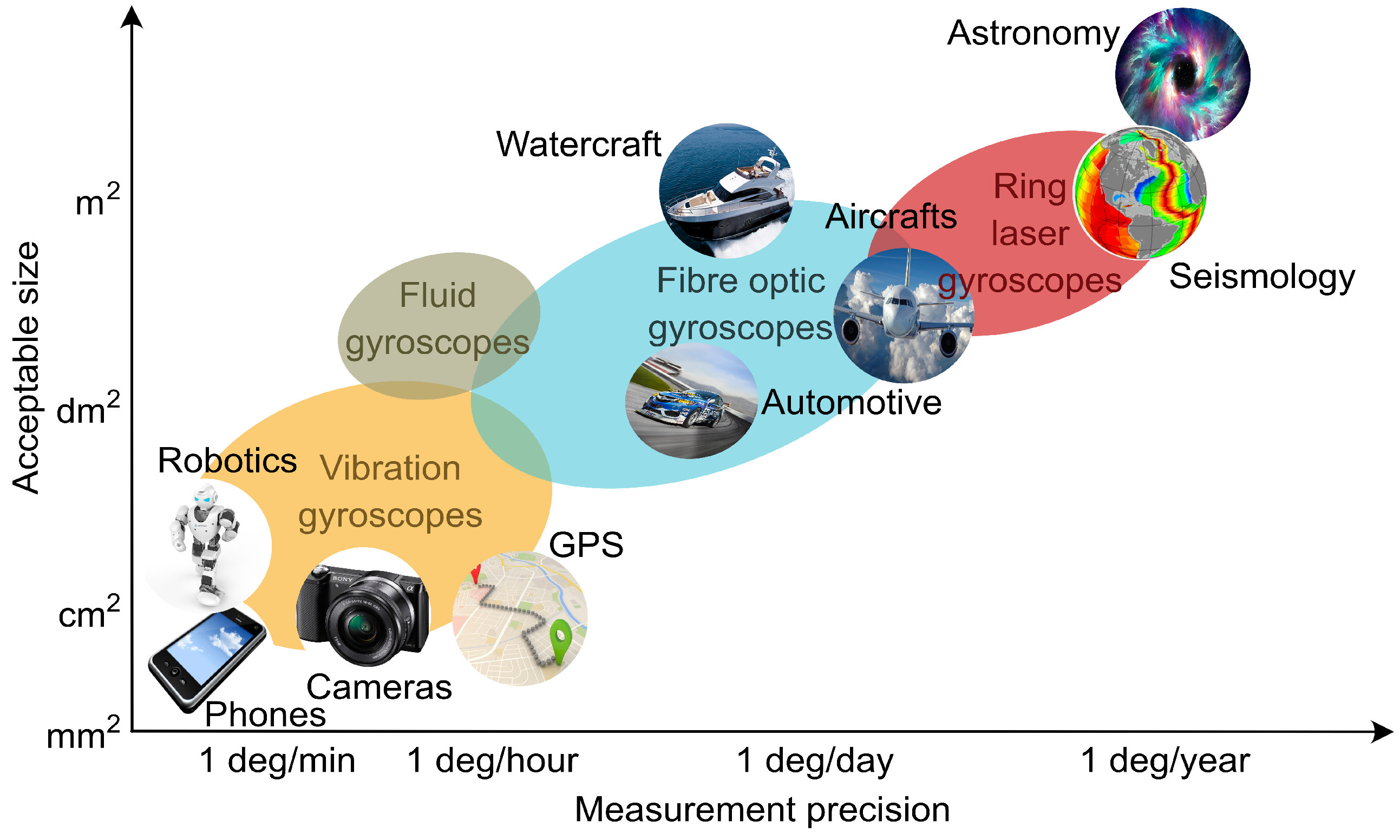
1. Introduction
2. Sagnac Effect
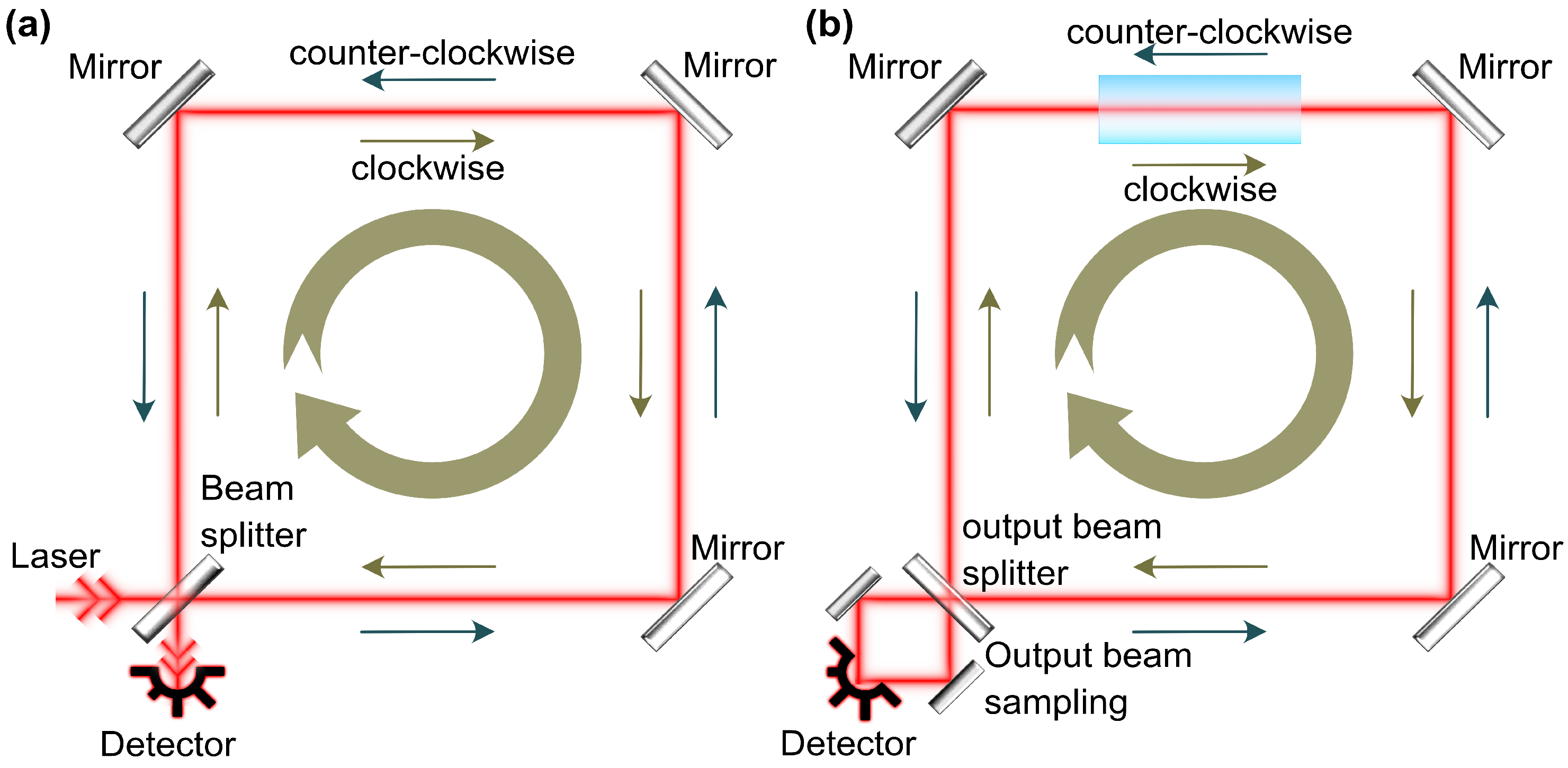
2.1. Methods for Sagnac Effect Detection
2.2. Measurement Errors of Angular Rotation in Laser Gyroscopes
- Gas degradation. He-Ne lasers generate the most desirable narrow-band radiation for gyroscopic measurements. However, gas lasers suffer from gas leaking from the cavity enclosure, which affects the laser gain and, therefore, the scale factor of the gyroscopes. Moreover, the scale factor is further reduced due to contamination of the laser gas with hydrogen, oxygen, nitrogen and water vapour [42,43]. Besides, gas laser gyroscopes face bias due to gas flow caused by temperature fluctuations or ionic flow due to electric discharge [44]. Gas degradation limits the long-term performance of the gyroscope and requires the usage of a solid-state gain medium.
- Variation of the scale factor. Under the influence of external conditions such as temperature and pressure, the scale factor tends to fluctuate, affecting the gyroscopic measurements. The intracavity conditions, such as instabilities of gain and losses, also affect the scale factor of the gyroscope. In fibre gyroscopes, time-dependent temperature fluctuations lead to travel time variation along the same sections of optical fibre for counter-propagating beams (known as the Shupe effect [45]), causing an additional parasitic difference in their optical paths.
- Intracavity non-reciprocal effects, the most significant among which are Magneto-optic effects [46,47] and Kerr effect. In fibre gyroscopes, the minimum detectable angular rate is usually limited by the Kerr effect. Owing to the very small silica fibre core and long distances in fibre interferometer, even small inequality in intensity between counter-propagating beams results in additional accumulated Kerr-induced phase shift [48]. This effect could be eliminated in hollow-core fibre gyros [49].
- Optical frequency fluctuations. All free-running lasers experience a variation of the oscillation frequency of the output radiation. One approach to mitigate this limitation is by applying a feedback loop with piezoelectric actuators [50]. For long-term operation, the oscillation frequency could be stabilised via a beat-note with an actively stabilised reference laser as a feedback reference signal [51].
- Polarisation instability. Counter-propagating beams can experience polarisation instability, leading to a variation of the optical paths caused by birefringence in optical fibres. The effect of polarisation instability could be mitigated by introducing a polariser inside the interferometer. The accuracy could also be enhanced by using a polarisation-maintaining fibre or polarising single-mode fibre [52].
- Acoustic noise and vibrations. Optical fibres are quite sensitive to acoustic noises, which are converted to phase noises of the counter-propagating beams through the photo-elastic effect [53]. Vibrations and input shock introduce additional noise and bias offset to the gyroscope performance. However, they could be minimised by a rigid design of the gyroscope.
2.3. Gyroscope Performance Consideration
3. Ultrafast Lasers
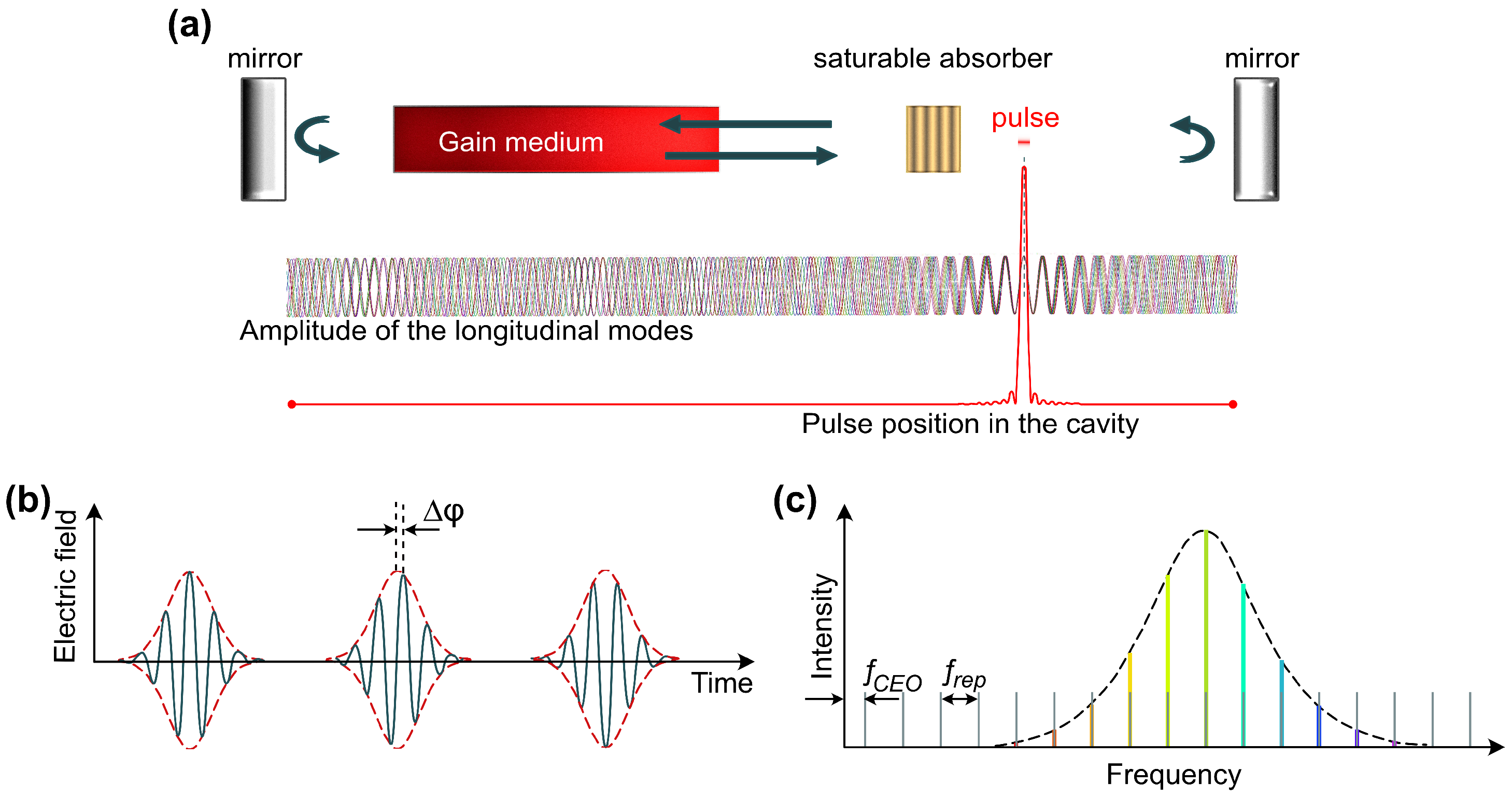
3.1. Principles of Mode-Locking Operation
3.2. Characterisation of Output Radiation in Ultrafast Lasers
3.3. Real-Time Measurements of Ultrashort Pulse Dynamic
3.3.1. Intensity Domain Methods
3.3.2. Spectral Domain Methods
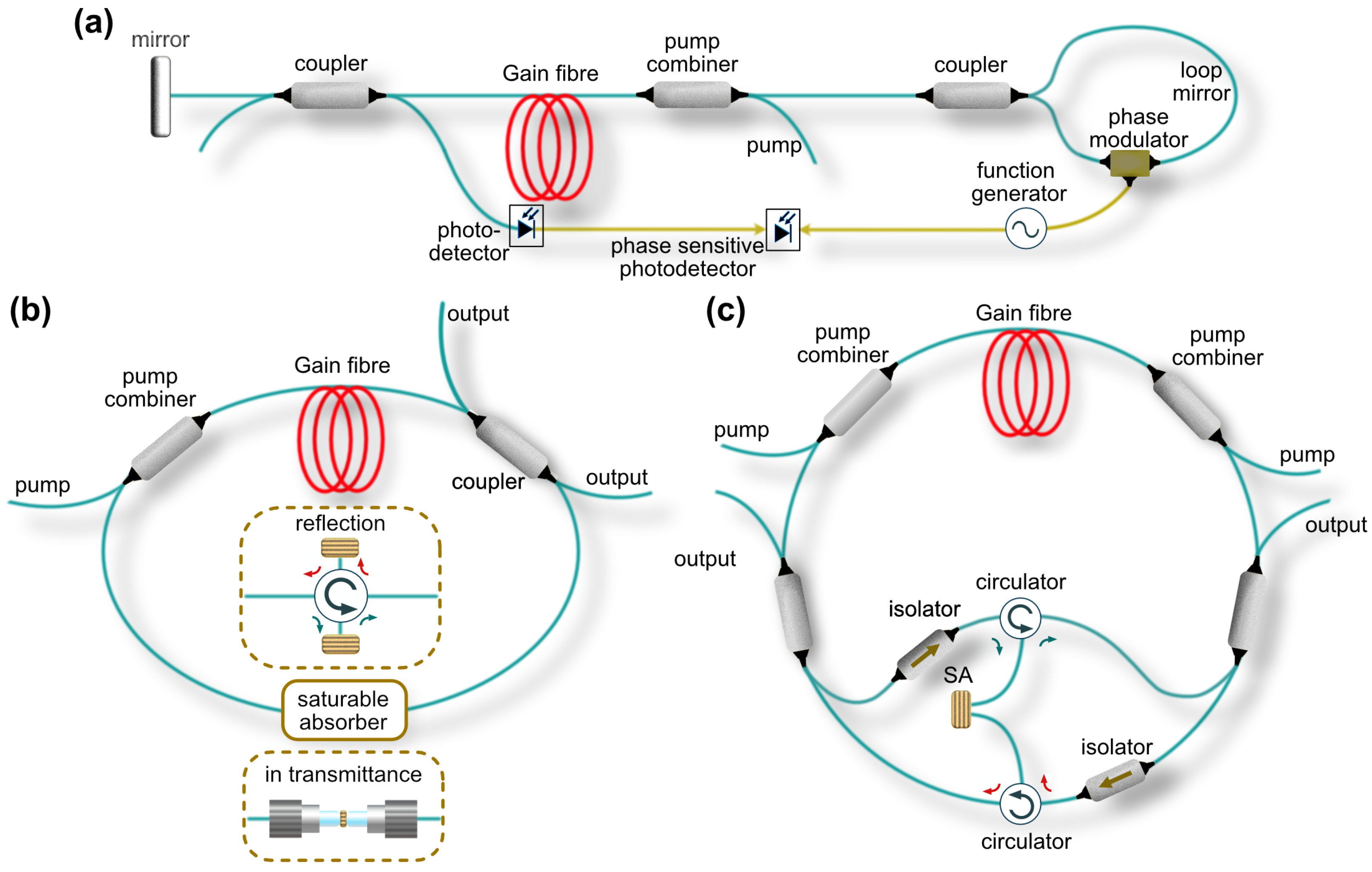
3.4. Mode-Locked Fibre Laser Designs for Gyroscopy
4. Highlights of Ultrashort Pulsed Fibre Laser Gyroscopes
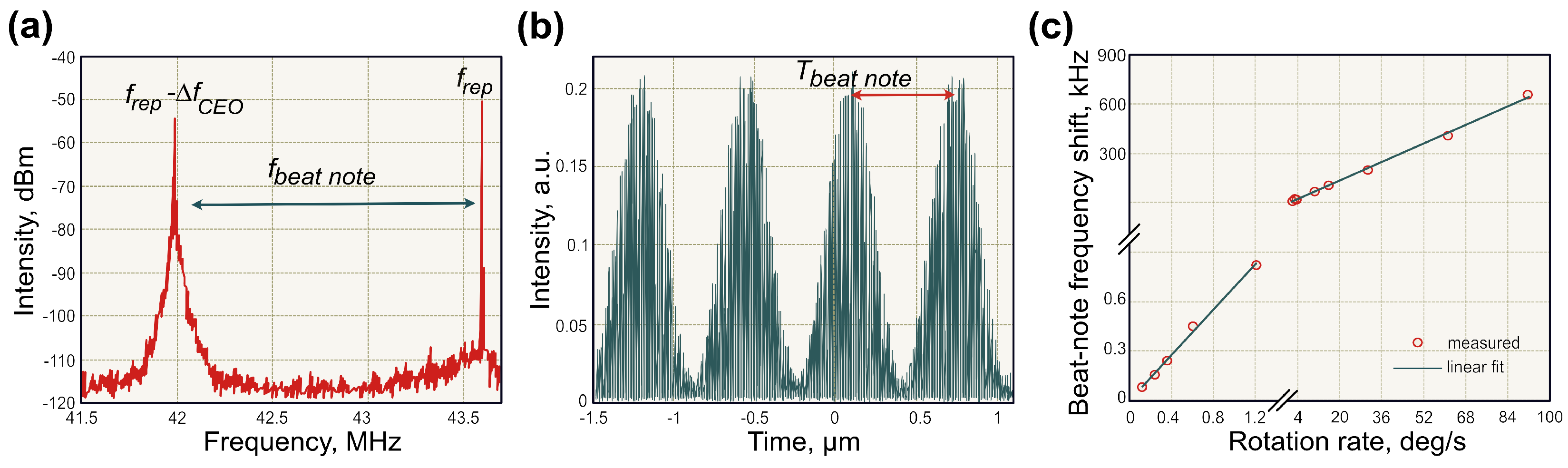
4.1. Beat-Note Measurements of the Optical Sagnac Effect
4.2. Beat-Note Measurements of the Optical Sagnac Effect Employing Dark-Soliton Fibre Laser
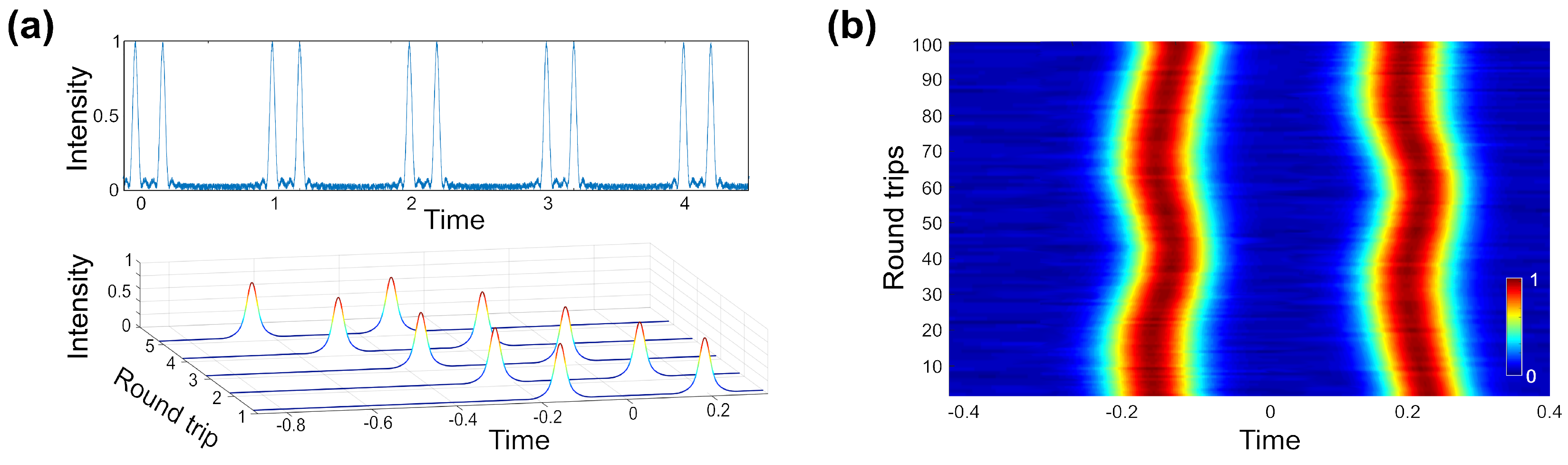
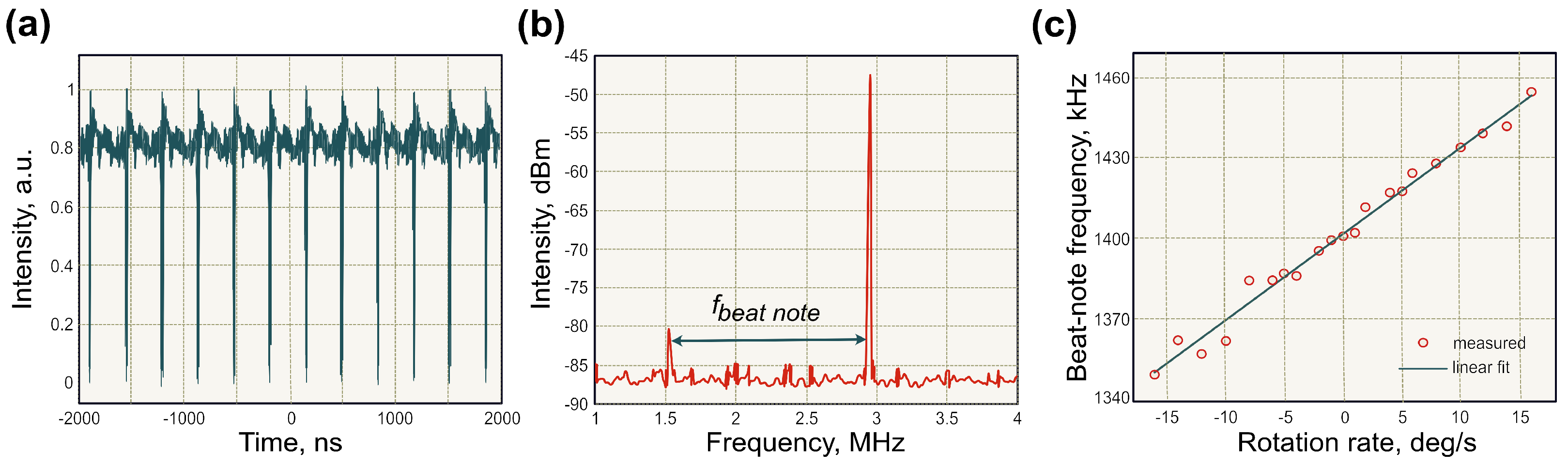
4.3. Real-Time Measurements of the Optical Sagnac Effect
Spatiotemporal Measurements
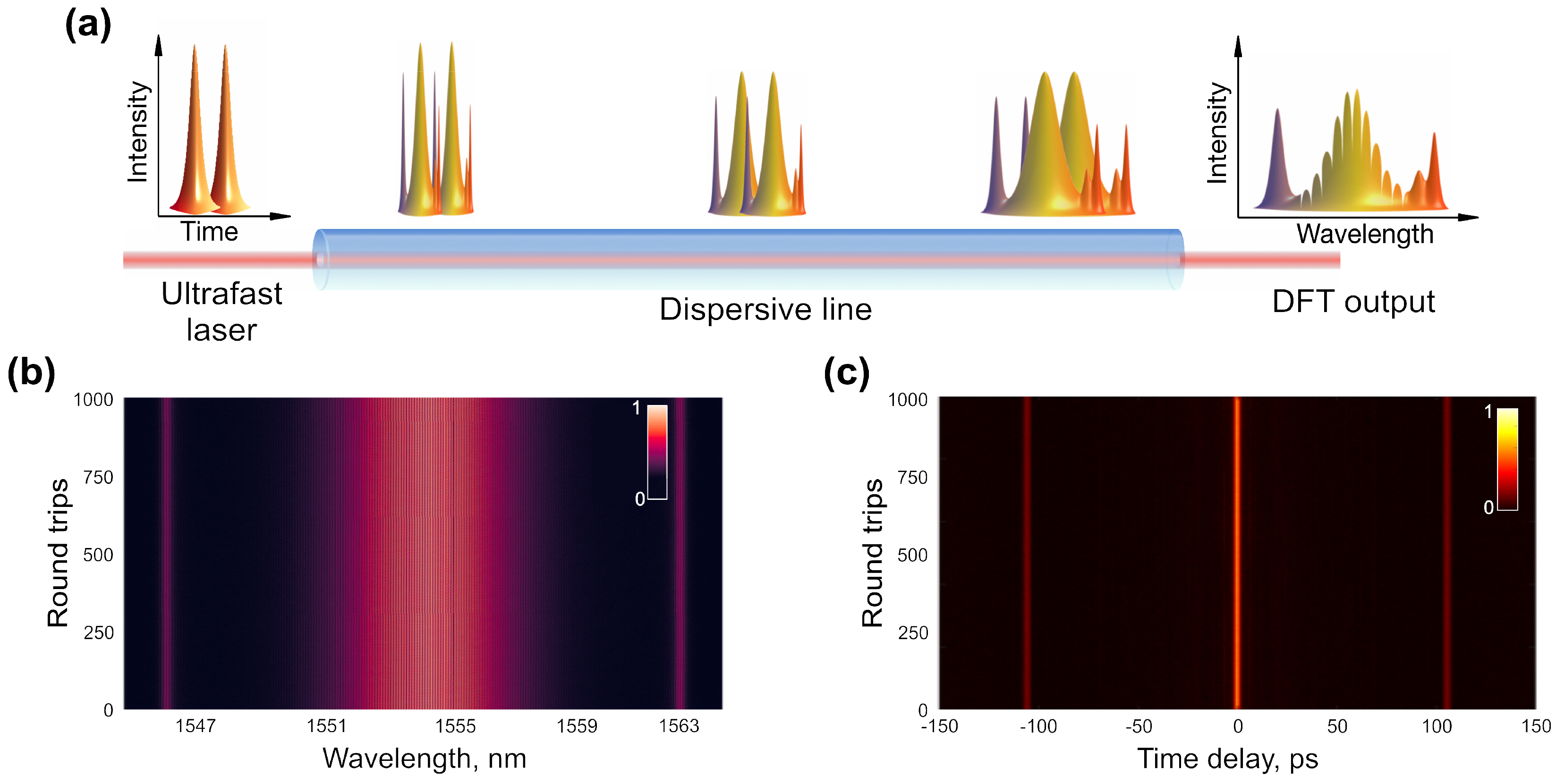
Dispersive Fourier Transform Measurements
4.4. Rotation Sensing by All-Fibre Bidirectional Optical Parametric Oscillator
5. Conclusions and Perspectives
Funding
Conflicts of Interest
References
- Scarborough, J.B. The Gyroscope; Interscience Publishers: London, UK, 1958. [Google Scholar]
- Johnson, W.R. Description of an Apparatus called the Rotascope, for exhibiting several phenomena and illustrating certain laws of rotary motion. Am. J. Sci. Arts (1820–1879) 1832, 21, 264B. [Google Scholar]
- Passaro, V.; Cuccovillo, A.; Vaiani, L.; De Carlo, M.; Campanella, C.E. Gyroscope technology and applications: A review in the industrial perspective. Sensors 2017, 17, 2284. [Google Scholar] [CrossRef] [PubMed]
- Macek, W.M.; Davis, D.T.M. Rotation rate sensing with traveling-wave ring lasers. Appl. Phys. Lett. 1963, 2, 67–68. [Google Scholar] [CrossRef]
- Sagnac, G. L’ether lumineux demontre par l’effet du vent relatif d’ether dans un interferometre en rotation uniforme. Comptes Rendus 1913, 157, 708–710. [Google Scholar]
- Sagnac, G. Sur la preuve de la realite de l’ether lumineux par l’experience de l’interferographe tournant. C. R. Acad. Sci. 1913, 157, 1410–1413. [Google Scholar]
- Hadziioannou, C.; Gaebler, P.; Schreiber, U.; Wassermann, J.; Igel, H. Examining ambient noise using colocated measurements of rotational and translational motion. J. Seismol. 2012, 16, 787–796. [Google Scholar] [CrossRef]
- Schreiber, K.U.; Klügel, T.; Wells, J.P.R.; Hurst, R.B.; Gebauer, A. How to Detect the Chandler and the Annual Wobble of the Earth with a Large Ring Laser Gyroscope. Phys. Rev. Lett. 2011, 107, 173904. [Google Scholar] [CrossRef]
- Vali, V.; Shorthill, R.W. Fiber ring interferometer. Appl. Opt. 1976, 15, 1099–1100. [Google Scholar] [CrossRef]
- Udd, E.; Watanabe, S.F.; Cahill, R.F. Comparison of Ring Laser and Fiber-Optic Gyro Technology; McDonnell Douglas Astronautics Company: Berkeley, MO, USA, 1985. [Google Scholar]
- Napolitano, F. Fiber-Optic Gyroscopes Key Technological Advantages. iXBlue 2010. Available online: https://www.ixblue.com/m/publication/fog-key-advantages.pdf (accessed on 19 May 2021).
- Korkishko, Y.N.; Fedorov, V.; Prilutskii, V.; Ponomarev, V.; Morev, I.; Skripnikov, S.; Khmelevskaya, M.; Buravlev, A.; Kostritskii, S.; Fedorov, I.; et al. Strapdown inertial navigation systems based on fiber-optic gyroscopes. Gyroscopy Navig. 2014, 5, 195–204. [Google Scholar] [CrossRef]
- Paturel, Y.; Honthaas, J.; Lefèvre, H.; Napolitano, F. One nautical mile per month FOG-based strapdown inertial navigation system: a dream already within reach? Gyroscopy Navig. 2014, 5, 1–8. [Google Scholar] [CrossRef]
- Aronowitz, F.; Collins, R. Mode Coupling due to back-scattering in a He–Ne travelling-wave ring laser. Appl. Phys. Lett. 1966, 9, 55–58. [Google Scholar] [CrossRef]
- Karwacki, F.A.; Shishkov, M.; Hasan, Z.; Sanzari, M.; Cui, H.-L. Optical biasing of a ring laser gyroscope with a quantum well mirror. In Proceedings of the IEEE 1998 Position Location and Navigation Symposium (Cat. No.98CH36153), Palm Springs, CA, USA, 20–23 April 1996; pp. 161–168. [Google Scholar]
- Geen, J.A. Dithered Ring Laser Gyroscope with Residual Lock-in Error Compensation. US Patent 4,606,637, 19 August 1986. [Google Scholar]
- Schreiber, K.U.; Wells, J.P.R. Invited review article: Large ring lasers for rotation sensing. Rev. Sci. Instrum. 2013, 84, 041101. [Google Scholar] [CrossRef]
- Kanamori, H.; Yokota, H.; Tanaka, G.; Watanabe, M.; Ishiguro, Y.; Yoshida, I.; Kakii, T.; Itoh, S.; Asano, Y.; Tanaka, S. Transmission characteristics and reliability of pure-silica-core single-mode fibers. J. Light. Technol. 1986, 4, 1144–1150. [Google Scholar] [CrossRef]
- Chesnoy, J. Picosecond gyrolaser. Opt. Lett. 1989, 14, 990–992. [Google Scholar] [CrossRef]
- Dennis, M.L.; Diels, J.C.M.; Lai, M. Femtosecond ring dye laser: a potential new laser gyro. Opt. Lett. 1991, 16, 529–531. [Google Scholar] [CrossRef]
- Gnass, D.; Ernsting, N.; Schäfer, F. Sagnac effect in the colliding-pulse-mode-locked dye ring laser. Appl. Phys. B 1991, 53, 119–120. [Google Scholar] [CrossRef]
- Christian, W.R.; Rosker, M.J. Picosecond pulsed diode ring-laser gyroscope. Opt. Lett. 1991, 16, 1587–1589. [Google Scholar] [CrossRef]
- Arissian, L.; Diels, J.C. Intracavity phase interferometry: frequency combs sensor inside a laser cavity. Laser Photonics Rev. 2014, 8, 799–826. [Google Scholar] [CrossRef]
- Hendrie, J.; Lenzner, M.; Afkhamiardakani, H.; Diels, J.C.; Arissian, L. Impact of resonant dispersion on the sensitivity of intracavity phase interferometry and laser gyros. Opt. Express 2016, 24, 30402–30410. [Google Scholar] [CrossRef]
- Jeon, M.; Jeong, H.; Kim, B.Y. Mode-locked fiber laser gyroscope. Opt. Lett. 1993, 18, 320–322. [Google Scholar] [CrossRef]
- Diddams, S.A. The evolving optical frequency comb. J. Opt. Soc. Am. B 2010, 2010 27, B51–B62. [Google Scholar] [CrossRef]
- Lezius, M.; Wilken, T.; Deutsch, C.; Giunta, M.; Mandel, O.; Thaller, A.; Schkolnik, V.; Schiemangk, M.; Dinkelaker, A.; Kohfeldt, A.; et al. Space-borne frequency comb metrology. Optica 2016, 2016 3, 1381–1387. [Google Scholar] [CrossRef]
- Fermann, M.E.; Hartl, I. Ultrafast fibre lasers. Nat. Photonics 2013, 7, 868–874. [Google Scholar] [CrossRef]
- Chernysheva, M.; Sugavanam, S.; Turitsyn, S. Real-time observation of the optical Sagnac effect in ultrafast bidirectional fibre lasers. APL Photonics 2020, 5, 016104. [Google Scholar] [CrossRef]
- Ciminelli, C.; Dell’Olio, F.; Campanella, C.E.; Armenise, M.N. Photonic technologies for angular velocity sensing. Adv. Opt. Photonics 2010, 2, 370–404. [Google Scholar] [CrossRef]
- Tartaglia, A. General relativistic corrections to the Sagnac effect. Phys. Rev. D 1998, 58, 064009. [Google Scholar] [CrossRef]
- Ori, A.; Avron, J.E. Generalized Sagnac-Wang-Fizeau formula. Phys. Rev. A 2016, 94, 063837. [Google Scholar] [CrossRef]
- Kaplan, A.; Meystre, P. Enhancement of the Sagnac effect due to nonlinearly induced nonreciprocity. Opt. Lett. 1981, 6, 590–592. [Google Scholar] [CrossRef]
- Hau, L.V.; Harris, S.E.; Dutton, Z.; Behroozi, C.H. Light speed reduction to 17 metres per second in an ultracold atomic gas. Nature 1999, 397, 594–598. [Google Scholar] [CrossRef]
- Leonhardt, U.; Piwnicki, P. Ultrahigh sensitivity of slow-light gyroscope. Phys. Rev. A 2000, 62, 055801. [Google Scholar] [CrossRef]
- Shahriar, M.S.; Pati, G.S.; Tripathi, R.; Gopal, V.; Messall, M.; Salit, K. Ultrahigh enhancement in absolute and relative rotation sensing using fast and slow light. Phys. Rev. A 2007, 75, 053807. [Google Scholar] [CrossRef]
- Smith, D.D.; Chang, H.; Arissian, L.; Diels, J.C. Dispersion-enhanced laser gyroscope. Phys. Rev. A 2008, 78, 053824. [Google Scholar] [CrossRef]
- Eliseev, P. Theory of nonlinear Sagnac effect. Opto-Electron. Rev. 2008, 16, 118–123. [Google Scholar] [CrossRef]
- Yum, H.N.; Salit, M.; Yablon, J.; Salit, K.; Wang, Y.; Shahriar, M.S. Superluminal ring laser for hypersensitive sensing. Opt. Express 2010, 18, 17658–17665. [Google Scholar] [CrossRef]
- Ezekiel, S.; Balsamo, S. Passive ring resonator laser gyroscope. Appl. Phys. Lett. 1977, 30, 478–480. [Google Scholar] [CrossRef]
- Sanders, G.A.; Sanders, S.J.; Strandjord, L.K.; Qiu, T.; Wu, J.; Smiciklas, M.; Mead, D.; Mosor, S.; Arrizon, A.; Ho, W.; et al. Fiber optic gyro development at Honeywell. In Proceedings of the Fiber Optic Sensors and Applications XIII. International Society for Optics and Photonics, Baltimore, MD, USA, 17–21 April 2016; Volume 9852, p. 985207. [Google Scholar]
- Hochuli, U.; Haldemann, P.; Li, H. Factors influencing the relative frequency stabiltiy of He–Ne laser structures. Rev. Sci. Instrum. 1974, 45, 1378–1381. [Google Scholar] [CrossRef]
- Ahearn, W.E.; Horstmann, R.E. Nondestructive Analysis for He–Ne Lasers. IBM J. Res. Dev. 1979, 23, 128–131. [Google Scholar] [CrossRef]
- Aronowitz, F. Fundamentals of the ring laser gyro. In Optical Gyros and Their Application; Loukianov, D., Rodloff, R., Sorg, H., Stieler, B., Eds.; NATO Research and Technology Organization: Brussels, Belgium, 1999; Volume 339, ISBN 92-837-1014-2. [Google Scholar]
- Shupe, D.M. Thermally induced nonreciprocity in the fiber-optic interferometer. Appl. Opt. 1980, 19, 654–655. [Google Scholar] [CrossRef]
- Hotate, K.; Tabe, K. Drift of an optical fiber gyroscope caused by the Faraday effect: influence of the earth’s magnetic field. Appl. Opt. 1986, 25, 1086–1092. [Google Scholar] [CrossRef]
- Logozinskii, V. Magnetically induced non-Faraday nonreciprocity in a fiber-optic gyroscope. J. Commun. Technol. Electron. 2006, 51, 836–840. [Google Scholar] [CrossRef]
- Ezekiel, S.; Davis, J.; Hellwarth, R. Intensity dependent nonreciprocal phase shift in a fiberoptic gyroscope. In Fiber-Optic Rotation Sensors and Related Technologies; Springer: Berlin/Heidelberg, Germany, 1982; pp. 332–336. [Google Scholar]
- Kim, H.K.; Digonnet, M.J.F.; Kino, G.S. Air-Core Photonic-Bandgap Fiber-Optic Gyroscope. J. Light. Technol. 2006, 24, 3169. [Google Scholar]
- Schreiber, U.K.; Rowe, C.H.; Wright, D.N.; Cooper, S.J.; Stedman, G.E. Precision stabilization of the optical frequency in a large ring laser gyroscope. Appl. Opt. 1998, 37, 8371–8381. [Google Scholar] [CrossRef] [PubMed]
- Schreiber, K.U.; Gebauer, A.; Wells, J.P.R. Long-term frequency stabilization of a 16 m2 ring laser gyroscope. Opt. Lett. 2012, 37, 1925–1927. [Google Scholar] [CrossRef]
- Wang, Z.; Yang, Y.; Lu, P.; Luo, R.; Li, Y.; Zhao, D.; Peng, C.; Li, Z. Dual-polarization interferometric fiber-optic gyroscope with an ultra-simple configuration. Opt. Lett. 2014, 39, 2463–2466. [Google Scholar] [CrossRef] [PubMed]
- Bucaro, J.A.; Dardy, H.D.; Carome, E.F. Optical fiber acoustic sensor. Appl. Opt. 1977, 16, 1761–1762. [Google Scholar] [CrossRef]
- Tur, M.; Shafir, E.; Blotekjaer, K. Source-induced noise in optical systems driven by low-coherence sources. J. Light. Technol. 1990, 8, 183–189. [Google Scholar] [CrossRef]
- Dunn, R.W.; Shabalin, D.E.; Thirkettle, R.J.; MacDonald, G.J.; Stedman, G.E.; Schreiber, K.U. Design and initial operation of a 367-m2 rectangular ring laser. Appl. Opt. 2002, 41, 1685–1688. [Google Scholar] [CrossRef]
- Hurst, R.B.; Stedman, G.E.; Schreiber, K.U.; Thirkettle, R.J.; Graham, R.D.; Rabeendran, N.; Wells, J.P.R. Experiments with an 834 m2 ring laser interferometer. J. Appl. Phys. 2009, 105, 113115. [Google Scholar] [CrossRef]
- Schreiber, K.U.; Gebauer, A.; Wells, J.P.R. Closed-loop locking of an optical frequency comb to a large ring laser. Opt. Lett. 2013, 38, 3574–3577. [Google Scholar] [CrossRef]
- Chao, B.F.; Dehant, V.; Gross, R.S.; Ray, R.D.; Salstein, D.A.; Watkins, M.M.; Wilson, C.R. Space geodesy monitors mass transports in global geophysical fluids. Trans. Am. Geophys. Union 2000, 81, 247–250. [Google Scholar] [CrossRef]
- Liu, K.; Zhang, F.L.; Li, Z.Y.; Feng, X.H.; Li, K.; Lu, Z.H.; Schreiber, K.U.; Luo, J.; Zhang, J. Large-scale passive laser gyroscope for earth rotation sensing. Opt. Lett. 2019, 44, 2732–2735. [Google Scholar] [CrossRef]
- Kuritsky, M.M.; Goldstein, M.S.; Greenwood, I.; Lerman, H.; McCarthy, J.; Shanahan, T.; Silver, M.; Simpson, J. Inertial navigation. Proc. IEEE 1983, 71, 1156–1176. [Google Scholar] [CrossRef]
- Kuznetsov, A.G.; Molchanov, A.V.; Chirkin, M.V.; Izmailov, E.A. Precise laser gyroscope for autonomous inertial navigation. Quantum Electron. 2015, 45, 78. [Google Scholar] [CrossRef]
- El-Sheimy, N.; Youssef, A. Inertial sensors technologies for navigation applications: State of the art and future trends. Satell. Navig. 2020, 1, 1–21. [Google Scholar] [CrossRef]
- Beghi, A.; Belfi, J.; Beverini, N.; Bouhadef, B.; Cuccato, D.; Virgilio, A.D.; Ortolan, A. Compensation of the laser parameter fluctuations in large ring-laser gyros: A Kalman filter approach. Appl. Opt. 2012, 51, 7518–7528. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Bernauer, F.; Wassermann, J.; Guattari, F.; Frenois, A.; Bigueur, A.; Gaillot, A.; de Toldi, E.; Ponceau, D.; Schreiber, U.; Igel, H. Full characterization of a 3C broadband rotational seismometer. Seismol. Res. Lett. 2018, 89, 620–629. [Google Scholar] [CrossRef]
- Li, H.; Lin, Y.; Liu, L.; Ma, H.; Jin, Z. Signal processing improvement of passive resonant fiber optic gyroscope using a reciprocal modulation-demodulation technique. Opt. Express 2020, 28, 18103–18111. [Google Scholar] [CrossRef] [PubMed]
- Ravaille, A.; Feugnet, G.; Debord, B.; Gérôme, F.; Benabid, F.; Bretenaker, F. Rotation measurements using a resonant fiber optic gyroscope based on Kagome fiber. Appl. Opt. 2019, 58, 2198–2204. [Google Scholar] [CrossRef]
- Zheng, Y.; Xu, H.; Song, J.; Li, L.; Zhang, C. Excess Relative-Intensity-Noise Reduction in a Fiber Optic Gyroscope Using a Faraday Rotator Mirror. J. Light. Technol. 2020, 38, 6939–6947. [Google Scholar] [CrossRef]
- Zhu, W.; Fokoua, E.N.; Chen, Y.; Bradley, T.; Petrovich, M.; Poletti, F.; Zhao, M.; Richardson, D.; Slavík, R. Temperature insensitive fiber interferometry. Opt. Lett. 2019, 44, 2768–2770. [Google Scholar] [CrossRef]
- Mutugala, U.S.; Fokoua, E.N.; Chen, Y.; Bradley, T.; Sandoghchi, S.R.; Jasion, G.; Curtis, R.; Petrovich, M.; Poletti, F.; Richardson, D.; et al. Hollow-core fibres for temperature-insensitive fibre optics and its demonstration in an Optoelectronic oscillator. Sci. Rep. 2018, 8, 18015. [Google Scholar] [CrossRef] [PubMed]
- Dell’Olio, F.; Tatoli, T.; Ciminelli, C.; Armenise, M. Recent advances in miniaturized optical gyroscopes. J. Eur. Opt. Soc. Rapid Publ. 2014, 9, 14013. [Google Scholar] [CrossRef]
- Mahmoud, M.; Mahmoud, A.; Cai, L.; Khan, M.; Mukherjee, T.; Bain, J.; Piazza, G. Novel on chip rotation detection based on the acousto-optic effect in surface acoustic wave gyroscopes. Opt. Express 2018, 26, 25060–25075. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Suh, M.G.; Vahala, K. Microresonator Brillouin gyroscope. Optica 2017, 4, 346–348. [Google Scholar] [CrossRef]
- Lai, Y.H.; Suh, M.G.; Lu, Y.K.; Shen, B.; Yang, Q.F.; Wang, H.; Li, J.; Lee, S.H.; Yang, K.Y.; Vahala, K. Earth rotation measured by a chip-scale ring laser gyroscope. Nat. Photonic 2020, 14, 345–349. [Google Scholar] [CrossRef]
- Qin, T.; Yang, J.; Zhang, F.; Chen, Y.; Shen, D.; Liu, W.; Chen, L.; Jiang, X.; Chen, X.; Wan, W. Fast-and slow-light-enhanced light drag in a moving microcavity. Commun. Phys. 2020, 3, 1–8. [Google Scholar] [CrossRef]
- Ren, J.; Hodaei, H.; Harari, G.; Hassan, A.U.; Chow, W.; Soltani, M.; Christodoulides, D.; Khajavikhan, M. Ultrasensitive micro-scale parity-time-symmetric ring laser gyroscope. Opt. Lett. 2017, 42, 1556–1559. [Google Scholar] [CrossRef]
- Grant, M.J.; Digonnet, M.J.F. Enhanced rotation sensing and exceptional points in a parity–time-symmetric coupled-ring gyroscope. Opt. Lett. 2020, 45, 6538–6541. [Google Scholar] [CrossRef]
- Hargrove, L.; Fork, R.L.; Pollack, M. Locking of He–Ne laser modes induced by synchronous intracavity modulation. Appl. Phys. Lett. 1964, 5, 4–5. [Google Scholar] [CrossRef]
- Morgner, U.; Kärtner, F.X.; Cho, S.H.; Chen, Y.; Haus, H.A.; Fujimoto, J.G.; Ippen, E.P.; Scheuer, V.; Angelow, G.; Tschudi, T. Sub-two-cycle pulses from a Kerr-lens mode-locked Ti:sapphire laser. Opt. Lett. 1999, 24, 411–413. [Google Scholar] [CrossRef] [PubMed]
- Sotor, J.; Sobon, G. 24 fs and 3 nJ pulse generation from a simple, all polarization maintaining Er-doped fiber laser. Laser Phys. Lett. 2016, 13, 125102. [Google Scholar] [CrossRef]
- Danson, C.N.; Haefner, C.; Bromage, J.; Butcher, T.; Chanteloup, J.C.F.; Chowdhury, E.A.; Galvanauskas, A.; Gizzi, L.A.; Hein, J.; Hillier, D.I.; et al. Petawatt and exawatt class lasers worldwide. High Power Laser Sci. Eng. 2019, 7, e54. [Google Scholar] [CrossRef]
- Brabec, T.; Krausz, F. Intense few-cycle laser fields: Frontiers of nonlinear optics. Rev. Mod. Phys. 2000, 72, 545. [Google Scholar] [CrossRef]
- Di Piazza, A.; Müller, C.; Hatsagortsyan, K.; Keitel, C.H. Extremely high-intensity laser interactions with fundamental quantum systems. Rev. Mod. Phys. 2012, 84, 1177. [Google Scholar] [CrossRef]
- Zhang, P.; Bulanov, S.; Seipt, D.; Arefiev, A.; Thomas, A. Relativistic plasma physics in supercritical fields. Phys. Plasmas 2020, 27, 050601. [Google Scholar] [CrossRef]
- Coddington, I.; Newbury, N.; Swann, W. Dual-comb spectroscopy. Optica 2016, 3, 414–426. [Google Scholar] [CrossRef]
- Udem, T.; Holzwarth, R.; Hänsch, T.W. Optical frequency metrology. Nature 2002, 416, 233. [Google Scholar] [CrossRef]
- Gaal, P.; Raschke, M.B.; Reimann, K.; Woerner, M. Measuring optical frequencies in the 0–40 THz range with non-synchronized electro–optic sampling. Nat. Photonics 2007. [Google Scholar] [CrossRef]
- Leopardi, H.; Davila-Rodriguez, J.; Quinlan, F.; Olson, J.; Sherman, J.A.; Diddams, S.A.; Fortier, T.M. Single-branch Er:fiber frequency comb for precision optical metrology with 10-18 fractional instability. Optica 2017, 4, 879–885. [Google Scholar] [CrossRef]
- Ippen, E.P. Principles of passive mode locking. Appl. Phys. B 1994, 58, 159–170. [Google Scholar] [CrossRef]
- Haus, H.A. Mode-locking of lasers. IEEE J. Sel. Top. Quantum Electron. 2000, 6, 1173–1185. [Google Scholar] [CrossRef]
- Kryukov, P.; Letokhov, V. Fluctuation mechanism of ultrashort pulse generation by laser with saturable absorber. IEEE J. Quantum Electron. 1972, 8, 766–782. [Google Scholar] [CrossRef]
- Glenn, W. The fluctuation model of a passively mode-locked laser. IEEE J. Quantum Electron. 1975, 11, 8–17. [Google Scholar] [CrossRef]
- Agrawal, G.P. Nonlinear fiber optics. In Nonlinear Science at the Dawn of the 21st Century; Springer: Berlin/Heidelberg, Germany, 2000; pp. 195–211. [Google Scholar]
- Fermann, M.E.; Galvanauskas, A.; Sucha, G. Ultrafast Lasers: Technology and Applications; CRC Press: Boca Raton, FL, USA, 2002; Volume 80. [Google Scholar]
- Lariontsev, E.G.; Serkin, V.N. Possibility of using self-focusing for increasing contrast and narrowing of ultrashort light pulses. Sov. J. Quantum Electron. 1975, 5, 796. [Google Scholar] [CrossRef]
- Fermann, M.; Andrejco, M.; Silberberg, Y.; Stock, M. Passive mode locking by using nonlinear polarization evolution in a polarization-maintaining erbium-doped fiber. Opt. Lett. 1993, 18, 894–896. [Google Scholar] [CrossRef]
- Doran, N.; Wood, D. Nonlinear-optical loop mirror. Opt. Lett. 1988, 13, 56–58. [Google Scholar] [CrossRef]
- Fermann, M.E.; Haberl, F.; Hofer, M.; Hochreiter, H. Nonlinear amplifying loop mirror. Opt. Lett. 1990, 15, 752–754. [Google Scholar] [CrossRef]
- Mocker, H.W.; Collins, R. Mode competition and self-locking effects in a Q-switched ruby laser. Appl. Phys. Lett. 1965, 7, 270–273. [Google Scholar] [CrossRef]
- Glenn, W.; Brienza, M.; DeMaria, A. Mode locking of an organic dye laser. Appl. Phys. Lett. 1968, 12, 54–56. [Google Scholar] [CrossRef]
- Keller, U.; Weingarten, K.J.; Kartner, F.X.; Kopf, D.; Braun, B.; Jung, I.D.; Fluck, R.; Honninger, C.; Matuschek, N.; Aus der Au, J. Semiconductor saturable absorber mirrors (SESAM’s) for femtosecond to nanosecond pulse generation in solid-state lasers. IEEE J. Sel. Top. Quantum Electron. 1996, 2, 435–453. [Google Scholar] [CrossRef]
- Okhotnikov, O.; Grudinin, A.; Pessa, M. Ultra-fast fibre laser systems based on SESAM technology: new horizons and applications. New J. Phys. 2004, 6, 177. [Google Scholar] [CrossRef]
- Keller, U. Ultrafast solid-state lasers. Prog. Opt. 2004, 46, 1–116. [Google Scholar]
- Tilma, B.W.; Mangold, M.; Zaugg, C.A.; Link, S.M.; Waldburger, D.; Klenner, A.; Mayer, A.S.; Gini, E.; Golling, M.; Keller, U. Recent advances in ultrafast semiconductor disk lasers. Light Sci. Appl. 2015, 4, e310. [Google Scholar] [CrossRef]
- Gaponenko, M.; Metz, P.W.; Härkönen, A.; Heuer, A.; Leinonen, T.; Guina, M.; Südmeyer, T.; Huber, G.; Kränkel, C. SESAM mode-locked red praseodymium laser. Opt. Lett. 2014, 39, 6939–6941. [Google Scholar] [CrossRef] [PubMed]
- Hasan, T.; Sun, Z.; Wang, F.; Bonaccorso, F.; Tan, P.H.; Rozhin, A.G.; Ferrari, A.C. Nanotube–polymer composites for ultrafast photonics. Adv. Mater. 2009, 21, 3874–3899. [Google Scholar] [CrossRef]
- Zhang, H.; Tang, D.; Zhao, L.; Bao, Q.; Loh, K. Large energy mode locking of an erbium-doped fiber laser with atomic layer graphene. Opt. Express 2009, 17, 17630–17635. [Google Scholar] [CrossRef]
- Martinez, A.; Sun, Z. Nanotube and graphene saturable absorbers for fibre lasers. Nat. Photonics 2013, 7, 842–845. [Google Scholar] [CrossRef]
- Zhao, G.; Han, S.; Wang, A.; Wu, Y.; Zhao, M.; Wang, Z.; Hao, X. “Chemical Weathering” Exfoliation of Atom-Thick Transition Metal Dichalcogenides and Their Ultrafast Saturable Absorption Properties. Adv. Funct. Mater. 2015, 25, 5292–5299. [Google Scholar] [CrossRef]
- Woodward, R.I.; Kelleher, E.J. 2D saturable absorbers for fibre lasers. Appl. Sci. 2015, 5, 1440–1456. [Google Scholar] [CrossRef]
- Jiang, X.; Liu, S.; Liang, W.; Luo, S.; He, Z.; Ge, Y.; Wang, H.; Cao, R.; Zhang, F.; Wen, Q.; et al. Broadband nonlinear photonics in few-layer MXene Ti3C2Tx (T= F, O, or OH). Laser Photonics Rev. 2018, 12, 1700229. [Google Scholar] [CrossRef]
- Jhon, Y.I.; Koo, J.; Anasori, B.; Seo, M.; Lee, J.H.; Gogotsi, Y.; Jhon, Y.M. Metallic MXene saturable absorber for femtosecond mode-locked lasers. Adv. Mater. 2017, 29, 1702496. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Jiang, G.; Chen, S.; Guo, Z.; Yu, X.; Zhao, C.; Zhang, H.; Bao, Q.; Wen, S.; Tang, D.; et al. Mechanically exfoliated black phosphorus as a new saturable absorber for both Q-switching and mode-locking laser operation. Optics Express 2015, 23, 12823–12833. [Google Scholar] [CrossRef]
- Qin, Z.; Xie, G.; Zhao, C.; Wen, S.; Yuan, P.; Qian, L. Mid-infrared mode-locked pulse generation with multilayer black phosphorus as saturable absorber. Opt. Lett. 2016, 41, 56–59. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Coillet, A.; Demichel, O.; Wang, Z.; Rego, D.; Bouhelier, A.; Grelu, P.; Cluzel, B. Saturable plasmonic metasurfaces for laser mode locking. Light Sci. Appl. 2020, 9, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Kashiwagi, K.; Yamashita, S. Deposition of carbon nanotubes around microfiber via evanascent light. Optics Express 2009, 17, 18364–18370. [Google Scholar] [CrossRef] [PubMed]
- Hu, G.; Albrow-Owen, T.; Jin, X.; Ali, A.; Hu, Y.; Howe, R.C.; Shehzad, K.; Yang, Z.; Zhu, X.; Woodward, R.I.; et al. Black phosphorus ink formulation for inkjet printing of optoelectronics and photonics. Nat. Commun. 2017, 8, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Mou, C.; Rozhin, A.G.; Arif, R.; Zhou, K.; Turitsyn, S. Polarization insensitive in-fiber mode-locker based on carbon nanotube with N-methyl-2-pryrrolidone solvent filled fiber microchamber. Appl. Phys. Lett. 2012, 100, 101110. [Google Scholar] [CrossRef]
- Mollenauer, L.F.; Stolen, R.H.; Gordon, J.P. Experimental observation of picosecond pulse narrowing and solitons in optical fibers. Phys. Rev. Lett. 1980, 45, 1095. [Google Scholar] [CrossRef]
- Turitsyn, S.K.; Bale, B.G.; Fedoruk, M.P. Ispersion-managed solitons in fibre systems and lasers. Phys. Rep. 2012, 521, 135–203. [Google Scholar] [CrossRef]
- Chong, A.; Buckley, J.; Renninger, W.; Wise, F. All-normal-dispersion femtosecond fiber laser. Opt. Express 2006, emph14, 10095–10100. [Google Scholar] [CrossRef] [PubMed]
- Oktem, B.; Ülgüdür, C.; Ilday, F.Ö. Soliton–similariton fibre laser. Nat. Photonics 2010, 4, 307–311. [Google Scholar] [CrossRef]
- Kivshar, Y.S.; Luther-Davies, B. Dark optical solitons: physics and applications. Phys. Rep. 1998, 298, 81–197. [Google Scholar] [CrossRef]
- Krylov, A.A.; Chernykh, D.S.; Obraztsova, E.D. Gyroscopic effect detection in the colliding-pulse hybridly mode-locked erbium-doped all-fiber ring soliton laser. Opt. Lett. 2017, 42, 2439–2442. [Google Scholar] [CrossRef]
- Newbury, N.R.; Swann, W.C. Low-noise fiber-laser frequency combs. JOSA B 2007, 24, 1756–1770. [Google Scholar] [CrossRef]
- Haus, H.; Ippen, E. Group velocity of solitons. Opt. Lett. 2001, 26, 1654–1656. [Google Scholar] [CrossRef] [PubMed]
- Sala, K.; Kenney-Wallace, G.; Hall, G. CW autocorrelation measurements of picosecond laser pulses. IEEE J. Quantum Electron. 1980, 16, 990–996. [Google Scholar] [CrossRef]
- Stolen, R.; Lin, C. Self-phase-modulation in silica optical fibers. Phys. Rev. A 1978, 17, 1448. [Google Scholar] [CrossRef]
- Kane, D.J.; Trebino, R. Characterization of arbitrary femtosecond pulses using frequency-resolved optical gating. IEEE J. Quantum Electron.s 1993, 29, 571–579. [Google Scholar] [CrossRef]
- Akturk, S.; Kimmel, M.; O’Shea, P.; Trebino, R. Measuring pulse-front tilt in ultrashort pulses using GRENOUILLE. Opt. Express 2003, 11, 491–501. [Google Scholar] [CrossRef] [PubMed]
- Iaconis, C.; Walmsley, I.A. Spectral phase interferometry for direct electric-field reconstruction of ultrashort optical pulses. Opt. Lett. 1998, 23, 792–794. [Google Scholar] [CrossRef]
- Trebino, R. Frequency-Resolved Optical Gating: The Measurement of Ultrashort Laser Pulses: The Measurement of Ultrashort Laser Pulses; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Budunoğlu, I.L.; Ülgüdür, C.; Oktem, B.; Ilday, F.Ö. Intensity noise of mode-locked fiber lasers. Optics Lett. 2009, 34, 2516–2518. [Google Scholar] [CrossRef]
- Kim, J.; Song, Y. Ultralow-noise mode-locked fiber lasers and frequency combs: principles, status, and applications. Adv. Opt. Photonics 2016, 8, 465–540. [Google Scholar] [CrossRef]
- Paschotta, R.; Schlatter, A.; Zeller, S.; Telle, H.; Keller, U. Optical phase noise and carrier-envelope offset noise of mode-locked lasers. Appl. Phys. B 2006, 82, 265–273. [Google Scholar] [CrossRef]
- Jones, D.J.; Diddams, S.A.; Ranka, J.K.; Stentz, A.; Windeler, R.S.; Hall, J.L.; Cundiff, S.T. Carrier-envelope phase control of femtosecond mode-locked lasers and direct optical frequency synthesis. Science 2000, 288, 635–639. [Google Scholar] [CrossRef] [PubMed]
- Roudnev, V.; Esry, B. General theory of carrier-envelope phase effects. Phys. Rev. Lett. 2007, 99, 220406. [Google Scholar] [CrossRef]
- Von der Linde, D. Characterization of the noise in continuously operating mode-locked lasers. Appl. Phys. B 1986, 39, 201–217. [Google Scholar] [CrossRef]
- Dvoretskiy, D.A.; Sazonkin, S.G.; Orekhov, I.O.; Kudelin, I.S.; Pnev, A.B.; Karasik, V.E.; Krylov, A.A.; Denisov, L.K. High-energy ultrashort-pulse all-fiber erbium-doped ring laser with improved free-running performance. JOSA B 2018, 35, 2010–2014. [Google Scholar] [CrossRef]
- Haus, H.A.; Mecozzi, A. Noise of mode-locked lasers. IEEE J. Quantum Electron. 1993, 29, 983–996. [Google Scholar] [CrossRef]
- Hou, D.; Lee, C.C.; Yang, Z.; Schibli, T. Timing jitter characterization of mode-locked lasers with< 1 zs/ Hz resolution using a simple optical heterodyne technique. Opt. Lett. 2015, 40, 2985–2988. [Google Scholar]
- Jung, K.; Kim, J. Characterization of timing jitter spectra in free-running mode-locked lasers with 340 dB dynamic range over 10 decades of Fourier frequency. Opt. Lett. 2015, 40, 316–319. [Google Scholar] [PubMed]
- Kwon, D.; Jeon, I.; Lee, W.K.; Heo, M.S.; Kim, J. Generation of multiple ultrastable optical frequency combs from an all-fiber photonic platform. Sci. Adv. 2020, 6, eaax4457. [Google Scholar] [CrossRef] [PubMed]
- Xie, X.; Bouchand, R.; Nicolodi, D.; Giunta, M.; Hänsel, W.; Lezius, M.; Joshi, A.; Datta, S.; Alexandre, C.; Lours, M.; et al. Photonic microwave signals with zeptosecond-level absolute timing noise. Nat. Photonics 2017, 11, 44–47. [Google Scholar] [CrossRef]
- Kwon, D.; Kim, J. All-fiber interferometer-based repetition-rate stabilization of mode-locked lasers to 10-14-level frequency instability and 1-fs-level jitter over 1 s. Opt. Lett. 2017, 42, 5186–5189. [Google Scholar] [CrossRef] [PubMed]
- Washburn, B.R.; Swann, W.C.; Newbury, N.R. Response dynamics of the frequency comb output from a femtosecond fiber laser. Opt. Express 2005, 13, 10622–10633. [Google Scholar] [CrossRef] [PubMed]
- Nugent-Glandorf, L.; Johnson, T.A.; Kobayashi, Y.; Diddams, S.A. Impact of dispersion on amplitude and frequency noise in a Yb-fiber laser comb. Opt. Lett. 2011, 36, 1578–1580. [Google Scholar] [CrossRef]
- Wahlstrand, J.K.; Willits, J.T.; Menyuk, C.R.; Cundiff, S.T. The quantum-limited comb lineshape of a mode-locked laser: Fundamental limits on frequency uncertainty. Opt. Express 2008, 16, 18624–18630. [Google Scholar] [CrossRef]
- Xu, L.; Spielmann, C.; Poppe, A.; Brabec, T.; Krausz, F.; Hänsch, T.W. Route to phase control of ultrashort light pulses. Opt. Lett. 1996, 21, 2008–2010. [Google Scholar] [CrossRef]
- Udem, T.; Reichert, J.; Holzwarth, R.; Hänsch, T.W. Accurate measurement of large optical frequency differences with a mode-locked laser. Opt. Lett. 1999, 24, 881–883. [Google Scholar] [CrossRef]
- Hartl, I.; Imeshev, G.; Fermann, M.E.; Langrock, C.; Fejer, M.M. Integrated self-referenced frequency-comb laser based on a combination of fiber and waveguide technology. Opt. Express 2005, 13, 6490–6496. [Google Scholar] [CrossRef]
- Wittmann, T.; Horvath, B.; Helml, W.; Schätzel, M.G.; Gu, X.; Cavalieri, A.L.; Paulus, G.; Kienberger, R. Single-shot carrier–envelope phase measurement of few-cycle laser pulses. Nat. Phys. 2009, 5, 357–362. [Google Scholar] [CrossRef]
- Gowda, R.; Nguyen, N.; Diels, J.C.; Norwood, R.A.; Peyghambarian, N.; Kieu, K. All-fiber bidirectional optical parametric oscillator for precision sensing. Opt. Lett. 2015, 40, 2033–2036. [Google Scholar] [CrossRef] [PubMed]
- Iwakuni, K.; Inaba, H.; Nakajima, Y.; Kobayashi, T.; Hosaka, K.; Onae, A.; Hong, F.L. Narrow linewidth comb realized with a mode-locked fiber laser using an intra-cavity waveguide electro-optic modulator for high-speed control. Opt. Express 2012, 20, 13769–13776. [Google Scholar] [CrossRef] [PubMed]
- Benko, C.; Ruehl, A.; Martin, M.; Eikema, K.; Fermann, M.; Hartl, I.; Ye, J. Full phase stabilization of a Yb: fiber femtosecond frequency comb via high-bandwidth transducers. Opt. Lett. 2012, 37, 2196–2198. [Google Scholar] [CrossRef] [PubMed]
- Paschotta, R. Noise in Laser Technology: Part 1: Intensity and Phase Noise. Opt. Photonik 2009, 4, 48–50. [Google Scholar] [CrossRef]
- McCumber, D.E. Intensity Fluctuations in the Output of cw Laser Oscillators. I. Phys. Rev. 1966, 141, 306–322. [Google Scholar] [CrossRef]
- Paschotta, R. Noise of mode-locked lasers (Part II): timing jitter and other fluctuations. Appl. Phys. B 2004, 79, 163–173. [Google Scholar] [CrossRef]
- Kane, T.J. Intensity noise in diode-pumped single-frequency Nd: YAG lasers and its control by electronic feedback. IEEE Photonics Technol. Lett. 1990, 2, 244–245. [Google Scholar] [CrossRef]
- Cranch, G. Frequency noise reduction in erbium-doped fiber distributed-feedback lasers by electronic feedback. Opt. Lett. 2002, 27, 1114–1116. [Google Scholar] [CrossRef]
- Holman, K.W.; Jones, R.J.; Marian, A.; Cundiff, S.T.; Ye, J. Detailed studies and control of intensity-related dynamics of femtosecond frequency combs from mode-locked Ti: sapphire lasers. IEEE J. Sel. Top. Quantum Electron. 2003, 9, 1018–1024. [Google Scholar] [CrossRef]
- Wang, Z.; Nithyanandan, K.; Coillet, A.; Tchofo-Dinda, P.; Grelu, P. Optical soliton molecular complexes in a passively mode-locked fibre laser. Nat. Commun. 2019, 10, 830. [Google Scholar] [CrossRef] [PubMed]
- Churkin, D.; Sugavanam, S.; Tarasov, N.; Khorev, S.; Smirnov, S.; Kobtsev, S.; Turitsyn, S. Stochasticity, periodicity and localized light structures in partially mode-locked fibre lasers. Nat. Commun. 2015, 6, 7004. [Google Scholar] [CrossRef] [PubMed]
- Sugavanam, S.; Tarasov, N.; Churkin, D.V. Real-time intensity domain characterization of fibre lasers using spatio-temporal dynamics. Appl. Sci. 2016, 6, 65. [Google Scholar] [CrossRef]
- Kolner, B.H. Space-time duality and the theory of temporal imaging. IEEE J. Quantum Electron. 1994, 30, 1951–1963. [Google Scholar] [CrossRef]
- Salem, R.; Foster, M.A.; Turner, A.C.; Geraghty, D.F.; Lipson, M.; Gaeta, A.L. Optical time lens based on four-wave mixing on a silicon chip. Opt. Lett. 2008, 33, 1047–1049. [Google Scholar] [CrossRef]
- Ryczkowski, P.; Närhi, M.; Billet, C.; Merolla, J.M.; Genty, G.; Dudley, J.M. Real-time full-field characterization of transient dissipative soliton dynamics in a mode-locked laser. Nat. Photonics 2018, 12, 221. [Google Scholar] [CrossRef]
- Turitsyna, E.; Smirnov, S.; Sugavanam, S.; Tarasov, N.; Shu, X.; Babin, S.; Podivilov, E.; Churkin, D.; Falkovich, G.; Turitsyn, S. The laminar–turbulent transition in a fibre laser. Nat. Photonics 2013, 7, 783. [Google Scholar] [CrossRef]
- Birkholz, S.; Nibbering, E.T.J.; Brée, C.; Skupin, S.; Demircan, A.; Genty, G.; Steinmeyer, G. Spatiotemporal Rogue Events in Optical Multiple Filamentation. Phys. Rev. Lett. 2013, 111, 243903. [Google Scholar] [CrossRef]
- Herink, G.; Jalali, B.; Ropers, C.; Solli, D. Resolving the build-up of femtosecond mode-locking with single-shot spectroscopy at 90 MHz frame rate. Nat. Photonics 2016, 10, 321. [Google Scholar] [CrossRef]
- Peng, J.; Sorokina, M.; Sugavanam, S.; Tarasov, N.; Churkin, D.V.; Turitsyn, S.K.; Zeng, H. Real-time observation of dissipative soliton formation in nonlinear polarization rotation mode-locked fibre lasers. Commun. Phys. 2018, 1, 20. [Google Scholar] [CrossRef]
- Kudelin, I.; Sugavanam, S.; Chernysheva, M. Pulse-onset dynamics in a bidirectional mode-locked fibre laser via instabilities. Commun. Phys. 2020, 3, 1–10. [Google Scholar] [CrossRef]
- Kudelin, I.; Sugavanam, S.; Chernysheva, M. Build-up dynamics in bidirectional soliton fiber lasers. Photonics Res. 2020, 8, 776–780. [Google Scholar] [CrossRef]
- Goda, K.; Jalali, B. Dispersive Fourier transformation for fast continuous single-shot measurements. Nat. Photonics 2013, 7, 102. [Google Scholar] [CrossRef]
- Herink, G.; Kurtz, F.; Jalali, B.; Solli, D.; Ropers, C. Real-time spectral interferometry probes the internal dynamics of femtosecond soliton molecules. Science 2017, 356, 50–54. [Google Scholar] [CrossRef] [PubMed]
- Goda, K.; Tsia, K.K.; Jalali, B. Amplified dispersive Fourier-transform imaging for ultrafast displacement sensing and barcode reading. Appl. Phys. Lett. 2008, 93, 131109. [Google Scholar] [CrossRef]
- Wong, T.T.; Lau, A.K.; Wong, K.K.; Tsia, K.K. Optical time-stretch confocal microscopy at 1 μm. Opt. Lett. 2012, 37, 3330–3332. [Google Scholar] [CrossRef]
- Goda, K.; Tsia, K.; Jalali, B. Serial time-encoded amplified imaging for real-time observation of fast dynamic phenomena. Nature 2009, 458, 1145–1149. [Google Scholar] [CrossRef]
- Goda, K.; Ayazi, A.; Gossett, D.R.; Sadasivam, J.; Lonappan, C.K.; Sollier, E.; Fard, A.M.; Hur, S.C.; Adam, J.; Murray, C.; et al. High-throughput single-microparticle imaging flow analyzer. Proc. Natl. Acad. Sci. USA 2012, 109, 11630–11635. [Google Scholar] [CrossRef]
- Jiang, Y.; Karpf, S.; Jalali, B. Time-stretch LiDAR as a spectrally scanned time-of-flight ranging camera. Nat. Photonics 2020, 14, 14–18. [Google Scholar] [CrossRef]
- Hong, J.B.; Yeo, Y.B.; Lee, B.W.; Kim, B.Y. Phase sensitive detection for mode-locked fiber laser gyroscope. IEEE Photonics Technol. Lett. 1999, 11, 1030–1032. [Google Scholar] [CrossRef]
- Zhao, L.; Tang, D.; Cheng, T.; Lu, C. Self-started unidirectional operation of a fibre ring soliton laser without an isolator. J. Opt. A Pure Appl. Opt. 2007, 9, 477. [Google Scholar] [CrossRef]
- Li, D.; Shen, D.; Li, L.; Chen, H.; Tang, D.; Zhao, L. Unidirectional dissipative soliton operation in an all-normal-dispersion Yb-doped fiber laser without an isolator. Appl. Opt. 2015, 54, 7912–7916. [Google Scholar] [CrossRef] [PubMed]
- Fork, R.; Greene, B.; Shank, C.V. Generation of optical pulses shorter than 0.1 psec by colliding pulse mode locking. Appl. Phys. Lett. 1981, 38, 671–672. [Google Scholar] [CrossRef]
- Smith, K.; Sibbett, W.; Taylor, J.R. Subpicosecond generation via hybrid mode-locking of styryl 9 in the near infra-red. Opt. Commun. 1984, 49, 359–361. [Google Scholar] [CrossRef]
- Kim, S.; Kim, Y.; Park, J.; Han, S.; Park, S.; Kim, Y.J.; Kim, S.W. Hybrid mode-locked Er-doped fiber femtosecond oscillator with 156 mW output powers. Opt. Express 2012, 20, 15054–15060. [Google Scholar] [CrossRef]
- Dvoretskiy, D.A.; Sazonkin, S.G.; Orekhov, I.O.; Kudelin, I.S.; Pnev, A.B.; Karasik, V.E.; Denisov, L.K.; Lyapin, S.G.; Davydov, V.A. Hybrid mode-locked erbium-doped all-fiber ring laser with high-density well-aligned single-walled carbon nanotubes. In Proceedings of the Progress In Electromagnetics Research Symposium-Spring (PIERS), St. Petersburg, Russia, 22–25 May 2017. [Google Scholar]
- Hata, Y.; Nakajima, Y.; Minoshima, K. Bidirectional mode-locked Er-fiber laser with symmetrical cavity configuration. In Proceedings of the Conference on Lasers and Electro-Optics/Pacific Rim. Optical Society of America, Hong Kong, China, 29 July–3 August 2018; pp. 2–3. [Google Scholar]
- Ouyang, C.; Shum, P.; Wu, K.; Wong, J.H.; Lam, H.Q.; Aditya, S. Bidirectional passively mode-locked soliton fiber laser with a four-port circulator. Opt. Lett. 2011, 36, 2089–2091. [Google Scholar] [CrossRef]
- Zhou, Y.; Ren, Y.X.; Shi, J.; Wong, K.K.Y. Breathing dissipative soliton explosions in a bidirectional ultrafast fiber laser. Photon. Res. 2020, 8, 1566–1572. [Google Scholar] [CrossRef]
- Li, Y.; Yin, K.; Zhang, X.; Zheng, X.; Cheng, X.; Jiang, T. All-fiber bidirectional mode-locked ultrafast fiber laser at 2 μm. IEEE Photonics J. 2019, 11, 1–8. [Google Scholar] [CrossRef]
- Abdukerim, N.; Kayes, M.I.; Rekik, A.; Rochette, M. Bidirectional mode-locked thulium-doped fiber laser. Appl. Opt. 2018, 57, 7198–7202. [Google Scholar] [CrossRef]
- Li, B.; Xing, J.; Kwon, D.; Xie, Y.; Prakash, N.; Kim, J.; Huang, S.W. Bidirectional mode-locked all-normal dispersion fiber laser. Optica 2020, 7, 961–964. [Google Scholar] [CrossRef]
- Yao, X. Generation of bidirectional stretched pulses in a nanotube-mode-locked fiber laser. Appl. Opt. 2014, 53, 27–31. [Google Scholar] [CrossRef]
- Yu, Y.; Kong, C.; Li, B.; Kang, J.; Ren, Y.X.; Luo, Z.C.; Wong, K.K. Behavioral similarity of dissipative solitons in an ultrafast fiber laser. Opt. Lett. 2019, 44, 4813–4816. [Google Scholar] [CrossRef] [PubMed]
- Jeong, H.J.; Koh, Y.W.; Lee, B.W.; Jeon, M.Y.; Kim, B.Y. Analysis of polarization properties of a mode-locked fiber lasergyroscope. Appl. Opt. 1996, 35, 2206–2210. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Lee, B.W.; Jeong, H.J.; Kim, B.Y. High-sensitivity mode-locked fiber laser gyroscope. Opt. Lett. 1997, 22, 129–131. [Google Scholar] [CrossRef][Green Version]
- Braga, A.; Diels, J.C.; Jain, R.; Kay, R.; Wang, L. Bidirectional mode-locked fiber ring laser using self-regenerative, passively controlled, threshold gating. Opt. Lett. 2010, 35, 2648–2650. [Google Scholar] [CrossRef] [PubMed]
- Krylov, A.A.; Chernykh, D.S.; Arutyunyan, N.R.; Grebenyukov, V.V.; Pozharov, A.S.; Obraztsova, E.D. Generation regimes of bidirectional hybridly mode-locked ultrashort pulse erbium-doped all-fiber ring laser with a distributed polarizer. Appl. Opt. 2016, 55, 4201–4209. [Google Scholar] [CrossRef]
- Zhang, W.; Zhan, L.; Xian, T.; Gao, L. Bidirectional dark-soliton fiber lasers for high-sensitivity gyroscopic application. Opt. Lett. 2019, 44, 4008–4011. [Google Scholar] [CrossRef]
- Zhang, H.; Tang, D.; Zhao, L.; Wu, X. Dark pulse emission of a fiber laser. Phys. Rev. A 2009, 80, 045803. [Google Scholar] [CrossRef]
- Zhao, W.; Bourkoff, E. Propagation properties of dark solitons. Opt. Lett. 1989, 14, 703–705. [Google Scholar] [CrossRef]
- Chen, Y.; Atai, J. Absorption and amplification of dark solitons. Opt. Lett. 1991, 16, 1933–1935. [Google Scholar] [CrossRef] [PubMed]
- Zhao, W.; Bourkoff, E. Interactions between dark solitons. Opt. Lett. 1989, 14, 1371–1373. [Google Scholar] [CrossRef]
- Chernysheva, M.; Al Araimi, M.; Kbashi, H.; Arif, R.; Sergeyev, S.V.; Rozhin, A. Isolator-free switchable uni-and bidirectional hybrid mode-locked erbium-doped fiber laser. Opt. Express 2016, 24, 15721–15729. [Google Scholar] [CrossRef]
- Kudelin, I.S.; Sugavanam, S.; Chernysheva, M. Ultrafast gyroscopic measurements in passive Mach-Zehnder interferometer via time-stretch technique. In Proceedings of the The European Conference on Lasers and Electro-Optics. Optical Society of America, Nice, France, 1–3 November 2021. [Google Scholar]
- Woodward, R.; Kelleher, E.J. Towards ‘smart lasers’: Self-optimisation of an ultrafast pulse source using a genetic algorithm. Sci. Rep. 2016, 6, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Kokhanovskiy, A.; Ivanenko, A.; Kobtsev, S.; Smirnov, S.; Turitsyn, S. Machine learning methods for control of fibre lasers with double gain nonlinear loop mirror. Sci. Rep. 2019, 9, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Suo, X.; Yu, H.; Li, J.; Wu, X. Transmissive resonant fiber-optic gyroscope employing Kagome hollow-core photonic crystal fiber resonator. Opt. Lett. 2020, 45, 2227–2230. [Google Scholar] [CrossRef] [PubMed]


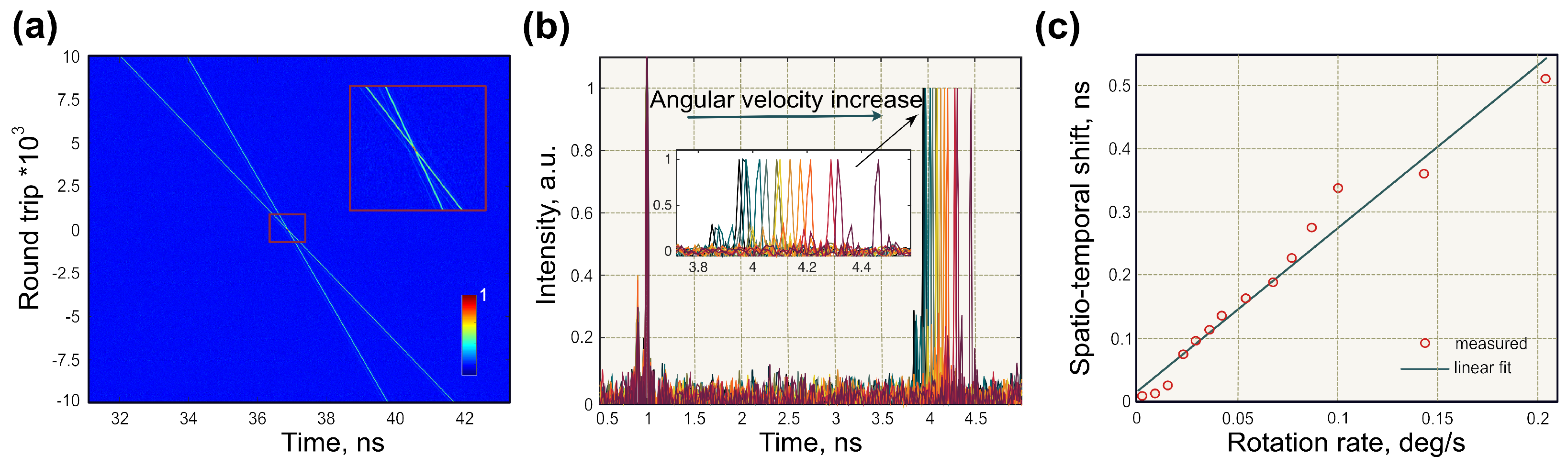
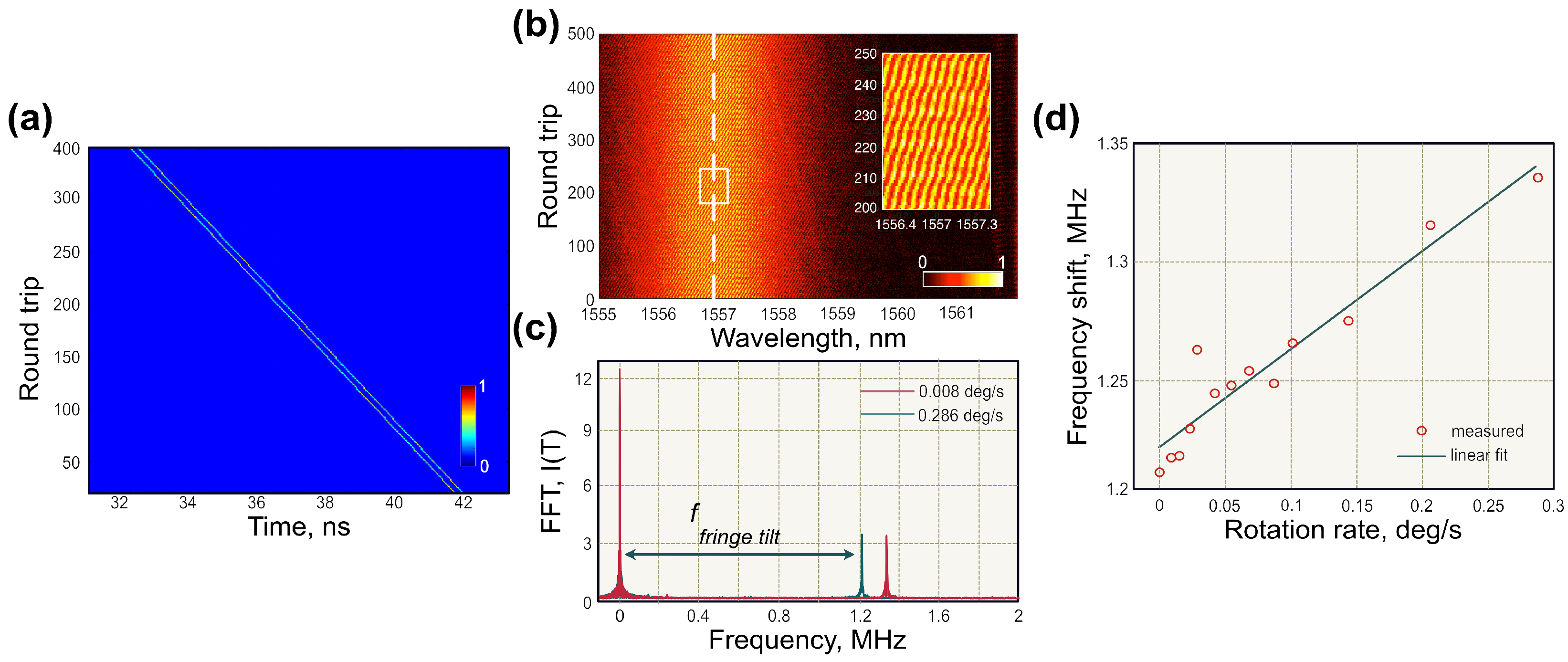

| Cavity | Gyroscope | Measurement | Angular Velocity | Resolution | Scale Factor | Stability | Advantages | Disadvantages | Ref. |
|---|---|---|---|---|---|---|---|---|---|
| configuration | length/area | method | range | performance | |||||
| NALM-based | phase noise | High stability | Sagnac effect is | ||||||
| NALM-based | random walk | laser configu- | through | ||||||
| with polariser | 150 m/0.07 m | time delay | up to 240 deg/s | 0.4 deg/ | 0.47 ps/(deg/h) | 0.06 deg/h | ration | roundtrips | [196] |
| zero bias drift | Well-established | Low stability | |||||||
| Ring cavity | 4.59 m/0.79 m | beat-note | 0.12–90 deg/s | 0.028 deg/s | 7 kHz/(deg/s) | 193 Hz | and simple | due to fluctuation | [123] |
| method | of the CEO frequency | ||||||||
| Ring cavity: | zero bias drift | Higher stability | Hard to achieve | ||||||
| dark solitons | 69.5 m/0.29 m | beat-note | ±16 deg/s | 0.05 deg/s | 3.31 kHz/(deg/s) | 72 Hz | of dark solitons | generation | [199] |
| Ring cavity: | real-time | time jitter | 100s kHz–10s MHz | Requires fast | |||||
| different rep rates | 13.5 m/0.3 m | spatiotemporal | 0.01–0.3 deg/s | 0.022 deg/s | 0.885 deg/s/ns | <0.8 ps | acquisition rate | photodetectors | [29] |
| and oscilloscope | |||||||||
| Ring cavity: | real-time | Highest resolution | Requires fast | ||||||
| equal rep rates | 13.5 m / 0.3 m | DFT | 0.01–0.3 deg/s | 0.007 deg/s | 0.017 deg/s/kHz | - | at high data | photodetectors | |
| acquisition rate | and oscilloscope | [29] | |||||||
| Sensitivity to | |||||||||
| the CEO phase | |||||||||
| Optical paramet- | estimated | f drift | Extremely narrow | No experimental | |||||
| ric oscillator | 13.5 m/0.3 m | beat-note | - | 3.22 × 10 deg/s | - | 10s kHz over 30 s | linewidth, possibility to scale | demonstration | [152] |
| at zero f drift | up performance | ||||||||
| Hollow-core fibre | bias stability 0.15 deg/h | Low environmental | High splice losses | ||||||
| optic gyroscope | 5.6 m/132 cm | ±100 deg/s | 0.05 deg/h | - | ARW 0.04 deg/ | sensitivity | demonstration | [208] | |
| Brillouin ring | ARW noise 0.068 deg/ | Highest resolution | Not at the point | ||||||
| laser gyroscope | 1017 mm | beat-note | up to 250 deg/h | 5 deg/h | 0.073 Hz/(deg/h) | bias stability 3.6 deg/h | Integrated design | of commercialisation | [73] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kudelin, I.; Sugavanam, S.; Chernysheva, M. Rotation Active Sensors Based on Ultrafast Fibre Lasers. Sensors 2021, 21, 3530. https://doi.org/10.3390/s21103530
Kudelin I, Sugavanam S, Chernysheva M. Rotation Active Sensors Based on Ultrafast Fibre Lasers. Sensors. 2021; 21(10):3530. https://doi.org/10.3390/s21103530
Chicago/Turabian StyleKudelin, Igor, Srikanth Sugavanam, and Maria Chernysheva. 2021. "Rotation Active Sensors Based on Ultrafast Fibre Lasers" Sensors 21, no. 10: 3530. https://doi.org/10.3390/s21103530
APA StyleKudelin, I., Sugavanam, S., & Chernysheva, M. (2021). Rotation Active Sensors Based on Ultrafast Fibre Lasers. Sensors, 21(10), 3530. https://doi.org/10.3390/s21103530






