A Lattice-Based Homomorphic Proxy Re-Encryption Scheme with Strong Anti-Collusion for Cloud Computing
Abstract
1. Introduction
1.1. Related Work
1.2. Our Contribution
- (1)
- (2)
- Then, based on the L-homomorphic encryption scheme proposed in this paper, we construct an HPRE-SAC scheme by using trapdoor sampling technology and a key switching algorithm.
- (3)
- Finally, a direct application of the HPRE-SAC scheme is given, that is, secure computing of personal health records (PHRs) in the cloud.
1.3. Paper Organization
2. Preliminaries
2.1. Lattice and Gaussian Distributions
2.2. HE: Definition and Security
- 1.
- Input the security parameter k. Output the public parameters .
- 2.
- Input the public parameters . Output the encryption key , the public evaluation key and the decryption key .
- 3.
- Input , and a message . Output a ciphertext .
- 4.
- : Input and a function f: . Output a ciphertext . (We consider homomorphic addition and multiplication of depth L arithmetic circuits f over in a gate-to-gate manner.)
- 5.
- Input and ciphertext under secret key . Output the message μ.
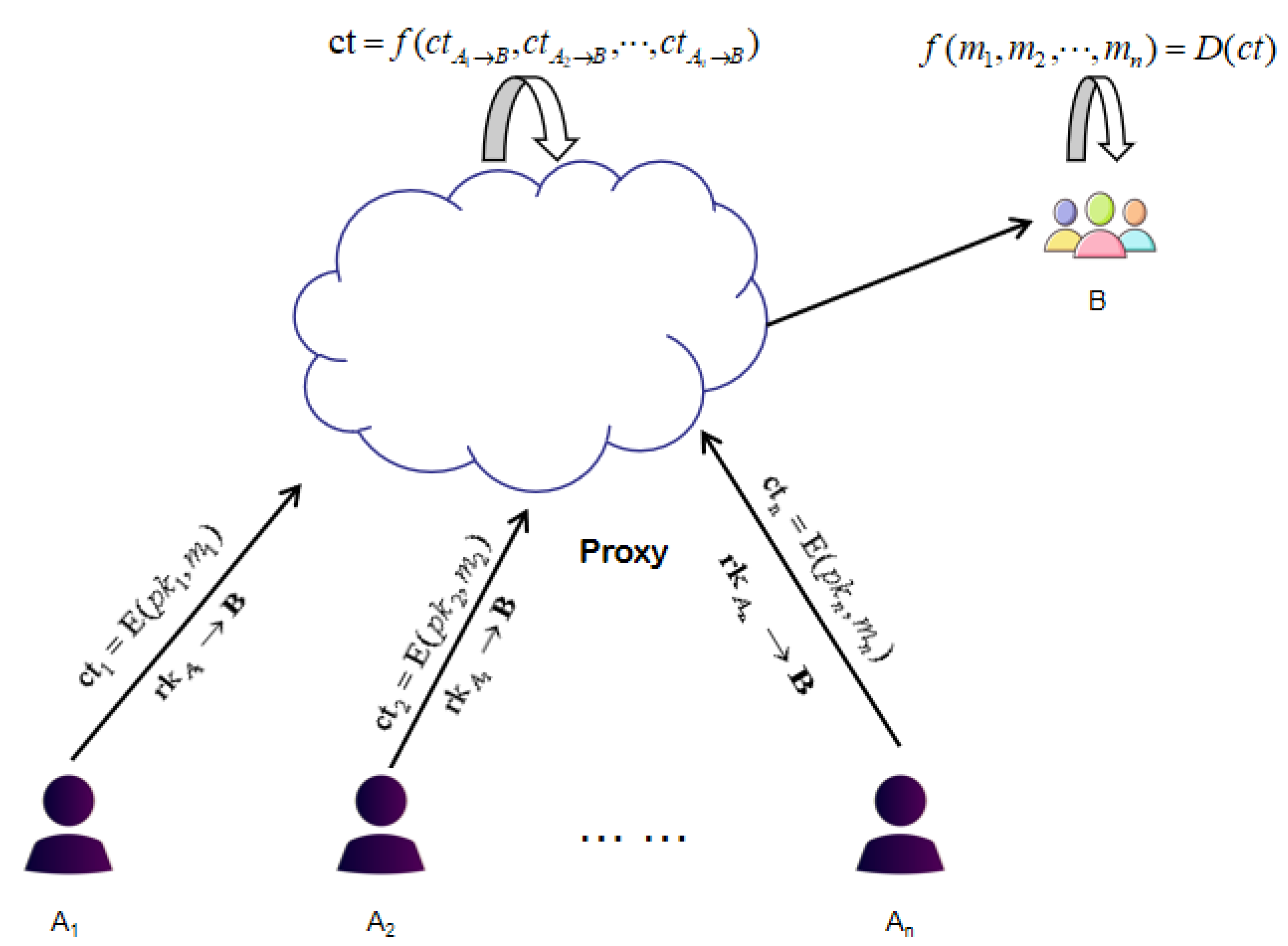
2.3. HPRE: Definition and Security Model
- (1)
- Trusted authority (TA). The TA is trusted by all participants. TA generates the public parameters .
- (2)
- Proxy. The proxy is semi-trusted by all participants. Proxy is generally a cloud service provider. Users use the cloud service provider to store and calculate data.
- (3)
- Data owner (DO). The DO encrypts the data and stores the encrypted data in the cloud, and generates a proxy re-encryption key for data users.
- (4)
- Data user (DU). The DU downloads the result of the homomorphic operation from the cloud service provider.
- 1.
- HPRE.Setup: For the security parameter k, the upper bound on the maximal multiplicative depth that the scheme can homomorphically evaluate, the TA outputs the public parameters .
- 2.
- HPRE.KeyGen: For , user i (DO or DU) outputs an encryption/decryption key pair , and public evaluation key .
- 3.
- HPRE.Enc: For , and a message μ, user (DO or DU) outputs an original ciphertext .
- 4.
- HPRE.Rekey: For , an encryption/decryption key pair of user i, and an encryption key of user j, user i outputs a re-encryption key .
- 5.
- HPRE.ReEnc For , a re-encryption key , and an original ciphertext of user i, the proxy outputs a re-encryption ciphertext for the user j.
- 6.
- HPRE.Eval: For and a function f: , the proxy outputs a ciphertext . (We consider homomorphic addition and multiplication of depth L arithmetic circuits f over in a gate-to-gate manner. In addition, it should be noted that the ciphertexts belonging to a user can be original ciphertext or re-encryption ciphertext.)
- 7.
- HPRE.Dec: For and a ciphertext under , user outputs the message μ.
3. Building Blocks
3.1. The Basic Encryption Scheme
- Input the security parameter k, sample . Output the public parameters .
- Input the public parameters , use algorithm TrapGen() to generate matrices with trapdoor basis T, where . Then use algorithm SamplePre to sample a vector , where . Output the encryption key and the decryption key . (Note that the decryption key T is redundant here, we can instead just let . The decryption key T is needed to construct the PRE scheme, as described below.)
- : Input the public parameters , the encryption key and a message . Output a ciphertext ,where , , .
- : Input the public parameters , the decryption key and a ciphertext . Compute and output
3.2. Correctness Analysis
- (1)
- (2)
- Algorithm TrapGen requires .
- (3)
- Algorithm SamplePre requires .
3.3. Security Analysis
3.4. Key Switching
- Input decryption keys , . Sample , , computeOutput a matrix
- Input a ciphertext under the decryption key , and . Output a ciphertext
4. An L- Homomorphic Encryption Scheme
4.1. Construction
- : Input the security parameter k, sample , and let L be the maximum depth of arithmetic circuit supporting homomorphic evaluation. Output the public parameters .
- : Input the public parameters , use algorithm TrapGen() to generate matrices with trapdoor basis T, where , use algorithm SamplePre to sample a vector , where , sample and computewhere . Output the encryption key , the decryption key , . (Note that the decryption key T is redundant here, we can instead just let . The decryption key T is needed to construct the PRE scheme, as described below.)
- : Identical to the basic encryption scheme, output .
- : As [41,47], We consider homomorphic addition and multiplication of depth L arithmetic circuits over in a gate-to-gate manner. That is, the decryption key of the ciphertexts operated by the gate at level i of the circuit is , and the decryption key of the ciphertexts output by the homomorphic operation is .: Input ciphertexts under secret key , computeand output: Input ciphertexts under secret key , computeand output
- : Input ciphertexts under secret key . Output .
4.2. Analysis for Homomorphism
4.3. Security Analysis
5. The HPRE-SAC Scheme
5.1. Construction
- Identical to the HE scheme, output .
- Identical to the HE scheme, output .
- : Identical to the HE scheme, output
- : Input , the encryption key and the decryption key of user i, the encryption key of user j, sample , use algorithm SamplePre() to sample a matrix , whereoutput the re-encryption key .
- Input , a original ciphertext of user i, and a re-encryption key . Output a re-encryption ciphertextfor user j, where .
- HPRE.Eval: Except for the ciphertexts that belongs to a user can be the original ciphertext or re-encryption ciphertext, the rest are the same as HE scheme, .
- HPRE.Dec: Identical to the HE scheme, output .
5.2. Correctness Analysis
5.3. Security Analysis
- If , it returns , where , , .
- If , it returns a random ciphertext
5.4. Comparisons
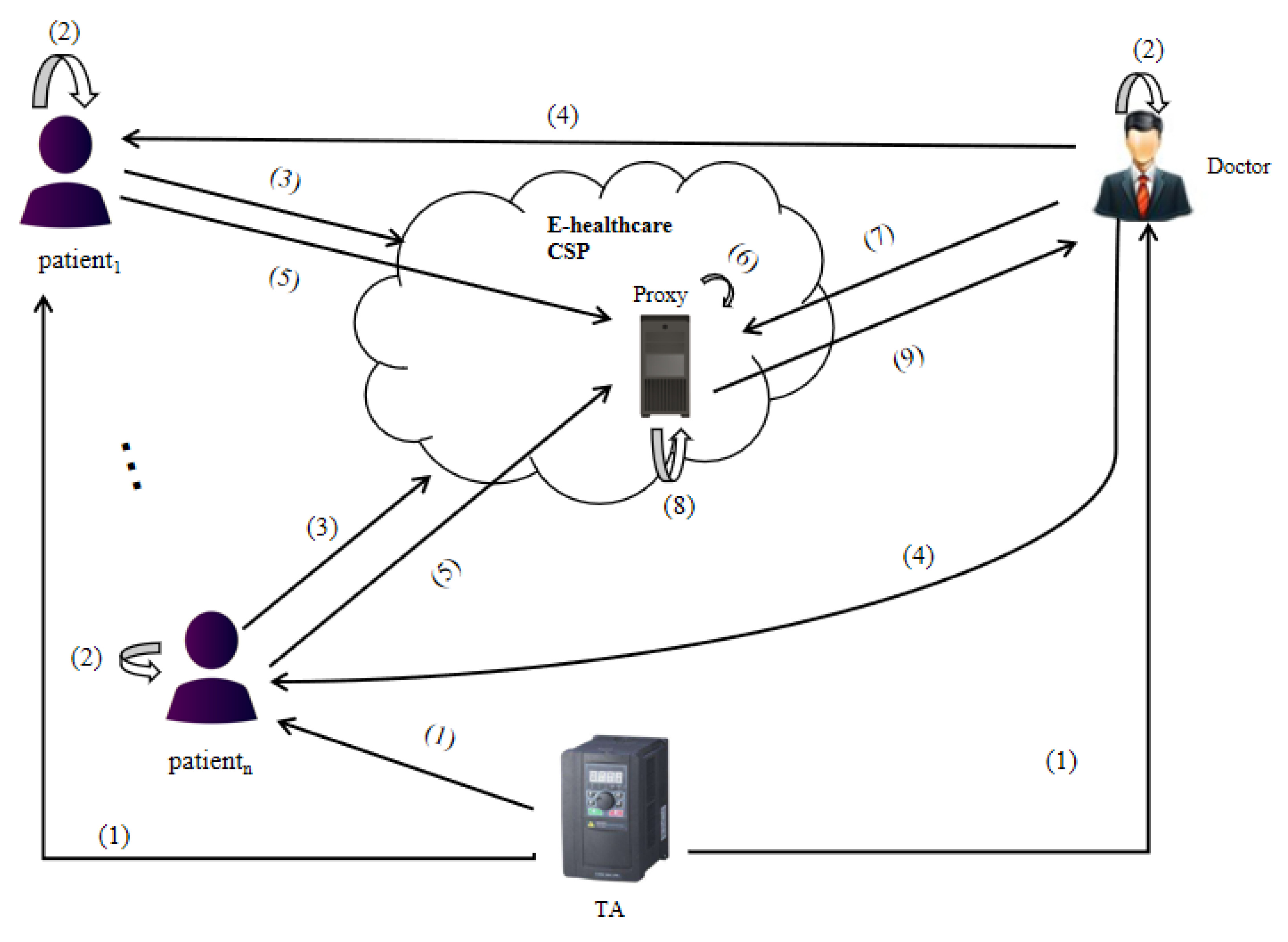
5.5. An Application
- (1)
- Patients and the doctor use the algorithm to register in TA to obtain the public parameters of the system.
- (2)
- Patients and the doctor use the algorithm to generate their own encryption key, public evaluation key and decryption key.
- (3)
- Patients use the algorithm to encrypt their PHRs and upload them to the E-healthcare cloud service provider for storage. The PHRs here includes not only diagnostic information from doctors, but also personal health information collected by smart wearable devices. We assume that the E-healthcare cloud service provider is not trusted, so the patients need to encrypt the data.
- (4)
- For a certain purpose (in addition to clinical purposes, it can also be for research purposes), the doctor asks patients for the right to decrypt their encrypted data.
- (5)
- After the patient agrees with the doctor’s request, the algorithm is used to generate the re-encryption key and send it to the proxy.
- (6)
- Suppose that the proxy residing in the cloud is semi-trusted, that is to say, it follows the protocol, but can collect information to infer private information, or collude with the data user to attack the data owner. The proxy re-encrypts the patient’s ciphertext to generate the doctor’s ciphertext by using the algorithm .
- (7)
- The doctor needs to analyze and calculate the PHRs of multiple patients for a certain purpose (in addition to clinical purpose, it can also be for research). In order to reduce the burden of local computation and communication, the doctor sends the function to the proxy.
- (8)
- The proxy uses the algorithm to perform homomorphic function operation on the re-encryption ciphertext belonging to the doctor.
- (9)
- The doctor downloads the results of homomorphic operation and decrypts them locally by using the algorithm to obtain the required data.
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Regev, O. On lattices, learning with errors, random linear codes, and cryptography. In Proceedings of the Thirty-Seventh Annual ACM Symposium on Theory of Computing, Baltimore, MD, USA, 22–24 May 2005; pp. 84–93. [Google Scholar]
- Regev, O. On lattices, learning with errors, random linear codes, and cryptography. J. ACM 2009, 56, 1–40. [Google Scholar] [CrossRef]
- Micciancio, D.; Regev, O. Worst-case to average-case reductions based on Gaussian measures. SIAM J. Comput. 2007, 37, 267–302. [Google Scholar] [CrossRef]
- Applebaum, B.; Cash, D.; Peikert, C.; Sahai, A. Fast cryptographic primitives and circular-secure encryption based on hard learning problems. In Proceedings of the 29th Annual International Cryptology Conference on Advances in Cryptology, Santa Barbara, CA, USA, 16–20 August 2009; pp. 595–618. [Google Scholar]
- Lindner, R.; Peikert, C. Better key sizes (and attacks) for LWE-based encryption. In Proceedings of the 11th International Conference on Topics in Cryptology: CT-RSA 2011, San Francisco, CA, USA, 14–18 February 2011; pp. 319–339. [Google Scholar]
- Orsini, E.; Smart, N.P. Bootstrapping BGV ciphertexts with a wider choice of p and q. In Proceedings of the 18th IACR International Conference on Practice and Theory in Public-Key Cryptography, Gaithersburg, MD, USA, 30 March–1 April 2015; pp. 673–698. [Google Scholar]
- Gentry, C. A Fully Homomorphic Encryption Scheme. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2009. [Google Scholar]
- Gentry, C. Fully homomorphic encryption using ideal lattices. In Proceedings of the 41st Annual ACM Symposium on Symposium on Theory of Computing, Bethesda, MD, USA, 31 May–2 June 2009; pp. 169–178. [Google Scholar]
- Mai, V.; Khalil, I. Design and implementation of a secure cloud-based billing model for smart meters as an Internet of things using homomorphic cryptography. Future Gener. Comput. Syst. 2017, 72, 327–338. [Google Scholar] [CrossRef]
- Ren, S.Q.; Tan, B.H.M.; Sundaram, S.; Wang, T.; Ng, Y.; Chang, V.; Aung, K.M.M. Secure searching on cloud storage enhanced by homomorphic indexing. Future Gener. Comput. Syst. 2016, 65, 102–110. [Google Scholar] [CrossRef]
- Blaze, M.; Bleumer, G.; Strauss, M. Divertible protocols and atomic proxy cryptography. In Proceedings of the International Conference on the Theory and Application of Cryptographic Techniques, Espoo, Finland, 31 May–4 June 1998; pp. 127–144. [Google Scholar]
- Ateniese, G.; Fu, K.; Green, M.; Hohenberger, S. Improved proxy re-encryption schemes with applications to secure distributed storage. ACM Trans. Inf. Syst. Secur. (TISSEC) 2006, 9, 1–30. [Google Scholar] [CrossRef]
- Yang, Y.; Zhu, H.; Lu, H.; Weng, J.; Zhang, Y.; Choo, K.K.R. Cloud based data sharing with fine-grained proxy re-encryption. Pervasive Mob. Comput. 2016, 28, 122–134. [Google Scholar] [CrossRef]
- Wang, D.; Li, W.; Wang, P. Measuring Two-Factor Authentication Schemes for Real-Time Data Access in Industrial Wireless Sensor Networks. IEEE Trans. Ind. Inform. 2018, 14, 4081–4092. [Google Scholar] [CrossRef]
- Jiang, L.; Guo, D. Dynamic Encrypted Data Sharing Scheme Based on Conditional Proxy Broadcast Re-Encryption for Cloud Storage. IEEE Access 2017, 5, 13336–13345. [Google Scholar] [CrossRef]
- Zhou, Y.; Deng, H.; Wu, Q.; Qin, B.; Liu, J.; Ding, Y. Identity-based proxy re-encryption version 2: Making mobile access easy in cloud. Future Gener. Comput. Syst. 2016, 62, 128–139. [Google Scholar] [CrossRef]
- Lu, Y.; Li, J. A pairing-free certificate-based proxy re-encryption scheme for secure data sharing in public clouds. Future Gener. Comput. Syst. 2016, 62, 140–147. [Google Scholar] [CrossRef]
- Zeng, P.; Choo, K.R. A New Kind of Conditional Proxy Re-Encryption for Secure Cloud Storage. IEEE Access 2018, 6, 70017–70024. [Google Scholar] [CrossRef]
- Ma, C.; Li, J.; Ouyang, W. Lattice-based identity-based homomorphic conditional proxy re-encryption for secure big data computing in cloud environment. Int. J. Found. Comput. Sci. 2017, 28, 645–660. [Google Scholar] [CrossRef]
- Li, J.; Ma, C.; Zhang, K. A Novel Lattice-Based CP-ABPRE Scheme for Cloud Sharing. Symmetry 2019, 11, 1262. [Google Scholar] [CrossRef]
- Liang, K.; Au, M.H.J.; Liu, K.J.; Susilo, W.; Wong, D.S.; Yang, G.; Yu, Y.; Yang, A. A secure and efficient ciphertext-policy attribute-based proxy re-encryption for cloud data sharing. Future Gener. Comput. Syst. 2015, 52, 95–108. [Google Scholar] [CrossRef]
- Sun, M.; Ge, C.; Fang, L.; Wang, J. A proxy broadcast re-encryption for cloud data sharing. Multimed. Tools Appl. 2018, 77, 10455–10469. [Google Scholar] [CrossRef]
- Xu, P.; Jiao, T.; Wu, Q.; Wang, W.; Jin, H. Conditional Identity-Based Broadcast Proxy Re-Encryption and Its Application to Cloud Email. IEEE Trans. Comput. 2016, 65, 66–79. [Google Scholar] [CrossRef]
- Ivan, A.; Dodis, Y. Proxy Cryptography Revisited. In Proceedings of the 10th Annual Network and Distributed System Security Symposium, 497 NDSS, DBLP, San Diego, CA, USA, 23–26 February 2003. [Google Scholar]
- Singh, K.; Pandu Rangan, C.; Banerjee, A.K. Lattice based identity based proxy re-encryption scheme. J. Internet Serv. Inf. Secur. (JISIS) 2013, 3, 38–51. [Google Scholar]
- Jiang, M.M.; Hu, Y.P.; Wang, B.C.; Wang, F.H.; Lai, Q.Q. Lattice-based multi-use unidirectional proxy re-encryption. Secur. Commun. Netw. 2015, 8, 3796–3803. [Google Scholar] [CrossRef]
- Li, J.; Ma, C.; Gu, Z. Multi-use Deterministic Public Key Proxy Re-Encryption from Lattices in the Auxiliary-Input Setting. Int. J. Found. Comput. Sci. 2020, 31, 551–567. [Google Scholar] [CrossRef]
- Ma, C.; Li, J.; Ouyang, W. A Homomorphic Proxy Re-encryption from Lattices. In Proceedings of the 10th International Conference, ProvSec 2016, Nanjing, China, 10–11 November 2016; pp. 353–372. [Google Scholar]
- Xagawa, K. Cryptography with Lattices. Ph.D. Thesis, Tokyo Institute of Technology, Tokyo, Japan, 2010. [Google Scholar]
- Aono, Y.; Boyen, X.; Wang, L. Key-private proxy re-encryption under LWE. In Proceedings of the International Conference on Cryptology in India, Mumbai, India, 7–10 December 2013; pp. 1–18. [Google Scholar]
- Ateniese, G.; Benson, K.; Hohenberger, S. Key-private proxy re-encryption. In Proceedings of the Cryptographers’ Track at the RSA Conference, San Francisco, CA, USA, 24–28 February 2009; pp. 279–294. [Google Scholar]
- Singh, K.; Rangan, C.P.; Banerjee, A.K. Cryptanalysis of unidirectional proxy re-encryption scheme. In Proceedings of the Information and Communication Technology-EurAsia Conference, Bali, Indonesia, 14–17 April 2014; pp. 564–575. [Google Scholar]
- Kirshanova, E. Proxy re-encryption from lattices. In Proceedings of the International Workshop on Public Key Cryptography, Buenos Aires, Argentina, 26–28 March 2014; pp. 77–94. [Google Scholar]
- Nishimaki, R.; Xagawa, K. Key-Private Proxy Re-Encryption from Lattices, Revisited, IEICE Transactions on Fundamentals of Electronics. Commun. Comput. Sci. 2015, 98, 100–116. [Google Scholar]
- Hou, J.; Jiang, M.; Guo, Y.; Song, W. Efficient identity-based multi-bit proxy re-encryption over lattice in the standard model. Inf. Secur. Tech. Rep. 2019, 47, 329–334. [Google Scholar] [CrossRef]
- Yin, W.; Wen, Q.; Li, W.; Zhang, H.; Jin, Z.P. Identity Based Proxy Re-encryption Scheme under LWE. KSII Trans. Internet Inf. Syst. 2017, 11, 6116–6132. [Google Scholar]
- Yin, W.; Wen, Q.; Li, W.; Zhang, H.; Jin, Z. A New Insigh-Proxy Re-encryption Under LWE with Strong Anti-collusion. In Proceedings of the International Conference on Information Security Practice and Experience, Kuala Lumpur, Malaysia, 26–28 November 2019; Springer: Cham, Switzerland, 2018; pp. 559–577. [Google Scholar]
- Zhong, H.; Cui, J.; Shi, R.; Xia, C. Many-to-one homomorphic encryption scheme. Secur. Commun. Netw. 2015, 9, 1007–1015. [Google Scholar] [CrossRef]
- Brakerski, Z.; Vaikuntanathan, V. Efficient fully homomorphic encryption from (Standard) LWE. In Proceedings of the 52nd Annual IEEE Symposium on Foundations of Computer Science, Palm Springs, CA, USA, 22–25 October 2011; pp. 97–106. [Google Scholar]
- Brakerski, Z.; Gentry, C.; Vaikuntanathan, V. (leveled) Fully Homomorphic Encryption without Bootstrapping. In Proceedings of the 3rd Innovations in Theoretical Computer Science Conference, Cambridge, MA, USA, 8–10 January 2012; pp. 309–325. [Google Scholar]
- Brakerski, Z. Fully Homomorphic Encryption without Modulus Switching from Classical Gapsvp. In Proceedings of the 32nd Annual Cryptology Conference, Santa Barbara, CA, USA, 19–23 August 2012; pp. 868–886. [Google Scholar]
- Gentry, C.; Sahaiy, A.; Waters, B. Homomorphic Encryption From Learning with Errors: Conceptually-Simpler, Asymptotically-Faster, Attribute-Based. In Proceedings of the 33rd Annual Cryptology Conference, Santa Barbara, CA, USA, 18–22 August 2013; pp. 75–92. [Google Scholar]
- Gentry, C.; Halevi, S.; Vaikuntanathan, V. A simple BGN-type cryptosystem from LWE. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, French Riviera, French, 30 May–3 June 2010; Springer: Berlin/Heidelberg, Germany, 2010; pp. 506–522. [Google Scholar]
- Li, Z.; Ma, C.; Wang, D. Towards Multi-Hop Homomorphic Identity-Based Proxy Re-Encryption via Branching Program. IEEE Access 2017, 5, 16214–16228. [Google Scholar] [CrossRef]
- Li, Z.; Ma, C.; Wang, D. Achieving Multi-Hop PRE via Branching Program. IEEE Trans. Cloud Comput. 2020, 8, 45–58. [Google Scholar] [CrossRef]
- Li, J.; Ma, C.; Zhang, L.; Yuan, Q. Unidirectional FHPRE Scheme from Lattice for Cloud Computing. Int. J. Netw. Secur. 2019, 21, 592–600. [Google Scholar]
- Ma, C.; Li, J.; Du, G. A Flexible Fully Homomorphic Encryption. Wirel. Pers. Commun. 2017, 95, 761–772. [Google Scholar] [CrossRef]
- Gentry, C.; Peikert, C.; Vaikuntanathan, V. Trapdoors for hard lattices and new cryptographic constructions. In Proceedings of the 40th Annual ACM Symposium on Theory of Computing, Victoria, BC, Canada, 17–20 May 2008; pp. 197–206. [Google Scholar]
- Alwen, J.; Peikert, C. Generating shorter bases for hard random lattices. Theory Comput. Syst. 2011, 48, 535–553. [Google Scholar] [CrossRef]
- Micciancio, D.; Peikert, C. Trapdoors for lattices: Simpler, tighter, faster, smaller. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, Cambridge, UK, 15–19 April 2012; pp. 700–718. [Google Scholar]
- Brakerski, Z.; Gentry, C.; Halevi, S. Packed Ciphertexts in LWE-Based Homomorphic Encryption. In Proceedings of the Public-Key Cryptography-PKC 2013, Lecture Notes in Computer Science, Nara, Japan, 26 February–1 March 2013; Springer: Berlin/Heidelberg, Germany, 2013; pp. 1–13. [Google Scholar]
- Lin, H.Y.; Hung, Y.M. An Improved Proxy Re-Encryption Scheme for IoT-Based Data Outsourcing Services in Clouds. Sensors 2021, 21, 67. [Google Scholar] [CrossRef]
- Qin, Z.; Xiong, H.; Wu, S.; Batamuliza, J. A survey of proxy re-encryption for secure data sharing in cloud computing. IEEE Trans. Serv. Comput. 2016. [Google Scholar] [CrossRef]
- Gai, K.; Qiu, M.; Zhao, H. Security-Aware Efficient Mass Distributed Storage Approach for Cloud Systems in Big Data. In Proceedings of the 2nd International Conference on Big Data Security on Cloud (BigDataSecurity), IEEE International Conference on High Performance and Smart Computing (HPSC), and IEEE International Conference on Intelligent Data and Security (IDS), New York, NY, USA, 9–10 April 2016; pp. 140–145. [Google Scholar]
- Qiu, M.; Xue, C.; Sha, H.M.; Jia, Z.; Shao, Z.; Sha, E.H.M. Voltage assignment with guaranteed probability satisfying timing constraint for real-time multiproceesor DSP. J. VLSI Signal Process. Syst. Signal Image Video Technol. 2017, 46, 55–73. [Google Scholar] [CrossRef]
- Dai, W.; Qiu, L.; Wu, A.; Qiu, M. Cloud infrastructure resource allocation for big data applications. IEEE Trans. Big Data 2016, 4, 313–324. [Google Scholar] [CrossRef]
- Bhatia, T.; Verma, A.K.; Sharma, G. Secure sharing of mobile personal healthcare records using certificateless proxy re-encryption in cloud. Trans. Emerg. Telecommun. Technol. 2018, 29, e3309. [Google Scholar] [CrossRef]
- Bhatia, T.; Verma, A.K.; Sharma, G. Towards a secure incremental proxy re-encryption for e-healthcare data sharing in mobile cloud computing. Concurr. Comput. Pract. Exp. 2020, 32, e5520. [Google Scholar] [CrossRef]

| Scheme | LWE | Security | Hop | Direction | HE | Anti-Collusion |
|---|---|---|---|---|---|---|
| Li et al. [20] | Y | CPA | Single | Uni- | N | weak |
| Singh et al. [25] | Y | CPA | Single | Uni- | N | weak |
| Xagawa [29] | Y | N | Single | Uni- | N | weak |
| Kirshanova [33] | Y | CCA | Single | Uni- | N | strong |
| Nishimaki et al. [34] | Y | CPA | Single | Uni- | N | weak |
| Hou et al. [35] | Y | CPA | Multi | Bi- | N | weak |
| Yin et al. [36] | Y | CPA | Single | Uni- | N | strong |
| Yin et al. [37] | Y | CPA | Single | Uni- | N | strong |
| Jiang et al. [26] | Y | CPA | Multi | Uni- | N | strong |
| Ma et al. [28] | Y | CPA | Single | Uni- | Y | weak |
| Li et al. [44] | Y | CPA | Multi | Uni- | Y | weak |
| Li et al. [45] | Y | CPA | Multi | Uni- | Y | weak |
| Li et al. [46] | Y | CPA | Single | Uni- | Y | weak |
| Our Scheme FHPR-SAC | Y | CPA | Multi | Uni- | Y | strong |
| x | scalar |
| rounding x to the nearest integer | |
| ) | rounding down (up) |
| vector | |
| A | matrix or set |
| norm of | |
| , where | |
| , where | |
| the concatenation of the columns of | |
| the concatenation of the rows of | |
| x is sampled according to a probability distribution | |
| x is sampled uniformly from a set S | |
| X and Y are computationally indistinguishable | |
| X and Y are statistically indistinguishable |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Qiao, Z.; Zhang, K.; Cui, C. A Lattice-Based Homomorphic Proxy Re-Encryption Scheme with Strong Anti-Collusion for Cloud Computing. Sensors 2021, 21, 288. https://doi.org/10.3390/s21010288
Li J, Qiao Z, Zhang K, Cui C. A Lattice-Based Homomorphic Proxy Re-Encryption Scheme with Strong Anti-Collusion for Cloud Computing. Sensors. 2021; 21(1):288. https://doi.org/10.3390/s21010288
Chicago/Turabian StyleLi, Juyan, Zhiqi Qiao, Kejia Zhang, and Chen Cui. 2021. "A Lattice-Based Homomorphic Proxy Re-Encryption Scheme with Strong Anti-Collusion for Cloud Computing" Sensors 21, no. 1: 288. https://doi.org/10.3390/s21010288
APA StyleLi, J., Qiao, Z., Zhang, K., & Cui, C. (2021). A Lattice-Based Homomorphic Proxy Re-Encryption Scheme with Strong Anti-Collusion for Cloud Computing. Sensors, 21(1), 288. https://doi.org/10.3390/s21010288





