Numerical and Experimental Investigation of the Opposite Influence of Dielectric Anisotropy and Substrate Bending on Planar Radiators and Sensors
Abstract
1. Introduction
2. Numerical and Experimental Methods and Materials
2.1. Two-Resonator Method for Measurement of the Uniaxial Anisotropy of Textile Fabrics
2.2. Numerical Models for Determination of the Dielectric Constant and Anisotropy of Textile Fabrics as Dielectric Mixtures
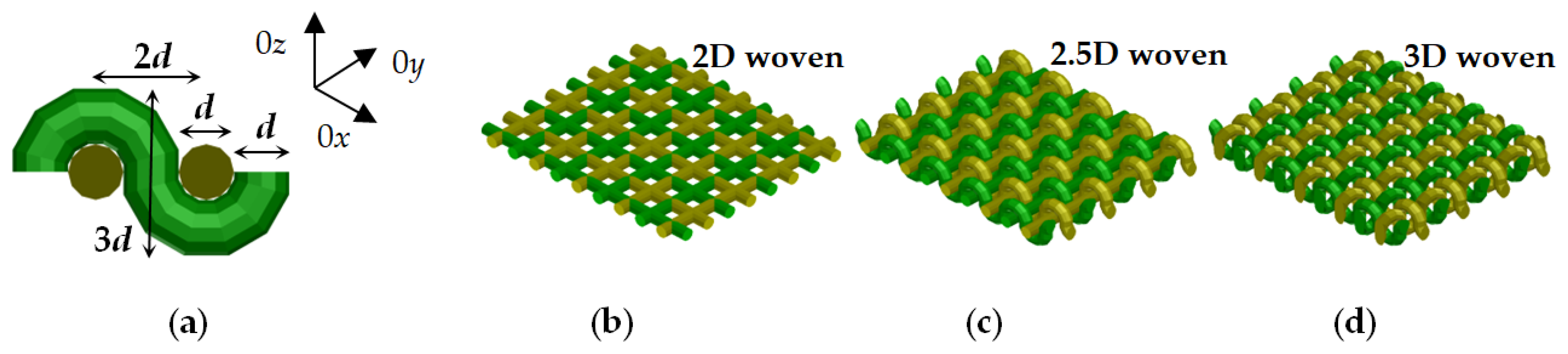
2.2.1. Limits for the Dielectric Parameters of Mixed Textile Threads
2.2.2. Numerical Models for Evaluation of the Dielectric Anisotropy of the Textile Fabrics
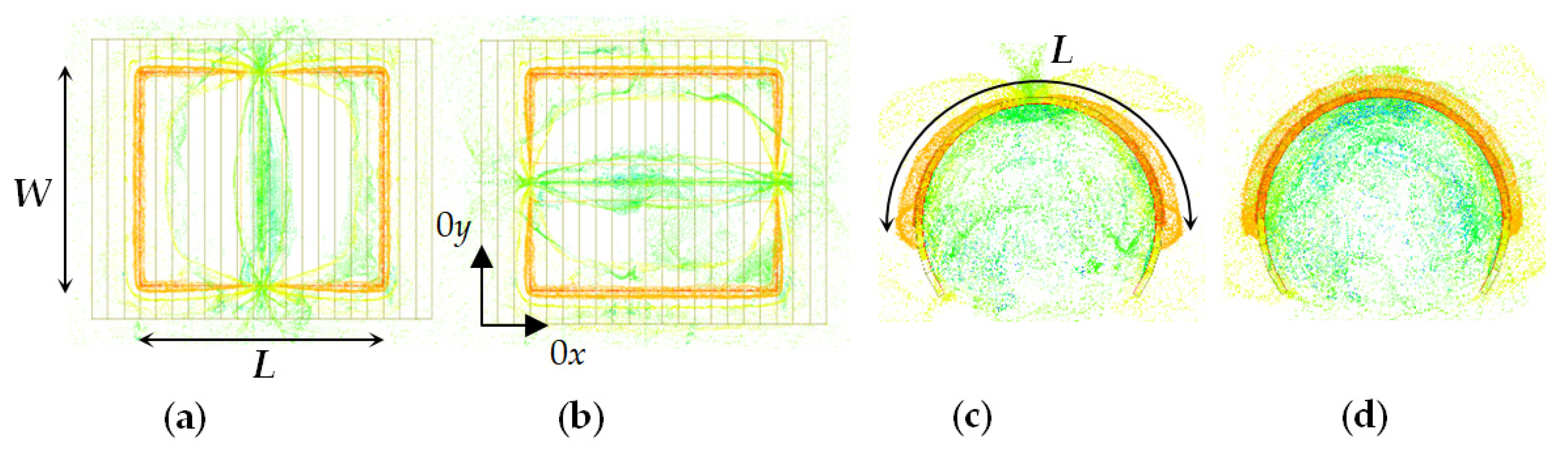
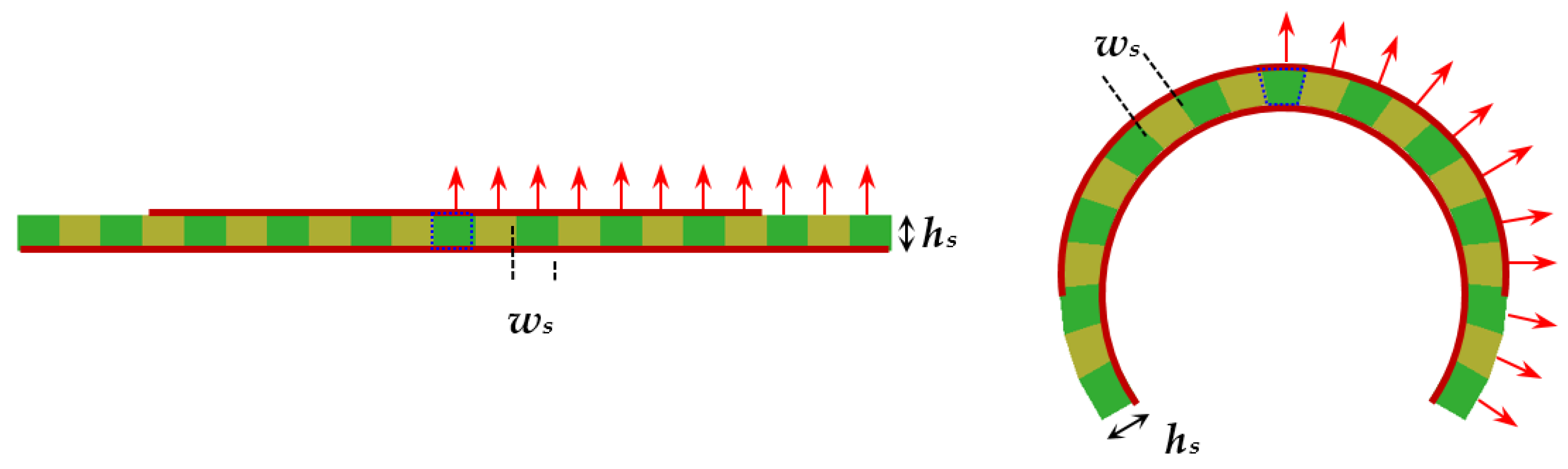
2.3. Procedure for Accurate Measurements of Bent Planar Resonators on Textile Fabrics
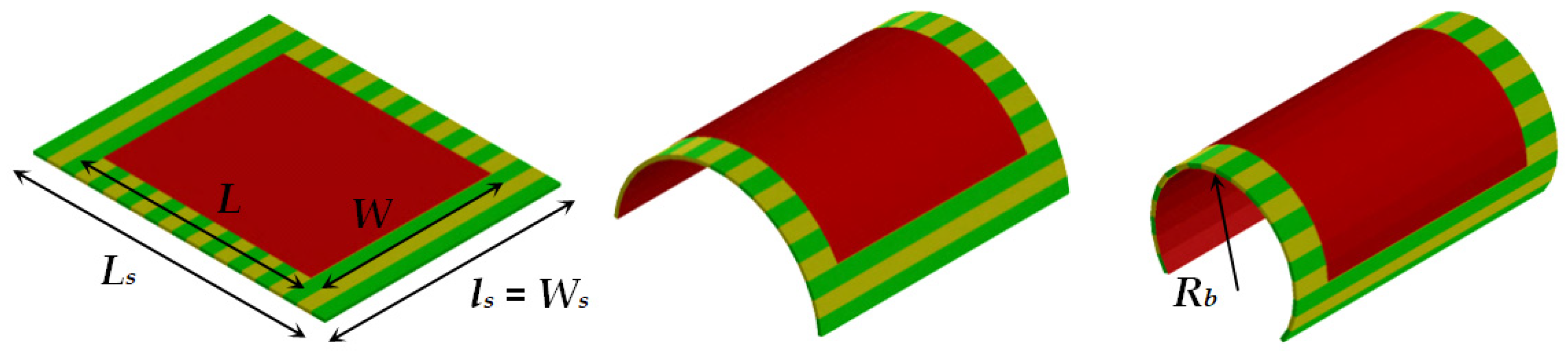
2.4. Numerical Models for Investigations of Bent Planar Resonators on Anisotropic Substrates
2.5. Materials Used in the Research
3. Results and Discussion
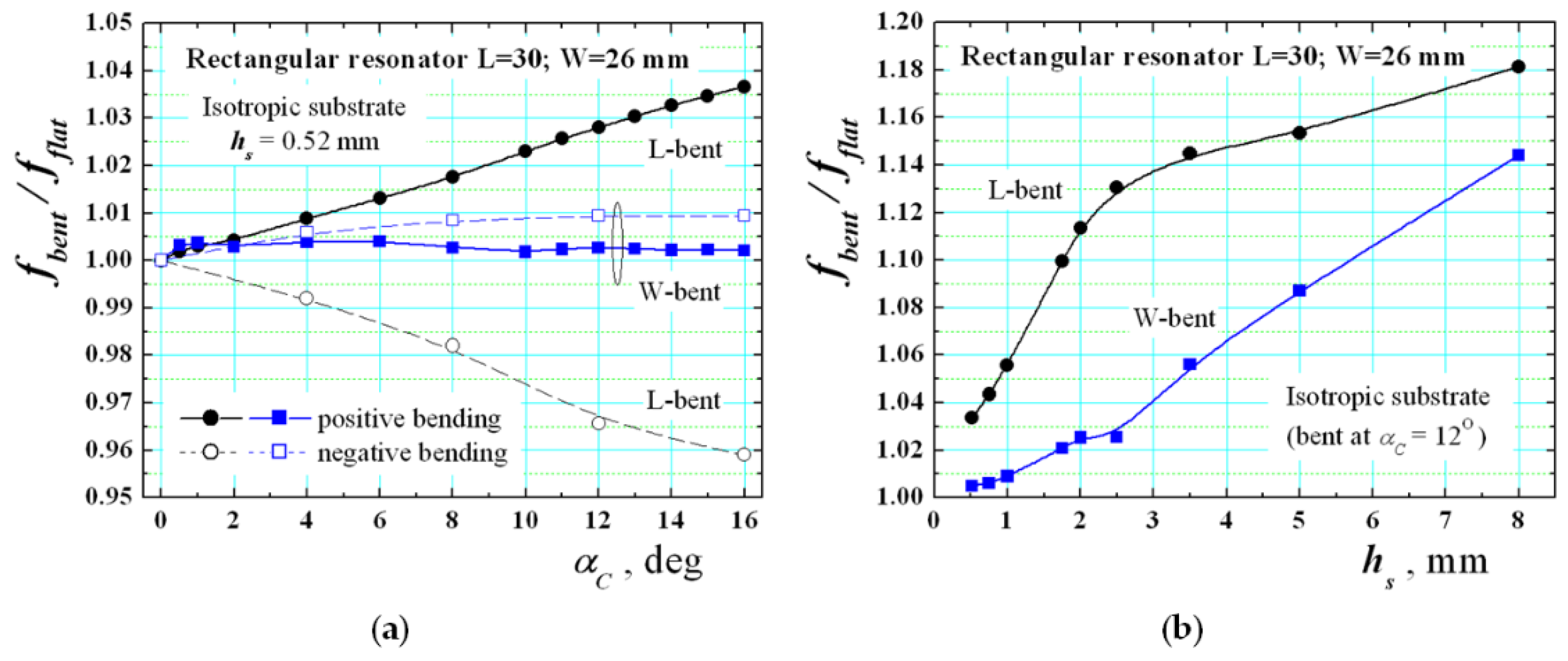
3.1. Pure Bending Effect
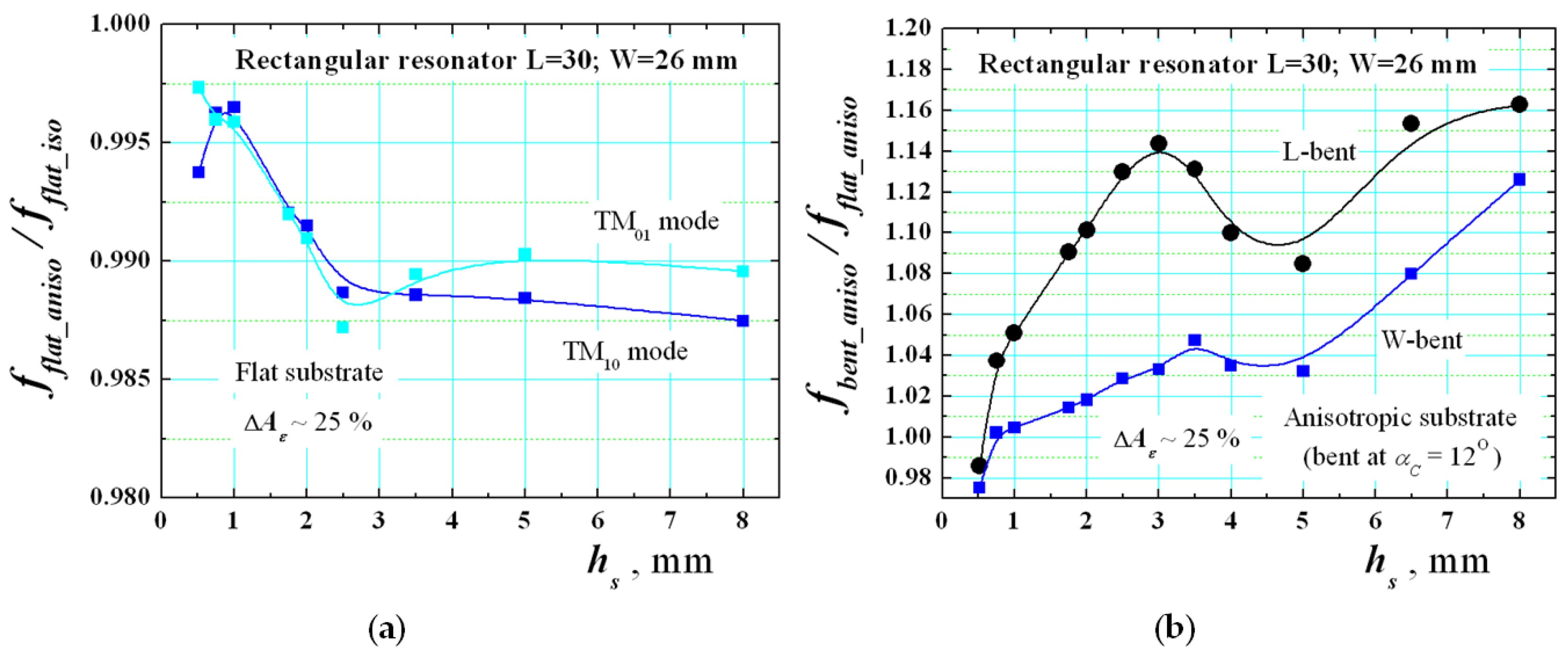
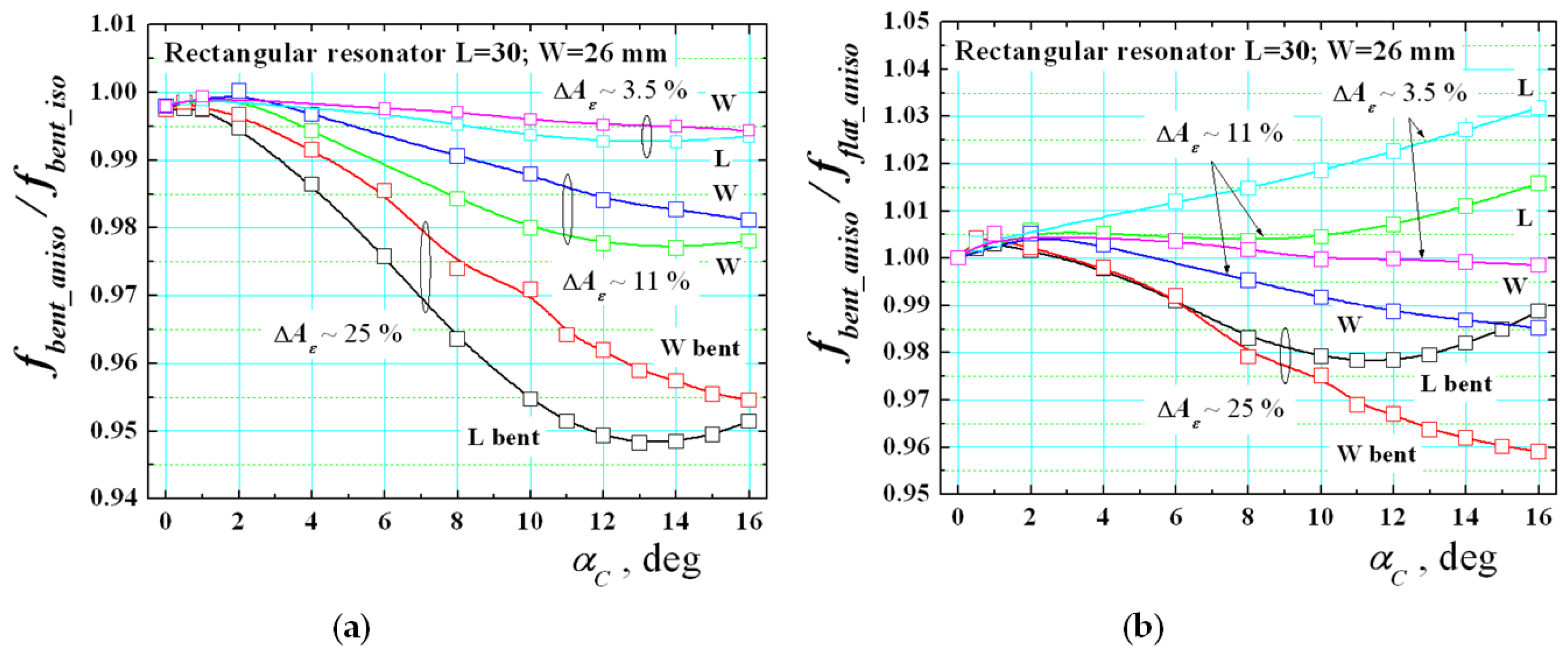
3.2. Investigation of the Simultaneous Effects of Anisotropy and Bending of Planar Resonators
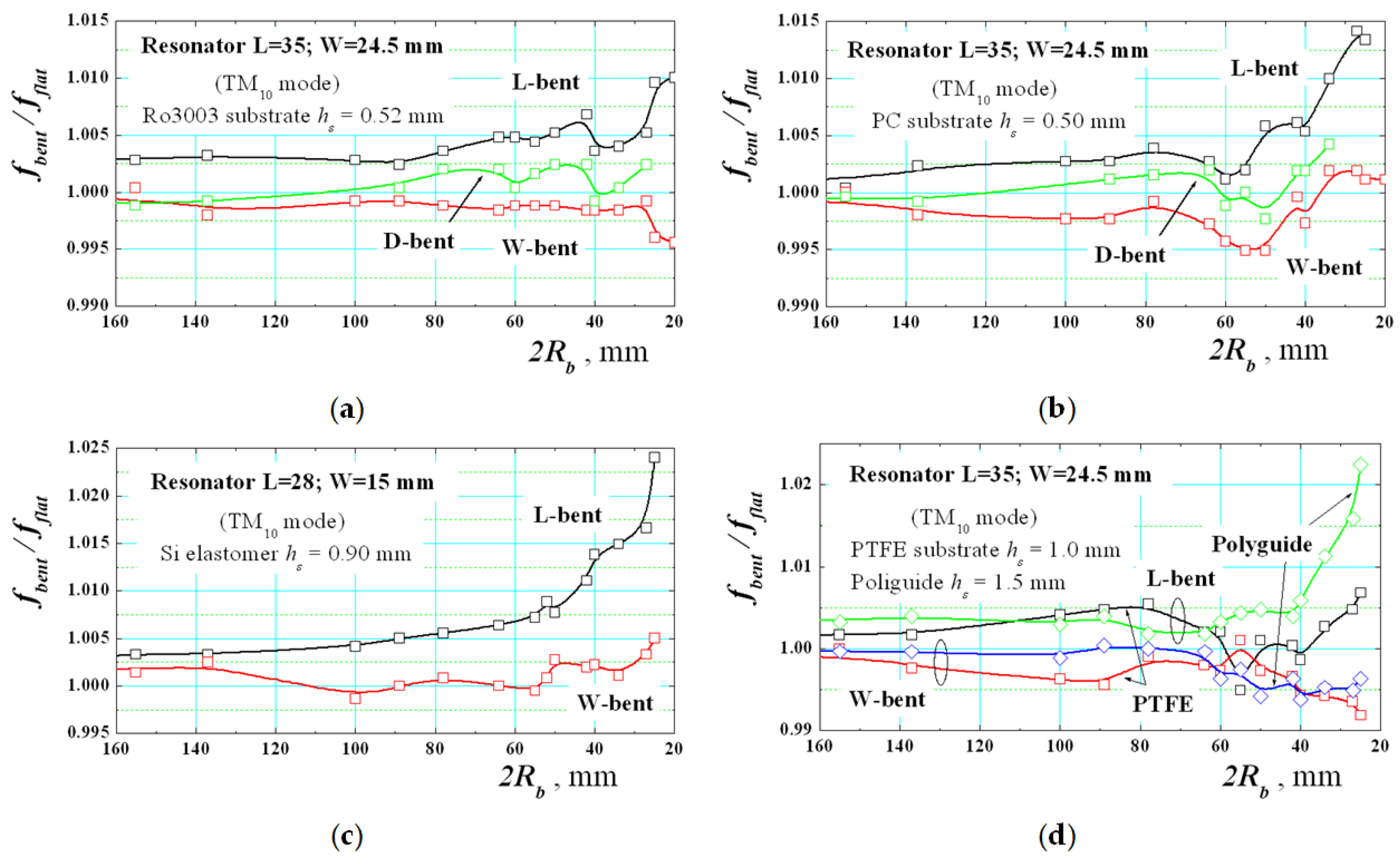
3.3. Effects of Anisotropy and Bending on More Sophisticated Planar Resonators
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Salvado, R.; Loss, C.; Gonçalves, R.; Pinho, P. Textile Materials for the Design of Wearable Antennas: A Survey. Sensors 2012, 12, 15841–15857. [Google Scholar] [CrossRef] [PubMed]
- Priya, A.; Kumar, A.; Chauhan, B. A Review of Textile and Cloth Fabric Wearable Antennas. Int. J. Comput. Appl. 2015, 116, 1–5. [Google Scholar] [CrossRef]
- Yadav, A.; Singh, V.K.; Chaudhary, M.; Mohan, H. A Review on Wearable Textile Antenna. J. Telecommun. Switch. Syst. Netw. 2015, 2, 37–41. [Google Scholar]
- Almohammed, B.; Ismail, A.; Sali, A. Electro-textile wearable antennas in wireless body area networks: Materials, antenna design, manufacturing techniques, and human body consideration—A review. Text. Res. J. 2020, 1–18. [Google Scholar] [CrossRef]
- Mohamadzade, B.; Hashmi, R.M.; Simorangkir, R.B.V.B.; Gharaei, R.; Rehman, S.-U.; Abbasi, Q.H. Recent Advances in Fabrication Methods for Flexible Antennas in Wearable Devices: State of the Art. Sensors 2019, 19, 2312. [Google Scholar] [CrossRef]
- Dankov, P.I. Material Characterization in the Microwave Range, When the Materials Become Composite, Reinforced, 3D-Printed, Artificially Mixed, Nanomaterials and Metamaterials. Forum for Electromagnetic Research Methods and Application Technologies (FERMAT Journal). Available online: https://www.e-fermat.org/articles.php (accessed on 20 December 2020).
- Ouyang, Y.; Chappell, W.J. High Frequency Properties of Electro-Textiles for Wearable Antenna Applications. IEEE Trans. Antennas Propag. 2008, 56, 381–389. [Google Scholar] [CrossRef]
- Sankaralingam, S.; Gupta, B. Determination of Dielectric Constant of Fabric Materials and Their Use as Substrates for Design and Development of Antennas for Wearable Applications. IEEE Trans. Instrum. Meas. 2010, 59, 3122–3130. [Google Scholar] [CrossRef]
- Bal, K.; Kothari, V.K. Measurement of dielectric properties of textile materials and their applications. Indian J. Fibre Text. 2009, 34, 191–199. [Google Scholar]
- Lesnikowski, J. Dielectric permittivity measurement methods of textile substrate of textile transmission lines. Electr. Rev. 2012, 3, 148–151. [Google Scholar]
- Mustata, F.S.C.; Mustata, A. Dielectric Behaviour of Some Woven Fabrics on the Basis of Natural Cellulosic Fibers. Adv. Mater. Sci. Eng. 2014, 2014, 216548. [Google Scholar] [CrossRef]
- Rahim, H.A.; Malek, F.; Soh, P.J.; Romli1, A.; Rani, K.A.; Isa, C.M.N.C.; Fuad, F.A.A. Measurement of Dielectric Properties of Textile Substrates. J. Teknol. Sci. Eng. 2015, 1, 1–6. [Google Scholar]
- Vassiliadis, S.; Kallivretaki, E.; Domvoglou, D.; Provatidis, C. Mechanical analysis of woven fabrics: The state of the art. In Advances in Modern Woven Fabrics Technology; Vassiliadis, S., Ed.; In-Tech Publ.: London, UK, 2011; pp. 41–64. ISBN 978-953-307-337-8. [Google Scholar]
- Morton, W.E.; Hearle, W.S. Physical Properties of Textile Fibres, 4th ed.; Woodhead Publishing: Cambridge, UK, 2008. [Google Scholar]
- Hu, J. Structure and Mechanics of Woven Fabrics; CRC, Woodhead Publ. Led.: Cambridge, UK, 2004. [Google Scholar]
- Raju, G.G. Dielectrics in Electric Fields; CRC Press: Boca Raton, FL, USA; Taylor & Francis Group: Abingdon-on-Thames, UK, 2017. [Google Scholar]
- Dankov, P.I.; Tsatsova, M.I.; Levcheva, V.P. Investigation of Uniaxial Dielectric Anisotropy of Textile Fabrics and Its Influence over the Wearable Antennas’ Behaviour. In Proceedings of the 2017 Progress in Electromagnetics Research Symposium-Fall (PIERS-FALL), Singapore, 19–22 November 2017. [Google Scholar] [CrossRef]
- Dankov, P.I. Dielectric anisotropy of modern microwave substrates. In Microwave and Millimeter Wave Technologies from Photonic Bandgap Devices to Antenna and Applications; Igor, M., Ed.; In-Tech. Publ.: London, UK, 2010. [Google Scholar] [CrossRef][Green Version]
- Mukai, Y.; Suh, M. Relationships between structure and microwave dielectric properties in cotton fabrics. Mater. Res. Express 2020, 7, 015105. [Google Scholar] [CrossRef]
- Ahmed, M.I.; Ahmed, M.F.; Shaalan, A.A. Investigation and Comparison of 2.4 GHz Wearable Antennas on Three Textile Substrates and Its Performance Characteristics. Open J. Antennas Propag. 2017, 5, 110–120. [Google Scholar] [CrossRef]
- Ibanez-Labiano, I.; Alomainy, A. Dielectric Characterization of Non-Conductive Fabrics for Temperature Sensing through Resonating Antenna Structures. Materials 2020, 13, 1271. [Google Scholar] [CrossRef] [PubMed]
- Zeouga, K.; Osman, L.; Gharsallah, A.; Manar, E.; Gupta, B. Truncated Patch Antenna on Jute Textile for Wireless Power Transmission at 2.45 GHz. Int. J. Adv. Comput. Sci. Appl. 2018, 9, 301–305. [Google Scholar] [CrossRef]
- Ahmed, M.I.; Ahmed, M.F.; Shaalan, A.-E.A. Novel Electrotextile Patch Antenna on Jeans Substrate for Wearable Applications. Prog. Electromagn. Res. C 2018, 83, 255–265. [Google Scholar] [CrossRef]
- Grilo, M.; Correra, F.S. Parametric Study of Rectangular Patch Antenna Using Denim Textile Material. In Proceedings of the SBMO/IEEE MTT-S International Microwave & Optoelectronics Conference (IMOC), Rio de Janeiro, Brazil, 28 October 2013. [Google Scholar] [CrossRef]
- Harmer, S.W.; Rezgui, N.; Bowring, N.; Luklinska, Z.; Ren, G. Determination of the Complex Permittivity of Textiles and Leather in the 14-40 GHz, mm wave band using a Free-Wave Transmittance Only Method. IET Microw. Antennas Propag. 2008, 2, 606–614. [Google Scholar] [CrossRef]
- Dankov, P.I. Concept for Equivalent Dielectric Constant of Planar Transmission Lines on Anisotropic Substrates. In Proceedings of the 46th European Microwave Conference (EuMC), London, UK, 3–7 October 2016; pp. 158–161. [Google Scholar] [CrossRef]
- Dankov, P. Two-resonator method for measurement of dielectric anisotropy in multilayer samples. IEEE Trans. Microw. Theory Tech. 2006, 54, 1534–1544. [Google Scholar] [CrossRef]
- Dankov, P.I.; Kondeva, M.I.; Baev, S.R. Influence of the Substrate Anisotropy in the Planar Antenna Simulations. In Proceedings of the International Workshop on Antenna Technology (iWAT) Conference, Lisbon, Portugal, 1–3 March 2010. [Google Scholar] [CrossRef]
- Wong, K.-L. Design of Nonplanar Microstrip Antennas and Transmission Lines; Wiley Series in Microwave and Optical Engineering; John Wiley & Sons: Hoboken, NJ, USA, 2004; ISBN 978-0-471-46390-0. [Google Scholar]
- Sanchez-Montero, R.; Lopez-Espi, P.-L.; Alen-Cordero, C.; Martinez-Rojas, J.-A. Bend and Moisture Effects on the Performance of a U-Shaped Slotted Wearable Antenna for Off-Body Communications in an Industrial Scientific Medical (ISM) 2.4 GHz Band. Sensors 2019, 19, 1804. [Google Scholar] [CrossRef]
- Escobedo, P.; de Pablos-Florido, J.; Carvajal, M.A.; Martínez-Olmos, A.; Capitán-Vallvey, L.F.; Palma, A. The effect of bending on laser-cut electro-textile inductors and capacitors attached on denim as wearable structures. Text. Res. J. 2020, 90, 2355–2366. [Google Scholar] [CrossRef]
- Gupta, N.P.; Kumar, M.; Maheshwari, R. Development and performance analysis of conformal UWB wearable antenna under various bending radii. IOP Conf. Ser. Mater. Sci. Eng. 2019, 594, 012025. [Google Scholar] [CrossRef]
- Gharbi, M.E.; Fernández-García, R.; Ahyoud, S.; Gil, I. A Review of Flexible Wearable Antenna Sensors: Design, Fabrication Methods, and Applications. Materials 2020, 13, 3781. [Google Scholar] [CrossRef] [PubMed]
- Jalil, M.E.; Rahim, M.K.A.; Samsuri, N.A.; Murad, N.A.; Majid, H.A.; Kamardin, K.; Abdullah, M.A. Fractal Koch Multiband Textile Antenna Performance with Bending, Wet Conditions and On the Human Body. Prog. Electromagn. Res. 2013, 140, 633–652. [Google Scholar] [CrossRef][Green Version]
- Ferreira, D.; Pires, P.; Rodrigues, R.; Caldeirinha, R.F.S. Wearable Textile Antennas: Examining the effect of bending on their performance. Antennas Propag. Mag. 2017, 59, 54–59. [Google Scholar] [CrossRef]
- Dankov, P.; Levcheva, V.; Sharma, P. Influence of Dielectric Anisotropy and Bending on Wearable Textile Antenna Properties. In Proceedings of the 2020 International Workshop on Antenna Technology (iWAT), Bucharest, Romania, 25–28 February 2020. [Google Scholar] [CrossRef]
- Ye, Y.; Yuan, J.; Su, K. A Volume-Surface Integral Equation Solver for Radiation from Microstrip Antenna on Anisotropic Substrate. Int. J. Antennas Propag. 2012, 2012, 1–4. [Google Scholar] [CrossRef]
- Odabasi, H.; Teixeira, F.L. Analysis of cylindrically conformal patch antennas on isoimpedance anisotropic substrates. In Proceedings of the 2011 30th URSI General Assembly and Scientific Symposium, Istanbul, Turkey, 13–20 August 2011; pp. 1–4. [Google Scholar] [CrossRef]
- Levcheva, V.P.; Hadjistamov, B.N.; Dankov, P.I. Two-Resonator Method for Characterization of Dielectric Substrate Anisotropy. Bulg. J. Phys. 2008, 35, 33–52. [Google Scholar]
- Silvestre, L. A characterization of optimal two-phase multifunctional composite designs. Proc. R. Soc. A Math. Phys. Eng. Sci. 2007, 463, 2543–2556. [Google Scholar] [CrossRef]
- Silvestre, L. Upper Bounds for Multiphase Composites in Any Dimension; Cornell University Library: Ithaca, NY, USA, 2010. [Google Scholar]
- Parnell, W.J.; Calvo-Jurado, C. On the computation of the Hashin–Shtrikman bounds for transversely isotropic two-phase linear elastic fibre-reinforced composites. J. Eng. Math. 2015, 95, 295–323. [Google Scholar] [CrossRef]
- Sihvola, A. Electromagnetic Mixing Formulas and Applications; The IEE, Electromagnetic Waves Series 47; IET: London, UK, 1999. [Google Scholar]
- Alonso-Gonz’alez, L.; Hoeye, S.V.; Vazquez, C.; Fernandez, M.; Hadarig, A.; Las-Heras, F. Novel Parametric Electromagnetic Modelling to Simulate Textile Integrated Circuits. In Proceedings of the IEEE MTT-S International Conference on Numerical Electromagnetic and Multiphysics Modeling and Optimization for RF, Microwave, and Terahertz Applications (NEMO), Seville, Spain, 17–19 May 2017. [Google Scholar] [CrossRef]
- Chen, T.; Chen, Y.; Jian, R. A Wideband Differential-Fed Microstrip Patch Antenna Based on Radiation of Three Resonant Modes. Int. J. Antennas Propag. 2019, 2019. [Google Scholar] [CrossRef]
- Abdelgwad, A.H. Microstrip Patch Antenna Enhancement Techniques. Int. Sch. Sci. Res. Innov. 2018, 12, 703–710. [Google Scholar] [CrossRef]
- V&V Article 3: Modeling Broadband and Circularly Polarized Patch Antennas Using EM. Picasso. Available online: http://www.emagtech.com/wiki/index.php/V%26V_Article_3:_Modeling_Broadband_And_Circularly_Polarized_Patch_Antennas_Using_EM.Picasso (accessed on 20 December 2020).
- Rathor, V.S.; Saini, J.P. A Design of Swastika Shaped Wideband Microstrip Patch Antenna for GSM/WLAN Application. J. Electromagn. Anal. Appl. 2014, 6, 31–37. [Google Scholar] [CrossRef]
- Khraisat, Y.S.H. Increasing Microstrip Patch Antenna Bandwidth by Inserting Ground Slots. J. Electromagn. Anal. Appl. 2018, 10, 1–11. [Google Scholar] [CrossRef]
- Souza, E.A.M.; Oliveira, P.S.; D’Assunção, A.G.; Mendonça, L.M.; Peixeiro, G. Miniaturization of a Microstrip Patch Antenna with a Koch Fractal Contour Using a Social Spider Algorithm to Optimize Shorting Post Position and Inset Feeding. Int. J. Antennas Propag. 2019, 2019. [Google Scholar] [CrossRef]
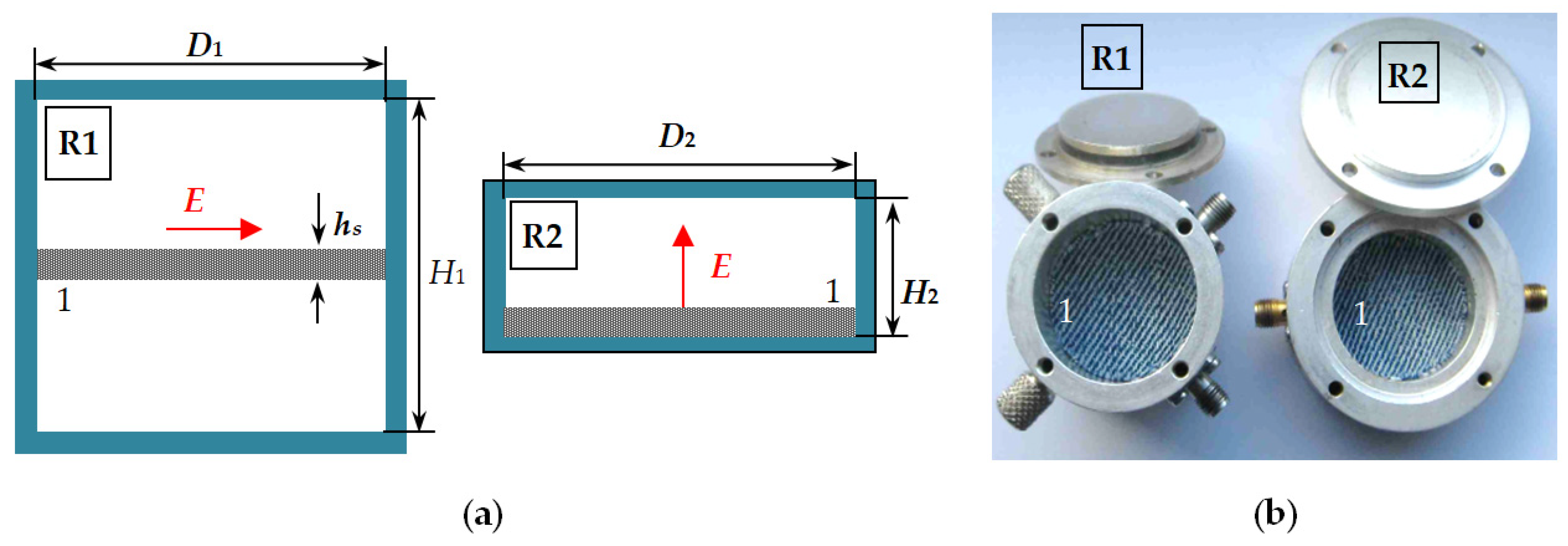
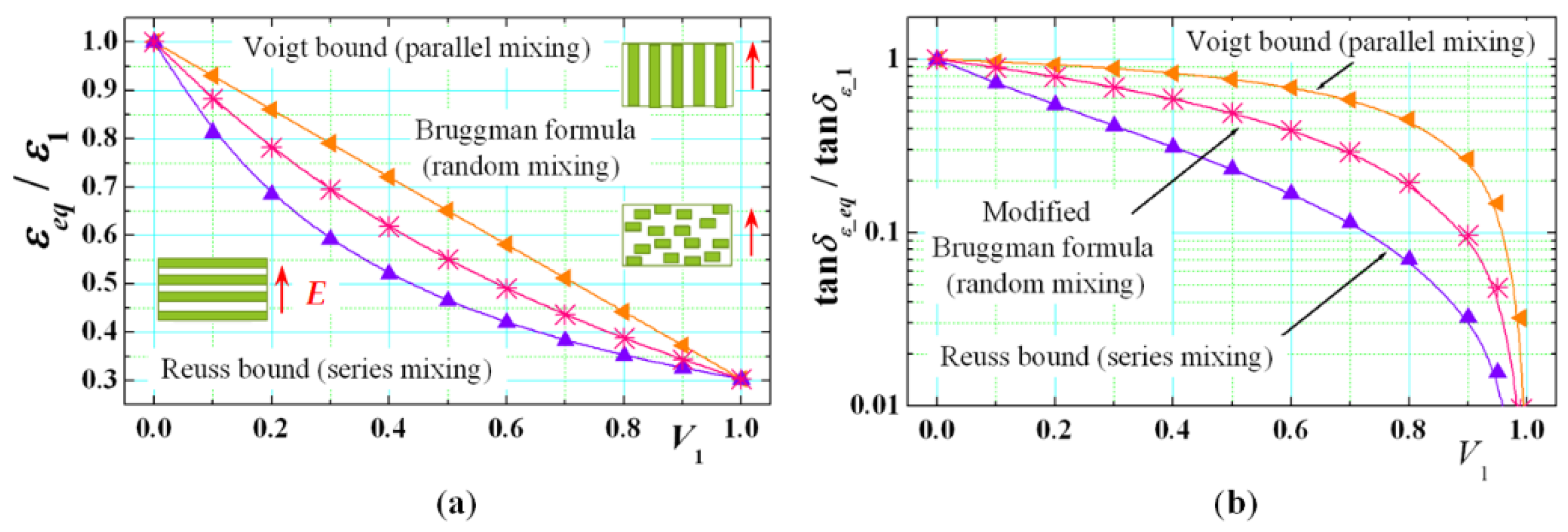
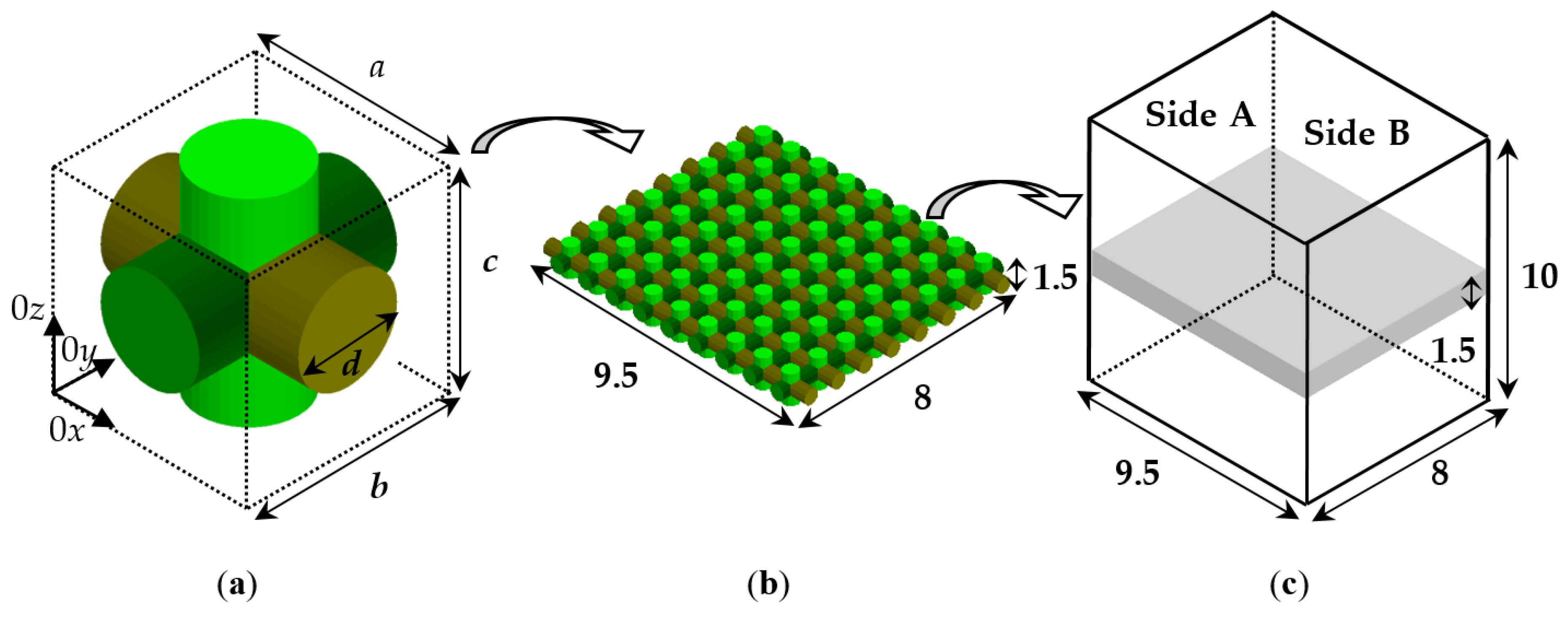

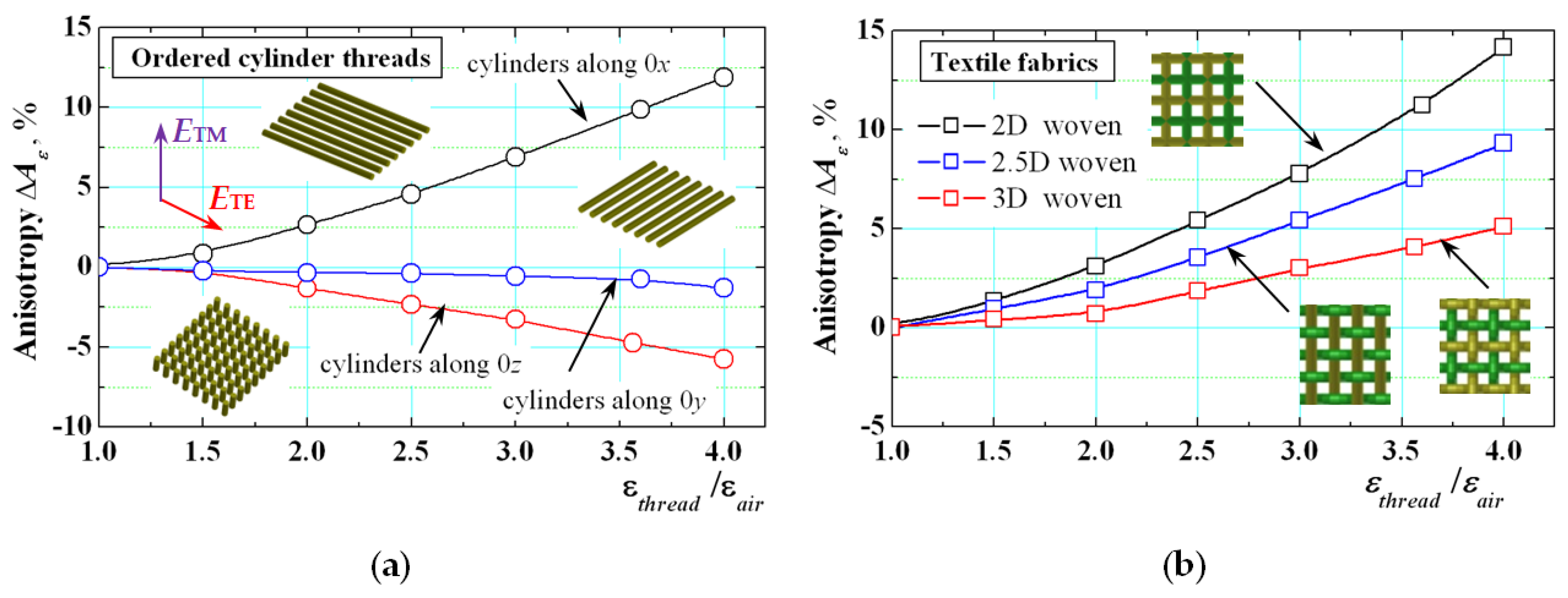



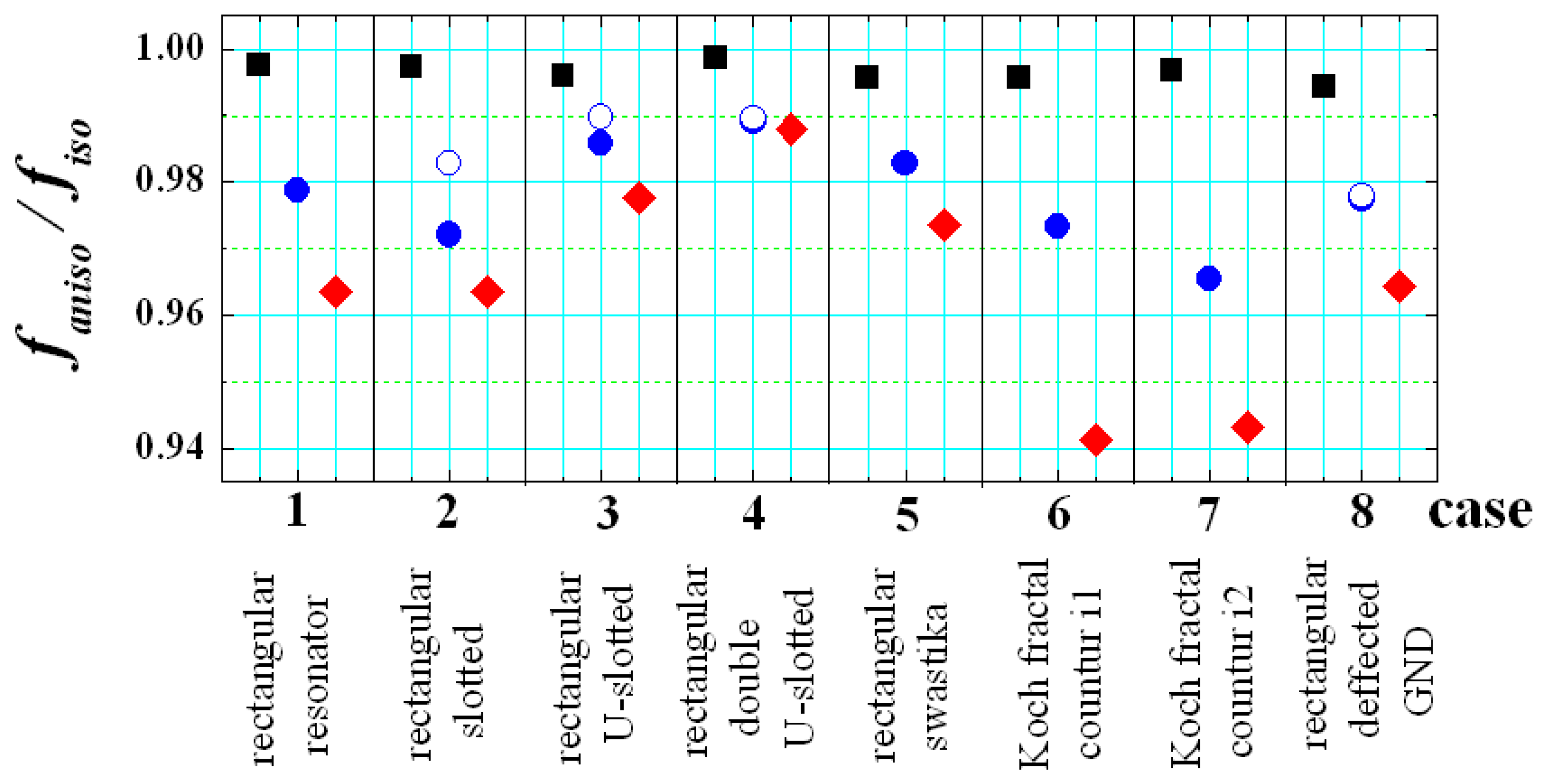
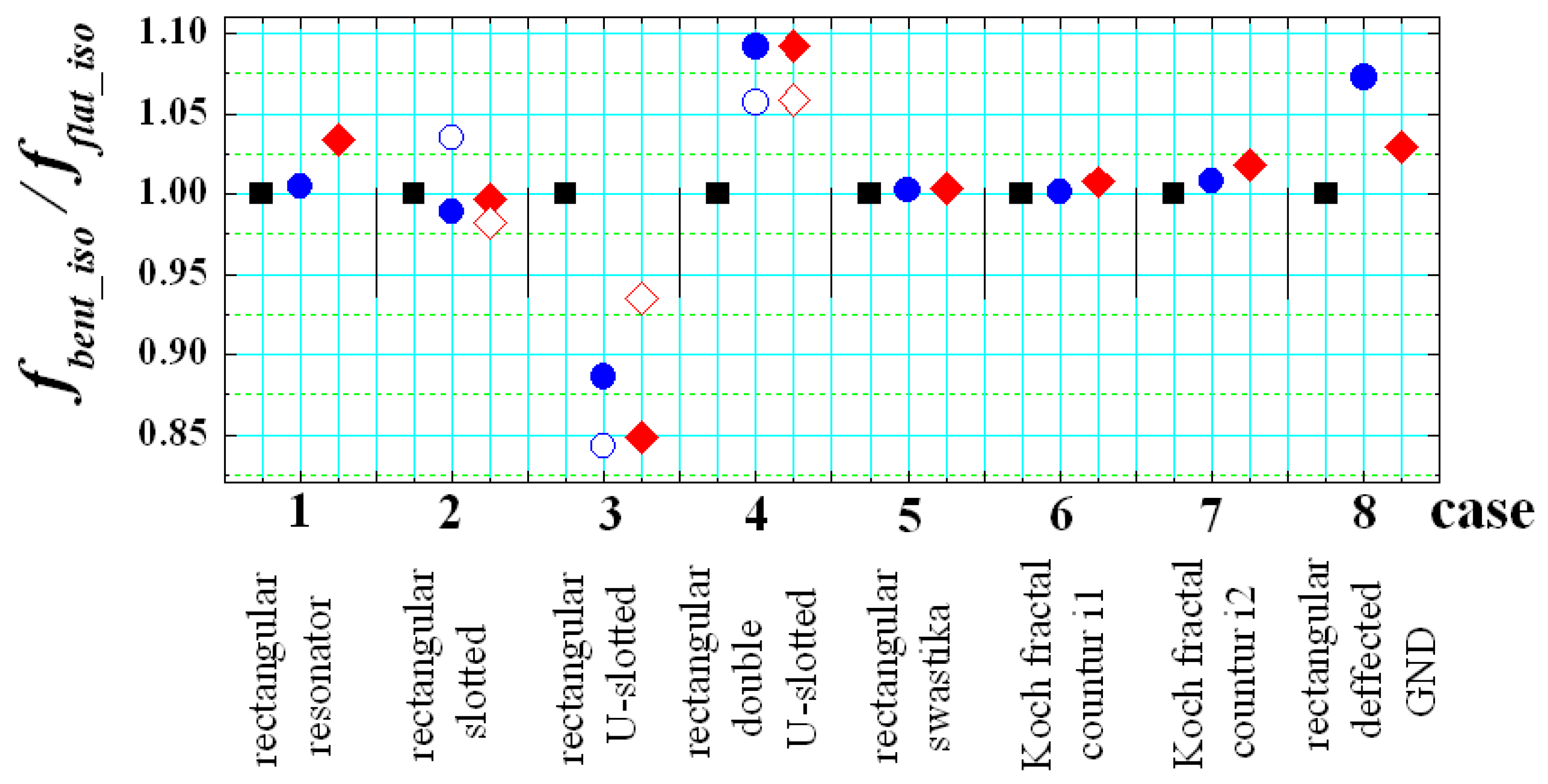

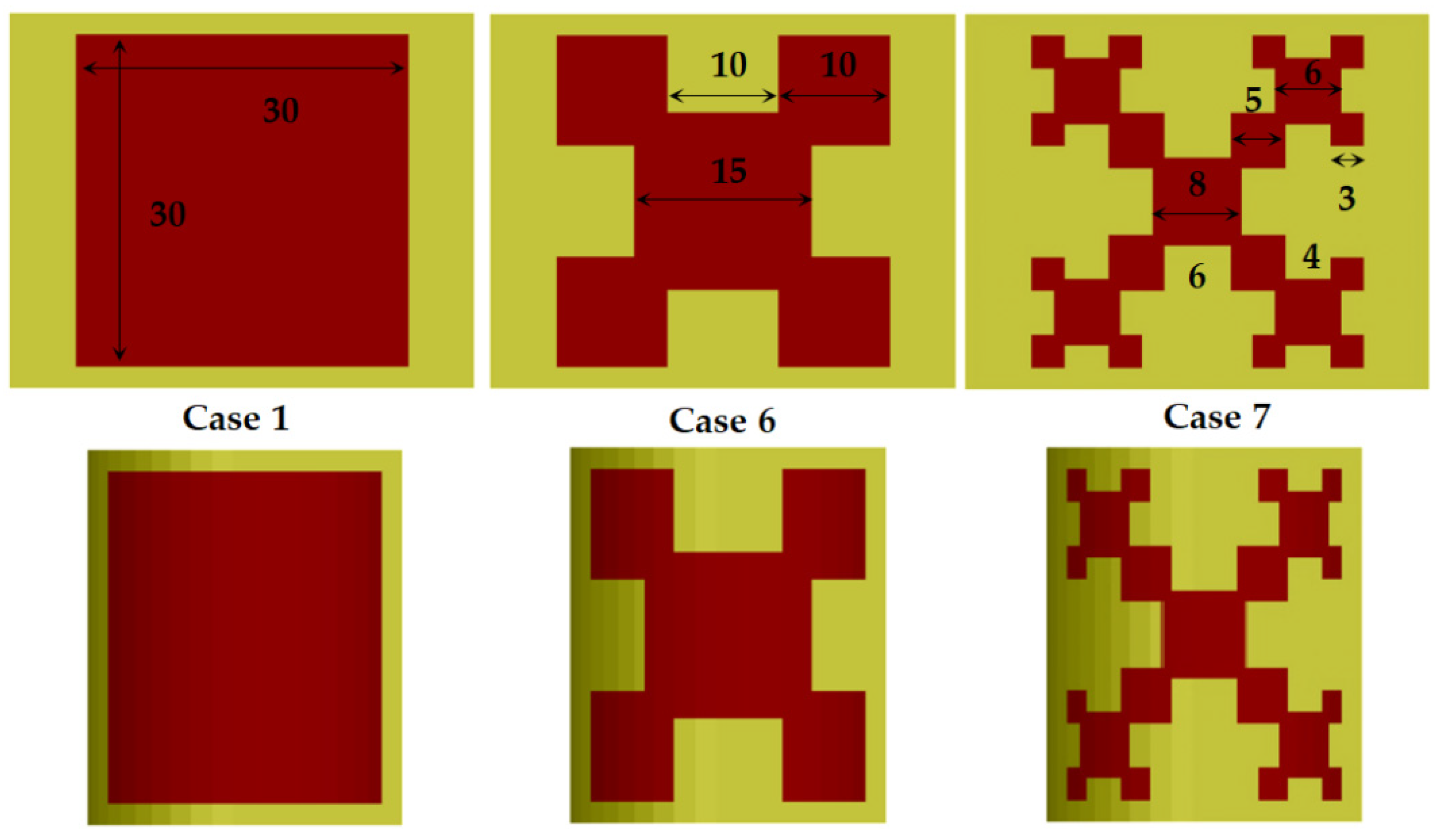
| Material | hs, mm | εpar/tan δε_par | εεperp/tan δε_perp | ΔAε/ΔAtanδε, % |
|---|---|---|---|---|
| Textile and polymer samples | ||||
| Denim | 0.90 | 1.74/0.048 | 1.61/0.030 | 7.8/38 |
| Linen | 0.65 | 1.65/0.043 | 1.58/0.044 | 4.3/−2.3 |
| Waterproof fabric with breathability GORE-TEX® | 0.20 | 1.53/0.0057 | 1.38/0.0043 | 10.3/28 |
| Polydimethylsiloxane (PDMS) | 0.70 | 2.73/0.022 | 2.57/0.019 | 6.00/15 |
| Flexible isotropic and near-to-isotropic samples | ||||
| Polytetrafluoroethylene (PTFE) | 0.45 | 2.05/0.00027 | 2.04/0.00026 | 0.49/3.8 |
| Polycarbonate (PC) | 0.50 | 2.77/0.0056 | 2.76/0.0055 | 0.36/1.8 |
| Silicone elastomer | 0.90 | 2.21/0.0010 | 2.19/0.0008 | 0.91/22 |
| Ro3003 | 0.51 | 3.00/0.0012 | 2.97/0.0013 | 1.0/−8 |
| Relatively flexible anisotropic reinforces substrates | ||||
| Ro4003 | 0.21 | 3.67/0.0037 | 3.38/0.0028 | 8.2/28 |
| NT9338 | 0.52 | 4.02/0.005 | 3.14/0.0025 | 24.6/67 |
| Relatively flexible anisotropic soft ceramics | ||||
| Ro3010 | 0.645 | 11.74/0.0025 | 10.13/0.0038 | 14.7/−41 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dankov, P.I.; Sharma, P.K.; Gupta, N. Numerical and Experimental Investigation of the Opposite Influence of Dielectric Anisotropy and Substrate Bending on Planar Radiators and Sensors. Sensors 2021, 21, 16. https://doi.org/10.3390/s21010016
Dankov PI, Sharma PK, Gupta N. Numerical and Experimental Investigation of the Opposite Influence of Dielectric Anisotropy and Substrate Bending on Planar Radiators and Sensors. Sensors. 2021; 21(1):16. https://doi.org/10.3390/s21010016
Chicago/Turabian StyleDankov, Plamen I., Praveen K. Sharma, and Navneet Gupta. 2021. "Numerical and Experimental Investigation of the Opposite Influence of Dielectric Anisotropy and Substrate Bending on Planar Radiators and Sensors" Sensors 21, no. 1: 16. https://doi.org/10.3390/s21010016
APA StyleDankov, P. I., Sharma, P. K., & Gupta, N. (2021). Numerical and Experimental Investigation of the Opposite Influence of Dielectric Anisotropy and Substrate Bending on Planar Radiators and Sensors. Sensors, 21(1), 16. https://doi.org/10.3390/s21010016







