Efficient Spectrum Occupancy Prediction Exploiting Multidimensional Correlations through Composite 2D-LSTM Models †
Abstract
1. Introduction
2. System Model and Preliminaries
2.1. Prediction with Autoregressive Model
2.2. Prediction with Bayesian-Inference
2.3. Prediction with Long Short-Term Memory
2.4. Prediction with Convolutional Long Short-Term Memory
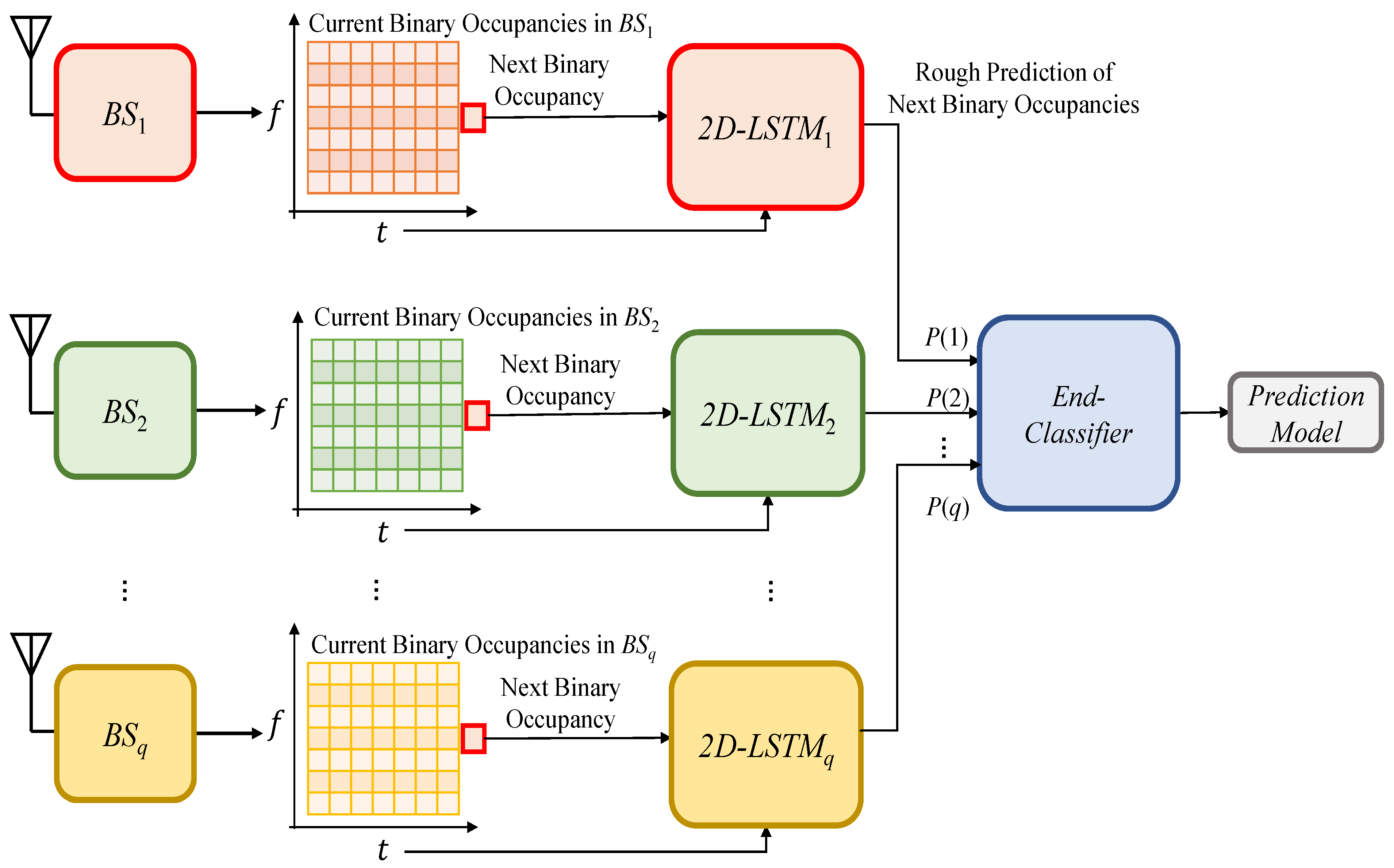
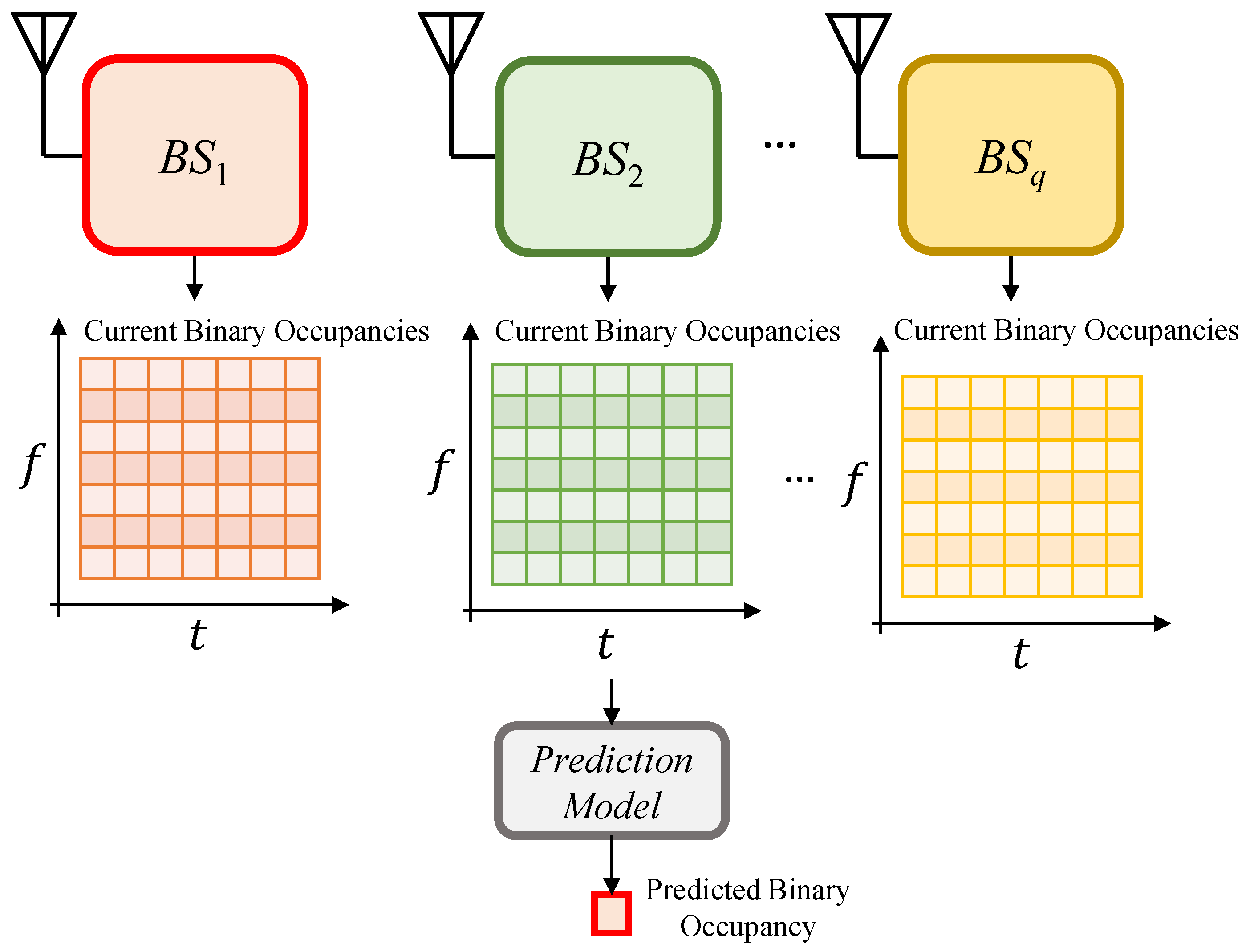
3. The Proposed Method for Spectrum Occupancy Prediction Exploiting Time, Frequency, and Space Correlations
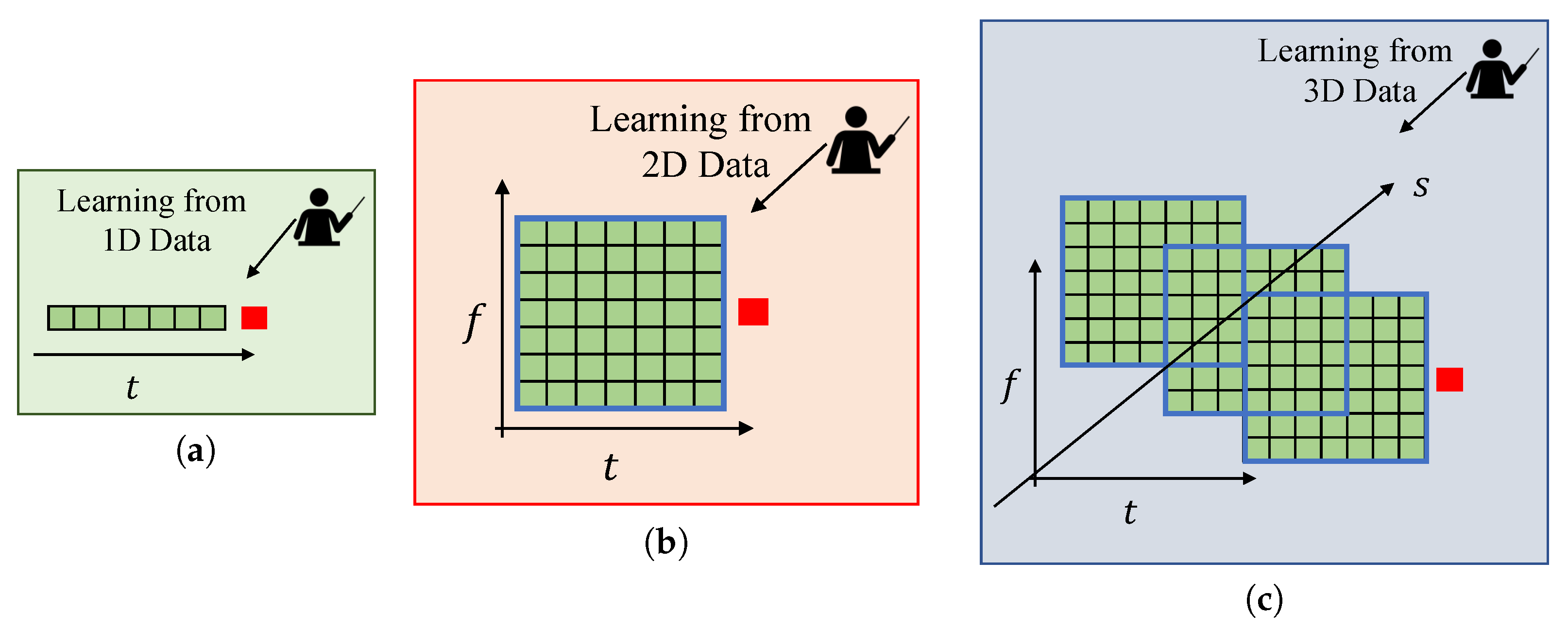
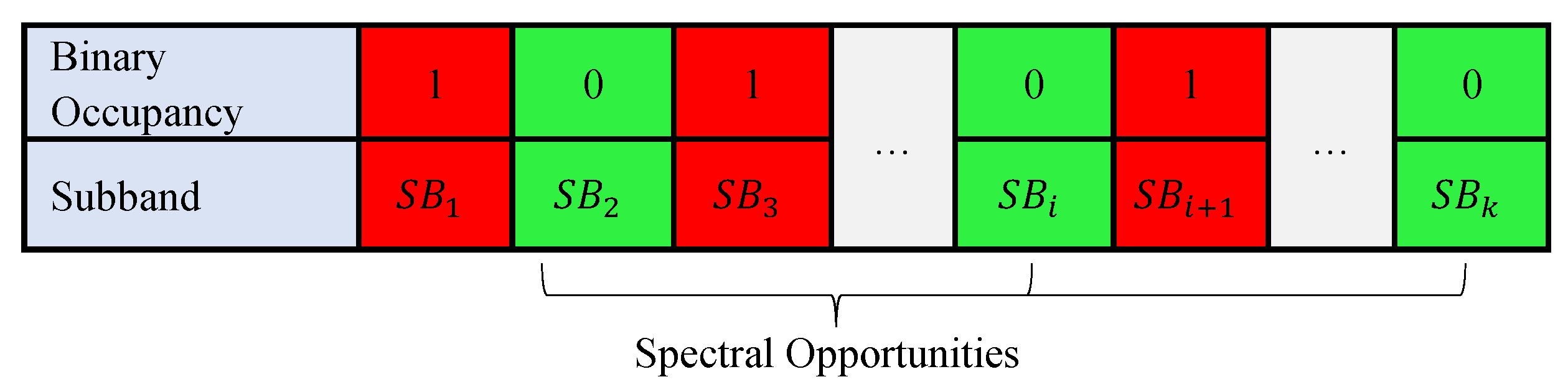
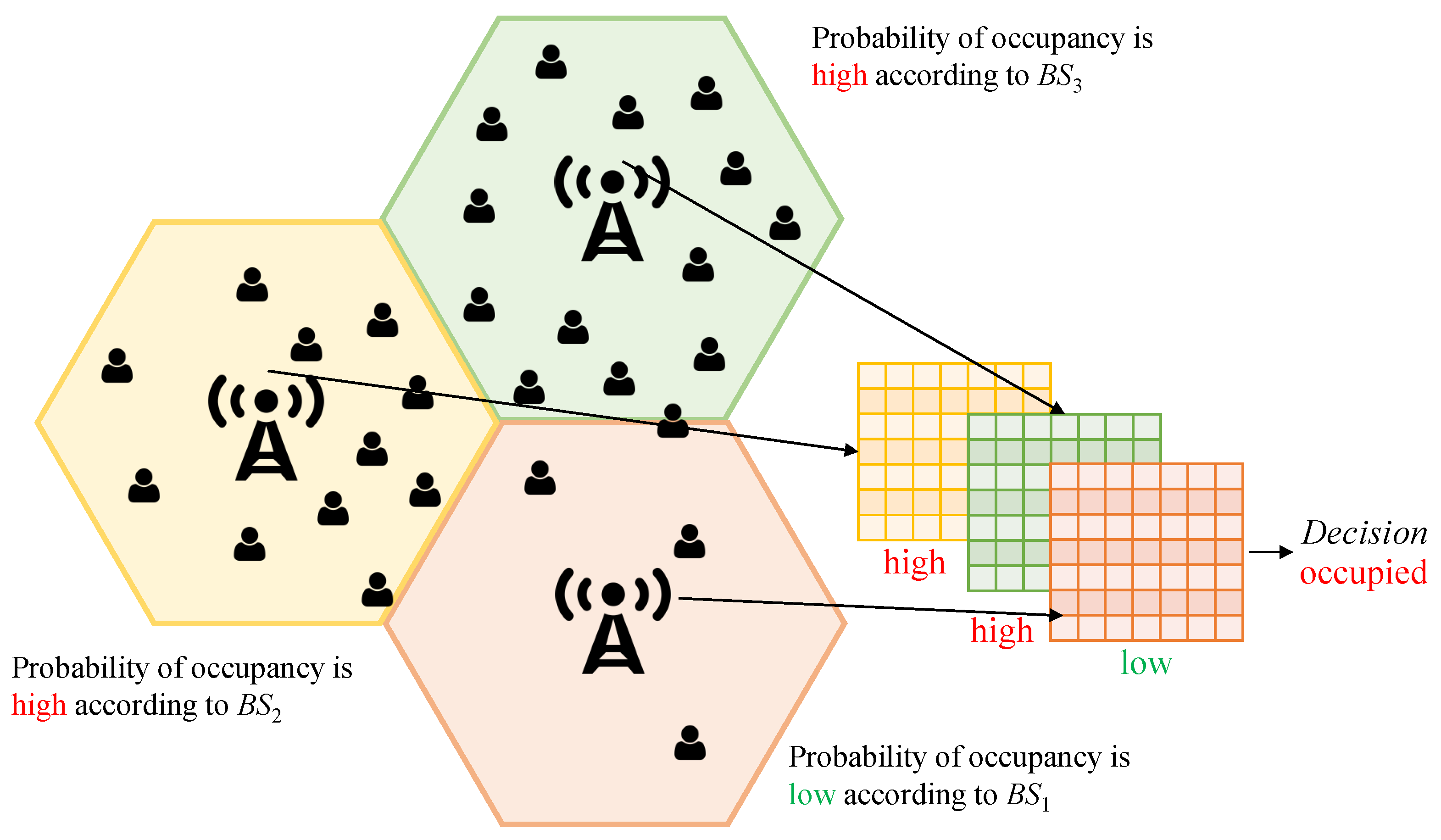
3.1. Motivations for Time, Frequency, and Space Correlation Exploitation and Problem Sub-Division
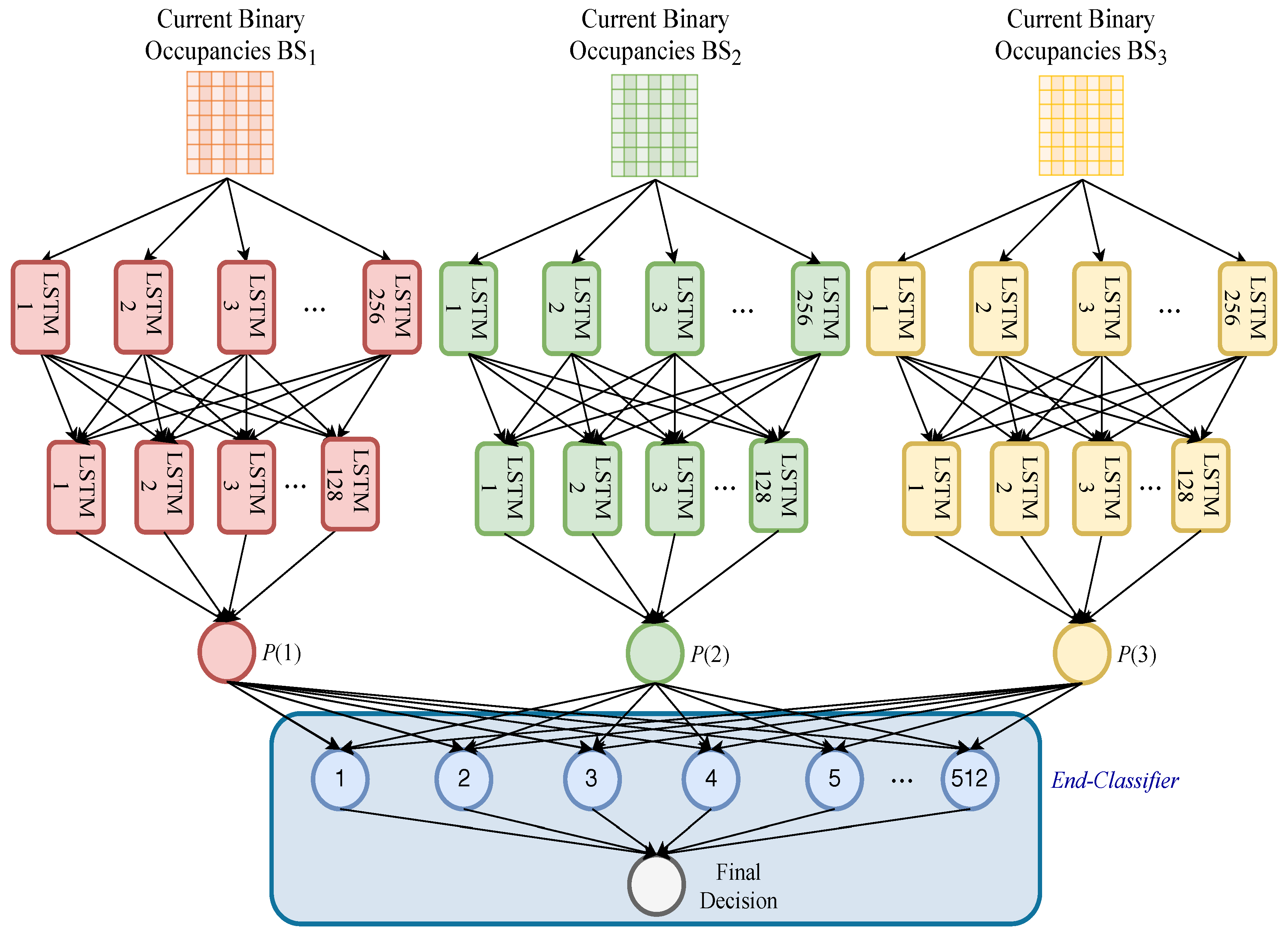
3.2. The Proposed Method
3.3. A Note on Computational Complexity
4. Dataset Generation
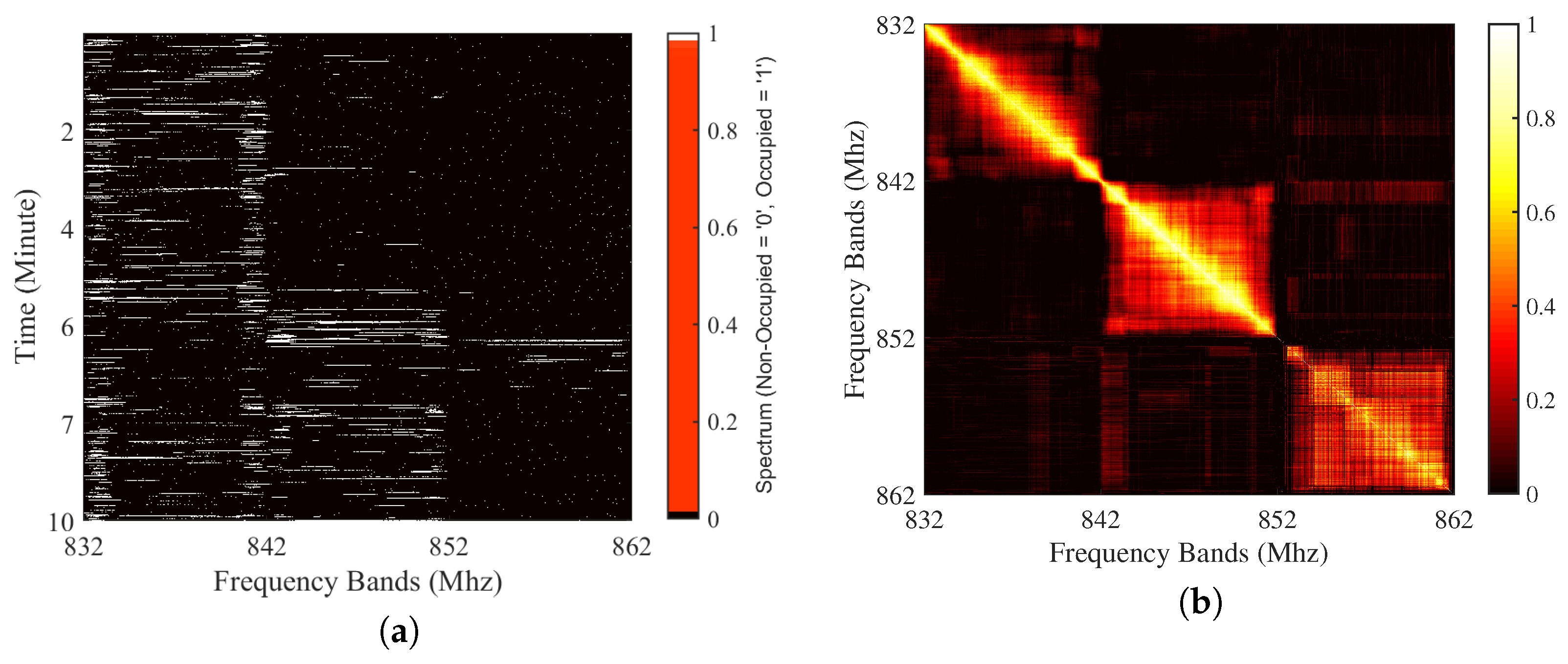
4.1. Measurement Setup
4.2. Measurement Procedure and Geographical Locations
4.2.1. City Center (Taksim)
4.2.2. Rural Area (Silivri)
5. Parameter Settings and Experimental Results
5.1. Hyperparameters of Deep Learning Models
- 1D-LSTM: This model uses two LSTM hidden layers and an output layer. Particularly, 256 and 128 hidden units were used in the first and second hidden layers, respectively. The rectified linear unit (ReLU) was used as activation functions. Afterward, the probability of the occupancies was calculated in the output layer, which uses a sigmoid activation function with 1 unit. We note that one unit is enough to represent the occupancies since there are only two classes (spectrum is occupied “1” or not “0”). In total, 461,441 parameters were used. Finally, the model was trained with a batch size of 256 and 18 epochs. Efficient adaptive moment estimation (ADAM) was used with an optimum learning rate of 0.0001 during the training. Also, the logarithmic loss function was used for binary classification.
- ConvLSTM: The ConvLSTM model was used with 3D data as the state-of-the-art method. The model includes two ConvLSTM layers, a flatten layer, and an output layer. In the first and second ConvLSTM layers, 256 and 128 units were used, respectively. Afterward, a flatten layer was used to prepare a vector for the output layer. Finally, an output layer WAS used with one unit. In the output layer, the sigmoid function was used. In total, 4,142,721 parameters were used. A batch size of 256 and 15 epochs were used to train the model. ADAM was used for the adaptive learning rate optimization with an optimum learning rate of 0.00005. Furthermore, the logarithmic loss function was used for binary classification.
- 2D-LSTM: This model uses two LSTM hidden layers and an output layer. More specifically, with ReLU activation functions 256 and 128 hidden units were used in the first and second LSTM hidden layers, respectively. Afterward, an output layer was used to calculate the probability of the occupancy. The sigmoid function was used in the output layer. In total, 467,585 parameters were used. Finally, the DL model was trained with a batch size of 256 and 15 epochs. ADAM was used for adaptive learning rate optimization and the optimum learning rate in this model was found at 0.00005. Again, for binary classification, the logarithmic loss function was employed.
- An end-classifier: A standard two-layer feed-forward network [47] was used as an end-classifier. This classifier consists of a hidden layer and an output layer. The sigmoid functions were used as activation functions. The MATLAB Neural-Network-Toolbox “nprtool” [47] was used for implementation. Scaled conjugate gradient (trainsscg), and cross-entropy (crossentropy) were used for training and performance metrics, respectively. The number of hidden neurons was set to 512 while the number of output neurons was set to one. Therefore, 25,600 parameters were used in total.
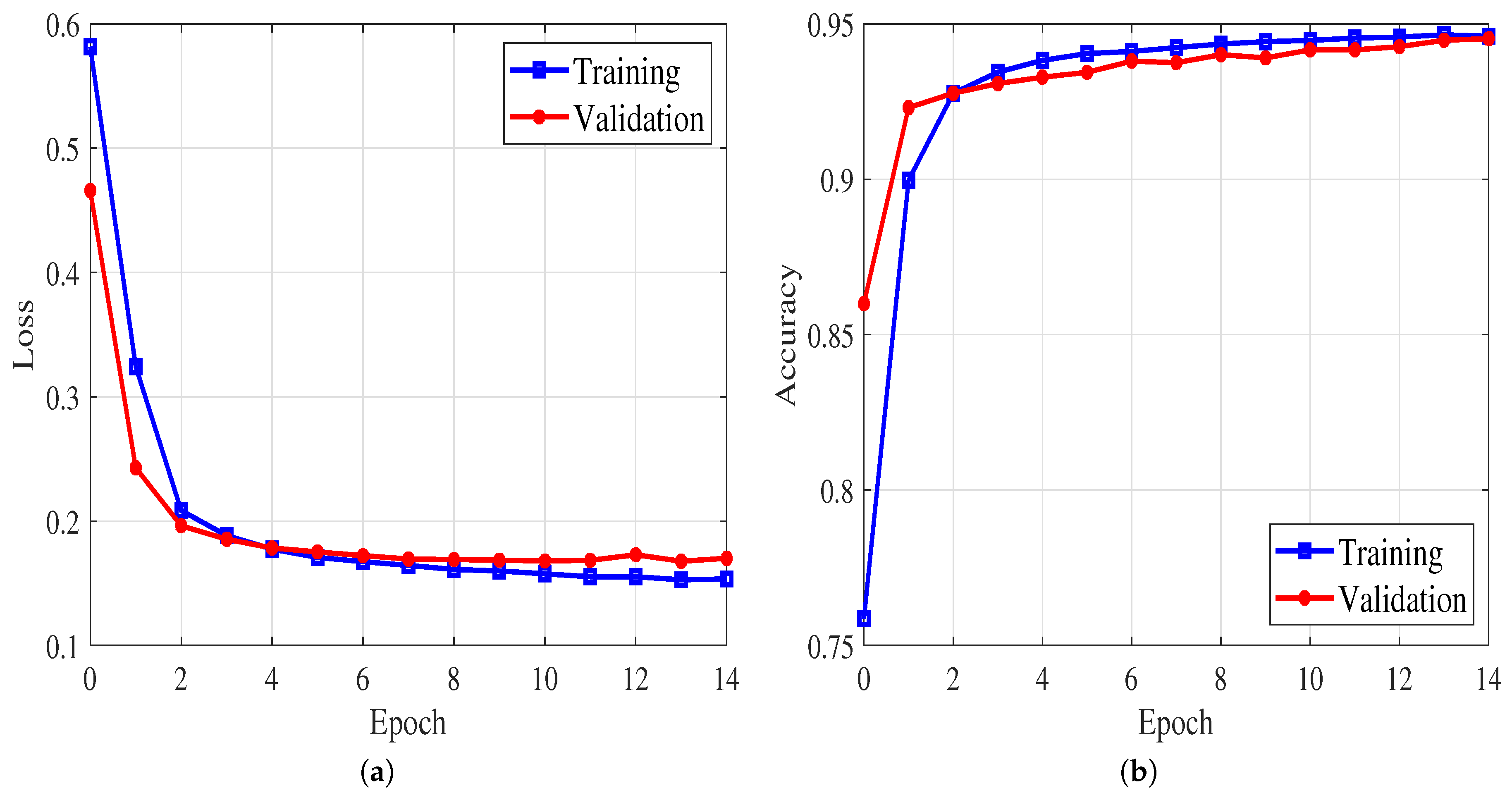
5.2. Performance Evaluation and Discussion
6. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| 1D | one-dimensional |
| 2D | two-dimensional |
| 3D | three-dimensional |
| 5G | fifth-generation |
| ADAM | adaptive moment estimation |
| ARM | autoregressive model |
| BIF | Bayesian inference |
| BS | base station |
| CNN | convolutional neural networks |
| ConvLSTM | convolutional long short-term memory |
| CPU | central processing unit |
| CR | cognitive radio |
| DL | deep learning |
| LSTM | long-short term memory |
| ML | machine learning |
| PRB | physical resource block basis |
| PUs | primary users |
| ReLU | rectified linear unit |
| RSSI | received signal strength indicator |
| SB | subband |
| SUs | secondary users |
| UL | uplink |
References
- Ancans, G.; Bobrovs, V.; Ancans, A.; Kalibatiene, D. Spectrum considerations for 5G mobile communication systems. Procedia Comput. Sci. 2017, 104, 509–516. [Google Scholar] [CrossRef]
- Dahlman, E.; Mildh, G.; Parkvall, S.; Peisa, J.; Sachs, J.; Selén, Y.; Sköld, J. 5G wireless access: Requirements and realization. IEEE Commun. Mag. 2014, 52, 42–47. [Google Scholar] [CrossRef]
- Amjad, M.; Rehmani, M.H.; Mao, S. Wireless multimedia cognitive radio networks: A comprehensive survey. IEEE Commun. Surv. Tutor. 2018, 20, 1056–1103. [Google Scholar] [CrossRef]
- Hong, X.; Wang, J.; Wang, C.X.; Shi, J. Cognitive radio in 5G: A perspective on energy-spectral efficiency trade-off. IEEE Commun. Mag. 2014, 52, 46–53. [Google Scholar] [CrossRef]
- Haykin, S. Cognitive radio: Brain-empowered wireless communications. IEEE J. Sel. Areas Commun. 2005, 23, 201–220. [Google Scholar] [CrossRef]
- Yucek, T.; Arslan, H. A survey of spectrum sensing algorithms for cognitive radio applications. IEEE Commun. Surv. Tutor. 2009, 11, 116–130. [Google Scholar] [CrossRef]
- Banavathu, N.R.; Khan, M.Z.A. Optimization of N-out-of-K rule for heterogeneous cognitive radio networks. IEEE Signal Process. Lett. 2019, 26, 445–449. [Google Scholar] [CrossRef]
- Arienzo, L.; Tarchi, D. Statistical modeling of spectrum sensing energy in multi-hop cognitive radio networks. IEEE Signal Process. Lett. 2015, 22, 356–360. [Google Scholar] [CrossRef]
- Arjoune, Y.; Kaabouch, N. A comprehensive survey on spectrum sensing in cognitive radio networks: Recent advances, new challenges, and future research directions. Sensors 2019, 19, 126. [Google Scholar] [CrossRef]
- Yu, L.; Chen, J.; Ding, G.; Tu, Y.; Yang, J.; Sun, J. Spectrum prediction based on Taguchi method in deep learning with long short-term memory. IEEE Access 2018, 6, 45923–45933. [Google Scholar] [CrossRef]
- Naikwadi, M.H.; Patil, K.P. A Survey of Artificial Neural Network based Spectrum Inference for Occupancy Prediction in Cognitive Radio Networks. In Proceedings of the 4th International Conference on Trends in Electronics and Informatics (ICOEI), Tirunelveli, India, 15–17 June 2020; pp. 903–908. [Google Scholar] [CrossRef]
- Lin, Z.; Jiang, X.; Huang, L.; Yao, Y. A energy prediction based spectrum sensing approach for cognitive radio networks. In Proceedings of the 5th International Conference on Wireless Communications, Networking and Mobile Computing (WICOM), Beijing, China, 24–26 September 2009; pp. 1–4. [Google Scholar] [CrossRef]
- Wen, Z.; Luo, T.; Xiang, W.; Majhi, S.; Ma, Y. Autoregressive spectrum hole prediction model for cognitive radio systems. In Proceedings of the IEEE International Conference on Communications Workshops (ICC), Beijing, China, 19–23 May 2008; pp. 154–157. [Google Scholar] [CrossRef]
- Xing, X.; Jing, T.; Huo, Y.; Li, H.; Cheng, X. Channel quality prediction based on Bayesian inference in cognitive radio networks. In Proceedings of the IEEE International Conference on Computer Communications (INFOCOM), Turin, Italy, 14–19 April 2013; pp. 1465–1473. [Google Scholar] [CrossRef]
- Tumuluru, V.K.; Wang, P.; Niyato, D. Channel status prediction for cognitive radio networks. Wireless Commun. Mob. Comput. 2012, 12, 862–874. [Google Scholar] [CrossRef]
- Eltholth, A.A. Spectrum prediction in cognitive radio systems using a wavelet neural network. In Proceedings of the International Conference on Software, Telecommunications and Computer Networks (SoftCOM), Split, Croatia, 22–24 September 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Ding, G.; Jiao, Y.; Wang, J.; Zou, Y.; Wu, Q.; Yao, Y.D.; Hanzo, L. Spectrum inference in cognitive radio networks: Algorithms and applications. IEEE Commun. Surv. Tutor. 2017, 20, 150–182. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, H.; MacKenzie, A.B.; Matinmikko, M. Predicting spectrum occupancies using a non-stationary hidden Markov model. IEEE Wireless Commun. Lett. 2014, 3, 333–336. [Google Scholar] [CrossRef]
- Selim, A.; Paisana, F.; Arokkiam, J.A.; Zhang, Y.; Doyle, L.; DaSilva, L.A. Spectrum monitoring for radar bands using deep convolutional neural networks. In Proceedings of the IEEE Global Communications Conference (GLOBECOM), Singapore, 4–8 December 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Shawel, B.; Woledegebre, D.; Pollin, S. Deep-learning based cooperative spectrum prediction for cognitive networks. In Proceedings of the International Conference on Information and Communication Technology Convergence (ICTC), Jeju, Korea, 17–19 October 2018; pp. 133–137. [Google Scholar] [CrossRef]
- Yu, L.; Chen, J.; Ding, G. Spectrum prediction via long short term memory. In Proceedings of the 3rd IEEE International Conference on Computer and Communications (ICCC), Chengdu, China, 13–16 December 2017; pp. 643–647. [Google Scholar] [CrossRef]
- Omotere, O.; Fuller, J.; Qian, L.; Han, Z. Spectrum occupancy prediction in coexisting wireless systems using deep learning. In Proceedings of the IEEE 88th Vehicular Technology Conference (VTC-Fall), Chicago, IL, USA, 27–30 August 2018; pp. 1–7. [Google Scholar] [CrossRef]
- Aygül, M.A.; Nazzal, M.; Ekti, A.R.; Görçin, A.; da Costa, D.B.; Ateş, H.F.; Arslan, H. Spectrum occupancy prediction exploiting time and frequency correlations through 2D-LSTM. In Proceedings of the IEEE 91st Vehicular Technology Conference (VTC2020-Spring), Antwerp, Belgium, 25–28 May 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Hisham, A.M.; Arslan, H. Multidimensional signal analysis and measurements for cognitive radio systems. In Proceedings of the 2008 IEEE Radio and Wireless Symposium, Orlando, FL, USA, 22–24 January 2008; pp. 639–642. [Google Scholar] [CrossRef]
- Sun, J.; Wang, J.; Ding, G.; Shen, L.; Yang, J.; Wu, Q.; Yu, L. Long-term spectrum state prediction: An image inference perspective. IEEE Access 2018, 6, 43489–43498. [Google Scholar] [CrossRef]
- Alkhouri, I.; Joneidi, M.; Hejazi, F.; Rahnavard, N. Large-scale spectrum occupancy learning via tensor decomposition and LSTM networks. In Proceedings of the IEEE International Radar Conference (RADAR), Washington, DC, USA, 28–30 April 2020; pp. 677–682. [Google Scholar] [CrossRef]
- Shawel, B.S.; Woldegebreal, D.H.; Pollin, S. Convolutional LSTM-based long-term spectrum prediction for dynamic spectrum access. In Proceedings of the 27th European Signal Processing Conference (EUSIPCO), A Coruna, Spain, 2–6 September 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Ioannidou, A.; Chatzilari, E.; Nikolopoulos, S.; Kompatsiaris, I. Deep learning advances in computer vision with 3D data: A survey. ACM Comput. Surv. (CSUR) 2017, 50, 1–38. [Google Scholar] [CrossRef]
- Gezawa, A.S.; Zhang, Y.; Wang, Q.; Yunqi, L. A review on deep learning approaches for 3D data representations in retrieval and classifications. IEEE Access 2020, 8, 57566–57593. [Google Scholar] [CrossRef]
- Fragkiadakis, A.G.; Tragos, E.Z.; Askoxylakis, I.G. A survey on security threats and detection techniques in cognitive radio networks. IEEE Commun. Surv. Tut. 2013, 15, 428–445. [Google Scholar] [CrossRef]
- Bassoy, S. Self-Organised Multi-Objective Network Clustering for Coordinated Communications in Future Wireless Networks. Ph.D. Thesis, University of Glasgow, Glasgow, UK, 2020. [Google Scholar]
- Jaqaman, K.; Loerke, D.; Mettlen, M.; Kuwata, H.; Grinstein, S.; Schmid, S.L.; Danuser, G. Robust single-particle tracking in live-cell time-lapse sequences. Nat. Methods 2008, 5, 695–702. [Google Scholar] [CrossRef]
- Khalfi, B.; Hamdaoui, B.; Guizani, M.; Zorba, N. Efficient spectrum availability information recovery for wideband DSA networks: A weighted compressive sampling approach. IEEE Trans. Wireless Commun. 2018, 17, 2162–2172. [Google Scholar] [CrossRef]
- LeCun, Y.; Boser, B.E.; Denker, J.S.; Henderson, D.; Howard, R.E.; Hubbard, W.E.; Jackel, L.D. Handwritten digit recognition with a back-propagation network. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 1990; pp. 396–404. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Tai, K.S.; Socher, R.; Manning, C.D. Improved semantic representations from tree-structured long short-term memory networks. arXiv 2015, arXiv:1503.00075. [Google Scholar] [CrossRef]
- Xingjian, S.; Chen, Z.; Wang, H.; Yeung, D.Y.; Wong, W.K.; Woo, W.c. Convolutional LSTM network: A machine learning approach for precipitation nowcasting. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2015; pp. 802–810. [Google Scholar]
- Sak, H.; Senior, A.; Beaufays, F. Long short-term memory based recurrent neural network architectures for large vocabulary speech recognition. arXiv 2014, arXiv:1402.1128. [Google Scholar]
- Sak, H.; Senior, A.W.; Beaufays, F. Long short-term memory recurrent neural network architectures for large scale acoustic modeling. In Proceedings of the Annual Conference of the International Speech Communication Association, (INTERSPEECH), Singapore, 14–18 September 2014; pp. 338–342. [Google Scholar]
- He, K.; Sun, J. Convolutional neural networks at constrained time cost. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 5353–5360. [Google Scholar]
- 3rd Generation Partnership Project (3GPP). Evolved Universal Terrestrial Radio Access (E-UTRA); (Release 16); 3GPP: Sophia Antipolis, France, 2020. [Google Scholar]
- Qaraqe, K.A.; Celebi, H.; Gorcin, A.; El-Saigh, A.; Arslan, H.; Alouini, M. Empirical results for wideband multidimensional spectrum usage. In Proceedings of the IEEE 20th International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC), Tokyo, Japan, 13–16 September 2009; pp. 1262–1266. [Google Scholar] [CrossRef]
- Zhang, G.; Wang, J.; Xiang, Y. Method, Apparatus and System for Spectrum Prediction. U.S. Patent 8,687,516, 1 April 2014. [Google Scholar]
- Comba. Outdoor Directional Quad-Band Antenna (ODI-065R17M18JJJ-G); Comba: Hongkong, China, 2020. [Google Scholar]
- Arimas. LTE Guard Band Calculation. Available online: https://arimas.com/lte-guard-band-calculation/ (accessed on 17 August 2020).
- Chollet, F. Keras. Available online: https://keras.io (accessed on 14 August 2020).
- Beale, M.H.; Hagan, M.T.; Demuth, H.B. Neural Network Toolbox User’s Guide; The Mathworks Inc.: Natick, MA, USA, 2010. [Google Scholar]




| Method | Execution Time (s) | |
|---|---|---|
| Training | Testing | |
| The tensor-based method | 608 | 2.8 |
| 2D-LSTM-based method | 57.8 | 0.7 |
| BS | Area | |
|---|---|---|
| Taksim | Silivri | |
| 6429 | 3178 | |
| 4442 | 3138 | |
| 3GPP Band | Bandwidth | Frequency | Duplex | Technology |
|---|---|---|---|---|
| B20 | 10 MHz | 852–862 Mhz (UL) | Frequency division duplexing | Long term evolution-Advanced Pro (4.5 G) |
| Method | Measure | ||
|---|---|---|---|
| -Score | |||
| ARM | 0.9210 | 0.9681 | 0.9440 |
| BIF | 0.9264 | 0.9738 | 0.9495 |
| 1D-LSTM | 0.9602 | 0.9780 | 0.9690 |
| 2D-LSTM | 0.9720 | 0.9732 | 0.9726 |
| ConvLSTM | 0.9760 | 0.9763 | 0.9762 |
| Composite 2D-LSTMs | 0.9727 | 0.9742 | 0.9735 |
| Method | Measure | ||
|---|---|---|---|
| -Score | |||
| ARM | 0.8863 | 0.8704 | 0.8783 |
| BIF | 0.9336 | 0.9130 | 0.9232 |
| 1D-LSTM | 0.9465 | 0.9165 | 0.9312 |
| 2D-LSTM | 0.9462 | 0.9216 | 0.9338 |
| ConvLSTM | 0.9479 | 0.9298 | 0.9388 |
| Composite 2D-LSTMs | 0.9476 | 0.9233 | 0.9353 |
| Method | Execution Time (s) | |
|---|---|---|
| Training | Testing | |
| ConvLSTM | 608.7 | 2.7 |
| Composite 2D-LSTMs | 58.1 | 0.7 |
| Method | Execution Time (s) | |
|---|---|---|
| Training | Testing | |
| ConvLSTM | 610.3 | 2.9 |
| Composite 2D-LSTMs | 58.9 | 0.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aygül, M.A.; Nazzal, M.; Sağlam, M.İ.; da Costa, D.B.; Ateş, H.F.; Arslan, H. Efficient Spectrum Occupancy Prediction Exploiting Multidimensional Correlations through Composite 2D-LSTM Models. Sensors 2021, 21, 135. https://doi.org/10.3390/s21010135
Aygül MA, Nazzal M, Sağlam Mİ, da Costa DB, Ateş HF, Arslan H. Efficient Spectrum Occupancy Prediction Exploiting Multidimensional Correlations through Composite 2D-LSTM Models. Sensors. 2021; 21(1):135. https://doi.org/10.3390/s21010135
Chicago/Turabian StyleAygül, Mehmet Ali, Mahmoud Nazzal, Mehmet İzzet Sağlam, Daniel Benevides da Costa, Hasan Fehmi Ateş, and Hüseyin Arslan. 2021. "Efficient Spectrum Occupancy Prediction Exploiting Multidimensional Correlations through Composite 2D-LSTM Models" Sensors 21, no. 1: 135. https://doi.org/10.3390/s21010135
APA StyleAygül, M. A., Nazzal, M., Sağlam, M. İ., da Costa, D. B., Ateş, H. F., & Arslan, H. (2021). Efficient Spectrum Occupancy Prediction Exploiting Multidimensional Correlations through Composite 2D-LSTM Models. Sensors, 21(1), 135. https://doi.org/10.3390/s21010135






