Representations and Benchmarking of Modern Visual SLAM Systems
Abstract
1. Introduction
- Intelligent transportation: whether talking about autonomous vehicles on open roads or Automatic Guided Vehicles (AGVs) within campuses, office buildings, or factories, transportation is a time and safety-critical problem that would benefit strongly from either partial or full automation.
- Domestic robotics: demographic changes are increasingly impacting our availability to do household management or take care of elderly people. Service robots able to execute complex tasks such as moving and manipulating arbitrary objects could provide an answer to this problem.
- Intelligence augmentation: eye-wear such as the Microsoft Hololens is already pointing at the future form of highly portable, smart devices capable of assisting humans during the execution of everyday tasks. The potential advancement over current devices such as smartphones originates from the superior spatial awareness provided by onboard Simultaneous Localisation And Mapping (SLAM) and Artificial Intelligence (AI) capabilities.
- We provide a concise review of currently existing Spatial AI systems along with an exposition of their most important characteristics.
- We discuss the structure of current and possible future environment representations and its implications on the structure of their underlying optimisation problems.
- We introduce novel synthetic datasets for Spatial AI with all required ground-truth information including camera calibration, sensor trajectories, object-level scene composition, as well as all object attributes such as poses, classes, and shapes readily available.
- We propose a set of clear evaluation metrics that will analyse all aspects of the output of a Spatial AI system, including localisation accuracy, scene label distributions, the accuracy of the geometry and positioning of all scene elements, as well as the completeness and compactness of the entire scene representation.
2. Review of Current SLAM Systems and Their Evolution into Spatial AI
3. What Representations Are Pursued by Spatial AI?
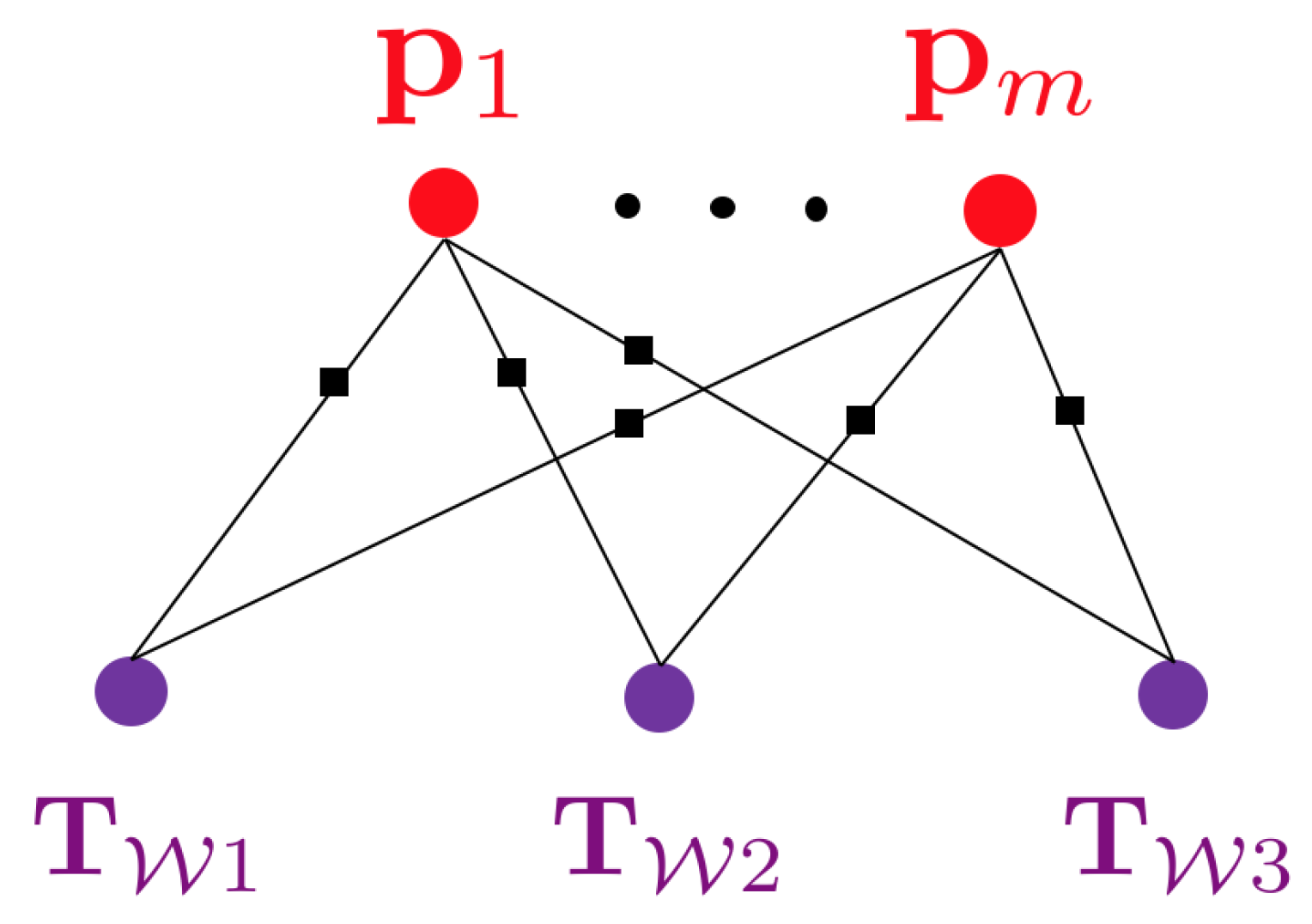
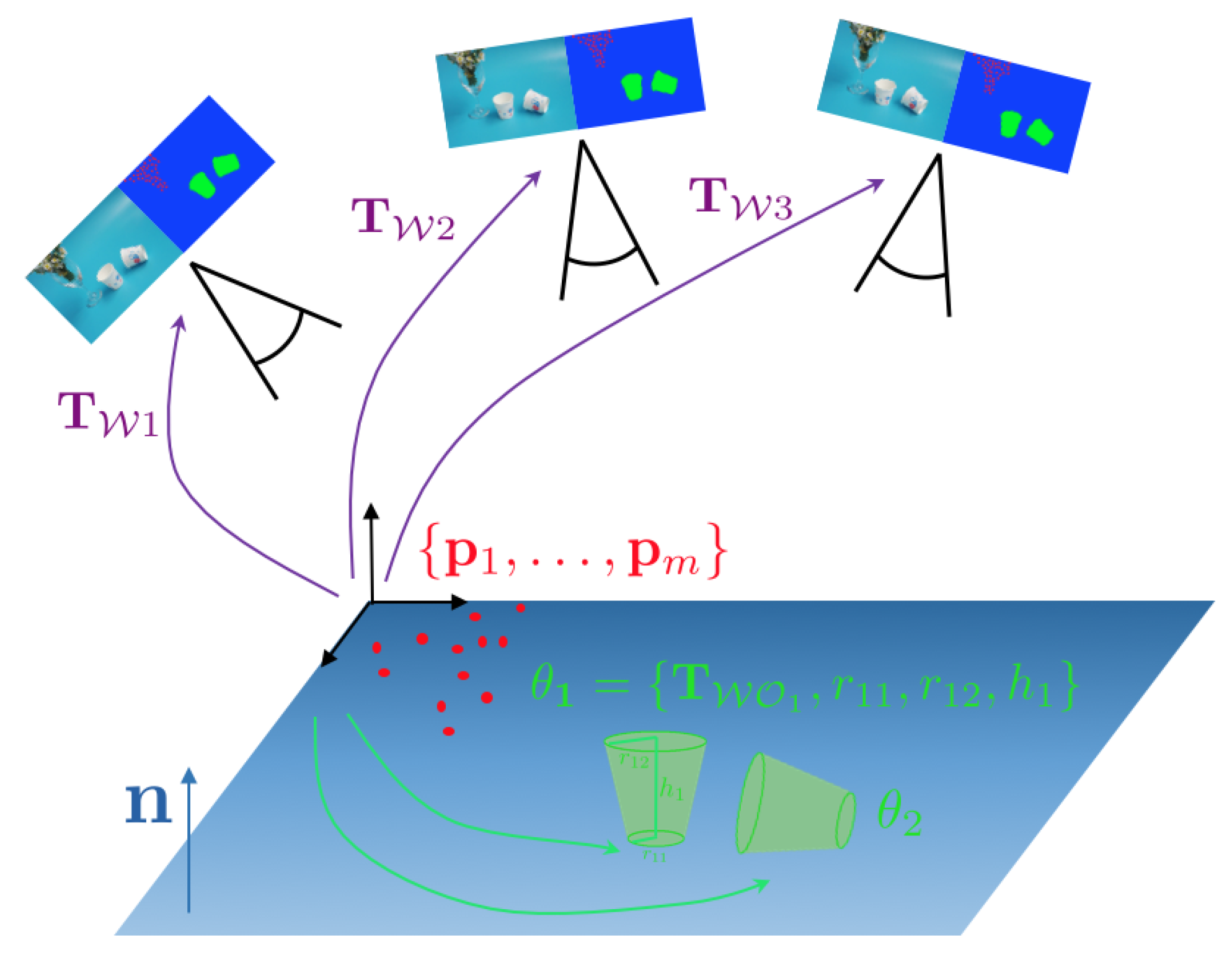
3.1. Hybrid Graphical Models
- It gives us more flexibility in choosing different but more appropriate parametrisations for the geometry of each segment.
- It gives us a reasonable partitioning according to human standards enabling us to assign a class or—more generally—semantic attributes to each segment.
- Two instances of a thin conical object with location and shape parameters. Due to rotational symmetry, the pose would have 5 Degree of Freedom (DoF), and the number of shape parameters would be 3 (bottom radius , top radius , and height of the object h).
- One set of 3D points to represent the plant. The cardinality of the set is, for the example, given by the number of sparse, multiview feature correspondences between the images.
- A plane vector to represent the background structure.
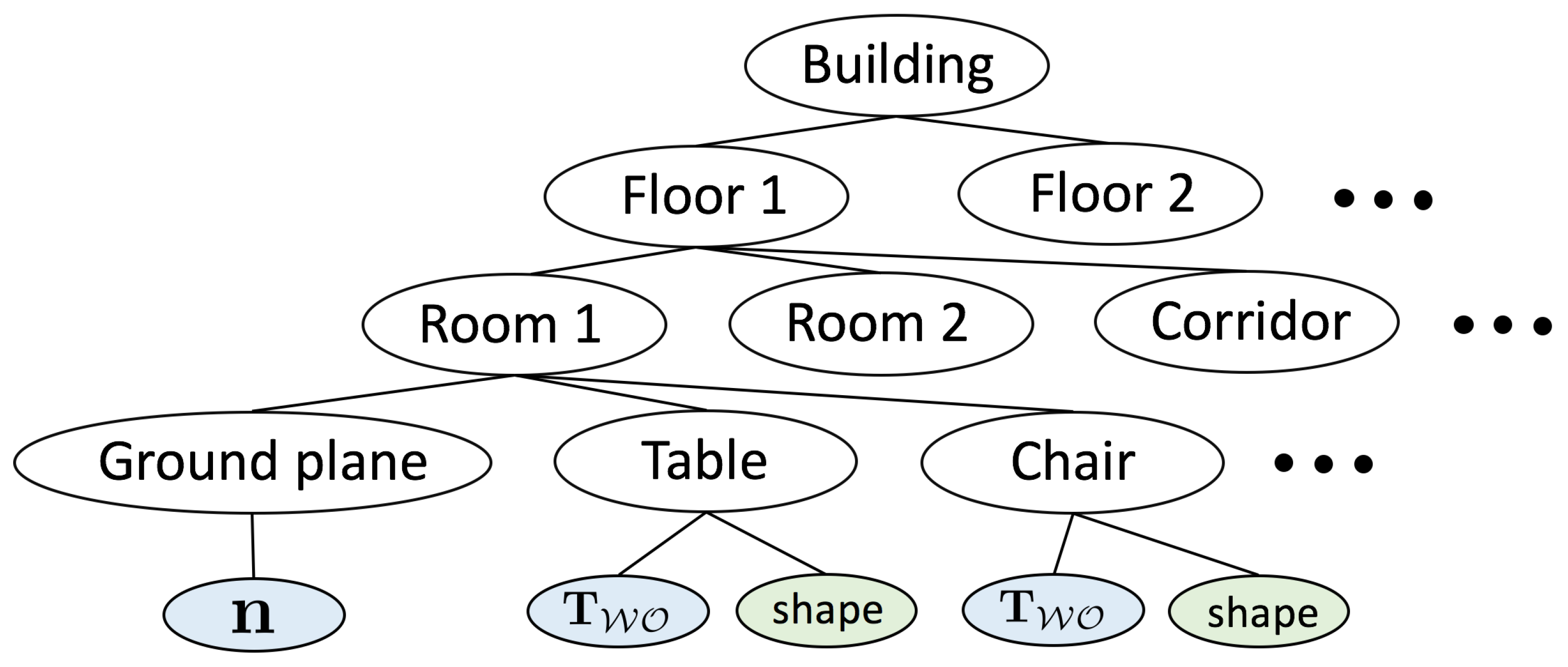
3.2. Hierarchical Hybrid Graphical Models
- A natural subdivision of the graph into multiple subgraphs, which is a requirement in larger-scale applications where the complete map can no longer be loaded into memory. The hierarchical, tree-based structure of the map permits loading submaps of different scales (e.g., entire floors or just single rooms).
- An agreement between the tree structure of the map and the natural segmentations and hierarchical subdivisions used by humans, which simplifies man-machine interaction.
- Parent structures appearing as separate nodes in the optimisation graph and enabling the construction of higher-order residual errors.
3.3. Expected Advantages of the Proposed Environment Representations
- Compact map representations: whether talking about a planar surface representing a wall or a more complex object shape, the object-level partitioning permits the choice of class-specific implicit low-dimensional representations. While choosing a simple three-vector to parametrise a plane, more complex objects could be modelled using the above-introduced, artificial intelligence based low-dimensional shape representations. The compact representations have obvious benefits in terms of memory efficiency, a critical concern in the further development of next-generation Spatial AI systems.
- Low-dimensional representations: by employing class-specific, we implicitly force optimised shapes to satisfy available priors about their geometry. In contrast to current approaches which use high-dimensional, semantically unaware representations that only employ low-level priors such as local smoothness, the (possibly learned) higher-level priors we may employ for certain objects of known classes are much more powerful and implicitly impose the correct amount of smoothness for each part of the object. It is conceivable that such techniques will have a much better ability to deal with measurement disturbances such as missing data or highly reflective surfaces.
- Current low-level representations enable the automated solution of low-level problems such as the efficient, collision-free point-to-point navigation in an environment but do not yet enable the execution of more complex instructions that would require an understanding of semantics and composition. Hierarchical hybrid graphical models would give machines a much more useful understanding of man-made environments and notably one that is presumably much closer to our own, human reasoning.
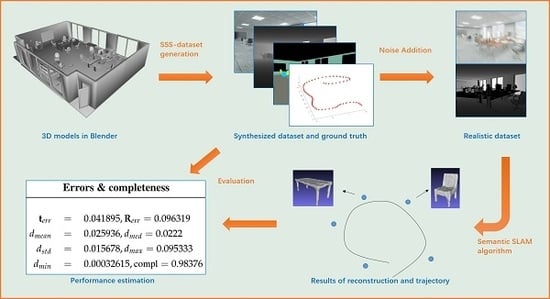
4. A New Benchmark
4.1. Review of Existing Datasets and Benchmarks
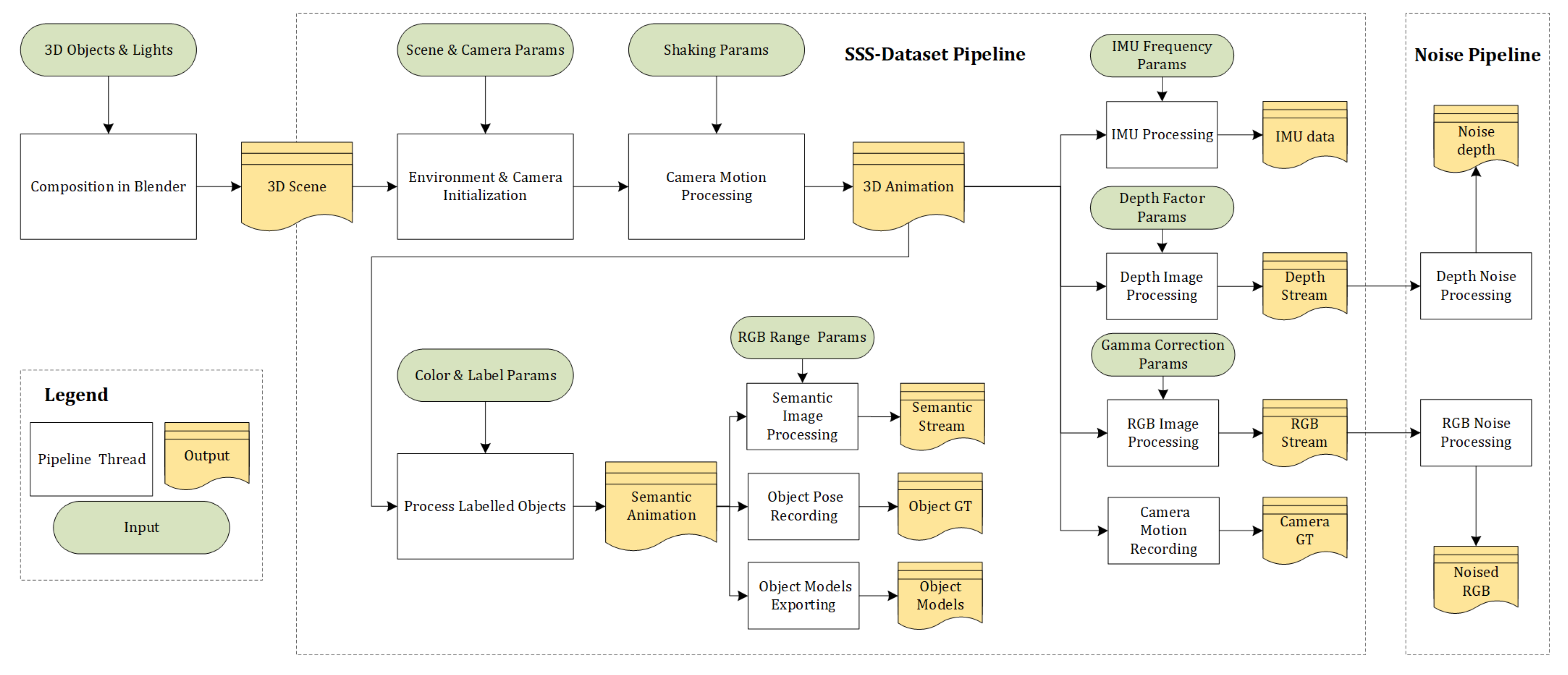
4.2. Dataset Creation
- Rendering engines model the imaging process according to some preset parameters and with a unified computer clock for each virtual sensor. This effectively saves the effort for intrinsic and extrinsic calibration of the multisensor system, including the tedious time stamp alignment between RGB, depth, and semantic images as well as the IMU readings.
- The convenience given by the software-based adjustment and replacement of objects and cameras vastly increases the efficiency of the entire dataset generation process.
- The diversity of the freely available, virtual 3D object models including the variability of their texture maps enables the automatic generation of a large number of highly variable datasets, which improves the generality of the subsequently developed Spatial AI, SLAM, and deep learning algorithms. If designed well, the dataset properties including the virtual multisensor setup, the sensor trajectory, the scene layout, and the objects’ composition, arrangement, and appearance can be steered at the hand of a simple input script.
4.2.1. RGB Map
4.2.2. Depth Map
4.2.3. Segmentation Map
4.2.4. Camera Trajectories
4.2.5. IMU Data
4.2.6. Semantic Object Data
4.3. Dataset Toolset
4.4. Evaluation Metrics
4.4.1. Evaluation of Sensor Poses
- Average Trajectory Error (ATE): The Average Trajectory Error directly measures the differences between corresponding points of the ground truth and the calculated trajectories. The evaluation is preceded by a spatial alignment of these two trajectories using a Procrustes alignment step. The latter identifies a Euclidean or similarity transformation that aligns the two trajectories as good as possible under an L2-error criterion. The residual errors are due to drift or gross errors in the sensor motion estimation, which the ATE characterises by either the mean, median, or standard deviation of the distance between the estimated and the ground truth position:where and are the trajectory alignment parameters recovered from the Procrustes alignment step.
- Relative Pose Error (RPE): The ATE is not very robust as a large number of absolute locations may easily be affected by only few gross estimation errors along the trajectory. The RPE in turn evaluates relative pose estimates between pairs of frames in the sequence. Particularly if the chosen pairs of frames are drawn from local windows, the RPE is a good measure of average local tracking accuracy:where represents the Riemannian logarithmic map.
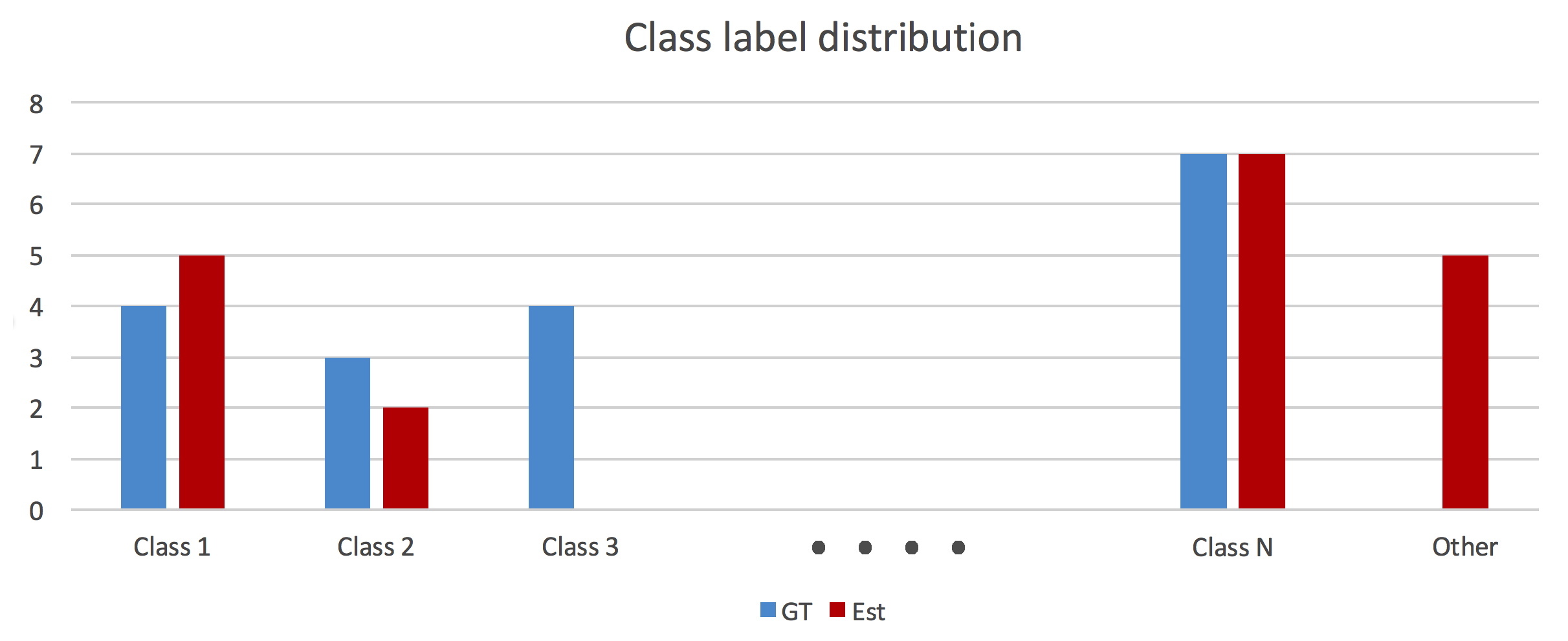
4.4.2. Scene Label Distribution
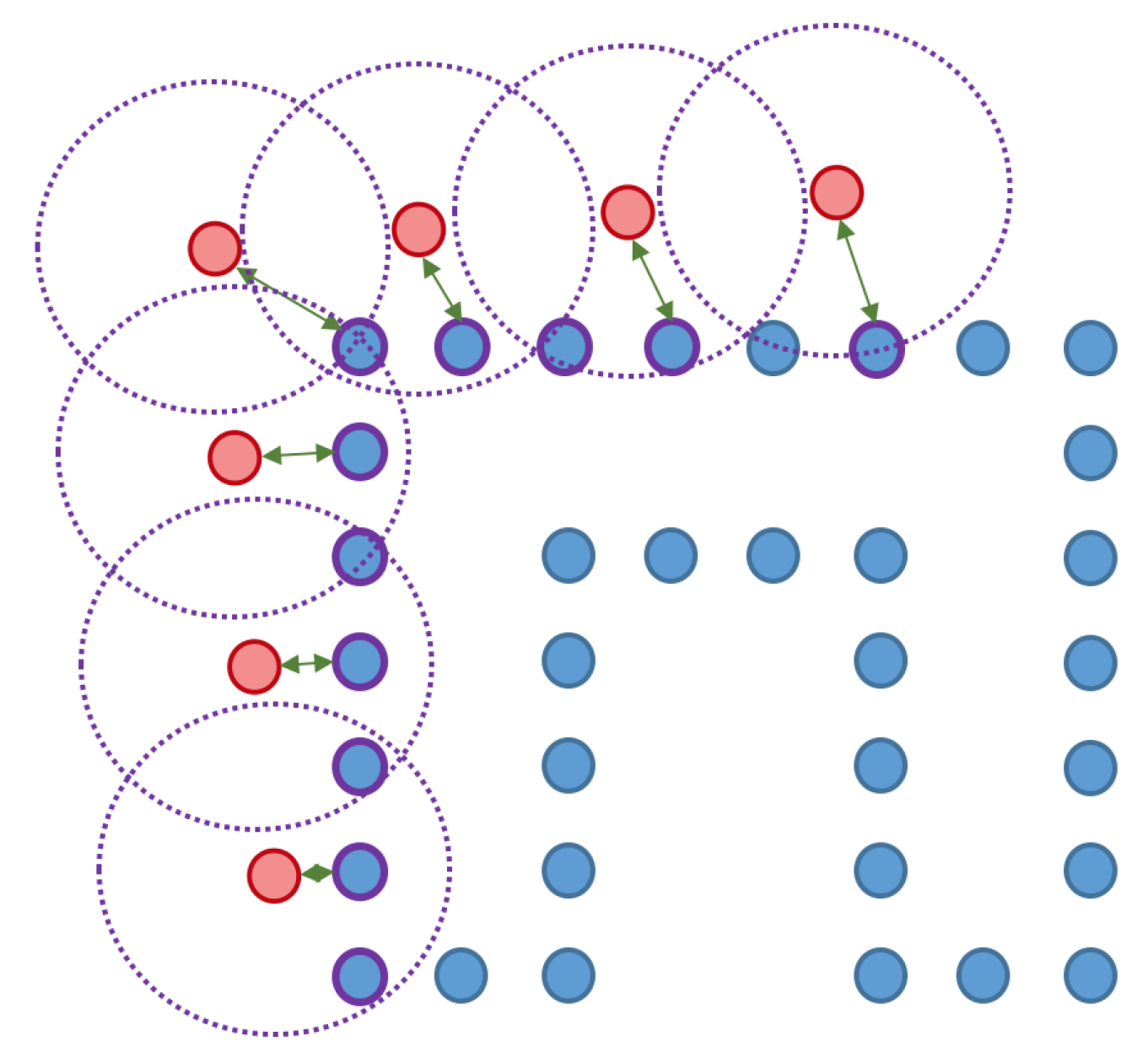
4.4.3. Object Class, Pose, Shape, and Completeness
- For each object, we pick the nearest and the second nearest object judged by their object centers.
- We first ensure that the distance to the best is below a certain threshold.
- We then ensure that the ratio between the distance to the second best and the distance to the best is below a certain threshold.
- First, we need to express the geometries in a common reference frame. We reuse the similarity transformation given by and identified by the prealignment step in the trajectory’s ATE evaluation and combine it with the individual object-to-world transformations to transfer all shape representations into a common global frame.
- The next step consists of expressing geometries in comparable representations. We choose point-clouds as there exist many algorithms and techniques to deal with point clouds. For the ground truth data, we generate point-clouds by simply using the vertices of each CAD mesh. However, in order to ensure sufficiently dense surface sampling, larger polygons are recursively subdivided into smaller subtriangles until the surface of each triangle is below a certain threshold. For the reconstructed model, we also transfer the employed representation into a point cloud:
- –
- If it is a point cloud already, we leave it unchanged.
- –
- For a polygon mesh, we simply employ the above-outlined strategy to ensure a sufficiently dense sampling of the surface.
- –
- For binary occupancy grids, we employ the marching cubes algorithm to transfer the representation into a mesh, and then employ the above-outlined technique to obtain a sufficiently dense point cloud.
- –
- For a signed distance field, we employ the Poisson surface interpolation method, by which we again obtain a mesh that is transformed as above.
- Once both the ground truth and the estimated object of each correspondence are expressed as point clouds in the same global reference frame, we proceed to their alignment. We choose the GoICP algorithm [73] for their alignment as it enables us to find the globally optimal alignment requiring neither a prior about the transformation nor correspondences between the two-point sets.
- Pose: The accuracy of the object pose is simply evaluated by the magnitude of the translation and the angle of rotation of the aligning transformation identified by GoICP [73].
- Shape: The accuracy of the shape is assessed by first applying the aligning transformation identified by GoICP and then taking the mean and median of the Euclidean distances between each point in the estimated point cloud and their nearest neighbour in the ground truth point set. Further shape accuracy measured such as the standard deviation and the maximum and minimum of the point-to-point distances are given as well.
- Completeness: We conclude by assessing the model completeness of each object. This is done by—again—first applying the aligning transformation to the estimated point set. We then mark each point in the ground truth point set as either observed or not. A point is observed if it is within a certain threshold distance of one of the inferred points. The final completeness measure is simply given asHowever, this measure obviously depends on a good choice of the threshold distance, which is why the completeness measure is evaluated for multiple such distances. This leads to a curve that expresses the quality of the shape as a function of this radius. The final measure to evaluate the shape completeness or quality is given by taking the area under this curve.
4.4.4. Background Model
4.4.5. Computational Aspects
5. Application to An Example Spatial AI System
5.1. Application to Kimera
5.2. Application to Deep-SLAM++
- We run an object detector over the left images of each estimated stereo frame and use both depth and semantic information in the bounding box to perform a segmentation of each observed object.
- For each detected object, we find all neighbouring frames in which the object is observable, detect redundancies, and initialise unique object representations with a list of frames in which each object is observable.
- We use Pix3D [60] to predict complete object geometries from the partial, image-based observations. For each object, the initialisation is performed by using the centre observing frame.
- We refine the latent code of each object shape representation by minimising depth errors in all observing frames. This finds a compromise between measurement fidelity and the application of prior shape knowledge.
- To conclude, the individual object shape optimisations are alternated by object pose optimisations in which the entire object shape is aligned with their respective observations.
6. Discussion
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Davison, A.J. FutureMapping: The Computational Structure of Spatial AI Systems. arXiv 2018, arXiv:1803.11288. [Google Scholar]
- Leonard, J.J.; Durrant-Whyte, H.F. Mobile robot localization by tracking geometric beacons. IEEE Trans. Robot. (T-RO) 1991, 7, 376–382. [Google Scholar] [CrossRef]
- Cadena, C.; Carlone, L.; Carrillo, H.; Latif, Y.; Scaramuzza, D.; Neira, J.; Reid, I.; Leonard, J.J. Past, Present, and Future of Simultaneous Localization and Mapping: Toward the Robust-Perception Age. IEEE Trans. Robot. (T-RO) 2016, 32, 1309–1332. [Google Scholar] [CrossRef]
- Davison, A.; Reid, D.; Molton, D.; Stasse, O. MonoSLAM: Real-Time Single Camera SLAM. IEEE Trans. Pattern Anal. Mach. Intell. (PAMI) 2007, 26, 1052–1067. [Google Scholar] [CrossRef]
- Klein, G.; Murray, D. Parallel Tracking and Mapping for Small AR Workspaces. In Proceedings of the International Symposium on Mixed and Augmented Reality (ISMAR), Naples, Italy, 12–13 April 2007. [Google Scholar]
- Mur-Artal, R.; Tardós, J.D. ORB-SLAM2: An Open-Source SLAM System for Monocular, Stereo, and RGB-D Cameras. IEEE Trans. Robot. (T-RO) 2017, 33, 1255–1262. [Google Scholar] [CrossRef]
- Triggs, B.; McLauchlan, P.; Hartley, R.; Fitzgibbon, A. Bundle Adjustment—A Modern Synthesis. In Proceedings of the International Workshop on Vision Algorithms: Theory and Practice (ICCV), Corfu, Greece, 21–22 September 1999; pp. 298–372. [Google Scholar]
- Agarwal, S.; Snavely, N.; Simon, I.; Seitz, S.; Szeliski, R. Building Rome in a day. In Proceedings of the International Conference on Computer Vision (ICCV), Kyoto, Japan, 27 September–4 October 2009; pp. 72–79. [Google Scholar]
- Schönberger, J.L.; Frahm, J.M. Structure-from-Motion Revisited. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), LasVegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Schönberger, J.L.; Zheng, E.; Pollefeys, M.; Frahm, J.M. Pixelwise View Selection for Unstructured Multi-View Stereo. In Proceedings of the European Conference on Computer Vision (ECCV), Amsterdam, The Netherlands, 11–14 October 2016. [Google Scholar]
- Qin, T.; Li, P.; Shen, S. VINS-Mono: A Robust and Versatile Monocular Visual-Inertial State Estimator. IEEE Trans. Robot. (T-RO) 2018, 34, 1004–1020. [Google Scholar] [CrossRef]
- Delaunoy, A.; Pollefeys, M. Photometric bundle adjustment for dense multi-view 3d modeling. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Columbus, OH, USA, 23–28 June 2014. [Google Scholar]
- Newcombe, R.A.; Lovegrove, S.J.; Davison, A.J. DTAM: Dense Tracking and Mapping in Real-Time. In Proceedings of the International Conference on Computer Vision (ICCV), Barcelona, Spain, 6–13 November 2011. [Google Scholar]
- Hornung, A.; Wurm, K.M.; Bennewitz, M.; Stachniss, C.; Burgard, W. OctoMap: An efficient probabilistic 3D mapping framework based on octrees. Auton. Robot. 2013, 34, 189–206. [Google Scholar] [CrossRef]
- Vespa, E.; Nikolov, N.; Grimm, M.; Nardi, L.; Kelly, P.H.J.; Leutenegger, S. Efficient Octree-Based Volumetric SLAM Supporting Signed-Distance and Occupancy Mapping. IEEE Robot. Autom. Lett. 2018, 3, 1144–1151. [Google Scholar] [CrossRef]
- Curless, B.; Levoy, M. A volumetric method for building complex models from range images. In Proceedings of the 23rd Annual Conference on Computer Graphics and Interactive Techniques, SIGGRAPH 1996, New Orleans, LA, USA, 4–9 August 1996. [Google Scholar]
- Newcombe, R.A.; Izadi, S.; Hilliges, O.; Molyneaux, D.; Kim, D.; Davison, A.J.; Kohli, P.; Shotton, J.; Hodges, S.; Fitzgibbon, A. KinectFusion: Real-time dense surface mapping and tracking. In Proceedings of the International Symposium on Mixed and Augmented Reality (ISMAR), Basel, Switzerland, 26–29 October 2011. [Google Scholar]
- Oleynikova, H.; Taylor, Z.; Fehr, M.; Siegwart, R.; Nieto, J. Voxblox: Incremental 3D Euclidean Signed Distance Fields for on-board MAV planning. In Proceedings of the IEEE/RSJ Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017. [Google Scholar]
- Millane, A.; Taylor, Z.; Oleynikova, H.; Nieto, J.; Siegwart, R.; Cadena, C. C-blox: A Scalable and Consistent TSDF-based Dense Mapping Approach. In Proceedings of the IEEE/RSJ Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018. [Google Scholar]
- Pumarola, A.; Vakhitov, A.; Agudo, A.; Sanfeliu, A.; Moreno-Noguer, F. PL-SLAM: Real-time monocular visual SLAM with points and lines. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017. [Google Scholar]
- Gomez-Ojeda, R.; Moreno, F.; Scaramuzza, D.; González Jiménez, J. PL-SLAM: A Stereo SLAM System through the Combination of Points and Line Segments. arXiv 2017, arXiv:1705.09479. [Google Scholar] [CrossRef]
- Whelan, T.; Leutenegger, S.; Salas-Moreno, R.; Glocker, B.; Davison, A. ElasticFusion: Dense SLAM without a pose graph. In Proceedings of the Robotics: Science and Systems (RSS), Rome, Italy, 13–17 July 2015. [Google Scholar]
- Redmon, J.; Farhadi, A. YOLO9000: Better, Faster, Stronger. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- He, K.; Gkioxari, G.; Dollár, P.; Girshick, R. MASK R-CNN. In Proceedings of the International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017. [Google Scholar]
- Chen, K.; Pang, J.; Wang, J.; Xiong, Y.; Li, X.; Sun, A.; Feng, W.; Liu, Z.; Shi, J.; Ouyang, W.; et al. Hybrid task cascade for isntance segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019. [Google Scholar]
- Shi, S.; Wang, X.; Li, H. PointRCNN: 3D Object Proposal Generation and Detection from Point Cloud. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019. [Google Scholar]
- Davison, A.J.; Ortiz, J. FutureMapping 2: Gaussian Belief Propagation for Spatial AI. arXiv 2019, arXiv:1910.14139. [Google Scholar]
- Choudhary, S.; Trevor, A.J.B.; Christensen, H.I.; Dellaert, F. SLAM with object discovery, modeling and mapping. In Proceedings of the IEEE/RSJ Conference on Intelligent Robots and Systems (IROS), Chicago, IL, USA, 14–18 September 2014. [Google Scholar]
- Gálvez-López, D.; Salas, M.; Tardós, J.D.; Montiel, J.M.M. Real-time monocular object SLAM. Robot. Auton. Syst. 2016, 75, 435–449. [Google Scholar] [CrossRef]
- Sünderhauf, N.; Pham, T.; Latif, Y.; Milford, M.; Reid, I. Meaningful maps with object-oriented semantic mapping. In Proceedings of the IEEE/RSJ Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017. [Google Scholar]
- Nakajima, Y.; Saito, H. Efficient object-oriented semantic mapping with object detector. IEEE Access 2018, 7, 3206–3213. [Google Scholar] [CrossRef]
- Stückler, J.; Waldvogel, B.; Schulz, H.; Behnke, S. Dense real-time mapping of object-class semantics from RGB-D video. J. Real-Time Image Process. 2015, 15, 599–609. [Google Scholar] [CrossRef]
- McCormac, J.; Handa, A.; Davison, A.J.; Leutenegger, S. SemanticFusion: Dense 3D Semantic Mapping with Convolutional Neural Networks. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017. [Google Scholar]
- McCormac, J.; Clark, R.; Bloesch, M.; Davison, A.J.; Leutenegger, S. Fusion++: Volumetric object-level SLAM. In Proceedings of the International Conference on 3D Vision (3DV), Verona, Italy, 5–8 September 2018. [Google Scholar]
- Pham, Q.H.; Hua, B.S.; Nguyen, D.T.; Yeung, S.K. Real-time Progressive 3D Semantic Segmentation for Indoor Scenes. In Proceedings of the IEEE Winter Conference on Applications in Computer Vision (WACV), Waikoloa Village, HI, USA, 7–11 January 2019. [Google Scholar]
- Grinvald, M.; Furrer, F.; Novkovic, T.; Chung, J.J.; Cadena, C.; Siegwart, R.; Nieto, J. Volumetric Instance-Aware Semantic Mapping and 3D Object Discovery. IEEE Robot. Autom. Lett. 2019, 3, 3037–3044. [Google Scholar] [CrossRef]
- Rosinol, A.; Abate, M.; Chang, Y.; Carlone, L. Kimera: An Open-Source Library for Real-Time Metric-Semantic Localization and Mapping. arXiv 2019, arXiv:1910.02490. [Google Scholar]
- Salas-Moreno, R.F.; Newcombe, R.A.; Strasdat, H.; Kelly, P.H.J.; Davison, A.J. SLAM++: Simultaneous Localisation and Mapping at the Level of Objects. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Portland, OR, USA, 23–28 June 2013. [Google Scholar]
- Ulusoy, A.O.; Black, M.J.; Geiger, A. Semantic Multi-view Stereo: Jointly Estimating Objects and Voxels. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Gunther, M.; Wiemann, T.; Albrecht, S.; Hertzberg, J. Model-based furniture recognition for building semantic object maps. Artif. Intell. 2017, 247, 336–351. [Google Scholar] [CrossRef]
- Häne, C.; Zach, C.; Cohen, A.; Pollefeys, M. Dense semantic 3D reconstruction. IEEE Trans. Pattern Anal. Mach. Intell. (PAMI) 2016, 39, 1730–1743. [Google Scholar] [CrossRef]
- Xu, K.; Kim, V.G.; Huang, Q.; Kalogerakis, E. Data-driven shape analysis and processing. Comput. Graph. Forum 2017, 36, 101–132. [Google Scholar] [CrossRef]
- Güney, F.; Geiger, A. Displets: Resolving Stereo Ambiguities using Object Knowledge. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015. [Google Scholar]
- Chhaya, F.; Reddy, D.; Upadhyay, S.; Chari, V.; Zia, M.Z.; Krishna, K.M. Monocular reconstruction of vehicles: Combining SLAM with shape priors. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016. [Google Scholar]
- Hosseinzadeh, M.; Latif, Y.; Pham, T.; Sünderhauf, N.; Reid, I. Structure Aware SLAM using Quadrics and Planes. In Proceedings of the Asian Conference on Computer Vision (ACCV), Taipei, Taiwan, 20–24 November 2016. [Google Scholar]
- Gay, P.; Bansal, V.; Rubino, C.; Del Bue, A. Probabilistic Structure from Motion with Objects (PSfMO). In Proceedings of the International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017. [Google Scholar]
- Dame, A.; Prisacariu, V.A.; Ren, C.Y.; Reid, I. Dense Reconstruction using 3D object shape priors. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Portland, OR, USA, 23–28 June 2013. [Google Scholar]
- Engelmann, F.; Stückler, J.; Leibe, B. Joint object pose estimation and shape reconstruction in urban street scenes using 3D shape priors. In Proceedings of the German Conference on Pattern Recognition (GCPR), Hannover, Germany, 12–15 September 2016. [Google Scholar]
- Alismail, H.; Browning, B.; Lucey, S. Photometric bundle adjustment for vision-based SLAM. In Proceedings of the Asian Conference on Computer Vision (ACCV), Taipei, Taiwan, 20–24 November 2016. [Google Scholar]
- Zhu, R.; Lucey, S. Rethinking Reprojection: Closing the Loop for Pose-aware Shape Reconstruction from a Single Image. In Proceedings of the International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017. [Google Scholar]
- Hu, L.; Xu, W.; Huang, K.; Kneip, L. Deep-SLAM++: Object-level RGBD SLAM based on class-specific deep shape priors. arXiv 2019, arXiv:1907.09691. [Google Scholar]
- Bloesch, M.; Czarnowski, J.; Clark, R.; Leutenegger, S.; Davison, A.J. CodeSLAM - learning a compact, optimisable representation for dense visual SLAM. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–22 June 2018. [Google Scholar]
- Zhi, S.; Bloesch, M.; Leutenegger, S.; Davison, A.J. SceneCode: Monocular Dense Semantic Reconstruction using Learned Encoded Scene Representations. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019. [Google Scholar]
- Gupta, S.; Arbeláez, P.; Girshick, R.; Malik, J. Aligning 3D Models to RGB-D Images of Cluttered Scenes. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015. [Google Scholar]
- Li, Y.; Dai, A.; Guibas, L.; Niener, M. Database-Assisted Object Retrieval for Real-Time 3D Reconstruction. Comput. Graph. Forum 2015, 34, 435–446. [Google Scholar] [CrossRef]
- Chen, K.; Lai, Y.K.; Wu, Y.X.; Martin, R.; Hu, S.M. Automatic Semantic Modeling of Indoor Scenes from Low-quality RGB-D Data using Contextual Information. ACM Trans. Graph. 2014, 33, 1–12. [Google Scholar] [CrossRef]
- Huang, S.; Qi, S.; Zhu, Y.; Xiao, Y.; Xu, Y.; Zhu, S.C. Holistic 3D scene parsing and reconstruction from a single rgb image. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018. [Google Scholar]
- Grabner, A.; Roth, P.M.; Lepetit, V. Location Field Descriptors: Single Image 3D Model Retrieval in the Wild. In Proceedings of the International Conference on 3D Vision (3DV), Quebec City, QC, Canada, 16–19 September 2019. [Google Scholar]
- Dellaert, F.; Kaess, M. Square Root SAM: Simultaneous Localization and Mapping via Square Root Information Smoothing. Int. J. Robot. Res. (IJRR) 2016, 25, 1181–1203. [Google Scholar] [CrossRef]
- Sun, X.; Wu, J.; Zhang, X.; Zhang, Z.; Zhang, C.; Xue, T.; Tenenbaum, J.B.; Freeman, W.T. Pix3d: Dataset and methods for single-image 3d shape modeling. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–22 June 2018. [Google Scholar]
- Sturm, J.; Engelhard, N.; Endres, F.; Burgard, W.; Cremers, D. A benchmark for the evaluation of RGB-D SLAM systems. In Proceedings of the IEEE/RSJ Conference on Intelligent Robots and Systems (IROS), Algarve, Portugal, 7–12 October 2012; pp. 573–580. [Google Scholar]
- Alhaija, H.; Mustikovela, S.; Mescheder, L.; Geiger, A.; Rother, C. Augmented Reality Meets Computer Vision: Efficient Data Generation for Urban Driving Scenes. Int. J. Comput. Vis. (IJCV) 2018, 12, 961–972. [Google Scholar] [CrossRef]
- Lin, T.; Maire, M.; Belongie, S.J.; Bourdev, L.D.; Girshick, R.B.; Hays, J.; Perona, P.; Ramanan, D.; Dollár, P.; Zitnick, C.L. Microsoft COCO: Common Objects in Context. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014. [Google Scholar]
- Silberman, N.; Hoiem, D.; Kohli, P.; Fergus, R. Indoor Segmentation and Support Inference from RGBD Images. In Proceedings of the European Conference on Computer Vision, Florence, Italy, 7–13 October 2012. [Google Scholar]
- Zhou, B.; Zhao, H.; Puig, X.; Fidler, S.; Barriuso, A.; Torralba, A. Semantic understanding of scenes through the ade20k dataset. arXiv 2016, arXiv:1608.05442. [Google Scholar] [CrossRef]
- Zhou, B.; Zhao, H.; Puig, X.; Fidler, S.; Barriuso, A.; Torralba, A. Scene Parsing through ADE20K Dataset. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Xiao, J.; Owens, A.; Torralba, A. SUN3D: A Database of Big Spaces Reconstructed using SfM and Object Labels. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Sydney, NSW, Australia, 1–8 December 2013. [Google Scholar]
- Dai, A.; Chang, A.X.; Savva, M.; Halber, M.; Funkhouser, T.; Nießner, M. ScanNet: Richly-annotated 3D Reconstructions of Indoor Scenes. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Chang, A.X.; Funkhouser, T.; Guibas, L.; Hanrahan, P.; Huang, Q.; Li, Z.; Savarese, S.; Savva, M.; Song, S.; Su, H.; et al. ShapeNet: An Information-Rich 3D Model Repository. arXiv 2015, arXiv:1512.03012. [Google Scholar]
- Handa, A.; Whelan, T.; McDonald, J.B.; Davison, A.J. A Benchmark for RGB-D Visual Odometry, 3D Reconstruction and SLAM. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014. [Google Scholar]
- Grossberg, M.D.; Nayar, S.K. Determining the camera response from images: What is knowable? IEEE Trans. Pattern Anal. Mach. Intell. 2003, 25, 1455–1467. [Google Scholar] [CrossRef]
- Iversen, T.M.; Kraft, D. Generation of synthetic Kinect depth images based on empirical noise model. Electron. Lett. 2017, 53, 856–858. [Google Scholar] [CrossRef]
- Yang, J.; Li, H.; Campbell, D.; Jia, Y. Go-ICP: A globally optimal solution to 3D ICP point-set registration. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 38, 2241–2254. [Google Scholar] [CrossRef]







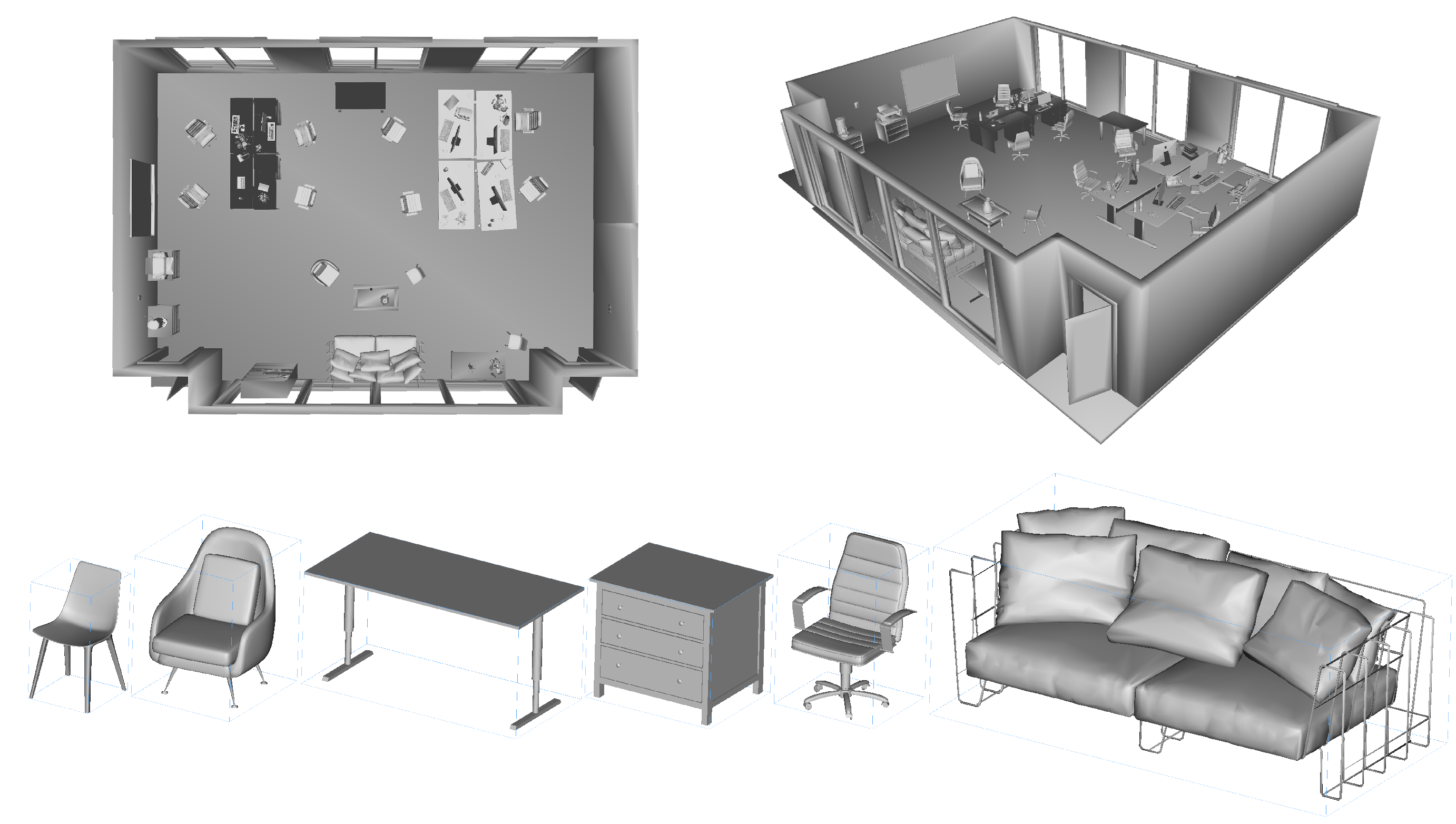
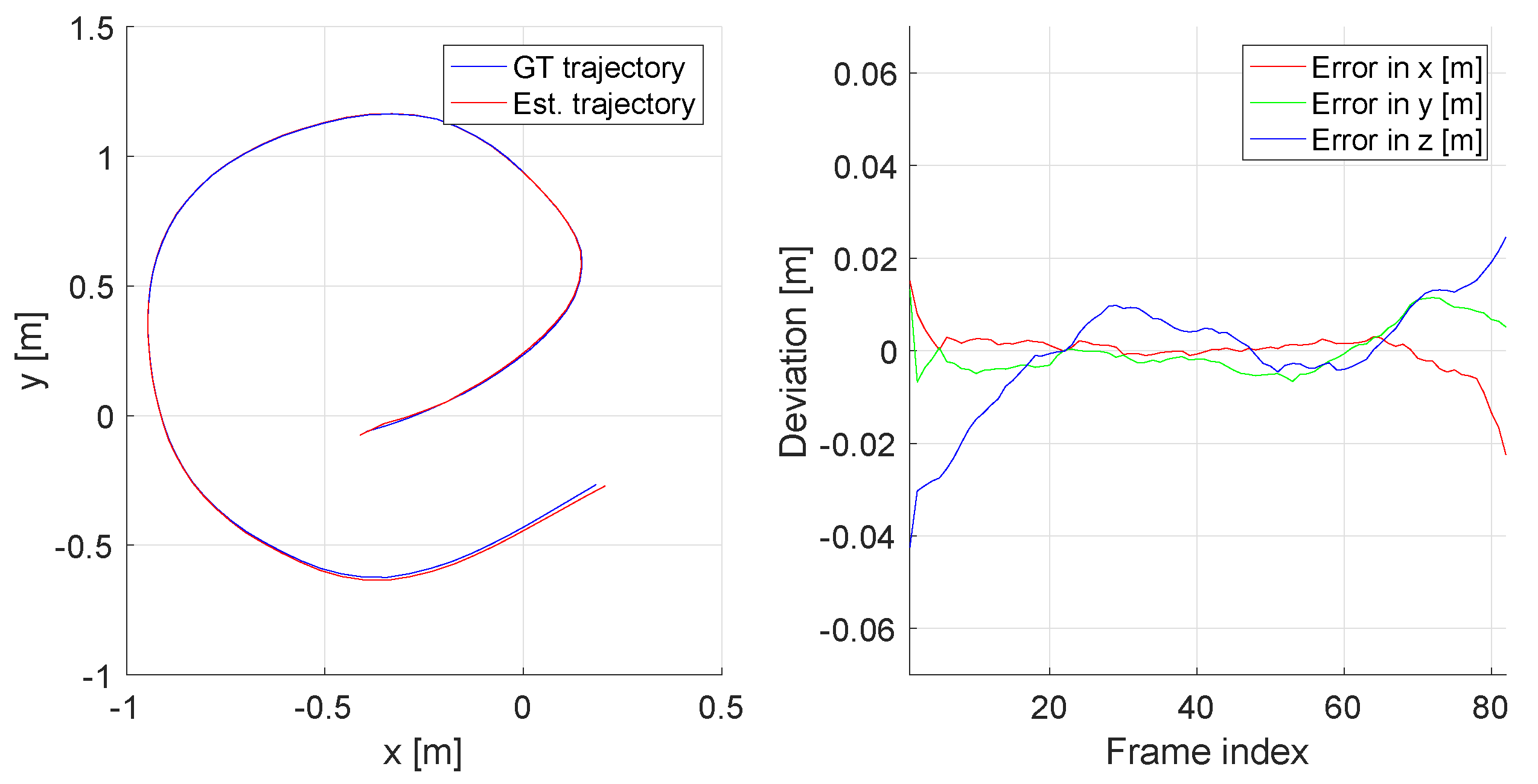
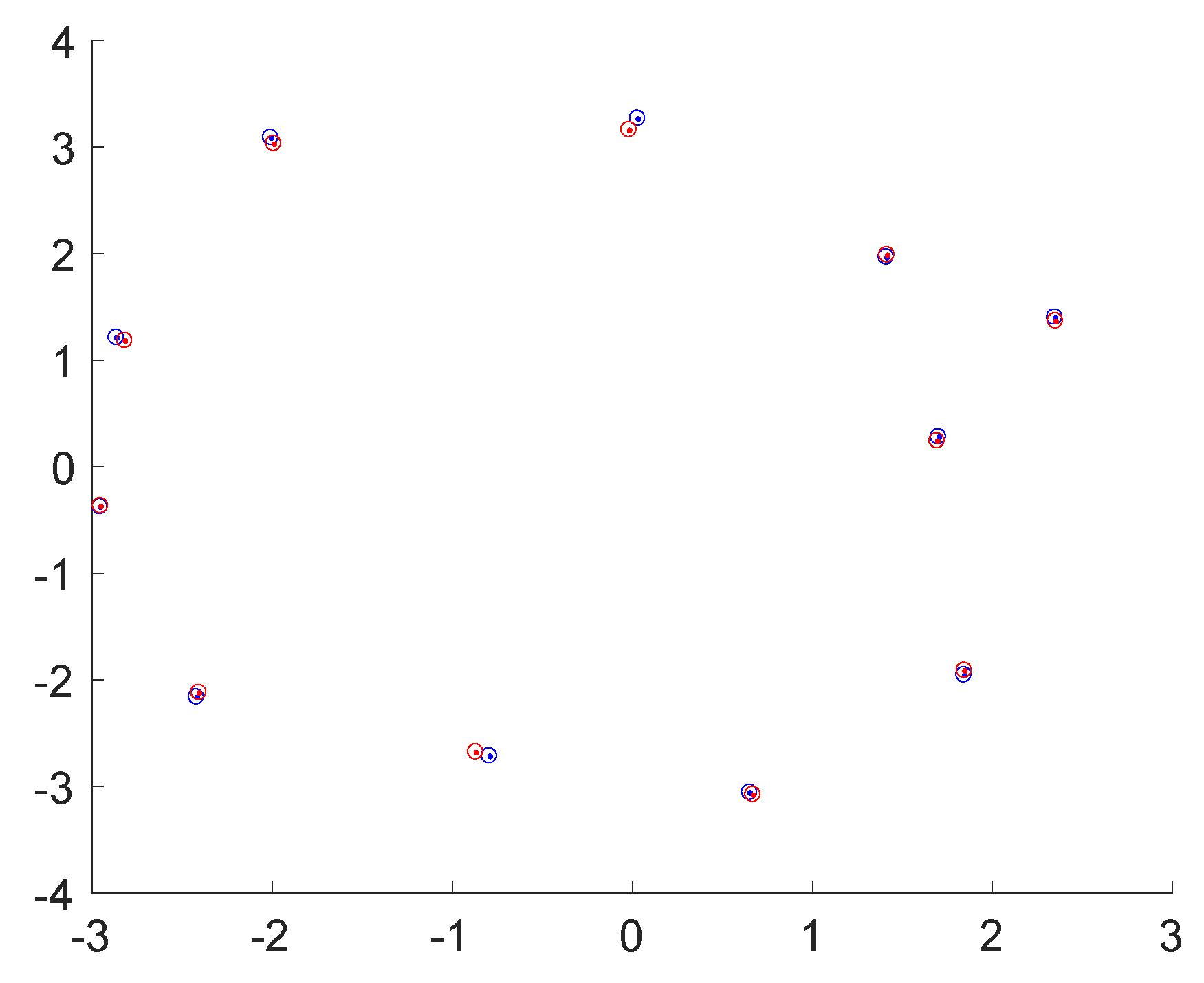

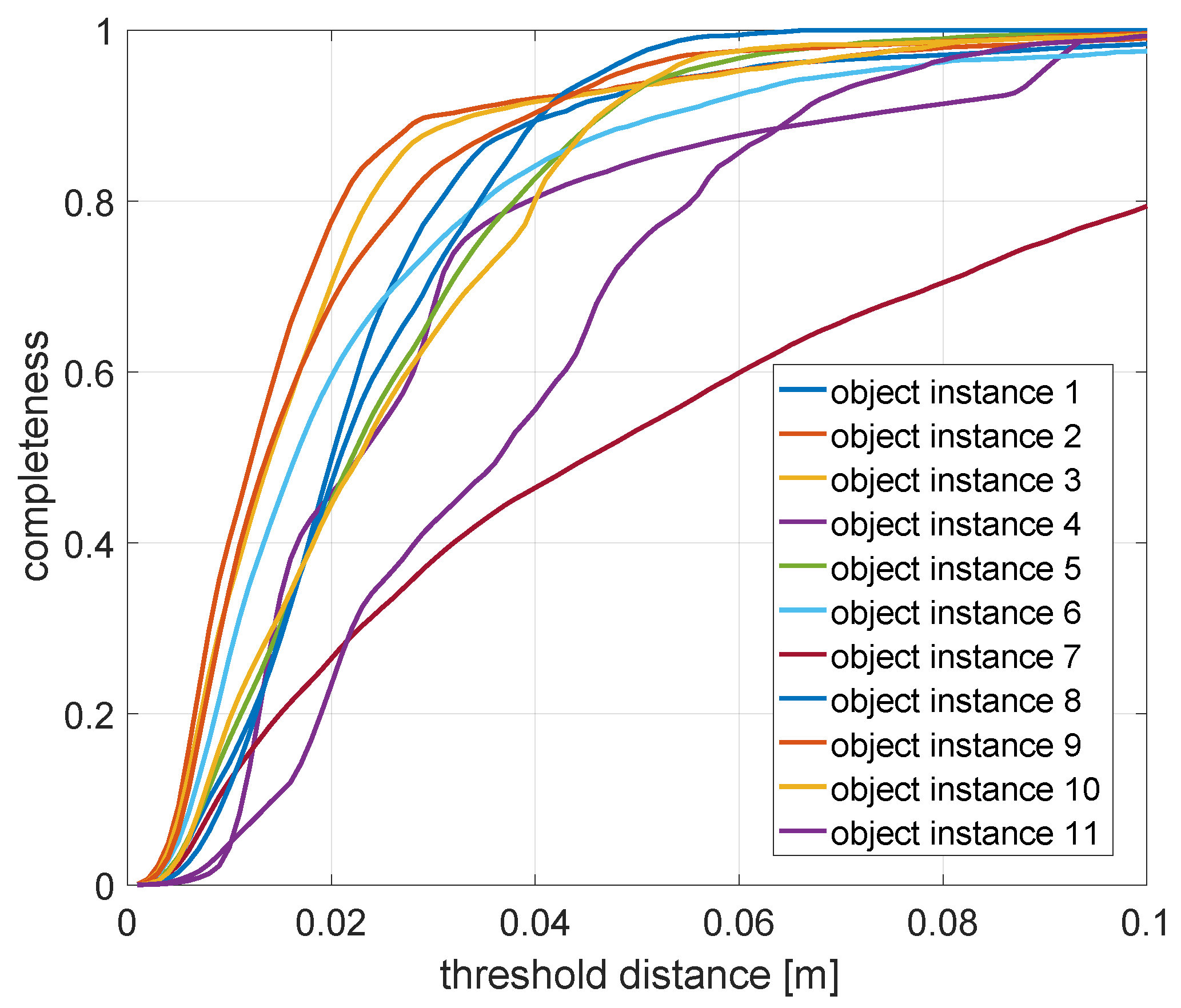
| Datasets | Duration [s] | Semantic Objects | Properties |
|---|---|---|---|
| Single Room Datasets | |||
| rm1 | 70 | 2C1, 1C2, 1T1, 1T2, 1S1, 1TV1 | 6.4 × 6.5 × 3.1 m slight shaking slight occlusion |
| rm2 | 60 | 1C1, 2C2, 2C3, 1C4, 1T1, 1T2 | 8.0 × 6.0 × 3.2 m heavy shaking slight occlusion |
| rm3 | 40 | 8C1, 2C2, 1C3, 1T1, 1T2, 4T3 2T4, 1T5, 4T6, 1S1 | 10.0 × 14.0 × 2.8 m slight shaking heavy occlusion |
| rm4 | 16.7 | 3C1, 2C2, 2C3, 2T1, 1T2, 1T3 | 12.1 × 12.0 × 3.2 m no shaking no occlusion |
| Multiroom Dataset | |||
| rm5 | 60 | 2C1, 1C2, 2C3, 1C4, 2C5, 1C6 1T1, 1T2, 1T3, 1T4, 1S1, 1TV1 | combo of rm1 and rm2 slight shaking slight occlusion |
| SSIM | MSE | PSNR | SSIM | MSE | PSNR | |
|---|---|---|---|---|---|---|
| rm1 | 0.9514 | 71.3171 | 29.5989 | 0.9530 | 23.5196 | 34.4165 |
| rm2 | 0.8980 | 720.4544 | 19.5547 | 0.8990 | 625.2354 | 20.1704 |
| rm3 | 0.9258 | 436.6094 | 21.7299 | 0.8677 | 167.2929 | 19.2812 |
| rm4 | 0.9031 | 327.233 | 22.4227 | 0.9593 | 177.5349 | 25.6380 |
| rm5 | 0.9191 | 230.0157 | 24.5132 | 0.9264 | 35.2029 | 32.6650 |
| RGB | Depth | Seg | |
|---|---|---|---|
| rm1 | 5.07 | 4.75 | 2.31 |
| rm2 | 5.07 | 1.79 | 1.15 |
| rm3 | 10.17 | 8.89 | 4.72 |
| rm4 | 7.87 | 7.19 | 1.29 |
| rm5 | 6.57 | 6.54 | 2.89 |
| RGB noise | 5.02 | Depth noise | 16.32 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| rmse | 0.014061 | std.-dev. | 0.0088741 |
| mean error | 0.010951 | min error | 0.00018726 |
| median error | 0.0071863 | max error | 0.046873 |
| Instance | GT Model | Estimated Model | Alignment | Errors & Completeness |
|---|---|---|---|---|
| 1 GT: chair1 Est: chair |  |  |  | |
| 2 GT: chair1 Est: chair |  |  |  | |
| 3 GT: chair1 Est: chair |  |  |  | |
| 4 GT: table1 Est: table |  |  |  | |
| 5 GT: chair2 Est: chair |  |  |  | |
| 6 GT: chair3 Est: chair |  |  |  | |
| 7 GT: table3 Est: table |  |  |  | |
| 8 GT: table1 Est: table |  |  |  | |
| 9 GT: chair2 Est: chair |  |  | 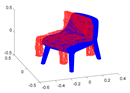 | |
| 10 GT: chair3 Est: chair |  |  |  | |
| 11 GT: table2 Est: table |  |  |  |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, Y.; Hu, L.; Kneip, L. Representations and Benchmarking of Modern Visual SLAM Systems. Sensors 2020, 20, 2572. https://doi.org/10.3390/s20092572
Cao Y, Hu L, Kneip L. Representations and Benchmarking of Modern Visual SLAM Systems. Sensors. 2020; 20(9):2572. https://doi.org/10.3390/s20092572
Chicago/Turabian StyleCao, Yuchen, Lan Hu, and Laurent Kneip. 2020. "Representations and Benchmarking of Modern Visual SLAM Systems" Sensors 20, no. 9: 2572. https://doi.org/10.3390/s20092572
APA StyleCao, Y., Hu, L., & Kneip, L. (2020). Representations and Benchmarking of Modern Visual SLAM Systems. Sensors, 20(9), 2572. https://doi.org/10.3390/s20092572