Research on Visualization and Error Compensation of Demolition Robot Attachment Changing
Abstract
1. Introduction
- The forward kinematics model of the BROKK 160 (BROKK MACHINES CO. LTD., Beijing, China) robot was established through measurement and calibration, and then error analysis of the motion trajectory of the robot’s end-effector was carried out. The results show that the large-sized robot driven by a hydraulic system could not achieve high-precision motion control through the conventional off-line calibration method.
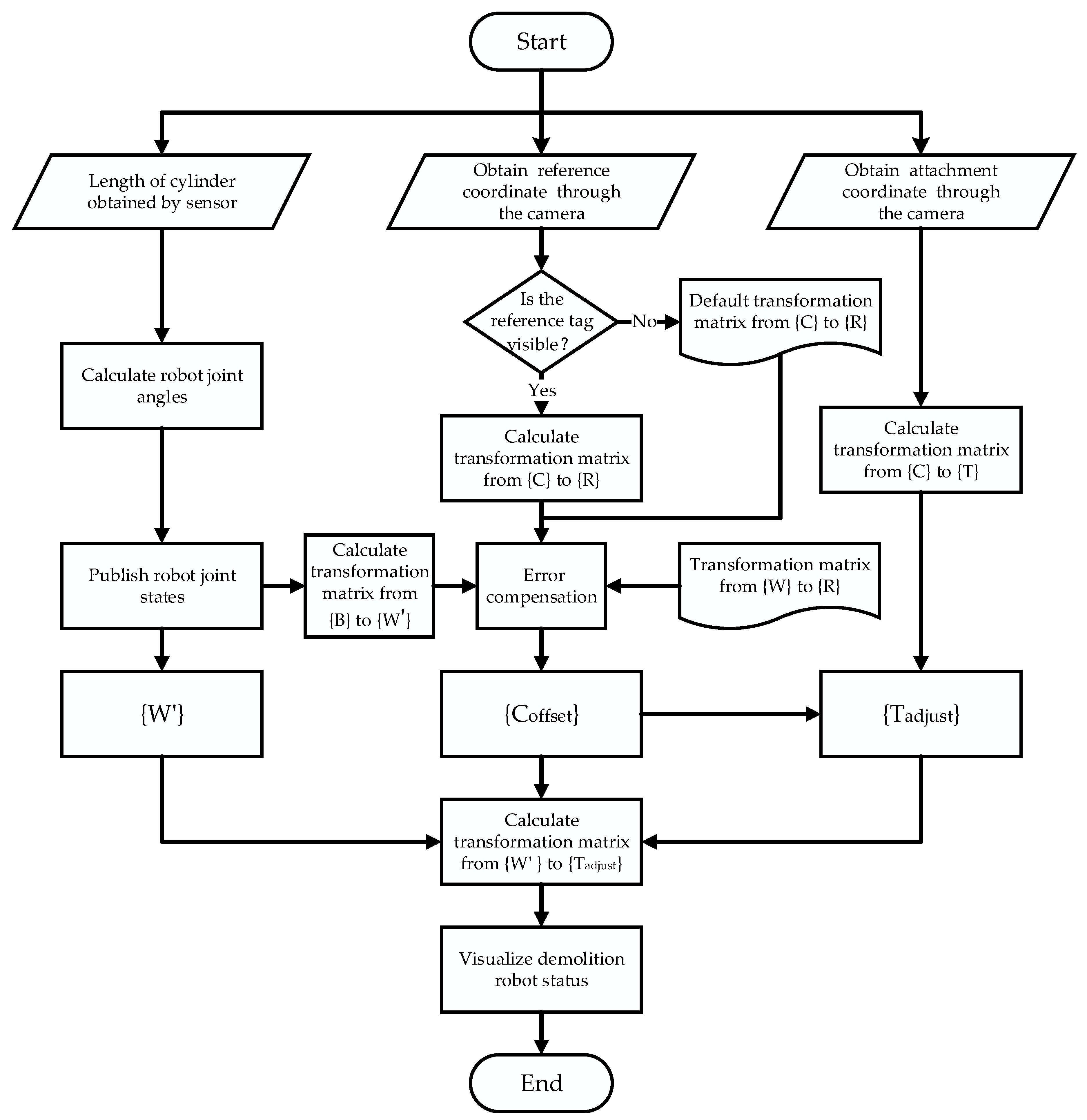
- Based on this problem, a method of real-time error compensation for the attachment changing of large-size demolition robots was proposed. By introducing a reference coordinate system that was fixed near the dock spot of the robot quick-hitch equipment, this method was able to complete the coordinate transformation from the dock spot of the robot quick-hitch equipment to the dock spot of the attachment, thereby achieving the error compensation.
- Both indoor and outdoor experiments were carried out to verify this method. It was shown that the error compensation method proposed in this paper could reduce the level of error in the attachment changing process from the centimeter to the millimeter scale, thereby meeting the accuracy requirements.
2. Kinematics
3. Error Estimation
4. Improvement
4.1. Reference Coordinates Frame
4.2. Offsetting the Camera Coordinate Frame {Coffset}
4.3. Error Compensation Algorithm
5. Experimental Research
5.1. Experimental Scene 1: Contrasting Experiment of Error Compensation
5.1.1. Initialization
5.1.2. Preparation
5.1.3. The Alignment Range
5.1.4. The Angle Alignment and Operation Stages
5.1.5. Discussion
- In a safe scenario, the operator can observe the movement trajectory of the quick-hitch equipment from a close distance and multiple angles during the whole procedure until the task of demolition robot attachment changing can be finished.
- In a hazardous scenario, the operator remote attachment changing needs to be done through cameras, the third stage cannot be completed.
- In a hazardous scenario, the operator remote attachment changing is done through a visualization system. During the fourth and fifth stages, {W} and {T} are aligned and the relative distance between {W} and {T} should be 0. In this experiment, the distance without the error compensation from {W} to {T} increased along with the upward movement of {W}, with an average value of 26.68 mm, a minimum value of 16.65 mm, and a maximum value of 39.2 mm. The third stage could not be completed.
- The mean value of the distance with error compensation from {W} to {T} was 2.89 mm, the minimum value was 1.57 mm, and the maximum value was 4.53 mm. The task of the demolition robot attachment changing could be finished.
5.2. Experiment Scene 2: Attachment Remote Changing Indoors
5.3. Experiment Scene 3: Attachment Remote Changing Outdoors
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bogue, R. Robots in the nuclear industry: A review of technologies and applications. Ind. Robot Int. J. 2011, 38, 113–118. [Google Scholar] [CrossRef]
- Delmerico, J.; Mintchev, S.; Giusti, A.; Gromov, B.; Melo, K.; Horvat, T.; Cadena, C.; Hutter, M.; Ijspeert, A.; Floreano, D.; et al. The current state and future outlook of rescue robotics. J. Field Robot. 2019, 36, 1171–1191. [Google Scholar] [CrossRef]
- Kawatsuma, S.; Mimura, R.; Asama, H. Unitization for portability of emergency response surveillance robot system: Experiences and lessons learned from the deployment of the JAEA-3 emergency response robot at the Fukushima Daiichi Nuclear Power Plants. ROBOMECH J. 2017, 4. [Google Scholar] [CrossRef]
- Buckingham, R. Nuclear snake-arm robots. Ind. Robot Int. J. 2012, 39, 6–11. [Google Scholar] [CrossRef]
- Burrell, T.; Montazeri, A.; Monk, S.; Taylor, C.J. Feedback Control—Based Inverse Kinematics Solvers for a Nuclear Decommissioning Robot. IFAC Pap. 2016, 49, 177–184. [Google Scholar] [CrossRef]
- Brokk Global. Available online: https://www.brokk.com (accessed on 10 January 2020).
- Takeyasu, M.; Nakano, M.; Fujita, H.; Nakada, A.; Watanabe, H.; Sumiya, S.; Furuta, S. Results of environmental radiation monitoring at the Nuclear Fuel Cycle Engineering Laboratories, JAEA, following the Fukushima Daiichi Nuclear Power Plant accident. J. Nucl. Sci. Technol. 2012, 49, 281–286. [Google Scholar] [CrossRef]
- Yoshida, T.; Nagatani, K.; Tadokoro, S.; Nishimura, T.; Koyanagi, E. Improvements to the Rescue Robot Quince Toward Future Indoor Surveillance Missions in the Fukushima Daiichi Nuclear Power Plant. In Field and Service Robotics: Results of the 8th International Conference; Yoshida, K., Tadokoro, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 19–32. [Google Scholar]
- Denavit, J.; Hartenberg, R.S. Notation for lower-pair mechanisms based on matrices. J. Appl. Mech. 1995, 22, 215–221. [Google Scholar]
- Assenov, E.; Bosilkov, E.; Dimitrov, R.; Damianov, T. Kinematics and dynamics of working mechanism of hydraulic excavator. Annu. Univ. Min. Geol. 2003, 46, 47–49. [Google Scholar]
- Fujino, K.; Moteki, M.; Nishiyama, A.; Yuta, S. Towards Autonomous Excavation by Hydraulic Excavator—Measurement and Consideration on Bucket Posture and Body Stress in Digging Works. In Proceedings of the 2013 IEEE Workshop on Advanced Robotics and Its Social Impacts, Tokyo, Japan, 7–9 November 2013; pp. 231–236. [Google Scholar]
- Chang, P.H.; Lee, S.-J. A straight-line motion tracking control of hydraulic excavator system. Mechatronics 2002, 12, 119–138. [Google Scholar] [CrossRef]
- Yamamoto, H.; Moteki, M.; Shao, H.; Ootuki, K.; Yanagisawa, Y.; Sakaida, Y.; Nozue, A.; Yamaguchi, T.; Yuta, S. Development of the autonomous hydraulic excavator prototype using 3-D information for motion planning and control. Trans. Soc. Instrum. Control Eng. 2010, 48. [Google Scholar] [CrossRef]
- Rezazadeh Azar, E.; McCabe, B. Part based model and spatial–temporal reasoning to recognize hydraulic excavators in construction images and videos. Autom. Constr. 2012, 24, 194–202. [Google Scholar] [CrossRef]
- Wu, L.; Ren, H. Finding the Kinematic Base Frame of a Robot by Hand-Eye Calibration Using 3D Position Data. IEEE Trans. Autom. Sci. Eng. 2017, 14, 314–324. [Google Scholar] [CrossRef]
- John, C. Introduction to Robotics: Mechanics and Control, 4th ed.; Pearson: London, UK, 2017. [Google Scholar]
- Peter, C. Robotics, Vision & Control; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Olson, E. AprilTag: A Robust and Flexible Visual Fiducial System. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011. [Google Scholar]
- Wang, J.; Olson, E. AprilTag 2: Efficient and Robust Fiducial Detection. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems, Daejeon, Korea, 9–14 October 2016. [Google Scholar]
- Maximilian, K.; Acshi, H.; Edwin, O. Flexible Layouts for Fiducial Tags. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 25–29 October 2020. [Google Scholar]
- Brommer, C.; Malyuta, D.; Hentzen, D.; Brockers, R. Long-Duration Autonomy for Small Rotorcraft UAS Including Recharging. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems, Madrid, Spain, 1–5 October 2018; pp. 7252–7258. [Google Scholar]




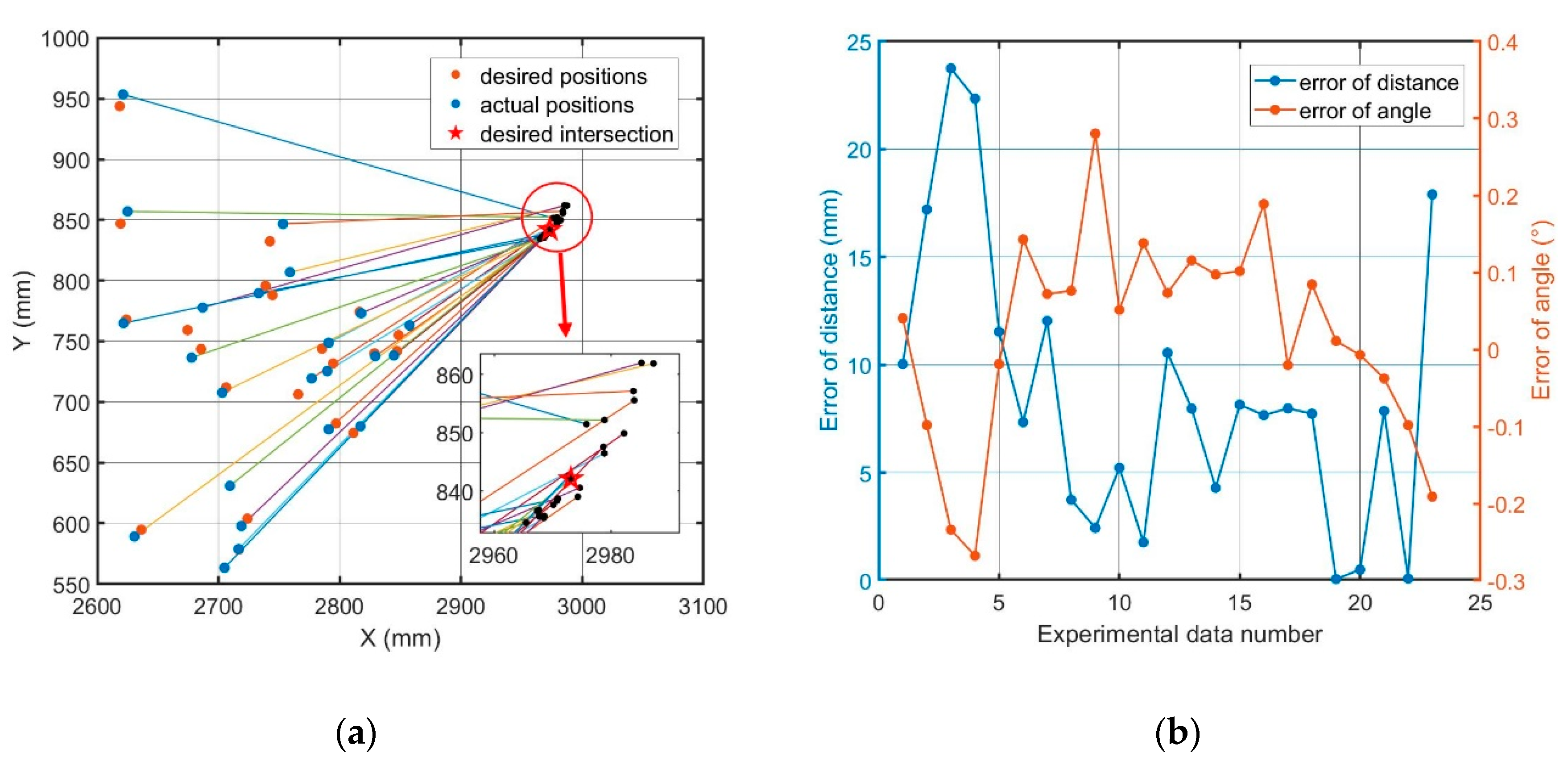






| θ1 | θ2 | θ3 | θ4 | θ5 | Angle | Distance | Angle Error | Distance Error |
|---|---|---|---|---|---|---|---|---|
| 0° | 102.94° | −92.04° | −46.13° | 19.18° | −16.0° | 369 mm | 0.04° | 10.0 mm |
| 0° | 102.94° | −108.86° | −30.09° | 69.31° | 33.2° | 248 mm | −0.10° | 17.2 mm |
| 0° | 107.47° | −110.56° | −23.92° | 40.54° | 13.3° | 235 mm | −0.23° | 23.8 mm |
| 0° | 111.16° | −112.94° | −28.94° | 46.49° | 15.5° | 310 mm | −0.27° | 22.3 mm |
| 0° | 105.87° | −98.57° | −45.74° | 37.67° | −0.8° | 354 mm | −0.02° | 11.5 mm |
| 0° | 94.88° | −94.49° | −45.74° | 72.82° | 27.6° | 212 mm | 0.14° | 7.3 mm |
| 0° | 94.85° | −97.91° | −36.99° | 74.88° | 34.9° | 152 mm | 0.07° | 12.0 mm |
| 0° | 91.12° | −81.95° | −67.79° | 70.54° | 12.0° | 357 mm | 0.08° | 3.7 mm |
| 0° | 84.47° | −81.95° | −57.33° | 89.73° | 35.2° | 177 mm | 0.28° | 2.4 mm |
| 0° | 84.36° | −78.59° | −68.45° | 88.62° | 26.0° | 297 mm | 0.05° | 5.2 mm |
| 0° | 82.44° | −75.65° | −62.72° | 79.20° | 23.4° | 171 mm | 0.14° | 1.8 mm |
| 0° | 78.20° | −67.83° | −78.58° | 87.03° | 18.9° | 304 mm | 0.07° | 10.6 mm |
| 0° | 75.12° | −67.83° | −73.19° | 97.49° | 31.7° | 210 mm | 0.12° | 8.0 mm |
| 0° | 73.92° | −67.83° | −70.07° | 102.37° | 38.5° | 161 mm | 0.10° | 4.3 mm |
| 0° | 74.92° | −61.35° | −78.71° | 76.24° | 11.2° | 239 mm | 0.10° | 8.1 mm |
| 0° | 74.86° | −71.24° | −70.81° | 109.19° | 42.2° | 238 mm | 0.19° | 7.7 mm |
| 0° | 86.10° | −85.96° | −67.41° | 103.59° | 36.3° | 418 mm | −0.02° | 8.0 mm |
| 0° | 84.92° | −87.15° | −60.40° | 106.25° | 43.7° | 345 mm | 0.08° | 7.7 mm |
| 0° | 93.32° | −96.09° | −51.75° | 93.21° | 38.7° | 338 mm | 0.01° | 0.1 mm |
| 0° | 93.30° | −100.01° | −46.85° | 99.36° | 45.8° | 368 mm | −0.01° | 0.5 mm |
| 0° | 93.28° | −99.32° | −39.63° | 91.71° | 46.0° | 233 mm | −0.04° | 7.9 mm |
| 0° | 93.26° | −100.34° | −47.32° | 100.60° | 46.1° | 387 mm | −0.10° | 0.1 mm |
| 0° | 103.00° | −100.86° | −33.54° | 33.99° | 2.4° | 231 mm | −0.19° | 17.9 mm |
| Time | {W} Position | Error Compensation | Without Error Compensation | ||
|---|---|---|---|---|---|
| {T} Position | Distance from {W} to {T} | {T} Position | Distance from {W} to {T} | ||
| 0 s | (2.777 m, 0 m, 1.284 m) | (2.863 m, 0.002 m, 0.826 m) | 466.7 mm | (2.863 m, 0.002 m, 0.826 m) | 466.7 mm |
| 9.6 s | (2.696 m, 0 m, 0.858 m) | (2.863 m, 0.002 m, 0.826 m) | 170.0 mm | (2.863 m, 0.002 m, 0.826 m) | 170.0 mm |
| 12.0 s | (2.646 m, 0 m, 0.705 m) | (2.853 m, 0.004 m, 0.816 m) | 234.2 mm | (2.863 m, 0.002 m, 0.826 m) | 245.8 mm |
| 32.0 s | (2.849 m, 0 m, 0.865 m) | (2.849 m, 0.002 m, 0.866 m) | 1.88 mm | (2.863 m, 0.002 m, 0.826 m) | 16.93 mm |
| 40.2 s | (2.863 m, 0 m, 1.077 m) | (2.864 m, 0.002 m, 1.079 m) | 2.41 mm | (2.878 m, 0.001 m, 1.058 m) | 24.93 mm |
| 52 s | (2.894 m, 0 m, 1.336 m) | (2.896 m, 0.001 m, 1.338 m) | 2.93 mm | (2.909 m, −0.001 m, 1.302 m) | 36.81 mm |
| Min Value from 40.2 to 52 s | ― | ― | 1.57 mm | ― | 16.65 mm |
| Max Value from 40.2 to 52 s | ― | ― | 4.53 mm | ― | 39.20 mm |
| Mean Value from 40.2 to 52 s | ― | ― | 2.89 mm | ― | 26.68 mm |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, Q.; Zou, S.; Chen, H.; Duan, W. Research on Visualization and Error Compensation of Demolition Robot Attachment Changing. Sensors 2020, 20, 2428. https://doi.org/10.3390/s20082428
Deng Q, Zou S, Chen H, Duan W. Research on Visualization and Error Compensation of Demolition Robot Attachment Changing. Sensors. 2020; 20(8):2428. https://doi.org/10.3390/s20082428
Chicago/Turabian StyleDeng, Qian, Shuliang Zou, Hongbin Chen, and Weixiong Duan. 2020. "Research on Visualization and Error Compensation of Demolition Robot Attachment Changing" Sensors 20, no. 8: 2428. https://doi.org/10.3390/s20082428
APA StyleDeng, Q., Zou, S., Chen, H., & Duan, W. (2020). Research on Visualization and Error Compensation of Demolition Robot Attachment Changing. Sensors, 20(8), 2428. https://doi.org/10.3390/s20082428





