A New Construction of High Performance LDPC Matrices for Mobile Networks
Abstract
1. Introduction
1.1. Case Study
1.1.1. LDPC User Cases in 5G
1.1.2. LDPC User Cases in IoT
1.1.3. Would LDPC Be a Candidate for 6G
1.1.4. Potential Applications of the Proposed Scheme
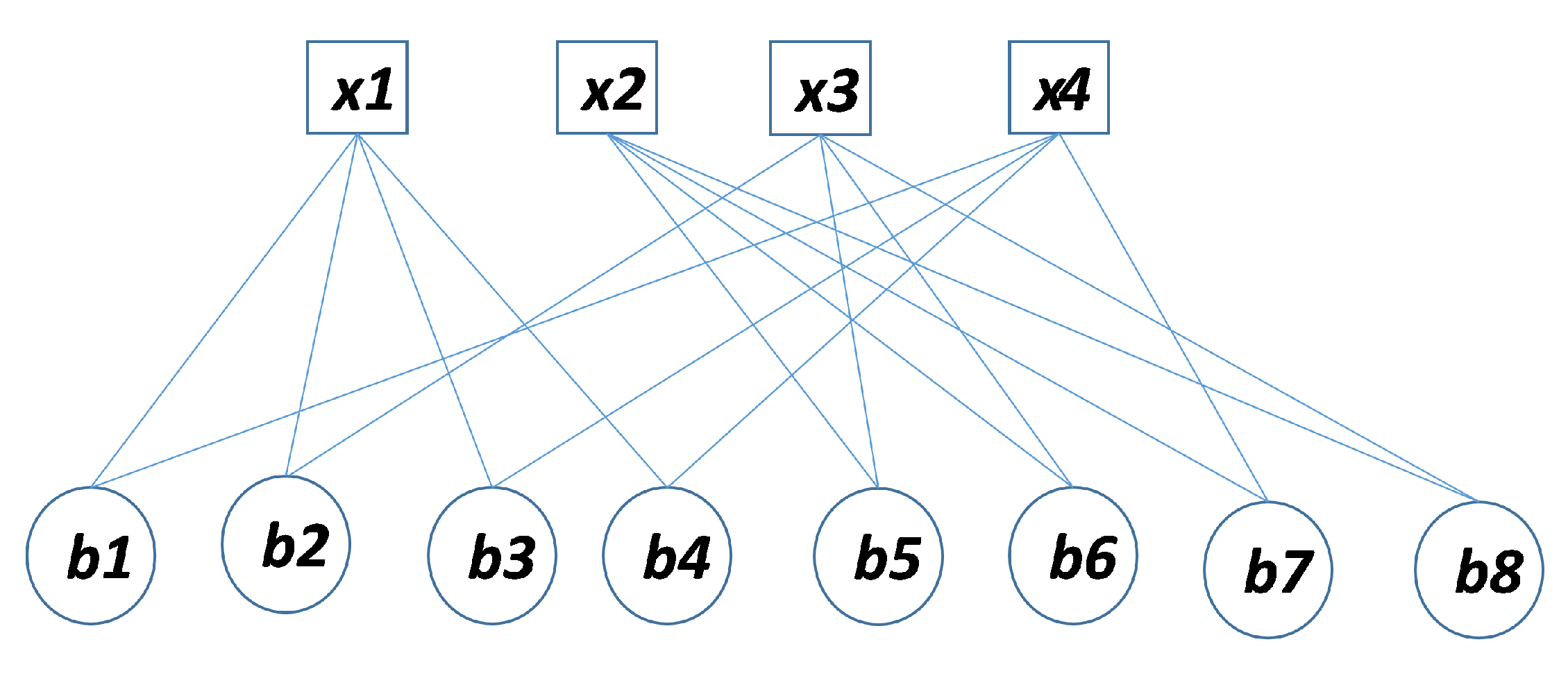
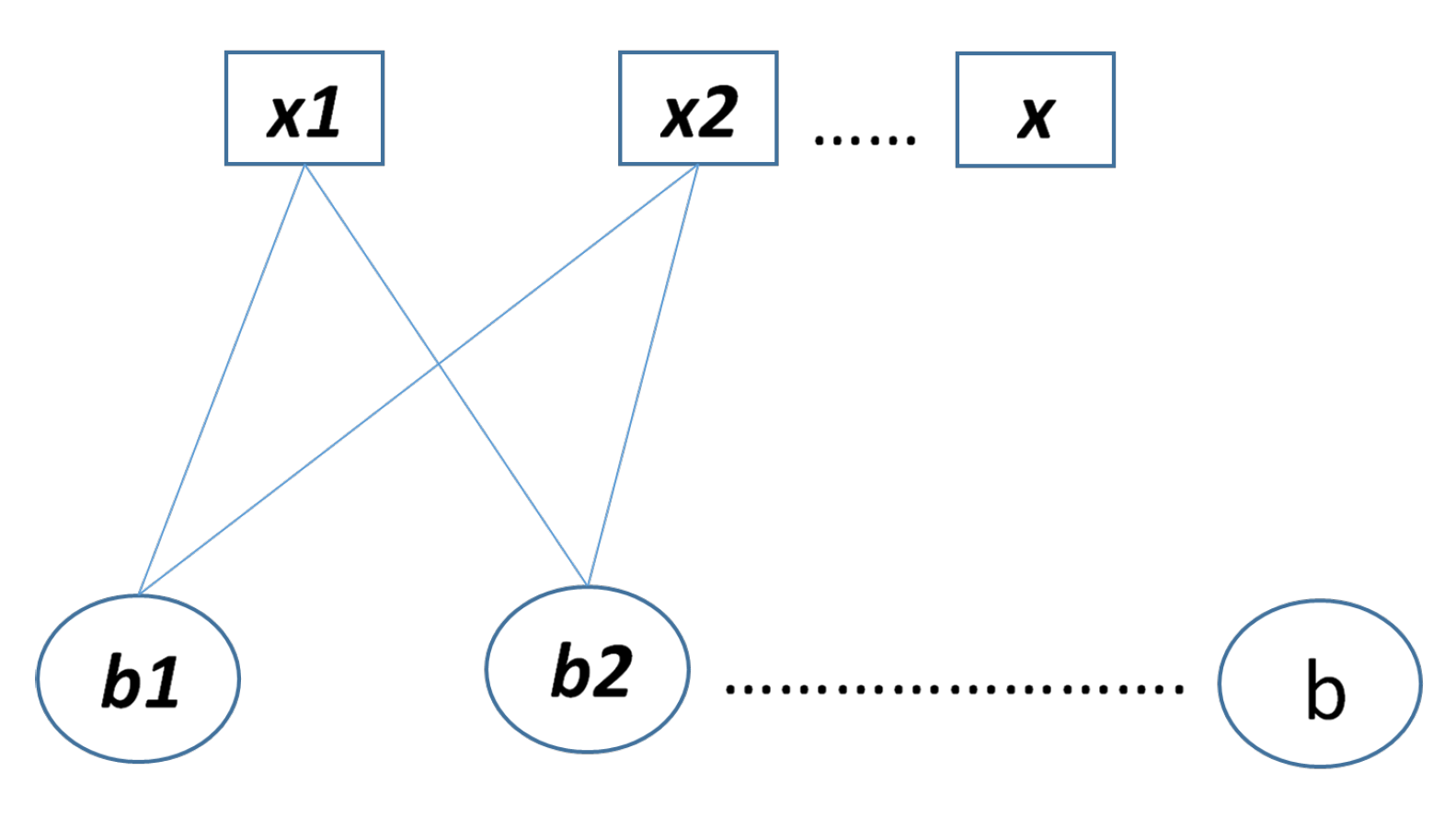
1.2. LDPC Code Structure
1.3. Standards Including LDPC Codes and Recent Protograph Codes
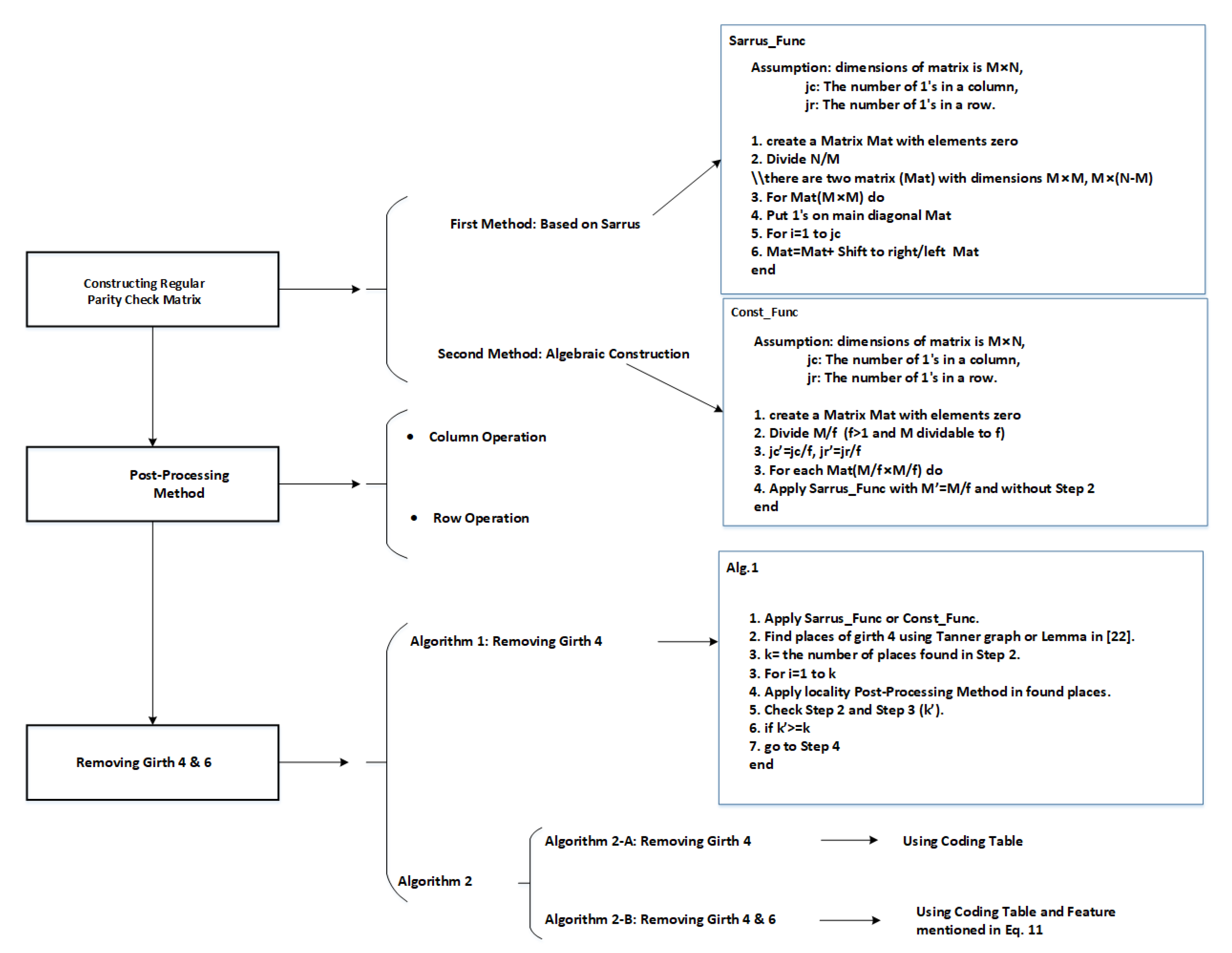
2. Proposed Methods for Construction of Parity Check Matrix
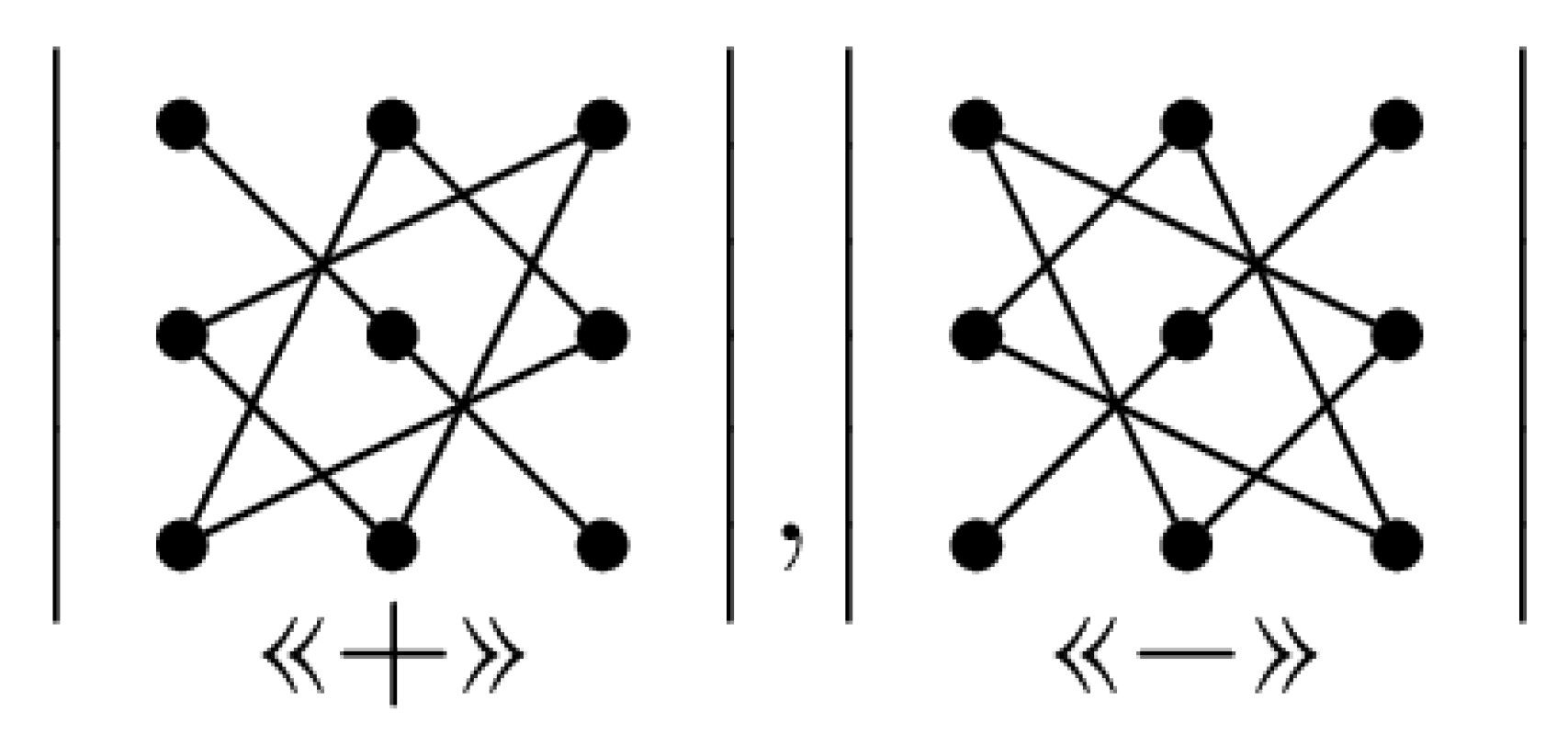
2.1. Method 1: Sarrus-Based Method
2.1.1. Background

2.1.2. The first Proposed Method
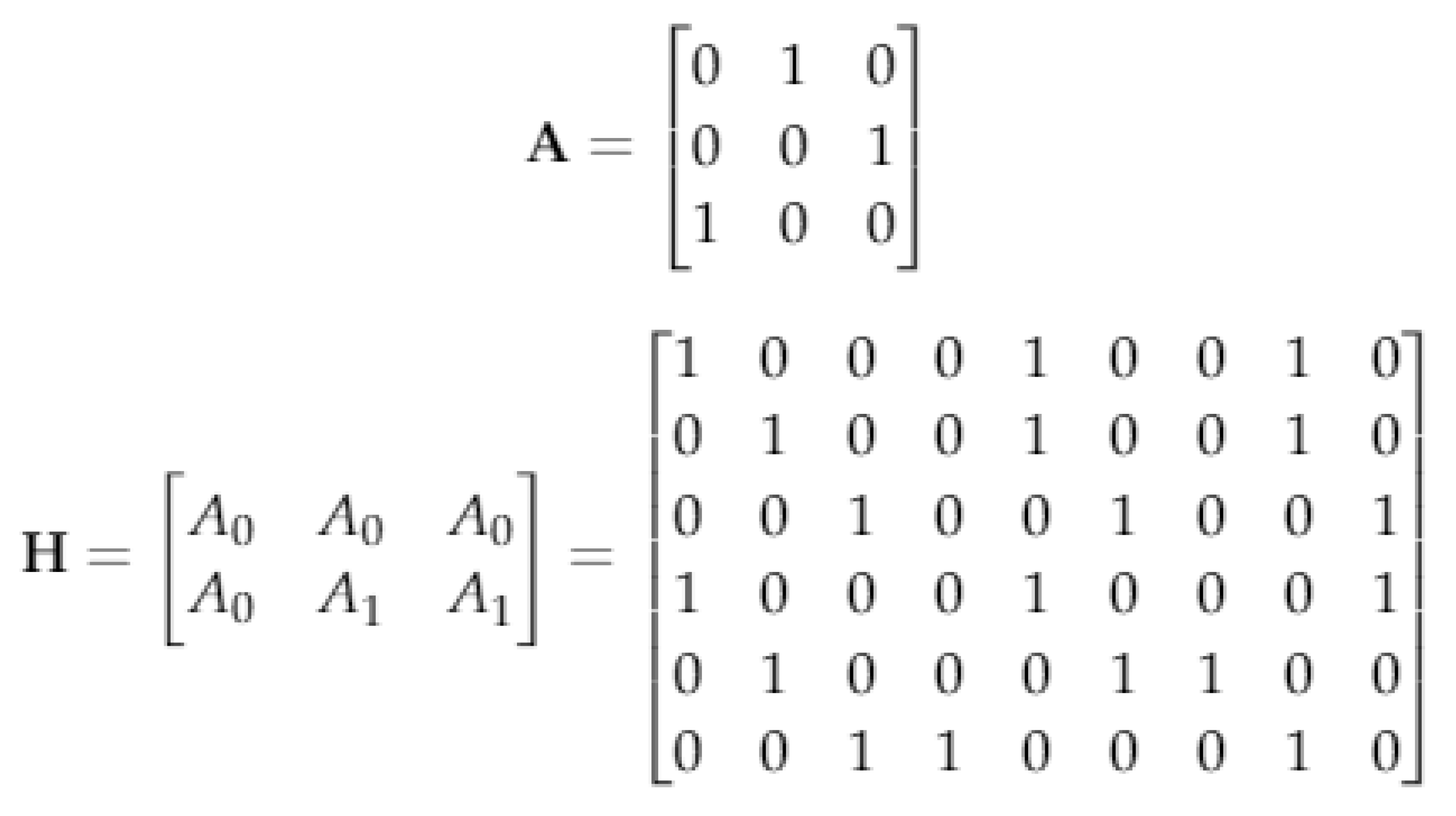
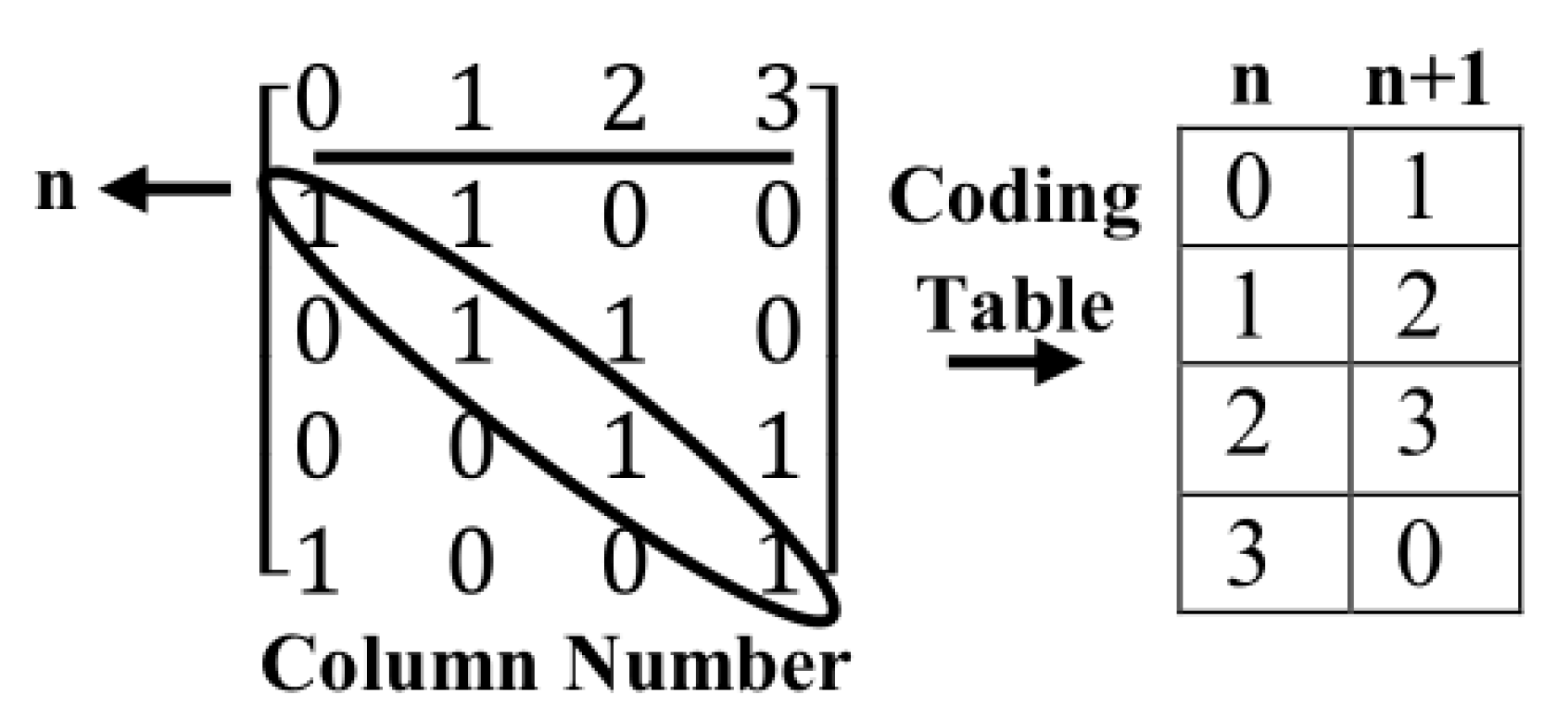
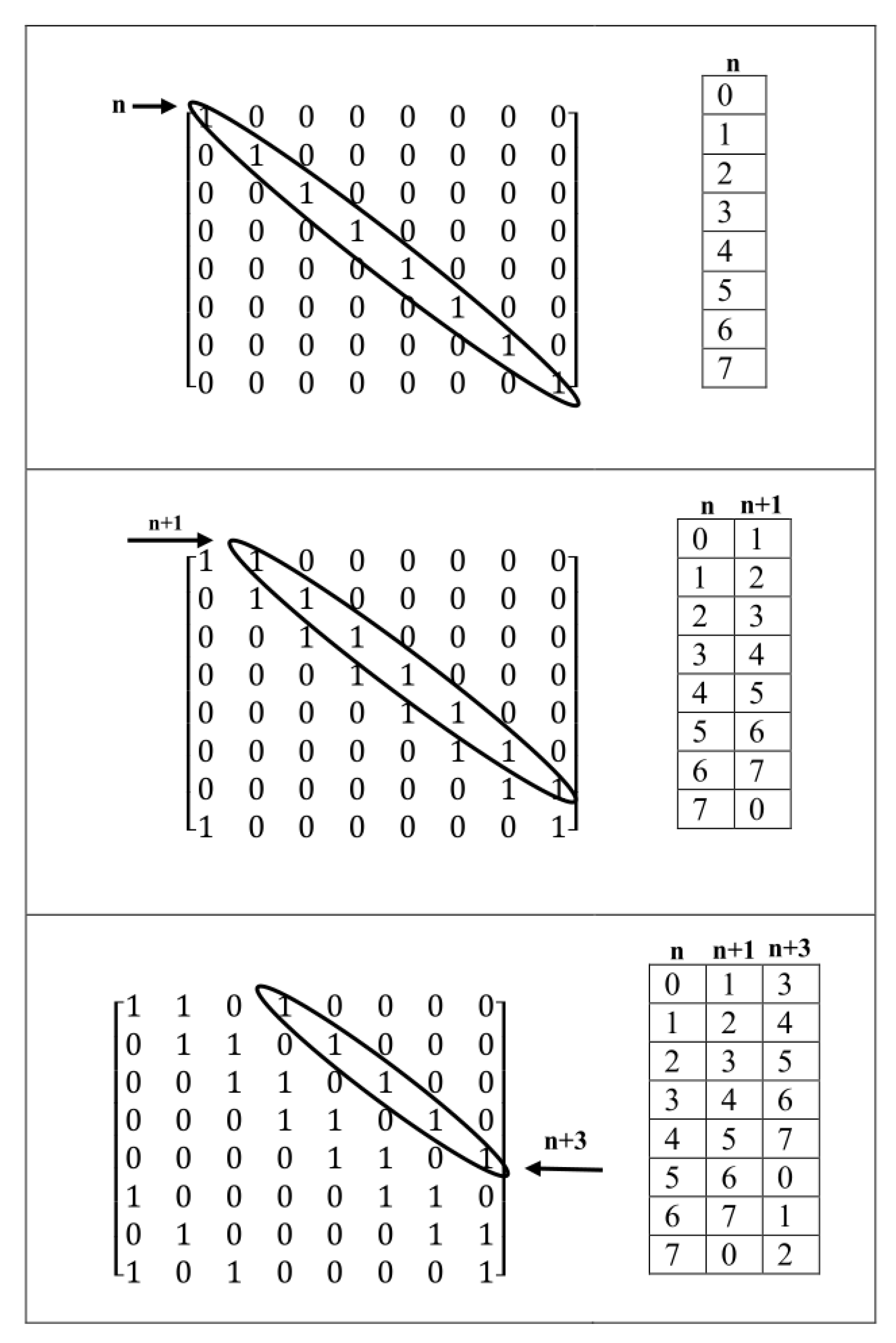
2.2. Second Method: Algebraic Construction
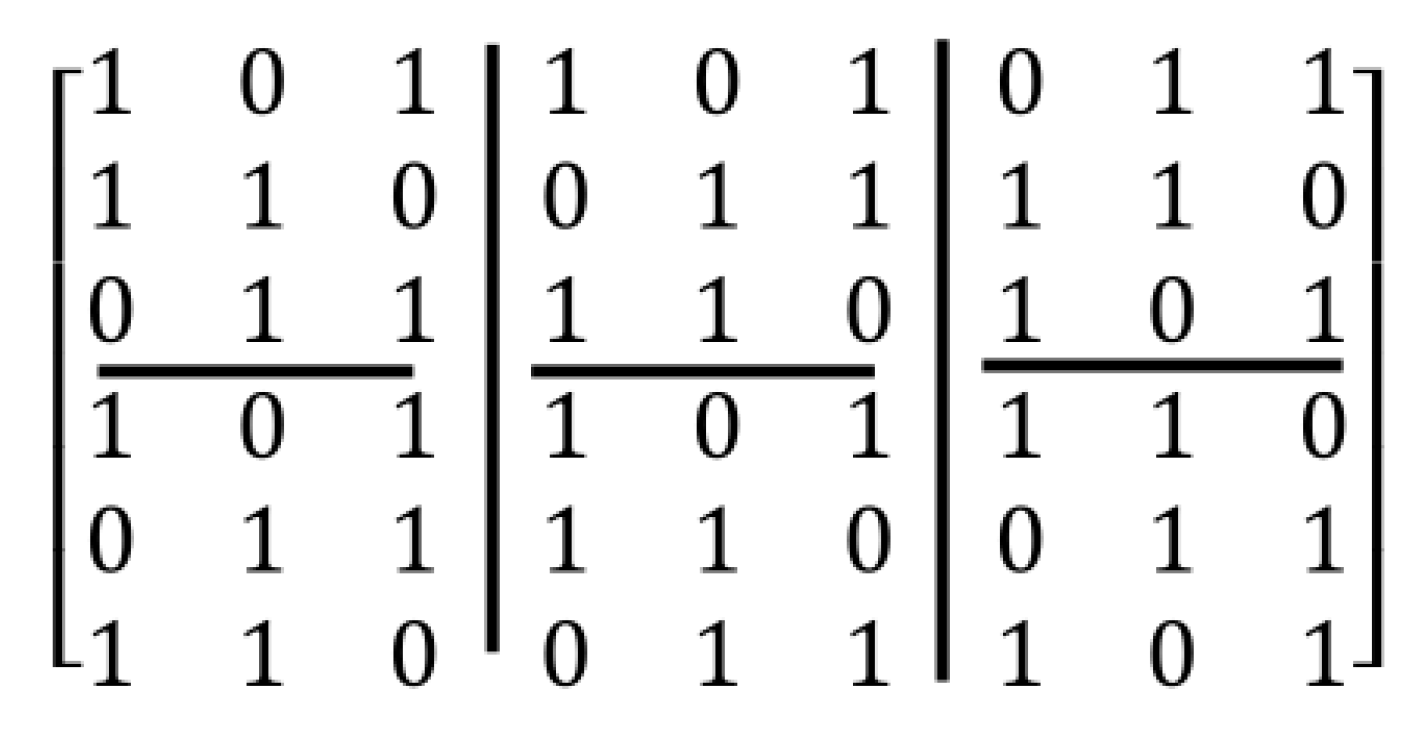
2.3. Post-Processing Method
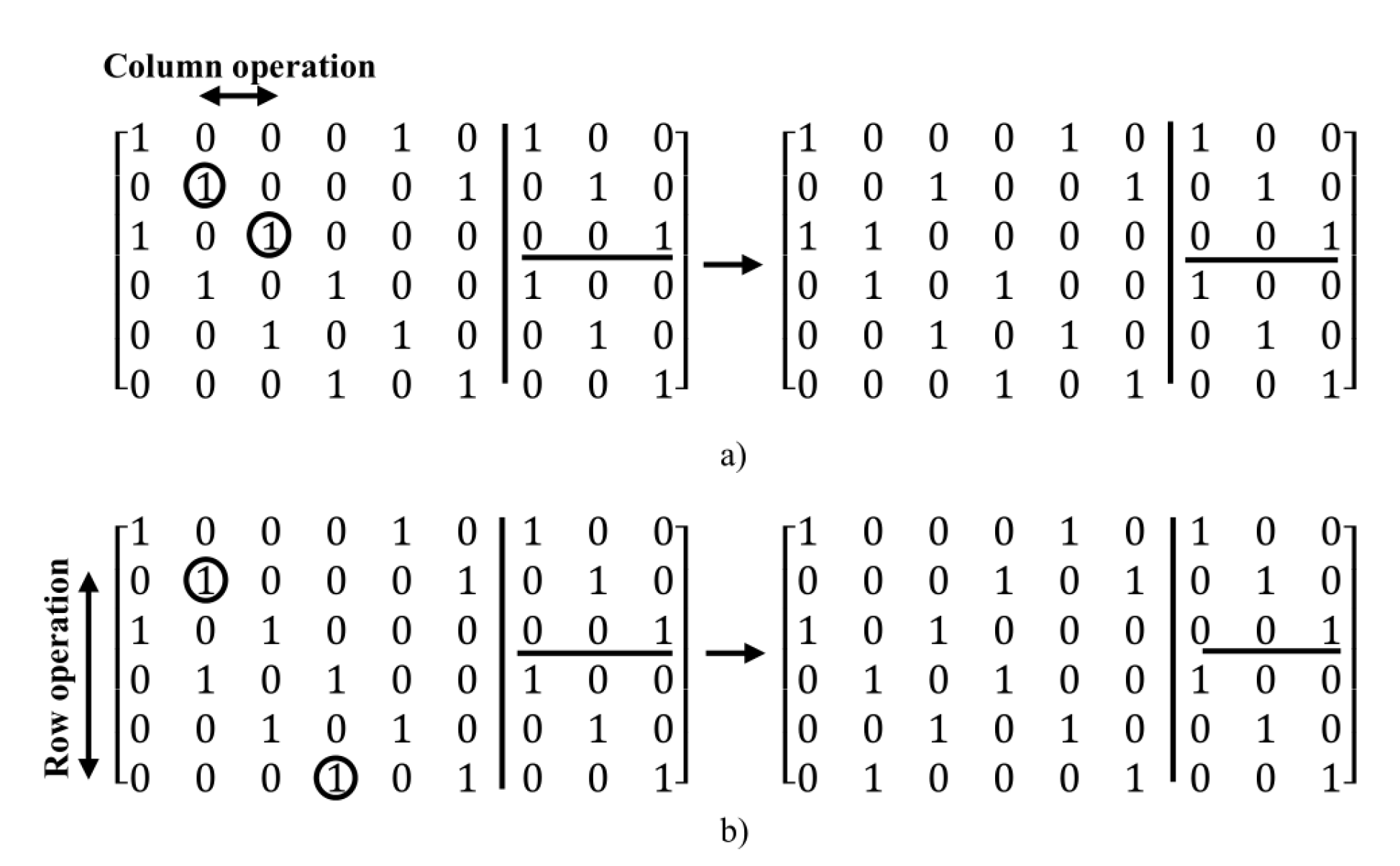
- Column operations: in this method, for creating of a new state of the matrix, for the specified two columns, the value of one in a column is exchanged with the value of zero of another column and vice versa, i.e. this operation for the value of one in a column and value of zero in other column is done.
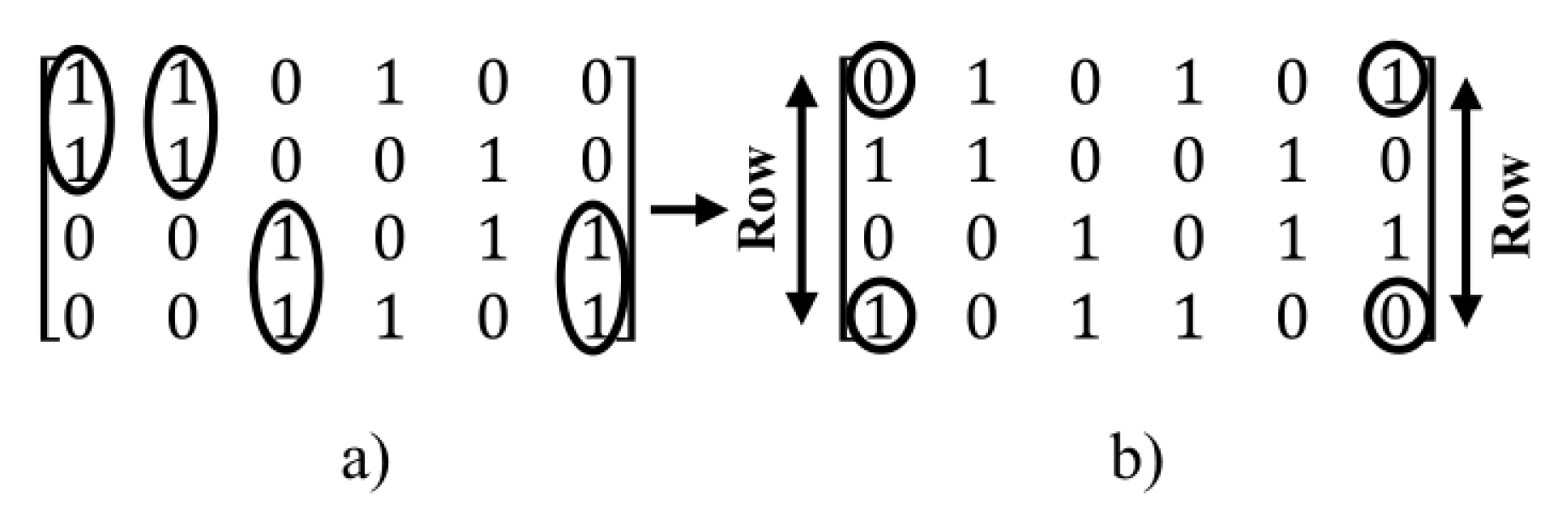
- Row operations: in this method, for creating a new state of the matrix, two rows are selected and then, the value of one in a row is exchanged with a value of zero in another row and vice versa.
3. Proposed Algorithms for Removing the Girths 4 and 6
3.1. Algorithm 1 for Removing Girth 4
3.2. Algorithm 2 for Removing Girth 4 and 6
3.2.1. Algorithm 2-A: Without Girths 4
3.2.2. Algorithm 2-B: Without Girths 6 and 4
4. Simulation Results and Analysis
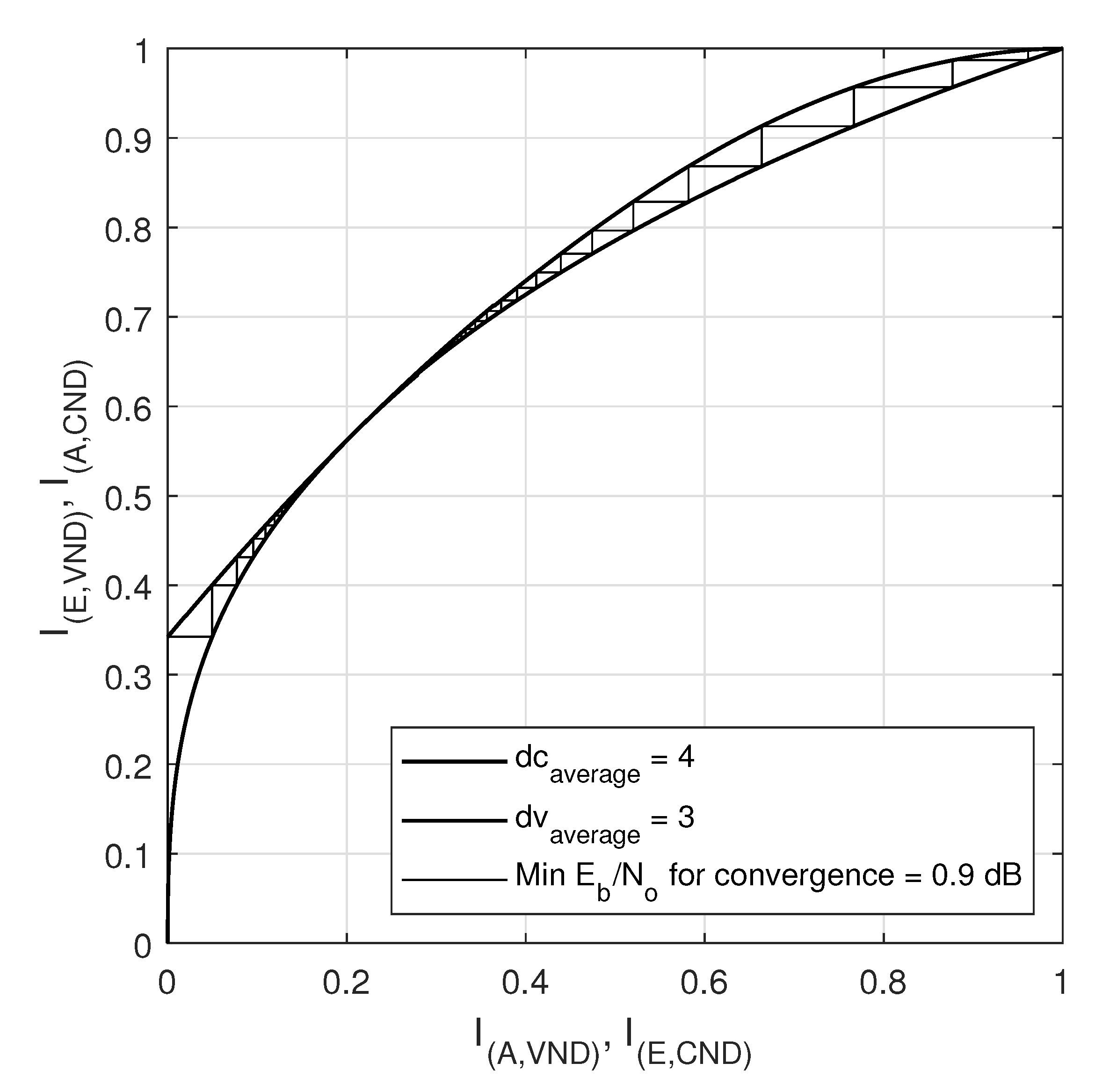
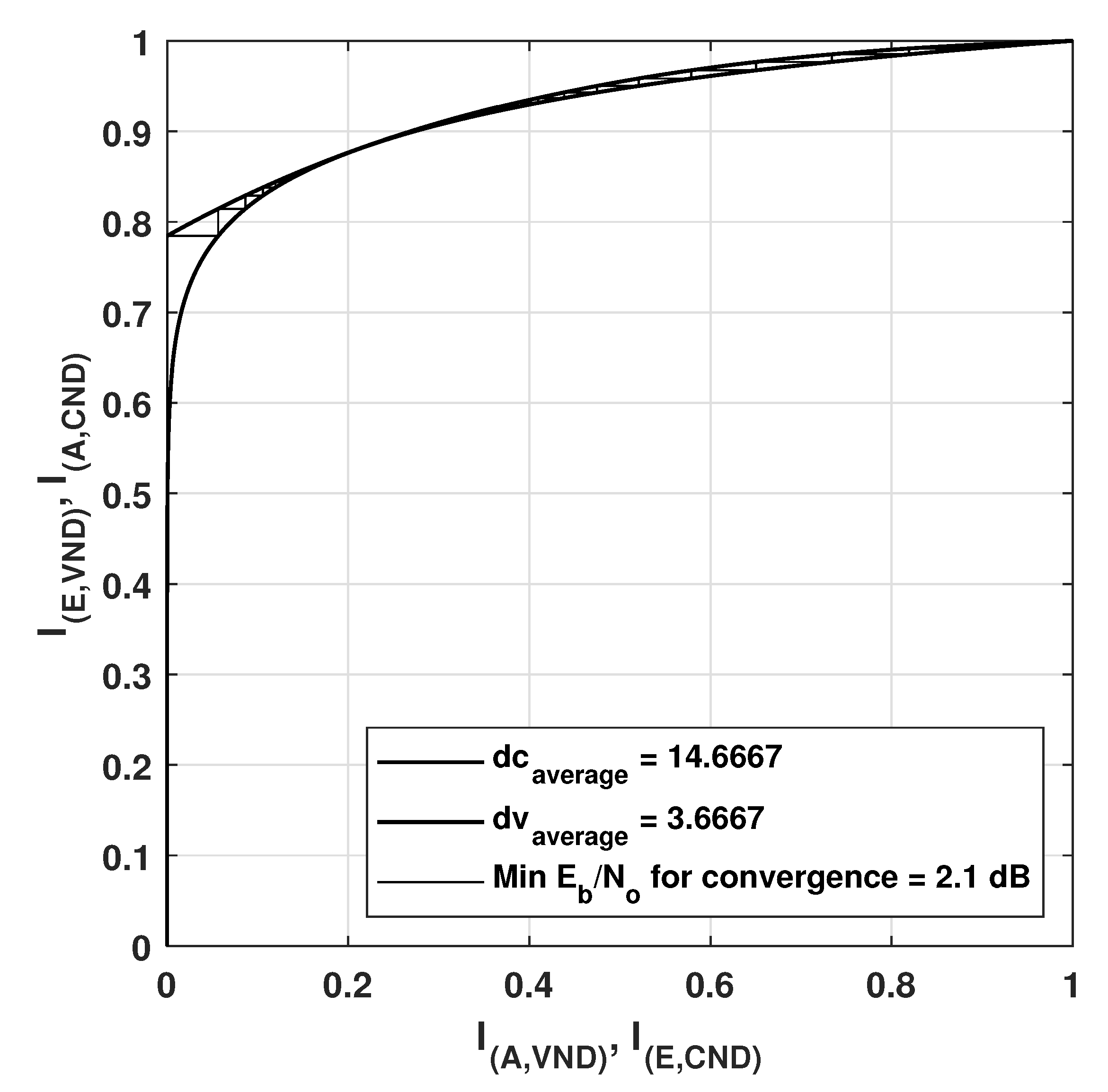
EXIT Chart Analysis
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lee, H.; Kwon, J. Survey and Analysis of Information Sharing in Social IoT. In Proceedings of the 2015 8th International Conference on Disaster Recovery and Business Continuity (DRBC), Jeju Island, Korea, 5–28 November 2015; pp. 15–18. [Google Scholar]
- Minh, T.N. Confidentiality and Integrity for IoT/Mobile Networks. In Recent Trends in Communication Networks; IntechOpen: London, UK, 2019. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Gallager, R.G. Low-density parity-check codes. Ire Trans. Inf. Theory 1962, 8, 21–28. [Google Scholar] [CrossRef]
- MacKay, D.J.C.; Neal, R.M. Near Shannon limit performance of low density parity check codes. Electron. Lett. 1997, 33, 457–458. [Google Scholar] [CrossRef]
- MacKay, D.J. Good error-correcting codes based on very sparse matrices. IEEE Trans. Inf. Theory 1999, 45, 399–431. [Google Scholar] [CrossRef]
- Ullah, W.; FengFan, Y. Improved Min-Sum Decoding Algorithm for Moderate Length Low Density Parity Check Codes. In Computer, Informatics, Cybernetics and Applications; Springer: Berlin/Heidelberg, Germany, 2012; pp. 935–943. [Google Scholar]
- Dai, W.; Milenkovic, O.; Pham, H.V. Structured sublinear compressive sensing via belief propagation. Phys. Commun. 2012, 5, 76–90. [Google Scholar] [CrossRef]
- Xu, K.; Lv, Z.; Xu, Y.; Zhang, D.; Zhong, X.; Liang, W. Joint physical network coding and LDPC decoding for two way wireless relaying. Phys. Commun. 2013, 6, 43–47. [Google Scholar] [CrossRef][Green Version]
- Third Generation Partnership Project Document 25.212. 2000. Available online: https://www.etsi.org/deliver/etsi_ts/125200_125299/125212/03.02.00_60/ts_125212v030200p.pdf (accessed on 25 March 2020).
- Ullah, W.; Fengfan, Y.; Yahya, A. QC LDPC Codes for MIMO and Cooperative Networks using Two Way Normalized Min-Sum Decoding. Telkomnika Indones. J. Electr. Eng. 2014, 12, 5448–5457. [Google Scholar] [CrossRef]
- Ullah, W.; Jiang, T.; Yang, F.; Aziz, S.M. Two-way normalization of min-sum decoding algorithm for medium and short length low density parity check codes. In Proceedings of the 2011 7th International Conference on Wireless Communications, Networking and Mobile Computing, Wuhan, China, 23–25 September 2011; pp. 1–5. [Google Scholar]
- Roth, R.M.; Zeh, A. On spectral design methods for quasi-cyclic codes. In Proceedings of the 2016 IEEE International Symposium on Information Theory (ISIT), Barcelona, Spain, 10–15 July 2016; pp. 1108–1112. [Google Scholar]
- Tanner, R.M. A recursive approach to low complexity codes. IEEE Trans. Inf. Theory 1981, 27, 533–547. [Google Scholar] [CrossRef]
- Chung, S.Y.; Forney, G., Jr.; Richardson, T.; Urbanke, R. On the design of low-density parity-check codes within 0.0045 dB of the Shannon limit. IEEE Commun. Lett. 2001, 5, 58–60. [Google Scholar] [CrossRef]
- Fossorier, M.P.C. Quasi cyclic low-density parity-check codes from circulant permutation matrices. IEEE Trans. Inf. Theory 2004, 50, 1788–1793. [Google Scholar] [CrossRef]
- Smarandache, R.; Vontobel, P.O. Quasi-Cyclic LDPC Codes: Influence of Proto- and Tanner-Graph Structure on Minimum Hamming Distance Upper Bounds. IEEE Trans. Inf. Theory 2012, 58, 585–607. [Google Scholar] [CrossRef]
- Okamura, T. Designing LDPC codes using cyclic shifts. In Proceedings of the IEEE International Symposium on Information Theory, Yokohama, Japan, 29 June–4 July 2003; p. 151. [Google Scholar] [CrossRef]
- Virmani, S.H.G. LDPC for Wi-Fi and WiMAX technologies. In Proceedings of the 2009 International Conference, n Emerging Trends in Electronic and Photonic Devices & Systems, Varanasi, India, 22–24 December 2009; pp. 262–265. [Google Scholar] [CrossRef]
- Marchand, C.; Boutillon, E. LDPC decoder architecture for DVB-S2 and DVB-S2X standards. In Proceedings of the 2015 IEEE Workshop on Signal Processing Systems (SiPS), Hangzhou, China, 14–16 October 2015; pp. 1–5. [Google Scholar] [CrossRef]
- Sybis, M.; Wesolowski, K.; Jayasinghe, K.; Venkatasubramanian, V.; Vukadinovic, V. Channel coding for ultra-reliable low-latency communication in 5G systems. In Proceedings of the 2016 IEEE 84th vehicular technology conference (VTC-Fall), Montreal, QC, Canada, 18–21 September 2016; pp. 1–5. [Google Scholar]
- Ateya, A.A.; Muthanna, A.; Makolkina, M.; Koucheryavy, A. Study of 5G services standardization: Specifications and requirements. In Proceedings of the 2018 10th International Congress on Ultra Modern Telecommunications and Control Systems and Workshops (ICUMT), Moscow, Russia, 5–9 November 2018; pp. 1–6. [Google Scholar]
- Bae, J.H.; Abotabl, A.; Lin, H.P.; Song, K.B.; Lee, J. An overview of channel coding for 5G NR cellular communications. Apsipa Trans. Signal Inf. Process. 2019, 8, e17. [Google Scholar] [CrossRef]
- Chen, P.; Xie, Z.; Fang, Y.; Chen, Z.; Mumtaz, S.; Rodrigues, J.J. Physical-layer network coding: An efficient technique for wireless communications. IEEE Netw. 2019. [Google Scholar] [CrossRef]
- Mohd, S.A.A.M.F.; Fadi, S. LCPC Error Correction Code for IoT Applications. IEEE Trans. Commun. 2010, 58, 1365–1375. [Google Scholar]
- Li, B.; Fei, Z.; Zhang, Y. UAV communications for 5G and beyond: Recent advances and future trends. IEEE Internet Things J. 2018, 6, 2241–2263. [Google Scholar] [CrossRef]
- Richardson, T.J.; Shokrollahi, M.A.; Urbanke, R.L. Design of capacity-approaching irregular low-density parity-check codes. IEEE Trans. Inf. Theory 2001, 47, 619–637. [Google Scholar] [CrossRef]
- Hu, X.Y.; Eleftheriou, E.; Arnold, D.M. Progressive edge-growth Tanner graphs. In Proceedings of the IEEE Globecom, San Antonio, TX, USA, 25–29 November 2001; Volume 2, pp. 995–1001. [Google Scholar]
- Luby, M.G.; Mitzenmacher, M.; Shokrollahi, M.A.; Spielman, D.A. Improved low-density parpity-check codes using irregular graphs. IEEE Trans. Inf. Theory 2001, 47, 585–598. [Google Scholar] [CrossRef]
- Richardson, T.J.; Urbanke, R.L. The capacity of low-density parity-check codes under message-passing decoding. IEEE Trans. Inf. Theory 2001, 47, 599–618. [Google Scholar] [CrossRef]
- Kschischang, F.R.; Frey, B.J.; Loeliger, H.A. Extended bit-filling and LDPC code design. In Proceedings of the IEEE Globecom, San Antonio, TX, USA, 25–29 November 2001; pp. 674–679. [Google Scholar]
- Battaglioni, M.; Baldi, M.; Paolini, E. Complexity-constrained spatially coupled LDPC codes based on protographs. In Proceedings of the 2017 International Symposium on Wireless Communication Systems (ISWCS), Bologna, Italy, 28–31 August 2017; pp. 49–53. [Google Scholar]
- Genga, Y.; Ogundile, O.; Oyerinde, O.; Versfeld, J. A low complexity encoder construction for systematic quasi-cyclic LDPC codes. In Proceedings of the 2017 IEEE AFRICON, Cape Town, South Africa, 18–20 September 2017; pp. 167–170. [Google Scholar]
- Fan, J.L. Array Codes as LDPC Codes. In Constrained Coding and Soft Iterative Decoding; Springer: Boston, MA, USA, 2001; pp. 195–203. [Google Scholar] [CrossRef]
- Zhang, L.; Huang, Q.; Lin, S.; Abdel-Ghaffar, K.; Blake, I.F. Quasi-cyclic LDPC codes: An algebraic construction, rank analysis, and codes on Latin squares. IEEE Trans. Commun. 2010, 58, 3126–3139. [Google Scholar] [CrossRef]
- Recommendation, I.; G9960. Unified High-Speed Wireline-Based Home Networking Transceivers–System Architecture and Physical Layer Specification. 2011. Available online: https://www.itu.int/rec/T-REC-G.9960 (accessed on 28 March 2020).
- CCSDS. TM Synchronization and Channel Coding. Blue Book 2011. Available online: https://public.ccsds.org/Pubs/131x0b2ec1s.pdf (accessed on 28 March 2020).
- Declercq, D.; Fossorier, M.; Biglieri, E. Channel Coding: Theory, Algorithms, and Applications: Academic Press Library in Mobile and Wireless Communications; Academic Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Fang, Y.; Bi, G.; Guan, Y.L.; Lau, F.C. A survey on protograph LDPC codes and their applications. IEEE Commun. Surv. Tutor. 2015, 17, 1989–2016. [Google Scholar] [CrossRef]
- Tang, C.; Shen, H.; Jiang, M.; Zhao, C. Optimization of generalized VDMM for protograph-based LDPC coded BICM. IEEE Commun. Lett. 2014, 18, 853–856. [Google Scholar] [CrossRef]
- Fang, Y.; Chen, P.; Cai, G.; Lau, F.C.; Liew, S.C.; Han, G. Outage-limit-approaching channel coding for future wireless communications: Root-protograph low-density parity-check codes. IEEE Veh. Technol. Mag. 2019, 14, 85–93. [Google Scholar] [CrossRef]
- Hajrizaj, D. New method to compute determinant of a 3x3 matrix. Int. J. Algebra 2009, 3, 211–219. [Google Scholar]
- Lin, S.; Costello, D.J. Error control coding; Pearson Education India: Delhi/Chennai/Bangalore, India, 2004. [Google Scholar]
- Ullah, W.; Yahya, A. Comprehensive Algorithmic Review and Analysis of LDPC Codes. Indones. J. Electr. Eng. Comput. Sci. 2015, 16, 111–130. [Google Scholar]
- Malema, G. Flexible Construction of High-Girth Qc-Ldpc Codes. Int. J. Comput. Sci. Appl. 2012, 1, 19–25. [Google Scholar]
- Fan, J.; Xiao, Y. A design of LDPC codes with large girth based on the sub-matrix shifting. In Proceedings of the 2006 IET International Conference on Wireless, Mobile and Multimedia Networks, Hangzhou, China, 6–9 November 2006; pp. 1–4. [Google Scholar]
- Ryan, W.; Lin, S. Channel Codes: Classical and Modern; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
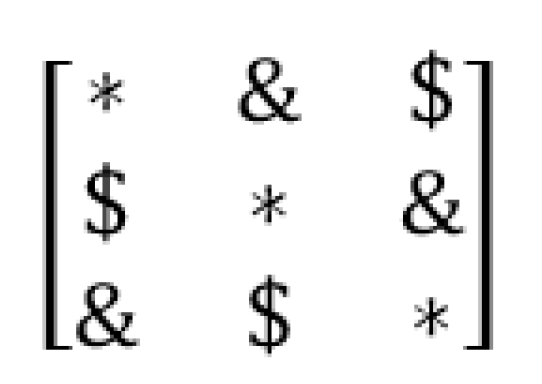

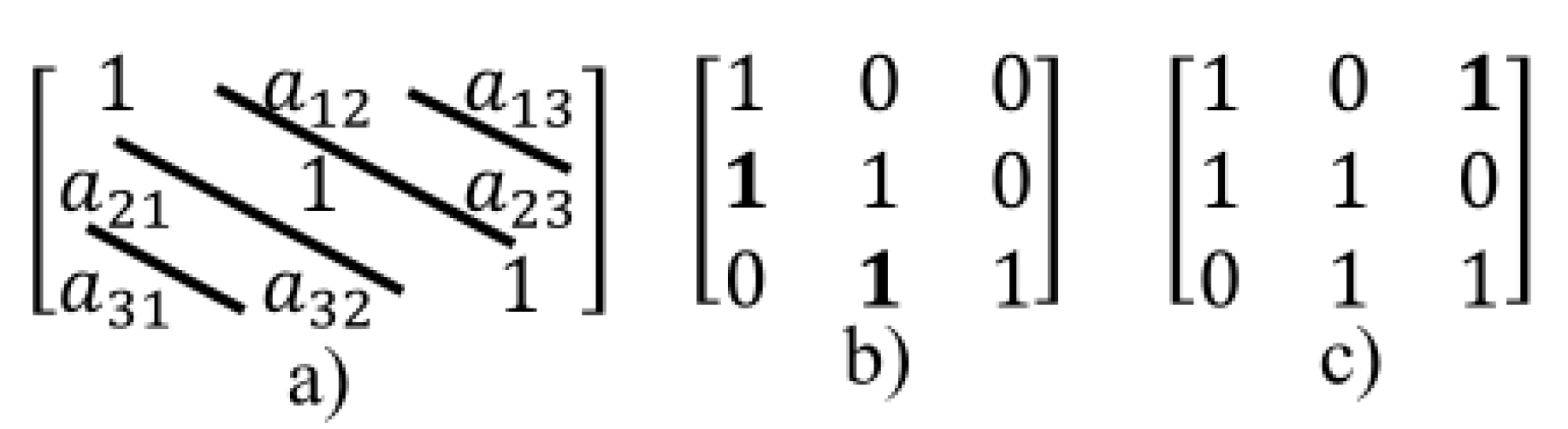







© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sarvaghad-Moghaddam, M.; Ullah, W.; Jayakody, D.N.K.; Affes, S. A New Construction of High Performance LDPC Matrices for Mobile Networks. Sensors 2020, 20, 2300. https://doi.org/10.3390/s20082300
Sarvaghad-Moghaddam M, Ullah W, Jayakody DNK, Affes S. A New Construction of High Performance LDPC Matrices for Mobile Networks. Sensors. 2020; 20(8):2300. https://doi.org/10.3390/s20082300
Chicago/Turabian StyleSarvaghad-Moghaddam, Moein, Waheed Ullah, Dushantha Nalin K. Jayakody, and Sofiène Affes. 2020. "A New Construction of High Performance LDPC Matrices for Mobile Networks" Sensors 20, no. 8: 2300. https://doi.org/10.3390/s20082300
APA StyleSarvaghad-Moghaddam, M., Ullah, W., Jayakody, D. N. K., & Affes, S. (2020). A New Construction of High Performance LDPC Matrices for Mobile Networks. Sensors, 20(8), 2300. https://doi.org/10.3390/s20082300







