Estimating Exerted Hand Force via Force Myography to Interact with a Biaxial Stage in Real-Time by Learning Human Intentions: A Preliminary Investigation
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Setup
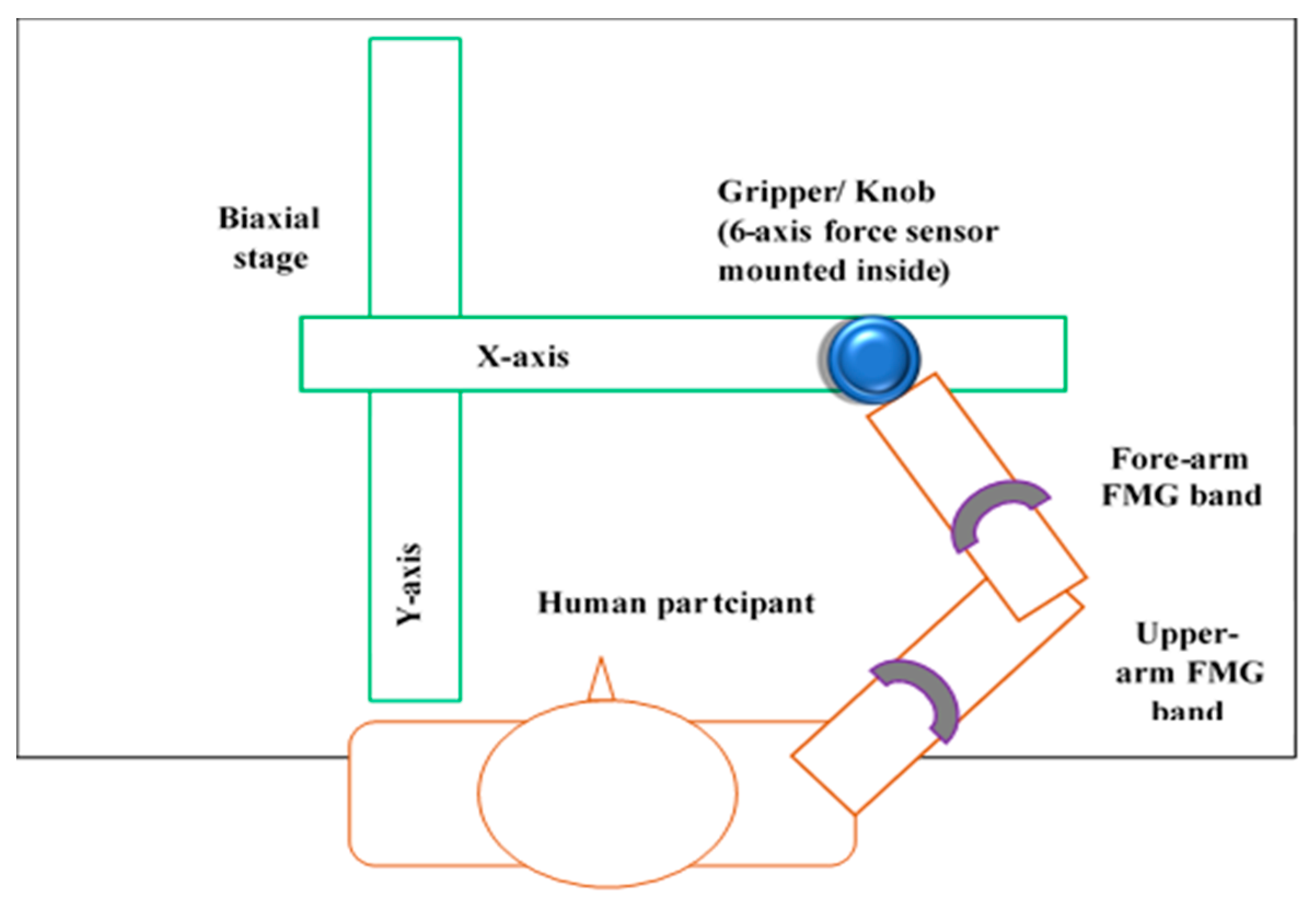
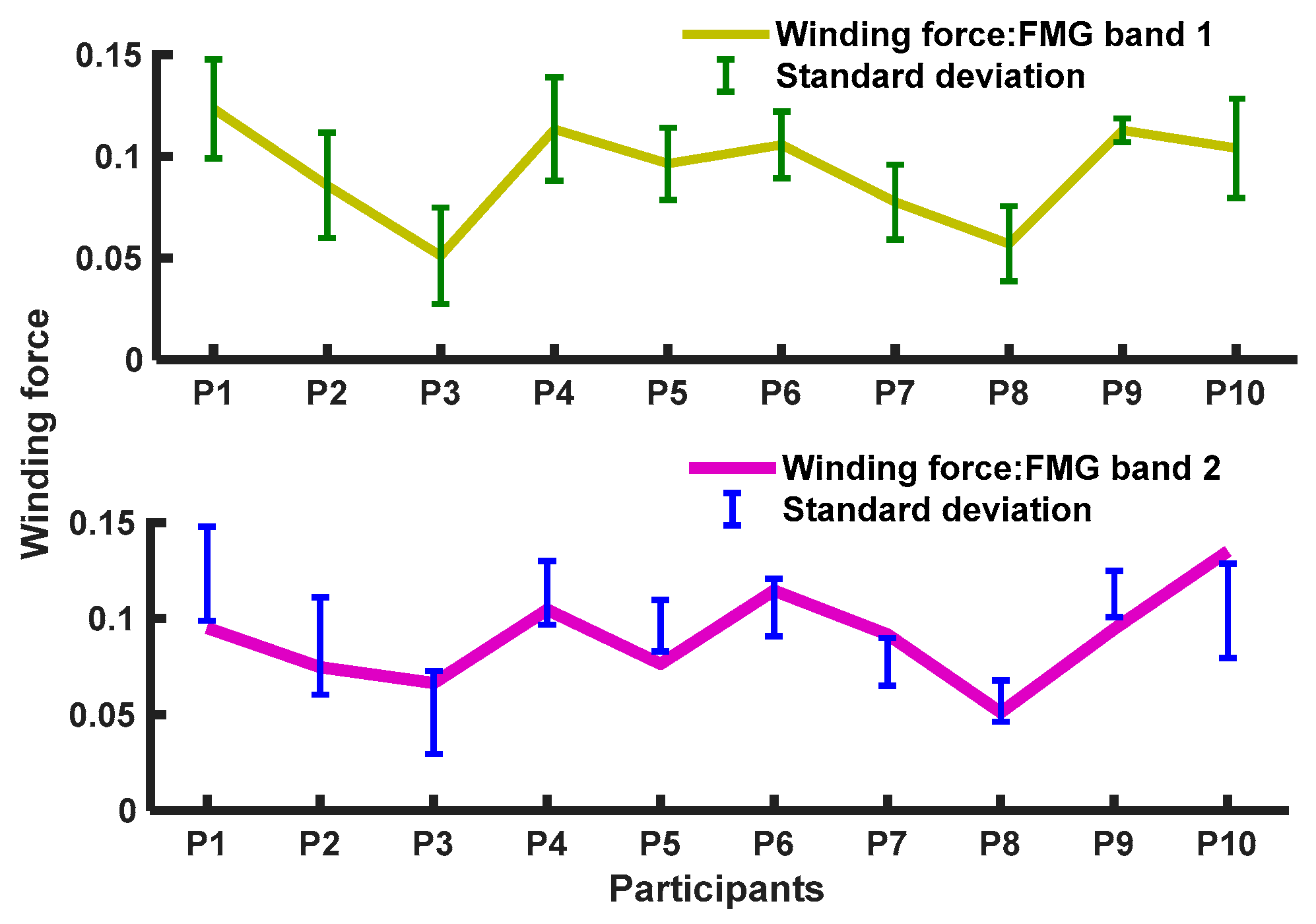
2.1.1. FMG Bands
2.1.2. The Biaxial Stage
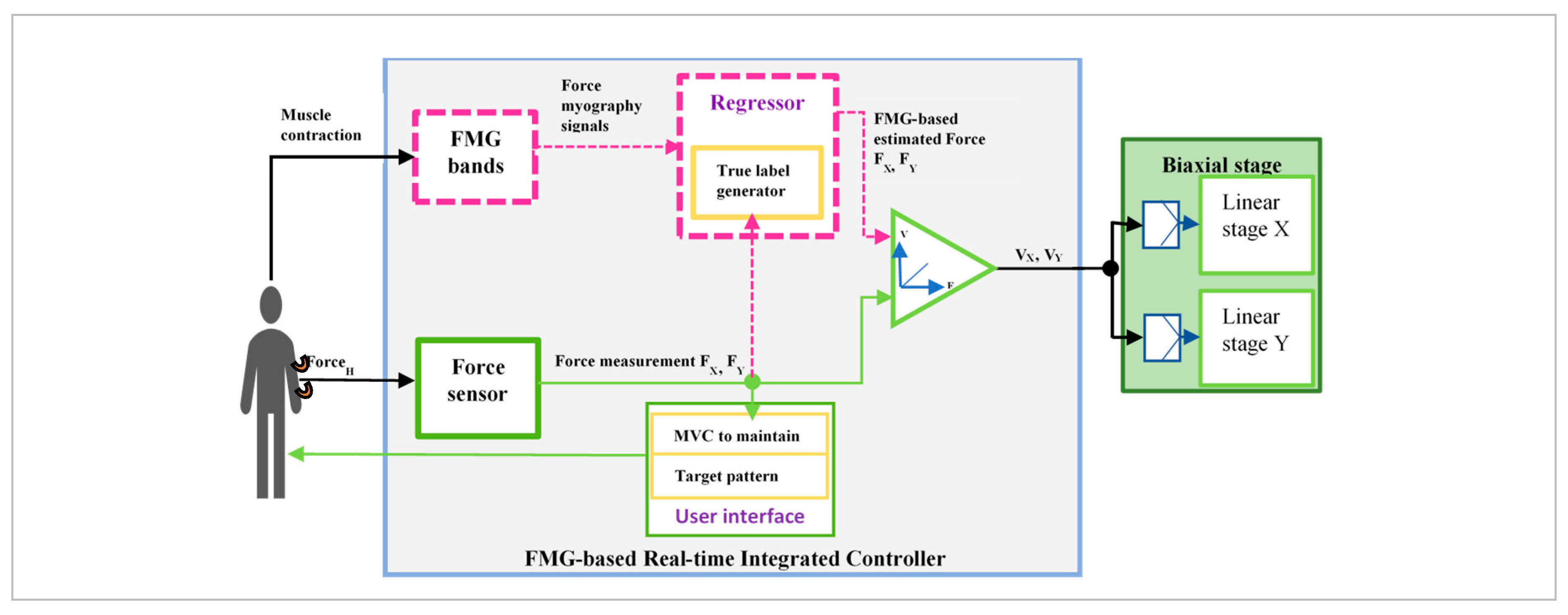
2.2. Real-Time FMG-Based Integrated Control
2.3. Regression Methods
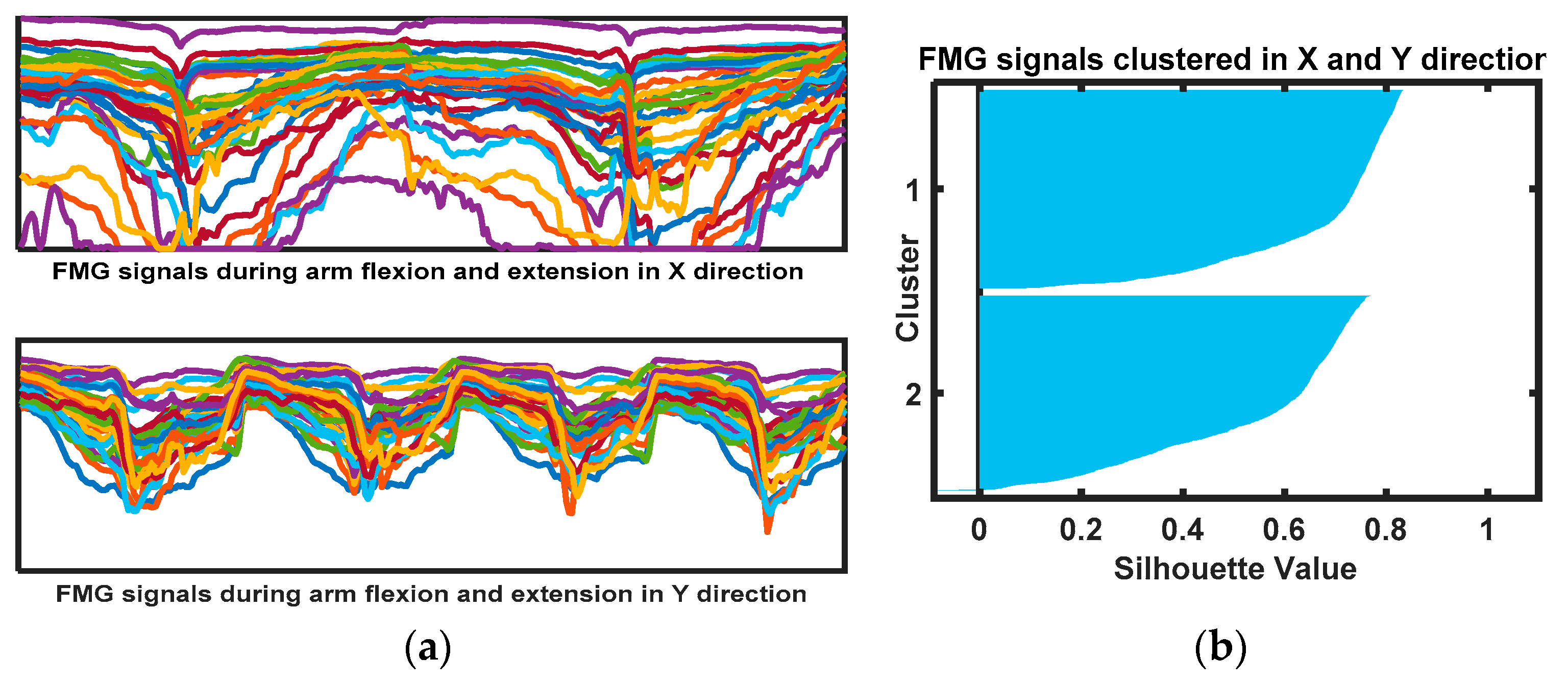
2.4. Dynamic Arm Motion Patterns
2.4.1. Intended 1-DoF Arm Motion Patterns
2.4.2. Intended 2-DoF Arm Motion Patterns
2.5. Performance Metrics
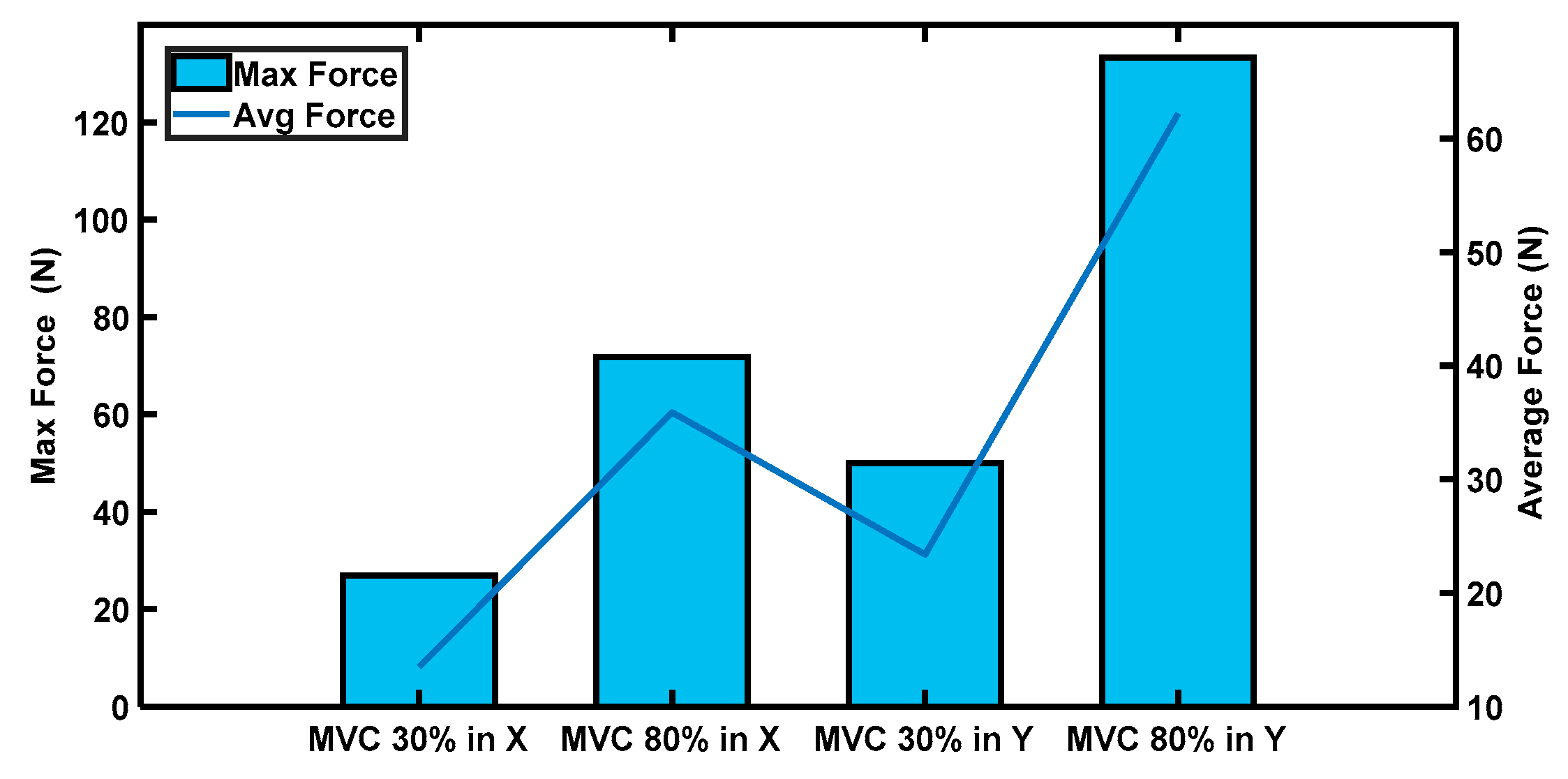
2.6. Protocol
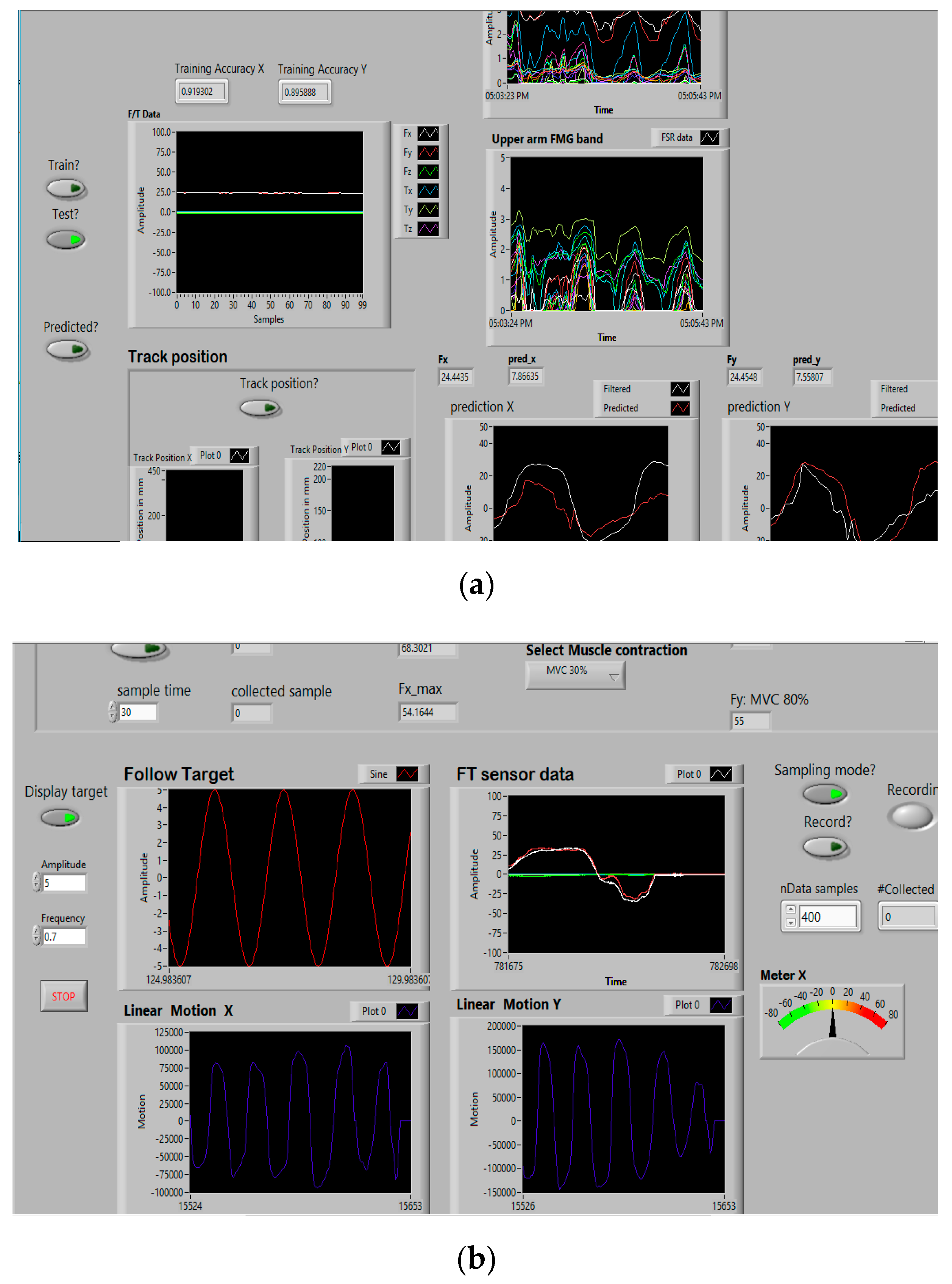
2.6.1. Data Collection Phase
2.6.2. Training Phase
2.6.3. Test Phase
3. Results
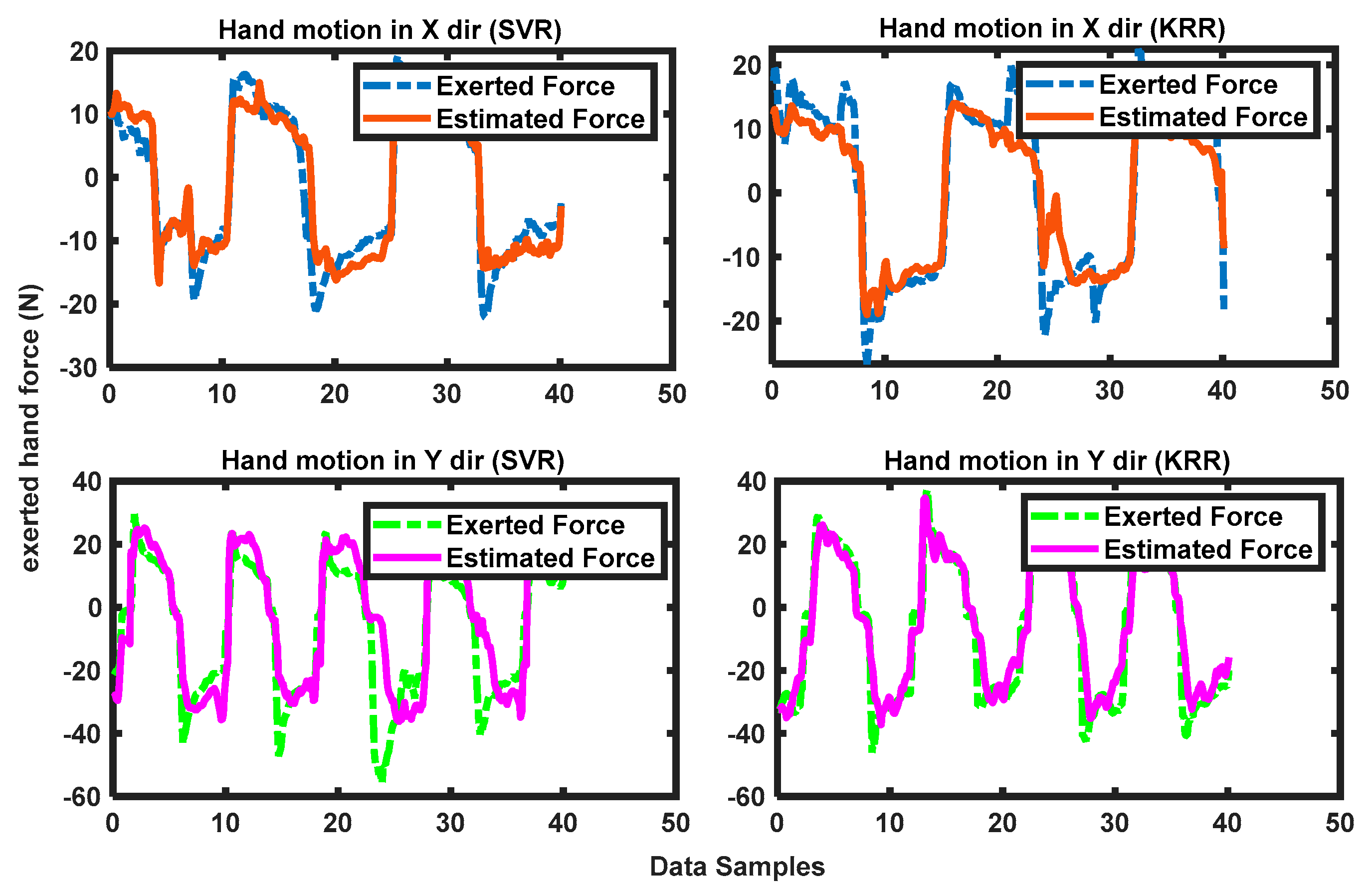
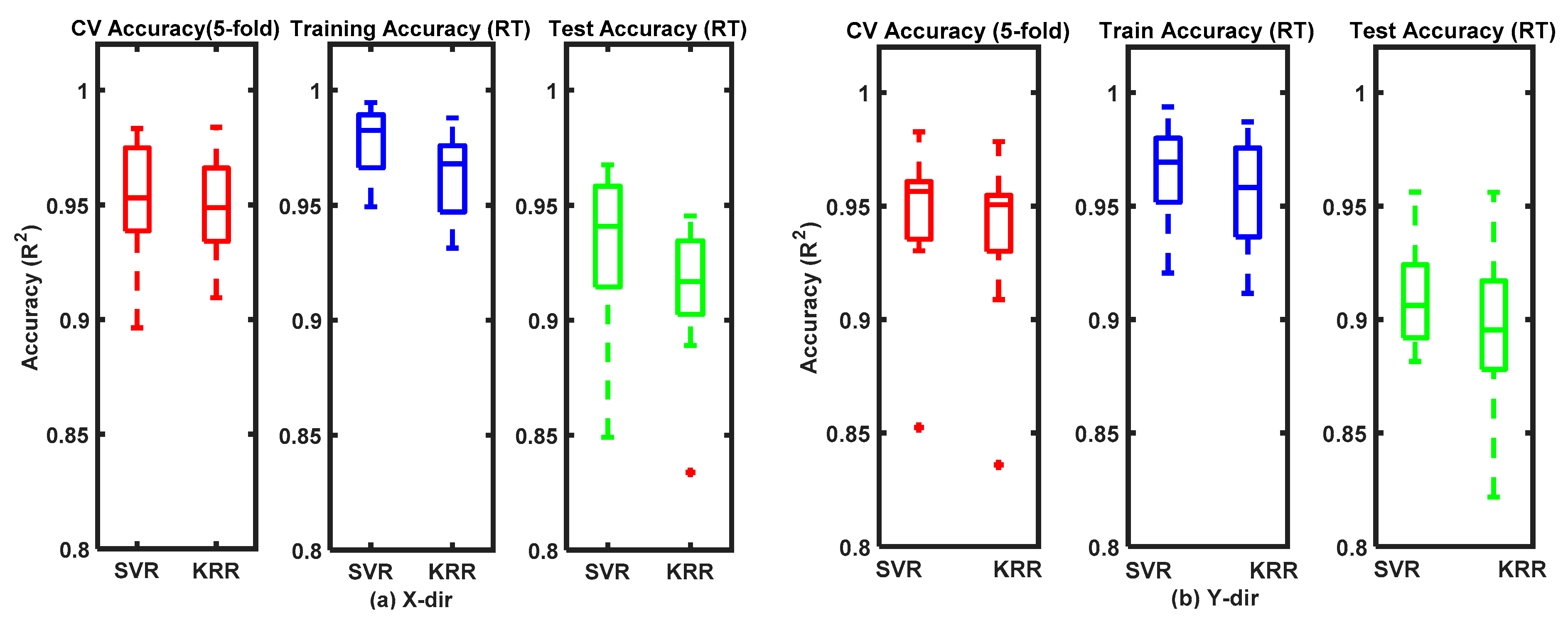
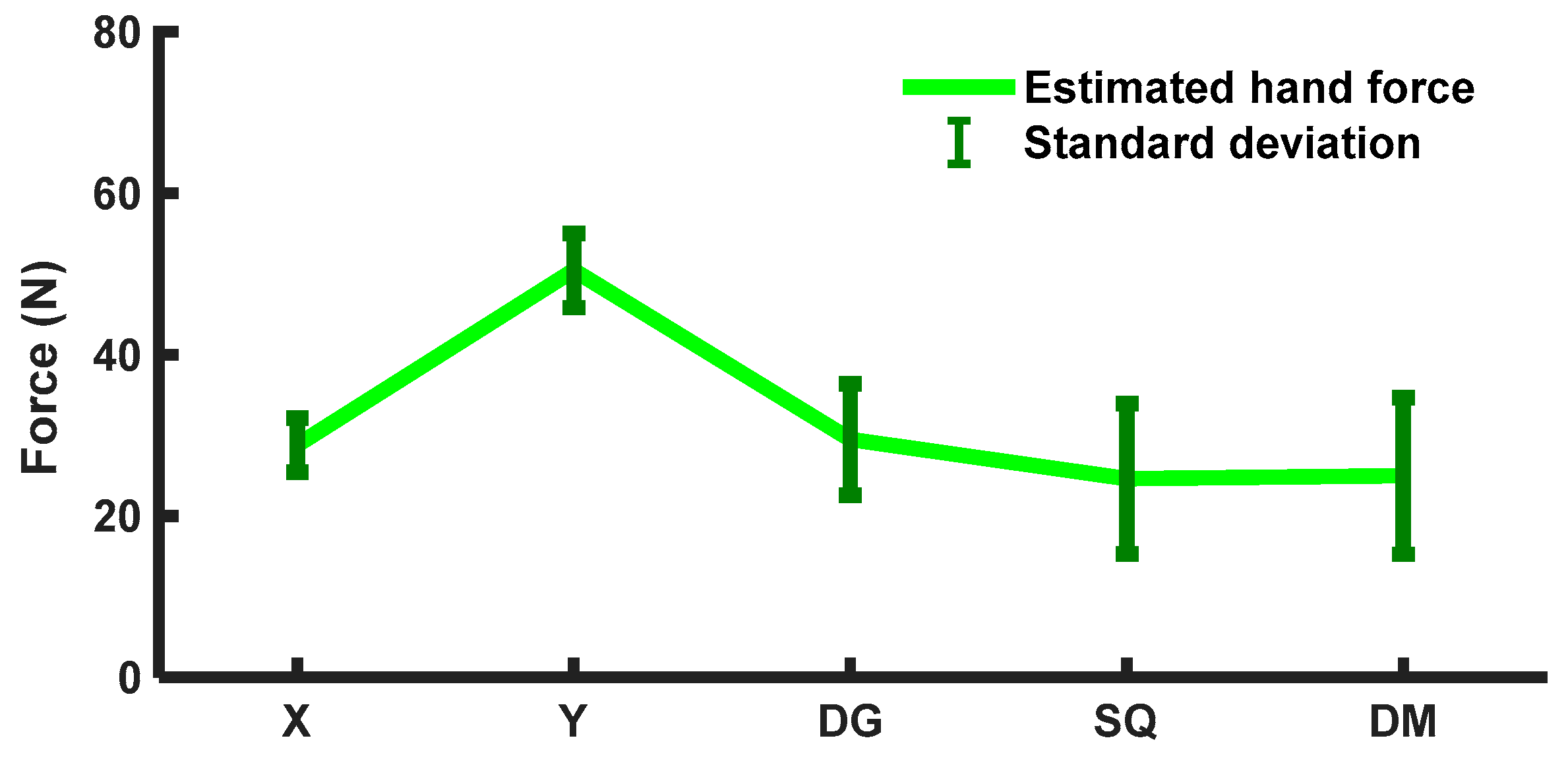
3.1. Real-Time FMG-Based 1-DoF Interactions
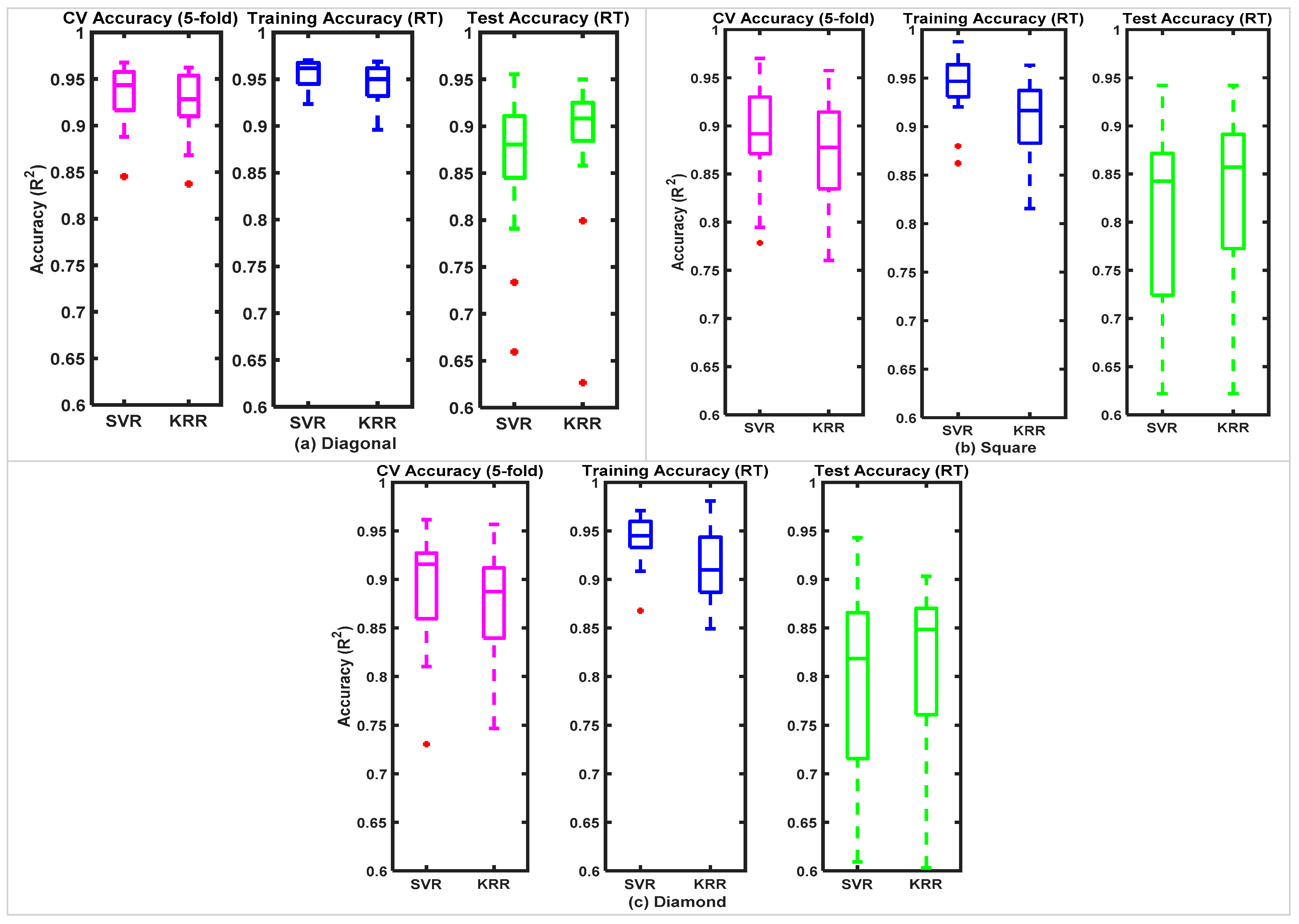
3.2. Real-Time FMG-Based 2-DoF Interactions
3.3. Comparison of Force Estimations in Dynamic Motions
3.4. Significance in Estimations
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Helms, E.; Hägele, M.; Schaaf, W. Robot assistants at manual workplaces: Effective co-operation and safety aspects. In Proceedings of the 33rd ISR (International Symposium on Robotics), Stockholm, Sweden, 7–11 October 2002; pp. 7–11. [Google Scholar]
- Santis, A.D.; Siciliano, B.; Luca, A.D.; Bicchi, A. An atlas of physical human-robot interaction. Mech. Mach. Theory 2008, 43, 253–270. [Google Scholar] [CrossRef]
- Matthias, I.L.; Kock, S.; Jerregard, H.; Källman, M.; Lundberg, I.; Mellander, R. Safety of collaborative industrial robots certification possibilities for a collaborative assembly robot concept. In Proceedings of the 2011 IEEE International Symposium on Assembly and Manufacturing (ISAM), Tampere, Finland, 25–27 May 2011; pp. 1–6. [Google Scholar]
- Malamas, E.N.; Petrakis, E.G.; Zervakis, M.; Petit, L.; Legat, J.D. A survey on industrial vision systems, applications and tools. Image Vis. Comput. 2003, 21, 171–188. [Google Scholar] [CrossRef]
- Bass, L.N.B.; Henry, E. Ultrasonic background noise in industrial environments. J. Acoust. Soc. Am. 1985, 78, 2013–2016. [Google Scholar] [CrossRef]
- Lee, C.; Choi, H.; Park, J.; Park, K.; Lee, S. Collision avoidance by the fusion of different beamwidth ultrasonic sensors. In Proceedings of the 2007 IEEE SENSORS, Atlanta, GA, USA, 28–31 October 2007; pp. 985–988. [Google Scholar]
- Haddadin, S.; Albu-Schaffer, A.; de Luca, A.; Hirzinger, G. Collision detection and reaction: A contribution to safe physical human-robot interaction. In Proceedings of the 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22–26 September 2008; pp. 3356–3363. [Google Scholar]
- Carmichael, M.G.; Liu, D.; Waldron, K.J. Investigation of reducing fatigue and musculoskeletal disorder with passive actuators. In Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems, Taipei, Taiwan, 18–22 October 2010; pp. 2481–2486. [Google Scholar]
- Nelson, N.A.; Park, R.M.; Silverstein, M.A.; Mirer, F.E. Cumulative trauma disorders of the hand and wrist in the auto industry. Am. J. Public Health 1992, 82, 1550–1552. [Google Scholar] [CrossRef] [PubMed]
- Mukhopadhyay, S.C. Wearable sensors for human activity monitoring: A review. IEEE Sens. J. 2015, 15, 1321–1330. [Google Scholar] [CrossRef]
- Cornacchia, M.; Ozcan, K.; Zheng, Y.; Velipasalar, S. A survey on activity detection and classification using wearable sensors. IEEE Sens. J. 2017, 17, 386–403. [Google Scholar] [CrossRef]
- Geethanjali, P.; Ray, K.K. A low-cost real-time research platform for EMG pattern recognition-based prosthetic hand. IEEE/ASME Trans. Mechatron. 2015, 20, 1948–1955. [Google Scholar] [CrossRef]
- Gui, K.; Liu, H.; Zhang, D. A practical and adaptive method to achieve EMG-based torque estimation for a robotic exoskeleton. IEEE/ASME Trans. Mechatron. 2019, 24, 483–494. [Google Scholar] [CrossRef]
- Yokoyama, M.; Koyama, R.; Yanagisawa, M. An evaluation of hand-force prediction using artificial neural-network regression models of surface EMG signals for handwear devices. J. Sens. 2017, 2017. [Google Scholar] [CrossRef]
- Zhang, Q.; Hayashibe, M.; Fraisse, P.; Guiraud, D. FES-Induced torque prediction with evoked EMG sensing for muscle fatigue tracking. IEEE/ASME Trans. Mechatron. 2011, 16, 816–826. [Google Scholar] [CrossRef]
- Xiao, Z.G.; Menon, C. Towards the development of a wearable feedback system for monitoring the activities of the upper-extremities. J. NeuroEng. Rehabil. 2014, 11, 2. [Google Scholar] [CrossRef] [PubMed]
- Xiao, Z.G.; Menon, C. A Review of Force Myography Research and Development. Sensors 2019, 19, 4557. [Google Scholar] [CrossRef] [PubMed]
- Kadkhodayan, A.; Jiang, X.; Menon, C. Continuous prediction of finger movements using force myography. J. Med. Biol. Eng. 2016, 36, 594–604. [Google Scholar] [CrossRef]
- Chegani, R.S.; Menon, C. Regressing grasping using force myography: An exploratory study. BioMed. Eng. Online 2018, 17, 159. [Google Scholar] [CrossRef]
- Jiang, X.; Merhi, L.-K.; Menon, C. Force exertion affects grasp classification using force myography. IEEE Trans. Hum.-Mach. Syst. 2018, 48, 219–226. [Google Scholar] [CrossRef]
- Sakr, M.; Menon, C. On the estimation of isometric wrist/forearm torque about three axes using force myography. In Proceedings of the 2016 6th IEEE International Conference on Biomedical Robotics and Biomechatronics (BioRob), Singapore, 26–29 June 2016; pp. 827–832. [Google Scholar]
- Delva, M.L.; Sakr, M.; Chegani, R.S.; Khoshnam, M.; Menon, C. Investigation into the Potential to Create a Force Myography-based Smart-home Controller for Aging Populations. In Proceedings of the 2018 7th IEEE International Conference on Biomedical Robotics and Biomechatronics (Biorob), Enschede, The Netherlands, 26–29 August 2018; pp. 770–775. [Google Scholar]
- Sanford, J.; Patterson, R.; Popa, D.O. Concurrent surface electromyography and force myography classification during times of prosthetic socket shift and user fatigue. J. Rehab. Asst. Tech. Eng. 2017, 4. [Google Scholar] [CrossRef]
- Jiang, X.; Merhi, L.K.; Xiao, Z.G.; Menon, C. Exploration of force myography and surface electromyography in hand gesture classification. Med. Eng. Phys. 2017, 41, 63–73. [Google Scholar] [CrossRef]
- Belyea, A.; Englehart, K.; Scheme, E. FMG Versus EMG: A comparison of usability for real-time pattern recognition based control. IEEE Trans. Biomed. Eng. 2019, 66, 3098–3104. [Google Scholar] [CrossRef]
- Li, Y.; Ge, S.S. Human-robot collaboration based on motion intention estimation. IEEE/ASME Trans. Mechatron. 2014, 19, 1007–1014. [Google Scholar] [CrossRef]
- Ravichandar, H.C.; Dani, A.P. Human intention inference using expectation-maximization algorithm with online model learning. IEEE Trans. Auto. Sci. Eng. 2017, 14, 855–868. [Google Scholar] [CrossRef]
- Owoyemi, J.; Hashimoto, K. Learning human motion intention with 3D convolutional neural network. In Proceedings of the 2017 IEEE International Conference on Mechatronics and Automation (ICMA), Takamatsu, Japan, 6–9 August 2017; pp. 1810–1815. [Google Scholar]
- Yu, X.; He, W.; Li, Y.; Yang, C.; Sun, C. Neural control for constrained human-robot interaction with human motion intention estimation and impedance learning. In Proceedings of the 2017 Chinese Automation Congress (CAC), Jinan, China, 20–22 October 2017; pp. 2682–2687. [Google Scholar]
- Stroeve, S. Impedance characteristics of a neuromusculoskeletal model of the human arm I. Posture control. Biol. Cybern. 1999, 81, 475–494. [Google Scholar] [CrossRef] [PubMed]
- Tanzio Printed Electronics. Available online: https://tangio.co/collections/frontpage (accessed on 27 January 2020).
- Zaber Technologies Inc. Available online: https://www.zaber.com/products/linear-stages/X-LSQ/details/X-LSQ450B (accessed on 27 January 2020).
- ATI Industrial Automation. Available online: https://www.ati-ia.com/products/ft/.ft_models.aspx?id=Mini45 (accessed on 27 January 2020).
- Ergonomics. Available online: http://www.ergonomics4schools.com/lzone/workspace.htm (accessed on 27 January 2020).
- Karwowski, W. International Encyclopedia of Ergonomics and Human Factors, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2006; Volume 3, ISBN 9780415304306. [Google Scholar]
- Komati, B.; Pac, M.R.; Clévy, C.; Popa, D.O.; Lutz, P. Explicit force control vs. impedance control for micromanipulation. In ASME 2013 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference; American Society of Mechanical Engineers Digital Collection: Portland, OR, USA, 2013; pp. 1–8. [Google Scholar]
- Pozdnoukhov, A.; Bengio, S. Semi-supervised kernel methods for regression estimation. In Proceedings of the 2006 IEEE International Conference on Acoustics Speech and Signal Processing Proceedings, Toulouse, France, 14–19 May 2006; Volume 5, pp. 577–580. [Google Scholar]
- Ferris, D.P.; Sawicki, G.S.; Daley, M.A. A physiologist’s perspective on robotic exoskeletons for human locomotion. Int. J. Humanoid Robot. 2007, 4, 507–528. [Google Scholar] [CrossRef] [PubMed]
- Zhou, L.; Bai, S.; Li, Y. Energy Optimal Trajectories in Human Arm Motion Aiming for Assistive Robots. J. Model. Identif. Control 2017, 38, 11–19. [Google Scholar] [CrossRef]
- Malosio, M.; Pedrocchi, N.; Vicentini, F.; Tosatti, L.M. Analysis of Elbow-Joints Misalignment in Upper-Limb Exoskeleton. In Proceedings of the 2011 IEEE International Conference on Rehabilitation Robotics, Zurich, Switzerland, 29 June–1 July 2011; pp. 456–461. [Google Scholar]
- Field, A. Discovering Statistics Using IBM SPSS, 5th ed.; Sage: Los Angeles, CA, USA, 2017. [Google Scholar]
- Ju, Z.; Liu, H. Human arm motion analysis with multisensory information. IEEE/ASME Trans. Mechatron. 2014, 19, 456–466. [Google Scholar] [CrossRef]
- Suzuki, Y.; Pan, Y.; Suzuki, S.; Kurihara, K.; Furuta, K. Human Operation with XY-Stages-Human Adaptive Mechatronics. In Proceedings of the 2006 IEEE International Conference on Systems, Man and Cybernetics, Taipei, Taiwan, 8–11 October 2006; pp. 4034–4039. [Google Scholar]
- Jiang, N.; Muceli, S.; Graimann, B.; Farina, D. Effect of arm position on the prediction of kinematics from EMG in amputees. Med. Biol. Eng. Comput. 2013, 51, 143–151. [Google Scholar] [CrossRef]
- Xu, Y.; Terekhov, A.V.; Latash, M.L.; Zatsiorsky, V.M. Forces and moments generated by the human arm: Variability and control. Exp. Brain Res. 2012, 223, 159–175. [Google Scholar] [CrossRef]
- Xiao, Z.G.; Menon, C. Performance of forearm FMG and sEMG for estimating elbow, forearm and wrist positions. J. Bionic Eng. 2017, 14, 284–295. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, Q.; Zeng, N.; Chen, J.; Zhang, Q. Discrete hand motion intention decoding based on transient myoelectric signals. IEEE Access 2019, 7, 81360–81369. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, G.; Han, B.; Wang, Z.; Zhang, T. sEMG based human motion intention recognition. J. Robot. 2019. [Google Scholar] [CrossRef]
- Côté-Allard, U.; Gagnon-Turcotte, G.; Phinyomark, A.; Glette, K.; Scheme, E.; LaViolette, F.; Gosselin, B. Virtual Reality to Study the Gap Between Offline and Real-Time EMG-based Gesture Recognition. arXiv 2009, arXiv:1912.09380. (submitted on December 2019). [Google Scholar]
- Sakr, M.; Menon, C. Exploratory evaluation of the force myography (FMG) signals usage for force control of a linear actuator. In Proceedings of the 2018 7th IEEE International Conference on Biomedical Robotics and Biomechatronics (Biorob), Enschede, The Netherlands, 26–29 August 2018; pp. 903–908. [Google Scholar]



| Devices | |
|---|---|
| Two force myography (FMG) bands with 16 force-sensing resistors (FSRs) each |
|
| |
| Biaxial stage with a gripper/knob (9600 bps) |
|
| |
| Force sensor |
|
| Model | Hyperparameters Ranges | Parameter Selection | Matlab Toolbox |
|---|---|---|---|
| Support vector regressor (SVR) | Cost = 20, Gamma = 1 | Grid search | livsvm |
| Kernel ridge regressor (KRR) | Lambda = 1, Kernel width parameter = 0.9 | Trial & Error | Kernel methods toolbox |
| X | Y | Diagonal | Square | Diamond |
|---|---|---|---|---|
 |  |  |  |  |
| Measures of Estimations | ||
|---|---|---|
| Accuracy | Coefficient of determination (R2) | Equation (3) |
| Error | Normalized root mean square error (NRMSE) | Equation (4) |
| Feature | Age (year) | Height (cm) | Arm Length (cm) | Upper Arm (cm) | Forearm (cm) |
|---|---|---|---|---|---|
| Mean | 33 | 175 | 74 | 29 | 27 |
| Standard deviation | 8 | 5 | 4 | 3 | 3 |
| Mode | 35 | 178 | 78 | 29 | 27 |
| Real-time (RT) FMG-based admittance control of a biaxial stage by an estimated hand force in an intended arm motion pattern | |
| Input: Forearm and upper-arm FMG signals, x = [x1, x2, …, x32] True labels from a force sensor, y = [Fx, Fy] | |
| Output: FMG-based estimated force, y’ = [Fx’, Fy’] to control the velocity of the biaxial stage | |
| Initialization:z seconds, n data samples, r repetitions, m reg.model {SVR, KRR} | |
| 1: | forzdo |
| 2: | Compute maximum voluntary contraction (MVC) in a planar surface |
| 3: | end for |
| 4: | Target_forceH ← above MVCs of 30% and below MVCs of 80% |
| 5: | Display ← (Target_forceH, Intended_motion) |
| 6: | while (RT_Data_collection_phase = = true) do |
| 7: | r = 1; |
| 8: | repeat |
| 9: | for n samples do |
| 10: | while (exerted_force = = true) do |
| 11: | Collect x and y and save them in comma-separated values (csv) format |
| 12: | end for |
| 13: | r = r + 1; |
| 14: | until r = 5; |
| 15: | end while |
| 16: | while (RT_Training_phase = = true) do |
| 17: | Select m reg_model |
| 18: | Select r rep csv files |
| 19: | Trained_model ← {x, y} |
| 20: | end while |
| 21: | while (RT_Test_phase = = true) do |
| 22: | Select m reg_model |
| 23: | while (exerted_force = = true) do |
| 24: | FMG-based estimated force, y′ ← Equation (3) |
| 25: | Velocity of the biaxial stage ← Equation (2) |
| 26: | end while |
| 27: | end while |
| Collaborative Task | Training Data (Labeled FMG Signals) | Test Data (Estimated Forces and Labeled FMG Signals) |
|---|---|---|
| A participant interacting with the stage by sliding its gripper with an exerted hand force in an intended motion | 2000 records or 68,000 data samples | 1000 records or 36,000 data samples |
| Data Sample | Regression Model | Test Accuracy (R2) | Test Error (NRMSE) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| X | Y | DG * | SQ * | DM * | X | Y | DG * | SQ * | DM * | ||
| Training: 2000 records | SVR | 0.94 ± 0.04 | 0.91 ± 0.04 | 0.88 ± 0.07 | 0.84 ± 0.09 | 0.82 ± 0.09 | 0.10 ± 0.05 | 0.11 ± 0.03 | 0.10 ± 0.03 | 0.10 ± 0.04 | 0.11 ± 0.03 |
| Testing: 1000 records | KRR | 0.92 ± 0.03 | 0.90 ± 0.05 | 0.91 ± 0.07 | 0.86 ± 0.09 | 0.85 ± 0.10 | 0.10 ± 0.04 | 0.12 ± 0.017 | 0.09 ± 0.02 | 0.10 ± 0.04 | 0.13 ± 0.02 |
| X | Y | Diagonal | Square | Diamond | |
|---|---|---|---|---|---|
| SVR | 0.1091 | 0.1114 | 0.1055 | 0.1092 | 0.1188 |
| KRR | 0.1174 | 0.1154 | 0.0997 | 0.1069 | 0.1262 |
| Arm Motion Patterns | Mean Difference | SD | Corrected p-Value |
|---|---|---|---|
| X–SQ | 0.103 | 0.013 | 0.000 |
| X–DM | 0.121 | 0.019 | 0.000 |
| Y–SQ | 0.074 | 0.022 | 0.048 |
| Y–DM | 0.092 | 0.026 | 0.049 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zakia, U.; Menon, C. Estimating Exerted Hand Force via Force Myography to Interact with a Biaxial Stage in Real-Time by Learning Human Intentions: A Preliminary Investigation. Sensors 2020, 20, 2104. https://doi.org/10.3390/s20072104
Zakia U, Menon C. Estimating Exerted Hand Force via Force Myography to Interact with a Biaxial Stage in Real-Time by Learning Human Intentions: A Preliminary Investigation. Sensors. 2020; 20(7):2104. https://doi.org/10.3390/s20072104
Chicago/Turabian StyleZakia, Umme, and Carlo Menon. 2020. "Estimating Exerted Hand Force via Force Myography to Interact with a Biaxial Stage in Real-Time by Learning Human Intentions: A Preliminary Investigation" Sensors 20, no. 7: 2104. https://doi.org/10.3390/s20072104
APA StyleZakia, U., & Menon, C. (2020). Estimating Exerted Hand Force via Force Myography to Interact with a Biaxial Stage in Real-Time by Learning Human Intentions: A Preliminary Investigation. Sensors, 20(7), 2104. https://doi.org/10.3390/s20072104






