Smart Soft Sensor Design with Hierarchical Sampling Strategy of Ensemble Gaussian Process Regression for Fermentation Processes
Abstract
1. Introduction
2. Preliminaries
2.1. Gaussian Process Regression
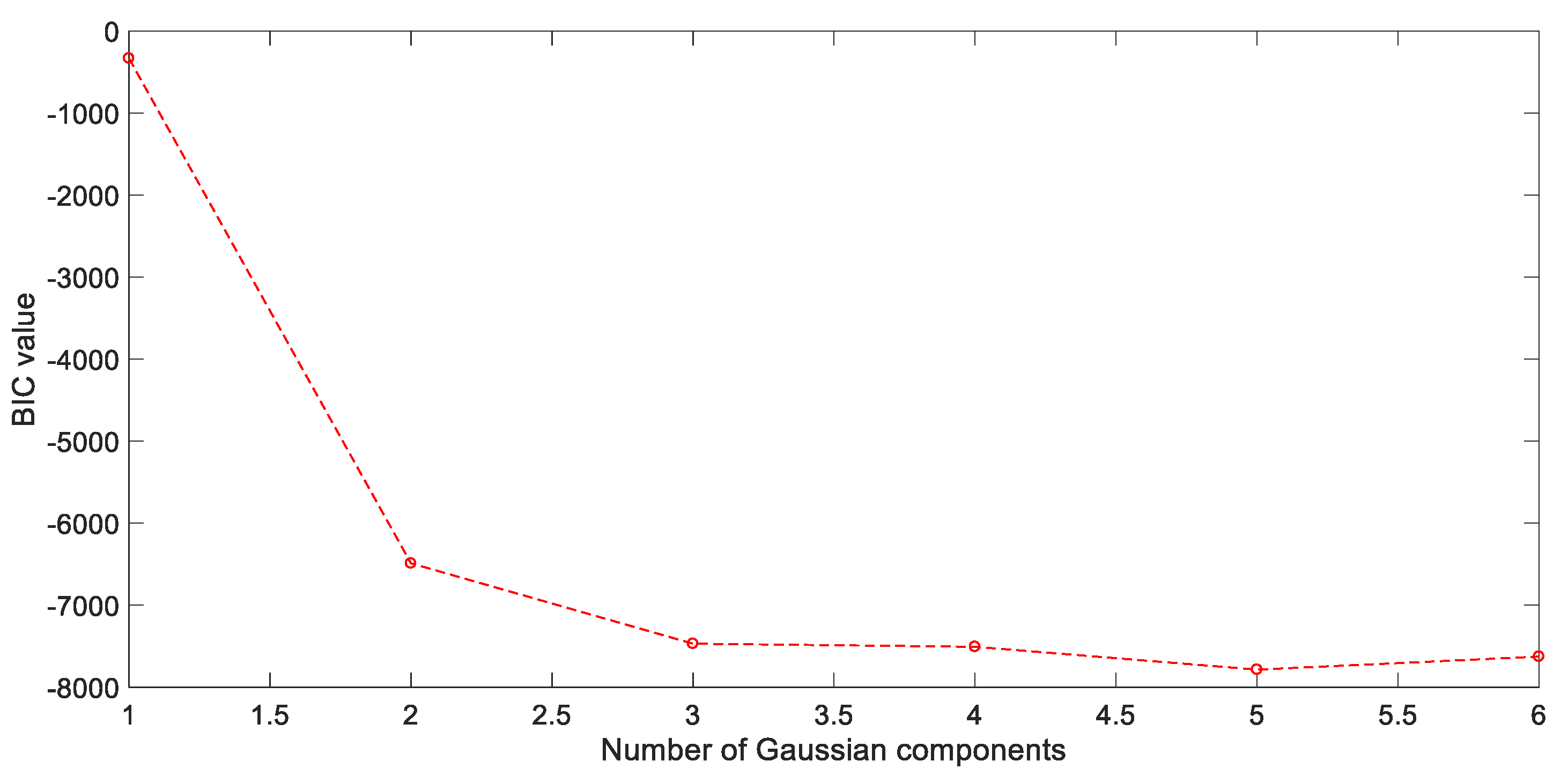
2.2. Gaussian Mixture Model
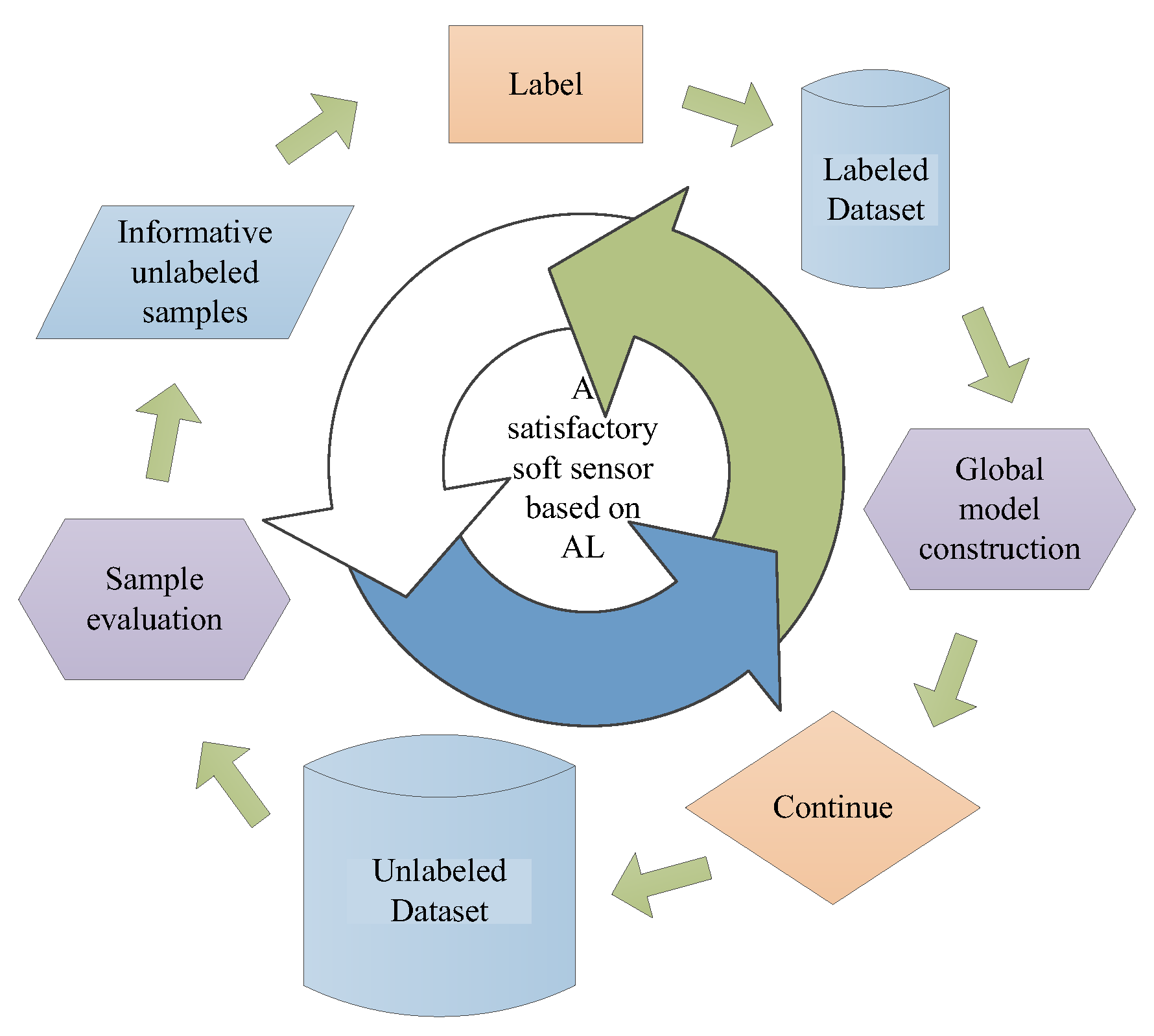
3. Hierarchical Sampling Strategy Based Active Learning Framework
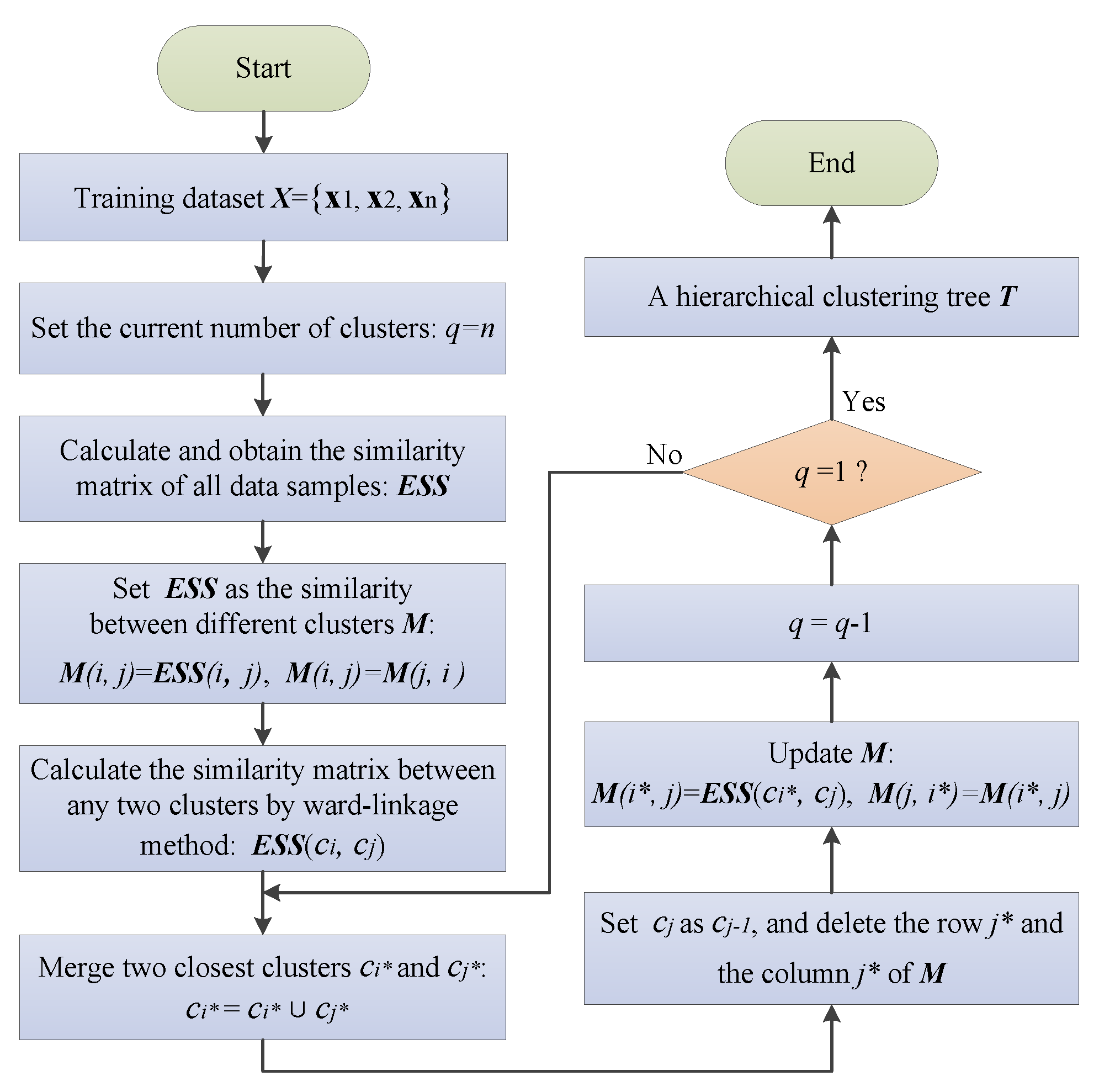
3.1. Hierarchical Clustering Algorithm
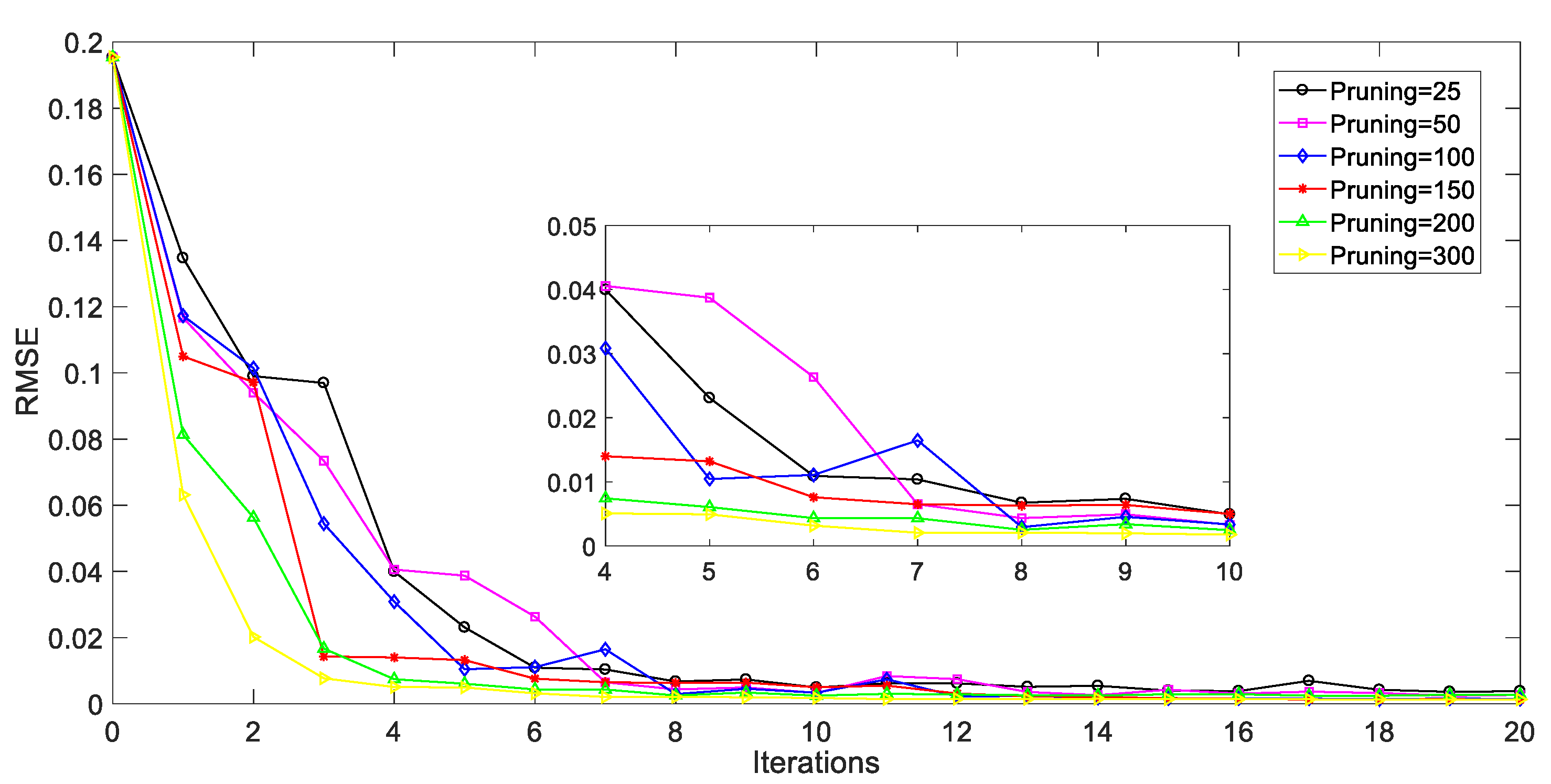
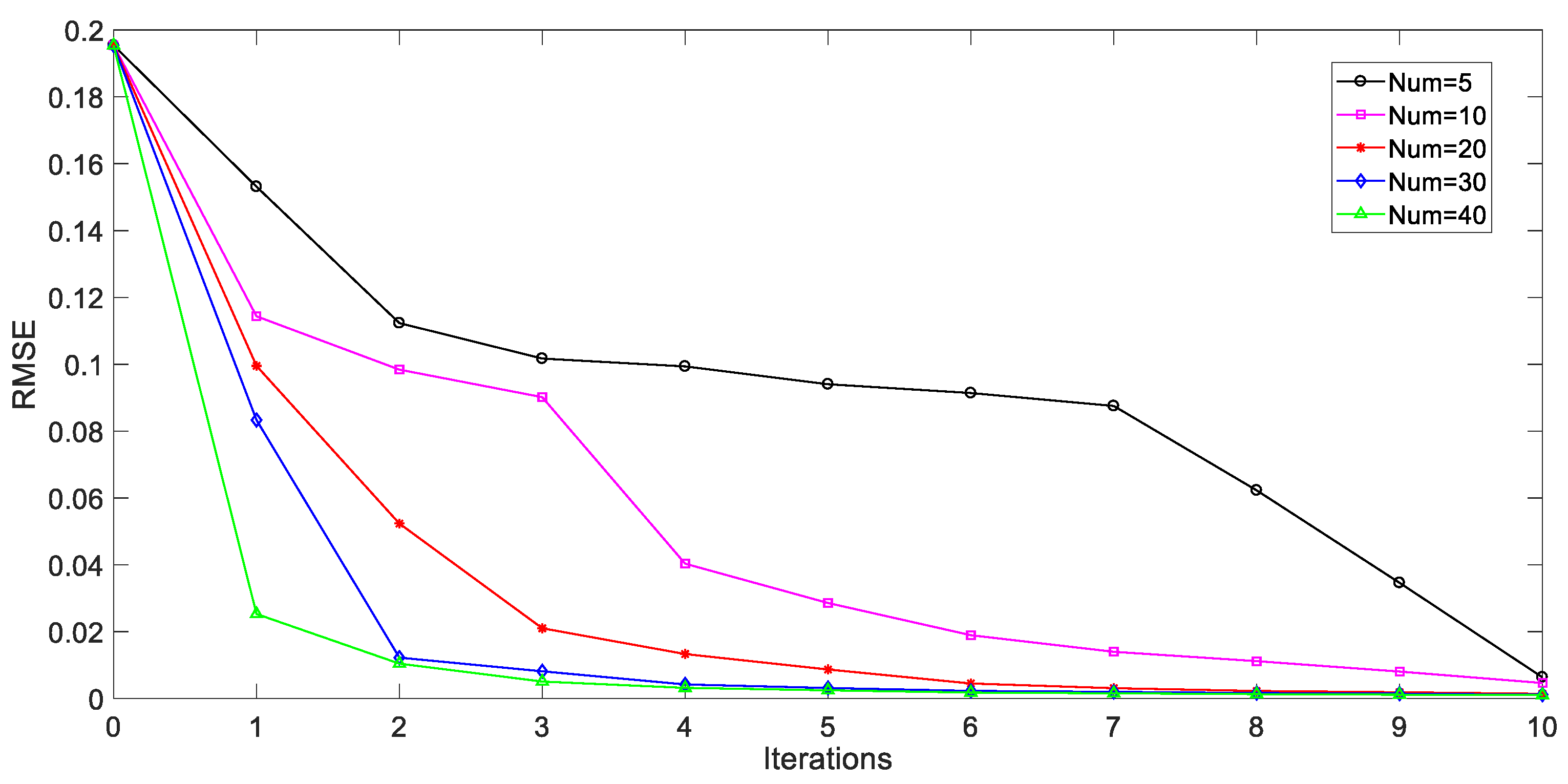
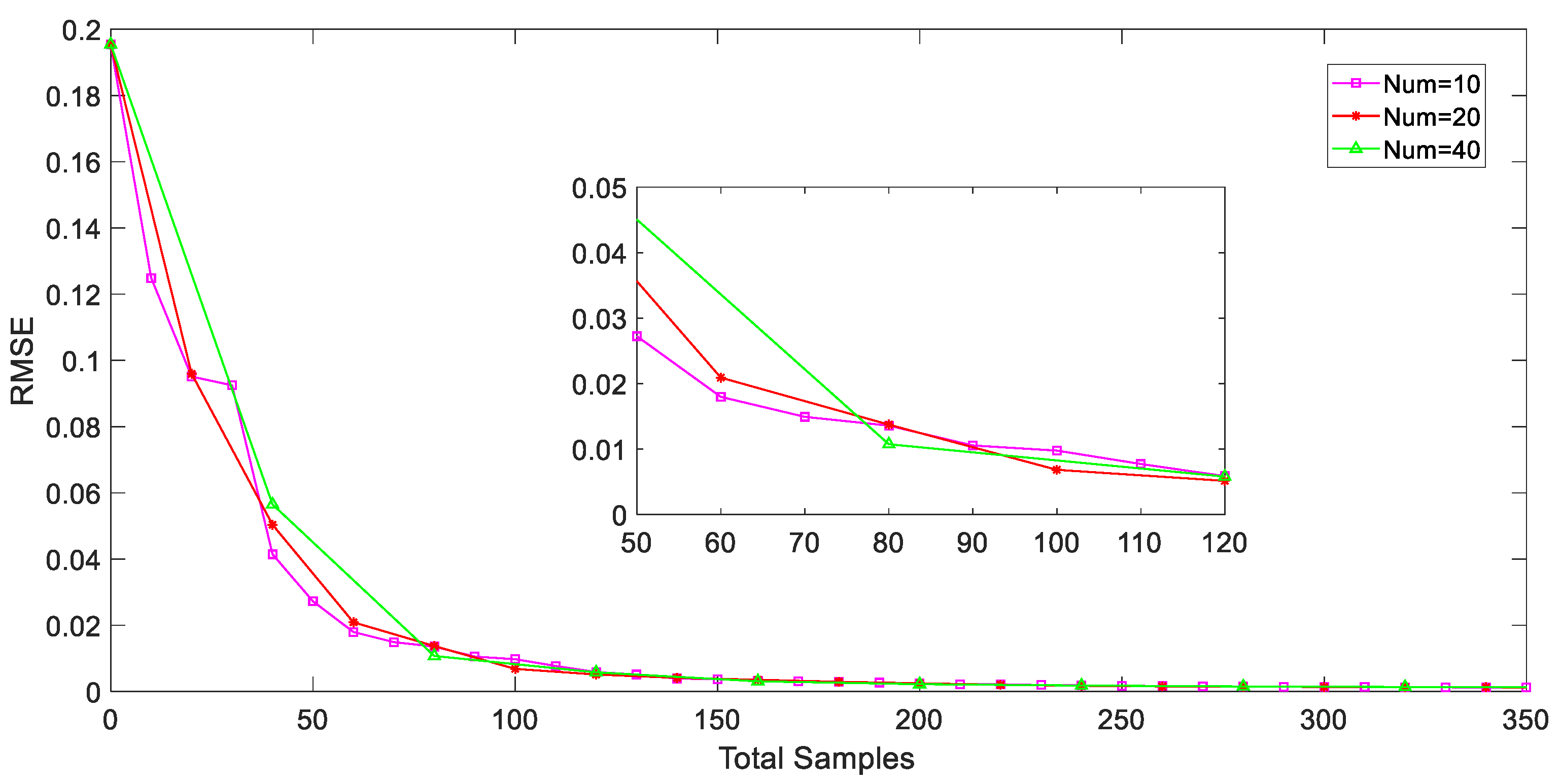
3.2. Adaptive Sampling Strategy
| Algorithm 1. The proposed hierarchical sampling strategy under AL framework. |
| Input: a HC tree of unlabeled data samples; iteration step Process:
Output: Newly labeled dataset , . |
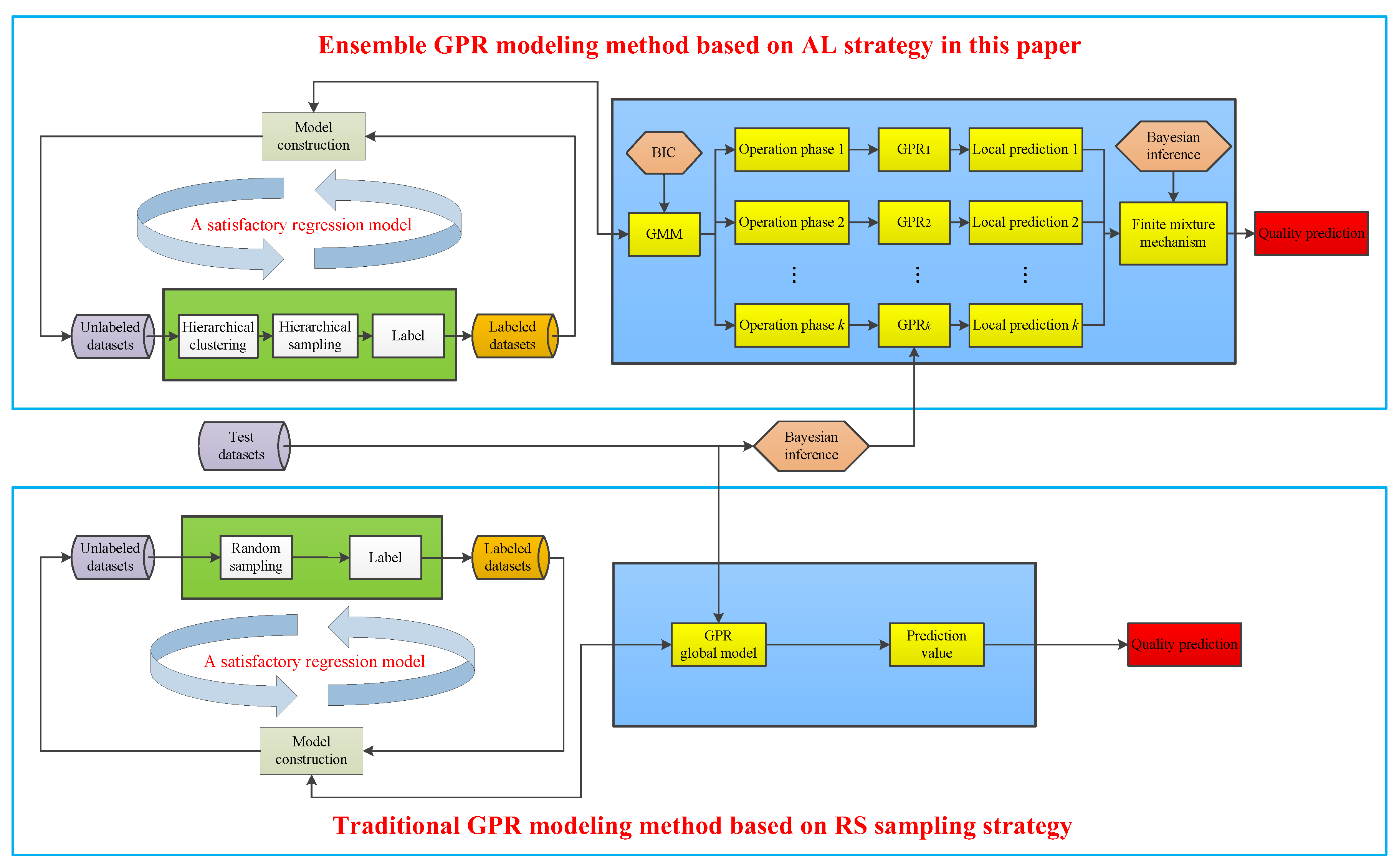
4. Ensemble GPR Modelling Method Under AL Framework
5. Case Study
5.1. Process Introduction
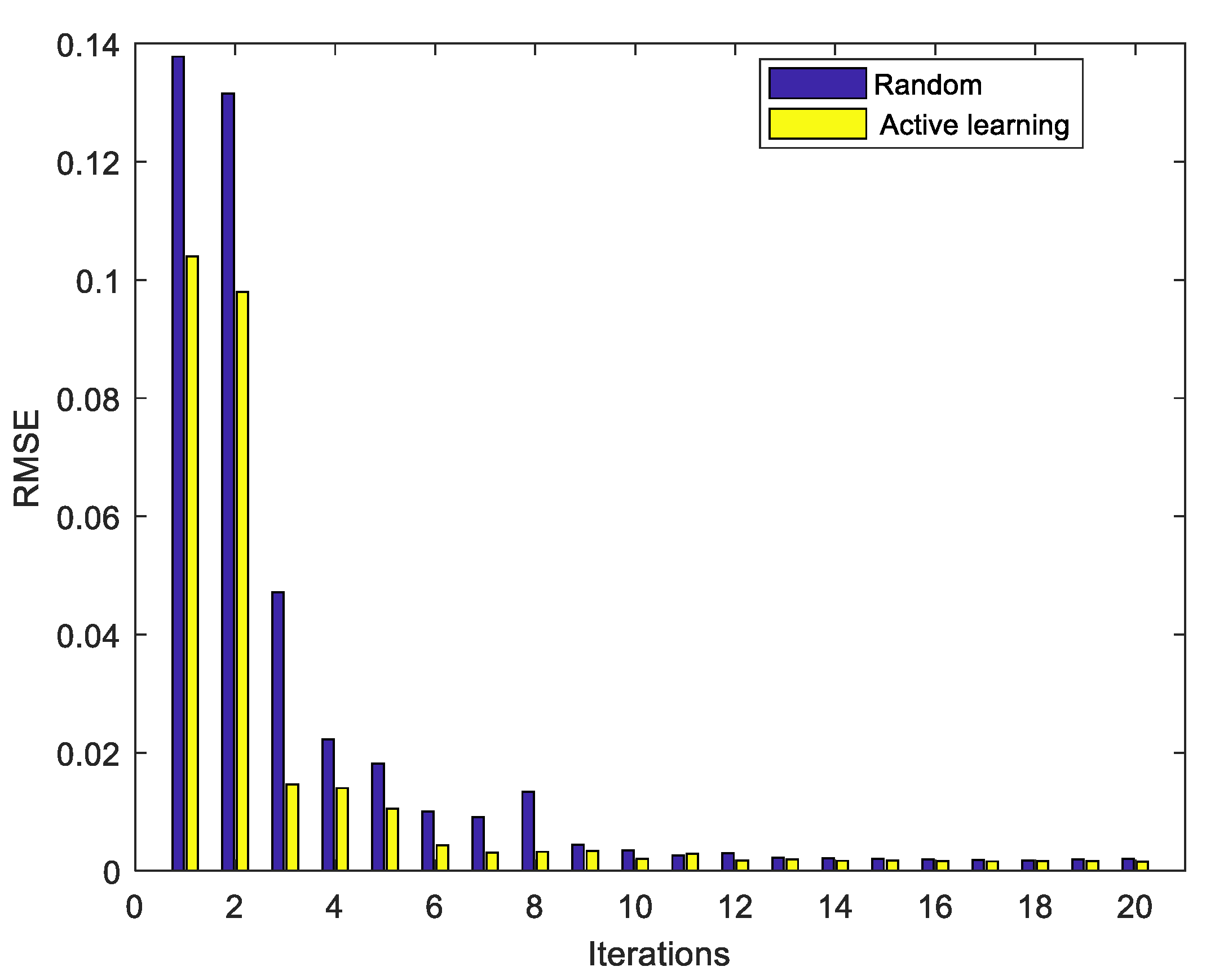
5.2. Performance Evaluation of the Proposed AL Strategy
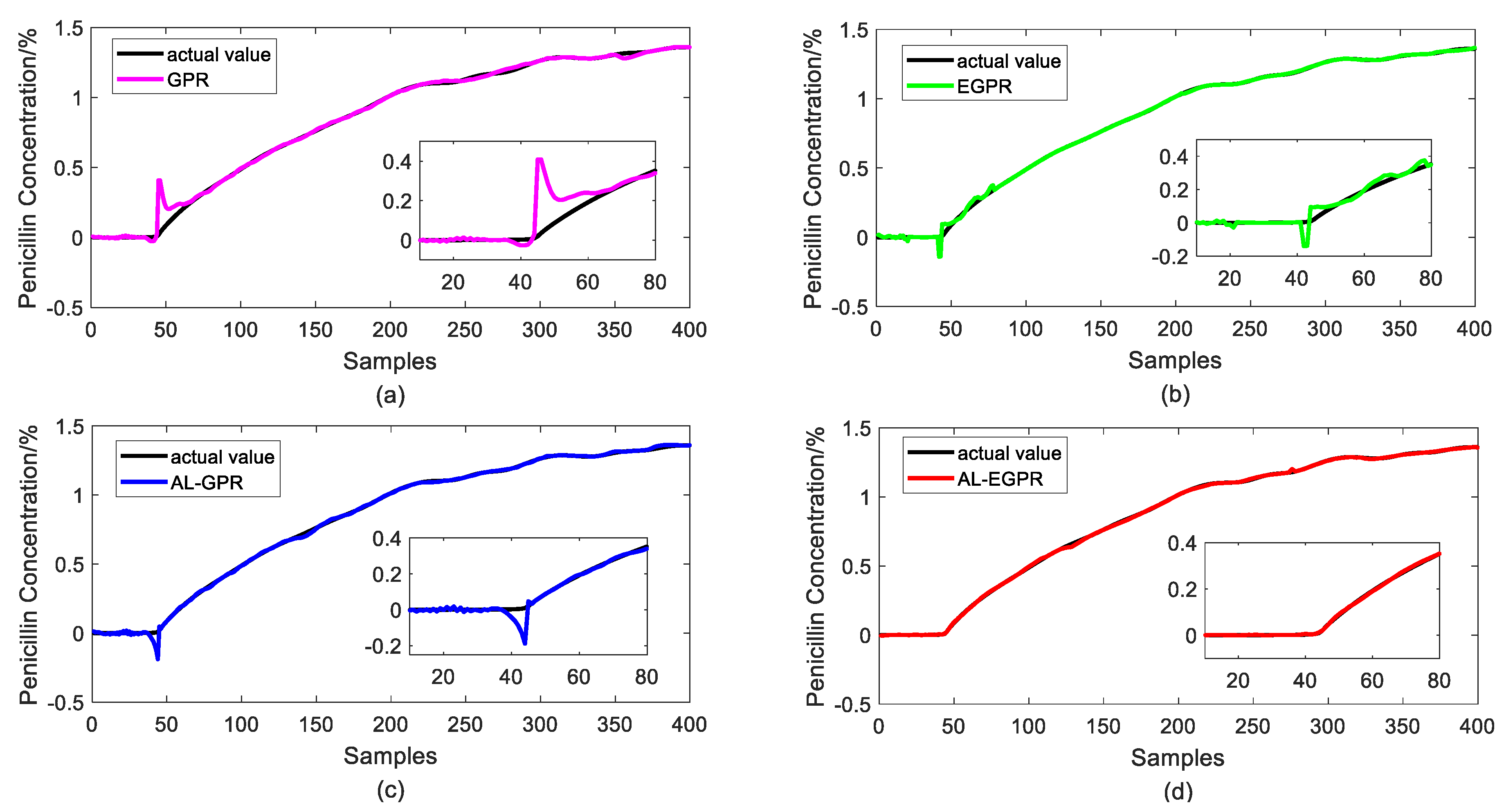
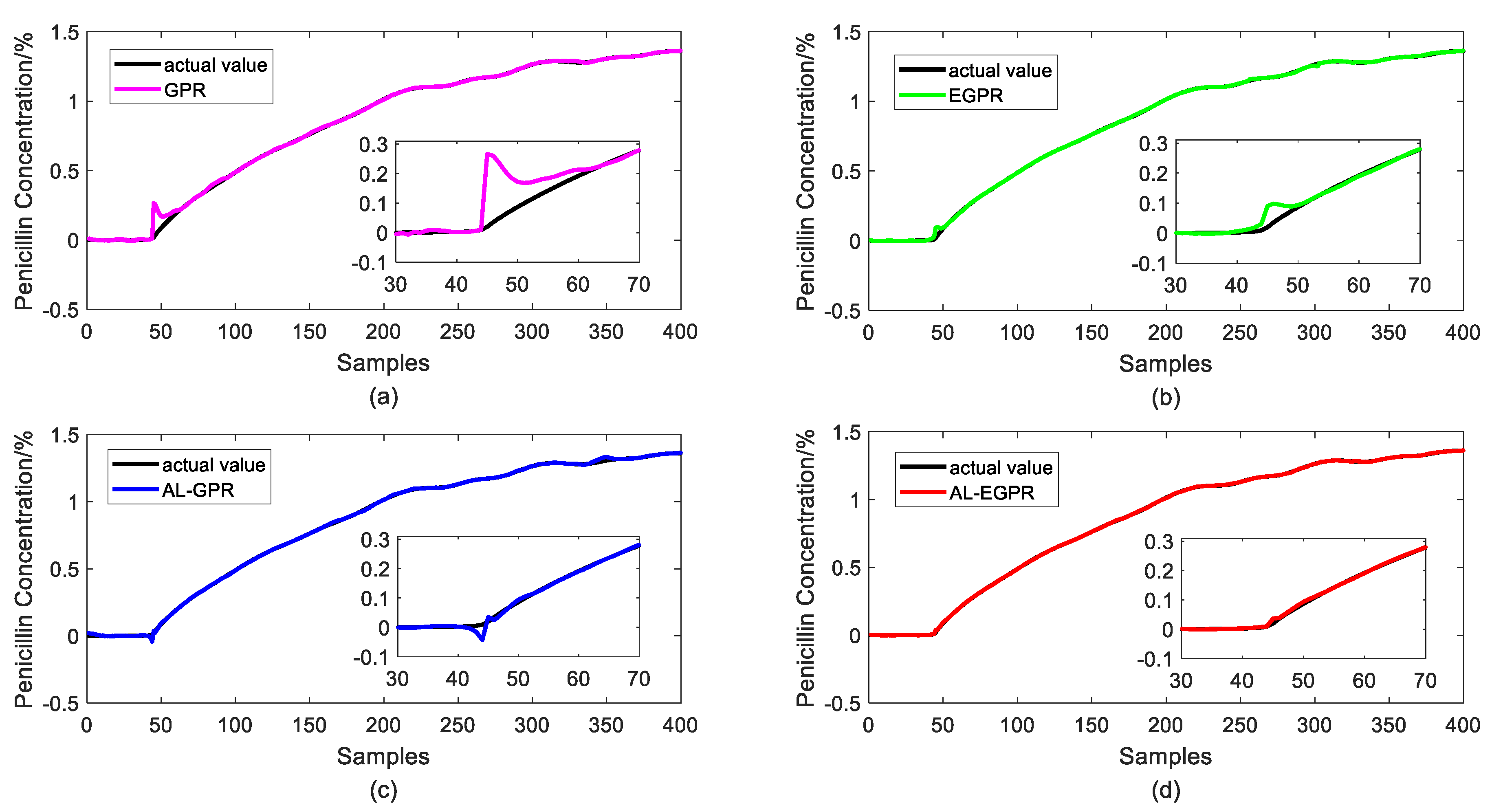
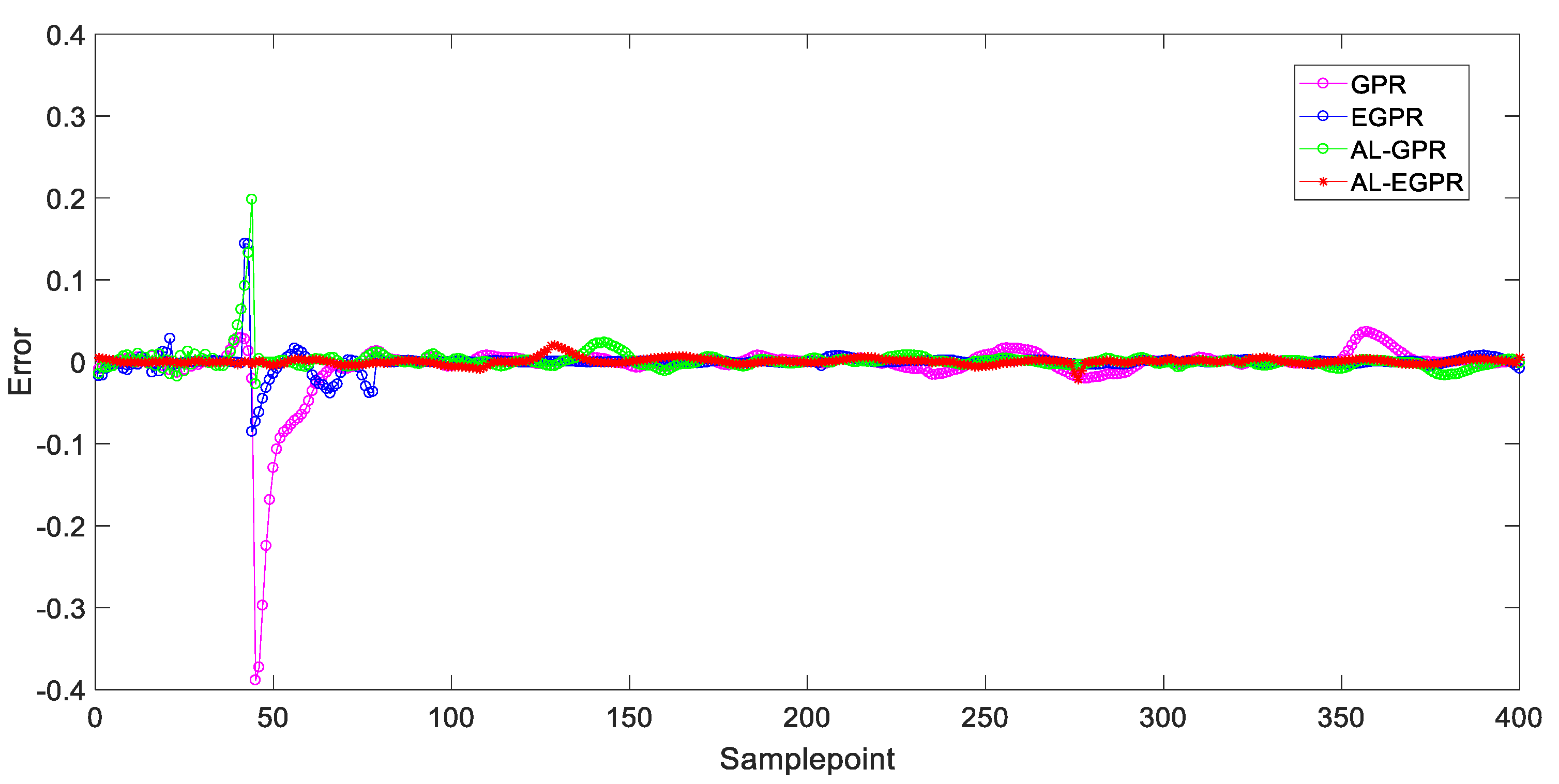
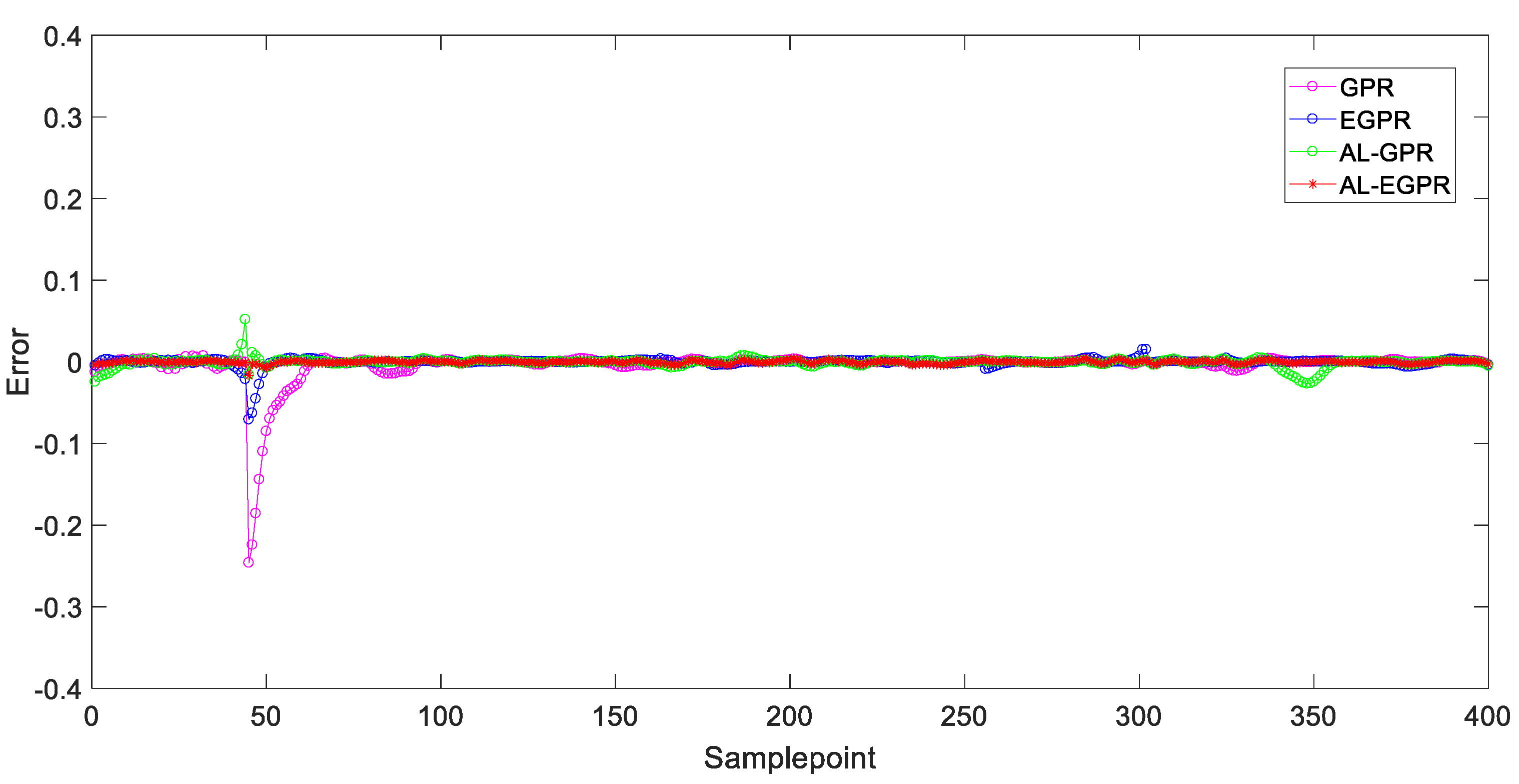
5.3. Prediction Results and Discussions
- (1)
- GPR (GPR based on RS strategy): To iteratively select unlabeled samples for labeling with RS sampling strategy, and to construct a global GPR model.
- (2)
- EGPR (ensemble GPR based on RS strategy): Firstly, to iteratively select unlabeled samples for labeling with RS sampling strategy, to further construct local GPR models on different regions divided by GMM method, and finally to integrate the base predictors by applying the Bayesian fusion strategy.
- (3)
- AL-GPR (GPR based on AL strategy): To iteratively select unlabeled samples for labeling with hierarchical sampling based AL strategy and construct a global GPR model.
- (4)
- AL-EGPR (ensemble GPR based on AL strategy): the proposed method.
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| AI | artificial intelligence |
| AL | active learning |
| AL-GPR | Gaussian process regression based on active learning |
| AL-EGPR | ensemble Gaussian process regression based on active learning |
| ANN | artificial neural network |
| BIC | Bayesian information criterion |
| EGPR | ensemble Gaussian process regression with random selection strategy |
| EM | expectation maximization |
| FCM | fuzzy C-means |
| GMM | Gaussian mixture model |
| GP | Gaussian process |
| GPR | Gaussian process regression |
| HC | hierarchical clustering |
| ML | machine learning |
| PCR | principal component regression |
| PFP | penicillin fermentation process |
| PLS | partial least squares |
| RMSE | root-mean-square error |
| RS | random selection |
| SVM | support vector machine |
| TP | tracking precision |
References
- Jordan, M.I.; Mitchell, T.M. Machine learning: Trends, perspectives, and prospects. Science 2015, 349, 255–260. [Google Scholar] [CrossRef]
- Villalba-Diez, J.; Schmidt, D.; Gevers, R.; Ordieres-Meré, J.; Buchwitz, M.; Wellbrock, W. Deep Learning for Industrial Computer Vision Quality Control in the Printing Industry 4.0. Sensors 2019, 19, 3987. [Google Scholar] [CrossRef] [PubMed]
- Fortuna, L.; Graziani, S.; Rizzo, A.; Xibilia, M.G. Soft Sensors for Monitoring and Control of Industrial Processes; Springer: London, UK, 2007. [Google Scholar]
- Kadlec, P.; Gabrys, B.; Strandt, S. Data-driven soft sensors in the process industry. Comput. Chem. Eng. 2009, 33, 795–814. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, J. Integrated soft sensor using just-in-time support vector regression and probabilistic analysis for quality prediction of multi-grade processes. J. Process Control 2013, 23, 793–804. [Google Scholar] [CrossRef]
- Hou, S.; Zhang, X.; Dai, W.; Han, X.; Hua, F. Multi-Model-and Soft-Transition-Based Height Soft Sensor for an Air Cushion Furnace. Sensors 2020, 20, 926. [Google Scholar] [CrossRef] [PubMed]
- Cang, W.; Yang, H. Adaptive soft sensor method based on online selective ensemble of partial least squares for quality prediction of chemical process. Asia-Pac. J. Chem. Eng. 2019, 14, 2346. [Google Scholar] [CrossRef]
- Marengo, E.; Bobba, M.; Robotti, E.; Liparota, M.C. Modeling of the polluting emissions from a cement production plant by partial least-squares, principal component regression, and artificial neural networks. Environ. Sci. Technol. 2006, 40, 272–280. [Google Scholar] [CrossRef]
- Das, S.; Saha, S. Data mining and soft computing using support vector machine: A survey. Int. J. Comput. Appl. 2013, 77, 40–47. [Google Scholar] [CrossRef]
- Abdar, M.; Makarenkov, V. CWV-BANN-SVM ensemble learning classifier for an accurate diagnosis of breast cancer. Measurement 2019, 146, 557–570. [Google Scholar] [CrossRef]
- Xiong, W.; Shi, X. Soft sensor modeling with a selective updating strategy for Gaussian process regression based on probabilistic principle component analysis. J. Frankl. Inst. 2018, 355, 5336–5349. [Google Scholar]
- Yu, J. Online quality prediction of nonlinear and non-Gaussian chemical processes with shifting dynamics using finite mixture model based Gaussian process regression approach. Chem. Eng. Sci. 2012, 82, 22–30. [Google Scholar] [CrossRef]
- Wang, L.; Jin, H.; Chen, X. Soft sensor development based on the hierarchical ensemble of Gaussian process regression models for nonlinear and non-Gaussian chemical processes. Ind. Eng. Chem. Res. 2016, 55, 7704–7719. [Google Scholar] [CrossRef]
- Ni, W.; Nørgaard, L.; Mørup, M. Non-linear calibration models for near infrared spectroscopy. Anal. Chim. Acta 2014, 813, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Shao, W.; Tian, X. Semi-supervised selective ensemble learning based on distance to model for nonlinear soft sensor development. Neurocomputing 2017, 222, 91–104. [Google Scholar] [CrossRef]
- He, X.; Ji, J.; Liu, K.; Gao, Z.; Liu, Y. Soft Sensing of Silicon Content via Bagging Local Semi-Supervised Models. Sensors 2019, 19, 3814. [Google Scholar] [CrossRef]
- Skurichina, M.; Duin, R.P.W. Bagging, boosting and the random subspace method for linear classifiers. Pattern Anal. Appl. 2002, 5, 121–135. [Google Scholar] [CrossRef]
- He, Z.; Ho, C.-H. An improved clustering algorithm based on finite Gaussian mixture model. Multimed. Tools Appl. 2019, 78, 24285–24299. [Google Scholar] [CrossRef]
- Cebeci, Z.; Yildiz, F. Comparison of k-means and fuzzy c-means algorithms on different cluster structures. J. Agric. Inform. 2015, 6, 13–23. [Google Scholar] [CrossRef]
- Yang, Y.Y.; Mahfouf, M.; Panoutsos, G. Probabilistic characterisation of model error using Gaussian mixture model—With application to Charpy impact energy prediction for alloy steel. Control Eng. Pract. 2012, 20, 82–92. [Google Scholar] [CrossRef]
- Yu, J. Multiway Gaussian mixture model based adaptive kernel partial least squares regression method for soft sensor estimation and reliable quality prediction of nonlinear multiphase batch processes. Ind. Eng. Chem. Res. 2012, 51, 13227–13237. [Google Scholar] [CrossRef]
- Zhu, J.; Ge, Z.; Song, Z. Variational Bayesian Gaussian mixture regression for soft sensing key variables in non-Gaussian industrial processes. IEEE Trans. Control Syst. Technol. 2017, 25, 1092–1099. [Google Scholar] [CrossRef]
- Mehmood, A.; On, B.-W.; Lee, I.; Ashraf, I.; Choi, G.S. Spam comments prediction using stacking with ensemble learning. J. Phys. Conf. Ser. 2018, 933, 012012. [Google Scholar] [CrossRef]
- Shi, X.; Xiong, W. Approximate linear dependence criteria with active learning for smart soft sensor design. Chemom. Intell. Lab. Syst. 2018, 180, 88–95. [Google Scholar] [CrossRef]
- Zhang, S.; Deng, G.; Wang, F. Active learning strategy for online prediction of particle size distribution in cobalt oxalate synthesis process. IEEE Access 2019, 7, 40810–40821. [Google Scholar] [CrossRef]
- Ge, Z. Active learning strategy for smart soft sensor development under a small number of labeled data samples. J. Process Control 2014, 24, 1454–1461. [Google Scholar] [CrossRef]
- Tang, Q.; Li, D.; Xi, Y. A new active learning strategy for soft sensor modeling based on feature reconstruction and uncertainty evaluation. Chemom. Intell. Lab. Syst. 2018, 172, 43–51. [Google Scholar] [CrossRef]
- Dumarey, M.; van Nederkassel, A.M.; Stanimirova, I.; Daszykowski, M. Recognizing paracetamol formulations with the same synthesis pathway based on their trace-enriched chromatographic impurity profiles. Anal. Chim. Acta 2009, 655, 43–51. [Google Scholar] [CrossRef]
- Yu, W. A mathematical morphology based method for hierarchical clustering analysis of spatial points on street networks. Appl. Soft Comput. 2019, 85, 105785. [Google Scholar] [CrossRef]
- Zhang, Z.; Pasolli, E.; Crawford, M.M.; Tilton, J.C. An active learning framework for hyperspectral image classification using hierarchical segmentation. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2016, 9, 640–654. [Google Scholar] [CrossRef]
- Ward, J.H., Jr. Hierarchical Grouping to Optimize an Objective Function. J. Am. Stat. Assoc. 1963, 58, 236–244. [Google Scholar] [CrossRef]
- Dasgupta, S.; Hsu, D. Hierarchical sampling for active learning. In Proceedings of the 25th International Conference on Machine Learning (ICML 2008), Helsinki, Finland, 5–9 July 2008; pp. 208–215. [Google Scholar] [CrossRef]
- Gopakumar, V.; Tiwari, S.; Rahman, I. A deep learning based data driven soft sensor for bioprocesses. Biochem. Eng. J. 2018, 136, 28–39. [Google Scholar] [CrossRef]
- Jin, H.; Chen, X.; Yang, J.; Zhang, H.; Wu, L. Multi-model adaptive soft sensor modeling method using local learning and online support vector regression for nonlinear time-variant batch processes. Chem. Eng. Sci. 2015, 131, 282–303. [Google Scholar] [CrossRef]

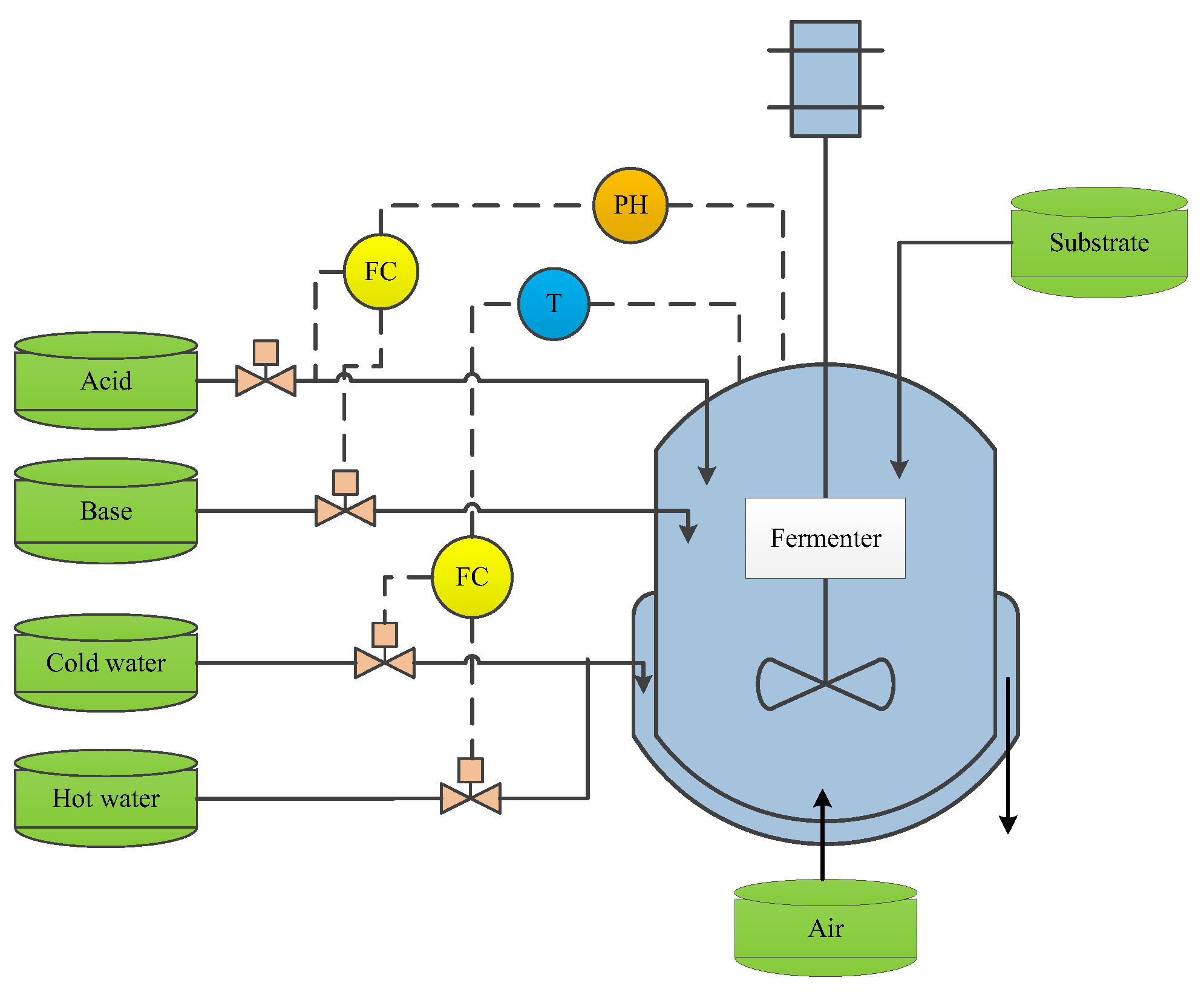
| Input Variables | Description | Unit |
|---|---|---|
| u1 | Culture volume | L |
| u2 | Agitator power | W |
| u3 | PH | - |
| u4 | Substrate feed temperature | K |
| u5 | Fermenter temperature | K |
| u6 | Substrate feed rate | g/h |
| u7 | Aeration rate | L/h |
| Methods | Sample Selection | Learning |
|---|---|---|
| GPR | Random | Global |
| EGPR | Random | Ensemble learning |
| AL-GPR | Active learning | Global |
| AL-EGPR | Active learning | Ensemble learning |
| Method | After the 3rd Iteration | After the 7th Iteration | ||
|---|---|---|---|---|
| RMSE | TP | RMSE | TP | |
| GPR | 0.0472 | 0.9894 | 0.0106 | 0.9995 |
| EGPR | 0.0155 | 0.9988 | 0.0069 | 0.9997 |
| AL-GPR | 0.0143 | 0.9991 | 0.0065 | 0.9997 |
| AL-EGPR | 0.0039 | 0.9998 | 0.0017 | 0.9999 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sheng, X.; Ma, J.; Xiong, W. Smart Soft Sensor Design with Hierarchical Sampling Strategy of Ensemble Gaussian Process Regression for Fermentation Processes. Sensors 2020, 20, 1957. https://doi.org/10.3390/s20071957
Sheng X, Ma J, Xiong W. Smart Soft Sensor Design with Hierarchical Sampling Strategy of Ensemble Gaussian Process Regression for Fermentation Processes. Sensors. 2020; 20(7):1957. https://doi.org/10.3390/s20071957
Chicago/Turabian StyleSheng, Xiaochen, Junxia Ma, and Weili Xiong. 2020. "Smart Soft Sensor Design with Hierarchical Sampling Strategy of Ensemble Gaussian Process Regression for Fermentation Processes" Sensors 20, no. 7: 1957. https://doi.org/10.3390/s20071957
APA StyleSheng, X., Ma, J., & Xiong, W. (2020). Smart Soft Sensor Design with Hierarchical Sampling Strategy of Ensemble Gaussian Process Regression for Fermentation Processes. Sensors, 20(7), 1957. https://doi.org/10.3390/s20071957




