A Systematic Methodology to Evaluate Prediction Models for Driving Style Classification
Abstract
1. Introduction
2. Background and Related Work
2.1. Driving Styles
2.2. Driving Styles Classification
2.2.1. Data Collection
2.2.2. Feature Space or Input
2.2.3. Output
2.2.4. Classification Models
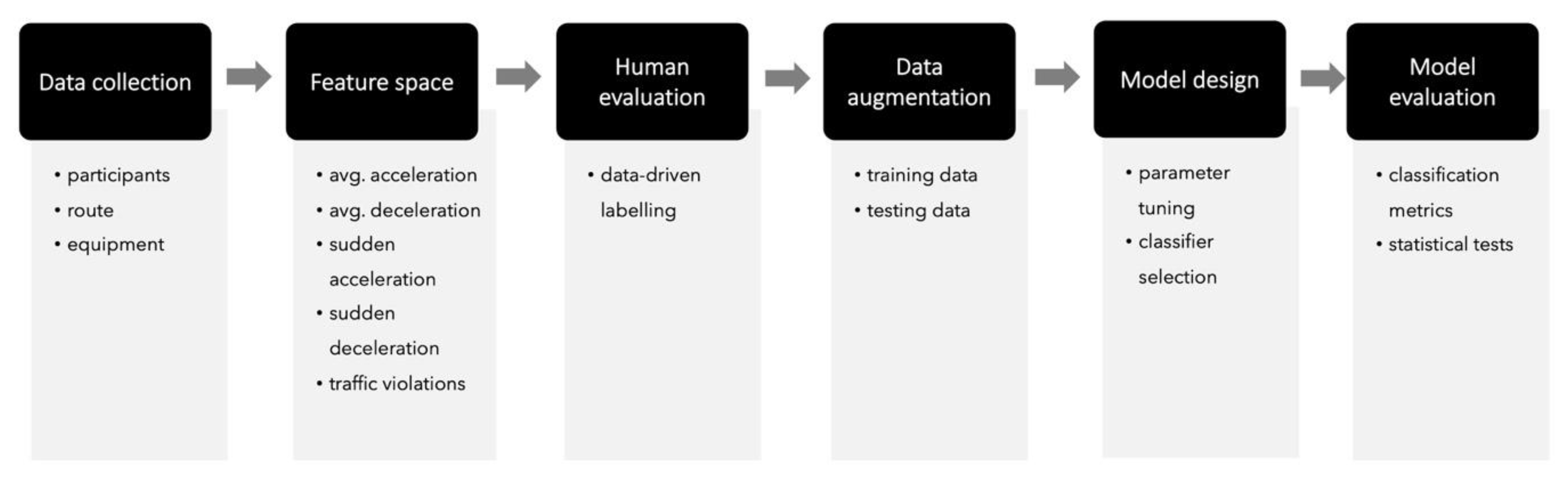
3. Methodology
- Data collection: The first step consists of gathering the in-vehicle data. Depending on the context, drivers are invited to participate in a data-capture session. The driver’s characteristics (e.g., experience, age) will be determined by the aim of the study being conducted. In addition, this step will define the route or routes to conduct driving tests and the equipment needed for capturing and synchronizing in-vehicle and external data. Depending on the research aim, we may consider recording timestamped data (e.g., for time-series or temporal analyses).
- Feature Space: Based on the data collected during the previous step, several features can be derived. The feature selection is a crucial step for machine-learning models, as these will define the performance of such models [41]. For driving styles-classification tasks, no consensus has been proposed among researchers to convey using a specific set of features. This disagreement is mainly due to the myriad of driving-styles applications (e.g., ADAS development, fuel consumption detection, safety road prevention) and research aims, as these will determine the set of features needed to perform the classification task [9].
- Human Evaluation: This step involves data evaluation by experts to get the ground truth. This step is a standard procedure to follow, when the overall purpose is to mimic experts’ decisions through automated algorithms or models. Usually, two or more raters (experts) inspect the data and assign a category or a score to each instance (a driver, in our particular case). The final category or score from each rater is then processed to calculate an inter-rater agreement score (e.g., inter-rater reliability (IRR) coefficient). A low score means that experts did not get similar results in the dataset evaluation, whereas a high score means that experts achieved a similar evaluation. Experts should iterate over their evaluation until they reach a good inter-rater agreement score.
- Data augmentation: A common classification problem in real-world scenarios is the lack of big-data availability, forcing researchers to work with small datasets, which in turn can be noisy or present unbalanced class distribution. A way to address this challenge is to produce synthetic data through a generative model, based on the original dataset. This process is called data augmentation [43] and takes the human labeled data to generate new datapoints that are close to the real data points. The data-augmentation process results in a new dataset, which can be used for model training purposes.
- Model design: Most machine-learning models need to be designed in order to find the best prediction model for the particular problem. Researchers should be aware of the configuration needed to implement a model. Some configuration steps require expert knowledge, for example, the design of fuzzy logic membership functions. Other configuration values can be defined semi-automatically by performing a grid search on model parameters. For example, in SVM models, the kernel function, C, and gamma parameters are crucial to find a model that performs a good classification task. To this end, prior research has developed a set of guidelines to implement SVM models and define such parameter values [44], which includes a grid search process.
- Model Evaluation: As suggested by Sokolova and Lapalme [45], several classification metrics can be derived from the confusion matrix in order to evaluate and compare the performance of several machine-learning models. These classification metrics correspond to accuracy, specificity, recall, F1-score, the Area Under the Curve (AUC), Kappa, and so on. Accuracy is the most used metric in machine-learning problems to determine the precision of a model according to its correctly classified examples (from now this relates to each driver) and the total size of the dataset. Another useful metric that considers the dataset class distribution (e.g., balanced vs. unbalanced data) is the F1-score. This metric is helpful as it takes false positives and false negatives to determine the performance of a model, which is essential in real-world datasets. In addition, the AUC is used to determine whether a model is capable of differentiating among classes by comparing the rates of false-positive and true-positive instances. As opposed to the accuracy, this measure does not consider dataset size to evaluate the performance of the model. Finally, the Kappa statistic measure considers the observed and expected accuracy in evaluating the performance of the model, which is more robust than merely relying on accuracy. This Kappa results in a measure that evaluates the agreement between model output and the ground truth.
4. Illustrative Study
4.1. Data Collection
4.1.1. Participants
4.1.2. Route
4.1.3. Equipment and Data
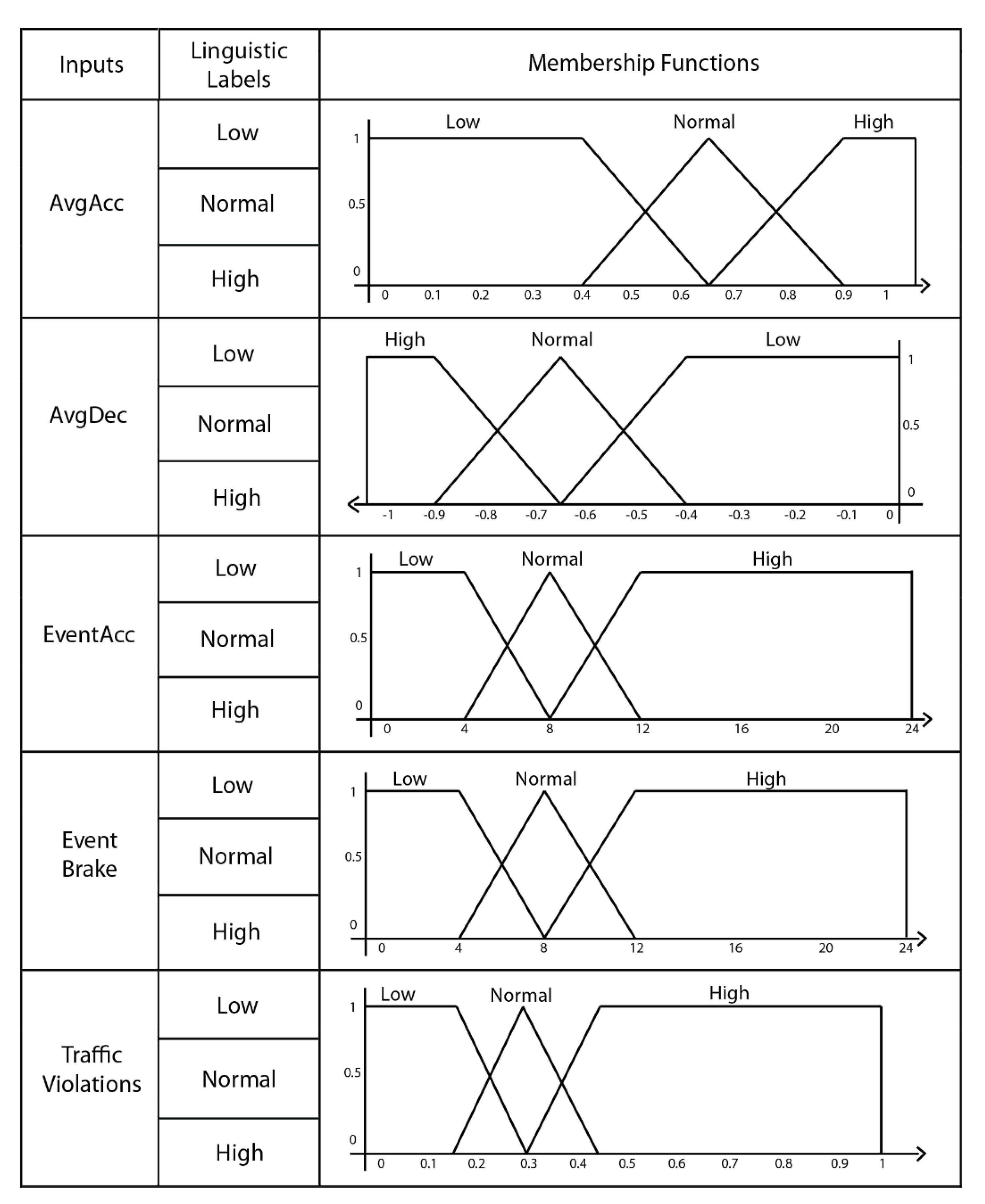
4.2. Feature Space
4.3. Human Evaluation
4.4. Data Augmentation
4.5. Model Design
4.5.1. Fuzzy Logic
4.5.2. Artificial Neural Networks
4.5.3. Support Vector Machines
4.5.4. Random Forests
4.5.5. kNN
4.6. Model Evaluation
4.6.1. Classification Metrics
4.6.2. Statistical Tests
5. Discussion
5.1. A Six-Step Methodology for Driving-Styles Classification
5.2. Performance and Statistical Evaluation
5.3. Limitations
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Elander, J.; West, R.; French, D. Behavioral correlates of individual differences in road-traffic crash risk: An examination of methods and findings. Psychol. Bull. 1993, 113, 279. [Google Scholar] [CrossRef]
- Petridou, E.; Moustaki, M. Human factors in the causation of road traffic crashes. Eur. J. Epidemiol. 2000, 16, 819–826. [Google Scholar] [CrossRef]
- World Health Organization. Global Status Report on Road Safety 2015; World Health Organization: Geneva, Switzerland, 2015. [Google Scholar]
- Arnold, L.S. Traffic Safety Culture Index; AAA Foundation for Traffic Safety: Washington, DC, USA, 2017. [Google Scholar]
- Aljaafreh, A.; Alshabatat, N.; Al-Din, M.S.N. Driving style recognition using fuzzy logic. In Proceedings of the 2012 IEEE International Conference on Vehicular Electronics and Safety (ICVES), Istanbul, Turkey, 24–27 July 2012; pp. 460–463. [Google Scholar]
- Houston, J.M.; Harris, P.B.; Norman, M. The aggressive driving behavior scale: Developing a self-report measure of unsafe driving practices. N. Am. J. Psychol. 2003, 5, 269–278. [Google Scholar]
- Lewis, D.J.; Russell, J.D.; Tuttle, C.S. Driver Feedback to Improve Vehicle Performance. U.S. Patent 7798578B2, 21 September 2010. [Google Scholar]
- Peng, J.; Fields, B.; Rutkowski, P.; Bowne, B. Systems and Methods for Providing Driver Feedback Using a Handheld Mobile Device. U.S. Patent 20110307188A1, 15 December 2011. [Google Scholar]
- Martinez, C.M.; Heucke, M.; Wang, F.-Y.; Gao, B.; Cao, D. Driving style recognition for intelligent vehicle control and advanced driver assistance: A survey. IEEE Trans. Intell. Transp. Syst. 2017, 19, 666–676. [Google Scholar] [CrossRef]
- Castignani, G.; Frank, R.; Engel, T. An evaluation study of driver profiling fuzzy algorithms using smartphones. In Proceedings of the 2013 21st IEEE International Conference on Network Protocols (ICNP), Goettingen, Germany, 7–10 October 2013; pp. 1–6. [Google Scholar]
- Doshi, A.; Trivedi, M.M. Examining the impact of driving style on the predictability and responsiveness of the driver: Real-world and simulator analysis. In Proceedings of the 2010 IEEE Intelligent Vehicles Symposium, San Diego, CA, USA, 21–24 June 2010; pp. 232–237. [Google Scholar]
- Meseguer, J.E.; Calafate, C.T.; Cano, J.C.; Manzoni, P. Drivingstyles: A smartphone application to assess driver behavior. In Proceedings of the 2013 IEEE Symposium on Computers and Communications (ISCC), Split, Croatia, 7–10 July 2013. [Google Scholar] [CrossRef]
- Castignani, G.; Derrmann, T.; Frank, R.; Engel, T. Driver behavior profiling using smartphones: A low-cost platform for driver monitoring. IEEE Intell. Transp. Syst. Mag. 2015, 7, 91–102. [Google Scholar] [CrossRef]
- Júnior, J.F.; Carvalho, E.; Ferreira, B.V.; de Souza, C.; Suhara, Y.; Pentland, A.; Pessin, G. Driver behavior profiling: An investigation with different smartphone sensors and machine learning. PLoS ONE 2017, 12, e0174959. [Google Scholar]
- Dörr, D.; Grabengiesser, D.; Gauterin, F. Online driving style recognition using fuzzy logic. In Proceedings of the 17th International IEEE Conference on Intelligent Transportation Systems (ITSC), Qingdao, China, 8–11 October 2014; pp. 1021–1026. [Google Scholar]
- Cheng, Z.-J.; Jeng, L.-W.; Li, K. Behavioral classification of drivers for driving efficiency related ADAS using artificial neural network. In Proceedings of the 2018 IEEE International Conference on Advanced Manufacturing (ICAM), Yunlin, Taiwan, 16–18 November 2018; pp. 173–176. [Google Scholar]
- Wang, W.; Xi, J.; Chong, A.; Li, L. Driving style classification using a semisupervised support vector machine. IEEE Trans. Hum. Mach. Syst. 2017, 47, 650–660. [Google Scholar] [CrossRef]
- Xue, Q.; Wang, K.; Lu, J.J.; Liu, Y. Rapid driving style recognition in car-following using machine learning and vehicle trajectory data. J. Adv. Transp. 2019. [Google Scholar] [CrossRef]
- Bejani, M.M.; Ghatee, M. A context aware system for driving style evaluation by an ensemble learning on smartphone sensors data. Transp. Res. Part C Emerg. Technol. 2018, 89, 303–320. [Google Scholar] [CrossRef]
- Meiring, G.; Myburgh, H. A review of intelligent driving style analysis systems and related artificial intelligence algorithms. Sensors 2015, 15, 30653–30682. [Google Scholar] [CrossRef]
- Blumer, A.; Ehrenfeucht, A.; Haussler, D.; Warmuth, M.K. Occam’s razor. Inf. Process. Lett. 1987, 24, 377–380. [Google Scholar] [CrossRef]
- Vilaca, A.; Cunha, P.; Ferreira, A.L. Systematic literature review on driving behavior. In Proceedings of the 2017 IEEE 20th International Conference on Intelligent Transportation Systems (ITSC), Yokohama, Japan, 16–19 October 2017; pp. 1–8. [Google Scholar]
- Sagberg, F.; Selpi; Bianchi Piccinini, G.F.; Engström, J. A review of research on driving styles and road safety. Hum. Factors 2015, 57, 1248–1275. [Google Scholar] [CrossRef] [PubMed]
- Ericsson, E. Variability in urban driving patterns. Transp. Res. Part D Transp. Environ. 2000, 5, 337–354. [Google Scholar] [CrossRef]
- Taubman-Ben-Ari, O.; Mikulincer, M.; Gillath, O. The multidimensional driving style inventory—Scale construct and validation. Accid. Anal. Prev. 2004, 36, 323–332. [Google Scholar] [CrossRef]
- Useche, S.A.; Cendales, B.; Alonso, F.; Pastor, J.C.; Montoro, L. Validation of the Multidimensional Driving Style Inventory (MDSI) in professional drivers: How does it work in transportation workers? Transp. Res. Part F Traffic Psychol. Behav. 2019, 67, 155–163. [Google Scholar] [CrossRef]
- Taubman-Ben-Ari, O.; Skvirsky, V. The multidimensional driving style inventory a decade later: Review of the literature and re-evaluation of the scale. Accid. Anal. Prev. 2016, 93, 179–188. [Google Scholar] [CrossRef]
- Mudgal, A.; Hallmark, S.; Carriquiry, A.; Gkritza, K. Driving behavior at a roundabout: A hierarchical Bayesian regression analysis. Transp. Res. Part D Transp. Environ. 2014, 26, 20–26. [Google Scholar] [CrossRef]
- Kanarachos, S.; Christopoulos, S.-R.G.; Chroneos, A. Smartphones as an integrated platform for monitoring driver behaviour: The role of sensor fusion and connectivity. Transp. Res. Part C Emerg. Technol. 2018, 95, 867–882. [Google Scholar] [CrossRef]
- Jiménez, F.; Amarillo, J.C.; Naranjo, J.E.; Serradilla, F.; Díaz, A. Energy consumption estimation in electric vehicles considering driving style. In Proceedings of the 2015 IEEE 18th International Conference on Intelligent Transportation Systems, Las Palmas, Spain, 15–18 September 2015; pp. 101–106. [Google Scholar]
- Van Ly, M.; Martin, S.; Trivedi, M.M. Driver classification and driving style recognition using inertial sensors. In Proceedings of the 2013 IEEE Intelligent Vehicles Symposium (IV), Gold Coast, QLD, Australia, 23–26 June 2013; pp. 1040–1045. [Google Scholar]
- López, J.O.; Pinilla, A.C.C.; Quintero, G.C.M. Driver behavior classification model based on an intelligent driving diagnosis system. In Proceedings of the 15th International IEEE Conference on Intelligent Transportation Systems, Anchorage, AK, USA, 16–19 September 2012; pp. 894–899. [Google Scholar]
- Brombacher, P.; Masino, J.; Frey, M.; Gauterin, F. Driving event detection and driving style classification using artificial neural networks. In Proceedings of the 2017 IEEE International Conference on Industrial Technology (ICIT), Toronto, ON, Canada, 22–25 March 2017; pp. 997–1002. [Google Scholar]
- Osafune, T.; Takahashi, T.; Kiyama, N.; Sobue, T.; Yamaguchi, H.; Higashino, T. Analysis of accident risks from driving behaviors. Int. J. Intell. Transp. Syst. Res. 2017, 15, 192–202. [Google Scholar] [CrossRef]
- Hong, J.-H.; Margines, B.; Dey, A.K. A smartphone-based sensing platform to model aggressive driving behaviors. In Proceedings of the SIGCHI Conference on Human Factors in Computing Systems, Toronto, ON, Canada, 26 April–1 May 2014; pp. 4047–4056. [Google Scholar]
- Murphey, Y.L.; Milton, R.; Kiliaris, L. Driver’s style classification using jerk analysis. In Proceedings of the 2009 IEEE Workshop on Computational Intelligence in Vehicles and Vehicular Systems, Nashville, TN, USA, 30 March–2 April 2009; pp. 23–28. [Google Scholar]
- Feraud, I.S.; Lara, M.a.M.; Naranjo, J.E. A fuzzy logic model to estimate safe driving behavior based on traffic violation. In Proceedings of the 2017 IEEE Ecuador Technical Chapters Meeting (ETCM), Salinas, Ecuador, 16–20 October 2017; pp. 1–6. [Google Scholar]
- Zhang, C.; Patel, M.; Buthpitiya, S.; Lyons, K.; Harrison, B.; Abowd, G.D. Driver classification based on driving behaviors. In Proceedings of the 21st International Conference on Intelligent User Interfaces, Sonoma, CA, USA, 7–10 March 2016; pp. 80–84. [Google Scholar]
- Karginova, N.; Byttner, S.; Svensson, M. Data-driven methods for classification of driving styles in buses. SAE Tech. Pap. 2012. [Google Scholar] [CrossRef]
- Vaitkus, V.; Lengvenis, P.; Žylius, G. Driving style classification using long-term accelerometer information. In Proceedings of the 2014 19th International Conference on Methods and Models in Automation and Robotics (MMAR), Miedzyzdroje, Poland, 2–5 September 2014; pp. 641–644. [Google Scholar]
- Montgomery, D.C. Design and Analysis of Experiments; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Langley, P. Machine learning as an experimental science. Mach. Learn. 1988, 3, 5–8. [Google Scholar] [CrossRef]
- Van Dyk, D.A.; Meng, X.-L. The art of data augmentation. J. Comput. Graph. Stat. 2001, 10, 1–50. [Google Scholar] [CrossRef]
- Ben-Hur, A.; Weston, J. A user’s guide to support vector machines. In Data Mining Techniques for the Life Sciences; Springer: Berlin, Germany, 2010; pp. 223–239. [Google Scholar]
- Sokolova, M.; Lapalme, G. A systematic analysis of performance measures for classification tasks. Inf. Process. Manag. 2009, 45, 427–437. [Google Scholar] [CrossRef]
- Japkowicz, N.; Shah, M. Evaluating Learning Algorithms: A Classification Perspective; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Paefgen, J.; Kehr, F.; Zhai, Y.; Michahelles, F. Driving behavior analysis with smartphones: insights from a controlled field study. In Proceedings of the 11th International Conference on Mobile and Ubiquitous Multimedia, Ulm, Germany, 4–6 December 2012; ACM: New York, NY, USA, 2012; p. 36. [Google Scholar]
- Landis, J.R.; Koch, G.G. An application of hierarchical kappa-type statistics in the assessment of majority agreement among multiple observers. Biometrics 1977, 33, 363–374. [Google Scholar] [CrossRef]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic minority over-sampling technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Hall, M.; Frank, E.; Holmes, G.; Pfahringer, B.; Reutemann, P.; Witten, I.H. The WEKA data mining software: An update. ACM SIGKDD Explor. Newsl. 2009, 11, 10–18. [Google Scholar] [CrossRef]
- Guney, K.; Sarikaya, N. Comparison of Mamdani and Sugeno fuzzy inference system models for resonant frequency calculation of rectangular microstrip antennas. Prog. Electromagn. Res. 2009, 12, 81–104. [Google Scholar] [CrossRef]
- Jassbi, J.J.; Serra, P.J.A.; Ribeiro, R.A.; Donati, A. A comparison of mandani and sugeno inference systems for a space fault detection application. In Proceedings of the Automation Congress (WAC’06. World), Budapest, Hungary, 24–26 July 2006; pp. 1–8. [Google Scholar]
- Hush, D.R. Classification with neural networks: A performance analysis. In Proceedings of the IEEE International Conference on Systems Engineering, Fairborn, OH, USA, 24–26 August 1989; pp. 277–280. [Google Scholar]
- Bergmeir, C.N.; Benàtez Sánchez, J.M. Neural networks in R using the Stuttgart neural network simulator: RSNNS. Neural Netw. 2012. [Google Scholar] [CrossRef]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Wang, C. A Theory of Generalization in Learning Machines with Neural Network Applications; University of Pennsylvania: Philadelphia, PA, USA, 1994. [Google Scholar]
- Ripley, B.D. Statistical aspects of neural networks. Netw. Chaos Stat. Probabilistic Asp. 1993, 50, 40–123. [Google Scholar]
- Kaastra, I.; Boyd, M. Designing a neural network for forecasting financial and economic time series. Neurocomputing 1996, 10, 215–236. [Google Scholar] [CrossRef]
- Hecht-Nielsen, R. Kolmogorov’s mapping neural network existence theorem. In Proceedings of the IEEE International Conference on Neural Networks III, San Diego, CA, USA, 21–24 June 1987; pp. 11–13. [Google Scholar]
- Boser, B.E.; Guyon, I.M.; Vapnik, V.N. A training algorithm for optimal margin classifiers. In Proceedings of the Fifth Annual Workshop on Computational Learning Theory, Pittsburgh, PA, USA, 27–29 July 1992; pp. 144–152. [Google Scholar]
- Steinwart, I.; Christmann, A. Support Vector Machines; Springer Science & Business Media: Berlin, Germany, 2008. [Google Scholar]
- Burges, J.C. A tutorial on support vector machines for pattern recognition. Data Min. Knowl. Discov. 1998, 2, 121–167. [Google Scholar] [CrossRef]
- Chang, C.-C.; Lin, C.-J. LIBSVM: A library for support vector machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 1–27. [Google Scholar] [CrossRef]
- Zhou, Y.; Pei, S. An effective adaptive multi-objective particle swarm for multimodal constrained function optimization. JCP 2010, 5, 1144–1151. [Google Scholar] [CrossRef]
- Witten, I.H.; Frank, E. Data mining: practical machine learning tools and techniques with Java implementations. ACM Sigmod Record 2002, 31, 76–77. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Fix, E.; Hodges, J.L., Jr. Discriminatory Analysis-Nonparametric Discrimination: Consistency Properties; USAF school of Aviation Medicine: Dayton, OH, USA, 1951. [Google Scholar]
- Han, J.; Pei, J.; Kamber, M. Data Mining: Concepts and Techniques; Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Shreve, J.; Schneider, H.; Soysal, O. A methodology for comparing classification methods through the assessment of model stability and validity in variable selection. Decis. Support Syst. 2011, 52, 247–257. [Google Scholar] [CrossRef]
- Wilcoxon, F. Individual comparisons by ranking methods. Biom. Bull. 1945, 1, 80–83. [Google Scholar] [CrossRef]
- af Wåhlberg, A. Driver Behaviour and Accident Research Methodology: Unresolved Problems; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Enders, C.K. A primer on the use of modern missing-data methods in psychosomatic medicine research. Psychosom. Med. 2006, 68, 427–436. [Google Scholar] [CrossRef]
- Perez, L.; Wang, J. The effectiveness of data augmentation in image classification using deep learning. arXiv 2017, arXiv:1712.04621. [Google Scholar]
- Ko, T.; Peddinti, V.; Povey, D.; Khudanpur, S. Audio augmentation for speech recognition. In Proceedings of the 16th Annual Conference of the International Speech Communication Association, Dresden, Germany, 6–10 September 2015. [Google Scholar]
- Ho, Y.-C.; Pepyne, D.L. Simple explanation of the no-free-lunch theorem and its implications. J. Optim. Theory Appl. 2002, 115, 549–570. [Google Scholar] [CrossRef]
- Godil, S.S.; Shamim, M.S.; Enam, S.A.; Qidwai, U. Fuzzy logic: A “simple” solution for complexities in neurosciences. Surg. Neurol. Int. 2011, 2. [Google Scholar] [CrossRef]
- Mitrovic, D. Reliable method for driving events recognition. IEEE Trans. Intell. Transp. Syst. 2005, 6, 198–205. [Google Scholar] [CrossRef]
- Miyajima, C.; Nishiwaki, Y.; Ozawa, K.; Wakita, T.; Itou, K.; Takeda, K.; Itakura, F. Driver modeling based on driving behavior and its evaluation in driver identification. Proc. IEEE 2007, 95, 427–437. [Google Scholar] [CrossRef]
| Event Types | Traffic-Flow Levels | ||
|---|---|---|---|
| Low | Medium | High | |
| EventAcc | a >= 2 m/s2 | a >= 1.5 m/s2 | a >= 1 m/s2 |
| EventBrake | a <= 2 m/s2 | a <= 1.5 m/s2 | a <= 1 m/s2 |
| Rules | Antecedents | Consequent | Weight | |
|---|---|---|---|---|
| 1 | EventAcc AvgAcc | High High | aggressive | 1 |
| 2 | EventBrake AvgDec | High High | aggressive | 1 |
| 3 | AvgAcc | Low | calm | 0.8 |
| 4 | EventAcc EventBrake | High High | aggressive | 1 |
| 5 | AvgDec EventBrake | Low Low | calm | 0.8 |
| 6 | AvgAcc AvgDec | Normal Normal | normal | 0.9 |
| 7 | Traffic violations | High | aggressive | 1 |
| 8 | Traffic violations | Low | calm | 0.8 |
| 9 | Traffic violations | Normal | normal | 0.9 |
| 10 | EventAcc EventBrake | Normal Normal | normal | 0.9 |
| Equations | Number of Neurons | Accuracy | Reference |
|---|---|---|---|
| + 1 | 3 | 0.84 | [56] |
| )/2 | 4 | 0.86 | [57] |
| 10 | 0.86 | [58] | |
| 12 | 0.84 | [59] |
| Parameters | Values |
|---|---|
| Kernel function | linear, polynomial, radial basis function (RBF), sigmoid |
| C | [2−5, 210] |
| γ | [2−5, 210] |
| Model | Accuracy | F1-Score | AUC | Kappa |
|---|---|---|---|---|
| Fuzzy Logic | 0.8800 | 0.8840 | 0.9072 | 0.8106 |
| ANN (sigmoid; lr = 0.4; N = 4) | 0.8600 | 0.8663 | 0.9030 | 0.7807 |
| SVM (RBF, C = 25; γ = 2−2 ) | 0.9600 | 0.9595 | 0.9730 | 0.9375 |
| RF (n = 100; m = 4) | 0.9200 | 0.9253 | 0.9451 | 0.8750 |
| kNN (k = 3) | 0.9200 | 0.9253 | 0.9451 | 0.8750 |
| Fuzzy Logic | ANN | SVM | KNN | RF | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Class | F1 | AUC | F1 | AUC | F1 | AUC | F1 | AUC | F1 | AUC |
| Calm | 0.9 | 0.9375 | 0.9091 | 0.9167 | 0.9524 | 0.9875 | 0.9524 | 0.9875 | 0.9524 | 0.9875 |
| Normal | 0.8696 | 0.8831 | 0.8511 | 0.8600 | 0.9545 | 0.9594 | 0.9091 | 0.9189 | 0.9091 | 0.9189 |
| Aggressive | 0.8823 | 0.9011 | 0.8387 | 0.8387 | 0.9714 | 0.9722 | 0.9143 | 0.9289 | 0.9143 | 0.9289 |
| Classifier 1 | Classifier 2 | p-Value |
|---|---|---|
| SVM | ANN | 0.025 |
| SVM | Fuzzy | 1 |
| SVM | kNN | 1 |
| SVM | RF | 1 |
| ANN | Fuzzy | 0.025 |
| ANN | kNN | 0.025 |
| ANN | RF | 0.025 |
| Fuzzy | kNN | 1 |
| Fuzzy | RF | 1 |
| kNN | RF | 1 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Silva, I.; Eugenio Naranjo, J. A Systematic Methodology to Evaluate Prediction Models for Driving Style Classification. Sensors 2020, 20, 1692. https://doi.org/10.3390/s20061692
Silva I, Eugenio Naranjo J. A Systematic Methodology to Evaluate Prediction Models for Driving Style Classification. Sensors. 2020; 20(6):1692. https://doi.org/10.3390/s20061692
Chicago/Turabian StyleSilva, Iván, and José Eugenio Naranjo. 2020. "A Systematic Methodology to Evaluate Prediction Models for Driving Style Classification" Sensors 20, no. 6: 1692. https://doi.org/10.3390/s20061692
APA StyleSilva, I., & Eugenio Naranjo, J. (2020). A Systematic Methodology to Evaluate Prediction Models for Driving Style Classification. Sensors, 20(6), 1692. https://doi.org/10.3390/s20061692






