Deep Active Learning for Surface Defect Detection
Abstract
1. Introduction
2. Related Work
2.1. Object Detection for Defect Detection
2.2. Active Learning
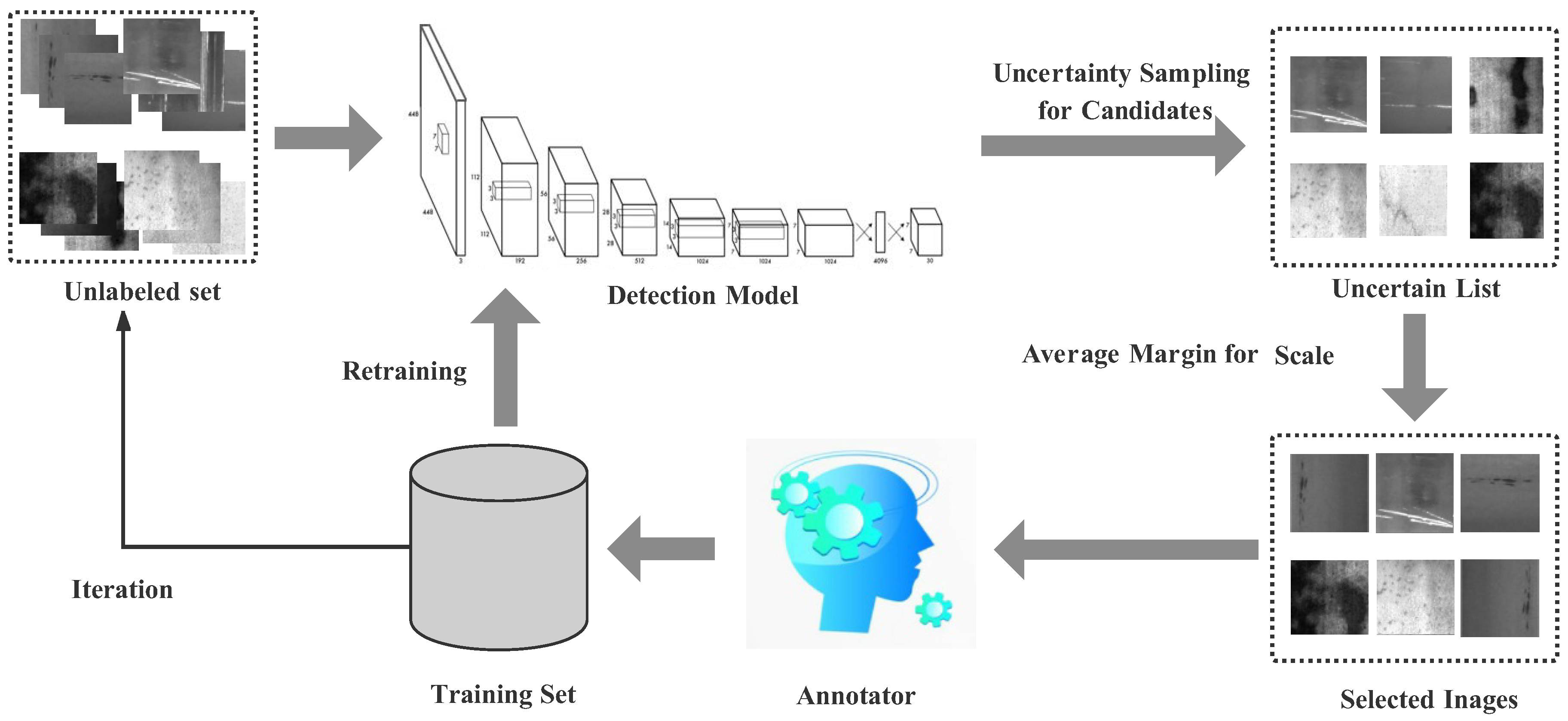
3. Active Learning for Defect Detection
3.1. Overall Framework
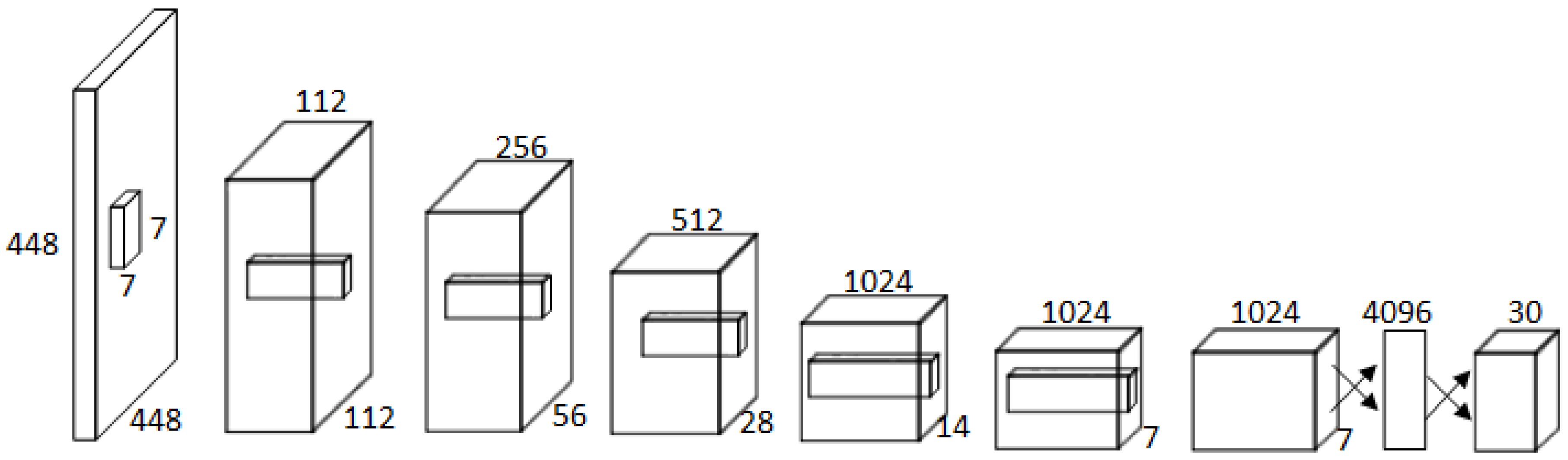
3.2. Detection Model
3.3. Active Learning for Detection
3.3.1. Uncertainty Sampling for Candidates
- A higher predicted value denotes the higher probability belonging to the corresponding defect.
- There is the maximum value that denotes the probability belonging to the corresponding defect.
- The probability belonging to the corresponding defect is higher than other probabilities of the remaining defects.
3.3.2. Average Margin for Scale
3.3.3. Overview Sampling Algorithm
| Algorithm 1: Active Learning for Defect Detection. |
 |
4. Experiments
4.1. Dataset Introduction
4.2. Comparisons
4.3. Evaluation
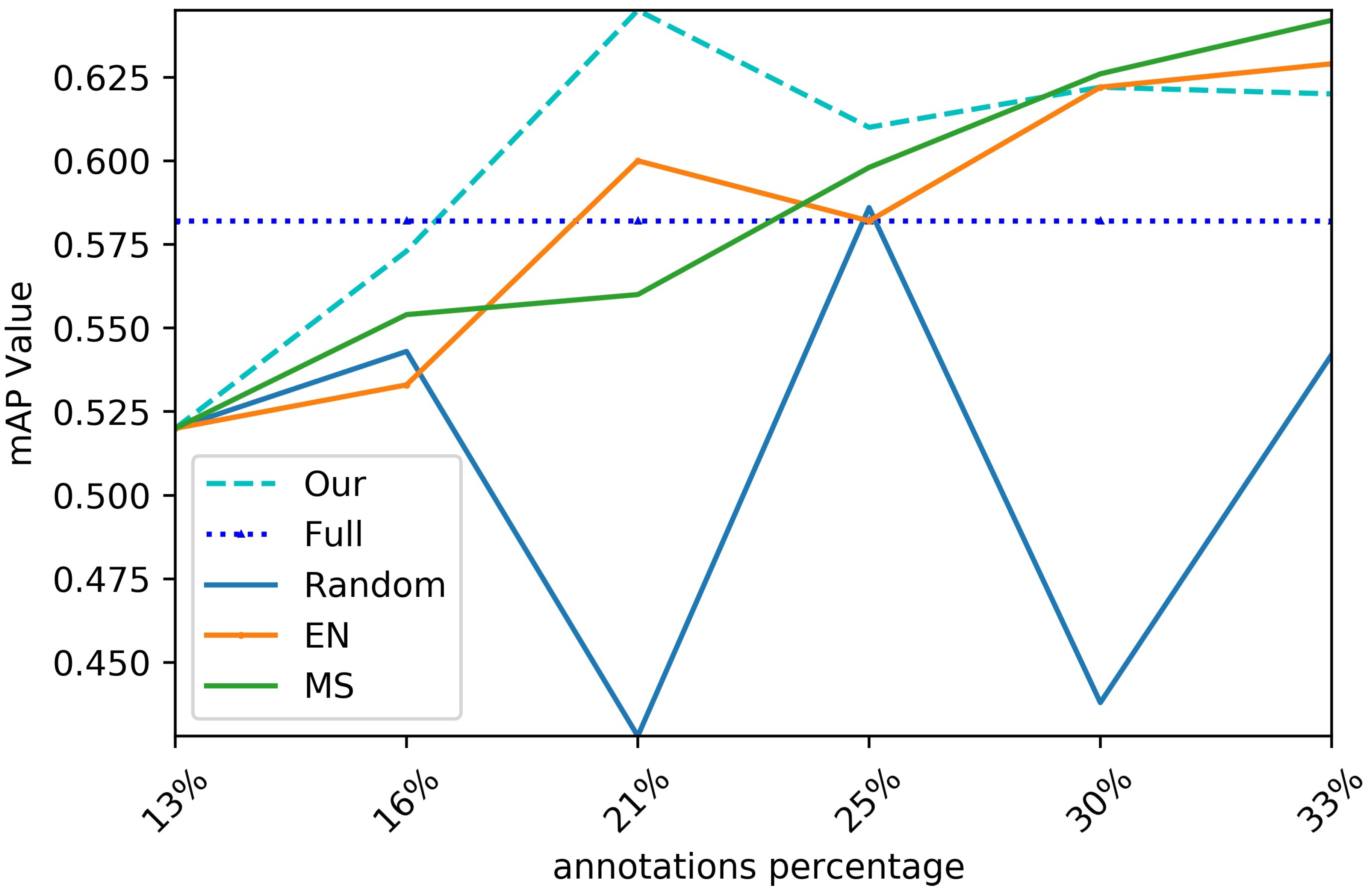
4.4. Comparison Results
4.4.1. Performance Improvement Comparison
4.4.2. Query Strategy Analysis
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Xie, X. A review of recent advances in surface defect detection using texture analysis techniques. Electron. Lett. Comput. Vision Image Anal. 2008, 7, 1–22. [Google Scholar] [CrossRef]
- Wu, X.; Cao, K.; Gu, X. A surface defect detection based on convolutional neural network. In Proceedings of the International Conference on Computer Vision Systems, Shenzhen, China, 10–13 July 2017; pp. 185–194. [Google Scholar]
- Liu, R.-X.; Yao, M.-H.; Wang, X.-B. Defects Detection Based on Deep Learning and Transfer Learning. Metal. Min. Ind. 2015. Available online: https://www.researchgate.net/publication/285367015_Defects_detection_based_on_deep_learning_and_transfer_learning (accessed on 12 March 2020).
- Masci, J.; Meier, U.; Ciresan, D.; Schmidhuber, J.; Fricout, G. Steel defect classification with max-pooling convolutional neural networks. In Proceedings of the 2012 International Joint Conference on Neural Networks (IJCNN), Brisbane, Australia, 10–15 June 2012; pp. 1–6. [Google Scholar]
- Liu, Z.; Wang, L.; Li, C.; Han, Z. A high-precision loose strands diagnosis approach for isoelectric line in high-speed railway. IEEE Trans. Ind. Inf. 2017, 14, 1067–1077. [Google Scholar] [CrossRef]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster r-cnn: Towards real-time object detection with region proposal networks. In Advances in Neural Information Processing Systems; 2015; pp. 91–99. Available online: http://papers.nips.cc/paper/5638-faster-r-cnn-towards-real-time-object-detection-with-region-proposal-networks (accessed on 12 March 2020).
- Sermanet, P.; Eigen, D.; Zhang, X.; Mathieu, M.; Fergus, R.; LeCun, Y. Overfeat: Integrated recognition, localization and detection using convolutional networks. arXiv 2013, arXiv:1312.6229. [Google Scholar]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You only look once: Unified, real-time object detection. In Proceedings of the IEEE conference on computer vision and pattern recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 779–788. [Google Scholar]
- Liu, W.; Anguelov, D.; Erhan, D.; Szegedy, C.; Reed, S.; Fu, C.Y.; Berg, A.C. Ssd: Single shot multibox detector. In Proceedings of the European conference on computer vision, Munich, Germany, 8–14 September 2016; pp. 21–37. [Google Scholar]
- Redmon, J.; Farhadi, A. YOLO9000: better, faster, stronger. In Proceedings of the IEEE conference on computer vision and pattern recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 7263–7271. [Google Scholar]
- Redmon, J.; Farhadi, A. Yolov3: An incremental improvement. arXiv 2018, arXiv:1804.02767. [Google Scholar]
- Hu, J.; Xu, W.; Gao, B.; Tian, G.Y.; Wang, Y.; Wu, Y.; Yin, Y.; Chen, J. Pattern deep region learning for crack detection in thermography diagnosis system. Metals 2018, 8, 612. [Google Scholar] [CrossRef]
- Fan, M.; Wu, G.; Cao, B.; Sarkodie-Gyan, T.; Li, Z.; Tian, G. Uncertainty metric in model-based eddy current inversion using the adaptive Monte Carlo method. Measurement 2019, 137, 323–331. [Google Scholar] [CrossRef]
- Song, K.; Yan, Y. A noise robust method based on completed local binary patterns for hot-rolled steel strip surface defects. Appl. Surf. Sci. 2013, 285, 858–864. [Google Scholar] [CrossRef]
- Kleiner, M.; Geiger, M.; Klaus, A. Manufacturing of lightweight components by metal forming. Magnesium 2003, 530, 26–66. [Google Scholar] [CrossRef]
- Feng, C.; Liu, M.Y.; Kao, C.C.; Lee, T.Y. Deep active learning for civil infrastructure defect detection and classification. In Proceedings of the ASCE International Workshop on Computing in Civil Engineering 2017, Seattle, DC, USA, 25–27 June 2017; pp. 298–306. [Google Scholar]
- Ren, R.; Hung, T.; Tan, K.C. A generic deep-learning-based approach for automated surface inspection. IEEE Trans. Cybern. 2017, 48, 929–940. [Google Scholar] [CrossRef] [PubMed]
- Azimi, S.M.; Britz, D.; Engstler, M.; Fritz, M.; Mücklich, F. Advanced steel microstructural classification by deep learning methods. Sci. Rep. 2018, 8, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Tong, S.; Koller, D. Support vector machine active learning with applications to text classification. J. Mach. Learn. Res. 2001, 2, 45–66. [Google Scholar]
- Tuia, D.; Volpi, M.; Copa, L.; Kanevski, M.; Munoz-Mari, J. A survey of active learning algorithms for supervised remote sensing image classification. IEEE J. Sel. Top. Sign. Proces. 2011, 5, 606–617. [Google Scholar] [CrossRef]
- Xu, Z.; Akella, R.; Zhang, Y. Incorporating diversity and density in active learning for relevance feedback. In Proceedings of the European Conference on Information Retrieval, Rome, Italy, 2–5 April 2007; pp. 246–257. [Google Scholar]
- Chakraborty, S.; Balasubramanian, V.; Panchanathan, S. Dynamic batch mode active learning. In Proceedings of the Computer Vision and Pattern Recognition (CVPR), Providence, RI, USA, 20–25 June 2011; pp. 2649–2656. [Google Scholar]
- Yuan, A.; Bai, G.; Yang, P.; Guo, Y.; Zhao, X. Handwritten English word recognition based on convolutional neural networks. In Proceedings of the 2012 International Conference on Frontiers in Handwriting Recognition, Bari, Italy, 18–20 September 2012; pp. 207–212. [Google Scholar]
- Zhu, J.; Wang, H.; Yao, T.; Tsou, B.K. Active learning with sampling by uncertainty and density for word sense disambiguation and text classification. In Proceedings of the 22nd International Conference on Computational Linguistics (Coling 2008), Manchester, UK, 18–22 August 2008; pp. 1137–1144. [Google Scholar]
- Yang, Y.; Ma, Z.; Nie, F.; Chang, X.; Hauptmann, A.G. Multi-class active learning by uncertainty sampling with diversity maximization. Int. J. Comput. Vision 2015, 113, 113–127. [Google Scholar] [CrossRef]


| Recall | Type | ||||
|---|---|---|---|---|---|
| Inclusion (In) | Patches (Pa) | Pitted Surface (Ps) | Scratches (Sc) | Data (%) | |
| Random | 0.8333 | 0.9322 | 0.6774 | 0.9394 | 50.0% |
| EN | 0.8636 | 0.9322 | 0.6774 | 0.9394 | 31.6% |
| MS | 0.9242 | 0.9322 | 0.4839 | 1.000 | 33.3% |
| Full | 0.8788 | 0.8983 | 0.6129 | 0.9091 | 100.0% |
| Ours | 0.8485 | 0.9153 | 0.7742 | 0.9091 | 21.7% |
| Precision | Defect | ||||
|---|---|---|---|---|---|
| Inclusion (In) | Patches (Pa) | Pitted Surface (Ps) | Scratches (Sc) | Data (%) | |
| Random | 0.1291 | 0.1672 | 0.0323 | 0.2583 | 50.0% |
| EN | 0.1839 | 0.2696 | 0.0669 | 0.2925 | 31.6% |
| MS | 0.1017 | 0.2183 | 0.0498 | 0.2409 | 33.3% |
| Full | 0.1213 | 0.2180 | 0.0617 | 0.1899 | 100% |
| Ours | 0.1965 | 0.3396 | 0.0774 | 0.3614 | 21.7% |
| AP | Defect | |||||
|---|---|---|---|---|---|---|
| Inclusion (In) | Patches (Pa) | Pitted Surface (Ps) | Scratches (Sc) | mAP | Data (%) | |
| Random | 0.5498 | 0.7498 | 0.3082 | 0.5658 | 0.542 | 50.0% |
| EN | 0.6359 | 0.8314 | 0.1959 | 0.8546 | 0.629 | 31.6% |
| MS | 0.6874 | 0.7944 | 0.1763 | 0.9104 | 0.642 | 33.3% |
| Full | 0.6183 | 0.7284 | 0.2103 | 0.7720 | 0.582 | 100% |
| Ours | 0.6390 | 0.8269 | 0.3277 | 0.7874 | 0.645 | 21.7% |
| Types | Inclusion (In) | Patches (Pa) | Pitted Surface (Ps) | Scratches (Sc) |
|---|---|---|---|---|
| Recall | 0.8788 | 0.8983 | 0.6129 | 0.9091 |
| Precision | 0.1213 | 0.2108 | 0.0617 | 0.1899 |
| AP | 0.6183 | 0.7284 | 0.2103 | 0.7720 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lv, X.; Duan, F.; Jiang, J.-J.; Fu, X.; Gan, L. Deep Active Learning for Surface Defect Detection. Sensors 2020, 20, 1650. https://doi.org/10.3390/s20061650
Lv X, Duan F, Jiang J-J, Fu X, Gan L. Deep Active Learning for Surface Defect Detection. Sensors. 2020; 20(6):1650. https://doi.org/10.3390/s20061650
Chicago/Turabian StyleLv, Xiaoming, Fajie Duan, Jia-Jia Jiang, Xiao Fu, and Lin Gan. 2020. "Deep Active Learning for Surface Defect Detection" Sensors 20, no. 6: 1650. https://doi.org/10.3390/s20061650
APA StyleLv, X., Duan, F., Jiang, J.-J., Fu, X., & Gan, L. (2020). Deep Active Learning for Surface Defect Detection. Sensors, 20(6), 1650. https://doi.org/10.3390/s20061650





