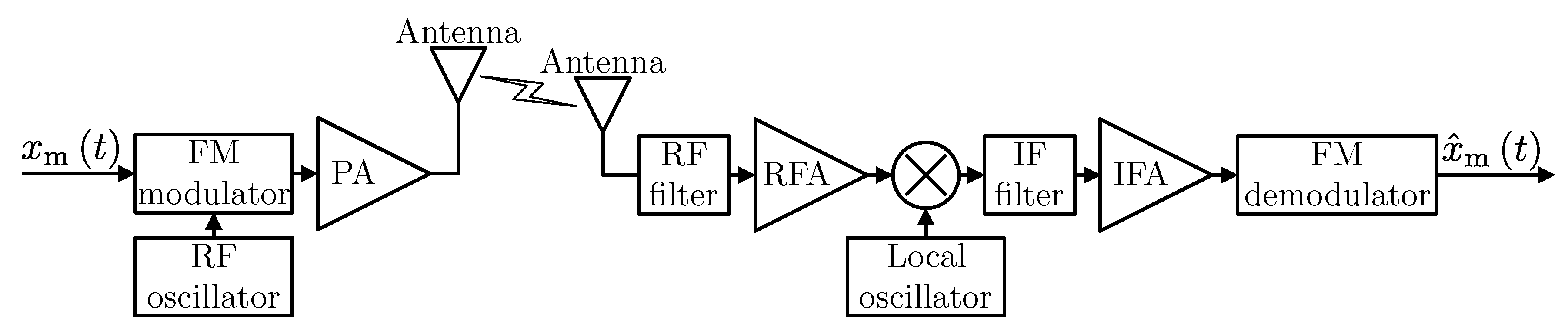
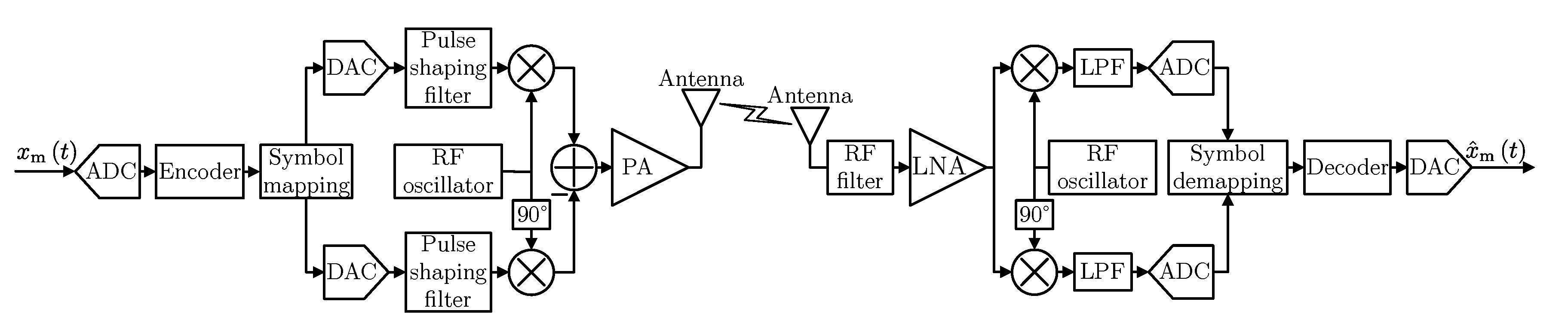
1. Introduction
In recent years, the number of devices connected to the Internet has rapidly increased. Mobile data traffic has grown 17-fold over the past five years [
1]. Mobile networks carried 686 petabytes per month in 2012 [
1]. According to Cisco predictions that monthly global mobile data traffic will be 77 exabytes by 2022, and annual traffic will reach almost one zettabyte [
1]. Moreover, communication of billions of machines and devices that are expected to comprise the Internet of Things (IoT) pose even greater challenges, never encountered before. This means a high density of devices per square meter, and in consequence, short distances between nodes of the network. Furthermore, some number of these devices, e.g., sensors, will be (are) battery powered, and thus, they have to be ultra-energy-efficient. Nowadays, most low-energy wireless systems adopt digital modulation and coding, and the baseband digital signal processing is often performed in software [
2]. Thus, besides the energy needed for signal transmission, energy is also required for signal processing at both a transmitter and a receiver. This processing energy may even dominate at short link distances and most often increases when approaching the Shannon capacity limit because of the implementation complexity [
3].
The inspiration for the design of new ultra-energy-efficient networks can be the human brain which can be compared to the ultra-dense network. The neurons of a human brain can be compared to nodes, while axons can be compared to links in a network. It is well-known that the current wireless-node power-consumption in wireless local-area and cellular networks is of the order of 0.1–2 W [
4] for just one transmission link. In comparison, the incredibly complex human brain works with less than
per node (neuron) with up to 10,000 links. Thus, even considering the shorter distances, the human brain for a massive network of neurons and synapses is many orders of magnitude more energy efficient than any human-made network. We believe that future IoT networks should borrow some mechanisms used in the nervous-system communication, since the number of nodes will be massive, and the distances and power levels will be extremely small. One mechanism in a human brain, making it ultra-energy-efficient, is the fact that neurons operate and communicate continuously in time. Moreover, inside each neuron, information incoming from the synapses, is integrated and processed in an analog manner and the neuron then decides whether to fire an action potential. This discrete, binary event is transmitted along the axon to other neurons. Thus, we pose the question whether in some energy-constricted, dense networks (with short-distance links and moderate distortions), the nervous-system-inspired analog transmission can be an alternative to digital transmission, whether adaptive digital and analog modulation is an energy-efficient link-adaptation option, and if so, in what network scenarios.
Bio-inspired systems have been studied intensively during the last 15 years, as can be seen from the review papers, see for example [
5,
6,
7,
8]. Nevertheless, these papers describe the general concept of bio-inspired systems or summarize the bio-inspired algorithms, e.g., genetic algorithm or ant-colony optimization. In the context of wireless networks, there are few articles that present specific, brain-inspired solutions. For instance, in [
9], the authors describe the topologies of a network which can be found in a human brain and show the trade-off between the complexity of the topology and the consumed power. The brain-inspired dynamic spectrum management for cognitive radio has been proposed in [
10]. Papers [
11,
12] describe the possibility of applying the artificial intelligence (AI) techniques (like machine learning, genetic algorithms, swarm intelligence, ant colony, artificial neural networks, fuzzy system) in the context of 5G networks. Moreover, in [
13] the microglia functionality from the human brain is applied in a dense network. It was already shown in [
14] that the digital system with coding can be more energy efficient for longer links while the uncoded digital system is more energy efficient for shorter links. We wanted to extend this research to an analog system that requires higher transmission power (to provide higher SNR at the receiver as confirmed by Figure 6), but lower power is consumed by signal processing. Finding the balance between these two factors and its relation to coded and uncoded digital systems is a novel research topic up to our knowledge.
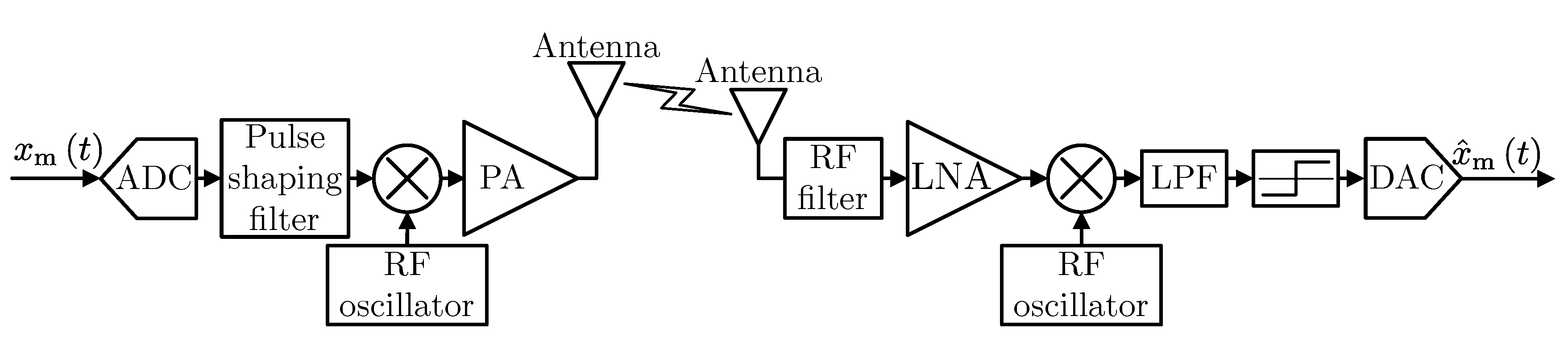
In this paper, we consider brain-inspired analog and digital transmission in the context of energy-efficient ultra-dense networks, i.e., consisting of short links with moderate attenuation and distortions. The energy-efficiency metric has been compared between these two types of communication taking the circuit power consumption model into account. Moreover, we assumed that the transmitted data came from analog sensors in the considered systems. Although currently many sensors are available as digital output only, a number of physical phenomenons are measured initially as analog signals, e.g., voltage or resistance. Therefore, in the case of the digital transmission, the input data are fed first to the analog-to-digital converter. At the receiving side, the decoded data are converted back to analog form. The rest of the paper is organized as follows. In
Section 2, the system model for analog and digital transmission is described. The numerical results with their detailed analysis are presented in
Section 3, while the conclusions are provided in
Section 5.
3. Simulation Results
Although the analog communication schemes can potentially be energy-efficient because of a small number of the transmitter- and receiver-components, most of the wireless communication systems nowadays are digital for the reason of relatively high transmission quality performance, especially in the hostile radio channel. However, in some short-distance channels (such as the ones that can be potentially the case in massive high-density networks) the former can be competitive for the energy-efficiency with reasonable performance. Therefore, let us evaluate both transmission types in terms of the energy-efficiency and MSE-based performance.
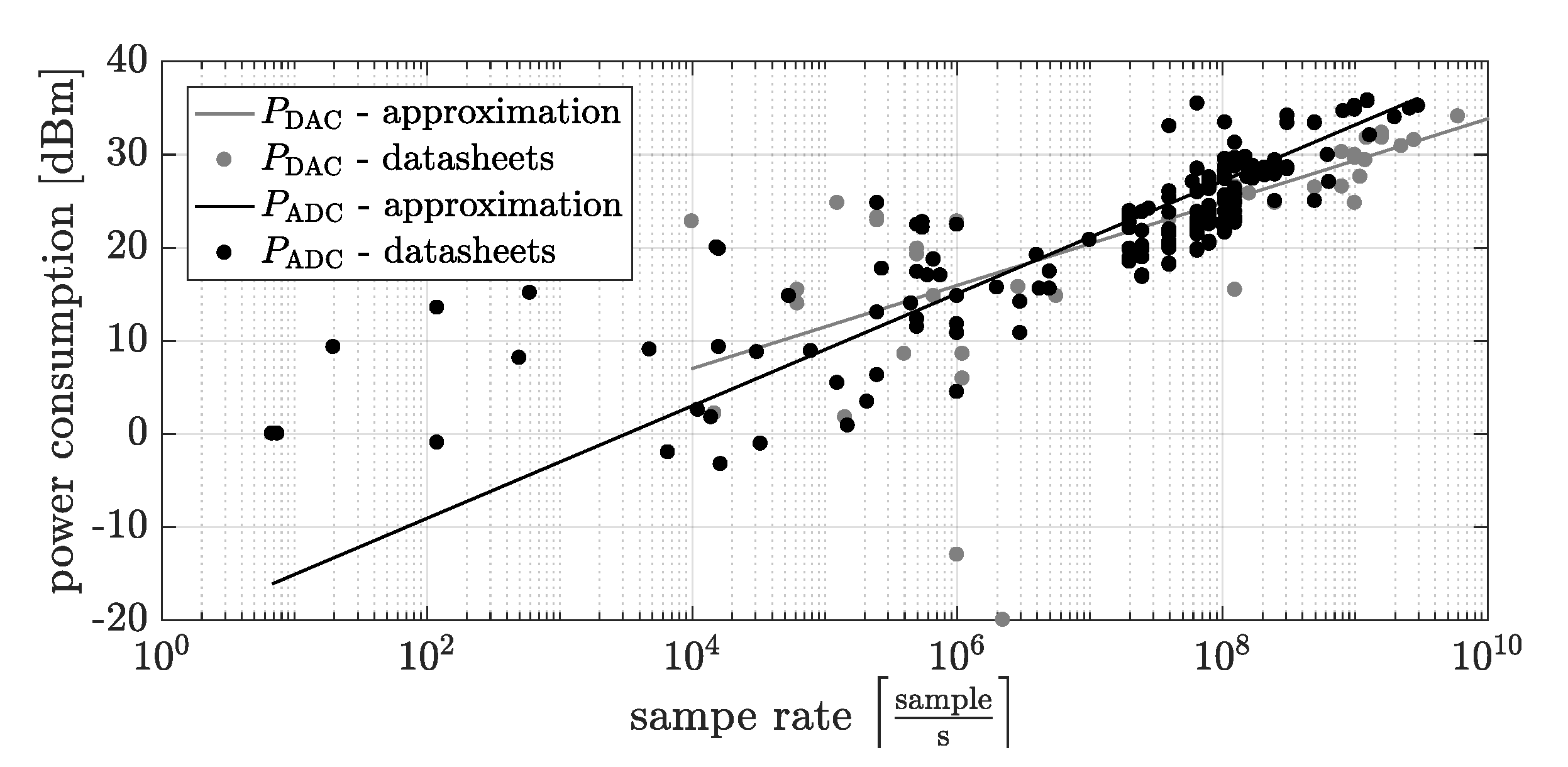
Here below, results obtained by the computer simulation using MATLAB software are presented. It can be observed that in the case of the digital transmission, the input data are fed first to the analog-to-digital converter. At the receiving side, the decoded data are converted back to analog form. As the input and output signal of all systems has the same structure, their performance can be compared without consideration of the further processing steps and the energy consumed by them. Firstly, let us define the relation between the power consumed by the transmitter and receiver components in the above models. The hypothesis that analog communication can be more energy efficient than the digital is based on the assumption that the analog transmitter and receiver are less complex than digital ones. However, this also depends on the implementation and application. On the other hand, the
or uncoded
transmitters and receivers use most of the blocks of the coded or uncoded digital system with
modulation. Thus, in our model, we introduce the factor
which determines the relation between
and
where
. The same operation can be applied in the case of the digital system with
modulation
, where
determines the relation between the power consumed by transmitter and receiver components in the digital transmission with
and
modulation. For the fair comparison of the analog and digital transmission in the considered scenario, both systems are compared for the same bandwidth
and the same
in the transmission band. Thus, for the given parameters of digital transmission defining the bandwidth (code rate, bits number of quantization, modulation order and frequency sampling), the frequency deviation for analog transmission is determined. The results have been obtained for
,
,
,
,
, modulation orders for the
scheme
, the code rate of the turbo code for the coded transmission
,
based on [
16,
24],
[
25],
,
, the values
and
based on literature [
16], channel attenuation
[
26], the noise power
[
26]. In all systems, perfect synchronization is assumed. The results have been generated using the Monte Carlo method and have been averaged over 1000 source signal realization. The source signal has been generated as the sum of the sin function with different amplitude, frequency and phase. The time duration of input signal is equal 0.1 s.
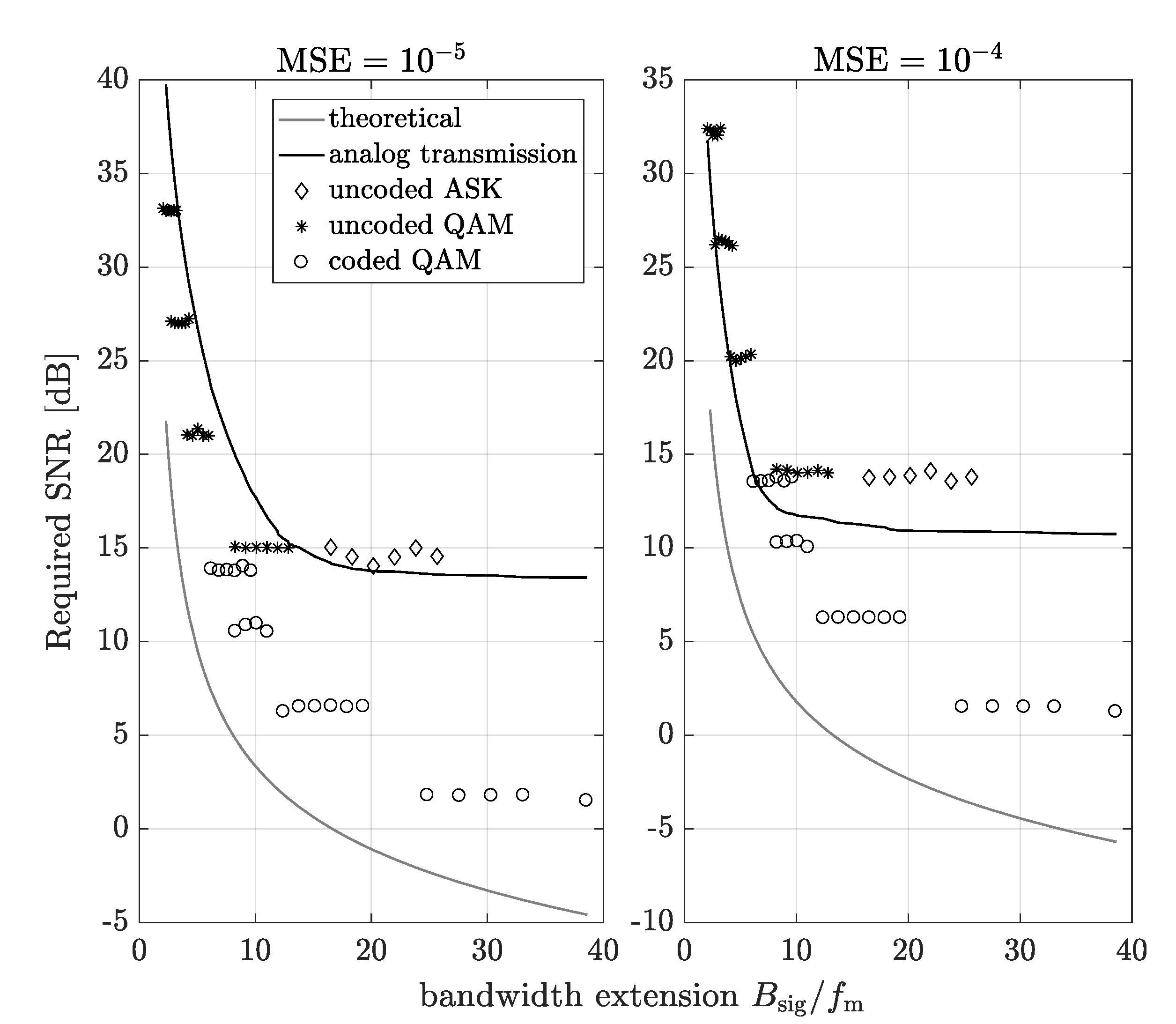
In the first step, the analog and digital transmission have been compared in the context of the
(corresponding to the transmit power) required to achieve a given quality of the received signal. Thus, in
Figure 6, the required
needed to achieve a given
(defined in
Section 2), as a function of the bandwidth extension for the analog, digital and the theoretical (ideal) scheme is presented. Based on [
27], in the theoretical scheme, the required
is calculated assuming that the throughput of the link is equal to the link capacity for the extension bandwidth:
where
S is a power of the analog source signal
, while
is the required value of
needed to achieve a given
, in the theoretical scheme. On the left-hand side of
Figure 6, required
for
is plotted. It is noticeable that in the most cases of the bandwidth extension, the digital transmissions achieve a given
for lower values of
than analog transmission. On the other hand, note that these results do not take the power consumed by the signal processing into account. Thus, from the energy efficiency perspective, the analog transmission may still be better. On the right-hand side of
Figure 6, the required
for
is plotted. There exist more cases where the analog transmission needs lower values of
, in order to achieve a given
.
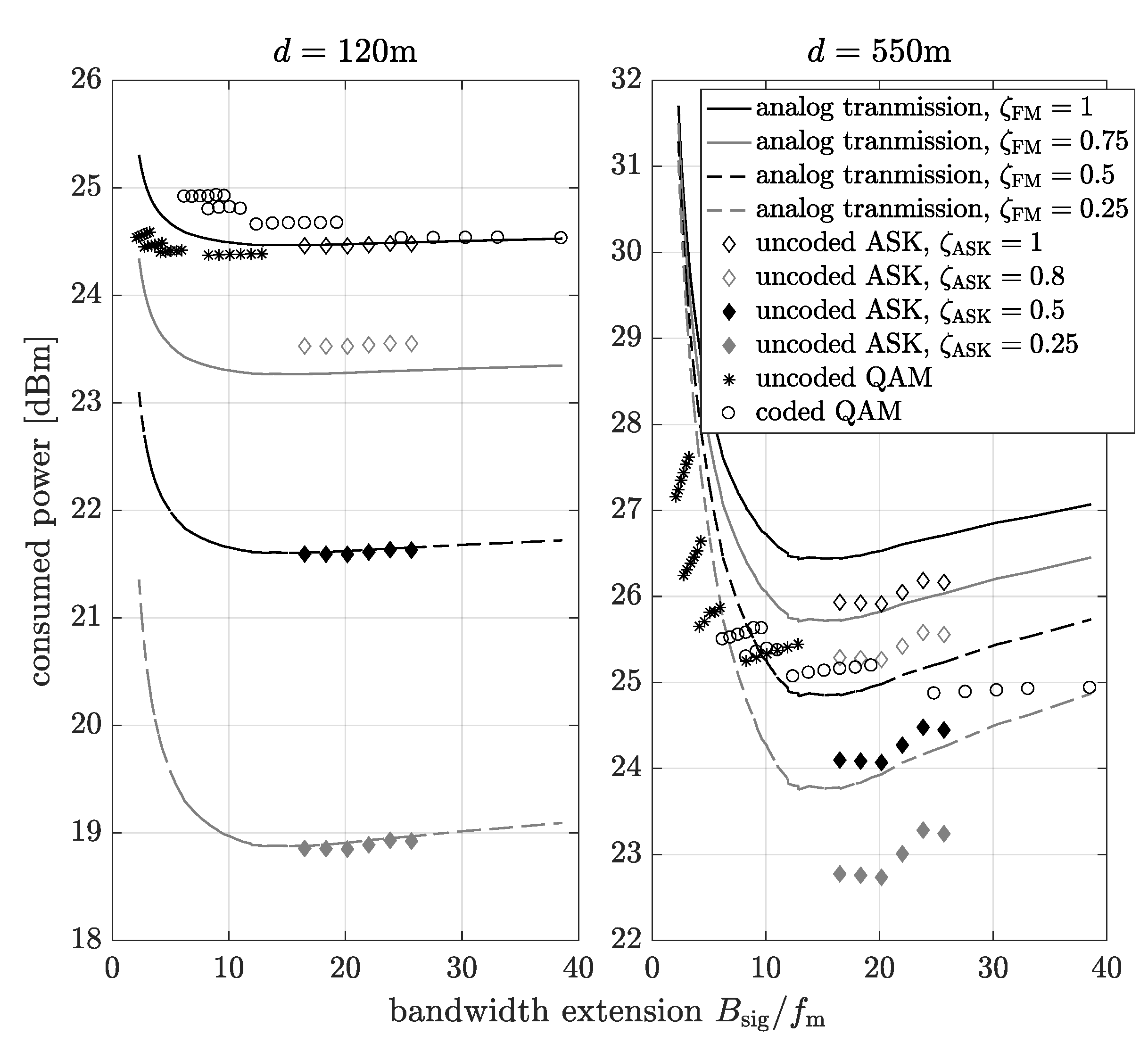
In
Figure 7 the total consumed power as a function of the bandwidth extension for different distances between the transmitter and the receiver, as well as factors
and
is plotted. Now, it can be observed that for a short distance between the transmitter and the receiver (
m, on the left-hand side plot) the digital transmission can consume less power only when
, i.e., when
and even in this case, some of the considered digital transmission schemes consume more power than the analog transmission. Moreover, the uncoded digital transmission with
modulation can consume similar power as analog communication system, thus, it can be considered as a good candidate transmission scheme for energy efficient communication in short links. In the case of the higher distance the between transmitter and receiver (
m, on the right-hand side plot), the analog transmission consumes more power than digital communication with
modulation for
, however, for
, there exist cases when the digital transmission is less energy efficient. Finally, for the considered analog as well as digital transmission, there exists the bandwidth extension which minimizes the consumed power.
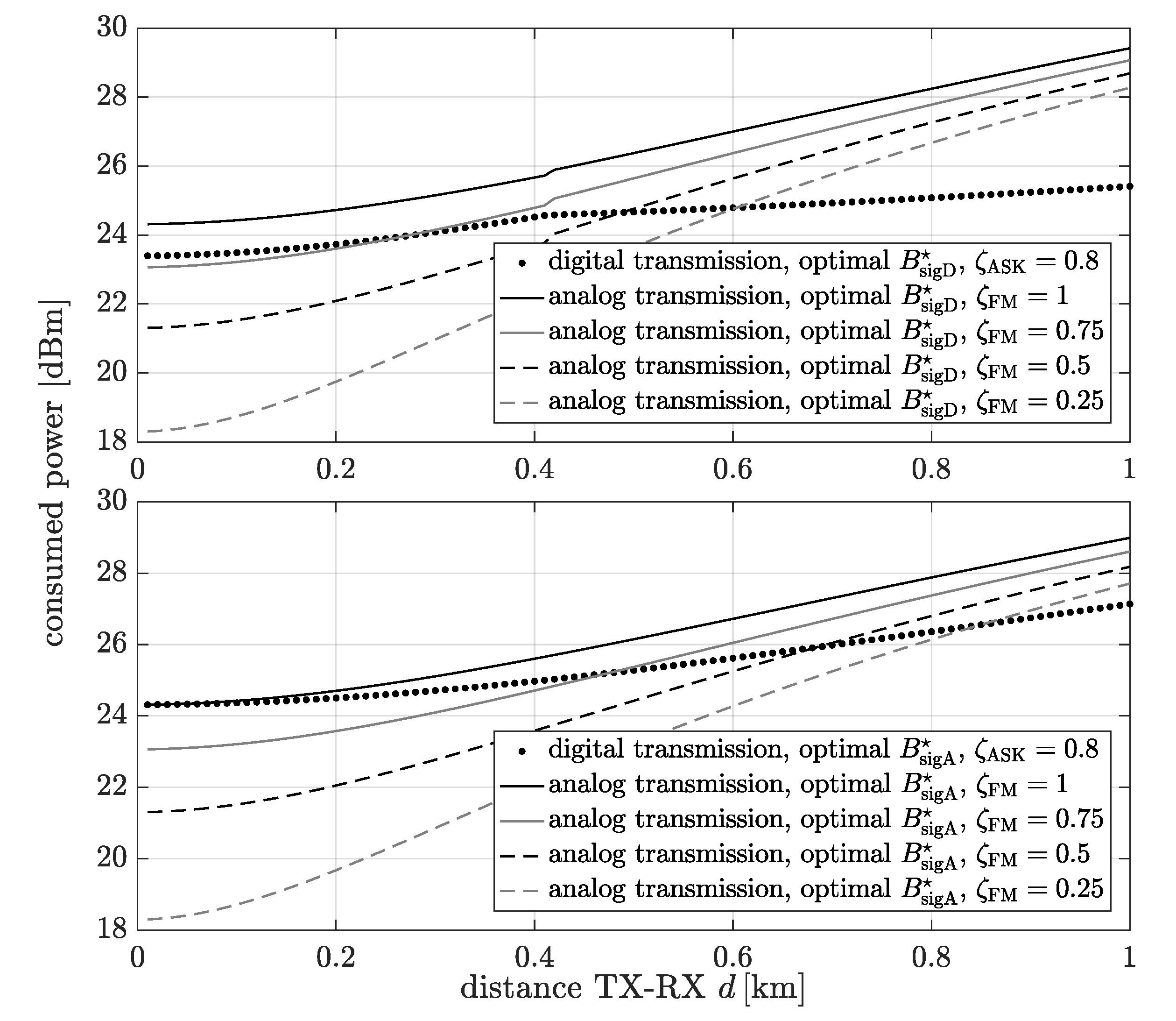
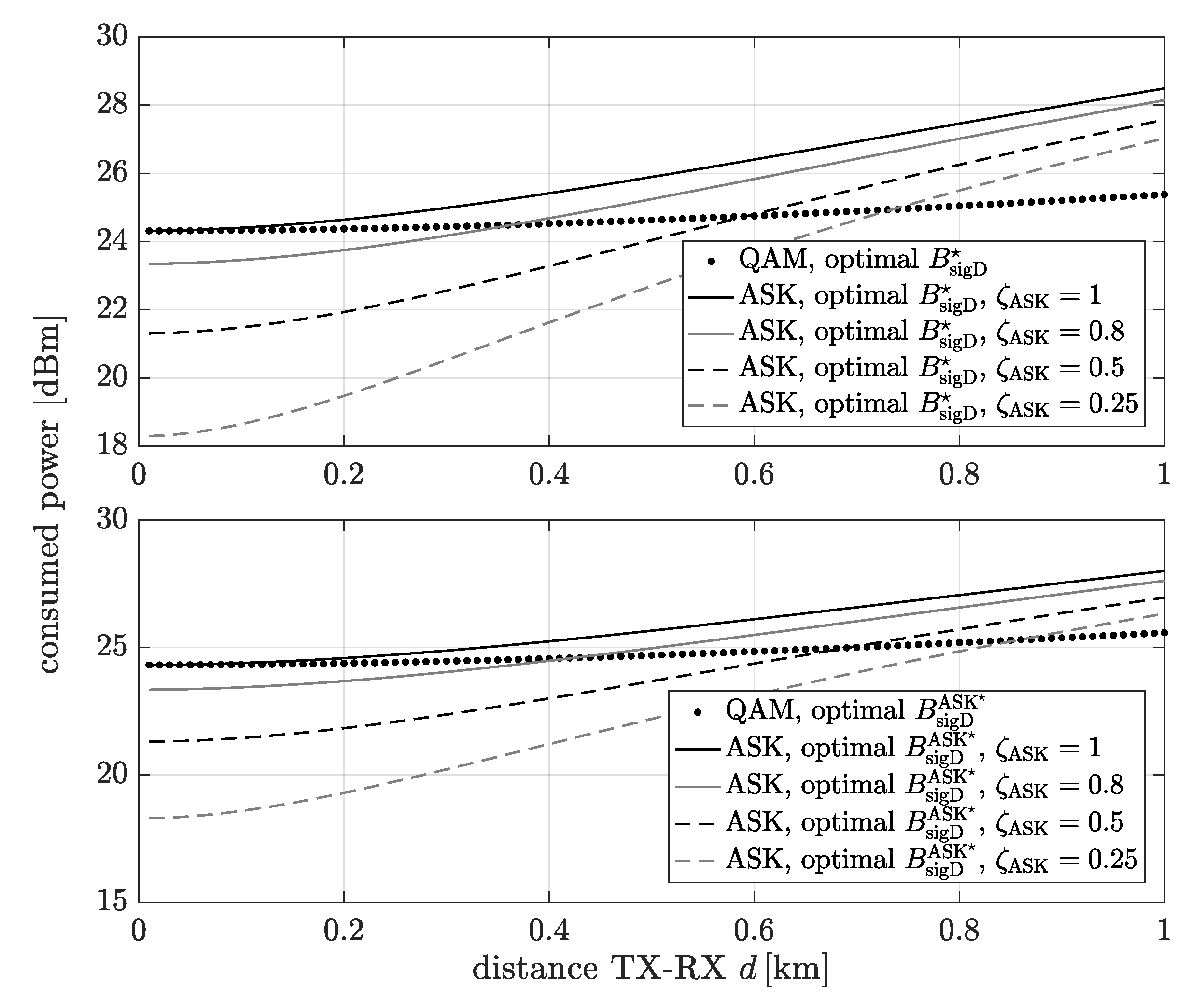
The power consumption of the analog and digital communication system schemes for the bandwidth extension which minimize the power consumption as a function of the distance between the transmitter and the receiver is shown in
Figure 8. The digital communication system means that data can be transmitted using
or
modulation. The consumed power has been determined for each distance and the bandwidth extension which minimize the consumption power for digital transmission (top figure)
or analog transmission (bottom figure)
for
. It is noticeable that only when
, the consumed power of the analog communication system is higher than the digital one for all considered distances. In the rest of the cases, for short distances, the analog transmission is more energy efficient. This is due to the domination of the power consumed by the transmitter and receiver components and the baseband signal processing power over the transmission (signal emission) power.
So far we have considered the source of the
signal to be time-continuous. Let us also consider the case, when the source generates digital data (discrete in time and in the set of values). For this case, in
Figure 9, the power consumption of the digital transmission with
and
modulation as a function of the distance between the transmitter and the receiver is compared. In the top figure, the results have been determined for the optimal bandwidth extension (in the context of the minimization of power consumption) of the digital transmission with
modulation
, while in the bottom figure, for the optimal bandwidth extension (in the context of the minimization of power consumption) of the digital transmission with
modulation
. There, one can observe that for short distances, the digital communication system with
modulation is more energy efficient than the one with
modulation due to the less complex transmitter and the receiver.
4. Analytical Power Consumption Model
In this section, the analytical power consumption model of the analyzed analog and digital transmission, based on the simulation results, have been proposed. Thus, let us approximate the required SNR for FM-based system vs. the bandwidth extension curves by the exponential function:
where
,
,
and
are the fitting parameters for a given
. The coefficients, obtained by least squares fitting to results visible in
Figure 6, are shown in
Table 2. Based on Equation (
11), the transmission power for a given channel attenuation and the noise power can be calculated by:
Substituting Equation (
12) to Equation (
5), the analytical power consumption model which depends on the distance between transmitter and receiver and bandwidth extension can be determined:
In the same way, the analytical power consumption model can be determined for the digital schemes. Due to the finite set of parameters, we determine the lower and upper bound for the required SNR in a function of bandwidth extension. The approximation of the required SNR for coded digital scheme can be defined by the exponential function:
while for the uncoded
scheme by the function:
where the fitting parameters are
,
,
,
,
,
and
. These coefficient values, obtained based on least squares fitting to data from
Figure 6, are given in
Table 3 and
Table 4 for coded and uncoded QAM system, respectively. Based on the above equations, the transmission power of digital scheme with
modulation can be calculated as:
Finally, substituting Equation (
16) to Equation (
8), the analytical power consumption model of the digital transmission with
modulation is obtained as:
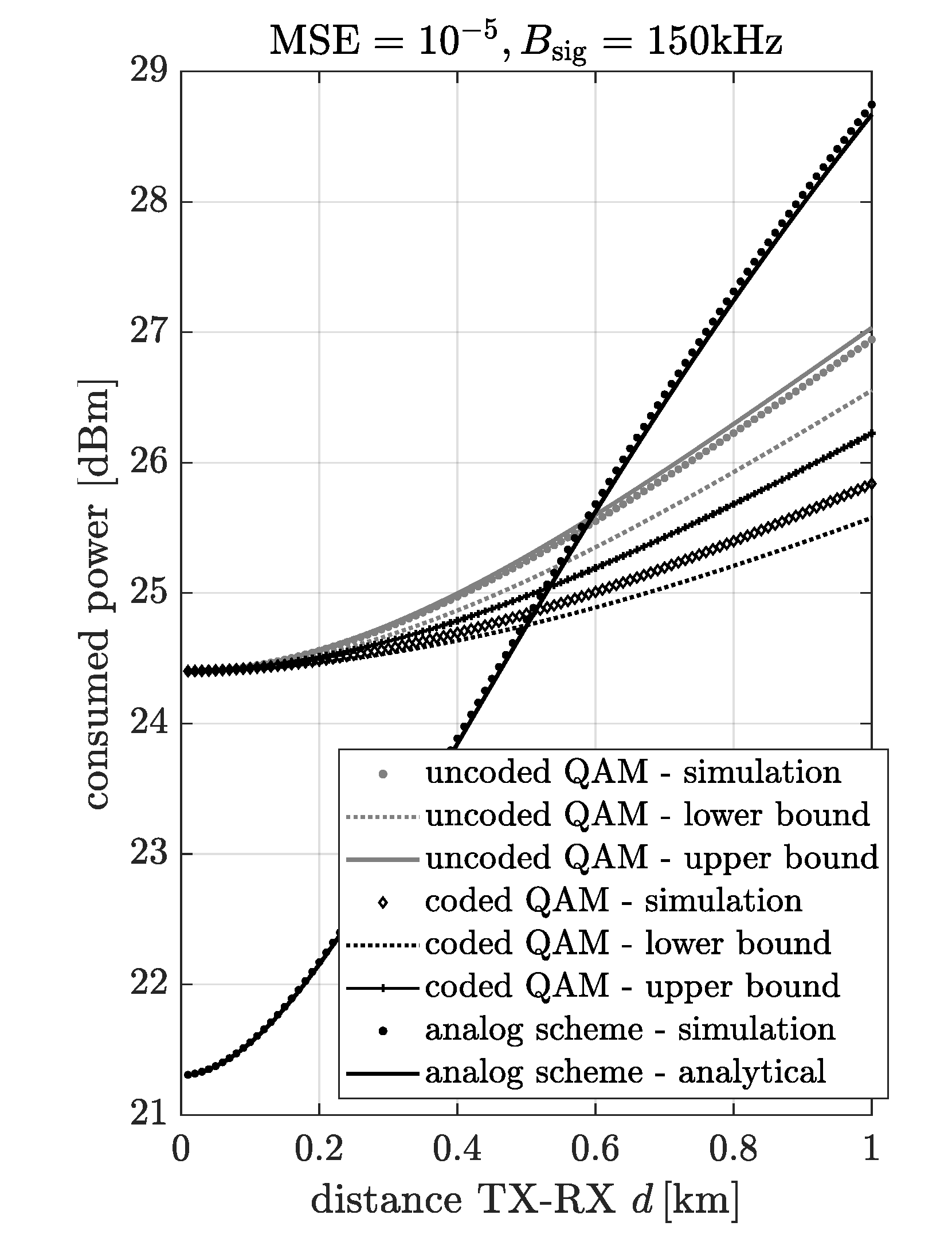
In
Figure 10, the power consumption of the digital and analog scheme resulting from the simulation and analytical model vs. distance between transmitter and receiver for
,
and
is presented. In the case of the digital scheme, the lower and upper bound of the power consumption are plotted. It can be observed that the simulation results are between curves obtained by the upper and lower bound. Moreover, in the case of the analog scheme, the approximation fits to the simulation results very well.
5. Conclusions
In this paper, inspired by the human brain, we have analyzed the analog and digital transmission from the energy-efficiency point of view. Our motivation was to flexibly choose between both schemes in a massive, short-links network to transfer information from various sources to various sinks, over moderately reliable channels with various QoS requirements. In our paper, we assumed that the transmitted data came from analog sensors in all systems. Therefore, in the case of the digital transmission, the input data are fed first to the analog-to-digital converter. At the receiving side, the decoded data are converted back to analog form. The following transmission schemes have been compared in the context of the performance as well as of the energy efficiency: simple analog, simple digital uncoded ASK and more complex digital uncoded and coded QAM scheme. For the energy efficiency analysis, the circuit power consumption models as well as datasheets have been studied and included in the total power consumption model. The high-level power consumption model and the relation factor have been applied in order to make the results independent from technologies. It can be observed that the power consumed when the transmitter and receiver are turned on is constant and and depend on this value, directly. Therefore, the change of this value causes the dilution of the power consumption about the difference between this value and the new value while the relations between transmission schemes will be the same. The simulation results have been obtained for the same bandwidth and the same in the occupied band and for the same MSE at the receiver output (related to the system performance). They show that in some cases, especially for relatively short links, the analog transmission can be beneficial, resulting in higher energy efficiency, while assuming the same performance level. Furthermore, the difference between energy consumption of frequency modulation and a simple digital modulation (ASK) is small and implementation dependent. Therefore, the proposed model gains importance providing not only qualitative but also quantitative guidance for energy efficient transmission mode selection. Moreover, due to the fact that the most data is represented in the digital form (sources are discrete), the simple uncoded digital communication system (with modulation) has also been compared with another digital system with modulation. The results show that there exist cases when the simple scheme minimizes the consumed power. Moreover, there exists optimal bandwidth extension which minimizes the power consumption for the considered analog and digital communication systems. Finally, the analytical power consumption model of the considered schemes has been proposed. The results show that the analytical model fits the simulation data very well and can be used to design the adaptive selection between analog and digital scheme in the link or in the multiuser network. In the case of multiuser interference, the proposed power consumption model can be easily adapted because in many cases for the considered narrowband system, the interference can be modeled as an increased noise floor. Therefore, the performance in the interference-limited environment can be estimated by calculating SINR value and using it for an SNR value in the presented results.