Method for Localization Aerial Target in AC Electric Field Based on Sensor Circular Array
Abstract
1. Introduction
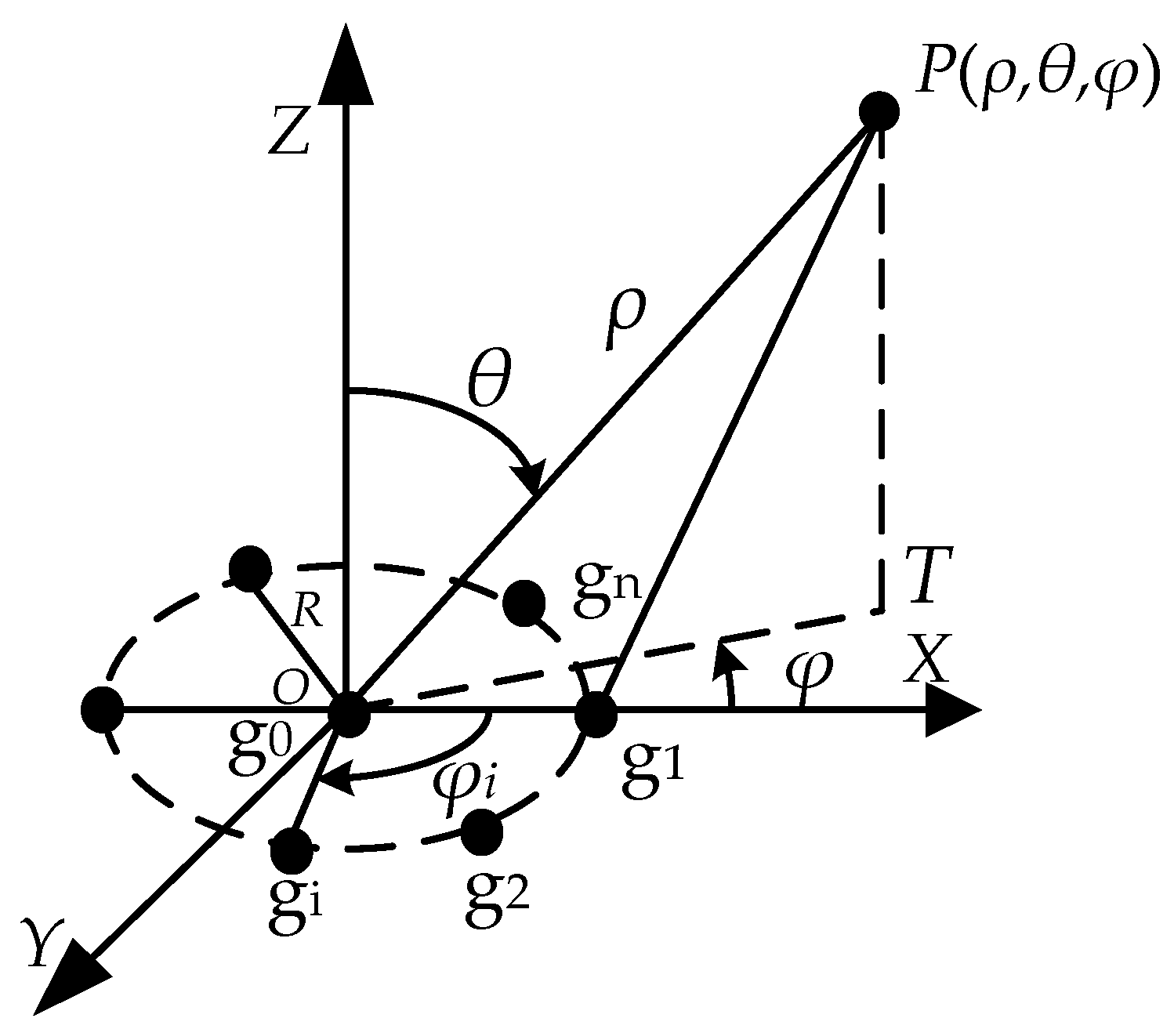
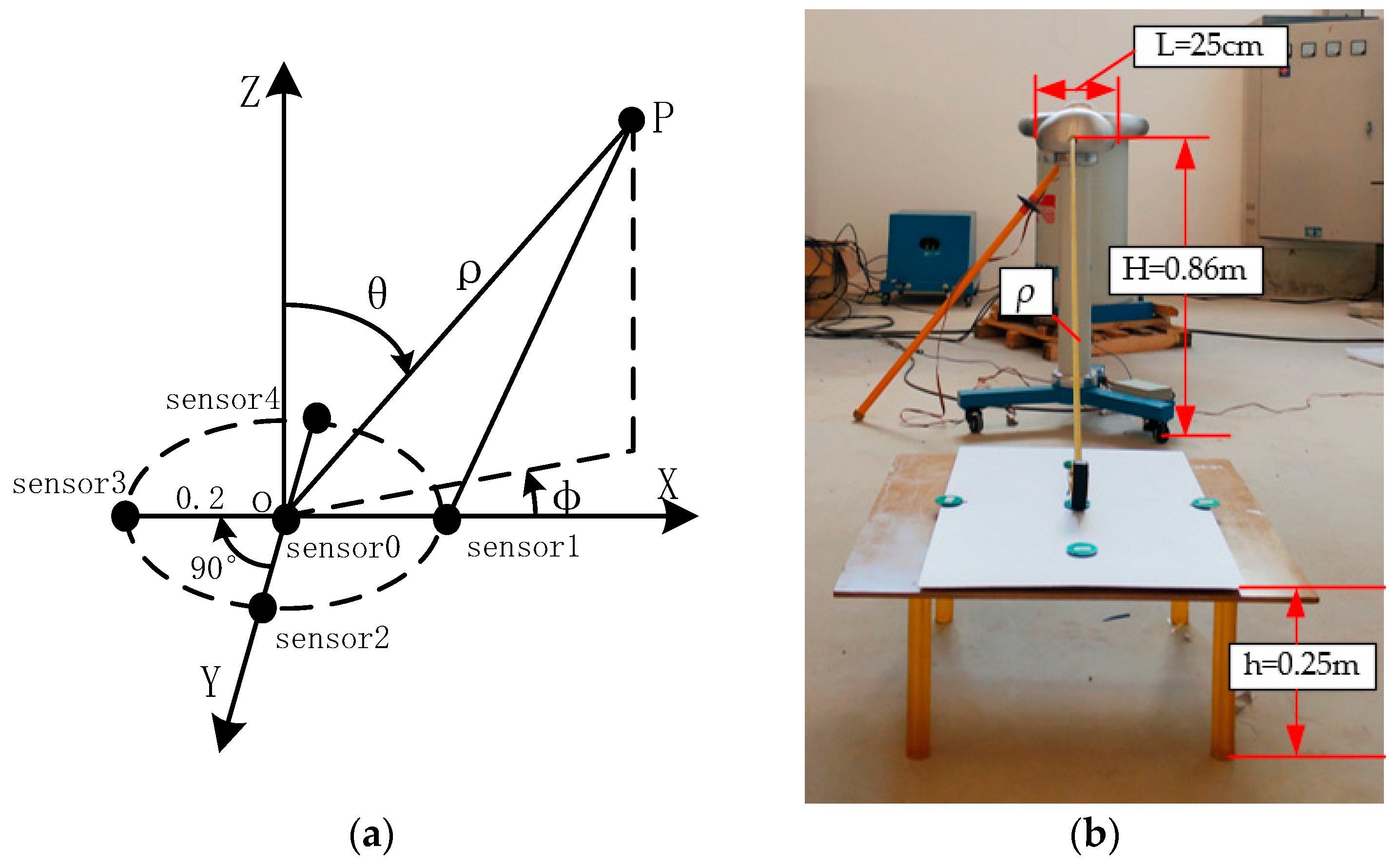
2. Localization Principle
3. Error Analysis
3.1. Error Model
3.2. Influence of Layout Parameters on Measurement Errors
3.2.1. Value Range of Layout Parameters
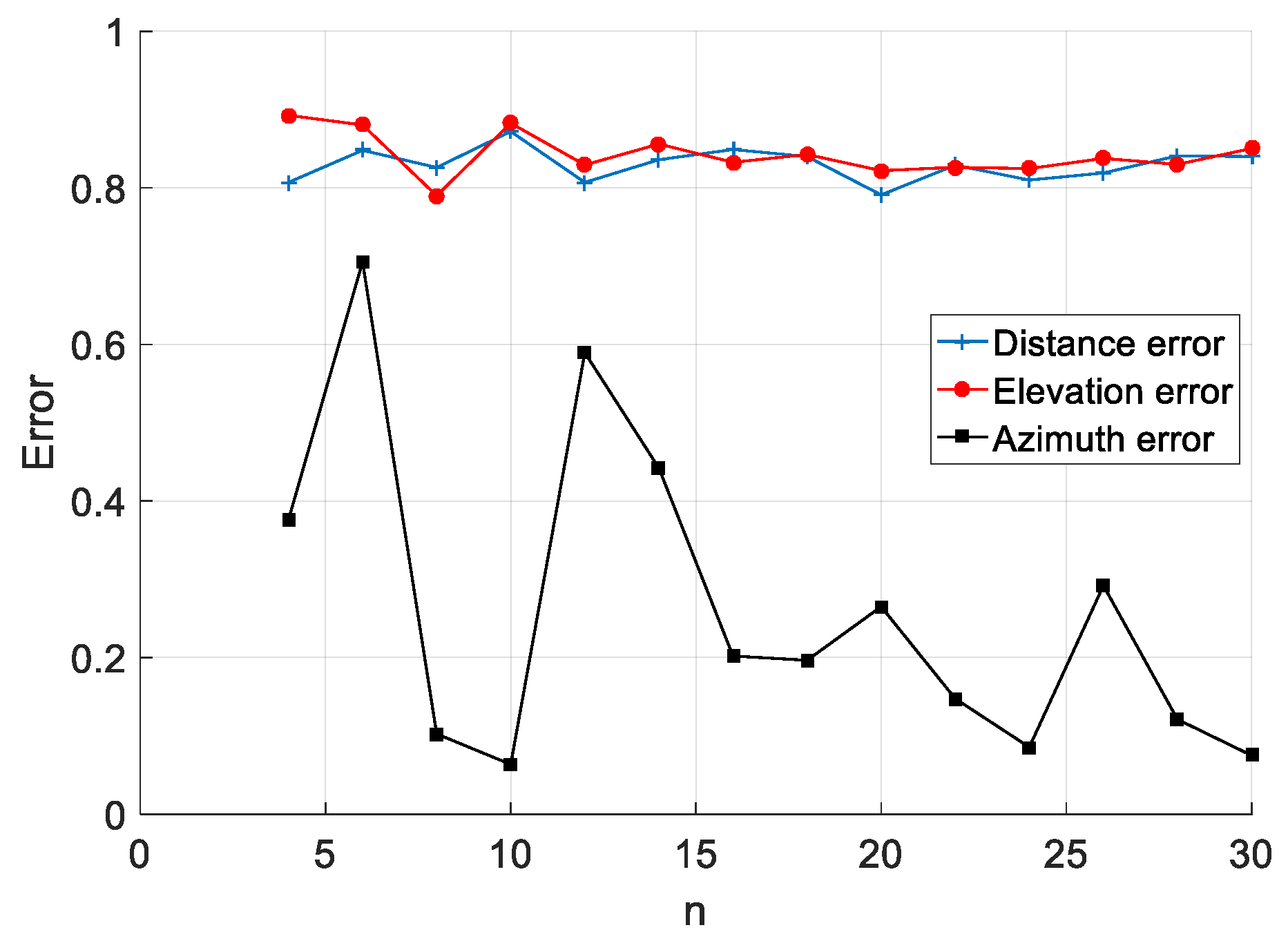
3.2.2. Simulation Analysis of the Effect of the Number of Sensors on the Localization Error
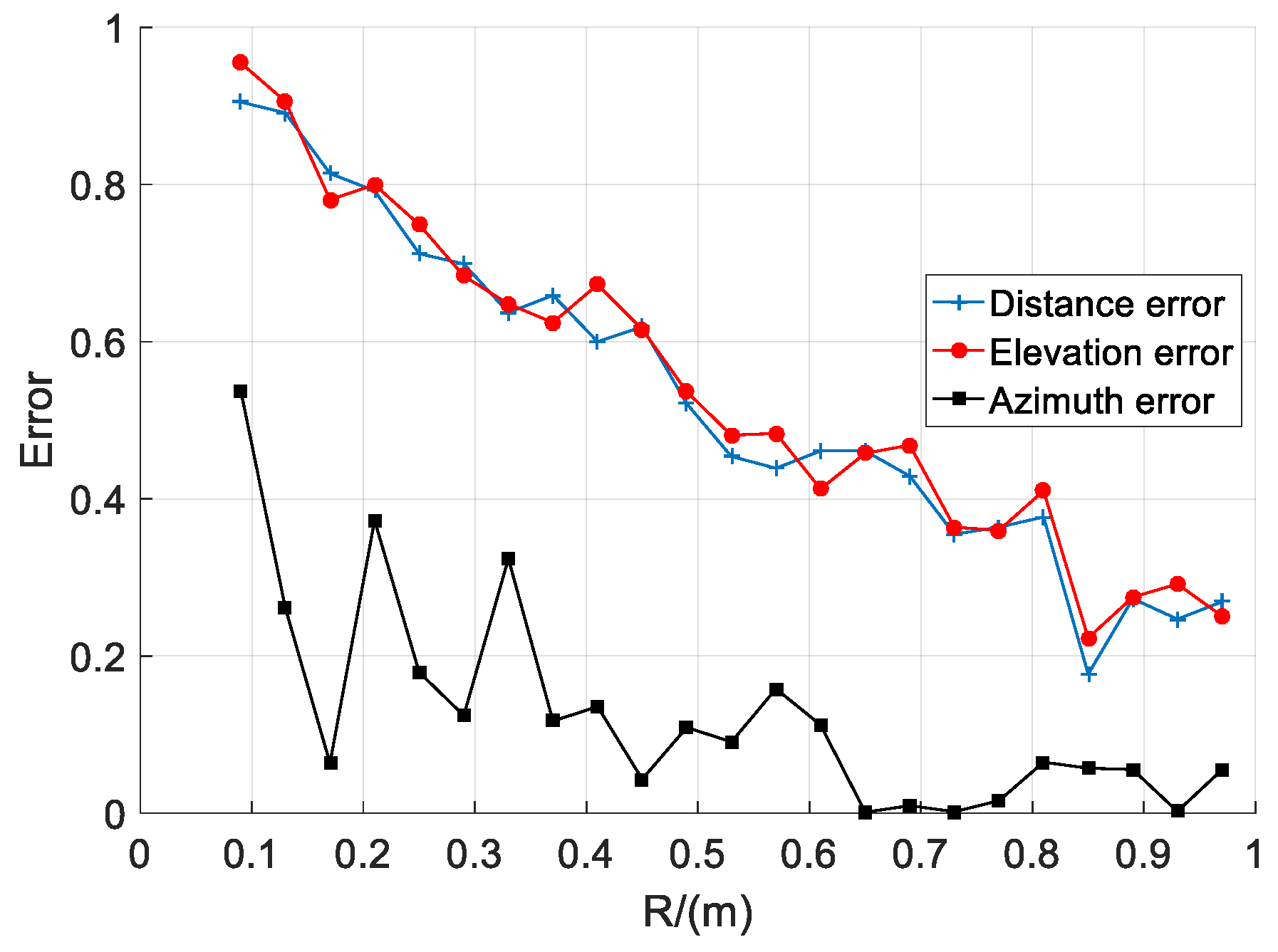
3.2.3. Simulation Analysis of the Influence of Array Radius on Localization Error
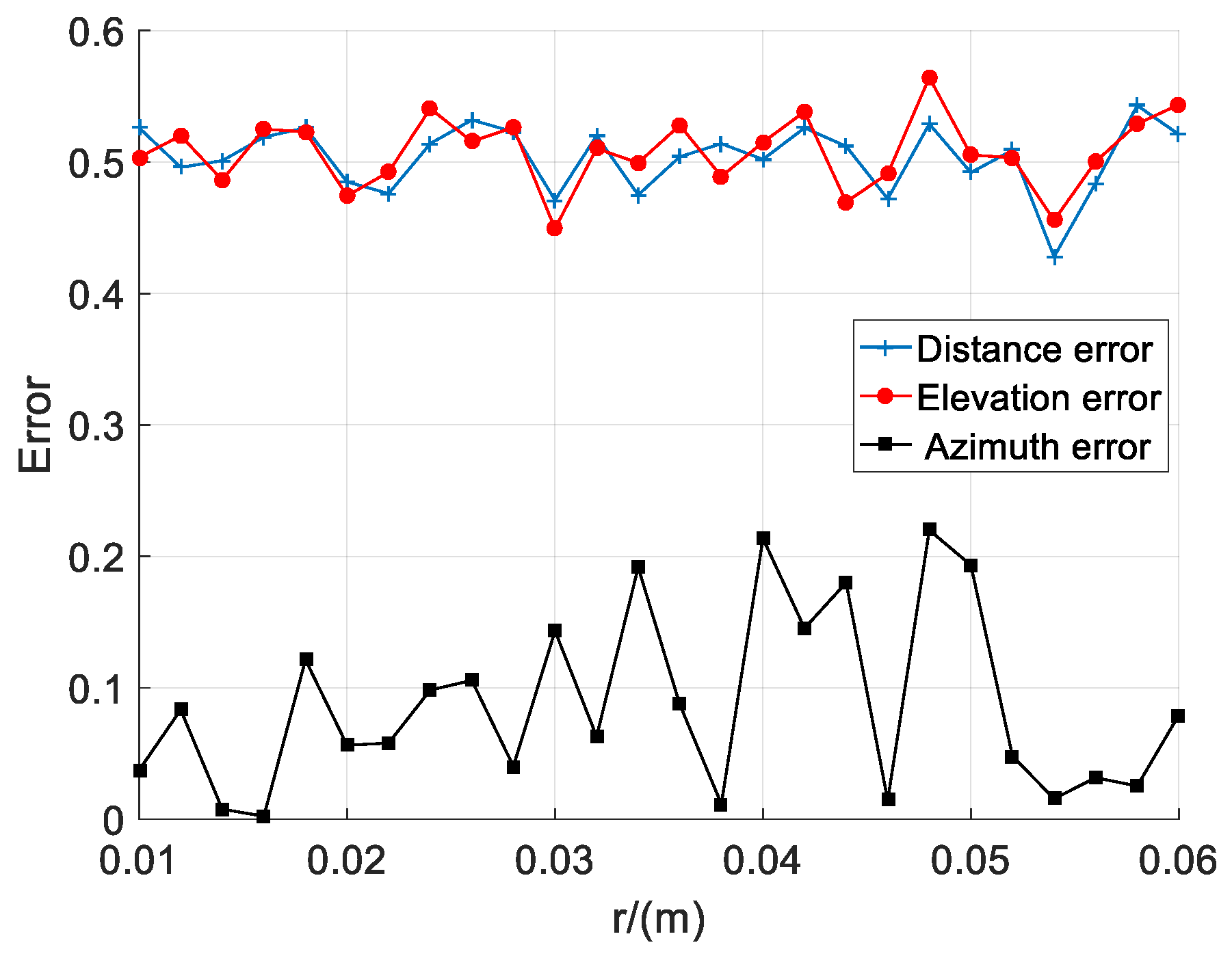
3.2.4. Simulation Analysis of the Effect of Sensor Radius on Localization Error
4. Building an Optimization Model
4.1. Determination of Constraints
4.2. Determination of the Objective Function
5. Optimization of Sensor Layout Parameters Based on Genetic Algorithm
5.1. The Solution Process of Genetic Algorithm
- Step 1:
- Establish an optimization model based on the localization principle and error analysis.
- Step 2:
- Determine the encoding method. The mathematical equation of the objective function and constraints in this article is a function optimization problem, so the real number encoding is selected.
- Step 3:
- Step 4:
- Initialize the population. The optimization of the layout parameters in this article belongs to a more complicated optimization problem. Therefore, the number of the initial population is set to 200, and the current generation number is g = 1.
- Step 5:
- According to Equation (27), calculate the fitness value of each individual in the contemporary population, and rank the fitness from large to small.
- Step 6:
- Judgment of termination condition. If g ≥ G = 500, the operation is terminated, and the most adaptive individual in the current population is the optimal solution; if g < G, the operation continues, and step 7 is performed.
- Step 7:
- Genetic evolution operation. Genetic evolution includes selection, crossing, and mutation. It is the most basic component of genetic algorithm [36]. After the operation is completed, a new generation of population will be generated. At this time, g = g + 1, go to Step 5.
5.2. Simulation Experiments and Optimization Results
6. Experimental Verification
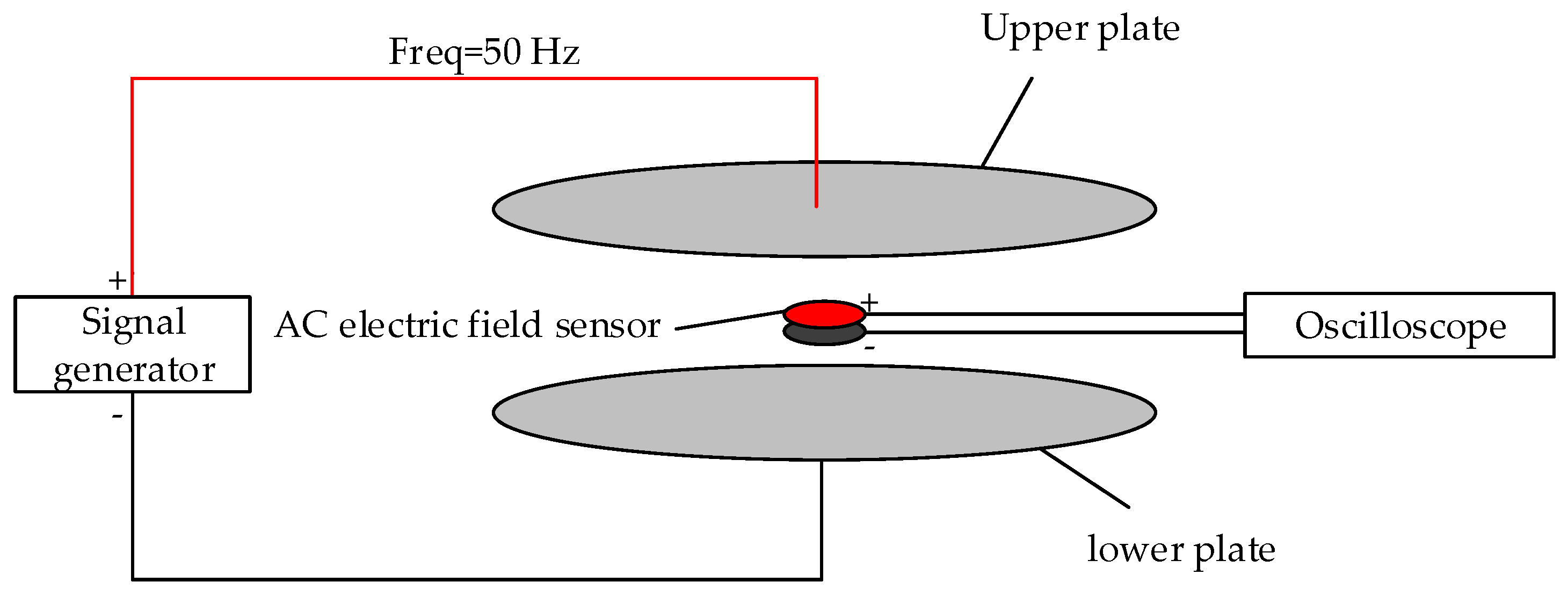
6.1. Detector Hardware Design
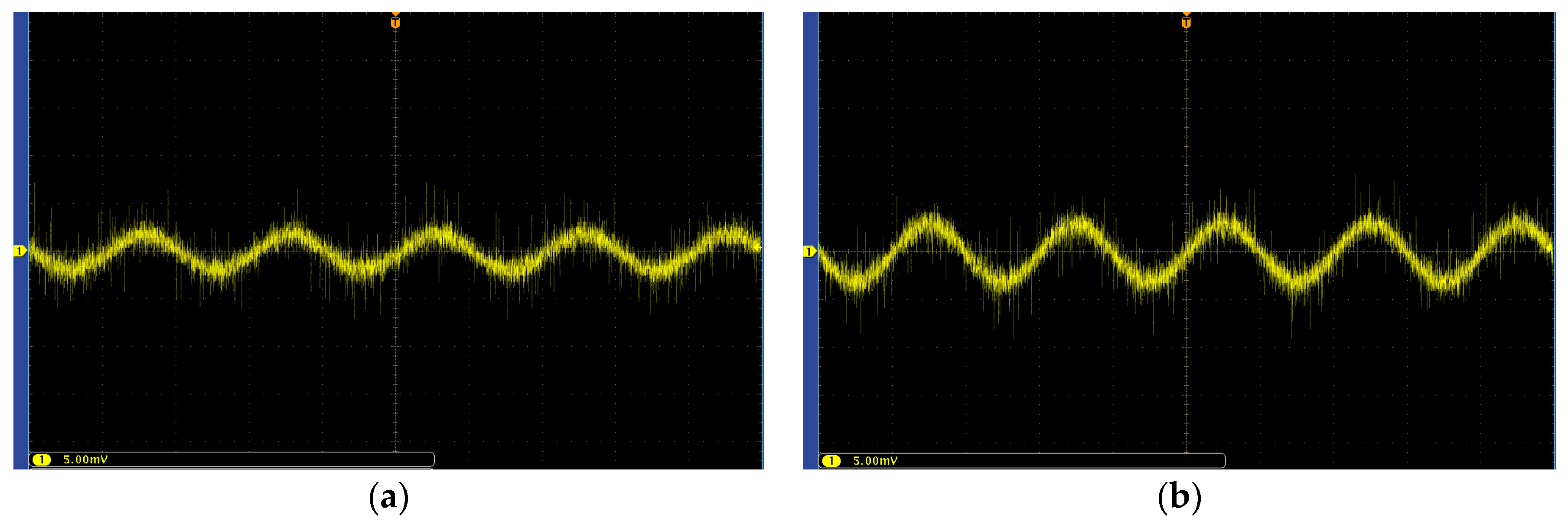
6.2. Experimental Platform Construction and Experimental Analysis
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Xiao, X.; Li, S. Impacts of flexible obstructive working environment on dynamic performances of inspection robot for power transmission line. J. Cent. South Univ. Technol. 2008, 15, 869–876. [Google Scholar] [CrossRef]
- Azevedo, F.; Dias, A.; Almeida, J.; Oliveira, A.; Ferreira, A.; Santos, T.; Martins, A.; Silva, E. LiDAR-Based Real-Time Detection and Modeling of Power Lines for Unmanned Aerial Vehicles. Sensors 2019, 19, 1812. [Google Scholar] [CrossRef] [PubMed]
- Fan, F.; Ji, Q.; Wu, G.; Wang, M.; Ye, X.; Mei, Q. Dynamic Barrier Coverage in a Wireless Sensor Network for Smart Grids. Sensors 2019, 19, 41. [Google Scholar] [CrossRef] [PubMed]
- Qin, X.; Wu, G.; Lei, J.; Fan, F.; Ye, X. Detecting Inspection Objects of Power Line from Cable Inspection Robot LiDAR Data. Sensors 2018, 18, 1284. [Google Scholar] [CrossRef] [PubMed]
- Hu, Y. Research and Development of Live Working Technology on Transmission and Distribution Lines. High Volt. Eng. 2006, 32, 1–10. [Google Scholar]
- Zhang, W.; Ning, Y.; Suo, C. A Method Based on Multi-Sensor Data Fusion for UAV Safety Distance Diagnosis. Electronics 2019, 8, 1467. [Google Scholar] [CrossRef]
- Xiao, D.; Ma, Q.; Xie, Y.; Zheng, Q.; Zhang, Z. A power electric field sensor for portable measurement. Sensor 2018, 18, 1053. [Google Scholar] [CrossRef]
- Liu, C.; He, W.; Wang, J. Design of Portable Power Frequency Electric Field Measurement Device. High Volt. Appar. 2012, 48, 57–62. [Google Scholar]
- Tong, J.; Lie, Y.; Liu, G.; Wang, H.; Jing, X.; Yang, P. Power-frequency Electric Field Measurement Using a Micromachined Electric Field Sensor. J. Electron. Inf. Technol. 2018, 12, 3036–3041. [Google Scholar]
- Ling, B.; Peng, C.; Ren, R.; Chu, Z.; Zhang, Z.; Lei, H.; Xia, S. Design, Fabrication and Characterization of a MEMS-Based Three-Dimensional Electric Field Sensor with Low Cross-Axis Coupling Interference. Sensors 2018, 18, 870. [Google Scholar] [CrossRef]
- Gu, Z.; Yang, P.; Peng, C. Electric field measurement safety warning system of live working based on MEMS structure. Transducer Microsyst. Technol. 2017, 36, 111–113. [Google Scholar]
- Zhou, N.; Fang, Z.; Tang, L.; Fan, L.; Zhang, W. Design and analysis of power frequency electric field sensing unit for high voltage near-electricity early warning. Transducer Microsyst. Technol. 2017, 36, 111–113. [Google Scholar]
- Wang, W.; Wen, G. Electric field examination and alarm display with Hall element. J. Suzhou Univ. (Nat. Sci.) 2003, 19, 47–50. [Google Scholar]
- Zhang, W.; Yang, C.; Zhou, N. Automatic identification method of voltage level of high voltage transmission line based on SVM. Ferroelectrics 2017, 521, 86–93. [Google Scholar] [CrossRef]
- Suo, C.; Sun, H.; Zhang, W.; Zhou, N.; Chen, W. Adaptive Safety Early Warning Device for Non-contact Measurement of HVDC Electric Field. Electronics 2020, 9, 329. [Google Scholar] [CrossRef]
- Hu, L.; Wang, S.; Zhang, E. Aspect-Aware Target Detection and Localization by Wireless Sensor Networks. Sensors 2018, 18, 2810. [Google Scholar] [CrossRef]
- Kan, Y.; Wang, P.; Zha, F.; Li, M.; Gao, W.; Song, B. Passive Acoustic Source Localization at a Low Sampling Rate Based on a Five-Element Cross Microphone Array. Sensors 2015, 15, 13326–13347. [Google Scholar] [CrossRef]
- Huang, S.; Wu, Z.; Misra, A. A Practical, Robust and Fast Method for Location Localization in Range-Based Systems. Sensors 2017, 17, 2869. [Google Scholar] [CrossRef]
- Wu, F.; Luo, L.; Jia, T.; Sun, A.; Sheng, G.; Jiang, X. RSSI-Power-Based Direction of Arrival Estimation of Partial Discharges in Substations. Energies 2019, 12, 3450. [Google Scholar] [CrossRef]
- Yan, J.; Qiao, R.; Tang, L.; Zheng, C.; Fan, B. A fuzzy decision based WSN localization algorithm for wise healthcare. China Commun. 2019, 4, 208–218. [Google Scholar]
- Fan, L.; Zheng, Q.; Kang, X. Baseline optimization for scalar magnetometer array and its application in magnetic target localization. Chin. Phys. B 2018, 27, 215–221. [Google Scholar] [CrossRef]
- Yin, J.; Xiong, C.; Wang, W. Acoustic Localization for a Moving Source Based on Cross Array Azimuth. Appl. Sci. 2018, 8, 1281. [Google Scholar] [CrossRef]
- Trinks, H.; Haseborg, J. Electric Field Detection and Ranging of Aircraft. IEEE Trans. Aerosp. Electron. Syst. 1982, AES-18, 268–274. [Google Scholar] [CrossRef]
- Chen, X.; Cui, Z.; Bi, J. Modeling on Passive Ground Electrostatic Detection System with Spherical Electrode. J. Beijing Inst. Technol. 2004, 24, 994–997. [Google Scholar]
- Li, M.; Feng, X.; Man, X. A Transformer Partial Discharge UHF Localization Method Based on TDOA and TS-PSO. Proc. CSEE 2019, 39, 1834–1842. [Google Scholar]
- Chen, H.; Zhu, C.; Li, Y.; Xu, D. Research on Calculation and Measurement of Power Frequency Electric Field for Transmission Line. J. Electr. Eng. 2016, 11, 40–45. [Google Scholar]
- Chen, X.; Cui, Z.; Chen, F. Analysis on the Properties of Electrostatic Target. Trans. Beijing Inst. Technol. 2005, 25, 159–163. [Google Scholar]
- Tian, D. Design and Implementation of Electrostatic Detection System. Master’s Thesis, Beijing Institute of Technology, Beijing, China, 2007. [Google Scholar]
- Hao, X.; Xu, L.; Cui, Z.; Chen, X. Design of fuze MEMS electrostatic detection array. Opt. Precis. Eng. 2009, 17, 1223–1227. [Google Scholar]
- Hu, Z.; He, W.; Yao, D.; Wang, J.; Wen, J.; Li, L. Research of High-voltage Power Frequency Electric Field Warning Instrument. Electr. Meas. Instrum. 2009, 9, 45–48. [Google Scholar]
- Chen, X.; Cui, Z.; Xu, L. Optimization of Round Array Passive Electrostatic Detection System. J. Beijing Inst. Technol. 2006, 26, 610–613. [Google Scholar]
- Chen, X.; Xu, L.; Bi, J.; Cui, Z. Location Method of Round Array Based Passive Electrostatic Detection System. J. Beijing Inst. Technol. 2005, 25, 159–163. [Google Scholar]
- Chen, F. Research on Target Identification of Electrostatic Detection. Ph.D. Thesis, Beijing Institute of Technology, Beijing, China, 2006. [Google Scholar]
- Xiao, D.; Liu, H.; Zhou, Q.; Xie, Y.; Ma, Q. Influence and Correction from the Human Body on the Measurement of a Power-Frequency Electric Field Sensor. Sensors 2016, 16, 859. [Google Scholar] [CrossRef] [PubMed]
- Zhu, L.; Zhuang, Z.; Zhang, Q. An Omni-Directional Passive Locatlization Technology of Acoustic Target with Plane Circular Array. Acta Acust. 1999, 2, 204–209. [Google Scholar]
- Chen, F.; Xu, S.; Zhao, Y.; Zhang, H. An Adaptive Genetic Algorithm of Adjusting Sensor Acquisition Frequency. Sensors 2020, 20, 990. [Google Scholar] [CrossRef] [PubMed]
- Misakian, M.; Fulcomer, P. Measurement of no uniform power frequency electric fields. IEEE Trans. Ind. Electron. 1983, 18, 657–661. [Google Scholar] [CrossRef]
- Bohnert, K.; Randle, H.; Frosido, G. Field test of interferometric optical fiber high-voltage and current sensors. Proc. SPIE 1994, 23, 16. [Google Scholar]



| Voltage level (kV) | 10 | 35 | 110 | 220 |
| Safe distance (m) | 0.7 | 1.0 | 1.5 | 3.0 |
| 9 | Numerical Value | Parameter | Numerical Value |
|---|---|---|---|
| 10−6C | 0.4 | ||
| 10 m | 0.3 | ||
| 60° | 0.2 | ||
| 0.1 | |||
| 1.3 × 10−12C | 5 to 30 mm | ||
| φ | 30° | 4 to 108 | |
| 8.58 × 10−12 | 0.01 | ||
| 0 to 20 cm |
| Parameter | Meaning | Set Value |
|---|---|---|
| m | Initial population | 200 |
| G | Maximal genetic algebra | 500 |
| Crossover probability | 80% | |
| Mutation probability | 1% |
| Serial Number | Distance Accuracy (%) | Array Radius (m) | Sensor Radius (m) | Number of Sensors | Evaluation Function Value |
|---|---|---|---|---|---|
| 1 | 7.2 | 0.2 | 0.015 | 4 | 8.67219 |
| 2 | 10.8 | 0.199 | 0.015 | 4 | 8.65989 |
| 3 | 11.5 | 0.199 | 0.015 | 4 | 8.68891 |
| 4 | 8 | 0.2 | 0.015 | 4 | 8.65807 |
| 5 | 8.4 | 0.2 | 0.015 | 4 | 8.65588 |
| 6 | 12.4 | 0.2 | 0.011 | 6 | 11.1286 |
| 7 | 12.2 | 0.2 | 0.011 | 6 | 11.1308 |
| 8 | 10.6 | 0.2 | 0.011 | 6 | 11.1282 |
| 9 | 8.5 | 0.2 | 0.011 | 6 | 11.1253 |
| 10 | 11.5 | 0.2 | 0.011 | 6 | 11.1303 |
| Target Coordinates | Target Measurement | Sensor0 (kV/m) | Sensor1 (kV/m) | Sensor2 (kV/m) | Sensor3 (kV/m) | Sensor4 (kV/m) | Measurement Error () |
|---|---|---|---|---|---|---|---|
| (1.05,35.52,0) | (0.92,30.89,1.16) | 3.30 | 4.01 | 3.16 | 2.60 | 3.13 | (0.13,4.63,1.16) |
| (1.05, 35.52,60) | (1.21,44.12,57.17) | 3.30 | 3.68 | 3.93 | 2.88 | 2.69 | (0.16,8.6,4.57) |
| (1.05,42.55, 0) | (0.87,36.40, 2.29) | 2.77 | 3.58 | 2.65 | 2.10 | 2.64 | (0.18,6.15,2.29) |
| (1.5,24,0) | (1.67,22.33, 5.14) | 1.34 | 1.49 | 1.30 | 1.24 | 1.28 | (0.17,1.67,5.14) |
| (1.5,24,30) | (1.30,18.67,26.10) | 1.34 | 1.4.4 | 1.36 | 1.21 | 1.25 | (0.2,4.8,3.9) |
| (1.5,28.25,0) | (1.31,33.05,−1.72) | 1.07 | 1.25 | 1.04 | 0.90 | 1.05 | (0.19,4.8,1.72) |
| (2.25,15.73,0) | (1.78,51.2,0) | 0.45 | 0.47 | 0.43 | 0.42 | 0.43 | (0.47,35.47,0) |
| (2.2.5,15.73,100) | (×,×,76.29) | 0.45 | 0.46 | 0.47 | 0.45 | 0.43 | (×,×,23.71) |
| (2.25,18.39,0) | (1.11,12.1,−11.86) | 0.35 | 0.37 | 0.33 | 0.32 | 0.33 | (1.14,6.29,11.86) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, W.; Li, P.; Zhou, N.; Suo, C.; Chen, W.; Wang, Y.; Zhao, J.; Li, Y. Method for Localization Aerial Target in AC Electric Field Based on Sensor Circular Array. Sensors 2020, 20, 1585. https://doi.org/10.3390/s20061585
Zhang W, Li P, Zhou N, Suo C, Chen W, Wang Y, Zhao J, Li Y. Method for Localization Aerial Target in AC Electric Field Based on Sensor Circular Array. Sensors. 2020; 20(6):1585. https://doi.org/10.3390/s20061585
Chicago/Turabian StyleZhang, Wenbin, Peng Li, Nianrong Zhou, Chunguang Suo, Weiren Chen, Yanyun Wang, Jiawen Zhao, and Yincheng Li. 2020. "Method for Localization Aerial Target in AC Electric Field Based on Sensor Circular Array" Sensors 20, no. 6: 1585. https://doi.org/10.3390/s20061585
APA StyleZhang, W., Li, P., Zhou, N., Suo, C., Chen, W., Wang, Y., Zhao, J., & Li, Y. (2020). Method for Localization Aerial Target in AC Electric Field Based on Sensor Circular Array. Sensors, 20(6), 1585. https://doi.org/10.3390/s20061585





