Ultrasensitive Magnetic Field Sensors for Biomedical Applications
Abstract
1. Introduction
- Capture, preconcentration, and separation of analytes bonded with the specifically functionalized surface of the particles;
- Mixing of lateral flows;
- Creation of contrast in magnetic susceptibility of the biological medium for future sensing.
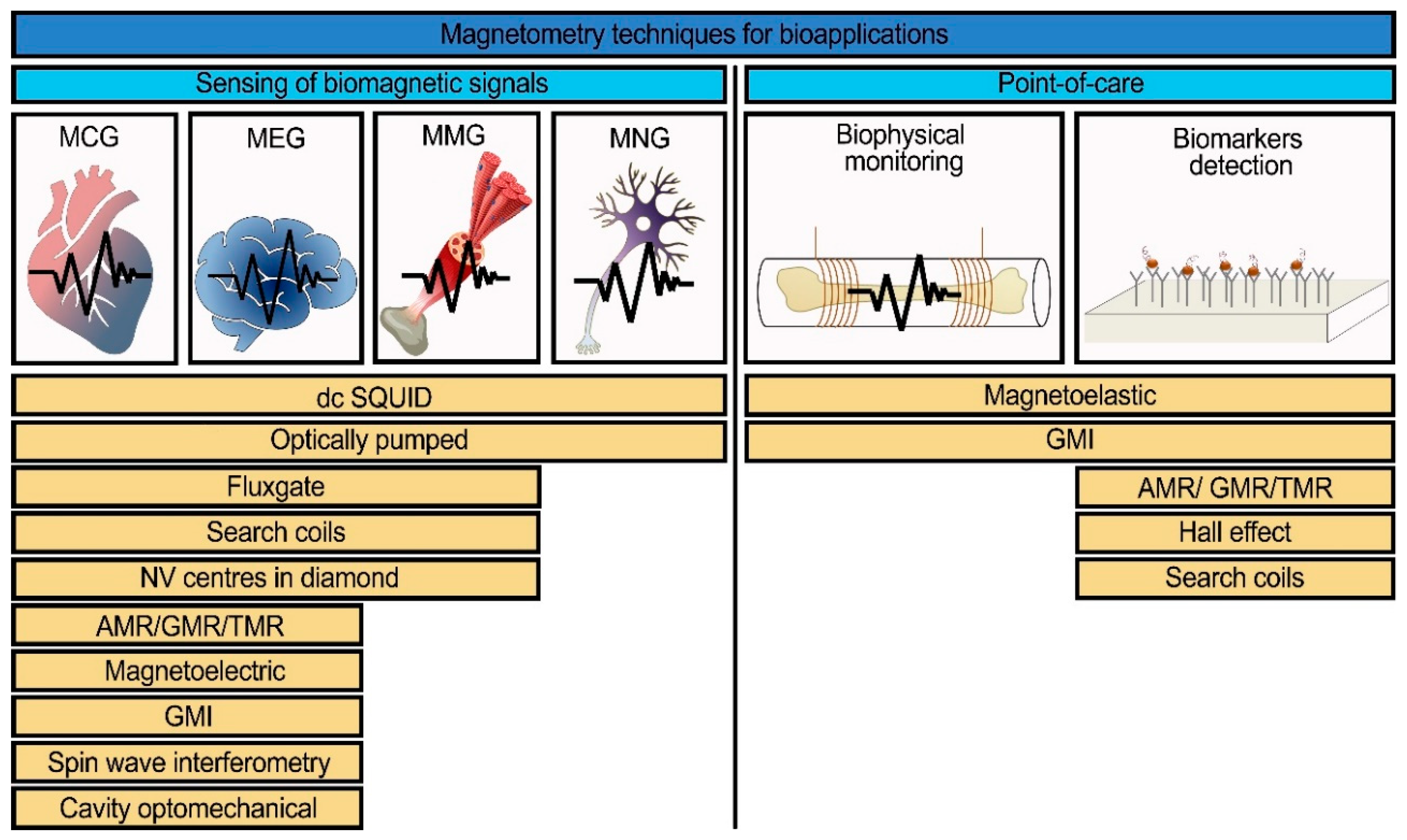
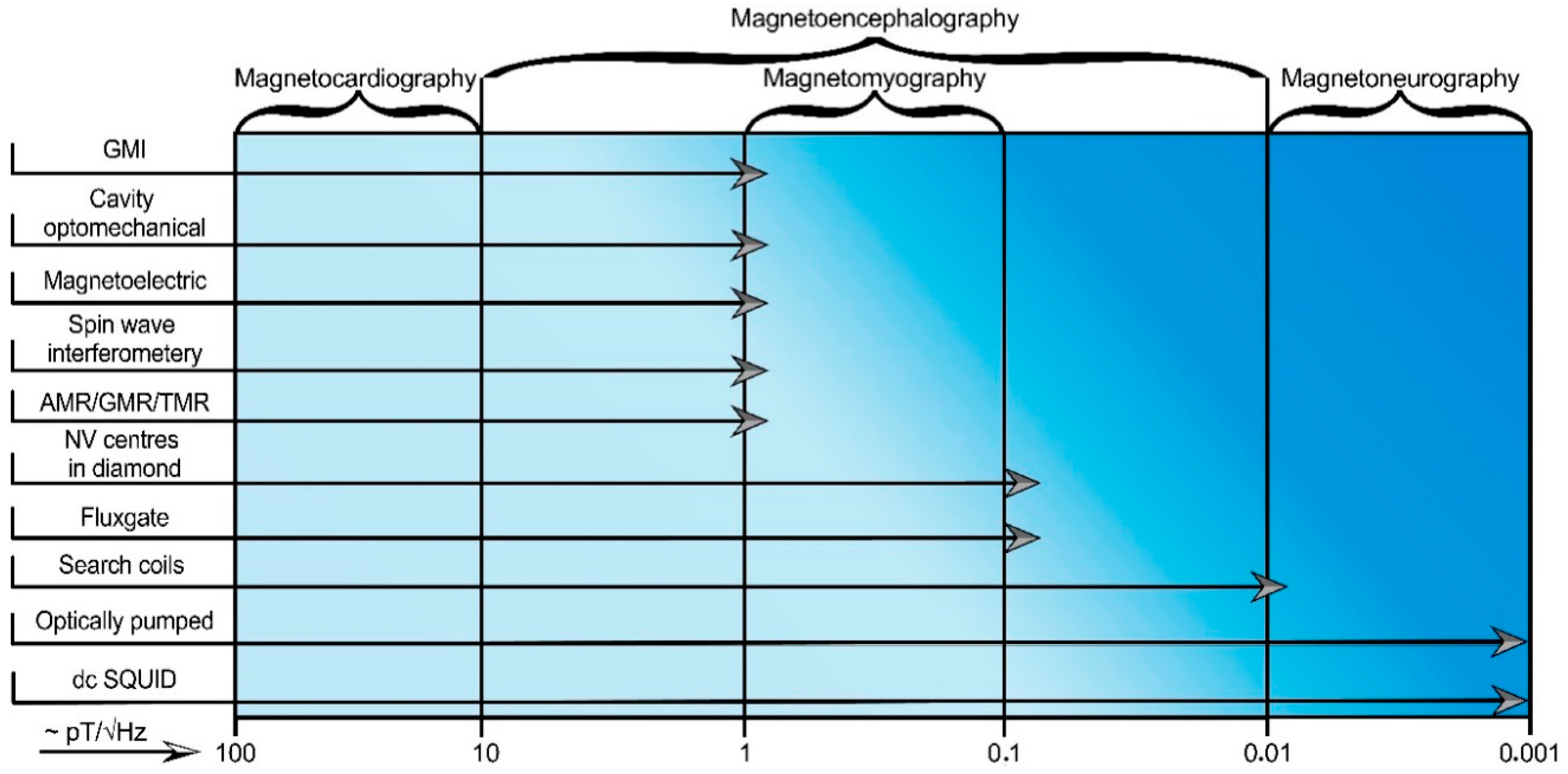
2. Types of Magnetic Field Sensors
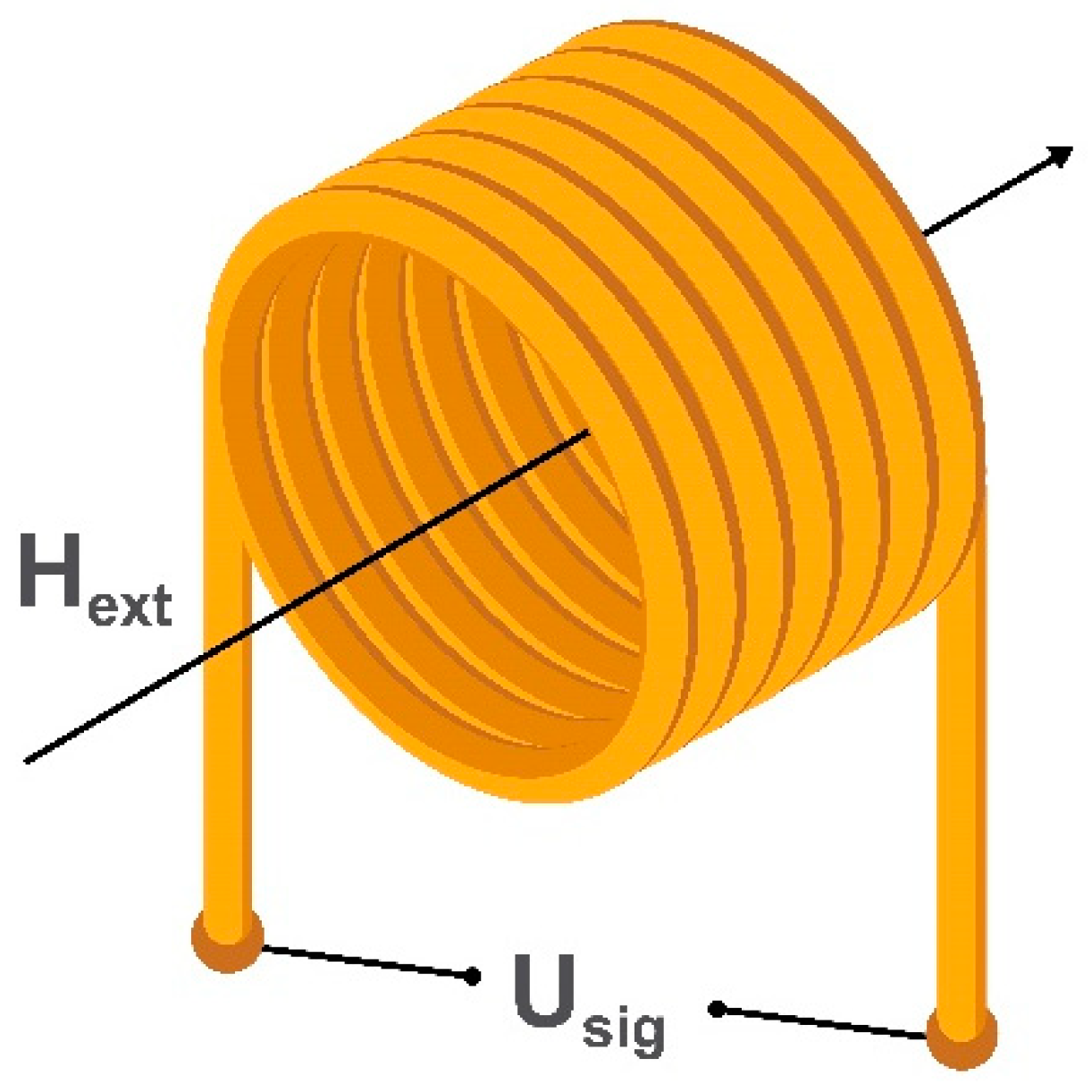
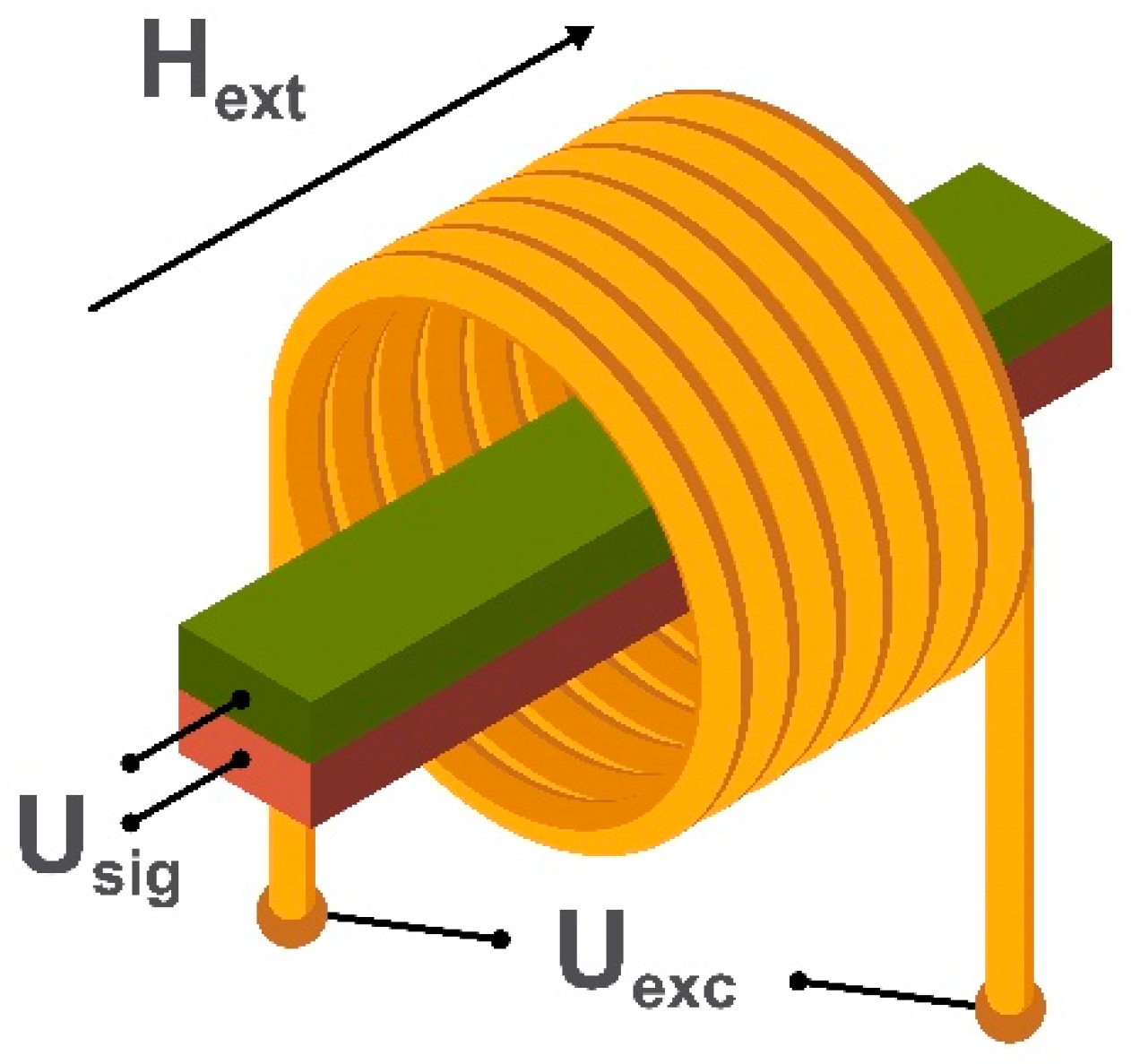
2.1. Search Coil Magnetometers
2.2. SQUID Magnetometers
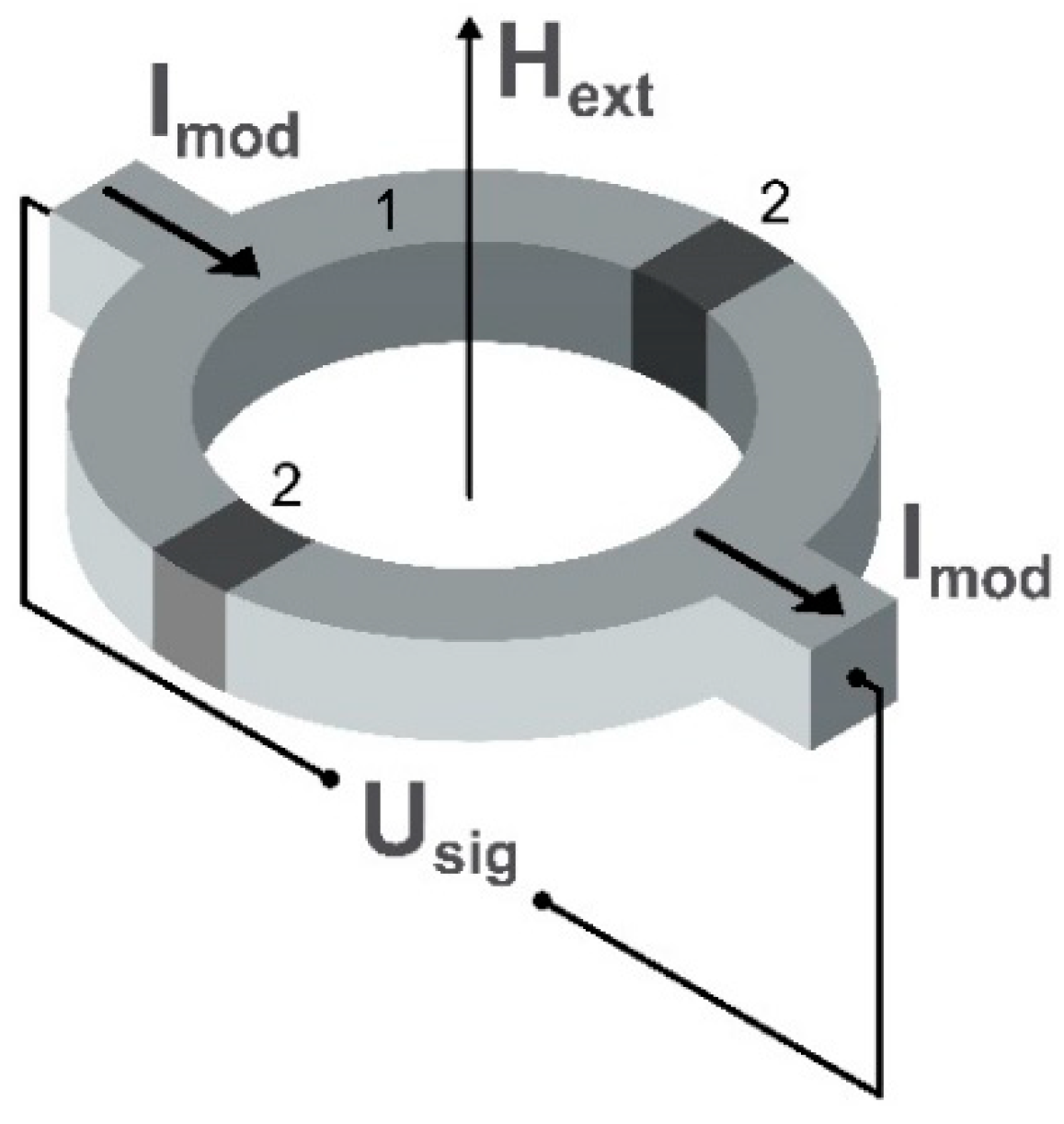
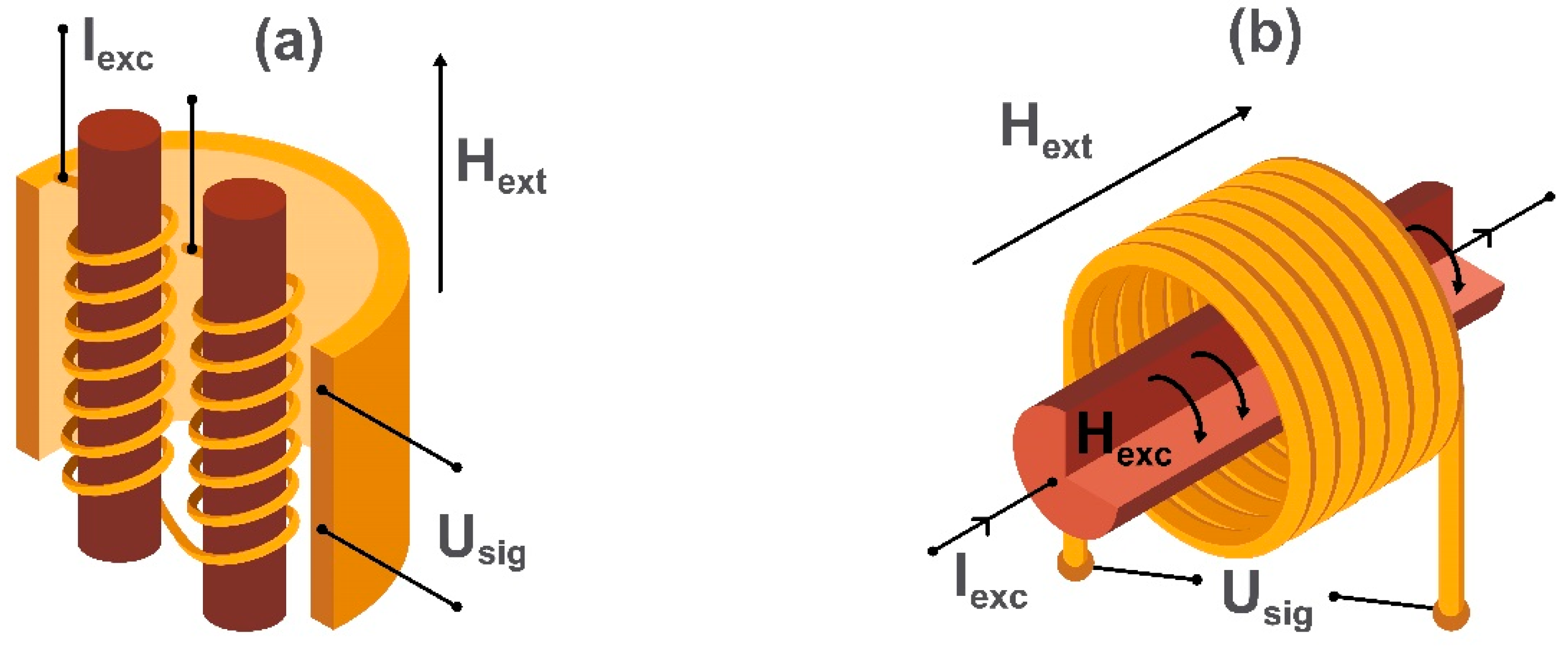
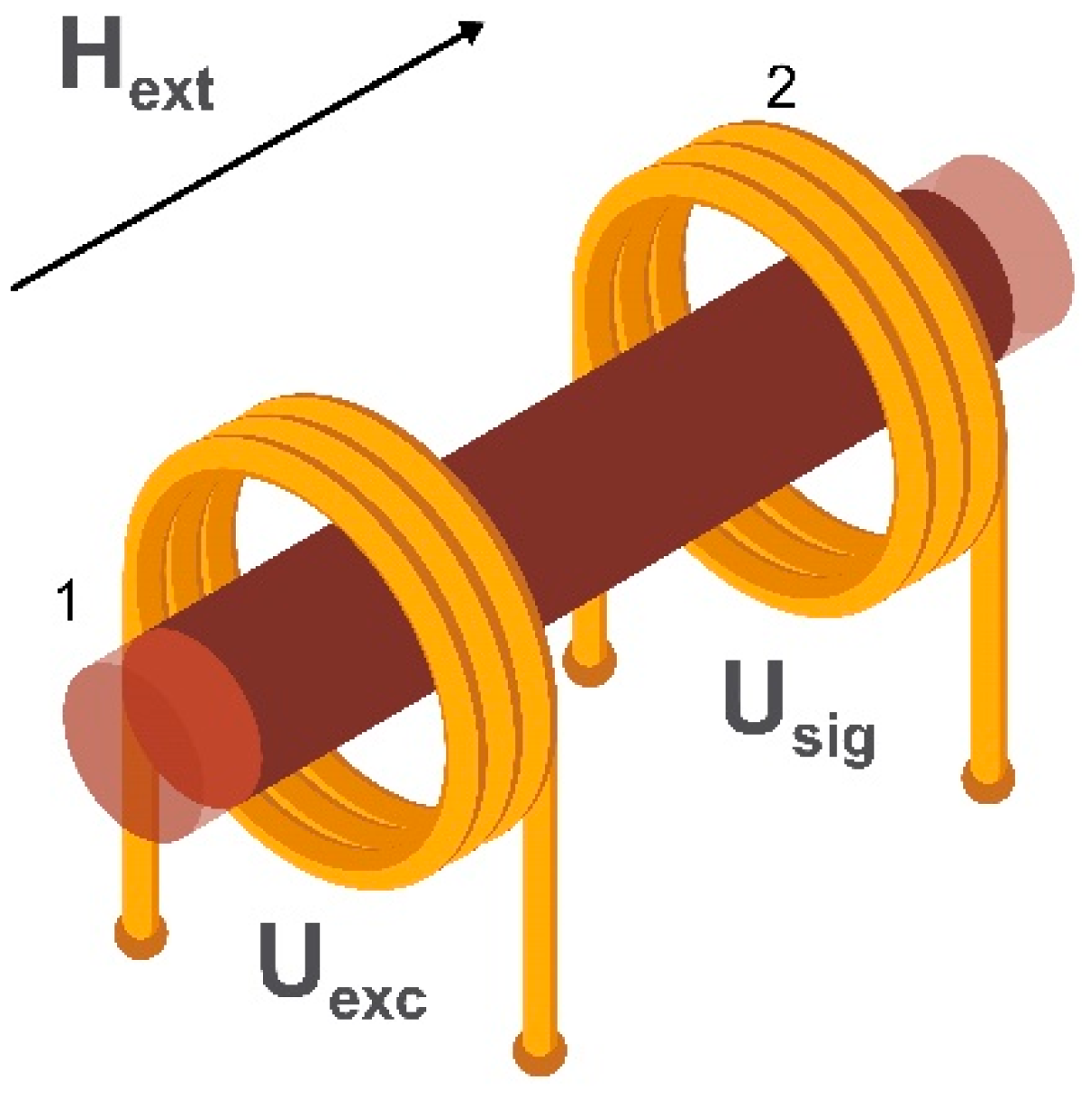
2.3. Fluxgate Magnetometers
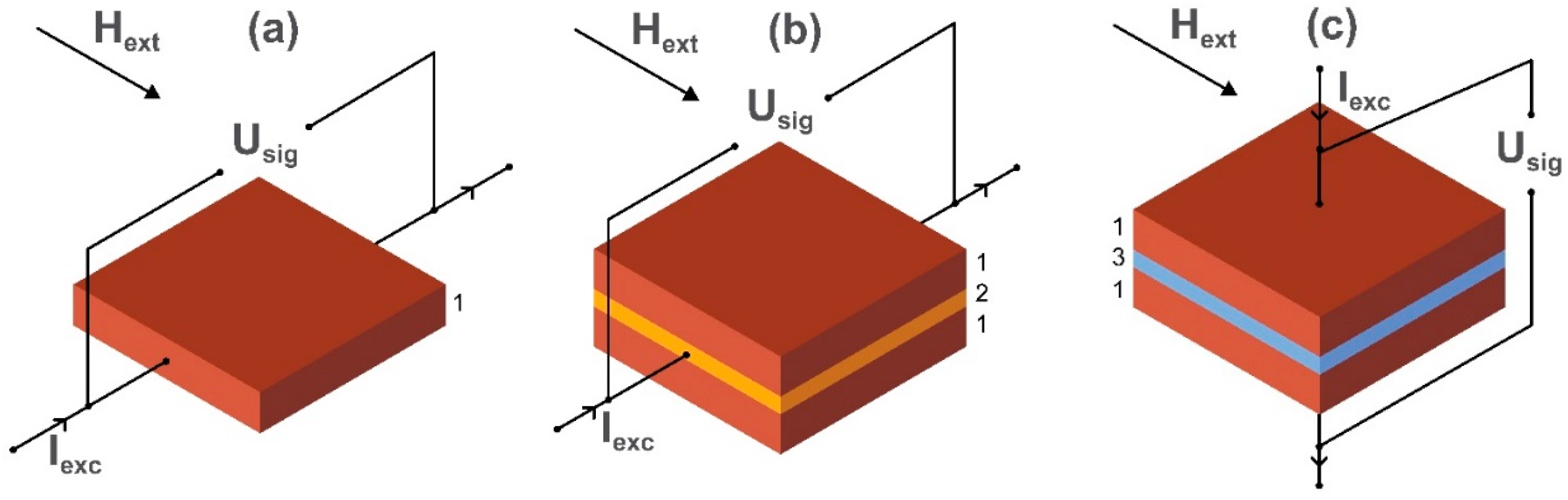
2.4. Magnetoresistance (MR) Effects
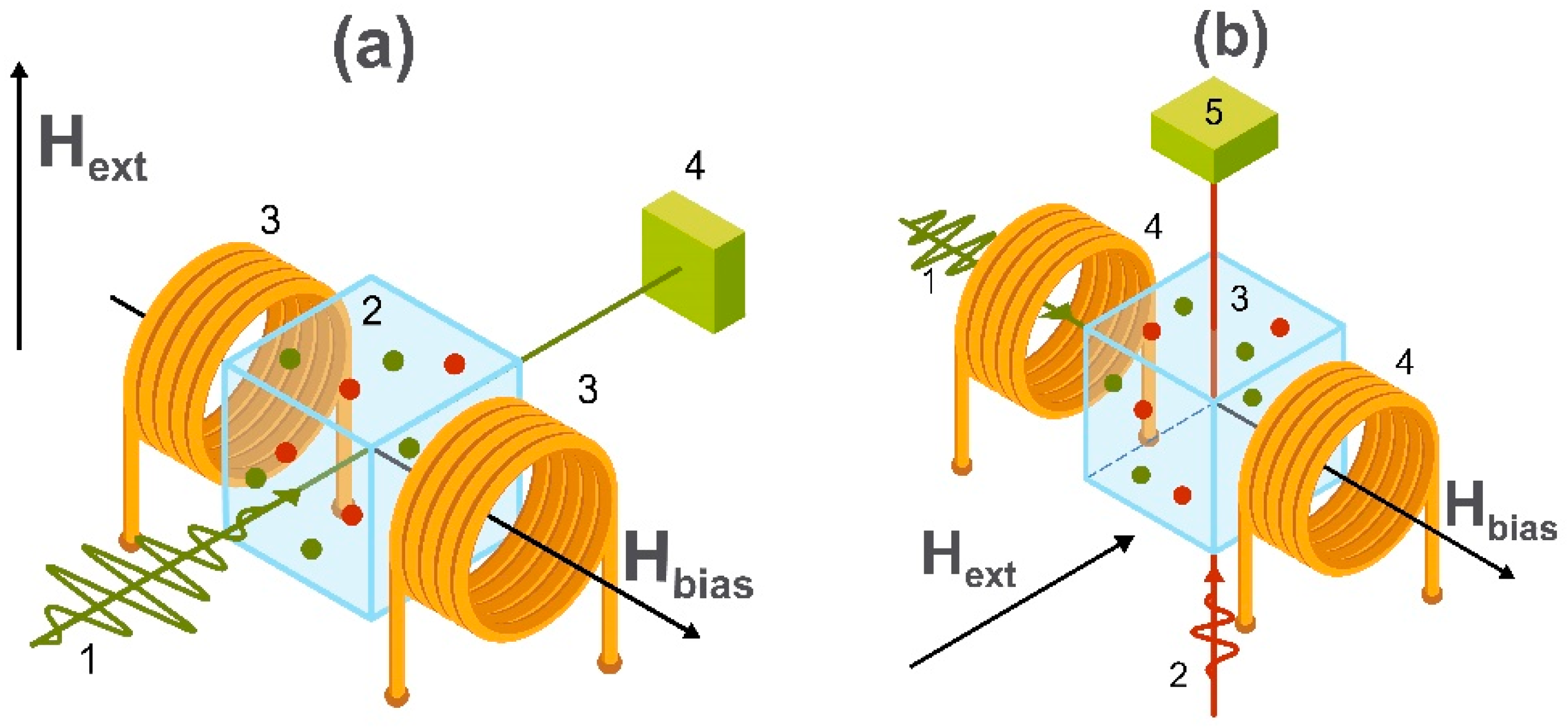
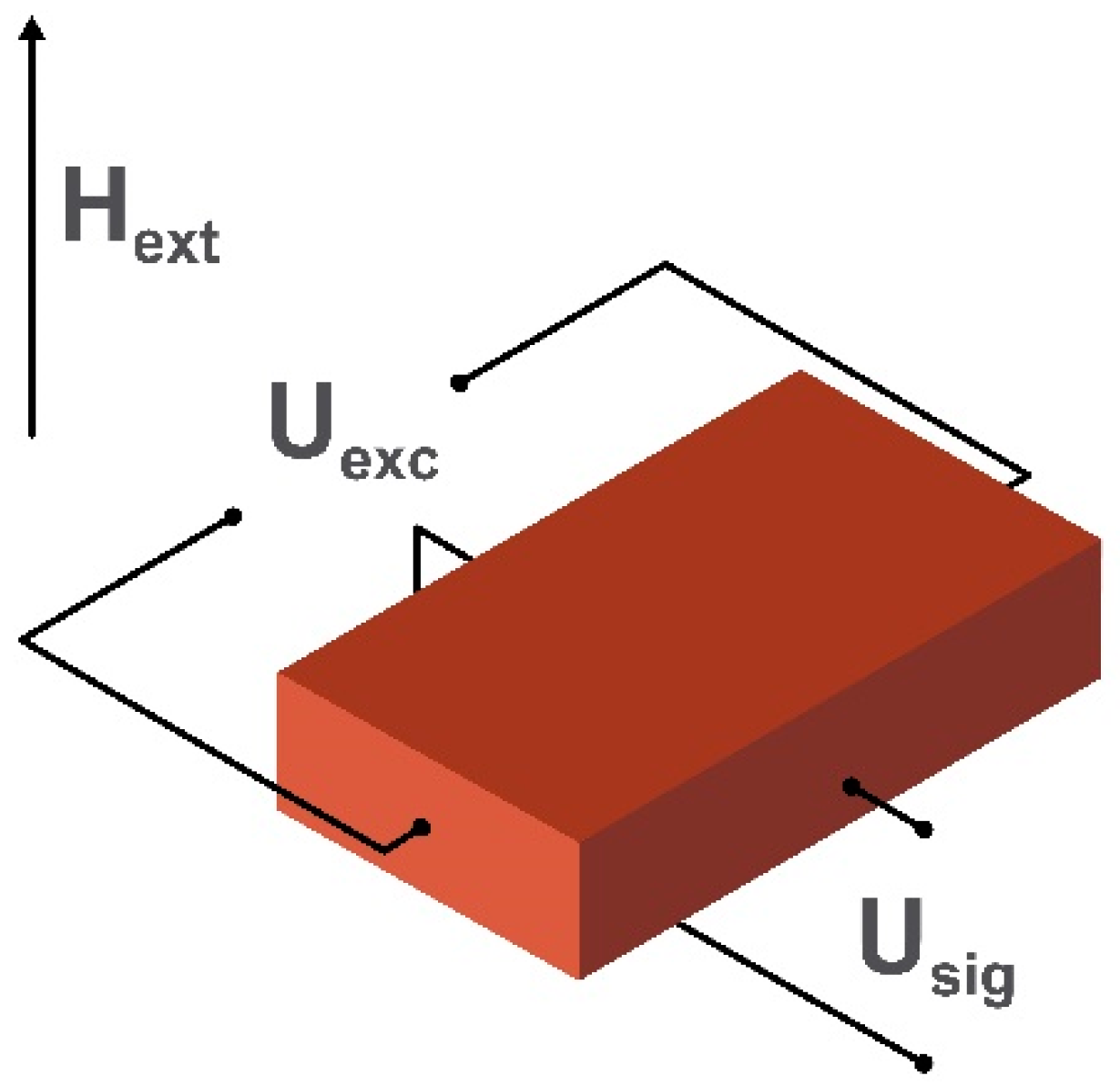
2.5. Magnetoelectric Magnetometers
2.6. Giant Magneto-Impedance (GMI) Magnetometers
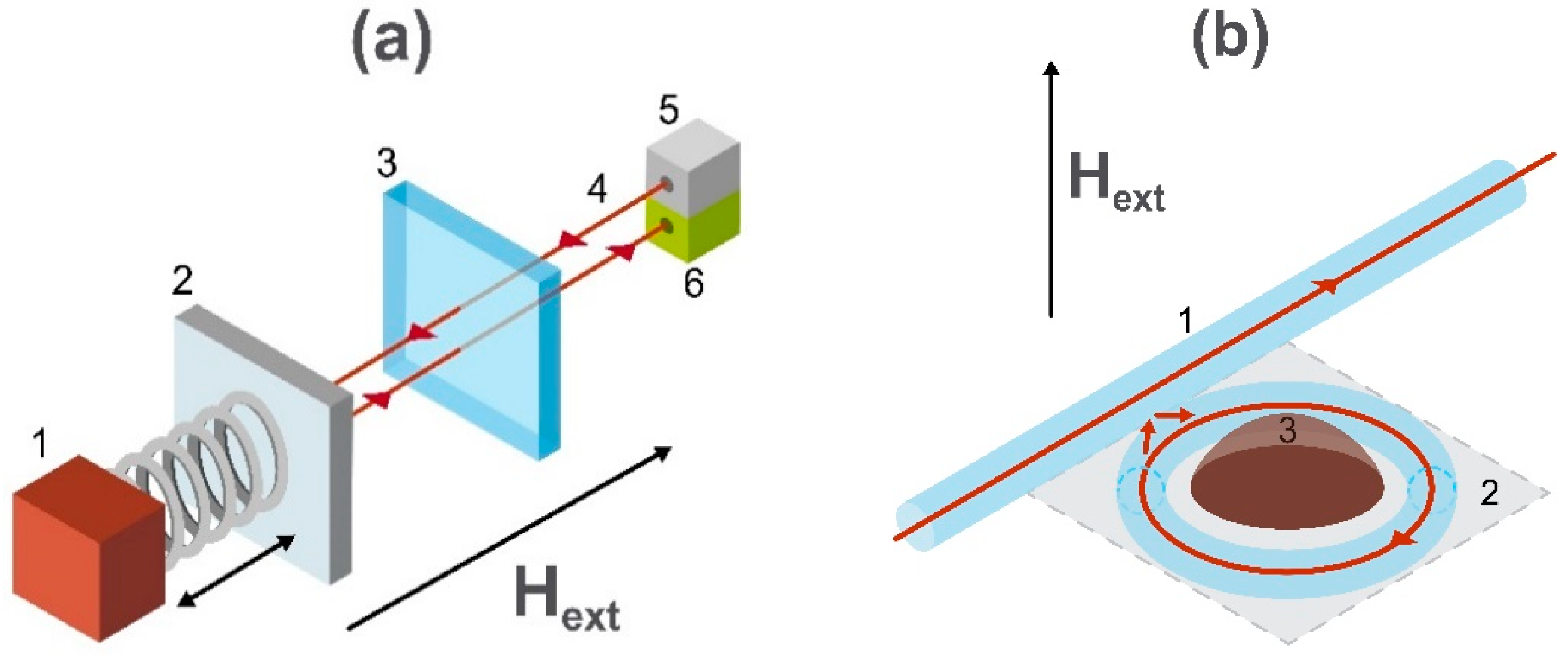
2.7. Optically Pumped Atomic Magnetometers
2.8. Cavity Optomechanical Magnetometers
2.9. Magnetometry Utilizing Nitrogen-Vacancy Centers in Diamond
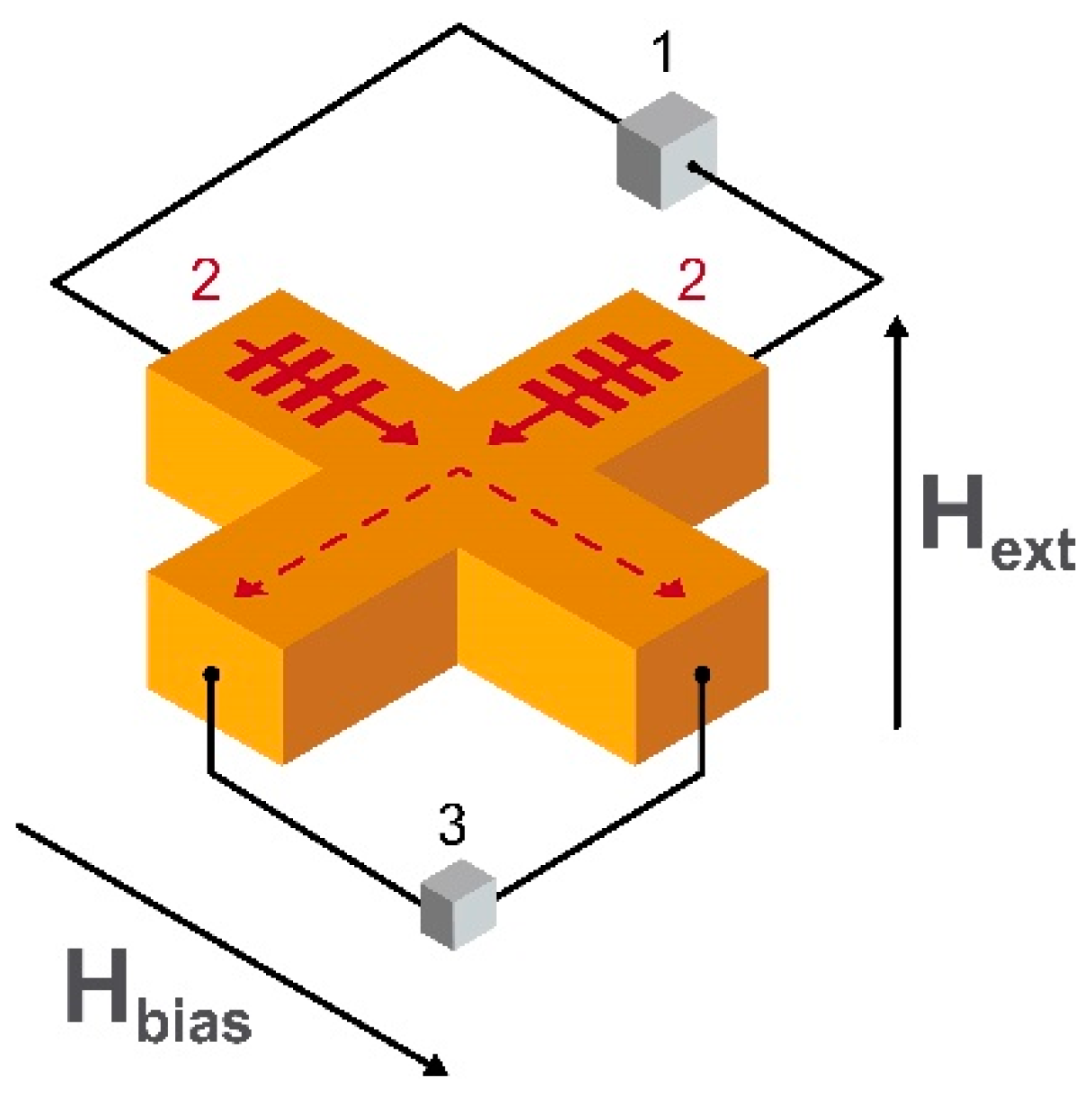
2.10. Hall Effect Magnetometers
2.11. Magnetoelastic Magnetometers
2.12. Spin Wave Interferometry Based Magnetometers
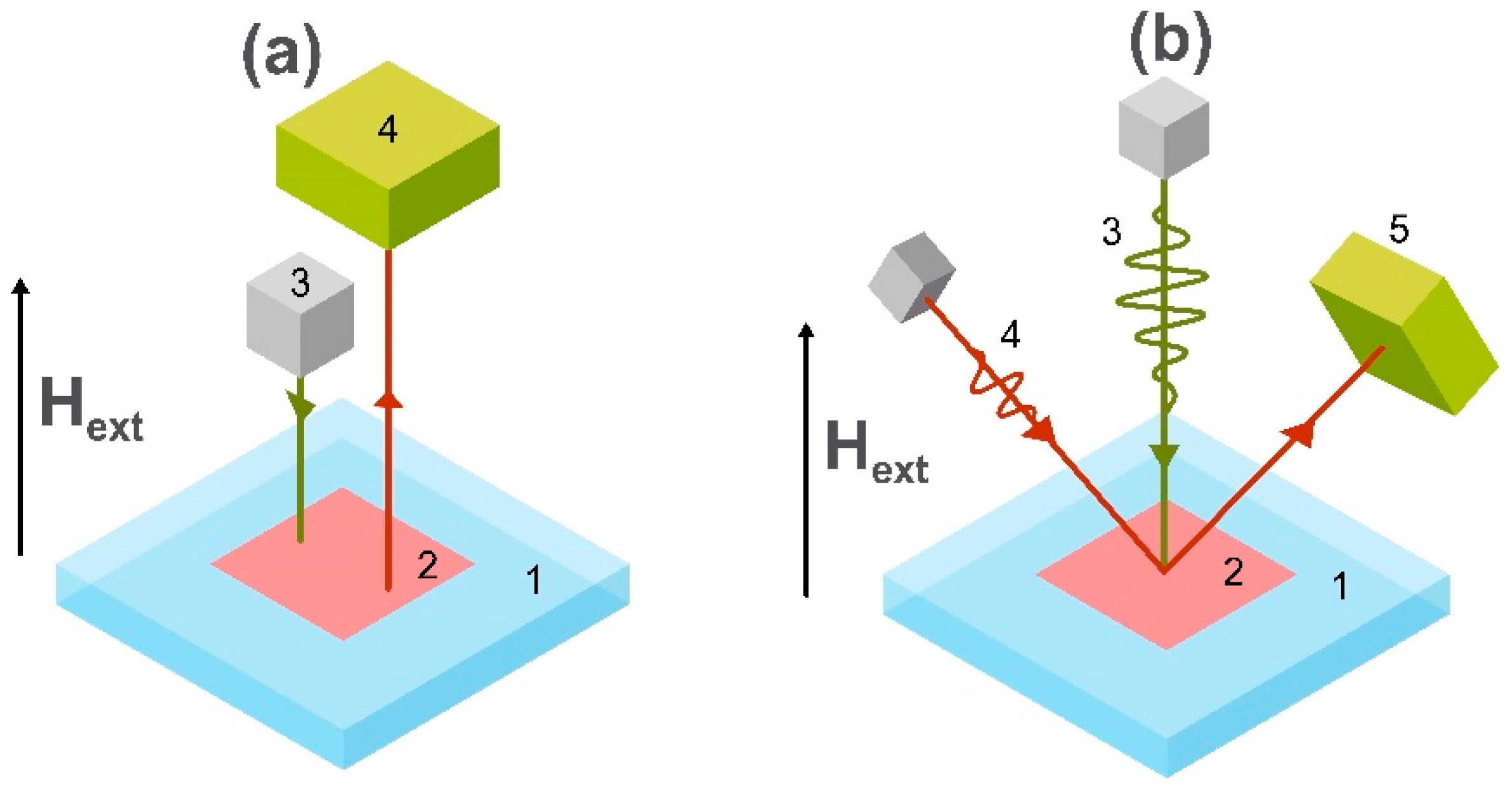
3. Applications of Magnetic Field Sensors
- (i)
- measuring a magnetic field produced by human organs
- (ii)
- detecting magnetically labelled biomolecules.
3.1. Detection of Biomagnetic Signals
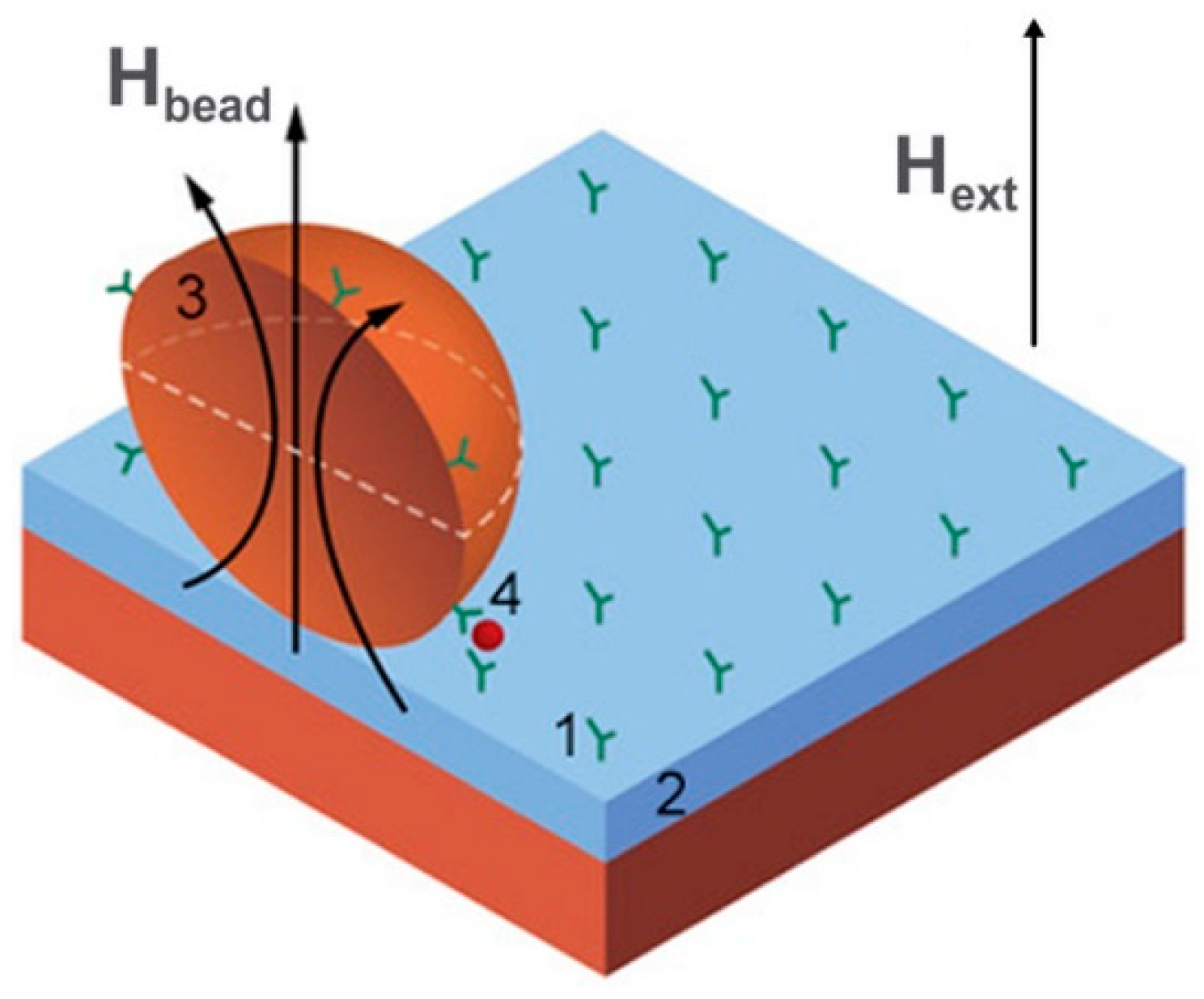
3.2. Point of Care Diagnostics
4. Conclusions and Future Perspectives
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Vitol, E.A.; Novosad, V.; Rozhkova, E.A. Microfabricated magnetic structures for future medicine: From sensors to cell actuators. Nanomedicine 2012, 7, 1611–1624. [Google Scholar] [CrossRef] [PubMed]
- Mapps, D.J. Remote magnetic sensing of people. Sens. Actuators A Phys. 2003, 106, 321–325. [Google Scholar] [CrossRef]
- Strand, S.A.; Strasburger, J.F.; Wakai, R.T. Fetal magnetocardiogram waveform characteristics. Physiol. Meas. 2019, 40, 035002. [Google Scholar] [CrossRef] [PubMed]
- Jensen, K.; Skarsfeldt, M.A.; Stærkind, H.; Arnbak, J.; Balabas, M.V.; Olesen, S.P.; Bentzen, B.H.; Polzik, E.S. Magnetocardiography on an isolated animal heart with a room-temperature optically pumped magnetometer. Sci. Rep. 2018, 8, 16218. [Google Scholar] [CrossRef]
- Sumiya, S.; Kawabata, S.; Hoshino, Y.; Adachi, Y.; Sekihara, K.; Tomizawa, S.; Tomori, M.; Ishii, S.; Sakaki, K.; Ukegawa, D.; et al. Magnetospinography visualizes electrophysiological activity in the cervical spinal cord. Sci. Rep. 2017, 7, 2192. [Google Scholar] [CrossRef]
- Bourguignon, M.; Jousmäki, V.; Dalal, S.S.; Jerbi, K.; De Tiège, X. Coupling between human brain activity and body movements: Insights from non-invasive electromagnetic recordings. Neuroimage 2019, 203, 116177. [Google Scholar] [CrossRef]
- García-Alba, J.; Ramírez-Toraño, F.; Esteba-Castillo, S.; Bruña, R.; Moldenhauer, F.; Novell, R.; Romero-Medina, V.; Maestú, F.; Fernández, A. Neuropsychological and neurophysiological characterization of mild cognitive impairment and Alzheimer’s disease in Down syndrome. Neurobiol. Aging 2019, 84, 70–79. [Google Scholar] [CrossRef]
- Heidari, H.; Zuo, S.; Krasoulis, A.; Nazarpour, K. CMOS Magnetic Sensors for Wearable Magnetomyography. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, EMBS, Honolulu, HI, USA, 17–21 July 2018; pp. 2116–2119. [Google Scholar]
- Lee, H.; Shin, T.H.; Cheon, J.; Weissleder, R. Recent Developments in Magnetic Diagnostic Systems. Chem. Rev. 2015, 115, 10690–10724. [Google Scholar] [CrossRef]
- Van Reenen, A.; De Jong, A.M.; Den Toonder, J.M.J.; Prins, M.W.J. Integrated lab-on-chip biosensing systems based on magnetic particle actuation-a comprehensive review. Lab Chip 2014, 14, 1966–1986. [Google Scholar] [CrossRef]
- Gloag, L.; Mehdipour, M.; Chen, D.; Tilley, R.D.; Gooding, J.J. Advances in the Application of Magnetic Nanoparticles for Sensing. Adv. Mater. 2019, 31, 1904385. [Google Scholar] [CrossRef]
- Anfossi, L.; Di Nardo, F.; Cavalera, S.; Giovannoli, C.; Baggiani, C. Multiplex lateral flow immunoassay: An overview of strategies towards high-throughput point-of-need testing. Biosensors 2018, 9, 2. [Google Scholar] [CrossRef] [PubMed]
- Ren, W.; Mohammed, S.I.; Wereley, S.; Irudayaraj, J. Magnetic Focus Lateral Flow Sensor for Detection of Cervical Cancer Biomarkers. Anal. Chem. 2019, 91, 2876–2884. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; Dong, M.; Zhang, C.; Wang, Y.; Xie, M.; Chen, Y. Magnetic lateral flow strip for the detection of cocaine in urine by naked eyes and smart phone camera. Sensors 2017, 17, 1286. [Google Scholar] [CrossRef] [PubMed]
- Rivas, M.; Lago-Cachón, D.; Martínez-García, J.C.; García, J.A.; Calleja, A.J. Eddy-current sensing of superparamagnetic nanoparticles with spiral-like copper circuits. Sens. Actuators A Phys. 2014, 216, 123–127. [Google Scholar] [CrossRef]
- Moyano, A.; Salvador, M.; Martínez-García, J.C.; Socoliuc, V.; Vékás, L.; Peddis, D.; Alvarez, M.A.; Fernández, M.; Rivas, M.; Blanco-López, M.C. Magnetic immunochromatographic test for histamine detection in wine. Anal. Bioanal. Chem. 2019, 411, 6615–6624. [Google Scholar] [CrossRef] [PubMed]
- Lago-Cachón, D.; Rivas, M.; Martínez-García, J.C.; García, J.A. Cu impedance-based detection of superparamagnetic nanoparticles. Nanotechnology 2013, 24, 245501. [Google Scholar] [CrossRef] [PubMed]
- Fujiwara, K.; Oogane, M.; Kanno, A.; Imada, M.; Jono, J.; Terauchi, T.; Okuno, T.; Aritomi, Y.; Morikawa, M.; Tsuchida, M.; et al. Magnetocardiography and magnetoencephalography measurements at room temperature using tunnel magneto-resistance sensors. Appl. Phys. Express 2018, 11, 023001. [Google Scholar] [CrossRef]
- Huang, H.T.; Garu, P.; Li, C.H.; Chang, W.C.; Chen, B.W.; Sung, S.Y.; Lee, C.M.; Chen, J.Y.; Hsieh, T.F.; Sheu, W.J.; et al. Magnetoresistive Biosensors for Direct Detection of Magnetic Nanoparticle Conjugated Biomarkers on a Chip. Spin 2019, 9, 1940002. [Google Scholar] [CrossRef]
- Wang, Y.; Li, J.; Heidari, H.; Qin, J. Wearable Fluxgate Sensors for the Magnetoencephalography (MEG) for Monitoring the Brain Activities. In Abstract Book of Magnetic Frontiers Magnetic Sensors 2019; Magnetic Frontiers: Lisbon, Portugal, 2019; pp. 2–7. [Google Scholar]
- Ren, L.; Yu, K.; Tan, Y. Applications and advances of magnetoelastic sensors in biomedical engineering: A review. Materials 2019, 12, 1135. [Google Scholar] [CrossRef]
- Yarar, E.; Salzer, S.; Hrkac, V.; Piorra, A.; Höft, M.; Knöchel, R.; Kienle, L.; Quandt, E. Inverse bilayer magnetoelectric thin film sensor. Appl. Phys. Lett. 2016, 109, 022901. [Google Scholar] [CrossRef]
- Krishna, V.D.; Wu, K.; Perez, A.M.; Wang, J.P. Giant magnetoresistance-based biosensor for detection of influenza a virus. Front. Microbiol. 2016, 7, 400. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Y.; Zhang, Q.; Li, X.; Pan, H.; Wang, J.; Zhao, Z. Detection of AFP with an ultra-sensitive giant magnetoimpedance biosensor. Sens. Actuators B Chem. 2019, 293, 53–58. [Google Scholar] [CrossRef]
- Zheng, C.; Zhu, K.; De Freitas, S.C.; Chang, J.Y.; Davies, J.E.; Eames, P.; Freitas, P.P.; Kazakova, O.; Kim, C.G.; Leung, C.W.; et al. Magnetoresistive Sensor Development Roadmap (Non-Recording Applications). IEEE Trans. Magn. 2019, 55, 1–30. [Google Scholar] [CrossRef]
- Nikitin, P.I.; Vetoshko, P.M.; Ksenevich, T.I. New type of biosensor based on magnetic nanoparticle detection. J. Magn. Magn. Mater. 2007, 311, 445–449. [Google Scholar] [CrossRef]
- Balynsky, M.; Gutierrez, D.; Chiang, H.; Kozhevnikov, A.; Dudko, G.; Filimonov, Y.; Balandin, A.A.; Khitun, A. A Magnetometer Based on a Spin Wave Interferometer. Sci. Rep. 2017, 7, 11539. [Google Scholar] [CrossRef] [PubMed]
- Zetter, R.; Iivanainen, J.; Parkkonen, L. Optical Co-registration of MRI and On-scalp MEG. Sci. Rep. 2019, 9, 1–9. [Google Scholar] [CrossRef]
- Korepanov, V.; Berkman, R.; Rakhlin, L.; Klymovych, Y.; Prystai, A.; Marussenkov, A.; Afanassenko, M. Advanced field magnetometers comparative study. Meas. J. Int. Meas. Confed. 2001, 29, 137–146. [Google Scholar] [CrossRef]
- MacKert, B.M. Magnetoneurography: Theory and application to peripheral nerve disorders. Clin. Neurophysiol. 2004, 115, 2667–2676. [Google Scholar] [CrossRef]
- Forstner, S.; Sheridan, E.; Knittel, J.; Humphreys, C.L.; Brawley, G.A.; Rubinsztein-Dunlop, H.; Bowen, W.P. Ultrasensitive optomechanical magnetometry. Adv. Mater. 2014, 26, 6348–6353. [Google Scholar] [CrossRef]
- Uchiyama, T.; Ma, J. Design and Demonstration of Novel Magnetoencephalogram Detectors. IEEE Trans. Magn. 2019, 55, 1–8. [Google Scholar] [CrossRef]
- Manzin, A.; Nabaei, V.; Ferrero, R. Quantification of Magnetic Nanobeads with Micrometer Hall Sensors. IEEE Sens. J. 2018, 18, 10058–10065. [Google Scholar] [CrossRef]
- Jensen, K.; Budvytyte, R.; Thomas, R.A.; Wang, T.; Fuchs, A.M.; Balabas, M.V.; Vasilakis, G.; Mosgaard, L.D.; Stærkind, H.C.; Muller, J.H.; et al. Non-invasive detection of animal nerve impulses with an atomic magnetometer operating near quantum limited sensitivity. Sci. Rep. 2016, 6, 29638. [Google Scholar] [CrossRef] [PubMed]
- Dale, M.W.; Morley, G.W. Medical applications of diamond magnetometry: Commercial viability. arXiv 2017, arXiv:1705.01994. [Google Scholar]
- Coillot, C.; Moutoussamy, J.; Lebourgeois, R.; Ruocco, S.; Chanteur, G. Principle and performance of a dual-band search coil magnetometer: A new instrument to investigate fluctuating magnetic fields in space. IEEE Sens. J. 2010, 10, 255–260. [Google Scholar] [CrossRef]
- Sudhakaran, K.; Komaragiri, R.; Suja, K.J. Fabrication, characterization, and modelling of a novel via-less single metal level magnetic microcoil sensor for biosensing applications. Sens. Actuators A Phys. 2019, 290, 190–197. [Google Scholar]
- Ulvr, M. Design of PCB search coils for AC magnetic flux density measurement. AIP Adv. 2018, 8, 047505. [Google Scholar] [CrossRef]
- Mooney, J.W.; Ghasemi-Roudsari, S.; Banham, E.R.; Symonds, C.; Pawlowski, N.; Varcoe, B.T.H. A portable diagnostic device for cardiac magnetic field mapping. Biomed. Phys. Eng. Express 2017, 3, 015008. [Google Scholar] [CrossRef]
- Li, C.; Jiang, Y.; Yang, G.; Liu, F. Search coil magnetometer based on multi-parameter joint optimization design in ultra low-frequency communication. J. Magn. 2018, 23, 312–317. [Google Scholar] [CrossRef]
- Ozaki, M.; Yagitani, S.; Kasahara, Y.; Kojima, H.; Kasaba, Y.; Kumamoto, A.; Tsuchiya, F.; Matsuda, S.; Matsuoka, A.; Sasaki, T.; et al. Magnetic Search Coil (MSC) of Plasma Wave Experiment (PWE) aboard the Arase (ERG) satellite. Earth Planets Space 2018, 70, 1–13. [Google Scholar] [CrossRef]
- Tumanski, S. Induction coil sensors—A review. Meas. Sci. Technol. 2007, 18, R31–R46. [Google Scholar] [CrossRef]
- Gleich, B.; Weizenecker, J. Tomographic imaging using the nonlinear response of magnetic particles. Nature 2005, 435, 1214–1217. [Google Scholar] [CrossRef] [PubMed]
- Clarke, J.; Braginski, A.I. The SQUID Handbook: Fundamentals and Technology of SQUIDs and SQUID Systems, 1st ed.; Clarke, J., Braginski, A.I., Eds.; Wiley-VCH: Weinheim, Germany, 2004; ISBN 3527402292. [Google Scholar]
- Sternickel, K.; Braginski, A.I. Biomagnetism using SQUIDs: Status and perspectives. Supercond. Sci. Technol. 2006, 19, S160. [Google Scholar] [CrossRef]
- Yang, K.; Chen, H.; Lu, L.; Kong, X.; Yang, R.; Wang, J. SQUID Array with Optimal Compensating Configuration for Magnetocardiography Measurement in Different Environments. IEEE Trans. Appl. Supercond. 2019, 29, 1–7. [Google Scholar] [CrossRef]
- Buchner, M.; Höfler, K.; Henne, B.; Ney, V.; Ney, A. Tutorial: Basic principles, limits of detection, and pitfalls of highly sensitive SQUID magnetometry for nanomagnetism and spintronics. J. Appl. Phys. 2018, 124, 161101. [Google Scholar] [CrossRef]
- Clarke, J.; Hatridge, M.; Mößle, M. SQUID-Detected Magnetic Resonance Imaging in Microtesla Fields. Annu. Rev. Biomed. Eng. 2007, 9, 389–413. [Google Scholar] [CrossRef] [PubMed]
- Körber, R.; Storm, J.-H.; Seton, H.; Mäkelä, J.P.; Paetau, R.; Parkkonen, L.; Pfeiffer, C.; Riaz, B.; Schneiderman, J.F.; Dong, H.; et al. SQUIDs in biomagnetism: A roadmap towards improved healthcare. Supercond. Sci. Technol. 2016, 29, 113001. [Google Scholar] [CrossRef]
- Trabaldo, E.; Arpaia, R.; Arzeo, M.; Andersson, E.; Golubev, D.; Lombardi, F.; Bauch, T. Transport and noise properties of YBCO nanowire based nanoSQUIDs. Supercond. Sci. Technol. 2019, 32, 073001. [Google Scholar] [CrossRef]
- Cho, E.Y.; Li, H.; Lefebvre, J.C.; Zhou, Y.W.; Dynes, R.C.; Cybart, S.A. Direct-coupled micro-magnetometer with Y-Ba-Cu-O nano-slit SQUID fabricated with a focused helium ion beam. Appl. Phys. Lett. 2018, 113, 162602. [Google Scholar] [CrossRef]
- Russo, R.; Esposito, E.; Granata, C.; Vettoliere, A.; Russo, M.; Cannas, C.; Peddis, D.; Fiorani, D. Magnetic nanoparticle characterization using nano-SQUID based on niobium Dayem bridges. Phys. Procedia 2012, 36, 293–299. [Google Scholar] [CrossRef]
- Lee, S.-J.; Jeong, K.; Shim, J.H.; Lee, H.J.; Min, S.; Chae, H.; Namgoong, S.K.; Kim, K. SQUID-based ultralow-field MRI of a hyperpolarized material using signal amplification by reversible exchange. Sci. Rep. 2019, 9, 1–8. [Google Scholar] [CrossRef]
- Clarke, J.; Weinstock, H. SQUID Sensors: Fundamentals, Fabrication and Applications, 1st ed.; Weinstock, H., Ed.; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Wang, J.; Yang, K.; Yang, R.; Kong, X.; Chen, W. SQUID Gradiometer Module for Fetal Magnetocardiography Measurements inside a Thin Magnetically Shielded Room. IEEE Trans. Appl. Supercond. 2019, 29, 1–4. [Google Scholar] [CrossRef]
- Pan, Y.P.; Wang, S.Y.; Liu, X.Y.; Lin, Y.S.; Ma, L.X.; Feng, Y.; Wang, Z.; Chen, L.; Wang, Y.H. 3D nano-bridge-based SQUID susceptometers for scanning magnetic imaging of quantum materials. Nanotechnology 2019, 30, 305303. [Google Scholar] [CrossRef] [PubMed]
- Faley, M.I.; Dammers, J.; Maslennikov, Y.V.; Schneiderman, J.F.; Winkler, D.; Koshelets, V.P.; Shah, N.J.; Dunin-Borkowski, R.E. High T c SQUID Precautions: Supercond. Sci. Technol. 2017, 30, 1–5. [Google Scholar]
- Watson Industries. Available online: https://watson-gyro.com/ (accessed on 15 September 2019).
- Foester. Available online: https://www.fluxgate-magnetometer.com/ (accessed on 15 September 2019).
- SENSYS Magnetometers & Survey Solutions. Available online: https://sensysmagnetometer.com/ (accessed on 15 September 2019).
- Sengottuvel, S.; Sharma, A.; Biswal, D.; Khan, P.F.; Swain, P.P.; Patel, R.; Gireesan, K. Feasibility study on measurement of magnetocardiography (MCG) using fluxgate magnetometer. AIP Conf. Proc. 2018, 1942, 060018. [Google Scholar]
- Elrefai, A.L.; Sasada, I.; Harada, S. Gradiometer and magnetometer integration by using a pair of fundamental mode orthogonal fluxgate sensor heads. IEEE Trans. Magn. 2015, 51, 1–4. [Google Scholar] [CrossRef]
- Jeng, J.T.; Lu, C.C.; Ku, H.W.; Huang, B.R.; Chia, M.H.; Trinh, X.T. Three-Axis Micofluxgate with a Fluxguide. IEEE Trans. Magn. 2019, 55, 1–4. [Google Scholar] [CrossRef]
- Miles, D.M.; Ciurzynski, M.; Barona, D.; Narod, B.B.; Bennest, J.R.; Kale, A.; Lessard, M.; Milling, D.K.; Larson, J.; Mann, I.R. Low-noise permalloy ring cores for fluxgate magnetometers. Geosci. Instrum. Methods Data Syst. 2019, 8, 227–240. [Google Scholar] [CrossRef]
- Vetoshko, P.M.; Gusev, N.A.; Chepurnova, D.A.; Samoilova, E.V.; Syvorotka, I.I.; Syvorotka, I.M.; Zvezdin, A.K.; Korotaeva, A.A.; Belotelov, V.I. Flux-gate magnetic field sensor based on yttrium iron garnet films for magnetocardiography investigations. Technol. Phys. Lett. 2016, 42, 860–864. [Google Scholar] [CrossRef]
- Janosek, M. Parallel Fluxgate Magnetometers. In High Sensitivity Magnetometers; Springer: Berlin/Heidelberg, Germany, 2017; pp. 41–61. [Google Scholar]
- Jie, F.; Ning, N.; Ji, W.; Chiriac, H.; Xiaoping, L. Study of the noise in multicore orthogonal fluxgate sensors based on Ni-Fe/Cu composite microwire arrays. IEEE Trans. Magn. 2009, 45, 4451–4454. [Google Scholar]
- Murata, N.; Karo, H.; Sasada, I.; Shimizu, T. Fundamental Mode Orthogonal Fluxgate Magnetometer Applicable for Measurements of DC and Low-Frequency Magnetic Fields. IEEE Sens. J. 2018, 18, 2705–2712. [Google Scholar] [CrossRef]
- Butta, M.; Janosek, M.; Schutte, B.P.; Vazquez, M.; Perez, R.; Ramirez, E.C.; Jimenez, A. Effect of Amorphous Wire Core Diameter on the Noise of an Orthogonal Fluxgate. IEEE Trans. Magn. 2018, 54, 1–5. [Google Scholar]
- Vetoshko, P.M.; Zvezdin, A.K.; Skidanov, V.A.; Syvorotka, I.I.; Syvorotka, I.M.; Belotelov, V.I. The effect of the disk magnetic element profile on the saturation field and noise of a magneto-modulation magnetic field sensor. Tech. Phys. Lett. 2015, 41, 458–461. [Google Scholar] [CrossRef]
- Lu, C.C.; Huang, J. A 3-axis miniature magnetic sensor based on a planar fluxgate magnetometer with an orthogonal fluxguide. Sensors 2015, 15, 14727–14744. [Google Scholar] [CrossRef] [PubMed]
- Knyazev, G.A.; Kapralov, P.O.; Gusev, N.A.; Kalish, A.N.; Vetoshko, P.M.; Dagesyan, S.A.; Shaposhnikov, A.N.; Prokopov, A.R.; Berzhansky, V.N.; Zvezdin, A.K.; et al. Magnetoplasmonic Crystals for Highly Sensitive Magnetometry. ACS Photonics 2018, 5, 4951–4959. [Google Scholar] [CrossRef]
- Belyaev, V.K.; Murzin, D.V.; Perova, N.N.; Grunin, A.A.; Fedyanin, A.A.; Rodionova, V.V. Permalloy-based magnetoplasmonic crystals for sensor applications. J. Magn. Magn. Mater. 2019, 482, 292–295. [Google Scholar] [CrossRef]
- Zhukova, V.; Mino, J.; Del Val, J.J.; Ipatov, M.; Martinez-Amesti, A.; Varga, R.; Churyukanova, M.; Zhukov, A. Magnetoresistance and Kondo-like behavior in Co5Cu95 microwires. J. Alloys Compd. 2016, 674, 266–271. [Google Scholar] [CrossRef]
- Silva, A.V.; Leitao, D.C.; Valadeiro, J.; Amaral, J.; Freitas, P.P.; Cardoso, S. Linearization strategies for high sensitivity magnetoresistive sensors. EPJ Appl. Phys. 2015, 72, 10601. [Google Scholar] [CrossRef]
- Luong, V.S.; Nguyen, A.T.; Hoang, Q.K.; Nguyen, T.N.; Nguyen, A.T.; Nguyen, T.A.; Giap, V.C. Magnetoresistive performances in exchange-biased spin valves and their roles in low-field magnetic sensing applications. J. Sci. Adv. Mater. Devices 2018, 3, 399–405. [Google Scholar] [CrossRef]
- Prinz, G.A. Magnetoelectronics. Science 1998, 282, 1660–1663. [Google Scholar] [CrossRef]
- Wolf, S.A.; Awschalom, D.D.; Buhrman, R.A.; Daughton, J.M.; Von Molnár, S.; Roukes, M.L.; Chtchelkanova, A.Y.; Treger, D.M. Spintronics: A spin-based electronics vision for the future. Science 2001, 294, 1488–1495. [Google Scholar] [CrossRef]
- Gaster, R.S.; Hall, D.A.; Nielsen, C.H.; Osterfeld, S.J.; Yu, H.; MacH, K.E.; Wilson, R.J.; Murmann, B.; Liao, J.C.; Gambhir, S.S.; et al. Matrix-insensitive protein assays push the limits of biosensors in medicine. Nat. Med. 2009, 15, 1327–1332. [Google Scholar] [CrossRef] [PubMed]
- Shen, H.M.; Hu, L.; Fu, X. Integrated giant magnetoresistance technology for approachable weak biomagnetic signal detections. Sensors 2018, 18, 148. [Google Scholar] [CrossRef] [PubMed]
- Cubells-Beltrán, M.D.; Reig, C.; Madrenas, J.; De Marcellis, A.; Santos, J.; Cardoso, S.; Freitas, P.P. Integration of GMR sensors with different technologies. Sensors 2016, 16, 939. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Wang, Y.; Peng, L.; Ye, C. Measurement of Triaxial Magnetocardiography Using High Sensitivity Tunnel Magnetoresistance Sensor. IEEE Sens. J. 2019, 19, 9610–9615. [Google Scholar] [CrossRef]
- Dias, T.M.; Cardoso, F.A.; Martins, S.A.M.; Martins, V.C.; Cardoso, S.; Gaspar, J.F.; Monteiro, G.; Freitas, P.P. Implementing a strategy for on-chip detection of cell-free DNA fragments using GMR sensors: A translational application in cancer diagnostics using ALU elements. Anal. Methods 2016, 8, 119–128. [Google Scholar] [CrossRef]
- Schulz, L.; Heinisch, P.; Richter, I. Calibration of off-the-shelf anisotropic magnetoresistance magnetometers. Sensors 2019, 19, 1850. [Google Scholar] [CrossRef]
- Djamal, M.; Ramli, R. Giant Magnetoresistance Sensors Based on Ferrite Material and Its Applications. In Magnetic Sensors: Development Trends and Applications; Asfour, A., Ed.; BoD–Books on Demand: Norderstedt, Germany, 2017; pp. 111–132. [Google Scholar]
- Yuasa, S.; Djayaprawira, D.D. Giant tunnel magnetoresistance in magnetic tunnel junctions with a crystalline MgO(0 0 1) barrier. J. Phys. D Appl. Phys. 2007, 40, R337. [Google Scholar] [CrossRef]
- Ennen, I.; Kappe, D.; Rempel, T.; Glenske, C.; Hütten, A. Giant Magnetoresistance: Basic concepts, microstructure, magnetic interactions and applications. Sensors 2016, 16, 904. [Google Scholar] [CrossRef]
- Zhukova, V.; Mino, J.; Del Val, J.J.; Varga, R.; Martinez, G.; Baibich, M.; Ipatov, M.; Zhukov, A. Kondo-like behavior and GMR effect in granular Cu90Co10 microwires. AIP Adv. 2017, 7, 055906. [Google Scholar] [CrossRef]
- Vovk, A.Y.; Golub, V.O.; Malkinski, L.; Kravets, A.F.; Pogorily, A.M.; Shypil, O.V. Tunneling magnetoresistance in granular cermet films with particle size distribution. J. Magn. Magn. Mater. 2004, 272–276, 2003–2005. [Google Scholar] [CrossRef]
- Dagotto, E.; Burgy, J.; Moreo, A. Nanoscale phase separation in colossal magnetoresistance materials: Lessons for the cuprates? Solid State Commun. 2003, 126, 9–22. [Google Scholar] [CrossRef][Green Version]
- Wang, Y.J.; Gao, J.Q.; Li, M.H.; Shen, Y.; Hasanyan, D.; Li, J.F.; Viehland, D. A review on equivalent magnetic noise of magnetoelectric laminate sensors. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2014, 372, 20120455. [Google Scholar] [CrossRef]
- Wang, Y.; Gray, D.; Berry, D.; Gao, J.; Li, M.; Li, J.; Viehland, D. An extremely low equivalent magnetic noise magnetoelectric sensor. Adv. Mater. 2011, 23, 4111–4114. [Google Scholar] [CrossRef]
- Viehland, D.; Wuttig, M.; McCord, J.; Quandt, E. Magnetoelectric magnetic field sensors. MRS Bull. 2018, 43, 834–840. [Google Scholar] [CrossRef]
- Spaldin, N.A.; Ramesh, R. Advances in magnetoelectric multiferroics. Nat. Mater. 2019, 18, 203–212. [Google Scholar] [CrossRef]
- Makarova, L.A.; Alekhina, Y.A.; Omelyanchik, A.S.; Rodionova, V.V.; Malyshkina, O.V.; Perov, N.S. Elastically coupled ferromagnetic and ferroelectric microparticles: New multiferroic materials based on polymer, NdFeB and PZT particles. J. Magn. Magn. Mater. 2019, 470, 89–92. [Google Scholar] [CrossRef]
- Makarova, L.A.; Rodionova, V.V.; Alekhina, Y.A.; Rusakova, T.S.; Omelyanchik, A.S.; Perov, N.S. New Multiferroic Composite Materials Consisting of Ferromagnetic, Ferroelectric, and Polymer Components. IEEE Trans. Magn. 2017, 53, 1–7. [Google Scholar] [CrossRef]
- Harrison, E.P.; Turney, G.L.; Rowe, H. Electrical Properties of Wires of High Permeability. Nature 1935, 135, 961. [Google Scholar] [CrossRef]
- Makhotkin, V.E.; Shurukhin, B.P.; Lopatin, V.A.; Marchukov, P.Y.; Levin, Y.K. Magnetic field sensors based on amorphous ribbons. Sens. Actuators A. Phys. 1991, 27, 759–762. [Google Scholar] [CrossRef]
- Beach, R.S.; Berkowitz, A.E. Giant magnetic field dependent impedance of amorphous FeCoSiB wire. Appl. Phys. Lett. 1994, 64, 3652–3654. [Google Scholar] [CrossRef]
- Panina, L.V.; Mohri, K. Magneto-impedance effect in amorphous wires. Appl. Phys. Lett. 1994, 65, 1189–1191. [Google Scholar] [CrossRef]
- Hika, K.; Panina, L.V.; Mohri, K. Magneto-impedance in sandwich film for magnetic sensor heads. IEEE Trans. Magn. 1996, 32, 4594–4596. [Google Scholar] [CrossRef]
- García-Arribas, A.; Fernández, E.; de Cos, D. Thin-Film Magneto-Impedance Sensors. In Magnetic Sensors—Development Trends and Applications; Asfour, A., Ed.; BoD–Books on Demand: Norderstedt, Germany, 2017; pp. 39–62. [Google Scholar]
- Zhukov, A.; Ipatov, M.; Churyukanova, M.; Talaat, A.; Blanco, J.M.; Zhukova, V. Trends in optimization of giant magnetoimpedance effect in amorphous and nanocrystalline materials. J. Alloys Compd. 2017, 727, 887–901. [Google Scholar] [CrossRef]
- Dzhumazoda, A.; Panina, L.V.; Nematov, M.G.; Ukhasov, A.A.; Yudanov, N.A.; Morchenko, A.T.; Qin, F.X. Temperature-stable magnetoimpedance (MI) of current-annealed Co-based amorphous microwires. J. Magn. Magn. Mater. 2019, 474, 374–380. [Google Scholar] [CrossRef]
- Vol, A. The Role of the Chemically Induced Polarization of Nuclei in Biology. SPG BioMed 2018, 18, 1–13. [Google Scholar] [CrossRef]
- Zhukov, A.; Talaat, A.; Ipatov, M.; Zhukova, V. Tailoring the High-Frequency Giant Magnetoimpedance Effect of Amorphous Co-Rich Microwires. IEEE Magn. Lett. 2015, 6, 1–4. [Google Scholar] [CrossRef]
- Nowicki, M.; Gazda, P.; Szewczyk, R.; Nosenko, A. Vasyl Kyrylchuk Strain Dependence of Hysteretic Giant Magnetoimpedance Effect in Co-Based Amorphous Ribbon. Materials 2019, 12, 2110. [Google Scholar] [CrossRef]
- Panina, L.V.; Dzhumazoda, A.; Evstigneeva, S.A.; Adam, A.M.; Morchenko, A.T.; Yudanov, N.A.; Kostishyn, V.G. Temperature effects on magnetization processes and magnetoimpedance in low magnetostrictive amorphous microwires. J. Magn. Magn. Mater. 2018, 459, 147–153. [Google Scholar] [CrossRef]
- Mohri, K.; Uchiyama, T.; Shen, L.P.; Cai, C.M.; Panina, L.V.; Honkura, Y.; Yamamoto, M. Amorphous wire and CMOS IC-based sensitive micromagnetic sensors utilizing magnetoimpedance (MI) and stress-impedance (SI) effects. IEEE Trans. Magn. 2002, 38, 3063–3068. [Google Scholar] [CrossRef]
- Mohri, K.; Honkura, Y. Amorphous Wire and CMOS IC Based Magneto-Impedance Sensors—Origin, Topics, and Future. Sens. Lett. 2007, 5, 267–270. [Google Scholar] [CrossRef]
- Honkura, Y. Development of amorphous wire type MI sensors for automobile use. J. Magn. Magn. Mater. 2002, 249, 375–381. [Google Scholar] [CrossRef]
- Sandacci, S.; Makhnovskiy, D.; Panina, L.; Mohri, K.; Honkura, Y. Off-diagonal impedance in amorphous wires and its application to linear magnetic sensors. IEEE Trans. Magn. 2004, 40, 3505–3511. [Google Scholar] [CrossRef]
- Uchiyama, T.; Mohri, K.; Honkura, Y.; Panina, L.V. Recent Advances of Pico-Tesla Resolution Magneto-Impedance Sensor Based on Amorphous Wire CMOS IC MI Sensor. IEEE Trans. Magn. 2012, 48, 3833–3839. [Google Scholar] [CrossRef]
- Panina, L.V.; Yudanov, N.A.; Morchenko, A.T.; Kostishyn, V.G.; Makhnovskiy, D.P. Off-diagonal magnetoimpedance in amorphous microwires for low-field magnetic sensors. Phys. Status Solidi Appl. Mater. Sci. 2016, 213, 341–349. [Google Scholar] [CrossRef]
- Dolabdjian, C.; Ménard, D. Giant Magneto-Impedance (GMI) Magnetometers. In High Sensitivity Magnetometers; Grosz, A., Haji-Sheikh, M.J., Mukhopadhyay, S.C., Eds.; Springer: Berlin/Heidelberg, Germany, 2017; pp. 103–126. [Google Scholar]
- Mohri, K.; Uchiyama, T.; Panina, L.V.; Yamamoto, M.; Bushida, K. Recent advances of amorphous wire CMOS IC magneto-impedance sensors: Innovative high-performance micromagnetic sensor chip. J. Sensors 2015, 2015, 718069. [Google Scholar] [CrossRef]
- Uchiyama, T.; Nakayama, S.; Mohri, K.; Bushida, K. Biomagnetic field detection using very high sensitivity magnetoimpedance sensors for medical applications. Phys. Status Solidi Appl. Mater. Sci. 2009, 206, 639–643. [Google Scholar] [CrossRef]
- Wang, Y.; Wen, Y.; Li, P.; Chen, L. Improved magnetic sensor using laminated magnetic multilayer with coupled exciting and sensing micro planar coils. Sens. Actuators A Phys. 2018, 284, 112–119. [Google Scholar] [CrossRef]
- Chen, J.; Li, J.; Li, Y.; Chen, Y.; Xu, L. Design and fabrication of a miniaturized GMI magnetic sensor based on amorphous wire by MEMS technology. Sensors 2018, 18, 732. [Google Scholar] [CrossRef]
- Chen, J.; Li, J.; Xu, L. Highly integrated MEMS magnetic sensor based on GMI effect of amorphous wire. Micromachines 2019, 10, 237. [Google Scholar] [CrossRef]
- Cooper, R.J.; Prescott, D.W.; Lee, G.J.; Sauer, K.L. RF atomic magnetometer array with over 40 dB interference suppression using electron spin resonance. J. Magn. Reson. 2018, 296, 36–46. [Google Scholar] [CrossRef]
- Du, P.C.; Li, J.J.; Yang, S.J.; Wang, X.T.; Zhuo, Y.; Wang, F.; Wang, R.Q. Observing the steady-state visual evoked potentials with a compact quad-channel spin exchange relaxation-free magnetometer. Chin. Phys. B 2019, 28, 040702. [Google Scholar] [CrossRef]
- Lee, H.J.; Lee, S.J.; Shim, J.H.; Moon, H.S.; Kim, K. In-situ Overhauser-enhanced nuclear magnetic resonance at less than 1 μT using an atomic magnetometer. J. Magn. Reson. 2019, 300, 149–152. [Google Scholar] [CrossRef] [PubMed]
- Borna, A.; Carter, T.R.; Derego, P.; James, C.D.; Schwindt, P.D.D. Magnetic Source Imaging Using a Pulsed Optically Pumped Magnetometer Array. IEEE Trans. Instrum. Meas. 2019, 68, 493–501. [Google Scholar] [CrossRef] [PubMed]
- Affolderbach, C.; Stähler, M.; Knappe, S.; Wynands, R. An all-optical, high-sensitivity magnetic gradiometer. Appl. Phys. B Lasers Opt. 2002, 75, 605–612. [Google Scholar] [CrossRef]
- Put, P.; Popiołek, K.; Pustelny, S. Different sensitivities of two optical magnetometers realized in the same experimental arrangement. Sci. Rep. 2019, 9, 2537. [Google Scholar] [CrossRef]
- Li, W.; Peng, X.; Li, S.; Liu, C.; Guo, H.; Lin, P.; Zhang, W. Unshielded scalar magnetometer based on nonlinear magneto-optical rotation with amplitude modulated light. In Proceedings of the 2016 IEEE International Frequency Control Symposium, New Orleans, LA, USA, 9–12 May 2016; pp. 1–4. [Google Scholar]
- Liang, S.-Q.; Yang, G.-Q.; Xu, Y.-F.; Lin, Q.; Liu, Z.-H.; Chen, Z.-X. Simultaneously improving the sensitivity and absolute accuracy of CPT magnetometer. Opt. Express 2014, 22, 6837–6843. [Google Scholar] [CrossRef]
- Sheng, D.; Perry, A.R.; Krzyzewski, S.P.; Geller, S.; Kitching, J.; Knappe, S. A microfabricated optically-pumped magnetic gradiometer. Appl. Phys. Lett. 2017, 110, 031106. [Google Scholar] [CrossRef]
- Zhang, G.; Huang, S.; Xu, F.; Hu, Z.; Lin, Q. Multi-channel spin exchange relaxation free magnetometer towards two-dimensional vector magnetoencephalography. Opt. Express 2019, 27, 597. [Google Scholar] [CrossRef]
- Zhang, G.; Huang, S.; Lin, Q. Magnetoencephalography using a compact multichannel atomic magnetometer with pump-probe configuration. AIP Adv. 2018, 8, 125028. [Google Scholar] [CrossRef]
- Sulai, I.A.; DeLand, Z.J.; Bulatowicz, M.D.; Wahl, C.P.; Wakai, R.T.; Walker, T.G. Characterizing atomic magnetic gradiometers for fetal magnetocardiography. Rev. Sci. Instrum. 2019, 90, 085003. [Google Scholar] [CrossRef] [PubMed]
- Boto, E.; Meyer, S.S.; Shah, V.; Alem, O.; Knappe, S.; Kruger, P.; Fromhold, T.M.; Lim, M.; Glover, P.M.; Morris, P.G.; et al. A new generation of magnetoencephalography: Room temperature measurements using optically-pumped magnetometers. Neuroimage 2017, 149, 404–414. [Google Scholar] [CrossRef] [PubMed]
- Perry, A.R.; Sheng, D.; Krzyzewski, S.P.; Geller, S.; Knappe, S. Microfabricated optically pumped magnetometer arrays for biomedical imaging. In Slow Light, Fast Light, and Opto-Atomic Precision Metrology X; International Society for Optics and Photonics: San Francisco, CA, USA, 2017; Volume 10119, p. 101190V. [Google Scholar]
- Iivanainen, J.; Zetter, R.; Grön, M.; Hakkarainen, K.; Parkkonen, L. On-scalp MEG system utilizing an actively shielded array of optically-pumped magnetometers. Neuroimage 2019, 194, 244–258. [Google Scholar] [CrossRef]
- Iivanainen, J.; Stenroos, M.; Parkkonen, L. Measuring MEG closer to the brain: Performance of on-scalp sensor arrays. Neuroimage 2017, 147, 542–553. [Google Scholar] [CrossRef] [PubMed]
- Strand, S.; Lutter, W.; Strasburger, J.F.; Shah, V.; Baffa, O.; Wakai, R.T. Low-Cost Fetal Magnetocardiography: A Comparison of Superconducting Quantum Interference Device and Optically Pumped Magnetometers. J. Am. Heart Assoc. 2019, 8, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Labyt, E.; Corsi, M.C.; Fourcault, W.; Palacios Laloy, A.; Bertrand, F.; Lenouvel, F.; Cauffet, G.; Le Prado, M.; Berger, F.; Morales, S. Magnetoencephalography with optically pumped 4 He magnetometers at ambient temperature. IEEE Trans. Med. Imaging 2019, 38, 90–98. [Google Scholar] [CrossRef]
- Zetter, R.; Iivanainen, J.; Stenroos, M.; Parkkonen, L. Requirements for Coregistration Accuracy in On-Scalp MEG. Brain Topogr. 2018, 31, 931–948. [Google Scholar] [CrossRef]
- Colombo, A.P.; Carter, T.R.; Borna, A.; Jau, Y.-Y.; Johnson, C.N.; Dagel, A.L.; Schwindt, P.D.D. Four-channel optically pumped atomic magnetometer for magnetoencephalography. Opt. Express 2016, 24, 15403. [Google Scholar] [CrossRef]
- Forstner, S.; Prams, S.; Knittel, J.; van Ooijen, E.D.; Swaim, J.D.; Harris, G.I.; Szorkovszky, A.; Bowen, W.P.; Rubinsztein-Dunlop, H. Cavity optomechanical magnetometer. Smart Sens. Meas. Instrum. 2012, 108, 12081. [Google Scholar]
- Li, B.-B.; Bílek, J.; Hoff, U.B.; Madsen, L.S.; Forstner, S.; Prakash, V.; Schäfermeier, C.; Gehring, T.; Bowen, W.P.; Andersen, U.L. Quantum enhanced optomechanical magnetometry. Optica 2018, 5, 850–856. [Google Scholar] [CrossRef]
- Li, B.-B.; Bulla, D.; Prakash, V.; Forstne, S.; Dehghan-Manshadi, A.; Dunlop, H.R.; Foster, S.; Bowen, W.P. Citation: Invited Article: Scalable high-sensitivity optomechanical magnetometers on a chip. APL Photonics 2018, 3, 120806. [Google Scholar] [CrossRef]
- Bowen, W.P.; Yu, C. Cavity Optomechanical Magnetometers. In High Sensitivity Magnetometers; Grosz, A., Haji-Sheikh, M., Mukhopadhyay, S.C., Eds.; Springer: Berlin/Heidelberg, Germany, 2016; pp. 313–338. [Google Scholar]
- Zheng, H.; Xu, J.; Iwata, G.Z.; Lenz, T.; Michl, J.; Yavkin, B.; Nakamura, K.; Sumiya, H.; Ohshima, T.; Isoya, J.; et al. Zero-Field Magnetometry Based on Nitrogen-Vacancy Ensembles in Diamond. Phys. Rev. Appl. 2019, 11, 064068. [Google Scholar] [CrossRef]
- Zhao, B.; Guo, H.; Zhao, R.; Du, F.; Li, Z.; Wang, L.; Wu, D.; Chen, Y.; Tang, J.; Liu, J. High-Sensitivity Three-Axis Vector Magnetometry Using Electron Spin Ensembles in Single-Crystal Diamond. IEEE Magn. Lett. 2019, 10, 1. [Google Scholar] [CrossRef]
- Yamaguchi, T.; Matsuzaki, Y.; Saito, S.; Saijo, S.; Watanabe, H.; Mizuochi, N.; Ishi-Hayase, J. Bandwidth analysis of AC magnetic field sensing based on electronic spin double-resonance of nitrogen-vacancy centers in diamond. Jpn. J. Appl. Phys. 2019, 58, 100901. [Google Scholar] [CrossRef]
- Yahata, K.; Matsuzaki, Y.; Saito, S.; Watanabe, H.; Ishi-Hayase, J. Demonstration of vector magnetic field sensing by simultaneous control of nitrogen-vacancy centers in diamond using multi-frequency microwave pulses. Appl. Phys. Lett. 2019, 114, 022404. [Google Scholar] [CrossRef]
- Glenn, D.R.; Lee, K.; Park, H.; Weissleder, R.; Yacoby, A.; Lukin, M.D.; Lee, H.; Walsworth, R.L.; Connolly, C.B. Single-cell magnetic imaging using a quantum diamond microscope. Nat. Methods 2015, 12, 736–738. [Google Scholar] [CrossRef]
- Le Sage, D.; Arai, K.; Glenn, D.R.; Devience, S.J.; Pham, L.M.; Rahn-Lee, L.; Lukin, M.D.; Yacoby, A.; Komeili, A.; Walsworth, R.L. Optical magnetic imaging of living cells. Nature 2013, 496, 486–489. [Google Scholar] [CrossRef] [PubMed]
- Fuchs, P.; Challier, M.; Neu, E. Optimized single-crystal diamond scanning probes for high sensitivity magnetometry. New J. Phys. 2018, 20, 125001. [Google Scholar] [CrossRef]
- Schloss, J.M.; Barry, J.F.; Turner, M.J.; Walsworth, R.L. Simultaneous Broadband Vector Magnetometry Using Solid-State Spins. Phys. Rev. Appl. 2018, 10, 034044. [Google Scholar] [CrossRef]
- Chatzidrosos, G.; Wickenbrock, A.; Bougas, L.; Leefer, N.; Wu, T.; Jensen, K.; Dumeige, Y.; Budker, D. Miniature Cavity-Enhanced Diamond Magnetometer. Phys. Rev. Appl. 2017, 8, 044019. [Google Scholar] [CrossRef]
- Wolf, T.; Neumann, P.; Nakamura, K.; Sumiya, H.; Ohshima, T.; Isoya, J.; Wrachtrup, J. Subpicotesla diamond magnetometry. Phys. Rev. X 2015, 5, 041001. [Google Scholar] [CrossRef]
- Schirhagl, R.; Chang, K.; Loretz, M.; Degen, C.L. Nitrogen-Vacancy Centers in Diamond: Nanoscale Sensors for Physics and Biology. Annu. Rev. Phys. Chem. 2014, 65, 83–105. [Google Scholar] [CrossRef] [PubMed]
- Balasubramanian, P.; Osterkamp, C.; Chen, Y.; Chen, X.; Teraji, T.; Wu, E.; Naydenov, B.; Jelezko, F. dc Magnetometry with Engineered Nitrogen-Vacancy Spin Ensembles in Diamond. Nano Lett. 2019, 19, 6681–6686. [Google Scholar] [CrossRef] [PubMed]
- Stürner, F.M.; Brenneis, A.; Kassel, J.; Wostradowski, U.; Rölver, R.; Fuchs, T.; Nakamura, K.; Sumiya, H.; Onoda, S.; Isoya, J.; et al. Compact integrated magnetometer based on nitrogen-vacancy centers in diamond. Diam. Relat. Mater. 2019, 93, 59–65. [Google Scholar] [CrossRef]
- Webb, J.L.; Clement, J.D.; Troise, L.; Ahmadi, S.; Johansen, G.J.; Huck, A.; Andersen, U.L. Nanotesla sensitivity magnetic field sensing using a compact diamond nitrogen-vacancy magnetometer. Appl. Phys. Lett. 2019, 114, 231103. [Google Scholar] [CrossRef]
- Davis, H.C.; Ramesh, P.; Bhatnagar, A.; Lee-Gosselin, A.; Barry, J.F.; Glenn, D.R.; Walsworth, R.L.; Shapiro, M.G. Mapping the microscale origins of magnetic resonance image contrast with subcellular diamond magnetometry. Nat. Commun. 2018, 9, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Girgin, A.; Karalar, T.C. Output offset in silicon Hall effect based magnetic field sensors. Sens. Actuators A Phys. 2019, 288, 177–181. [Google Scholar] [CrossRef]
- Henriksen, A.D.; Rizzi, G.; Hansen, M.F. Planar Hall effect bridge sensors with NiFe/Cu/IrMn stack optimized for self-field magnetic bead detection. J. Appl. Phys. 2016, 119, 093910. [Google Scholar] [CrossRef]
- Kim, H.; Reddy, V.; Kim, K.W.; Jeong, I.; Hu, X.H.; Kim, C.G. Single magnetic bead detection in a microfluidic chip using planar hall effect sensor. J. Magn. 2014, 19, 10–14. [Google Scholar] [CrossRef]
- Pişkin, H.; Akdoğan, N. Interface-induced enhancement of sensitivity in NiFe/Pt/IrMn-based planar hall sensors with nanoTesla resolution. Sens. Actuators A Phys. 2019, 292, 24–29. [Google Scholar] [CrossRef]
- Izci, D.; Dale, C.; Keegan, N.; Hedley, J. The Construction of a Graphene Hall Effect Magnetometer. IEEE Sens. J. 2018, 18, 9534–9541. [Google Scholar] [CrossRef]
- Granell, P.N.; Wang, G.; Cañon Bermudez, G.S.; Kosub, T.; Golmar, F.; Steren, L.; Fassbender, J.; Makarov, D. Highly compliant planar Hall effect sensor with sub 200 nT sensitivity. NPJ Flex. Electron. 2019, 3, 3. [Google Scholar] [CrossRef]
- Henriksen, A.D.; Rizzi, G.; Hansen, M.F. Experimental comparison of ring and diamond shaped planar Hall effect bridge magnetic field sensors. J. Appl. Phys. 2015, 118, 103901. [Google Scholar] [CrossRef]
- Østerberg, F.W.; Rizzi, G.; Henriksen, A.D.; Hansen, M.F. Planar Hall effect bridge geometries optimized for magnetic bead detection. J. Appl. Phys. 2014, 115, 184505. [Google Scholar] [CrossRef]
- Paun, M.A.; Sallèse, J.M.; Kayal, M. Geometry influence on the Hall effect devices performance. UPB Sci. Bull. Ser. A Appl. Math. Phys. 2010, 72, 257–271. [Google Scholar]
- Sinha, B.; Oh, S.; Ramulu, T.S.; Lim, J.; Kim, D.Y.; Kim, C.G. Planar hall effect ring sensors for high field-sensitivity. Adv. Mater. Res. 2011, 317–319, 1136–1140. [Google Scholar] [CrossRef]
- Quynh, L.K.; Hien, N.T.; Binh, N.H.; Dung, T.T.; Tu, B.D.; Duc, N.H.; Giang, D.T.H. Simple planar Hall effect based sensors for low-magnetic field detection. Adv. Nat. Sci. Nanosci. Nanotechnol. 2019, 10, 025002. [Google Scholar] [CrossRef]
- Atalay, S.; Kolat, V.S.; Atalay, F.E.; Bayri, N.; Kaya, H.; Izgi, T. Magnetoelastic sensor for magnetic nanoparticle detection. J. Magn. Magn. Mater. 2018, 465, 151–155. [Google Scholar] [CrossRef]
- Ong, K.G.; Tan, E.L.; Pereles, B.; Horton, B. Wireless, magnetic-based sensors for biomedical applications. In Proceedings of the 31st Annual International Conference of the IEEE Engineering in Medicine and Biology Society: Engineering the Future of Biomedicine, EMBC 2009, Minneapolis, MN, USA, 2–6 September 2009; pp. 5436–5439. [Google Scholar]
- Ren, L.; Yu, K.; Tan, Y. Wireless and Passive Magnetoelastic-Based Sensor for Force Monitoring of Artificial Bone. IEEE Sens. J. 2019, 19, 2096–2104. [Google Scholar] [CrossRef]
- Ren, L.; Yu, K.; Tan, Y. Monitoring and assessing the degradation rate of magnesium-based artificial bone in vitro using a wireless magnetoelastic sensor. Sensors 2018, 18, 3066. [Google Scholar] [CrossRef]
- Bras, Y.; Greneche, J.-M. Magneto-Elastic Resonance: Principles, Modeling and Applications. In Resonance; BoD–Books on Demand: Norderstedt, Germany, 2017; p. 13. [Google Scholar]
- Pannetier-Lecoeur, M.; Fermon, C.; Campiglio, P.; Herreros, Q.; Jasmin-Lebras, G. Spin Electronics Based Magnetic Sensors for Biomagnetic Measurements. In Magnetoencephalography: From Signals to Dynamic Cortical Networks; Supek, S., Aine, C.J., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 1001–1005. [Google Scholar]
- Nanayakkara, K.; Anferov, A.; Jacob, A.P.; Allen, S.J.; Kozhanov, A. Cross junction spin wave logic architecture. IEEE Trans. Magn. 2014, 50, 1–4. [Google Scholar] [CrossRef]
- Trabada, D.G.; Roussigne, Y.; Cherif, S.M.; Stashkevich, A.A.; Belmeguenai, M.; Vazquez, M. Spin Waves Modes in Cobalt Nanowires Arrays. IEEE Trans. Magn. 2015, 51, 3–6. [Google Scholar] [CrossRef]
- Wang, Q.; Pirro, P.; Verba, R.; Slavin, A.; Hillebrands, B.; Chumak, A.V. Reconfigurable nanoscale spin-wave directional coupler. Sci. Adv. 2018, 4, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Vetoshko, P.M.; Valeiko, M.V.; Nikitin, P.I. Epitaxial yttrium iron garnet film as an active medium of an even-harmonic magnetic field transducer. Sens. Actuators A Phys. 2003, 106, 270–273. [Google Scholar] [CrossRef]
- Reermann, J.; Elzenheimer, E.; Schmidt, G. Real-Time Biomagnetic Signal Processing for Uncooled Magnetometers in Cardiology. IEEE Sens. J. 2019, 19, 4237–4249. [Google Scholar] [CrossRef]
- Lau, S.; Petković, B.; Haueisen, J. Optimal magnetic sensor vests for cardiac source imaging. Sensors 2016, 16, 754. [Google Scholar] [CrossRef]
- Boto, E.; Bowtell, R.; Krüger, P.; Fromhold, T.M.; Morris, P.G.; Meyer, S.S.; Barnes, G.R.; Brookes, M.J. On the potential of a new generation of magnetometers for MEG: A beamformer simulation study. PLoS ONE 2016, 11, e0157655. [Google Scholar] [CrossRef] [PubMed]
- Garcia, M.A.C.; Baffa, O. Magnetic fields from skeletal muscles: A valuable physiological measurement? Front. Physiol. 2015, 6, 1–4. [Google Scholar] [CrossRef]
- Hari, R.; Parkkonen, L.; Nangini, C. The brain in time: Insights from neuromagnetic recordings. Ann. N. Y. Acad. Sci. 2010, 1191, 89–109. [Google Scholar] [CrossRef]
- Vettoliere, A.; Ruggiero, B.; Valentino, M.; Silvestrini, P.; Granata, C. Fine-Tuning and Optimization of Superconducting Quantum Magnetic Sensors by Thermal Annealing. Sensors 2019, 19, 3635. [Google Scholar] [CrossRef]
- Dang, H.B.; Maloof, A.C.; Romalis, M.V. Ultrahigh sensitivity magnetic field and magnetization measurements with an atomic magnetometer. Appl. Phys. Lett. 2010, 97, 151110. [Google Scholar] [CrossRef]
- Tierney, T.M.; Holmes, N.; Mellor, S.; López, J.D.; Roberts, G.; Hill, R.M.; Boto, E.; Leggett, J.; Shah, V.; Brookes, M.J.; et al. Optically pumped magnetometers: From quantum origins to multi-channel magnetoencephalography. Neuroimage 2019, 199, 598–608. [Google Scholar] [CrossRef] [PubMed]
- Krzyzewski, S.P.; Perry, A.R.; Gerginov, V.; Knappe, S. Characterization of noise sources in a microfabricated single-beam zero-field optically-pumped magnetometer. J. Appl. Phys. 2019, 126, 044504. [Google Scholar] [CrossRef] [PubMed]
- Knappe, S.; Alem, O.; Sheng, D.; Kitching, J. Microfabricated Optically-Pumped Magnetometers for Biomagnetic Applications. J. Phys. Conf. Ser. 2016, 723, 012055. [Google Scholar] [CrossRef]
- Zhou, F.; Zhu, C.J.; Hagley, E.W.; Deng, L. Symmetry-breaking inelastic wave-mixing atomic magnetometry. Sci. Adv. 2017, 3, 1–8. [Google Scholar] [CrossRef]
- Gerginov, V.; Krzyzewski, S.; Knappe, S. Pulsed operation of a miniature scalar optically pumped magnetometer. J. Opt. Soc. Am. B 2017, 34, 1429. [Google Scholar] [CrossRef] [PubMed]
- Wilson, N.; Light, P.; Luiten, A.; Perrella, C. Ultrastable Optical Magnetometry. Phys. Rev. Appl. 2019, 11, 044034. [Google Scholar] [CrossRef]
- Xu, L.; Yuan, H.; Zhang, N.; Zhang, J.; Bian, G.; Fan, P.; Li, M.; Zhang, C.; Zhai, Y.; Fang, J. High-efficiency fluorescence collection for NV—Center ensembles in diamond. Opt. Express 2019, 27, 10787. [Google Scholar] [CrossRef]
- Ma, Z.; Zhang, S.; Fu, Y.; Yuan, H.; Shi, Y.; Gao, J.; Qin, L.; Tang, J.; Liu, J.; Li, Y. Magnetometry for precision measurement using frequency-modulation microwave combined efficient photon-collection technique on an ensemble of nitrogen-vacancy centers in diamond. Opt. Express 2018, 26, 382–390. [Google Scholar] [CrossRef]
- Barry, J.F.; Turner, M.J.; Schloss, J.M.; Glenn, D.R.; Song, Y.; Lukin, M.D.; Park, H.; Walsworth, R.L. Optical magnetic detection of single-neuron action potentials using quantum defects in diamond. Proc. Natl. Acad. Sci. USA 2016, 113, 14133–14138. [Google Scholar] [CrossRef]
- Maayani, S.; Foy, C.; Englund, D.; Fink, Y. Distributed Quantum Fiber Magnetometry. Laser Photonics Rev. 2019, 13, 1–7. [Google Scholar] [CrossRef]
- Schwartz, I.; Rosskopf, J.; Schmitt, S.; Tratzmiller, B.; Chen, Q.; McGuinness, L.P.; Jelezko, F.; Plenio, M.B. Blueprint for nanoscale NMR. Sci. Rep. 2019, 9, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Hong, S.; Grinolds, M.S.; Pham, L.M.; Le Sage, D.; Luan, L.; Walsworth, R.L.; Yacoby, A. Nanoscale magnetometry with NV centers in diamond. MRS Bull. 2013, 38, 155–161. [Google Scholar] [CrossRef]
- Nowodzinski, A.; Chipaux, M.; Toraille, L.; Jacques, V.; Roch, J.F.; Debuisschert, T. Nitrogen-Vacancy centers in diamond for current imaging at the redistributive layer level of Integrated Circuits. Microelectron. Reliab. 2015, 55, 1549–1553. [Google Scholar] [CrossRef]
- Lovchinsky, I.; Sushkov, A.O.; Urbach, E.; de Leon, N.P.; Choi, S.; De Greve, K.; Evans, R.; Gertner, R.; Bersin, E.; Müller, C.; et al. Nuclear magnetic resonance detection and spectroscopy of single proteins using quantum logic. Science 2016, 351, 836–842. [Google Scholar] [CrossRef]
- Fukami, M.; Yale, C.G.; Andrich, P.; Liu, X.; Heremans, F.J.; Nealey, P.F.; Awschalom, D.D. All-Optical Cryogenic Thermometry Based on Nitrogen-Vacancy Centers in Nanodiamonds. Phys. Rev. Appl. 2019, 12, 1. [Google Scholar] [CrossRef]
- Dumeige, Y.; Roch, J.-F.; Bretenaker, F.; Debuisschert, T.; Acosta, V.; Becher, C.; Chatzidrosos, G.; Wickenbrock, A.; Bougas, L.; Wilzewski, A.; et al. Infrared laser threshold magnetometry with a NV doped diamond intracavity etalon. Opt. Express 2019, 27, 1706. [Google Scholar] [CrossRef]
- Savitski, V.G. Optical gain in NV-colour centers for highly-sensitive magnetometry: A theoretical study. J. Phys. D Appl. Phys. 2017, 50, 475602. [Google Scholar] [CrossRef]
- Barry, J.F.; Schloss, J.M.; Bauch, E.; Turner, M.J.; Hart, C.A.; Pham, L.M.; Walsworth, R.L. Sensitivity Optimization for NV-Diamond Magnetometry. arXiv 2019, arXiv:1903.08176. [Google Scholar]
- Yu, Y.; Forstner, S.; Rubinsztein-Dunlop, H.; Bowen, W.P. Modelling of cavity optomechanical magnetometers. Sensors 2018, 18, 1558. [Google Scholar] [CrossRef]
- Vetoshko, P.M.; Gusev, N.A.; Chepurnova, D.A.; Samoilova, E.V.; Zvezdin, A.K.; Korotaeva, A.A.; Belotelov, V.I. Rat Magnetocardiography Using a Flux-Gate Sensor Based on Iron Garnet Films. Biomed. Eng. 2016, 50, 1–4. [Google Scholar] [CrossRef]
- Uchiyama, T.; Takiya, T. Development of precise off-diagonal magnetoimpedance gradiometer for magnetocardiography. AIP Adv. 2017, 7, 3–8. [Google Scholar] [CrossRef]
- Jin, F.; Wang, J.; Zhu, L.; Mo, W.; Dong, K.; Song, J. Impact of Adjustment of the Static Working Point on the 1/ f Noise in a Negative Feedback GMI Magnetic Sensor. IEEE Sens. J. 2019, 19, 9172–9177. [Google Scholar] [CrossRef]
- Wang, K.; Tajima, S.; Asano, Y.; Okuda, Y.; Hamada, N.; Cai, C.; Uchiyama, T. Detection of P300 brain waves using a Magneto-Impedance sensor. Proc. Int. Conf. Sens. Technol. ICST 2014, 2014, 547–550. [Google Scholar]
- Uchiyama, T.; Mohri, K.; Nakayama, S. Measurement of Spontaneous Oscillatory Magnetic Field of Guinea-Pig Smooth Muscle Preparation Using Pico-Tesla Resolution Amorphous Wire Magneto-Impedance Sensor. IEEE Trans. Magn. 2011, 47, 3070–3073. [Google Scholar] [CrossRef]
- Turutin, A.V.; Vidal, J.V.; Kubasov, I.V.; Kislyuk, A.M.; Kiselev, D.A.; Malinkovich, M.D.; Parkhomenko, Y.N.; Kobeleva, S.P.; Kholkin, A.L.; Sobolev, N.A. Highly sensitive magnetic field sensor based on a metglas/bidomain lithium niobate composite shaped in form of a tuning fork. J. Magn. Magn. Mater. 2019, 486, 165209. [Google Scholar] [CrossRef]
- Shirai, Y.; Hirao, K.; Shibuya, T.; Okawa, S.; Hasegawa, Y.; Adachi, Y.; Sekihara, K.; Kawabata, S. Magnetocardiography using a magnetoresistive sensor array. Int. Heart J. 2019, 60, 50–54. [Google Scholar] [CrossRef] [PubMed]
- Cardoso, S.; Leitao, D.C.; Dias, T.M.; Valadeiro, J.; Silva, M.D.; Chicharo, A.; Silverio, V.; Gaspar, J.; Freitas, P.P. Challenges and trends in magnetic sensor integration with microfluidics for biomedical applications. J. Phys. D Appl. Phys. 2017, 50, 213001. [Google Scholar] [CrossRef]
- Gooneratne, C.P.; Kodzius, R.; Li, F.; Foulds, I.G.; Kosel, J. On-chip magnetic bead manipulation and detection using a magnetoresistive sensor-based micro-chip: Design considerations and experimental characterization. Sensors 2016, 16, 1369. [Google Scholar] [CrossRef] [PubMed]
- Nikitin, M.P.; Orlov, A.V.; Sokolov, I.L.; Minakov, A.A.; Nikitin, P.I.; Ding, J.; Bader, S.D.; Rozhkova, E.A.; Novosad, V. Ultrasensitive detection enabled by nonlinear magnetization of nanomagnetic labels. Nanoscale 2018, 10, 11642–11650. [Google Scholar] [CrossRef]
- Wang, H.; Mahdavi, A.; Tirrell, D.A.; Hajimiri, A. A magnetic cell-based sensor. Lab Chip 2012, 12, 4465–4471. [Google Scholar] [CrossRef]
- Wang, T.; Zhou, Y.; Lei, C.; Luo, J.; Xie, S.; Pu, H. Magnetic impedance biosensor: A review. Biosens. Bioelectron. 2017, 90, 418–435. [Google Scholar] [CrossRef] [PubMed]
- Issadore, D.; Park, Y.I.; Shao, H.; Min, C.; Lee, K.; Liong, M.; Weissleder, R.; Lee, H. Magnetic sensing technology for molecular analyses. Lab Chip 2014, 14, 2385–2397. [Google Scholar] [CrossRef] [PubMed]
- Dalponte, A.; Bastos, E.S.; Missell, F.P. Enhanced response from field-annealed magnetoelastic strain sensor. J. Appl. Phys. 2016, 120, 064502. [Google Scholar] [CrossRef]
- Yu, K.; Ren, L.; Tan, Y.; Wang, J. Wireless magnetoelasticity-based sensor for monitoring the degradation behavior of polylactic acid artificial bone in vitro. Appl. Sci. 2019, 9, 739. [Google Scholar] [CrossRef]
- Tan, Y.; Zhu, J.; Ren, L. A two-dimensional wireless and passive sensor for stress monitoring. Sensors 2019, 19, 135. [Google Scholar] [CrossRef] [PubMed]
- Kozejova, D.; Fecova, L.; Klein, P.; Sabol, R.; Hudak, R.; Sulla, I.; Mudronova, D.; Galik, J.; Varga, R. Biomedical applications of glass-coated microwires. J. Magn. Magn. Mater. 2019, 470, 2–5. [Google Scholar] [CrossRef]
- Barroso, T.G.; Martins, R.C.; Fernandes, E.; Cardoso, S.; Rivas, J.; Freitas, P.P. Detection of BCG bacteria using a magnetoresistive biosensor: A step towards a fully electronic platform for tuberculosis point-of-care detection. Biosens. Bioelectron. 2018, 100, 259–265. [Google Scholar] [CrossRef]
- Hien, L.T.; Quynh, L.K.; Huyen, V.T.; Tu, B.D.; Hien, N.T.; Phuong, D.M.; Nhung, P.H.; Giang, D.T.H.; Duc, N.H. DNA-magnetic bead detection using disposable cards and the anisotropic magnetoresistive sensor. Adv. Nat. Sci. Nanosci. Nanotechnol. 2016, 7, 045006. [Google Scholar] [CrossRef]
- Quynh, L.K.; Tu, B.D.; Dang, D.X.; Viet, D.Q.; Hien, L.T.; Huong Giang, D.T.; Duc, N.H. Detection of magnetic nanoparticles using simple AMR sensors in Wheatstone bridge. J. Sci. Adv. Mater. Devices 2016, 1, 98–102. [Google Scholar] [CrossRef]
- Nabaei, V.; Chandrawati, R.; Heidari, H. Magnetic biosensors: Modelling and simulation. Biosens. Bioelectron. 2018, 103, 69–86. [Google Scholar] [CrossRef]
- Hansen, M.F.; Rizzi, G. Exchange-Biased AMR Bridges for Magnetic Field Sensing and Biosensing. IEEE Trans. Magn. 2017, 53, 4000211. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, Y.; Zhan, Q.; Liu, J.P.; Li, R.W. Rapid detection of Escherichia coli O157:H7 using tunneling magnetoresistance biosensor. AIP Adv. 2017, 7, 056658. [Google Scholar] [CrossRef]
- Klein, T.; Wang, W.; Yu, L.; Wu, K.; Boylan, K.L.M.; Vogel, R.I.; Skubitz, A.P.N.; Wang, J.P. Development of a multiplexed giant magnetoresistive biosensor array prototype to quantify ovarian cancer biomarkers. Biosens. Bioelectron. 2019, 126, 301–307. [Google Scholar] [CrossRef] [PubMed]
- Suess, D.; Bachleitner-Hofmann, A.; Satz, A.; Weitensfelder, H.; Vogler, C.; Bruckner, F.; Abert, C.; Prügl, K.; Zimmer, J.; Huber, C.; et al. Topologically protected vortex structures for low-noise magnetic sensors with high linear range. Nat. Electron. 2018, 1, 362–370. [Google Scholar] [CrossRef]
- Giouroudi, I.; Hristoforou, E. Perspective: Magnetoresistive sensors for biomedicine. J. Appl. Phys. 2018, 124, 030902. [Google Scholar] [CrossRef]
- Feng, Z.; Zhi, S.; Guo, L.; Zhou, Y.; Lei, C. An integrated magnetic microfluidic chip for rapid immunodetection of the prostate specific antigen using immunomagnetic beads. Microchim. Acta 2019, 186, 252. [Google Scholar] [CrossRef]
- Feng, Z.; Zhi, S.; Guo, L.; Wei, M.; Zhou, Y.; Lei, C. A novel integrated microfluidic platform based on micro-magnetic sensor for magnetic bead manipulation and detection. Microfluid. Nanofluidics 2018, 22, 86. [Google Scholar] [CrossRef]
- Wang, T.; Chen, Y.; Wang, B.; He, Y.; Li, H.; Liu, M.; Rao, J.; Wu, Z.; Xie, S.; Luo, J. A giant magnetoimpedance-based separable-type method for supersensitive detection of 10 magnetic beads at high frequency. Sens. Actuators A Phys. 2019, 300, 111656. [Google Scholar] [CrossRef]
- Liu, P.P.; Skucha, K.; Duan, Y.; Megens, M.; Kim, J.; Izyumin, I.I.; Gambini, S.; Boser, B. Magnetic relaxation detector for microbead labels. IEEE J. Solid-State Circuits 2012, 47, 1056–1064. [Google Scholar] [CrossRef]
- Melzer, M.; Mönch, J.I.; Makarov, D.; Zabila, Y.; Bermúdez, G.S.C.; Karnaushenko, D.; Baunack, S.; Bahr, F.; Yan, C.; Kaltenbrunner, M.; et al. Wearable magnetic field sensors for flexible electronics. Adv. Mater. 2015, 27, 1274–1280. [Google Scholar] [CrossRef]
- Milici, S.; Lazaro, A.; Villarino, R.; Girbau, D.; Magnarosa, M. Wireless Wearable Magnetometer-Based Sensor for Sleep Quality Monitoring. IEEE Sens. J. 2018, 18, 2145–2152. [Google Scholar] [CrossRef]
- Seshadri, D.R.; Li, R.T.; Voos, J.E.; Rowbottom, J.R.; Alfes, C.M.; Zorman, C.A.; Drummond, C.K. Wearable sensors for monitoring the internal and external workload of the athlete. NPJ Digit. Med. 2019, 2, 71. [Google Scholar] [CrossRef] [PubMed]
- van Erp, J.B.F.; van Veen, H.A.H.C. Touch down: The effect of artificial touch cues on orientation in microgravity. Neurosci. Lett. 2006, 404, 78–82. [Google Scholar] [CrossRef]
- Cañón Bermúdez, G.S.; Karnaushenko, D.D.; Karnaushenko, D.; Lebanov, A.; Bischoff, L.; Kaltenbrunner, M.; Fassbender, J.; Schmidt, O.G.; Makarov, D. Magnetosensitive e-skins with directional perception for augmented reality. Sci. Adv. 2018, 4. [Google Scholar] [CrossRef]
- Dahiya, R.S.; Metta, G.; Valle, M.; Sandini, G. Tactile Sensing—From Humans to Humanoids. IEEE Trans. Robot. 2010, 26, 1–20. [Google Scholar] [CrossRef]
- Hua, Q.; Sun, J.; Liu, H.; Bao, R.; Yu, R.; Zhai, J.; Pan, C.; Wang, Z.L. Skin-inspired highly stretchable and conformable matrix networks for multifunctional sensing. Nat. Commun. 2018, 9, 244. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, Y.; Zhou, Y.; Man, Q.; Hu, C.; Asghar, W.; Li, F.; Yu, Z.; Shang, J.; Liu, G.; et al. A skin-inspired tactile sensor for smart prosthetics. Sci. Robot. 2018, 3. [Google Scholar] [CrossRef]
- Oh, S.; Jung, Y.; Kim, S.; Kim, S.; Hu, X.; Lim, H.; Kim, C. Remote tactile sensing system integrated with magnetic synapse. Sci. Rep. 2017, 7, 1–8. [Google Scholar] [CrossRef]
- Cooper, R.J.; Prescott, D.W.; Matz, P.; Sauer, K.L.; Dural, N.; Romalis, M.V.; Foley, E.L.; Kornack, T.W.; Monti, M.; Okamitsu, J. Atomic Magnetometer Multisensor Array for rf Interference Mitigation and Unshielded Detection of Nuclear Quadrupole Resonance. Phys. Rev. Appl. 2016, 6. [Google Scholar] [CrossRef]
- Holmes, N.; Leggett, J.; Boto, E.; Roberts, G.; Hill, R.M.; Tierney, T.M.; Shah, V.; Barnes, G.R.; Brookes, M.J.; Bowtell, R. A bi-planar coil system for nulling background magnetic fields in scalp mounted magnetoencephalography. Neuroimage 2018, 181, 760–774. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Murzin, D.; Mapps, D.J.; Levada, K.; Belyaev, V.; Omelyanchik, A.; Panina, L.; Rodionova, V. Ultrasensitive Magnetic Field Sensors for Biomedical Applications. Sensors 2020, 20, 1569. https://doi.org/10.3390/s20061569
Murzin D, Mapps DJ, Levada K, Belyaev V, Omelyanchik A, Panina L, Rodionova V. Ultrasensitive Magnetic Field Sensors for Biomedical Applications. Sensors. 2020; 20(6):1569. https://doi.org/10.3390/s20061569
Chicago/Turabian StyleMurzin, Dmitry, Desmond J. Mapps, Kateryna Levada, Victor Belyaev, Alexander Omelyanchik, Larissa Panina, and Valeria Rodionova. 2020. "Ultrasensitive Magnetic Field Sensors for Biomedical Applications" Sensors 20, no. 6: 1569. https://doi.org/10.3390/s20061569
APA StyleMurzin, D., Mapps, D. J., Levada, K., Belyaev, V., Omelyanchik, A., Panina, L., & Rodionova, V. (2020). Ultrasensitive Magnetic Field Sensors for Biomedical Applications. Sensors, 20(6), 1569. https://doi.org/10.3390/s20061569







