Abstract
Motion analysis is an important topic in the monitoring of physical activities and recognition of neurological disorders. The present paper is devoted to motion assessment using accelerometers inside mobile phones located at selected body positions and the records of changes in the heart rate during cycling, under different body loads. Acquired data include 1293 signal segments recorded by the mobile phone and the Garmin device for uphill and downhill cycling. The proposed method is based upon digital processing of the heart rate and the mean power in different frequency bands of accelerometric data. The classification of the resulting features was performed by the support vector machine, Bayesian methods, k-nearest neighbor method, and neural networks. The proposed criterion is then used to find the best positions for the sensors with the highest discrimination abilities. The results suggest the sensors be positioned on the spine for the classification of uphill and downhill cycling, yielding an accuracy of 96.5% and a cross-validation error of 0.04 evaluated by a two-layer neural network system for features based on the mean power in the frequency bands and Hz. This paper shows the possibility of increasing this accuracy to 98.3% by the use of more features and the influence of appropriate sensor positioning for motion monitoring and classification.
1. Introduction
Recognition of human activities based on acceleration data [1,2,3,4,5,6] and their analysis by signal processing methods, computational intelligence, and machine learning, forms the basis of many systems for rehabilitation monitoring and evaluation of physical activities. Extensive attention has been paid to the analysis of these signals and their multimodal processing with further biomedical data [7,8] for feature extraction, classification, and human–computer interactions. Methods of motion detection and its analysis by accelerometers and global positioning systems (GPS) are also used for studies of physical activities including cycling [9,10,11,12,13,14], as assessed in this paper.
Sensor systems used for motion monitoring include wireless motion sensors (accelerometers and gyrometers) [15,16], camera systems (thermal, depth and color cameras) [9,17], ultrasound systems [18], and satellite positioning systems [12,13,14]. Specific methods are used for respiratory data processing [19] as well. There are many studies devoted to the analysis of these signals, markerless systems [20], and associated three-dimensional modelling.
There are very wide applications of motion monitoring systems, including gait analysis [21,22,23,24,25,26], motion evaluation [27,28,29,30,31,32], stroke patients monitoring [18,33], recognition of physical activities [34,35,36,37,38], breathing [39], and detection of motion disorders during sleep [40]. The combination of accelerometer sensors at different body locations in possible combination with GPS and geographical information systems is useful in improving movement monitoring of humans [41], assessing road surface roughness [10], and activity recognition [30] as well.
The present paper is devoted to the use of these systems to recognize selected motion activities using data acquired by accelerometers in mobile phones [42,43,44] with positioning and heart rate (HR) data simultaneously recorded by the Garmin system [45,46]. The locations of the accelerometric and Garmin sensors used to monitor the motion and heart rate data are presented in Figure 1. The methods used for the data processing include data de-noising, statistical methods, neural networks [47], and deep learning [48,49,50,51] methods with convolutional neural networks.
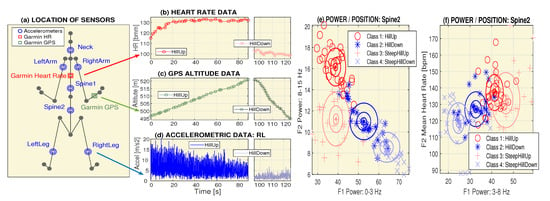
Figure 1.
The principle of motion data acquisition and their processing, presenting (a) location of accelerometric and Garmin system sensors during cycling, (b–d) sample signals recorded by the heart rate sensor, Garmin position system, and the RightLeg accelerometric data while moving up and down, (e) distribution of the mean power in the frequency ranges Hz and Hz, and (f) distribution of the mean power in the frequency range Hz and the mean heart rate for different cycling classes (route conditions) with cluster centers and ellipses showing multiples of the standard deviations.
The main goal of the present paper is the analysis of accelerometric and heart rate signals to contribute to monitoring physical activities and to the assesment of rehabilitation exercises [11,52]. Selected sensors were used for the analysis of data recorded during cycling in different conditions, extending the results recorded on the exercise bike [53,54]. The proposed mathematical tools include the use of neural networks [55], machine learning for pattern recognition, and the application of signal processing methods for data analysis to enable the monitoring of selected physiological functions.
2. Methods
2.1. Data Acquisition
Figure 1a presents the location of sensors for the acquisition of accelerometric, positioning, and heart rate data during cycling experiments with different loads. Both the mobile phone at different locations (for accelerometric data recording) and the Garmin system (for the simultaneous recording of GPS data and the heart rate) were used for data acquisition. Sample signals for uphill and downhill cycling are shown in Figure 1b–d.
The GPS and motion data (time stamps, longitude, latitude, altitude, cycling distance, and the cycling speed) were simultaneously measured by a Garmin fitness watch (Fenix 5S, Garmin Ltd., Schaffhausen, Switzerland). The heart rate data were acquired by a Garmin chest strap connected to a Garmin watch by the wireless data transmission technology. All data sets were acquired during the cycling experiments realised by a healthy and trained adult volunteer. Records were subsequently stored to the Garmin Connect website, exported in the specific Training Center (TCX) format (used for data exchange between fitness devices), converted to the comma-separated values (CSV), and imported into the MATLAB software for further processing.
A summary of the cycling segments for specific locations of the mobile phone used for accelerometric data acquisition is presented in Table 1.

Table 1.
Summary of cycling segments of individual positions used for classification.
The original mean sampling frequency was 142 Hz (changing in the range Hz with the standard deviation STD = 114) for accelerometric data and 0.48 Hz (changing in the range Hz, STD = 0.27) for heart rate data.
Table 2 presents the categories used for the classification. They were selected according to the profile of the terrain, its slope being evaluated by the Garmin GPS system. The individual categories include: (i) -HillUp; (ii) -HillDown; (iii) -SteepHillUp; and (iv) -SteepHillDown cycling.

Table 2.
The mean slope S [%] of the terrain segments, and its standard deviation (STD), as recorded by the Garmin GPS system.
A sample time segment of the modulus of the accelerometric data simultaneously recorded by the mobile phone at the selected location (the RightLeg) is presented in Figure 1d. All procedures involving human participants were in accordance with the ethical standards of the institutional research committee and with the 1964 Helsinki Declaration and its later amendments.
2.2. Signal Processing
The proposed data processing method included data analysis at first. The total number of 1293 cycling segments was reduced to 1254 segments in the initial step, to exclude those with the standard deviation of the speed higher than a selected fraction of its mean value. This process excluded 3% of the cycling segments with gross errors and problems on the cycling route, as specified in Table 1.
In the next step, the linear acceleration data without additional gravity components were processed. Their modulus of the accelerometric data was evaluated from the components , , and recorded in three directions:
for all values in each segment N values long, for all classes and at positions specified in Table 1. The Garmin data were used to evaluate the mean heart rate, cycling speed, and the mean slope in each segment. Owing to the slightly changing time period during each observation, the initial preprocessing step included the linear interpolation into a vector of uniformly spaced instants with the same endpoints and number of samples.
The processing of multimodal records of the accelerometric and heart rate signals was performed by similar numerical methods. In the initial stage, their de-noising was performed by finite impulse response (FIR) filtering of a selected order M, resulting in a new sequence using the relation
with coefficients forming a filter of the selected type and cutoff frequencies. In the present study, the selected cutoff frequency Hz was used for the antialiasing low pass FIR filter of the order . It allowed signal resampling for this new sampling frequency.
The accelerometric data were processed to evaluate the signal spectrum, covering the full frequency range of Hz related to the sampling theorem. The mean normalized power components in 4 sub-bands were then evaluated to define the features of each segment for each class and sensor position. The resulting feature vector includes in each of its columns q relative mean power values in the frequency bands Hz, which form a complete filter bank covering the frequency ranges of , , , and Hz. The next row of the feature vector includes the mean heart rate in each segment .
Each of the selected spectral features of a signal segment N samples long was evaluated using the discrete Fourier transform, in terms of the relative power in a specified frequency band Hz, as follows:
where is the set of indices for which the frequencies Hz.
Figure 1e,f presents selected features during different physical activities. Figure 1e shows the distribution of the mean power in the frequency ranges Hz and Hz, and Figure 1f presents the distribution of the mean power in the frequency range Hz and the mean heart rate for different categories of cycling (route conditions) with cluster centers and ellipses showing multiples of the standard deviations.
The validity of a pair of features selected from the feature vector for all segments related to specific classes and and positions was evaluated by the proposed criterion for cluster couples defined by the relation:
where
using the Euclidean distance between the cluster centers , of the features associated with classes k and l, respectively, and the sum of their standard deviations. For well-separated and compact clusters, this criterion should take a value larger than zero.
Signal analysis resulted in the evaluation of the feature matrix . The feature vector in each of its columns includes both the mean power in specific frequency ranges and the mean heart rate. The target vector includes the associated terrain specification according to Table 2 with selected results in Figure 2. Different classification methods were then applied to evaluate these features.

Figure 2.
The distribution of the mean power in the frequency ranges Hz and Hz for the accelerometer at (a) the LeftLeg, (b) the LeftArm, (c) the upper Spine1, and (d) the lower Spine2 position.
2.3. Pattern Recognition
Pattern values in the feature matrix and the associated target vector were then used for classifying all Q feature vectors into separate categories. System modelling was performed by a support vector machine (SVM), a Bayesian method, the k-nearest neighbour method, and a neural network [22,55,56,57]. network Both the accuracies and the cross-validation errors were then compared with the best results obtained by the two-layer neural network.
The machine learning [57,58] was based on the optimization of the classification system with R = 5 input values (that corresponded with the features evaluated as the mean power in four frequency bands and the mean heart rate) and output units in the learning stage. The target vector was transformed to the target matrix with units in the corresponding class rows in the range to enable evaluating the probability of each class.
In the case of the neural network classification model, the pattern matrix formed the input of the two-layer neural network structure with sigmoidal and softmax transfer functions presented in Figure 3a and used to evaluate the values by the following relations:
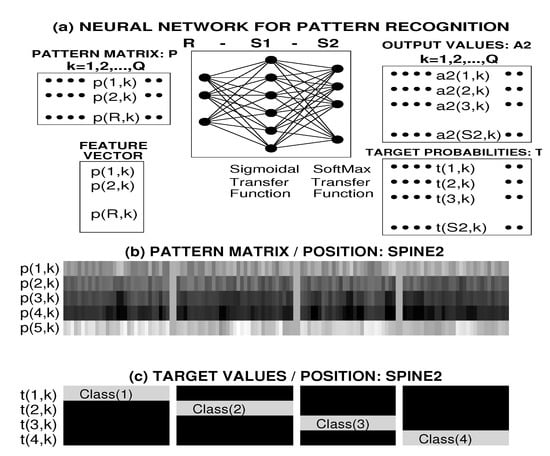
Figure 3.
Pattern matrix classification using (a) the two-layer neural network with sigmoidal and softmax transfer functions, (b) feature matrix values for classification of segment features and a given sensor position (Spine2) into a selected number of classes, and (c) associated target matrix.
For each column vector in the pattern matrix, the corresponding target vector has one unit element in the row pointing to the correct target value.
The network coefficients include the elements of the matrices and and associated vectors and . The proposed model uses the sigmoidal transfer function in the first layer and the probabilistic softmax transfer function in the second layer. The values of the output layer, based on the Bayes theorem [22], using the function
provide the probabilities of each class.
Figure 3b illustrates the pattern matrix formed by Q column vectors of R = 5 values representing the mean power in 4 frequency bands and the mean heart rate. Figure 3c presents the associated target matrix for a selected position of the accelerometric sensor.
Each column vector of grey shade pattern values was associated with one of the different target values during the learning process.
The receiver operating characteristic (ROC) curves were used as an efficient tool for the evaluation of classification results. The selected classifier finds in the negative/positive set the number of true-negative (TN), false-positive (FP), true-positive (TP), and false-negative (FP) experiments.
The associated performance metrics [59] can then be used to evaluate:
- Sensitivity (the true positive rate, the recall) and specificity (the true negative rate):
- Accuracy:
- Precision (the positive predictive value) and -score (the harmonic mean of the precision and sensitivity):
Cross-validation errors [60] were then evaluated as a measure of the generalization abilities of classification models using the leave-one-out method.
3. Results
Table 3 presents a summary of the mean features for classification into 4 classes (-SlopeUp, -SlopeDown, -SteepSlopeUp, and -SteepSlopeDown) for different positions of the sensors and selected features (the relative mean power [%] in frequency ranges Hz, Hz, Hz, Hz, and the heart rate [bpm]).

Table 3.
Mean features for classification into 4 classes (-SlopeUp, -SlopeDown, -SteepSlopeUp, and -SteepSlopeDown) for different positions of sensors and selected features (the percentage mean power , , , and , and the heart rate [bpm]).
The validity of pairs of features and for separating classes and was then evaluated using the proposed criterion specified by Equation (4). Figure 4 presents the evaluation of two classes (-SteepHillUp and -SteepHillDown) with cluster centers for different locations of the sensors, and associated values of the criterion function for features evaluated as the mean power in the frequency range Hz and the mean heart rate (Figure 4a,b) and the mean power in frequency ranges Hz and Hz (Figure 4c,d). The results presented here show that the highest discrimination abilities are possessed by a sensor located at the Spine2 position.

Figure 4.
The evaluation of two classes (-SteepHillUp and -SteepHillDown) presenting cluster centers for different locations of sensors and associated values of the criterion function for features evaluated as (a,b) the mean power in the frequency range Hz and the mean heart rate and (c,d) the mean power in frequency ranges Hz and Hz.
Figure 5 presents the classification of cycling segments into two categories (A-HillUp and B-HillDown) for two features evaluated as the mean power in the frequency ranges Hz and Hz for the sensor locations (a) the LeftLeg, (b) RightLeg, and (c) Spine2 with accuracy () and cross-validation () errors. More detailed results of this classification are presented in Table 4. Its separate rows present the accuracy [%] and cross-validation errors for the classification of class A (HillUp: +) and class B (HillDown: +) for different locations of the sensors, chosen features (—frequency range Hz, —frequency range Hz) and selected classification methods. The highest accuracy and the lowest cross-validation errors were achieved by the Spine2 location of the accelerometric sensors and all classification methods.
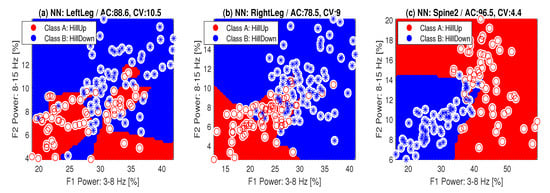
Figure 5.
Classification of cycling segments into two categories (A-HillUp and B-HillDown) for two features evaluated as the mean power in the frequency ranges Hz and Hz for sensor locations in (a) the LeftLeg, (b) the RightLeg, and (c) Spine2 with accuracy ( [%]) and cross-validation () errors.

Table 4.
Accuracy ( [%]) and cross-validation errors for classification of class A (HillUp: +) and class B (HillDown: +) for different locations of sensors, chosen features (—frequency range Hz, —frequency range Hz) and selected classification methods: support vector machine (SVM), Bayes, 5-nearest neighbour (5NN) and neural network (NN) methods (with the highest accuracy and the lowest cross-validations errors in bold).
Table 5 presents the accuracy [%], specificity (), sensitivity (), F1-score (), and cross-validation errors for classification into classes A and B by the neural network model for different locations of sensors and 5 features – including the power in all four frequency bands and the mean heart rate in each cycling segment. The highest accuracy, 98.3%, was achieved again for the Spine2 position of the accelerometric sensor with the highest F1-score of 98.2% as well.

Table 5.
Accuracy ( [%]), specificity ( [%]), sensitivity ( [%]), F1-score ( [%]), and cross-validation () errors for classification into classes A and B by the neural network model for different location of sensors and features – (with the highest accuracy and the lowest cross-validations errors in bold).
The comparison of neural network classification for two and five features is presented in Figure 6 related to Table 4 and Table 5. Cross-validation errors are evaluated by the leave-one-out method in all cases. Figure 6a shows that there is an increase in the accuracy by 6.17% on average that is most significant for locations with the lowest accuracy, including the arm and neck positions. In a similar way, an increase in the number of features from two to five decreased the cross-validation error on average by 8.72%, as presented in Figure 6b. This decrease was most significant for locations with the lowest accuracy and the highest error, which included the arm and neck positions again.

Figure 6.
Comparison of neural network classification presenting (a) accuracy and (b) cross-validation (CV) error using two and five features for different positions of the accelerometer.
4. Conclusions
This paper has presented the use of selected methods of machine learning and digital signal processing in the evaluation of motion and physical activities using wireless sensors for acquiring accelerometric and heart rate data. A mobile phone was used to record the accelerometric data at different body positions during cycling, under selected environmental conditions.
The results suggest that accelerometric data and the associated signal power in selected frequency bands can be used as features for the classification of different motion patterns to recognize cycling terrain and downhill and uphill cycling.
The proposed criterion selected the most appropriate position for classification of motion: it was the Spine2 position. All classification methods, including a support vector machine, a Bayesian method, the k-nearest neighbour method, and a two-layer neural network, were able to distinguish specific classes with an accuracy higher than 90%. The best results were achieved by the two-layer neural network and Spine2 position with an accuracy of 96.5% for two features, which was increased to 98.3% for five features.
These results correspond with those achieved during cycling on a home exercise bike [4,54] with different loads and additional sensors, including thermal cameras as well.
It is expected that further studies will be devoted to the analysis of more extensive data sets acquired by new non-invasive sensors, enabling the detection of further motion features with higher sampling frequencies. Special attention will be devoted to further multichannel data processing tools and deep learning methods with convolutional neural networks to improve the possibilities of remote monitoring of physiological functions.
Author Contributions
Data curation: H.C.; investigation: A.P.; methodology: O.V. All authors have read and agreed to the published version of the manuscript.
Acknowledgments
This research was supported by grant projects of the Ministry of Health of the Czech Republic (FN HK 00179906) and of the Charles University at Prague, Czech Republic (PROGRES Q40), as well as by the project PERSONMED—Centre for the Development of Personalized Medicine in Age-Related Diseases, Reg. No. CZ.02.1.010.00.017_0480007441, co-financed by the European Regional Development Fund (ERDF) and the governmental budget of the Czech Republic. No ethical approval was required for this study.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wannenburg, J.; Malekian, R. Physical Activity Recognition From Smartphone Accelerometer Data for User Context Awareness Sensing. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 3142–3149. [Google Scholar] [CrossRef]
- Slim, S.; Atia, A.; Elfattah, M.; Mostafa, M. Survey on Human Activity Recognition based on Acceleration Data. Intl. J. Adv. Comput. Sci. Appl. 2019, 10, 84–98. [Google Scholar] [CrossRef]
- Della Mea, V.; Quattrin, O.; Parpinel, M. A feasibility study on smartphone accelerometer-based recognition of household activities and influence of smartphone position. Inform. Health Soc. Care 2017, 42, 321–334. [Google Scholar] [CrossRef] [PubMed]
- Procházka, A.; Vyšata, O.; Charvátová, H.; Vališ, M. Motion Symmetry Evaluation Using Accelerometers and Energy Distribution. Symmetry 2019, 11, 871. [Google Scholar] [CrossRef]
- Li, R.; Kling, S.; Salata, M.; Cupp, S.; Sheehan, J.; Voos, J. Wearable Performance Devices in Sports Medicine. Sports Health 2016, 8, 74–78. [Google Scholar] [CrossRef] [PubMed]
- Rosenberger, M.; Haskell, W.; Albinali, F.; Mota, S.; Nawyn, J.; Intille, S. Estimating activity and sedentary behavior from an accelerometer on the hip or wrist. Med. Sci. Sports Exerc. 2013, 45, 964–975. [Google Scholar] [CrossRef] [PubMed]
- Monkaresi, H.; Calvo, R.A.; Yan, H. A Machine Learning Approach to Improve Contactless Heart Rate Monitoring Using a Webcam. IEEE J. Biomed. Health Informat. 2014, 18, 1153–1160. [Google Scholar] [CrossRef]
- Garde, A.; Karlen, W.; Ansermino, J.M.; Dumont, G.A. Estimating Respiratory and Heart Rates from the Correntropy Spectral Density of the Photoplethysmogram. PLoS ONE 2014, 9, e86427. [Google Scholar] [CrossRef]
- Procházka, A.; Charvátová, H.; Vyšata, O.; Kopal, J.; Chambers, J. Breathing Analysis Using Thermal and Depth Imaging Camera Video Records. Sensors 2017, 17, 1408. [Google Scholar] [CrossRef]
- Zang, K.; Shen, J.; Huang, H.; Wan, M.; Shi, J. Assessing and Mapping of Road Surface Roughness based on GPS and Accelerometer Sensors on Bicycle-Mounted Smartphones. Sensors 2018, 18, 914. [Google Scholar] [CrossRef]
- Ridgel, A.; Abdar, H.; Alberts, J.; Discenzo, F.; Loparo, K. Variability in cadence during forced cycling predicts motor improvement in individuals with Parkinson’s disease. IEEE Trans. Neural Syst. Rehabil. Eng. 2013, 21, 481–489. [Google Scholar] [CrossRef] [PubMed]
- Procházka, A.; Vaseghi, S.; Yadollahi, M.; Ťupa, O.; Mareš, J.; Vyšata, O. Remote Physiological and GPS Data Processing in Evaluation of Physical Activities. Med. Biol. Eng. Comput. 2014, 52, 301–308. [Google Scholar] [CrossRef] [PubMed]
- Charvátová, H.; Procházka, A.; Vaseghi, S.; Vyšata, O.; Vališ, M. GPS-based Analysis of Physical Activities Using Positioning and Heart Rate Cycling Data. Signal Image Video Process. 2017, 11, 251–258. [Google Scholar] [CrossRef]
- Procházka, A.; Vaseghi, S.; Charvátová, H.; Ťupa, O.; Vyšata, O. Cycling Segments Multimodal Analysis and Classification Using Neural Networks. Appl. Sci. 2017, 7, 581. [Google Scholar] [CrossRef]
- Zhang, J.; Macfarlane, D.; Sobko, T. Feasibility of a Chest-worn accelerometer for physical activity measurement. J. Sci. Med. Sport 2016, 19, 1015–1019. [Google Scholar] [CrossRef]
- Espinilla, M.; Medina, J.; Salguero, A.; Irvine, N.; Donnelly, M.; Cleland, I.; Nugent, C. Human Activity Recognition from the Acceleration Data of a Wearable Device. Which Features Are More Relevant by Activities? Proceedings 2018, 2, 1242. [Google Scholar] [CrossRef]
- Alkali, A.; Saatchi, R.; Elphick, H.; Burke, D. Thermal image processing for real-time non-contact respiration rate monitoring. IET Circ. Devices Syst. 2017, 11, 142–148. [Google Scholar] [CrossRef]
- Ambrosanio, M.; Franceschini, S.; Grassini, G.; Baselice, F. A Multi-Channel Ultrasound System for Non-Contact Heart Rate Monitoring. IEEE Sens. J. 2020, 20, 2064–2074. [Google Scholar] [CrossRef]
- Ruminski, J. Analysis of the parameters of respiration patterns extracted from thermal image sequences. Biocybern. Biomed. Eng. 2016, 36, 731–741. [Google Scholar] [CrossRef]
- Colyer, S.; Evans, M.; Cosker, D.; Salo, A. A Review of the Evolution of Vision-Based Motion Analysis and the Integration of Advanced Computer Vision Methods Towards Developing a Markerless System. Sport. Med. 2018, 4, 24.1–24.15. [Google Scholar] [CrossRef]
- Silsupadol, P.; Teja, K.; Lugade, V. Reliability and validity of a smartphone-based assessment of gait parameters across walking speed and smartphone locations: Body, bag, belt, hand, and pocket. Gait Posture 2017, 58, 516–522. [Google Scholar] [CrossRef] [PubMed]
- Procházka, A.; Vyšata, O.; Vališ, M.; Ťupa, O.; Schatz, M.; Mařík, V. Bayesian classification and analysis of gait disorders using image and depth sensors of Microsoft Kinect. Digit. Signal Prog. 2015, 47, 169–177. [Google Scholar] [CrossRef]
- Loprinzi, P.; Smith, B. Comparison between wrist-worn and waist-worn accelerometry. J. Phys. Act. Health 2017, 14, 539–545. [Google Scholar] [CrossRef] [PubMed]
- Mackintosh, K.; Montoye, A.; Pfeiffer, K.; McNarry, M. Investigating optimal accelerometer placement for energy expenditure prediction in children using a machine learning approach. Physiol. Meas. 2016, 37, 1728–1740. [Google Scholar] [CrossRef]
- Cooke, A.; Daskalopoulou, S.; Dasgupta, K. The impact of accelerometer wear location on the relationship between step counts and arterial stiffness in adults treated for hypertension and diabetes. J. Sci. Med. Sport 2018, 21, 398–403. [Google Scholar] [CrossRef]
- Rucco, R.; Sorriso, A.; Liparoti, M.; Ferraioli, G.; Sorrentino, P.; Ambrosanio, M.; Baselice, F. Type and location of wearable sensors for monitoring falls during static and dynamic tasks in healthy elderly: A review. Sensors 2018, 18, 1613. [Google Scholar] [CrossRef]
- Cvetkovic, B.; Szeklicki, R.; Janko, V.; Lutomski, P.; Luštrek, M. Real-time activity monitoring with a wristband and a smartphone. Inf. Fusion 2018, 43, 77–93. [Google Scholar] [CrossRef]
- Mannini, A.; Rosenberger, M.; Haskell, W.; Sabatini, A.; Intille, S. Activity recognition in youth using single accelerometer placed at wrist or ankle. Med. Sci. Sports Exerc. 2017, 49, 801–812. [Google Scholar] [CrossRef]
- Cleland, I.; Kikhia, B.; Nugent, C.; Boytsov, A.; Hallberg, J.; Synnes, K.; McClean, S.; Finlay, D. Optimal placement of accelerometers for the detection of everyday activities. Sensors 2013, 13, 9183–9200. [Google Scholar] [CrossRef]
- Mannini, A.; Intille, S.; Rosenberger, M.; Sabatini, A.; Haskell, W. Activity recognition using a single accelerometer placed at the wrist or ankle. Med. Sci. Sports Exerc. 2013, 45, 2193–2203. [Google Scholar] [CrossRef]
- Howie, E.; McVeigh, J.; Straker, L. Comparison of compliance and intervention outcomes between hip- and wrist-Worn accelerometers during a randomized crossover trial of an active video games intervention in children. J. Phys. Act. Health 2016, 13, 964–969. [Google Scholar] [CrossRef] [PubMed]
- Bertolotti, G.; Cristiani, A.; Colagiorgio, P.; Romano, F.; Bassani, E.; Caramia, N.; Ramat, S. A Wearable and Modular Inertial Unit for Measuring Limb Movements and Balance Control Abilities. IEEE Sens. J. 2016, 16, 790–797. [Google Scholar] [CrossRef]
- Lucas, A.; Hermiz, J.; Labuzetta, J.; Arabadzhi, Y.; Karanjia, N.; Gilja, V. Use of Accelerometry for Long Term Monitoring of Stroke Patients. IEEE J. Transl. Eng. Health Med. 2019, 7, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Crouter, S.; Flynn, J.; Bassett, D. Estimating physical activity in youth using a wrist accelerometer. Med. Sci. Sports Exerc. 2015, 47, 944–951. [Google Scholar] [CrossRef] [PubMed]
- Crouter, S.; Oody, J.; Bassett, D. Estimating physical activity in youth using an ankle accelerometer. J. Sports Sci. 2018, 36, 2265–2271. [Google Scholar] [CrossRef] [PubMed]
- Montoye, A.; Pivarnik, J.; Mudd, L.; Biswas, S.; Pfeiffer, K. Comparison of Activity Type Classification Accuracy from Accelerometers Worn on the Hip, Wrists, and Thigh in Young, Apparently Healthy Adults. Meas. Phys. Educ. Exerc. Sci. 2016, 20, 173–183. [Google Scholar] [CrossRef]
- Dutta, A.; Ma, O.; Toledo, M.; Pregonero, A.; Ainsworth, B.; Buman, M.; Bliss, D. Identifying free-living physical activities using lab-based models with wearable accelerometers. Sensors 2018, 18, 3893. [Google Scholar] [CrossRef]
- Ganea, R.; Paraschiv-Lonescu, A.; Aminian, K. Detection and classification of postural transitions in real-world conditions. IEEE Trans. Neural Syst. Rehabil. Eng. 2012, 20, 688–696. [Google Scholar] [CrossRef]
- Procházka, A.; Schätz, M.; Centonze, F.; Kuchyňka, J.; Vyšata, O.; Vališ, M. Extraction of Breathing Features Using MS Kinect for Sleep Stage Detection. Signal Image Video Process. 2016, 10, 1278–1286. [Google Scholar] [CrossRef]
- Procházka, A.; Kuchyňka, J.; Vyšata, O.; Schatz, M.; Yadollahi, M.; Sanei, S.; Vališ, M. Sleep Scoring Using Polysomnography Data Features. Signal Image Video Process. 2018, 12, 1043–1051. [Google Scholar] [CrossRef]
- Allahbakhshi, H.; Conrow, L.; Naimi, B.; Weibe, R. Using Accelerometer and GPS Data for Real-Life Physical Activity Type Detection. Sensors 2020, 20, 588. [Google Scholar] [CrossRef] [PubMed]
- Guiry, J.; van de Ven, P.; Nelson, J.; Warmerdam, L.; Ripe, H. Activity recognition with smartphone support. Med. Eng. Phys. 2014, 36, 670–675. [Google Scholar] [CrossRef] [PubMed]
- Bayat, A.; Pomplun, M.; Tran, D. A Study on Human Activity Recognition Using Accelerometer Data from Smartphones. Procedia Comput. Sci. 2014, 34, 450–457. [Google Scholar] [CrossRef]
- Shoaib, M.; Scholten, H.; Havinga, P. Towards physical activity recognition using smartphone sensors. In Proceedings of the 2013 IEEE 10th International Conference on Ubiquitous Intelligence and Computing and 2013 IEEE 10th International Conference on Autonomic and Trusted Computing, Vietri sul Mere, Italy, 18–21 December 2013; pp. 80–87. [Google Scholar]
- Gajda, R.; Biernacka, E.K.; Drygas, W. Are heart rate monitors valuable tools for diagnosing arrhythmias in endurance athletes? Scand. J. Med. 2018, 28, 496–516. [Google Scholar] [CrossRef] [PubMed]
- Collins, T.; Woolley, S.; Oniani, S.; Pires, I.; Garcia, N.; Ledger, S.; Pandyan, A. Version reporting and assessment approaches for new and updated activity and heart rate monitors. Sensors 2019, 19, 1705. [Google Scholar] [CrossRef]
- Yoshua, B.; Aaron, C.; Pascal, V. Representation Learning: A Review and New Perspectives. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1798–1828. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Antoniades, A.; Spyrou, L.; Martin-Lopez, D.; Valentin, A.; Alarcon, G.; Sanei, S.; Took, C. Detection of Interictal Discharges with Convolutional Neural Networks Using Discrete Ordered Multichannel Intracranial EEG. IEEE Trans. Neural Syst. Rehabil. Eng. 2017, 25, 2285–2294. [Google Scholar] [CrossRef]
- Mishra, C.; Gupta, D.L. Deep Machine Learning and Neural Networks: An Overview. IJHIT 2016, 9, 401–414. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Ar, I.; Akgul, Y. A Computerized Recognition System for the Home-Based Physiotherapy Exercises Using an RGBD Camera. IEEE Trans. Neural Syst. Rehabil. Eng. 2014, 22, 1160–1171. [Google Scholar] [CrossRef]
- Chauvin, R.; Hamel, M.; Briere, S.; Ferland, F.; Grondin, F.; Letourneau, D.; Tousignant, M.; Michaud, F. Contact-Free Respiration Rate Monitoring Using a Pan-Tilt Thermal Camera for Stationary Bike Telerehabilitation Sessions. IEEE Syst. J. 2016, 10, 1046–1055. [Google Scholar] [CrossRef]
- Procházka, A.; Charvátová, H.; Vaseghi, S.; Vyšata, O. Machine Learning in Rehabilitation Assesment for Thermal and Heart Rate Data Processing. IEEE Trans. Neural Syst. Rehabil. Eng. 2018, 26, 1209–12141. [Google Scholar] [CrossRef] [PubMed]
- Ou, G.; Murphey, Y. Multi-class pattern classification using neural networks. Pattern Recognit. 2007, 40, 4–8. [Google Scholar] [CrossRef]
- Shakhnarovich, M.; Darrell, T.; Indyk, P. Nearest-neighbor Methods in Learning and Vision: Theory and Practice; MIT Press: Cambridge, MA, USA, 2005. [Google Scholar]
- Theodoridis, S.; Koutroumbas, K. Pattern Recognition; Elsevier Science & Technology: Amsterdam, The Netherlands, 2008. [Google Scholar]
- Prashar, P. Neural Networks in Machine Learning. Int. J. Comput. Appl. Technol. 2014, 105, 1–3. [Google Scholar]
- Procházka, A.; Vyšata, O.; Ťupa, O.; Mareš, J.; Vališ, M. Discrimination of Axonal Neuropathy Using Sensitivity and Specificity Statistical Measures. SPRINGER: Neural Comput. Appl. 2014, 25, 1349–1358. [Google Scholar] [CrossRef]
- Fushiki, T. Estimation of prediction error by using K-fold cross-validation. Stat. Comput. 2011, 21, 137–146. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).