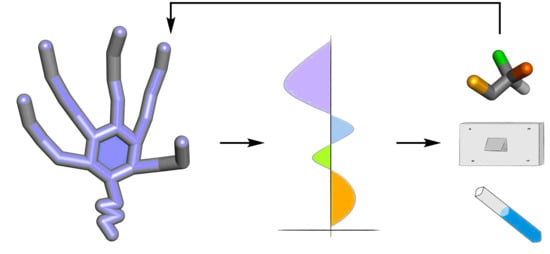
Chiroptical Sensing: A Conceptual Introduction
Abstract
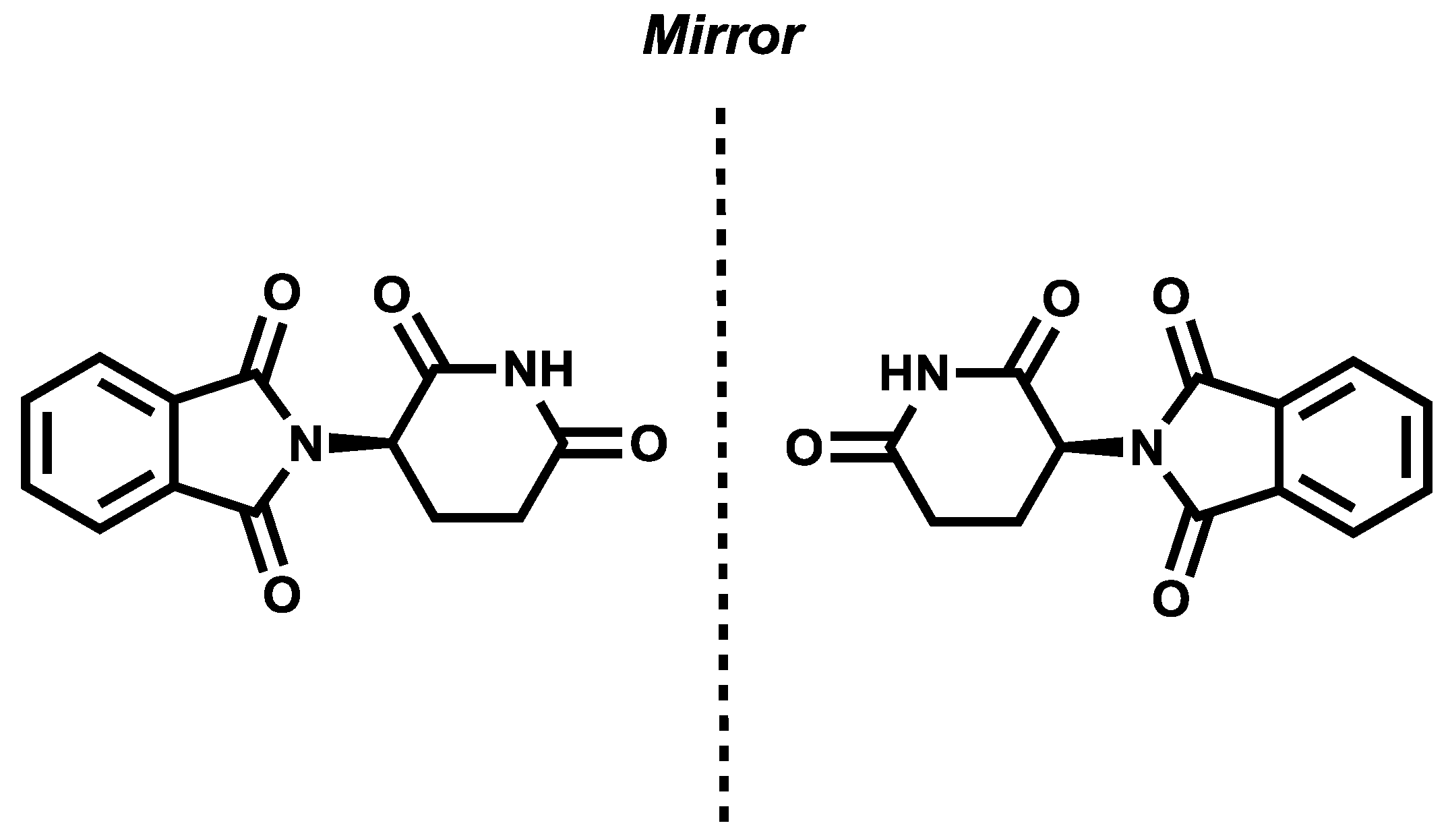
1. Introduction
2. Strategies for the Generation of Chiroptical Responses
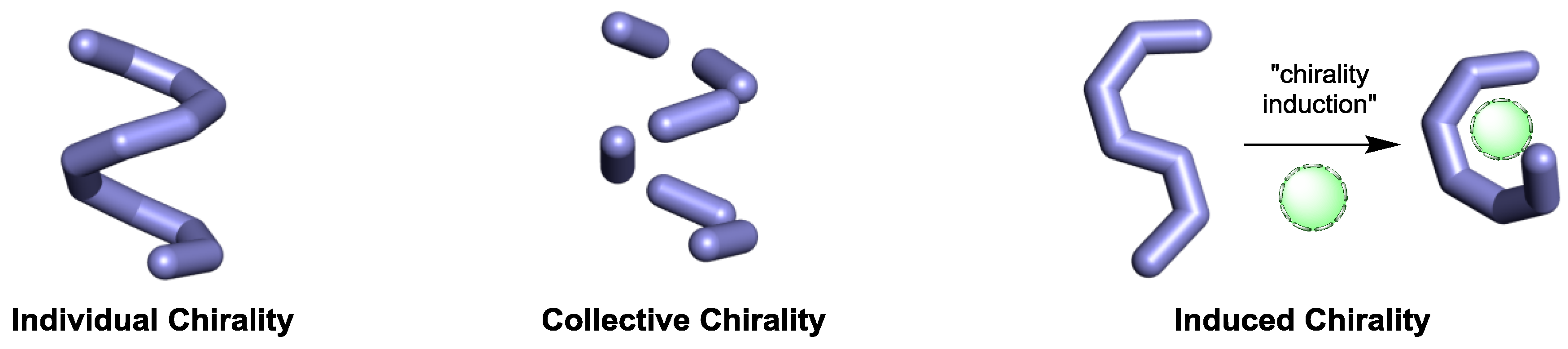
2.1. Individual Chirality
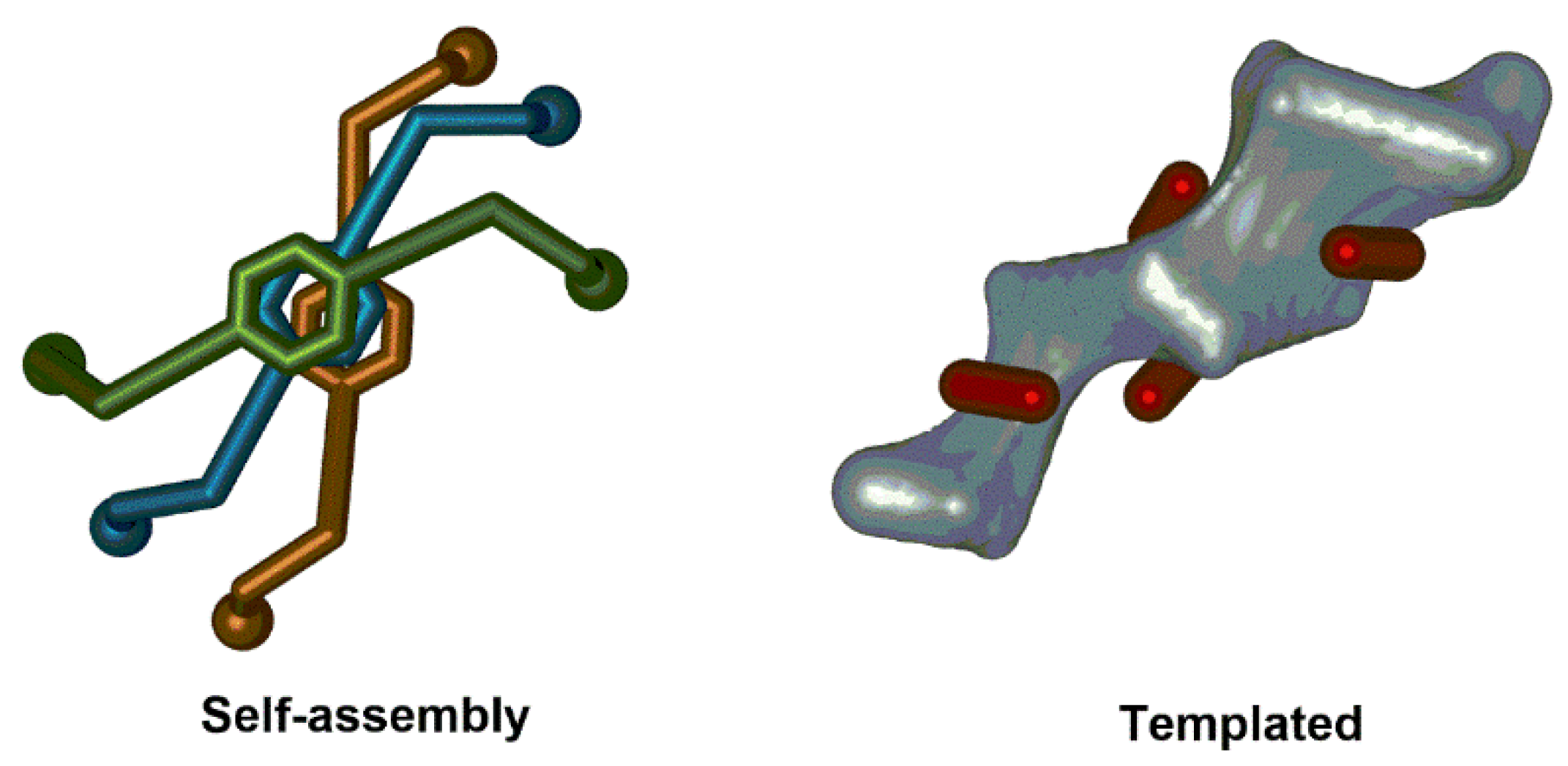
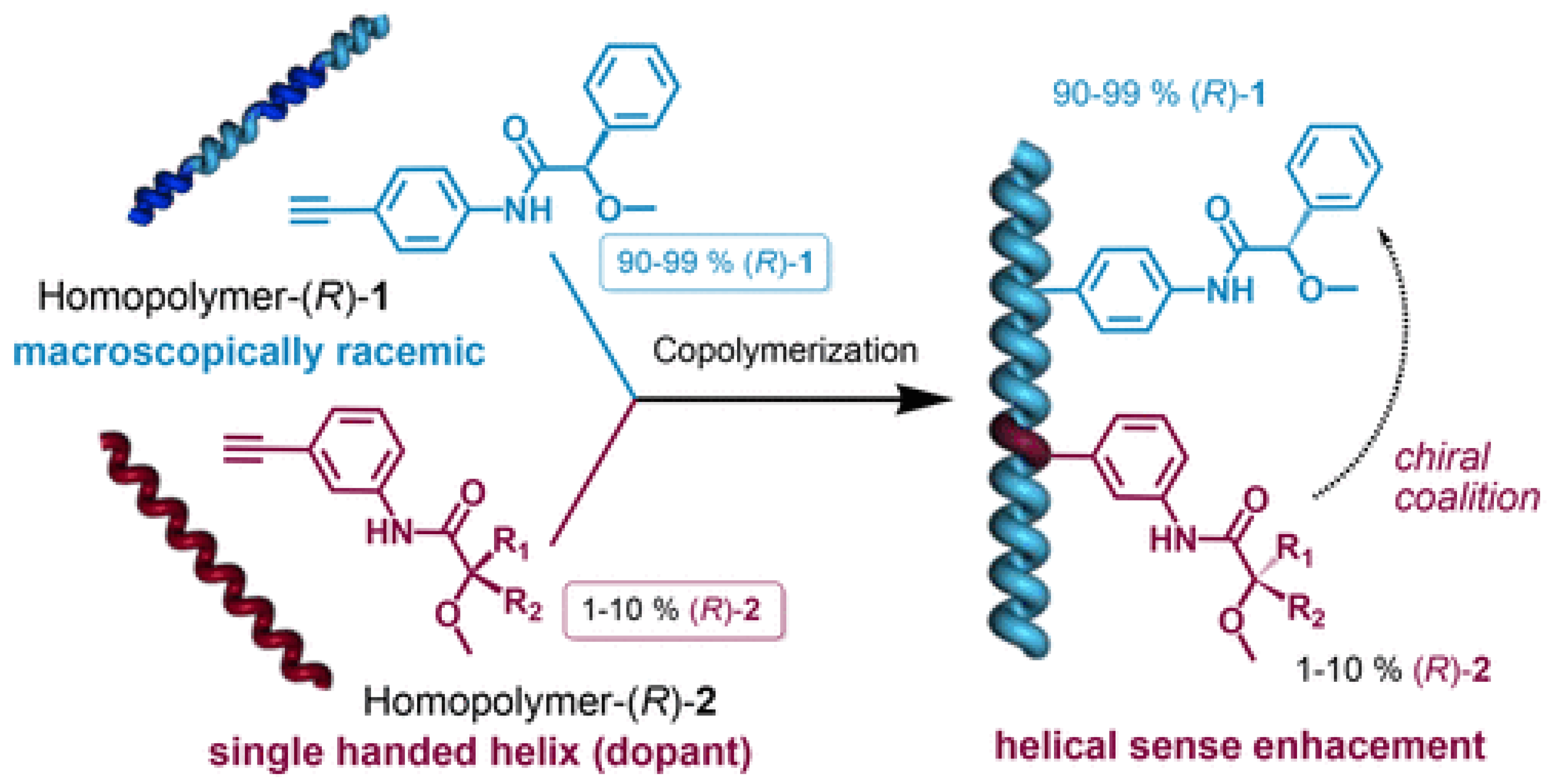
2.2. Collective Chirality
2.3. Induced Chirality
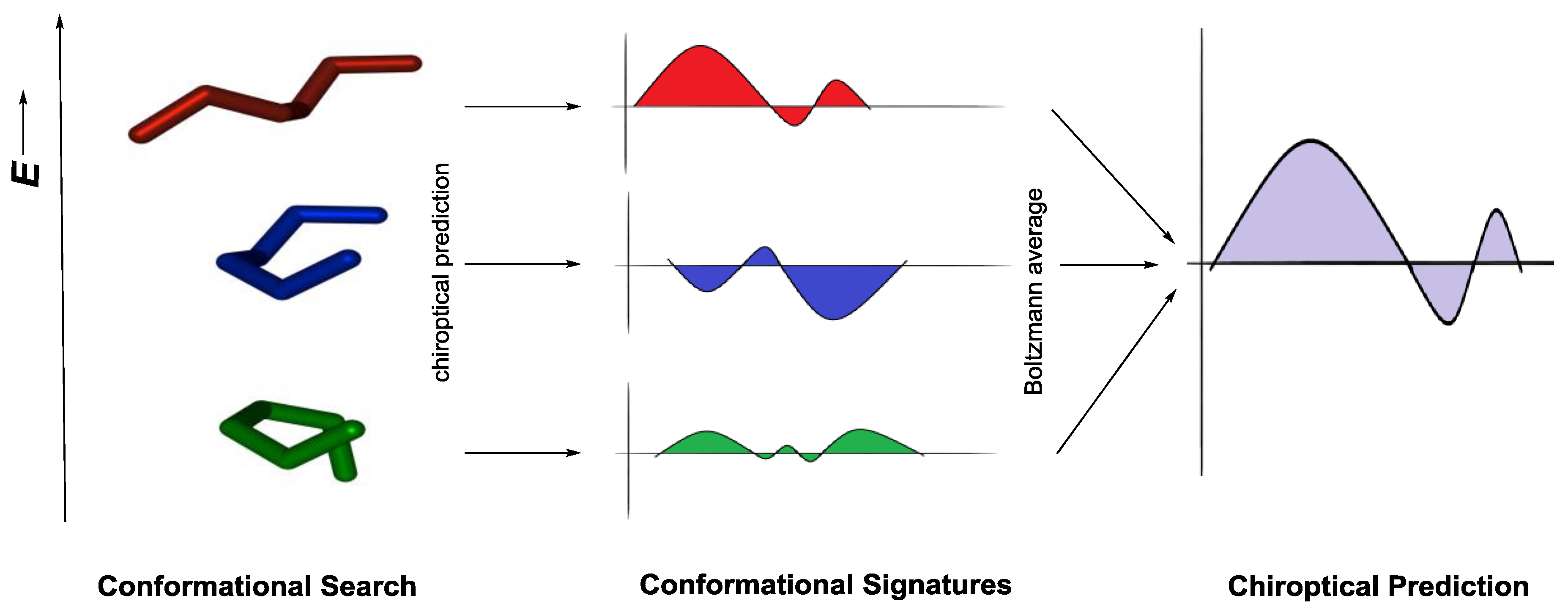
3. Approaches for the Prediction of Chiroptical Responses
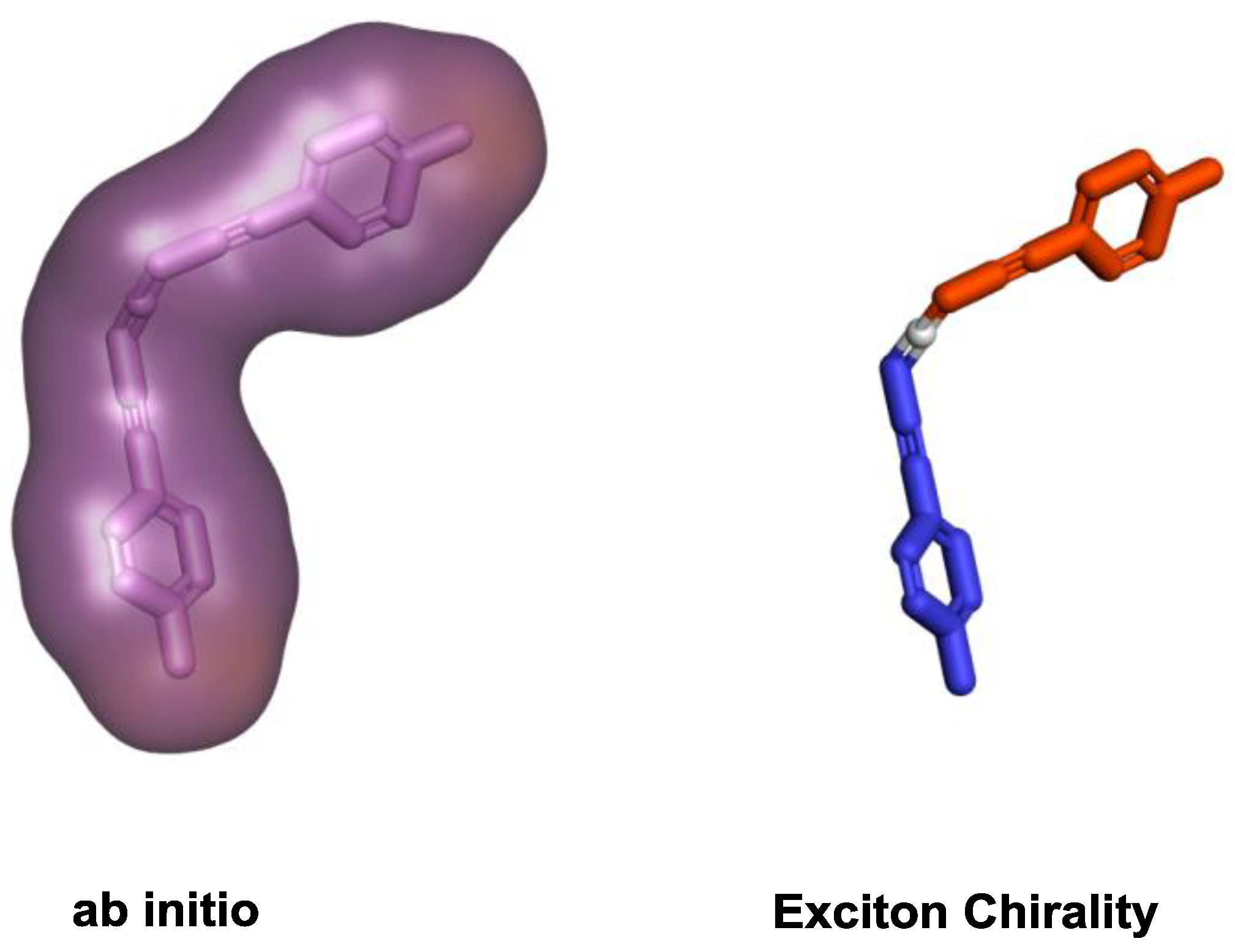
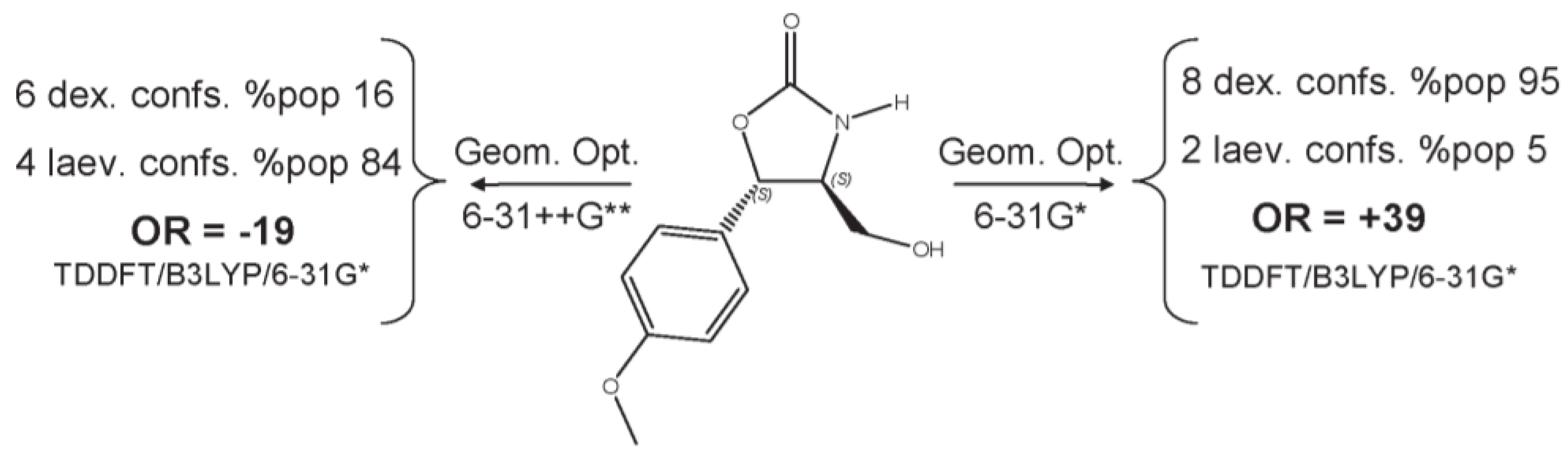
3.1. Ab Initio
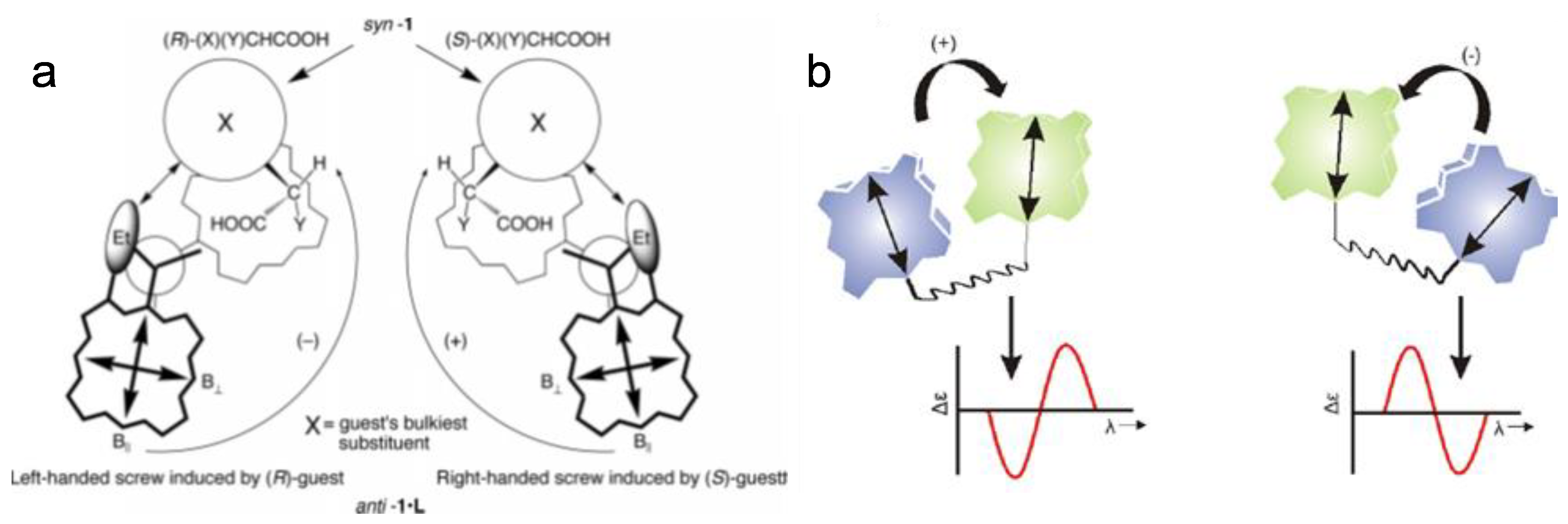
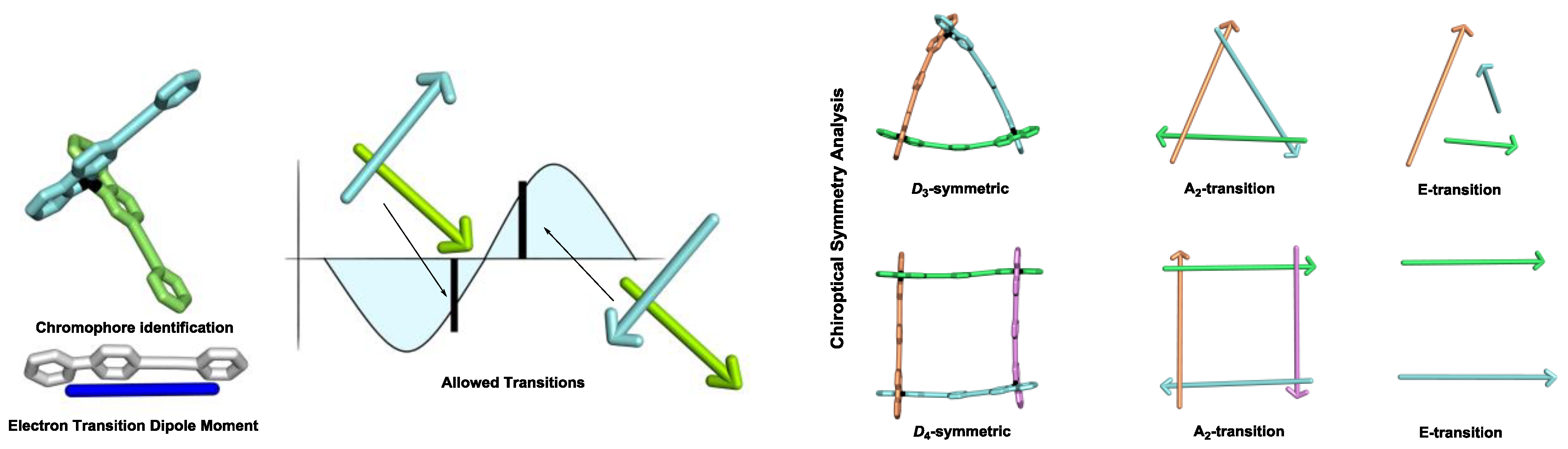
3.2. Exciton Chirality
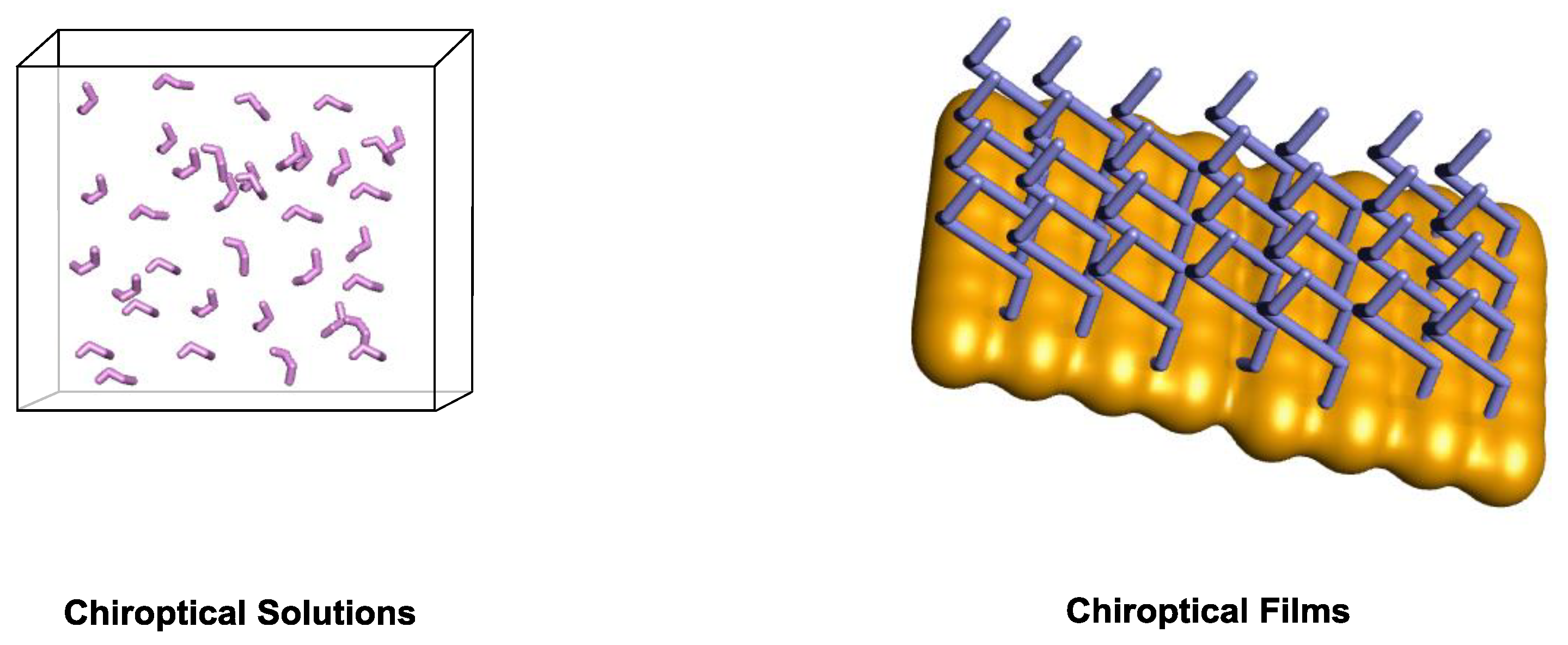
4. Chiroptical Systems on Different States of Matter
4.1. Chiroptical Solutions
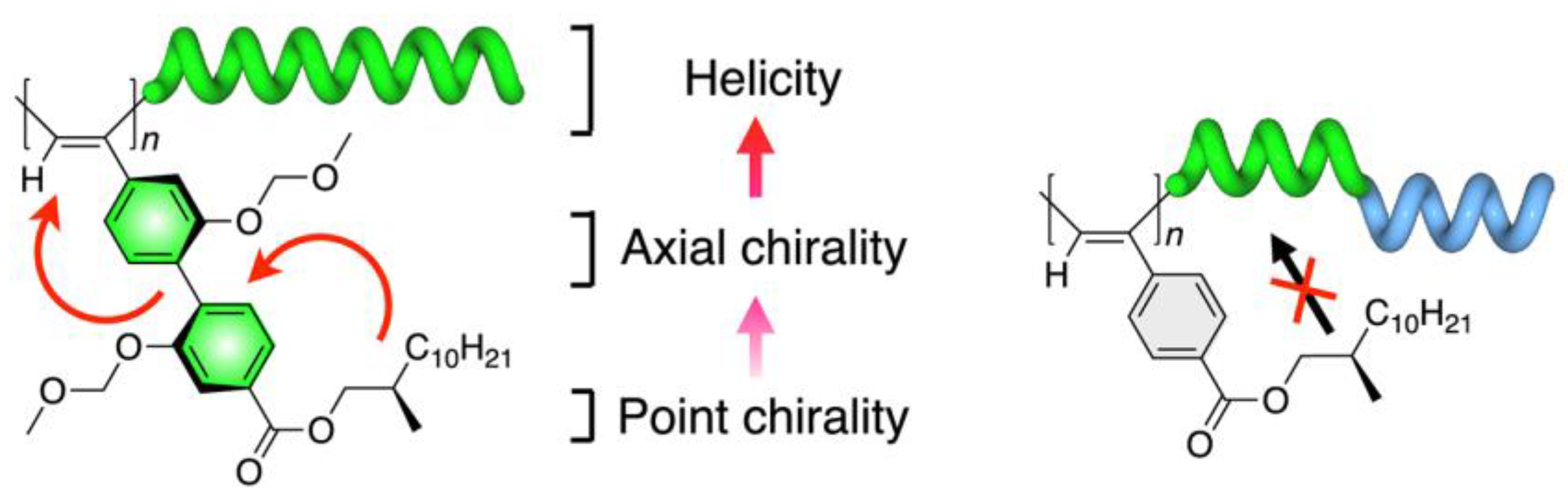
4.2. Two-dimensional (2D) Chiroptical Surfaces
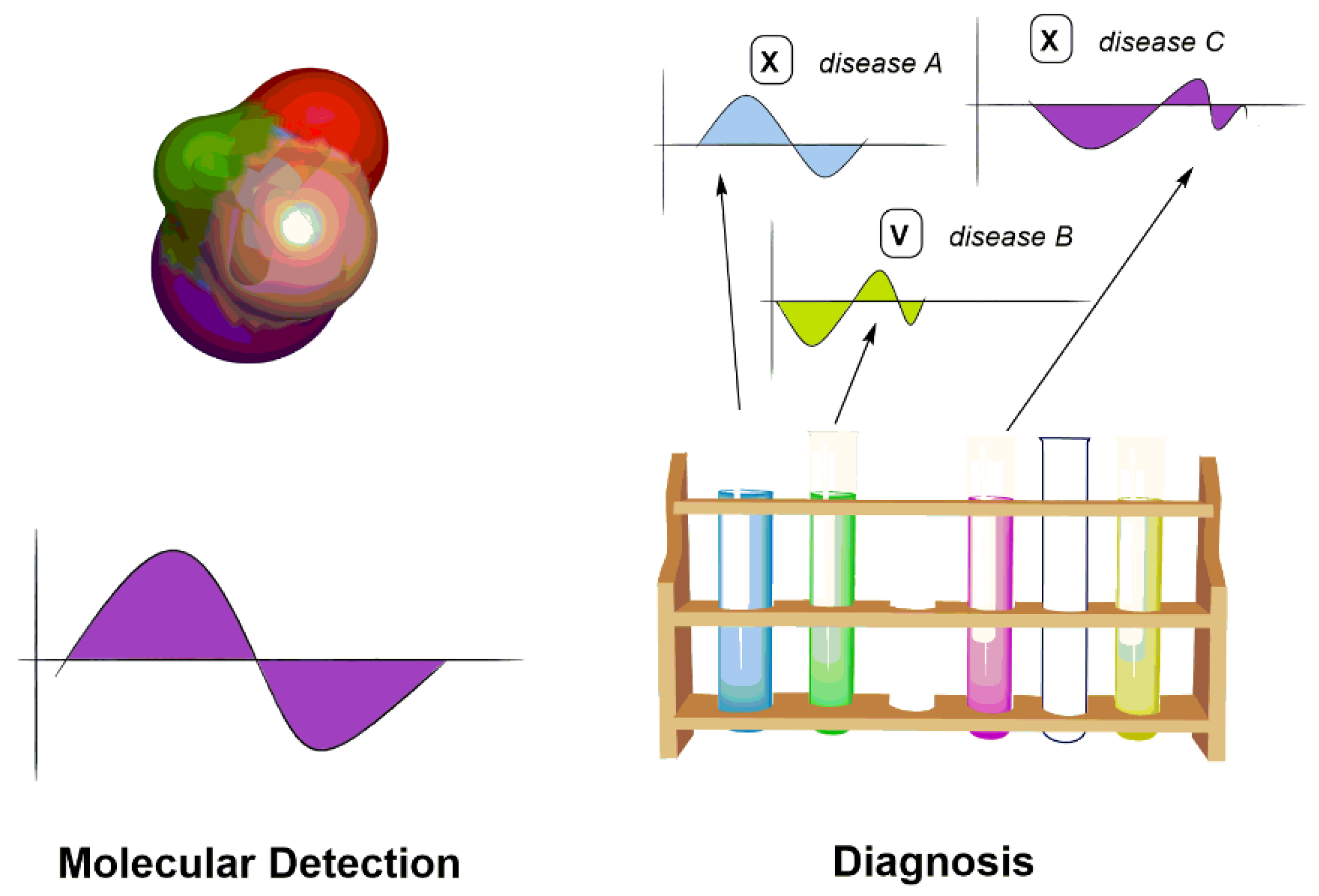
5. Chiroptical Sensing Applications
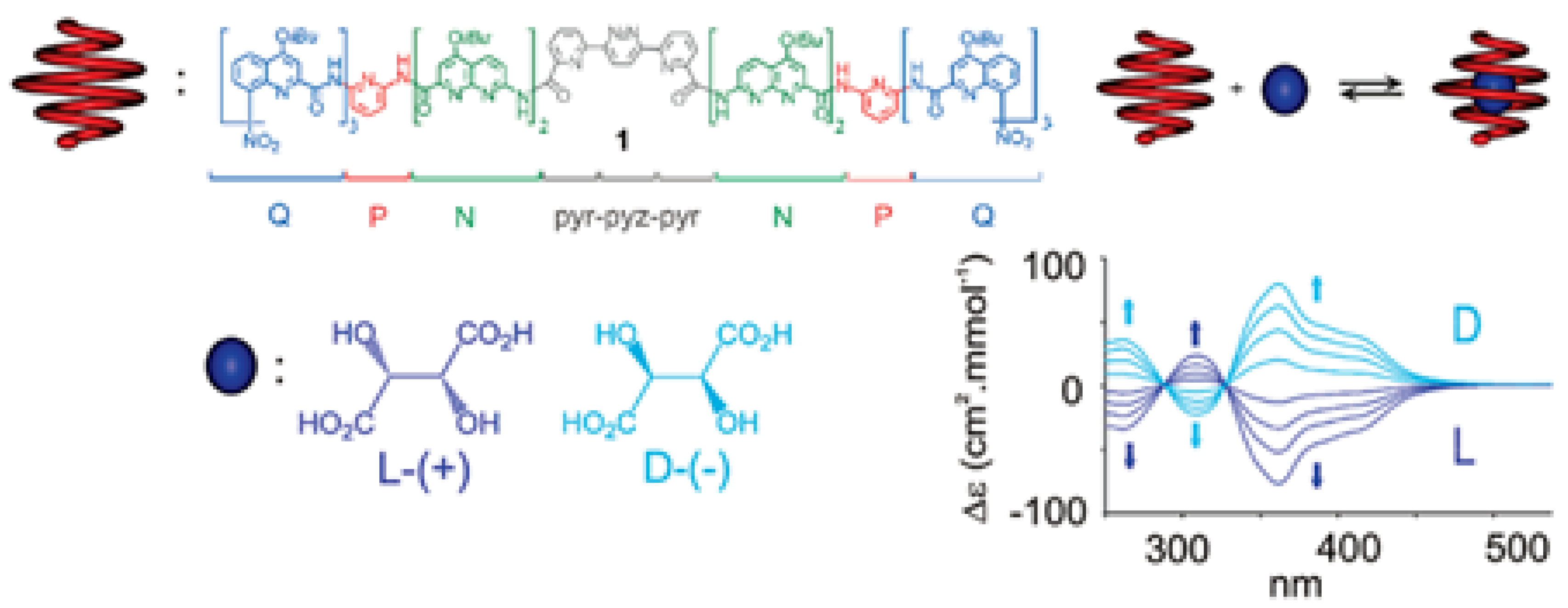
5.1. Chiroptical Molecular Detection
5.2. Chiroptical Diagnosis
6. Conclusions and Perspectives
Funding
Acknowledgments
Conflicts of Interest
References
- Riehl, J.P. Mirror-Image Asymmetry: An Introduction to the Origin and Consequences of Chirality; Wiley: Hoboken, NJ, USA, 2010; ISBN 9780470387597. [Google Scholar]
- Berova, N.; Alonso-Gómez, J.L.; Petrovic, A.G. Structure Elucidation in Organic Chemistry: The Search for the Right Tools. In Structure Elucidation in Organic Chemistry: The Search for the Right Tools; Cid, M.M., Bravo, J., Eds.; Wiley: Weinheim, Germany, 2015; pp. 65–100. ISBN 9783527664610. [Google Scholar]
- Gal, J. Louis Pasteur, language, and molecular chirality. I. Background and dissymmetry. Chirality 2011, 23, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Stephens, T.D.; Bunde, C.J.; Fillmore, B.J. Mechanism of action in thalidomide teratogenesis. Biochem. Pharmacol. 2000, 59, 1489–1499. [Google Scholar] [CrossRef]
- Pescitelli, G.; Di Bari, L.; Berova, N. Application of electronic circular dichroism in the study of supramolecular systems. Chem. Soc. Rev. 2014, 43, 5211–5233. [Google Scholar] [CrossRef] [PubMed]
- Petrovic, A.G.; Berova, N.; Alonso-Gómez, J.L. Absolute Configuration and Conformational Analysis of Chiral Compounds via Experimental and Theoretical Prediction of Chiroptical Properties: ORD, ECD, and VCD; Wiley: Weinheim, Germany, 2015; ISBN 9783527664610. [Google Scholar]
- Nakanishi, K.; Berova, N.; Polavarapu, P.L.; Woody, R.W. Comprehensive Chiroptical Spectroscopy, Volume 1, Instrumentation, Methodologies, and Theoretical Simulations; Wiley-VCH Verlag: Hoboken, NJ, USA, 2013. [Google Scholar]
- Barron, L.D. Molecular Light Scattering and Optical Activity; Cambridge University Press: New York, NY, USA, 2004. [Google Scholar]
- Bentley, K.W.; Wolf, C. Comprehensive Chirality Sensing: Development of Stereodynamic Probes with a Dual (Chir)optical Response. J. Org. Chem. 2014, 79, 6517–6531. [Google Scholar] [CrossRef] [PubMed]
- Rivera-Fuentes, P.; Alonso-Gómez, J.L.; Petrovic, A.G.; Santoro, F.; Harada, N.; Berova, N.; Diederich, F. Amplification of chirality in monodisperse, enantiopure alleno-acetylenic oligomers. Angew. Chem. Int. Ed. 2010, 49, 2247–2250. [Google Scholar] [CrossRef]
- Polavarapu, P.L. Why is it important to simultaneously use more than one chiroptical spectroscopic method for determining the structures of chiral molecules? Chirality 2008, 20, 664–672. [Google Scholar] [CrossRef]
- Polavarapu, P.L. Molecular structure determination using chiroptical spectroscopy: Where we may go wrong? Chirality 2012, 24, 909–920. [Google Scholar] [CrossRef]
- Comprehensive Chiroptical Spectroscopy, Instrumentation, Methodologies, and Theoretical Simulations; Wiley: Hoboken, NJ, USA, 2012; Volume 1, ISBN 1118120175.
- Lassen, P.R.; Skytte, D.M.; Hemmingsen, L.; Nielsen, S.F.; Freedman, T.B.; Nafie, L.A.; Christensen, S.B. Structure and absolute configuration of nyasol and hinokiresinol via synthesis and vibrational circular dichroism spectroscopy. J. Nat. Prod. 2005, 68, 1603–1609. [Google Scholar] [CrossRef]
- Petrovic, A.G.; Navarro-Vazquez, A.; Alonso-Gomez, J.L. ChemInform Abstract: From Relative to Absolute Configuration of Complex Natural Products. Interplay between NMR, ECD, VCD, and ORD Assisted by ab initio Calculations. Curr. Org. Chem. 2010, 1612–1628. [Google Scholar] [CrossRef]
- Daigle, M.; Miao, D.; Lucotti, A.; Tommasini, M.; Morin, J.-F. Helically Coiled Graphene Nanoribbons. Angew. Chem. Int. Ed. 2017. [Google Scholar] [CrossRef]
- Freire, F.; Seco, J.M.; Quiñoá, E.; Riguera, R. Chiral Amplification and Helical-Sense Tuning by Mono- and Divalent Metals on Dynamic Helical Polymers. Angew. Chem. Int. Ed. 2011, 50, 11692–11696. [Google Scholar] [CrossRef] [PubMed]
- Jeong, H.H.; Alarcón-Correa, M.; Mark, A.G.; Son, K.; Lee, T.C.; Fischer, P. Corrosion-Protected Hybrid Nanoparticles. Adv. Sci. 2017, 4, 1700234. [Google Scholar] [CrossRef]
- Iavicoli, P.; Xu, H.; Feldborg, L.N.; Linares, M.; Paradinas, M.; Stafström, S.; Ocal, C.; Nieto-Ortega, B.; Casado, J.; López Navarrete, J.T.; et al. Tuning the supramolecular chirality of one- and two-dimensional aggregates with the number of stereogenic centers in the component porphyrins. J. Am. Chem. Soc. 2010, 132, 9350–9362. [Google Scholar] [CrossRef] [PubMed]
- Guerrero-Martínez, A.; Auguié, B.; Alonso-Gómez, J.L.; Džolić, Z.; Gómez-Graña, S.; Žinić, M.; Cid, M.M.; Liz-Marzán, L.M.; Džolič, Z.; Gómez-Grańa, S.; et al. Intense optical activity from three-dimensional chiral ordering of plasmonic nanoantennas. Angew. Chem. Int. Ed. 2011, 50, 5499–5503. [Google Scholar] [CrossRef] [PubMed]
- Míguez-Lago, S.; Llamas-Saiz, A.L.; Magdalena Cid, M.; Alonso-Gómez, J.L. A Covalent Organic Helical Cage with Remarkable Chiroptical Amplification. Chem.-A Eur. J. 2015, 21, 18085–18088. [Google Scholar] [CrossRef]
- Wang, Z.; Cheng, F.; Winsor, T.; Liu, Y. Optical chiral metamaterials: A review of the fundamentals, fabrication methods and applications. Nanotechnology 2016, 27, 412001. [Google Scholar] [CrossRef]
- Suárez-Picado, E.; Quiñoá, E.; Riguera, R.; Freire, F. Poly(phenylacetylene) Amines: A General Route to Water-Soluble Helical Polyamines. Chem. Mater. 2018, 30, 6908–6914. [Google Scholar] [CrossRef]
- Castro-Fernández, S.; Yang, R.; García, A.P.; Garzón, I.L.; Xu, H.; Petrovic, A.G.; Alonso-Gómez, J.L. Diverse Chiral Scaffolds from Diethynylspiranes: All-Carbon Double Helices and Flexible Shape-Persistent Macrocycles. Chem.-A Eur. J. 2017, 23, 11747–11751. [Google Scholar] [CrossRef]
- Gidron, O.; Ebert, M.-O.; Trapp, N.; Diederich, F. Chiroptical detection of nonchromophoric, achiral guests by enantiopure alleno-acetylenic helicages. Angew. Chem. Int. Ed. 2014, 53, 13614–13618. [Google Scholar] [CrossRef]
- Si, S.; Gautier, C.; Boudon, J.; Taras, R.; Gladiali, S.; Bürgi, T. Ligand exchange on Au25 cluster with chiral thiols. J. Phys. Chem. C 2009, 113, 12966–12969. [Google Scholar] [CrossRef]
- Guerrero-Martínez, A.; Alonso-Gómez, J.L.J.L.; Auguié, B.; Cid, M.M.M.; Liz-Marzán, L.M.L.M. From individual to collective chirality in metal nanoparticles. Nano Today 2011, 6, 381–400. [Google Scholar] [CrossRef]
- Shao, K.; Lv, Z.; Xiong, Y.; Li, G.; Wang, D.; Zhang, H.; Qing, G. Circularly polarized light modulated supramolecular self-assembly for an azobenzene-based chiral gel. RSC Adv. 2019, 9, 10360–10363. [Google Scholar] [CrossRef]
- Cheng, J.; Le Saux, G.; Gao, J.; Buffeteau, T.; Battie, Y.; Barois, P.; Ponsinet, V.; Delville, M.-H.; Ersen, O.; Pouget, E.; et al. GoldHelix: Gold Nanoparticles Forming 3D Helical Superstructures with Controlled Morphology and Strong Chiroptical Property. ACS Nano 2017, 11, 3806–3818. [Google Scholar] [CrossRef] [PubMed]
- Gellman, S.H. Foldamers: A Manifesto. Acc. Chem. Res. 1998, 31, 173–180. [Google Scholar] [CrossRef]
- Li, C.Z.; Jiang, X.K.; Li, Z.T.; Gao, X.; Wang, Q.R. Foldamer-based molecular recognition. Chinese J. Org. Chem. 2007, 27, 188–196. [Google Scholar]
- Prince, R.B.; Barnes, S.A.; Moore, J.S. Foldamer-Based Molecular Recognition. J. Am. Chem. Soc. 2000, 122, 2758–2762. [Google Scholar] [CrossRef]
- Ferrand, Y.; Kendhale, A.M.; Kauffmann, B.; Grélard, A.; Marie, C.; Blot, V.; Pipelier, M.; Dubreuil, D.; Huc, I. Diastereoselective encapsulation of tartaric acid by a helical aromatic oligoamide. J. Am. Chem. Soc. 2010, 132, 7858–7859. [Google Scholar] [CrossRef]
- Valderrey, V.; Aragay, G.; Ballester, P. Porphyrin tweezer receptors: Binding studies, conformational properties and applications. Coord. Chem. Rev. 2014, 258–259, 137–156. [Google Scholar] [CrossRef]
- Berova, N.; Pescitelli, G.; Petrovic, A.G.; Proni, G. Probing molecular chirality by CD-sensitive dimeric metalloporphyrin hosts. Chem. Commun. 2009, 5958–5980. [Google Scholar] [CrossRef]
- Bhyrappa, P.; Borovkov, V.V.; Inoue, Y. Supramolecular Chirogenesis in Bis-porphyrins: Interaction with Chiral Acids and Application for the Absolute Configuration Assignment. Org. Lett. 2007, 9, 433–435. [Google Scholar] [CrossRef]
- Borovkov, V.; Yamamoto, T.; Higuchi, H.; Inoue, Y. Supramolecular Chirogenesis in Weakly Interacting Hosts: Role of the Temperature, Structural, and Electronic Factors in Enhancement of Chiroptical Sensitivity. Org. Lett. 2008, 10, 1283–1286. [Google Scholar] [CrossRef] [PubMed]
- Ikeda, C.; Zin, S.Y.; Park, M.; Inoue, H.; Kim, D.; Osuka, A. Helicity induction and two-photon absorbance enhancement in zinc(II) meso-meso linked porphyrin oligomers via intermodular hydrogen bonding interactions. J. Am. Chem. Soc. 2005, 127, 534–535. [Google Scholar] [CrossRef] [PubMed]
- Míguez-Lago, S.; Cid, M.M.; Alonso-Gómez, J.L. Covalent Organic Helical Cages as Sandwich Compound Containers. Eur. J. Org. Chem. 2016, 2016, 5716–5721. [Google Scholar] [CrossRef]
- Ajayaghosh, A.; Varghese, R.; Mahesh, S.; Praveen, V.K. From vesicles to helical nanotubes: A sergeant-and-soldiers effect in the self-assembly of oligo(p-phenyleneethynylene)s. Angew. Chem. Int. Ed. 2006, 45, 7729–7732. [Google Scholar] [CrossRef]
- Pal, D.S.; Kar, H.; Ghosh, S. Controllable supramolecular polymerization: Via a chain-growth mechanism. Chem. Commun. 2018, 54, 928–931. [Google Scholar] [CrossRef]
- Ishidate, R.; Markvoort, A.J.; Maeda, K.; Yashima, E. Unexpectedly Strong Chiral Amplification of Chiral/Achiral and Chiral/Chiral Copolymers of Biphenylylacetylenes and Further Enhancement/Inversion and Memory of the Macromolecular Helicity. J. Am. Chem. Soc. 2019, 141, 7605–7614. [Google Scholar] [CrossRef]
- Wen, T.; Shen, H.Y.; Wang, H.F.; Mao, Y.C.; Chuang, W.T.; Tsai, J.C.; Ho, R.M. Controlled Handedness of Twisted Lamellae in Banded Spherulites of Isotactic Poly(2-vinylpyridine) as Induced by Chiral Dopants. Angew. Chem. Int. Ed. 2015, 54, 14313–14316. [Google Scholar] [CrossRef]
- Arias, S.; Rodríguez, R.; Quiñoá, E.; Riguera, R.; Freire, F. Chiral Coalition in Helical Sense Enhancement of Copolymers: The Role of the Absolute Configuration of Comonomers. J. Am. Chem. Soc. 2018, 140, 667–674. [Google Scholar] [CrossRef]
- Pescitelli, G.; Di Bari, L. Revision of the Absolute Configuration of Preussilides A-F Established by the Exciton Chirality Method. J. Nat. Prod. 2017, 80, 2855–2859. [Google Scholar] [CrossRef]
- Asai, T.; Taniguchi, T.; Yamamoto, T.; Monde, K.; Oshima, Y. Structures of spiroindicumides a and B, unprecedented carbon skeletal spirolactones, and determination of the absolute configuration by vibrational circular dichroism exciton approach. Org. Lett. 2013, 15, 4320–4323. [Google Scholar] [CrossRef]
- Covington, C.L.; Nicu, V.P.; Polavarapu, P.L. Determination of the Absolute Con fi gurations Using Exciton Chirality Method for Vibrational Circular Dichroism: Right Answers for the Wrong Reasons? J. Phys. Chem. A 2015, 119, 10589–10601. [Google Scholar] [CrossRef] [PubMed]
- Hentschel, M.; Schäferling, M.; Duan, X.; Giessen, H.; Liu, N. Chiral plasmonics. Sci. Adv. 2017, 3, 1–13. [Google Scholar] [CrossRef]
- Noumeur, S.R.; Helaly, S.E.; Jansen, R.; Gereke, M.; Stradal, T.E.B.; Harzallah, D.; Stadler, M. Preussilides A-F, Bicyclic Polyketides from the Endophytic Fungus Preussia similis with Antiproliferative Activity. J. Nat. Prod. 2017, 80, 1531–1540. [Google Scholar] [CrossRef] [PubMed]
- Pecul, M.; Ruud, K. The Ab Initio Calculation of Optical Rotation and Electronic Circular Dichroism. Adv. Quantum Chem. 2005, 50, 185–212. [Google Scholar] [CrossRef]
- Crawford, T.D. Ab initio calculation of molecular chiroptical properties. Theor. Chem. Acc. 2005, 115, 227–245. [Google Scholar] [CrossRef]
- Polavarapu, P.L. Renaissance in chiroptical spectroscopic methods for molecular structure determination. Chem. Rec. 2007, 7, 125–136. [Google Scholar] [CrossRef]
- Autschbach, J. Computing chiroptical properties with first-principles theoretical methods: Background and illustrative examples. Chirality 2009, 21, E116–E152. [Google Scholar] [CrossRef]
- Pescitelli, G.; Bruhn, T. Good Computational Practice in the Assignment of Absolute Configurations by TDDFT Calculations of ECD Spectra. Chirality 2016, 28, 466–474. [Google Scholar] [CrossRef]
- Zuber, G.; Goldsmith, M.R.; Hopkins, T.D.; Beratan, D.N.; Wipf, P. Systematic assignment of the configuration of flexible natural products by spectroscopic and computational methods: The bistramide C analysis. Org. Lett. 2005, 7, 5269–5272. [Google Scholar] [CrossRef]
- Johnson, J.L.; Raghavan, V.; Cimmino, A.; Moeini, A.; Petrovic, A.G.; Santoro, E.; Superchi, S.; Berova, N.; Evidente, A.; Polavarapu, P.L. Absolute configurations of chiral molecules with multiple stereogenic centers without prior knowledge of the relative configurations: A case study of inuloxin C. Chirality 2018, 30, 1206–1214. [Google Scholar] [CrossRef]
- Brémond, E.; Savarese, M.; Adamo, C.; Jacquemin, D. Accuracy of TD-DFT Geometries: A Fresh Look. J. Chem. Theory Comput. 2018, 14, 3715–3727. [Google Scholar] [CrossRef]
- Berardozzi, R.; Guido, C.A.; Capozzi, M.A.M.; Cardellicchio, C.; Di Bari, L.; Pescitelli, G. Circular Dichroism and TDDFT Investigation of Chiral Fluorinated Aryl Benzyl Sulfoxides. Eur. J. Org. Chem. 2015, 5554–5562. [Google Scholar] [CrossRef]
- Bruhn, T.; Witterauf, F.; Götz, D.C.G.; Grimmer, C.T.; Würtemberger, M.; Radius, U.; Bringmann, G. C,C- and N,C-coupled dimers of 2-aminotetraphenylporphyrins: Regiocontrolled synthesis, spectroscopic properties, and quantum-chemical calculations. Chem.-A Eur. J. 2014, 20, 3998–4006. [Google Scholar] [CrossRef] [PubMed]
- Le Guennic, B.; Hieringer, W.; Görling, A.; Autschbach, J. Density functional calculation of the electronic circular dichroism spectra of the transition metal complexes [M(phen)3]2+ (M = Fe, Ru, Os). J. Phys. Chem. A 2005, 109, 4836–4846. [Google Scholar] [CrossRef] [PubMed]
- Brémond, É.; Savarese, M.; Su, N.Q.; Pérez-Jiménez, Á.J.; Xu, X.; Sancho-García, J.C.; Adamo, C. Benchmarking Density Functionals on Structural Parameters of Small-/Medium-Sized Organic Molecules. J. Chem. Theory Comput. 2016, 12, 459–465. [Google Scholar] [CrossRef]
- Howard, J.C.; Sowndarya, S.V.; Ansari, I.M.; Mach, T.J.; Baranowska-ŁAczkowska, A.; Crawford, T.D. Performance of Property-Optimized Basis Sets for Optical Rotation with Coupled Cluster Theory. J. Phys. Chem. A 2018, 122, 5962–5969. [Google Scholar] [CrossRef]
- Mazzeo, G.; Giorgio, E.; Zanasi, R.; Berova, N.; Rosini, C. Absolute configuration through the DFT simulation of the optical rotation. Importance of the correct selection of the input geometry: A caveat. J. Org. Chem. 2010, 75, 4600–4603. [Google Scholar] [CrossRef]
- Mennucci, B.; Cappelli, C.; Cammi, R.; Tomasi, J. Modeling solvent effects on chiroptical properties. Chirality 2011, 23, 717–729. [Google Scholar] [CrossRef]
- Petrovic, A.G.; Vantomme, G.; Negrón-Abril, Y.L.; Lubian, E.; Saielli, G.; Menegazzo, I.; Cordero, R.; Proni, G.; Nakanishi, K.; Carofiglio, T.; et al. Bulky melamine-based Zn-porphyrin tweezer as a CD probe of molecular chirality. Chirality 2011, 23, 808–819. [Google Scholar] [CrossRef]
- Troche-Pesqueira, E.; Pérez-Juste, I.; Navarro-Vázquez, A.; Cid, M.M. A β-cyclodextrin–resveratrol inclusion complex and the role of geometrical and electronic effects on its electronic induced circular dichroism. RSC Adv. 2013, 3, 10242. [Google Scholar] [CrossRef]
- Giner-Casares, J.J.; Liz-Marzán, L.M. Plasmonic nanoparticles in 2D for biological applications: Toward active multipurpose platforms. Nano Today 2014, 9, 365–377. [Google Scholar] [CrossRef]
- Tang, L.; Li, S.; Xu, L.; Ma, W.; Kuang, H.; Wang, L.; Xu, C. Chirality-based Au@Ag Nanorod Dimers Sensor for Ultrasensitive PSA Detection. ACS Appl. Mater. Interfaces 2015, 7, 12708–12712. [Google Scholar] [CrossRef]
- Perera, A.S.; Thomas, J.; Poopari, M.R.; Xu, Y. The clusters-in-a-liquid approach for solvation: New insights from the conformer specific gas phase spectroscopy and vibrational optical activity spectroscopy. Front. Chem. 2016, 4, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Lipparini, F.; Egidi, F.; Cappelli, C.; Barone, V. The optical rotation of methyloxirane in aqueous solution: A never ending story? J. Chem. Theory Comput. 2013, 9, 1880–1884. [Google Scholar] [CrossRef]
- Kumar, J.; Eraña, H.; López-Martínez, E.; Claes, N.; Martín, V.F.; Solís, D.M.; Bals, S.; Cortajarena, A.L.; Castilla, J.; Liz-Marzán, L.M. Detection of amyloid fibrils in Parkinson’s disease using plasmonic chirality. Proc. Natl. Acad. Sci. USA 2018, 115, 3225–3230. [Google Scholar] [CrossRef]
- Covington, C.L.; Polavarapu, P.L. Similarity in dissymmetry factor spectra: A quantitative measure of comparison between experimental and predicted vibrational circular dichroism. J. Phys. Chem. A 2013, 117, 3377–3386. [Google Scholar] [CrossRef]
- Junior, F.M.S.; Covington, C.L.; De Amorim, M.B.; Velozo, L.S.M.; Kaplan, M.A.C.; Polavarapu, P.L. Absolute configuration of a rare sesquiterpene: (+)-3-ishwarone. J. Nat. Prod. 2014, 77, 1881–1886. [Google Scholar] [CrossRef]
- Johnson, J.L.; Sadasivan Nair, D.; Muraleedharan Pillai, S.; Johnson, D.; Kallingathodi, Z.; Ibnusaud, I.; Polavarapu, P.L. Dissymmetry Factor Spectral Analysis Can Provide Useful Diastereomer Discrimination: Chiral Molecular Structure of an Analogue of (−)-Crispine A. ACS Omega 2019, 4, 6154–6164. [Google Scholar] [CrossRef] [PubMed]
- Harada, N.; Nakanishi, K. Exciton chirality method and its application to configurational and conformational studies of natural products. Acc. Chem. Res. 1972, 5, 257–263. [Google Scholar] [CrossRef]
- Berova, N.; Di Bari, L.; Pescitelli, G.; Di Bari, L.; Pescitelli, G. Application of electronic circular dichroism in configurational and conformational analysis of organic compounds. Chem. Soc. Rev. 2007, 36, 914–931. [Google Scholar] [CrossRef] [PubMed]
- Castro-Fernández, S.; Peña-Gallego, Á.; Mosquera, R.A.; Alonso-Gómez, J.L. Chiroptical symmetry analysis: Exciton Chirality-Based formulae to understand the chiroptical responses of Cn and Dn symmetric systems. Molecules 2019, 24, 141. [Google Scholar] [CrossRef] [PubMed]
- Ozcelik, A.; Pereira-Cameselle, R.; Mosquera, R.A.; Peña-Gallego, Á.; Alonso-Gómez, J.L. Chiroptical Symmetry Analysis of Trianglimines: A Case Study. Symmetry 2019, 11, 1245. [Google Scholar] [CrossRef]
- Walters, R.S.; Kraml, C.M.; Byrne, N.; Ho, D.M.; Qin, Q.; Coughlin, F.J.; Bernhard, S.; Pascal, R.A. Configurationally stable longitudinally twisted polycyclic aromatic compounds. J. Am. Chem. Soc. 2008, 130, 16435–16441. [Google Scholar] [CrossRef] [PubMed]
- Alonso-Gómez, J.L.J.L.; Rivera-Fuentes, P.; Harada, N.; Berova, N.; Diederich, F. An enantiomerically pure alleno-acetylenic macrocycle: Synthesis and rationalization of its outstanding chiroptical response. Angew. Chem. Int. Ed. 2009, 48, 5545–5548. [Google Scholar] [CrossRef] [PubMed]
- Pearlstein, R.M.; Davis, R.C.; Ditson, S.L. Giant circular dichroism of high molecular weight. Proc. Natl. Acad. Sci. USA 1982, 79, 400–402. [Google Scholar] [CrossRef]
- Yao, J.; Wu, W.; Liang, W.; Feng, Y.; Zhou, D.; Chruma, J.J.; Fukuhara, G.; Mori, T.; Inoue, Y.; Yang, C. Temperature-Driven Planar Chirality Switching of a Pillar[5]arene-Based Molecular Universal Joint. Angew. Chem. Int. Ed. 2017, 56, 6869–6873. [Google Scholar] [CrossRef]
- Fan, C.; Yao, J.; Li, G.; Guo, C.; Wu, W.; Su, D.; Zhong, Z.; Zhou, D.; Wang, Y.; Chruma, J.J.; et al. Precise Manipulation of Temperature-Driven Chirality Switching of Molecular Universal Joints through Solvent Mixing. Chem.-A Eur. J. 2019, 25, 12526–12537. [Google Scholar] [CrossRef]
- Lieberman, I.; Shemer, G.; Fried, T.; Kosower, E.M.; Markovich, G. Plasmon-resonance-enhanced absorption and circular dichroism. Angew. Chem. Int. Ed. Engl. 2008, 47, 4855–4857. [Google Scholar] [CrossRef]
- White, S.J.; Johnson, S.D.; Sellick, M.A.; Bronowska, A.; Stockley, P.G.; Wälti, C. The influence of two-dimensional organization on peptide conformation. Angew. Chem. Int. Ed. 2015, 54, 974–978. [Google Scholar] [CrossRef]
- Zhang, Y.-Q.; Oner, M.A.; Cirera, B.; Palma, C.-A.; Castro-Fernández, S.; Míguez-Lago, S.; Cid, M.M.; Barth, J.V.; Alonso-Gómez, J.L.; Klappenberger, F.; et al. Morphological self-assembly of enantiopure allenes for upstanding chiral architectures at interfaces. Chem. Commun. 2014, 50, 15022–15025. [Google Scholar] [CrossRef]
- Ozcelik, A.; Pereira-Cameselle, R.; Von Weber, A.; Paszkiewicz, M.; Carlotti, M.; Paintner, T.; Zhang, L.; Lin, T.; Zhang, Y.-Q.; Barth, J.V.V.; et al. Device-Compatible Chiroptical Surfaces through Self-Assembly of Enantiopure Allenes. Langmuir 2018, 34, 4548–4553. [Google Scholar] [CrossRef] [PubMed]
- Ariga, K.; Richards, G.J.; Ishihara, S.; Izawa, H.; Hill, J.P. Intelligent chiral sensing based on supramolecular and interfacial concepts. Sensors 2010, 10, 6796–6820. [Google Scholar] [CrossRef] [PubMed]
- Hendry, E.; Carpy, T.; Johnston, J.; Popland, M.; Mikhaylovskiy, R.V.; Lapthorn, A.J.; Kelly, S.M.; Barron, L.D.; Gadegaard, N.; Kadodwala, M. Ultrasensitive detection and characterization of biomolecules using superchiral fields. Nat. Nanotechnol. 2010, 5, 783–787. [Google Scholar] [CrossRef] [PubMed]
- Kelly, C.; Tullius, R.; Lapthorn, A.J.; Gadegaard, N.; Cooke, G.; Barron, L.D.; Karimullah, A.S.; Rotello, V.M.; Kadodwala, M. Chiral Plasmonic Fields Probe Structural Order of Biointerfaces. J. Am. Chem. Soc. 2018, 140, 8509–8517. [Google Scholar] [CrossRef] [PubMed]
- Tullius, R.; Platt, G.W.; Khosravi Khorashad, L.; Gadegaard, N.; Lapthorn, A.J.; Rotello, V.M.; Cooke, G.; Barron, L.D.; Govorov, A.O.; Karimullah, A.S.; et al. Superchiral Plasmonic Phase Sensitivity for Fingerprinting of Protein Interface Structure. ACS Nano 2017, 11, 12049–12056. [Google Scholar] [CrossRef] [PubMed]
- Schäferling, M.; Dregely, D.; Hentschel, M.; Giessen, H. Tailoring Enhanced Optical Chirality: Design Principles for Chiral Plasmonic Nanostructures. Phys. Rev. X 2012, 2, 031010. [Google Scholar] [CrossRef]
- Zhao, Y.; Askarpour, A.N.; Sun, L.; Shi, J.; Li, X.; Alù, A. Chirality detection of enantiomers using twisted optical metamaterials. Nat. Commun. 2017, 8. [Google Scholar] [CrossRef] [PubMed]
- Yoo, S.; Park, Q.H. Metamaterials and chiral sensing: A review of fundamentals and applications. Nanophotonics 2019, 8, 249. [Google Scholar] [CrossRef]
- Grimsdale, A.C.; Müllen, K. The chemistry of organic nanomaterials. Angew. Chem. Int. Ed. 2005, 44, 5592–5629. [Google Scholar] [CrossRef]
- Monti, D.; Nardis, S.; Stefanelli, M.; Paolesse, R.; Di Natale, C.; D’Amico, A. Porphyrin-based nanostructures for sensing applications. J. Sens. 2009. [Google Scholar] [CrossRef]
- Stefanelli, M.; Magna, G.; Zurlo, F.; Caso, F.M.; Di Bartolomeo, E.; Antonaroli, S.; Venanzi, M.; Paolesse, R.; Di Natale, C.; Monti, D. Chiral Selectivity of Porphyrin-ZnO Nanoparticle Conjugates. ACS Appl. Mater. Interfaces 2019, 11, 12077–12087. [Google Scholar] [CrossRef] [PubMed]
- Dai, L.; Wu, W.; Liang, W.; Chen, W.; Yu, X.; Ji, J.; Xiao, C.; Yang, C. Enhanced chiral recognition by γ-cyclodextrin-cucurbit[6]uril-cowheeled [4]pseudorotaxanes. Chem. Commun. 2018, 54, 2643–2646. [Google Scholar] [CrossRef] [PubMed]
- Li, P.; Lü, B.; Han, D.; Duan, P.; Liu, M.; Yin, M. Stoichiometry-controlled inversion of circularly polarized luminescence in co-assembly of chiral gelators with an achiral tetraphenylethylene derivative. Chem. Commun. 2019, 55, 2194–2197. [Google Scholar] [CrossRef] [PubMed]
- Št’ovíčková, L.; Tatarkovič, M.; Logerová, H.; Vavřinec, J.; Setnička, V. Identification of spectral biomarkers for type 1 diabetes mellitus using the combination of chiroptical and vibrational spectroscopy. Analyst 2015, 140, 2266–2272. [Google Scholar] [CrossRef]
- Jeong, H.-H.; Mark, A.G.; Lee, T.-C.; Alarcn-Correa, M.; Eslami, S.; Qiu, T.; Gibbs, J.G.; Fischer, P. Active Nanorheology with Plasmonics. Nano Lett. 2016, 16, 4887–4894. [Google Scholar] [CrossRef]







© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ozcelik, A.; Pereira-Cameselle, R.; Poklar Ulrih, N.; Petrovic, A.G.; Alonso-Gómez, J.L. Chiroptical Sensing: A Conceptual Introduction. Sensors 2020, 20, 974. https://doi.org/10.3390/s20040974
Ozcelik A, Pereira-Cameselle R, Poklar Ulrih N, Petrovic AG, Alonso-Gómez JL. Chiroptical Sensing: A Conceptual Introduction. Sensors. 2020; 20(4):974. https://doi.org/10.3390/s20040974
Chicago/Turabian StyleOzcelik, Ani, Raquel Pereira-Cameselle, Natasa Poklar Ulrih, Ana G. Petrovic, and José Lorenzo Alonso-Gómez. 2020. "Chiroptical Sensing: A Conceptual Introduction" Sensors 20, no. 4: 974. https://doi.org/10.3390/s20040974
APA StyleOzcelik, A., Pereira-Cameselle, R., Poklar Ulrih, N., Petrovic, A. G., & Alonso-Gómez, J. L. (2020). Chiroptical Sensing: A Conceptual Introduction. Sensors, 20(4), 974. https://doi.org/10.3390/s20040974