Analysis of a Cantilevered Piezoelectric Energy Harvester in Different Orientations for Rotational Motion
Abstract
1. Introduction
2. Materials and Methods
2.1. Modeling of the Proposed PEH
2.2. Experimental Setup
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Roundy, S.; Wright, P.K.; Rabaey, J. A study of low level vibrations as a power source for wireless sensor nodes. Comput. Commun. 2003, 26, 1131–1144. [Google Scholar] [CrossRef]
- Roundy, S.; Wright, P.K. A piezoelectric vibration based generator for wireless electronics. Smart Mater. Struct. 2004, 13, 1131–1142. [Google Scholar] [CrossRef]
- Reilly, E.K.; Burghardt, F.; Fain, R.; Wright, P. Powering a wireless sensor node with a vibration-driven piezoelectric energy harvester. Smart Mater. Struct. 2011, 20. [Google Scholar] [CrossRef]
- Ng, T.H.; Liao, W.H. Sensitivity Analysis and Energy Harvesting for a Self-Powered Piezoelectric Sensor. J. Intell. Mater. Syst. Struct. 2005, 16, 785–797. [Google Scholar] [CrossRef]
- Amin Karami, M.; Inman, D.J. Powering pacemakers from heartbeat vibrations using linear and nonlinear energy harvesters. Appl. Phys. Lett. 2012, 100. [Google Scholar] [CrossRef]
- Hwang, G.T.; Park, H.; Lee, J.H.; Oh, S.; Park, K.I.; Byun, M.; Park, H.; Ahn, G.; Jeong, C.K.; No, K.; et al. Self-powered cardiac pacemaker enabled by flexible single crystalline PMN-PT piezoelectric energy harvester. Adv. Mater. 2014, 26, 4880–4887. [Google Scholar] [CrossRef]
- Paradiso, J.A.; Starner, T. Energy scavenging for mobile and wireless electronics. IEEE Pervasive Comput. 2005, 4, 18–27. [Google Scholar] [CrossRef]
- Cook-Chennault, K.A.; Thambi, N.; Sastry, A.M. Powering MEMS portable devices—A review of non-regenerative and regenerative power supply systems with special emphasis on piezoelectric energy harvesting systems. Smart Mater. Struct. 2008, 17. [Google Scholar] [CrossRef]
- Nechibvute, A.; Chawanda, A.; Luhanga, P. Piezoelectric Energy Harvesting Devices: An Alternative Energy Source for Wireless Sensors. Smart Mater. Res. 2012, 2012, 1–13. [Google Scholar] [CrossRef]
- Erturk, A.; Inman, D.J. Issues in mathematical modeling of piezoelectric energy harvesters. Smart Mater. Struct. 2008, 17. [Google Scholar] [CrossRef]
- Erturk, A.; Inman, D.J. A Distributed Parameter Electromechanical Model for Cantilevered Piezoelectric Energy Harvesters. J. Vib. Acoust. 2008, 130. [Google Scholar] [CrossRef]
- Yang, Y.; Tang, L. Equivalent Circuit Modeling of Piezoelectric Energy Harvesters. J. Intell. Mater. Syst. Struct. 2009, 20, 2223–2235. [Google Scholar] [CrossRef]
- Erturk, A.; Inman, D.J. On Mechanical Modeling of Cantilevered Piezoelectric Vibration Energy Harvesters. J. Intell. Mater. Syst. Struct. 2008, 19, 1311–1325. [Google Scholar] [CrossRef]
- Dietl, J.M.; Wickenheiser, A.M.; Garcia, E. A Timoshenko beam model for cantilevered piezoelectric energy harvesters. Smart Mater. Struct. 2010, 19. [Google Scholar] [CrossRef]
- Hu, Y.; Xue, H.; Hu, H. A piezoelectric power harvester with adjustable frequency through axial preloads. Smart Mater. Struct. 2007, 16, 1961–1966. [Google Scholar] [CrossRef]
- Eichhorn, C.; Goldschmidtboeing, F.; Woias, P. Bidirectional frequency tuning of a piezoelectric energy converter based on a cantilever beam. J. Micromech. Microeng. 2009, 19. [Google Scholar] [CrossRef]
- Al-Ashtari, W.; Hunstig, M.; Hemsel, T.; Sextro, W. Frequency tuning of piezoelectric energy harvesters by magnetic force. Smart Mater. Struct. 2012, 21. [Google Scholar] [CrossRef]
- Dong, L.; Prasad, M.G.; Fisher, F.T. Two-dimensional resonance frequency tuning approach for vibration-based energy harvesting. Smart Mater. Struct. 2016, 25. [Google Scholar] [CrossRef]
- Bouhedma, S.; Zheng, Y.; Lange, F.; Hohlfeld, D. Magnetic Frequency Tuning of a Multimodal Vibration Energy Harvester. Sensors 2019, 19, 1149. [Google Scholar] [CrossRef]
- Morel, A.; Pillonnet, G.; Gasnier, P.; Lefeuvre, E.; Badel, A. Frequency tuning of piezoelectric energy harvesters thanks to a short-circuit synchronous electric charge extraction. Smart Mater. Struct. 2019, 28. [Google Scholar] [CrossRef]
- Brenes, A.; Morel, A.; Gibus, D.; Yoo, C.S.; Gasnier, P.; Lefeuvre, E.; Badel, A. Large-bandwidth piezoelectric energy harvesting with frequency-tuning synchronized electric charge extraction. Sens. Actuators A Phys. 2020, 302. [Google Scholar] [CrossRef]
- Xue, T.; Ma, X.; Rahn, C.; Roundy, S. Analysis of Upper Bound Power Output for a Wrist-Worn Rotational Energy Harvester from Real-World Measured Inputs. J. Phys. Conf. Ser. 2014, 557. [Google Scholar] [CrossRef]
- Pillatsch, P.; Yeatman, E.M.; Holmes, A.S. A piezoelectric frequency up-converting energy harvester with rotating proof mass for human body applications. Sens. Actuators A Phys. 2014, 206, 178–185. [Google Scholar] [CrossRef]
- Ramezanpour, R.; Nahvi, H.; Ziaei-Rad, S. Increasing the Performance of a Rotary Piezoelectric Frequency Up-Converting Energy Harvester Under Weak Excitations. J. Vib. Acoust. 2016, 139. [Google Scholar] [CrossRef]
- Fu, H.; Yeatman, E.M. A methodology for low-speed broadband rotational energy harvesting using piezoelectric transduction and frequency up-conversion. Energy 2017, 125, 152–161. [Google Scholar] [CrossRef]
- Shu, Y.C.; Wang, W.C.; Chang, Y.P. Electrically rectified piezoelectric energy harvesting induced by rotary magnetic plucking. Smart Mater. Struct. 2018, 27. [Google Scholar] [CrossRef]
- Janphuang, P.; Lockhart, R.; Henein, S.; Briand, D.; de Rooij, N.F. On the experimental determination of the efficiency of piezoelectric impact-type energy harvesters using a rotational flywheel. J. Phys. Conf. Ser. 2013, 476. [Google Scholar] [CrossRef]
- Gu, L.; Livermore, C. Passive self-tuning energy harvester for extracting energy from rotational motion. Appl. Phys. Lett. 2010, 97, 081904. [Google Scholar] [CrossRef]
- Hsu, J.-C.; Tseng, C.-T.; Chen, Y.-S. Analysis and experiment of self-frequency-tuning piezoelectric energy harvesters for rotational motion. Smart Mater. Struct. 2014, 23, 075013. [Google Scholar] [CrossRef]
- Rui, X.; Zeng, Z.; Zhang, Y.; Li, Y.; Feng, H.; Huang, X.; Sha, Z. Design and Experimental Investigation of a Self-Tuning Piezoelectric Energy Harvesting System for Intelligent Vehicle Wheels. IEEE Trans. Veh. Technol. 2019. [Google Scholar] [CrossRef]
- Guan, M.; Liao, W.-H. Design and analysis of a piezoelectric energy harvester for rotational motion system. Energy Convers. Manag. 2016, 111, 239–244. [Google Scholar] [CrossRef]
- Gu, L.; Livermore, C. Compact passively self-tuning energy harvesting for rotating applications. Smart Mater. Struct. 2012, 21, 015002. [Google Scholar] [CrossRef]
- Wang, Y.-J.; Chuang, T.-Y.; Yu, J.-H. Design and kinetic analysis of piezoelectric energy harvesters with self-adjusting resonant frequency. Smart Mater. Struct. 2017, 26, 095037. [Google Scholar] [CrossRef]
- Hsieh, T.T.; Chen, S.A.; Shu, Y.-C. Investigation of various cantilever configurations for piezoelectric energy harvesting under rotational motion. In Proceedings of the SPIE 10967, Active and Passive Smart Structures and Integrated Systems XIII, Denver, CO, USA, 21 March 2019; p. 1096719. [Google Scholar]
- Sadeqi, S.; Arzanpour, S.; Hajikolaei, K.H. Broadening the Frequency Bandwidth of a Tire-Embedded Piezoelectric-Based Energy Harvesting System Using Coupled Linear Resonating Structure. IEEE/ASME Trans. Mechatron. 2015, 20, 2085–2094. [Google Scholar] [CrossRef]
- Febbo, M.; Machado, S.P.; Gatti, C.D.; Ramirez, J.M. An out-of-plane rotational energy harvesting system for low frequency environments. Energy Convers. Manag. 2017, 152, 166–175. [Google Scholar] [CrossRef]
- Ramírez, J.M.; Gatti, C.D.; Machado, S.P.; Febbo, M. A piezoelectric energy harvester for rotating environment using a linked E-shape multi-beam. Extrem. Mech. Lett. 2019, 27, 8–19. [Google Scholar] [CrossRef]
- Zhang, Y.; Zheng, R.; Kaizuka, T.; Su, D.; Nakano, K.; Cartmell, M.P. Broadband vibration energy harvesting by application of stochastic resonance from rotational environments. Eur. Phys. J. Spec. Top. 2015, 224, 2687–2701. [Google Scholar] [CrossRef]
- Guo, B.; Chen, Z.; Cheng, C.; Yang, Y. Characteristics of a nonlinear rotating piezoelectric energy harvester under variable rotating speeds. Int. J. Appl. Electromagn. Mech. 2015, 47, 411–423. [Google Scholar] [CrossRef]
- Chen, Z.; Guo, B.; Xiong, Y.; Cheng, C.; Yang, Y. Melnikov-method-based broadband mechanism and necessary conditions of nonlinear rotating energy harvesting using piezoelectric beam. J. Intell. Mater. Syst. Struct. 2016, 27, 2555–2567. [Google Scholar] [CrossRef]
- Cheng, C.; Chen, Z.; Xiong, Y.; Shi, H.; Yang, Y. A high-efficiency, self-powered nonlinear interface circuit for bi-stable rotating piezoelectric vibration energy harvesting with nonlinear magnetic force. Int. J. Appl. Electromagn. Mech. 2016, 51, 235–248. [Google Scholar] [CrossRef]
- Zou, H.-X.; Zhang, W.-M.; Li, W.-B.; Wei, K.-X.; Gao, Q.-H.; Peng, Z.-K.; Meng, G. Design and experimental investigation of a magnetically coupled vibration energy harvester using two inverted piezoelectric cantilever beams for rotational motion. Energy Convers. Manag. 2017, 148, 1391–1398. [Google Scholar] [CrossRef]
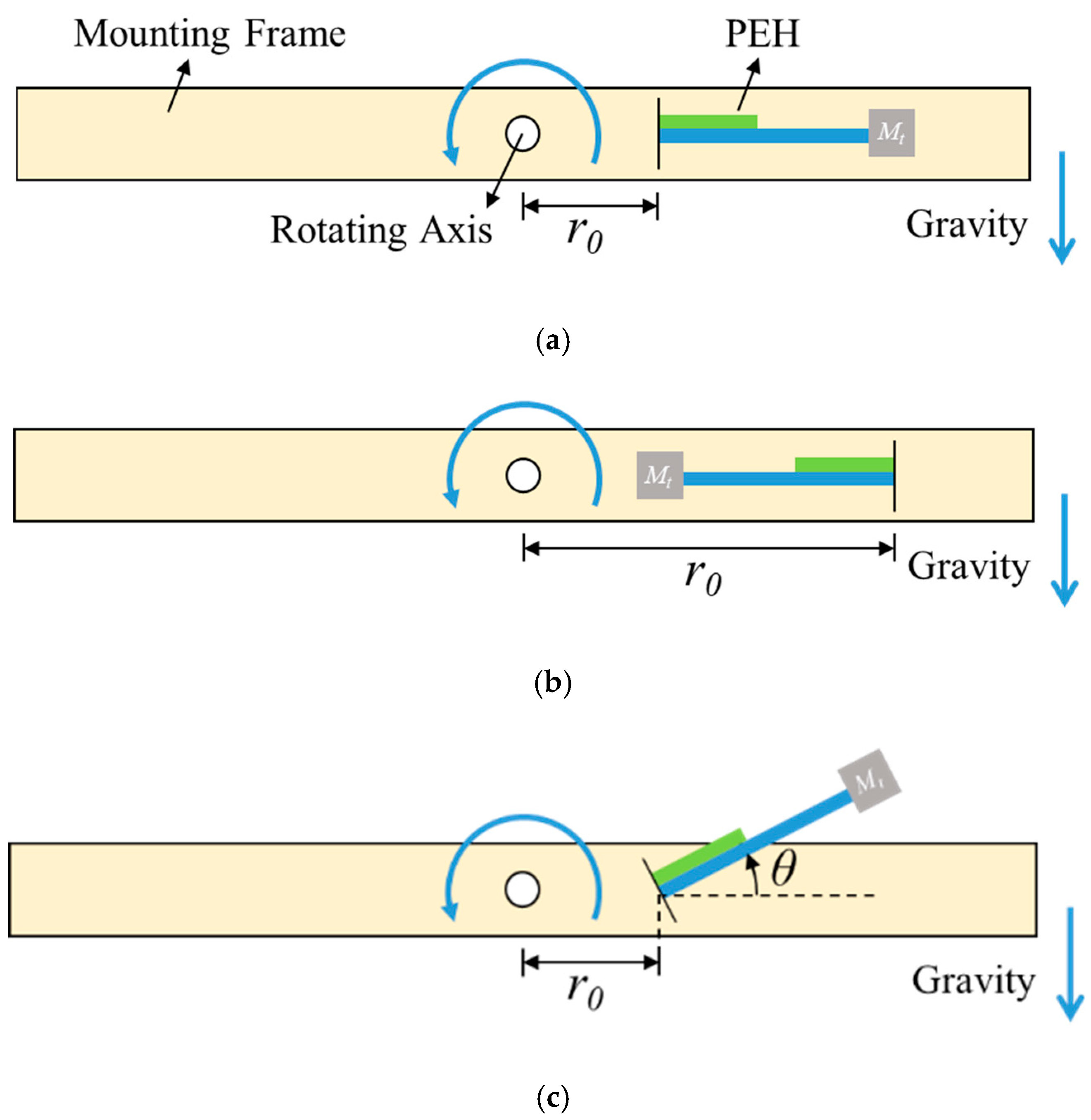






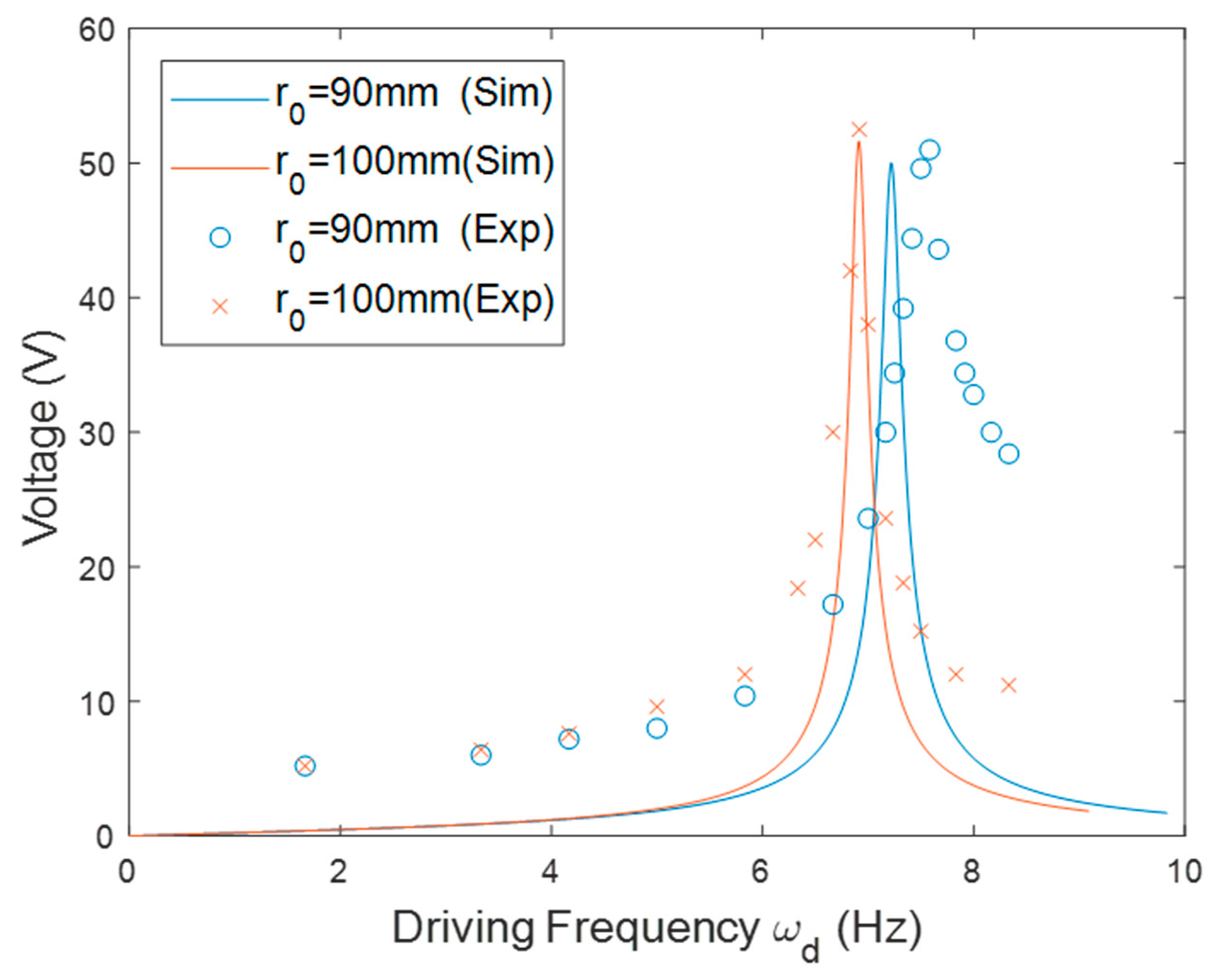

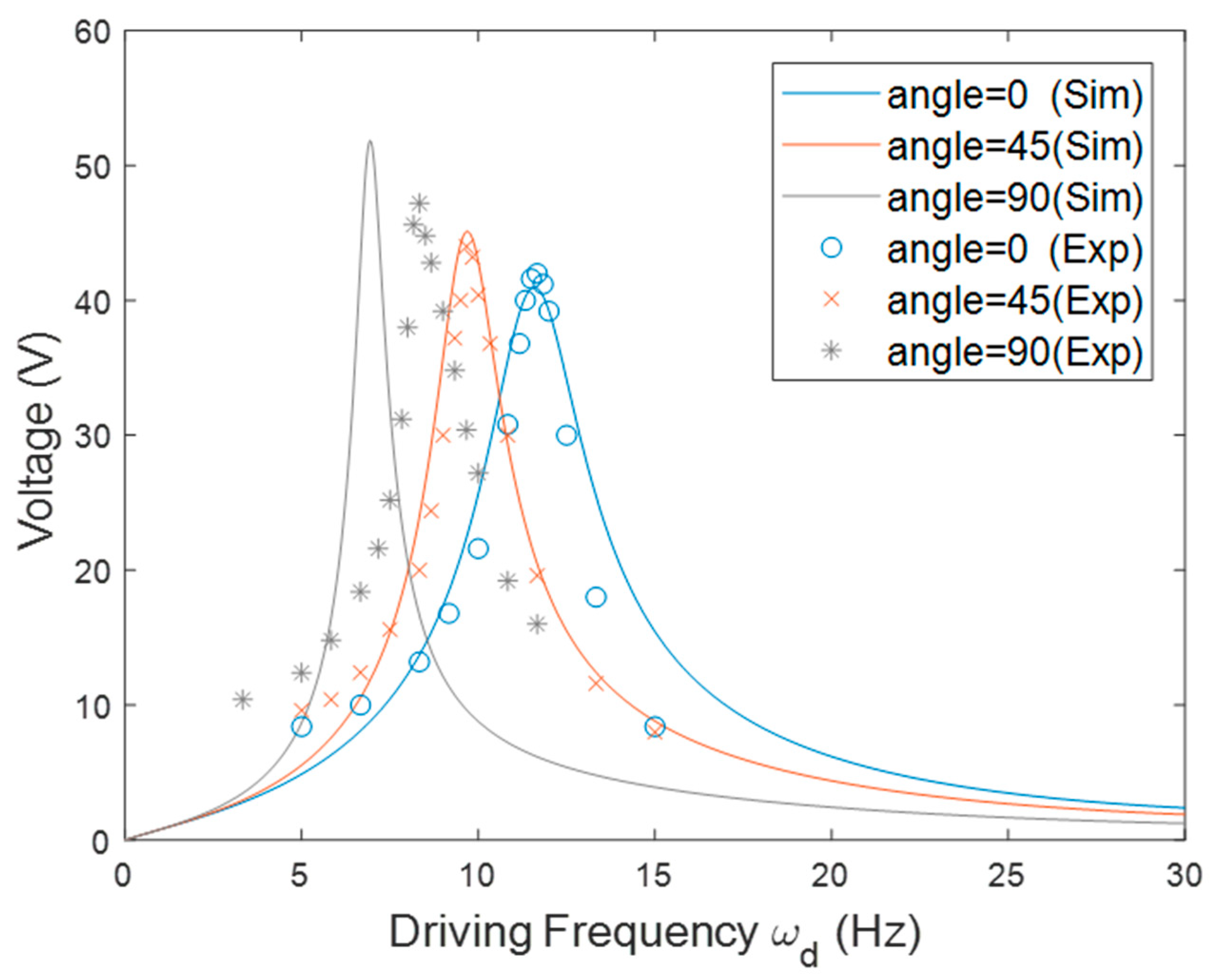
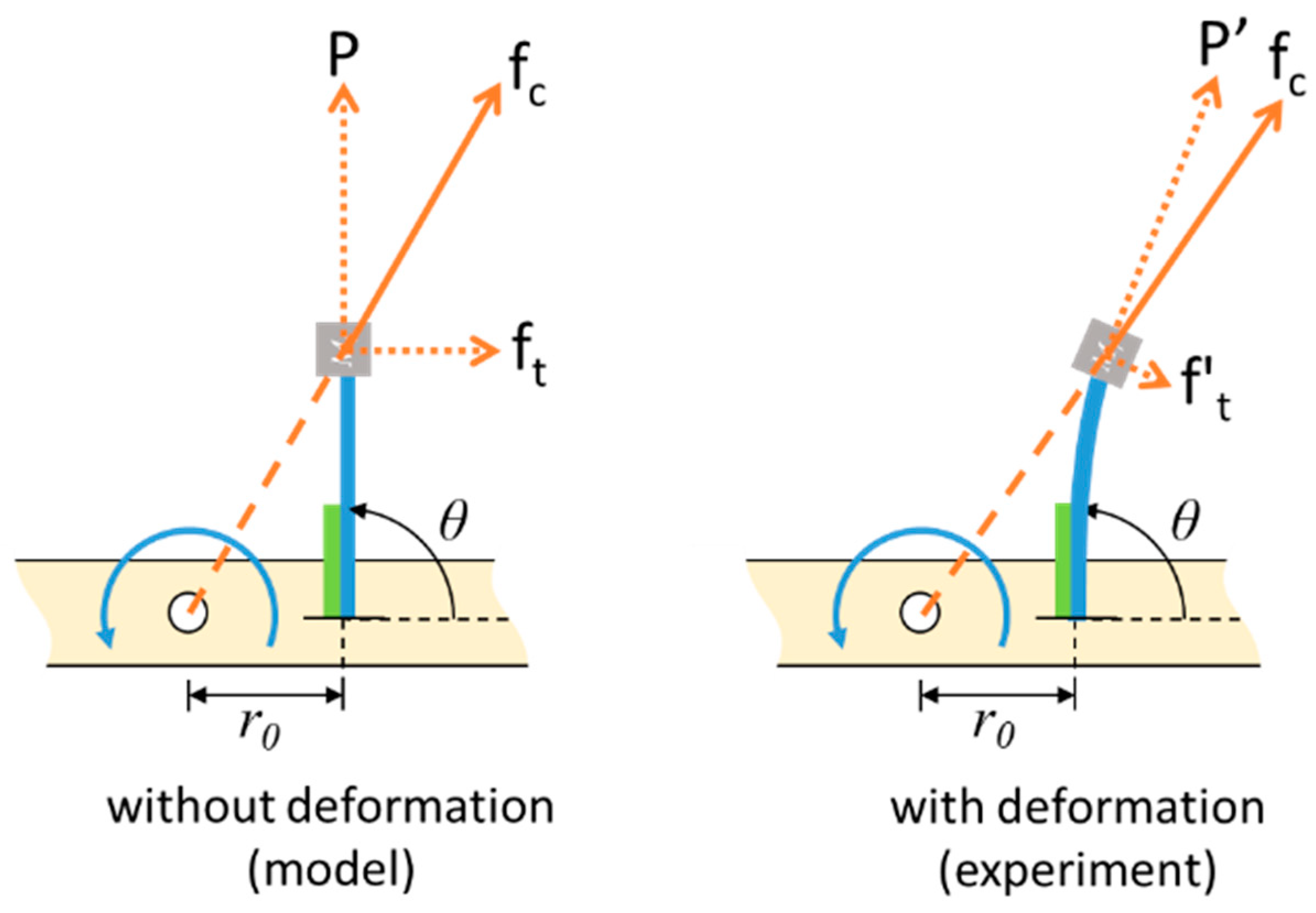
| Symbol | Description | Value |
|---|---|---|
| L | Length (beam) | 75 mm |
| bs | Width (beam) | 12.7 mm |
| hs | Thickness (beam) | 0.1 mm |
| ρs | Density (beam) | 7930 kg/m3 |
| Es | Young’s modulus (beam) | 193 GPa |
| L1 | Length (MFC) | 28 mm |
| bp | Width (MFC) | 7 mm |
| hp | Thickness (MFC) | 0.3 mm |
| ρp | Density (MFC) | 5440 kg/m3 |
| Ep | Young’s modulus (MFC) | 30.336 GPa |
| Mt | Tip mass | 3.04 g |
| R | Load resistance | 1 MΩ |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, W.-J.; Lin, J.-H.; Li, W.-C. Analysis of a Cantilevered Piezoelectric Energy Harvester in Different Orientations for Rotational Motion. Sensors 2020, 20, 1206. https://doi.org/10.3390/s20041206
Su W-J, Lin J-H, Li W-C. Analysis of a Cantilevered Piezoelectric Energy Harvester in Different Orientations for Rotational Motion. Sensors. 2020; 20(4):1206. https://doi.org/10.3390/s20041206
Chicago/Turabian StyleSu, Wei-Jiun, Jia-Han Lin, and Wei-Chang Li. 2020. "Analysis of a Cantilevered Piezoelectric Energy Harvester in Different Orientations for Rotational Motion" Sensors 20, no. 4: 1206. https://doi.org/10.3390/s20041206
APA StyleSu, W.-J., Lin, J.-H., & Li, W.-C. (2020). Analysis of a Cantilevered Piezoelectric Energy Harvester in Different Orientations for Rotational Motion. Sensors, 20(4), 1206. https://doi.org/10.3390/s20041206






