Precise Volumetric Measurements of Any Shaped Objects with a Novel Acoustic Volumeter
Abstract
1. Introduction
2. Materials and Methods
2.1. Sensor Design
2.2. Data Acquisition System
3. Working Principle
4. Results and Discussion
4.1. Single Frequency Operation
4.1.1. Measurement of Objects with Known Volumes; Calibration Curves
4.1.2. Measurement of Plant Seeds
4.2. Frequency Sweep Operation
4.2.1. Measurements of Total Volume of Pores
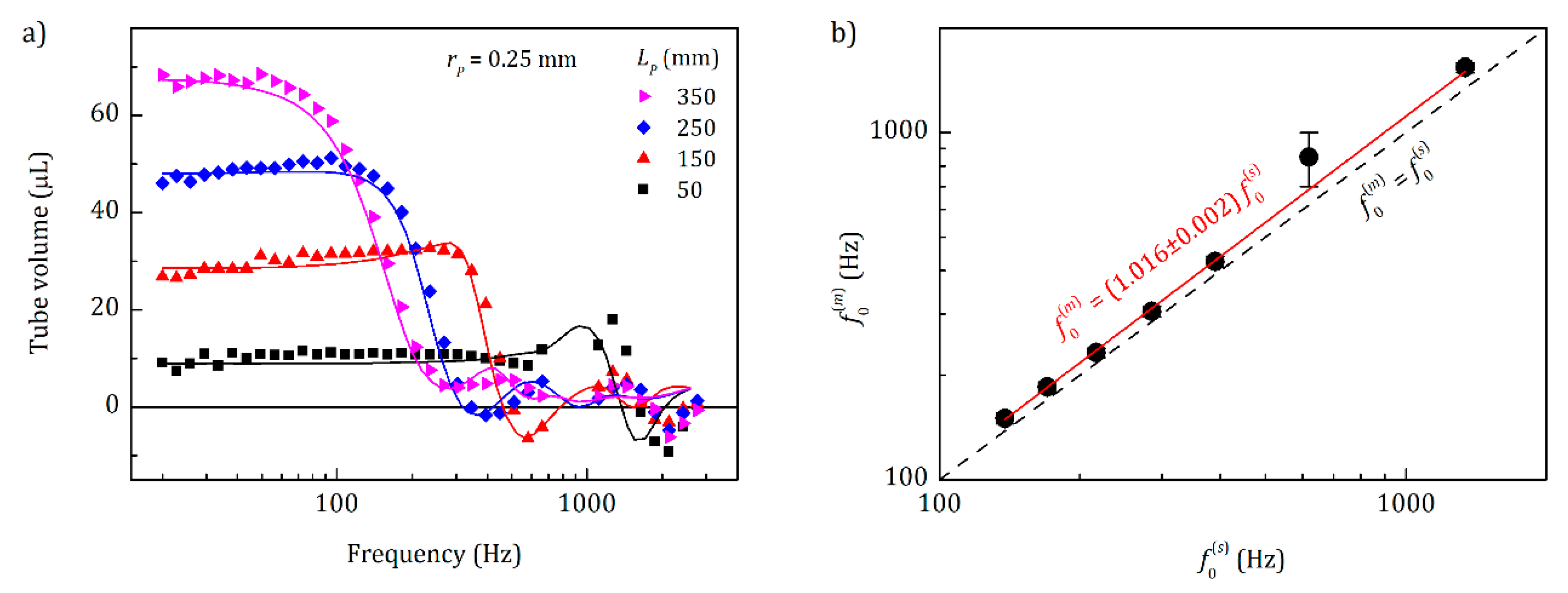
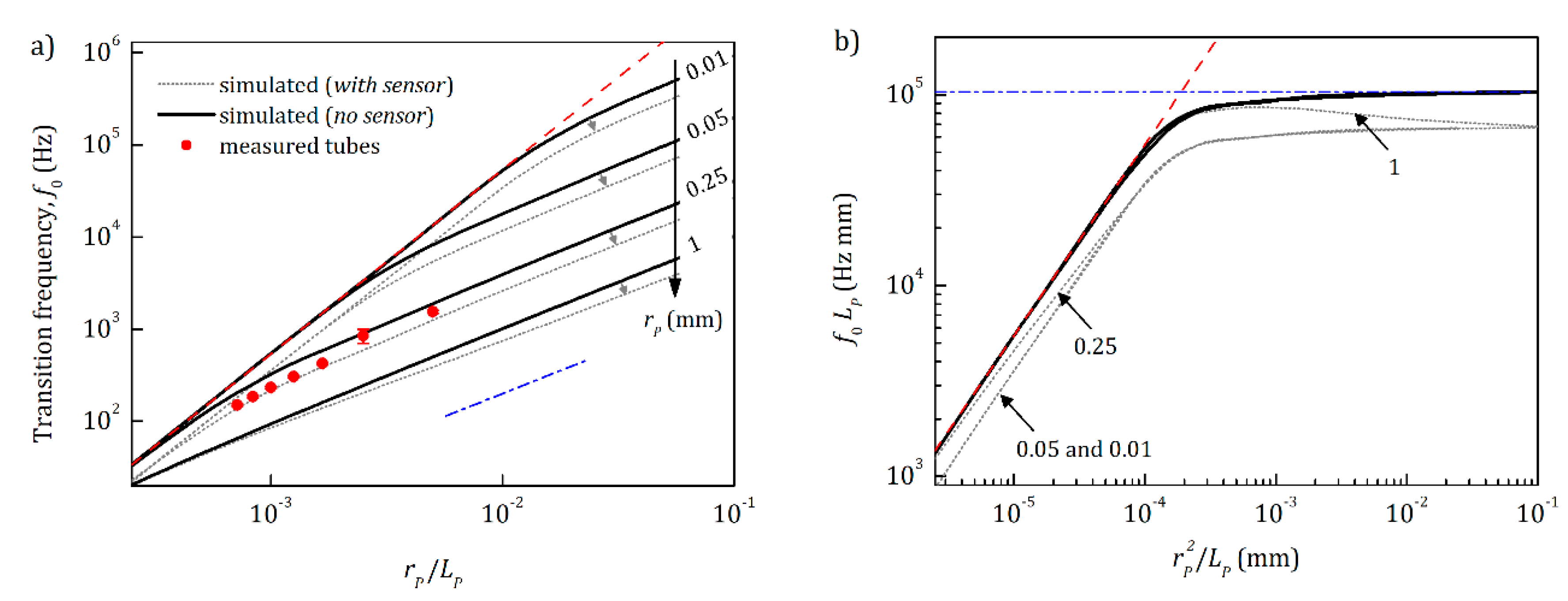
4.2.2. Teflon Tube Example; Theory Verification
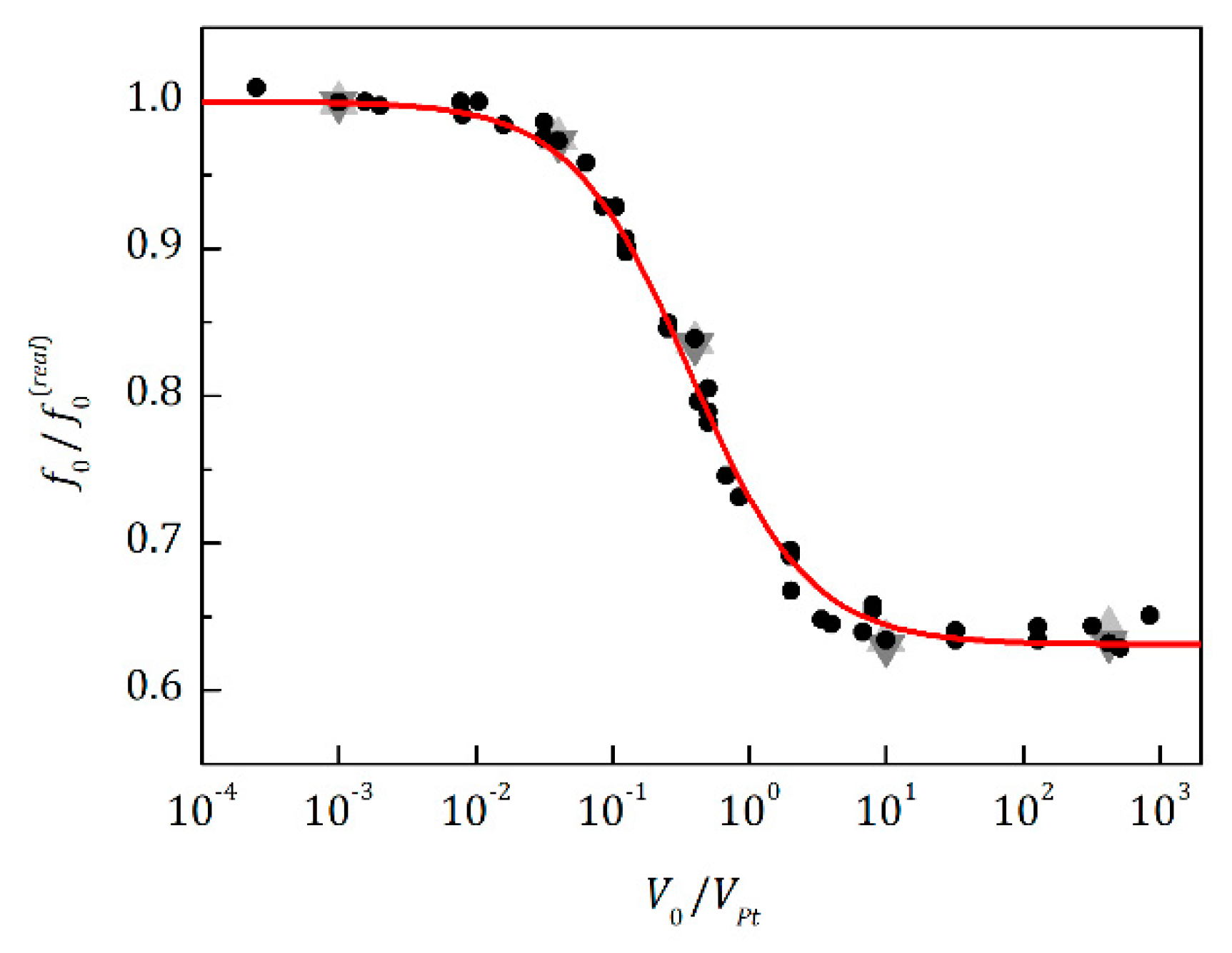
4.2.3. Influence of the Internal Volume of the Sensor and Pores Geometry
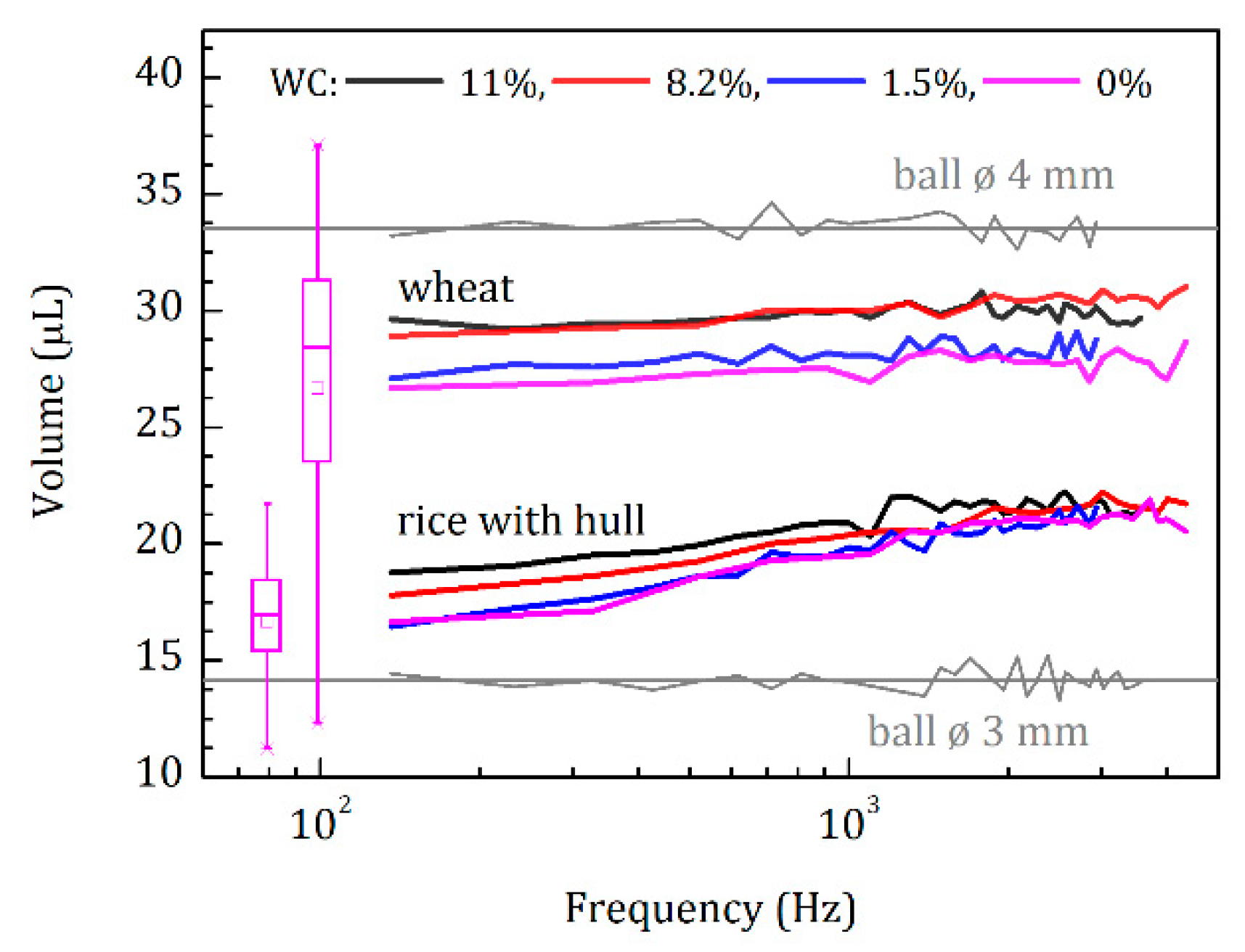
4.2.4. Plant Seed Example; Under the Husk
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| γair (-) | Adiabatic index of air |
| γP (-) | Polytropic index |
| Np (-) | Number of pores |
| ξ (-) | Visibility of the volume filled with air |
| Frequency response of the loudspeaker when the chamber is empty | |
| Frequency response of the loudspeaker when an object is present inside the chamber | |
| I0 (A) | Amplitude of applied sinusoidal current |
| f (Hz) | Frequency of applied sinusoidal current |
| f0 (Hz) | Transition frequency at which half of the pore volume is visible for the sensor |
| cP (J kg−1 K−1) | Specific heat capacity of air at constant pressure |
| T (K) | Temperature |
| ρ0 (kg m−3) | Density of air |
| ρp (kg m−3) | Density of air inside a pore |
| l1 (m) | Length of the wire in the coil of loudspeaker |
| l2 (m) | Length of the wire in the coil of microphone |
| rp (m) | Pore radius |
| Lp (m) | Pore length |
| S (m2) | Area of the loudspeaker membrane |
| V0 (m3) | Internal volume of the sensor chamber |
| ∆V (m3) | Volumetric change caused by the movements of the loudspeaker membrane |
| VS (m3) | Object volume |
| VPt (m3) | Total volume of pores |
| C (m−3) | Fit parameter |
| vS (m s−1) | Speed of sound |
| F (N) | Lorenz force |
| Floss (N) | Force which concerns losses in the loudspeaker |
| (N m−1) | Stiffness of the mechanical suspension of the loudspeaker |
| pa (Pa) | Atmospheric pressure |
| ∆p (Pa) | Change in pressure caused by the excitation membrane |
| ∆pmax (Pa) | Maximum change in pressure caused by the excitation membrane |
| µ (Pa s) | Air dynamic viscosity |
| t (s) | Time |
| B1 (T) | Magnetic flux density inside the coil of the loudspeaker |
| B2 (T) | Magnetic flux density inside the coil of the microphone |
| (V) | Electromotive force generated by the microphone |
| (V) | Root mean square value of the electromotive force generated by the microphone when sensor chamber is empty |
| (V) | Root mean square value of the electromotive force generated by the microphone when an object is in the sensor chamber |
| (-) | Relative value between the root mean square values of the electromotive forces generated by the microphone when the sensor chamber is empty and with an object inside |
| κ (W m−1 K−1) | Thermal conductivity of air |
Appendix A
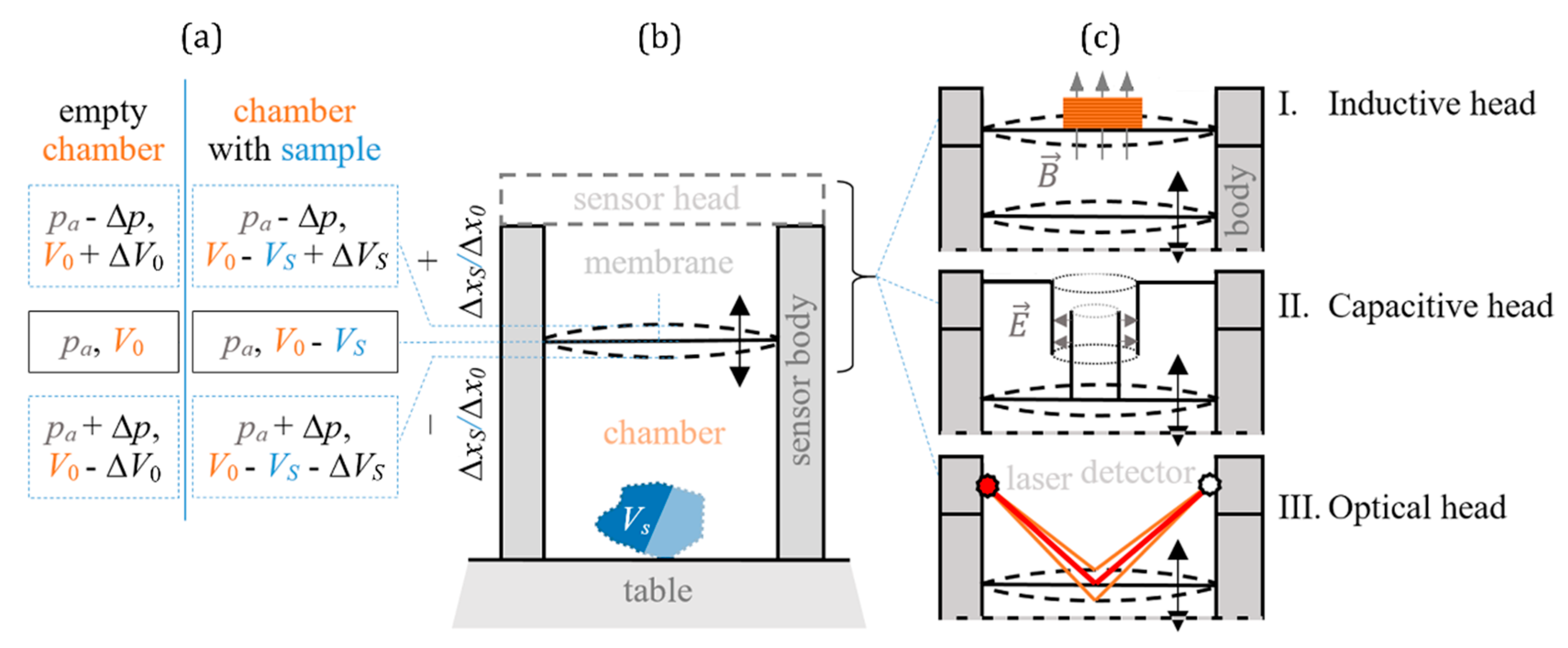
Appendix B
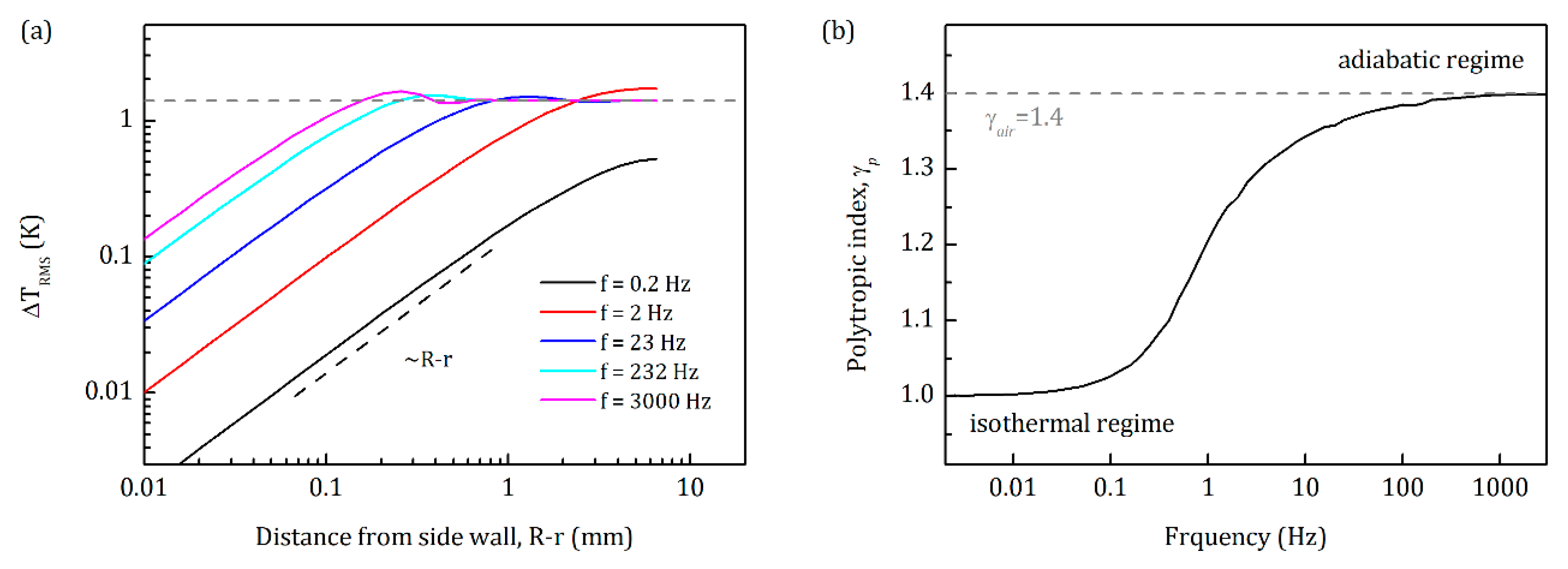

Appendix C
Appendix D

Appendix E
References
- Aghajani, N.; Ansaripour, E.; Kashaninejad, M. Effect of Moisture Content on Physical Properties of Barley Seeds. J. Agric. Sci. Tech. 2012, 14, 161–172. [Google Scholar]
- Bhattacharya, K.R.; Sowbhagya, C.M.; Swamy, Y.M.I. Some physical properties of paddy and rice and their interrelations. J. Sci. Food Agric. 1972, 23, 171–186. [Google Scholar] [CrossRef]
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision; Cambridge University Press: Cambridge, UK, 2003; ISBN 978-0-521-54051-3. [Google Scholar]
- Roussel, J.; Geiger, F.; Fischbach, A.; Jahnke, S.; Scharr, H. 3D Surface Reconstruction of Plant Seeds by Volume Carving: Performance and Accuracies. Front. Plant Sci. 2016, 7, 745. [Google Scholar] [CrossRef] [PubMed]
- Jahnke, S.; Roussel, J.; Hombach, T.; Kochs, J.; Fischbach, A.; Huber, G.; Scharr, H. phenoSeeder - A Robot System for Automated Handling and Phenotyping of Individual Seeds. Plant Physiol. 2016, 172, 1358–1370. [Google Scholar] [CrossRef]
- Agarwal, S.; Furukawa, Y.; Snavely, N.; Simon, I.; Curless, B.; Seitz, S.M.; Szeliski, R. Building Rome in a day. Commun. ACM 2011, 54, 105–112. [Google Scholar] [CrossRef]
- Seitz, S.M.; Curless, B.; Diebel, J.; Scharstein, D.; Szeliski, R. A Comparison and Evaluation of Multi-View Stereo Reconstruction Algorithms. In Proceedings of the 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition - Volume 1 (CVPR’06), New York, NY, USA, 17–22 June 2006; pp. 519–528. [Google Scholar] [CrossRef]
- Knapitsch, A.; Park, J.; Zhou, Q.-Y.; Koltun, V. Tanks and temples: benchmarking large-scale scene reconstruction. ACM Trans. Graphics 2017, 36, 1–13. [Google Scholar] [CrossRef]
- Furuse, A. Volume measuring apparatus and method. U.S. Patent US4888718A, 19 December 1989. [Google Scholar]
- Keng, E.Y.H. Air and belium pycnometer. Powder Technol. 1969, 3, 179–180. [Google Scholar] [CrossRef]
- Shea, J.E. Apparatus for measuring volumes of solid materials. U.S. Patent US2667782A, 2 February 1954. [Google Scholar]
- Tamari, S. Optimum design of the constant-volume gas pycnometer for determining the volume of solid particles. Meas. Sci. Technol. 2004, 15, 549–558. [Google Scholar] [CrossRef]
- Mathias, B.B. Apparatus for acoustically measuring volume. U.S. Patent US3075382A, 29 January 1963. [Google Scholar]
- Lao, B.Y. Acoustic pycnometer. U.S. Patent US4072046A, 7 February 1978. [Google Scholar]
- Torigoe, I.; Ishii, Y. Acoustic Bridge Volumeter. Trans. Soc. Instrum. Control Eng. 1994, 30, 1303–1309. [Google Scholar] [CrossRef][Green Version]
- Torigoe, I.; Ishii, Y. Acoustic Bridge Volumeter. Trans. Soc. Instrum. Control Eng. 2001, E-1, 164–170. [Google Scholar]
- Kobata, T.; Ueki, M.; Ooiwa, A.; Ishii, Y. Measurement of the volume of weights using an acoustic volumeter and the reliability of such measurement. Metrologia 2004, 41, S75–S83. [Google Scholar] [CrossRef]
- Sun, J.; Ueki, M.; Ueda, K. Investigation on the Volume Measurement of Weights Based on Boyle’s Law. Trans. Soc. Instrum. Control Eng. 2012, 48, 809–815. [Google Scholar] [CrossRef]
- Hu, M.-H.; Wang, J.; Cai, C.-Q.; Huang, T.; Zhong, R.-L.; Jiao, K. Numerical Study of Sound Pressure Distribution in Volume Determination with Acoustic Method. In Proceedings of the 3rd Annual International Conference on Mechanics and Mechanical Engineering (MME 2016), Chengdu, China, 16–18 December 2016; pp. 1035–1039. [Google Scholar] [CrossRef][Green Version]
- Hu, M.-H.; Wang, J.; Zhang, Y.; Cai, C.-Q.; Zhong, R.-L.; Ding, J.A.; Ren, X.P. Research on volume determination of mass standards with two acoustic measuring chambers. ACTA IMEKO 2017, 6, 8–12. [Google Scholar] [CrossRef]
- Nakano, A.; Torikata, Y.; Yamashita, T.; Sakamoto, T.; Futaya, Y.; Tateno, A.; Nishizu, T. Liquid volume measurement with a closed Helmholtz resonator under micro-gravity conditions. Cryogenics 2006, 46, 126–131. [Google Scholar] [CrossRef]
- Webster, E.S.; Davies, C.E. The Use of Helmholtz Resonance for Measuring the Volume of Liquids and Solids. Sensors 2010, 10, 10663–10672. [Google Scholar] [CrossRef]
- Hu, J. Acoustic resonance-based method and device for measuring liquid volume in container. WO2017049657A1, 30 March 2017. [Google Scholar]
- Imanishi, M.; Nagashima, A.; Moriyama, A.; Ishii, Y. Measurement of combustion-chamber volume using an acoustic resonance technique. In Proceedings of the 10th Anniversary. IMTC/94. Advanced Technologies in I M. 1994 IEEE Instrumentation and Measurement Technolgy Conference (Cat. No.94CH3424-9), Hamamatsu, Japan, 10–12 May 1994; pp. 589–592. [Google Scholar]
- Borisjuk, L.; Rolletschek, H.; Neuberger, T. Surveying the plant’s world by magnetic resonance imaging. Plant J. 2012, 70, 129–146. [Google Scholar] [CrossRef]
- Hughes, N.; Askew, K.; Scotson, C.P.; Williams, K.; Sauze, C.; Corke, F.; Doonan, J.H.; Nibau, C. Non-destructive, high-content analysis of wheat grain traits using X-ray micro computed tomography. Plant Methods 2017, 13, 76. [Google Scholar] [CrossRef]
- Sydoruk, V.A.; Kochs, J.; van Dusschoten, D.; Jahnke, S. Vorrichtung und Verfahren zur Bestimmung des Volumens und der Porosität von Objekten und Schüttgütern. DE102018009800.2; patent pending,
- Beranek, L.L.; Mellow, T. Acoustics: Sound Fields and Transducers; Elsevier Science & Technology: San Diego, CA, USA, 2012; ISBN 978-0-12-391486-6. [Google Scholar]
- Klippel, W. Nonlinear losses in electro-acoustical transducers. In Proceedings of the Acoustics 2012, Nantes, France, 23–27 April 2012; pp. 3484–3488. [Google Scholar]
- Kirkby, N.F. Polytropic process. THERMOPEDIATM A-to-Z Guide to Thermodynamics, Heat & Mass Transfer, and Fluids Engineering - Online 2006. Available online: http://www.thermopedia.com/content/1045/ (accessed on 30 January 2020).
- Bird, R.B.; Stewart, W.E.; Lightfoot, E.N. Transport Phenomena, 2nd ed.; Wiley: New York, NY, USA, 2007; ISBN 978-0-470-11539-8. [Google Scholar]
- Cramer, O. The variation of the specific heat ratio and the speed of sound in air with temperature, pressure, humidity, and CO2 concentration. J. Acoust. Soc. Am. 1993, 93, 2510–2516. [Google Scholar] [CrossRef]
- Pajdak, A.; Godyń, K.; Kudasik, M.; Murzyn, T. The use of selected research methods to describe the pore space of dolomite from copper ore mine, Poland. Environ Earth Sci 2017, 76, 389. [Google Scholar] [CrossRef]
- Evans, M.D.M.; Dalton, B.A.; Steele, J.G. Persistent adhesion of epithelial tissue is sensitive to polymer topography. J. Biomed. Mater. Res. 1999, 46, 485–493. [Google Scholar] [CrossRef]
- Dan, N. Drug release through liposome pores. Colloids Surf. B 2015, 126, 80–86. [Google Scholar] [CrossRef] [PubMed]
- Sologubik, C.A.; Campañone, L.A.; Pagano, A.M.; Gely, M.C. Effect of moisture content on some physical properties of barley. Ind. Crops Prod. 2013, 43, 762–767. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Fluid Mechanics, 2nd ed.; Pergamon Press: Oxford, UK, 1987; ISBN 978-0-08-033933-7. [Google Scholar] [CrossRef]


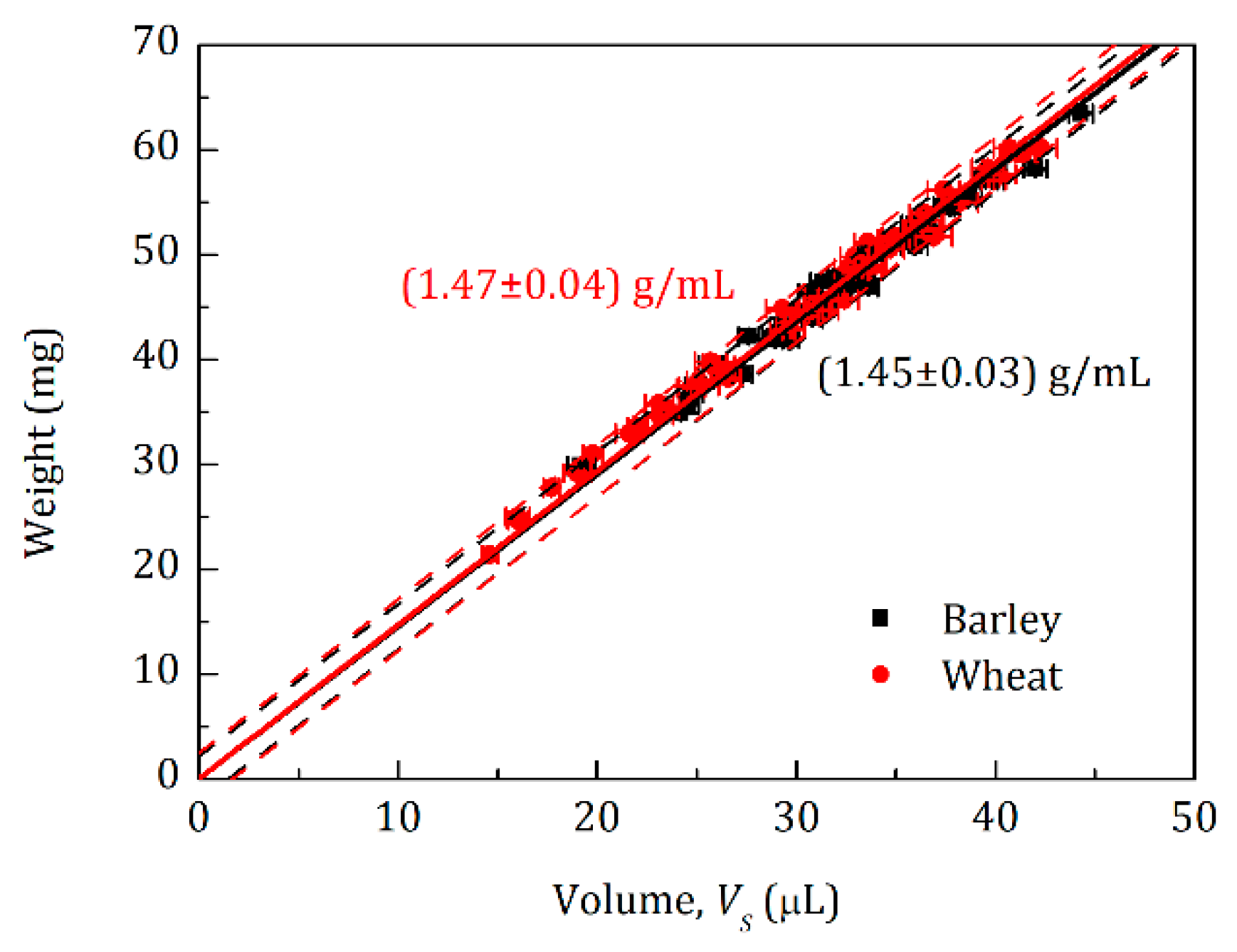
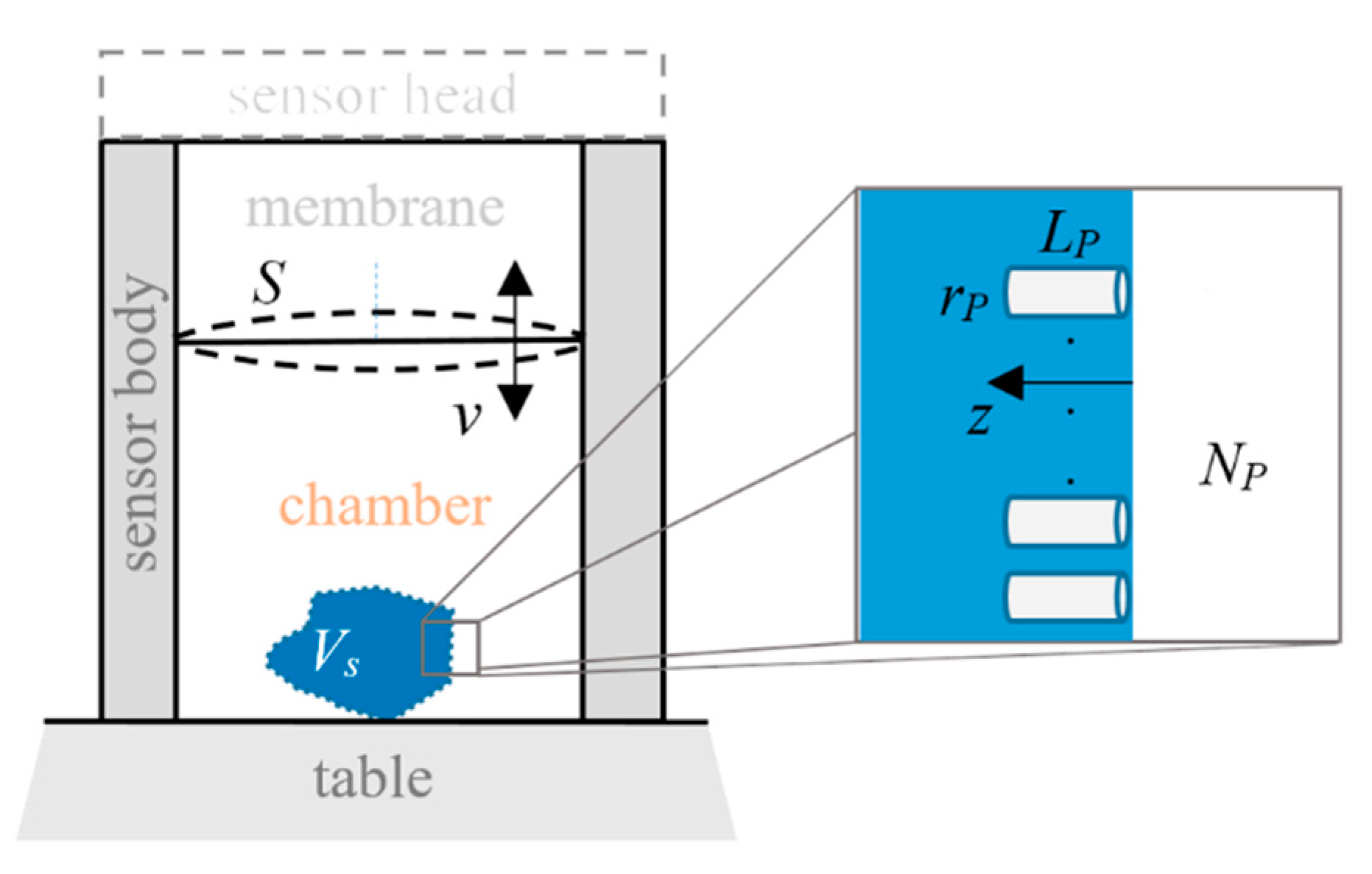
| Geometrically Estimated | Fitted by Equation (9) | Fitted by Equation (11) | |||
|---|---|---|---|---|---|
| V0 (µL) | V0 (µL) | V0 (µL) | C (µL−1), ×10−6 | ||
| 600 ± 70 1 | 693 ± 5 | 1.10 | 600 2 | 260 ± 20 2 | 1.05 2 |
| 1300 ± 70 1 | 1397 ± 3 | 19.3 | 1250 ± 20 | 130 ± 20 | 9.66 |
| 2630 ± 70 1 | 3160 ± 10 | 31.4 | 2570 ± 30 | 112 ± 9 | 3.47 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sydoruk, V.A.; Kochs, J.; van Dusschoten, D.; Huber, G.; Jahnke, S. Precise Volumetric Measurements of Any Shaped Objects with a Novel Acoustic Volumeter. Sensors 2020, 20, 760. https://doi.org/10.3390/s20030760
Sydoruk VA, Kochs J, van Dusschoten D, Huber G, Jahnke S. Precise Volumetric Measurements of Any Shaped Objects with a Novel Acoustic Volumeter. Sensors. 2020; 20(3):760. https://doi.org/10.3390/s20030760
Chicago/Turabian StyleSydoruk, Viktor A., Johannes Kochs, Dagmar van Dusschoten, Gregor Huber, and Siegfried Jahnke. 2020. "Precise Volumetric Measurements of Any Shaped Objects with a Novel Acoustic Volumeter" Sensors 20, no. 3: 760. https://doi.org/10.3390/s20030760
APA StyleSydoruk, V. A., Kochs, J., van Dusschoten, D., Huber, G., & Jahnke, S. (2020). Precise Volumetric Measurements of Any Shaped Objects with a Novel Acoustic Volumeter. Sensors, 20(3), 760. https://doi.org/10.3390/s20030760




