Inertial Sensor-Based Lower Limb Joint Kinematics: A Methodological Systematic Review
Abstract
1. Introduction
2. Methods
2.1. Eligibility Criteria
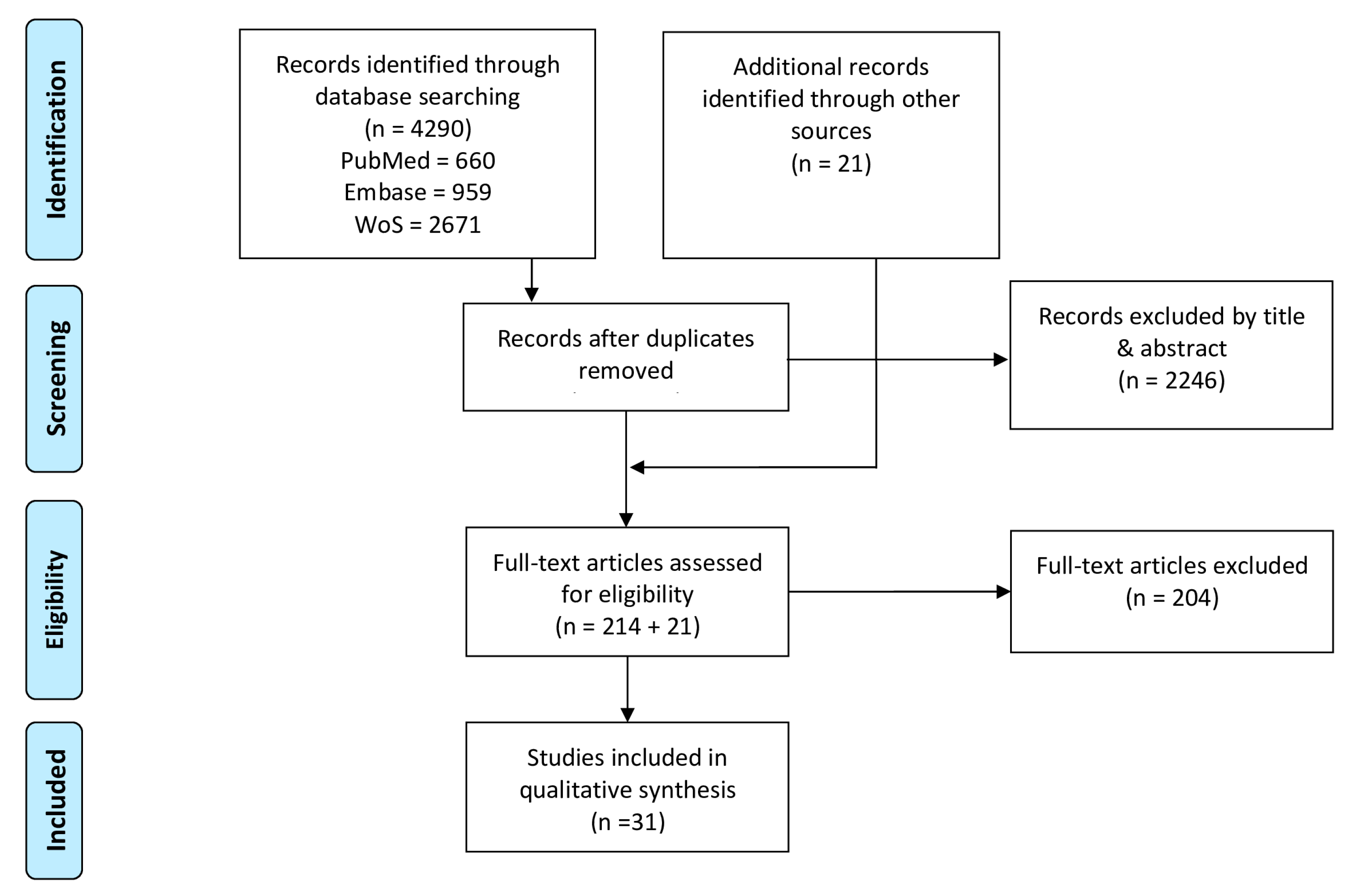
2.2. Search Strategy and Study Selection
2.3. Data Extraction
3. Results
3.1. Study Characteristics
3.2. Signal Processing Characteristics
3.2.1. Pre-Processing, Prior Information and Assumptions
3.2.2. Information Fusion
3.2.3. Drift Compensation, Initialization and Calibration
3.3. Study Evaluation and Results
4. Discussion
5. Future Research
5.1. Reporting Joint Kinematics
5.2. Biomechanical Joint Modeling
5.3. Validation with Respect to a Golden Standard Reference
5.4. Measurement Duration and Environment
5.5. Disturbed Movement Patterns
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Benson, L.C.; Clermont, C.A.; Bošnjak, E.; Ferber, R. The use of wearable devices for walking and running gait analysis outside of the lab: A systematic review. Gait & Posture 2018, 63, 124–138. [Google Scholar] [CrossRef]
- Hosseini Nasab, S.H.; List, R.; Oberhofer, K.; Fucentese, S.F.; Snedeker, J.G.; Taylor, W.R. Loading Patterns of the Posterior Cruciate Ligament in the Healthy Knee: A Systematic Review. PLoS ONE 2016, 11, e0167106. [Google Scholar] [CrossRef] [PubMed]
- Camomilla, V.; Cappozzo, A.; Vannozzi, G. Three-Dimensional Reconstruction of the Human Skeleton in Motion. In Handbook of Human Motion; Springer International Publishing: Cham, Switzerland, 2018; pp. 17–45. [Google Scholar] [CrossRef]
- McGinley, J.L.; Baker, R.; Wolfe, R.; Morris, M.E. The reliability of three-dimensional kinematic gait measurements: A systematic review. Gait & Posture 2009, 29, 360–369. [Google Scholar] [CrossRef]
- Stagni, R.; Fantozzi, S.; Cappello, A.; Leardini, A. Quantification of soft tissue artefact in motion analysis by combining 3D fluoroscopy and stereophotogrammetry: A study on two subjects. Clin. Biomech. 2005, 20, 320–329. [Google Scholar] [CrossRef]
- Camomilla, V.; Bergamini, E.; Fantozzi, S.; Vannozzi, G. Trends Supporting the In-Field Use of Wearable Inertial Sensors for Sport Performance Evaluation: A Systematic Review. Sensors 2018, 18, 873. [Google Scholar] [CrossRef]
- Wagner, J.F. About Motion Measurement in Sports Based on Gyroscopes and Accelerometers - an Engineering Point of View. Gyroscopy Navig. 2018, 9, 1–18. [Google Scholar] [CrossRef]
- Filippeschi, A.; Schmitz, N.; Miezal, M.; Bleser, G.; Ruffaldi, E.; Stricker, D. Survey of Motion Tracking Methods Based on Inertial Sensors: A Focus on Upper Limb Human Motion. Sensors 2017, 17, 40. [Google Scholar] [CrossRef]
- Lopez-Nava, I.H.; Munoz-Melendez, A. Wearable Inertial Sensors for Human Motion Analysis: A Review. IEEE Sens. J. 2016, 16, 7821–7834. [Google Scholar] [CrossRef]
- van der Straaten, R.; De Baets, L.; Jonkers, I.; Timmermans, A. Mobile assessment of the lower limb kinematics in healthy persons and in persons with degenerative knee disorders: A systematic review. Gait & Posture 2018, 59, 229–241. [Google Scholar] [CrossRef]
- Fong, D.T.; Chan, Y.Y. The use of wearable inertial motion sensors in human lower limb biomechanics studies: A systematic review. Sensors 2010, 10, 11556–11565. [Google Scholar] [CrossRef] [PubMed]
- Picerno, P. 25 years of lower limb joint kinematics by using inertial and magnetic sensors: A review of methodological approaches. Gait & Posture 2017, 51, 239–246. [Google Scholar] [CrossRef]
- Iosa, M.; Picerno, P.; Paolucci, S.; Morone, G. Wearable inertial sensors for human movement analysis. Expert Rev. Med. Devices 2016, 13, 641–659. [Google Scholar] [CrossRef] [PubMed]
- O’Reilly, M.; Caulfield, B.; Ward, T.; Johnston, W.; Doherty, C. Wearable Inertial Sensor Systems for Lower Limb Exercise Detection and Evaluation: A Systematic Review. Sports Med. 2018, 48, 1221–1246. [Google Scholar] [CrossRef]
- Moher, D.; Liberati, A.; Tetzlaff, J.; Altman, D.G.; The, P.G. Preferred Reporting Items for Systematic Reviews and Meta-Analyses: The PRISMA Statement. PLOS Med. 2009, 6, e1000097. [Google Scholar] [CrossRef]
- Djuric-Jovicic, M.D.; Jovicic, N.S.; Popovic, D.B. Kinematics of Gait: New Method for Angle Estimation Based on Accelerometers. Sensors 2011, 11, 10571–10585. [Google Scholar] [CrossRef]
- Rouhani, H.; Favre, J.; Crevoisier, X.; Aminian, K. Measurement of multi-segment foot joint angles during gait using a wearable system. J. Biomech. Eng. 2012, 134, 061006. [Google Scholar] [CrossRef]
- Lin, J.F.S.; Kulić, D. Human pose recovery using wireless inertial measurement units. Physiol. Meas. 2012, 33, 2099–2115. [Google Scholar] [CrossRef]
- Choi, S.; Shin, Y.B.; Kim, S.Y.; Kim, J. A novel sensor-based assessment of lower limb spasticity in children with cerebral palsy. J. NeuroEng. Rehabil. 2018, 15, 16. [Google Scholar] [CrossRef]
- Seel, T.; Raisch, J.; Schauer, T. IMU-Based Joint Angle Measurement for Gait Analysis. Sensors 2014, 14, 6891–6909. [Google Scholar] [CrossRef]
- Tong, K.; Granat, M.H. A practical gait analysis system using gyroscopes. Med Eng. Phys. 1999, 21, 87–94. [Google Scholar] [CrossRef]
- Joukov, V.; Bonnet, V.; Karg, M.; Venture, G.; Kulic, D. Rhythmic Extended Kalman Filter for Gait Rehabilitation Motion Estimation and Segmentation. IEEE Trans. Neural Syst. Rehabil. Eng. 2018, 26, 407–418. [Google Scholar] [CrossRef]
- Dejnabadi, H.; Jolles, B.M.; Aminian, K. A new approach to accurate measurement of uniaxial joint angles based on a combination of accelerometers and gyroscopes. IEEE Trans. Biomed. Eng. 2005, 52, 1478–1484. [Google Scholar] [CrossRef]
- Slajpah, S.; Kamnik, R.; Munih, M. Kinematics based sensory fusion for wearable motion assessment in human walking. Comput. Methods Programs Biomed. 2014, 116, 131–144. [Google Scholar] [CrossRef]
- Favre, J.; Jolles, B.M.; Aissaoui, R.; Aminian, K. Ambulatory measurement of 3D knee joint angle. J. Biomech. 2008, 41, 1029–1035. [Google Scholar] [CrossRef]
- Favre, J.; Aissaoui, R.; Jolles, B.M.; de Guise, J.A.; Aminian, K. Functional calibration procedure for 3D knee joint angle description using inertial sensors. J. Biomech. 2009, 42, 2330–2335. [Google Scholar] [CrossRef]
- Djuric-Jovicic, M.D.; Jovicic, N.S.; Popovic, D.B.; Djordjevic, A.R. Nonlinear optimization for drift removal in estimation of gait kinematics based on accelerometers. J. Biomech. 2012, 45, 2849–2854. [Google Scholar] [CrossRef]
- Liu, K.; Liu, T.; Shibata, K.; Inoue, Y.; Zheng, R. Novel approach to ambulatory assessment of human segmental orientation on a wearable sensor system. J. Biomech. 2009, 42, 2747–2752. [Google Scholar] [CrossRef]
- Kok, M.; Hol, J.D.; Schon, T.B. An optimization-based approach to human body motion capture using inertial sensors. IFAC-PapersOnLine 2014, 47, 79–85. [Google Scholar] [CrossRef]
- Goulermas, J.Y.; Findlow, A.H.; Nester, C.J.; Liatsis, P.; Zeng, X.J.; Kenney, L.P.J.; Tresadern, P.; Thies, S.B.; Howard, D. An instance-based algorithm with Auxiliary Similarity Information for the estimation of gait kinematics from wearable sensors. IEEE Trans. Neural Netw. 2008, 19, 1574–1582. [Google Scholar] [CrossRef]
- Findlow, A.; Goulermas, J.Y.; Nester, C.; Howard, D.; Kenney, L.P.J. Predicting lower limb joint kinematics using wearable motion sensors. Gait & Posture 2008, 28, 120–126. [Google Scholar] [CrossRef]
- O’Donovan, K.J.; Kamnik, R.; O’Keeffe, D.T.; Lyons, G.M. An inertial and magnetic sensor based technique for joint angle measurement. J. Biomech. 2007, 40, 2604–2611. [Google Scholar] [CrossRef]
- Takeda, R.; Tadano, S.; Natorigawa, A.; Todoh, M.; Yoshinari, S. Gait posture estimation using wearable acceleration and gyro sensors. J. Biomech. 2009, 42, 2486–2494. [Google Scholar] [CrossRef] [PubMed]
- Tadano, S.; Takeda, R.; Miyagawa, H. Three Dimensional Gait Analysis Using Wearable Acceleration and Gyro Sensors Based on Quaternion Calculations. Sensors 2013, 13, 9321–9343. [Google Scholar] [CrossRef] [PubMed]
- Ohtaki, Y.; Sagawa, K.; Inooka, H. A method for gait analysis in a daily living environment by body-mounted instruments. JSME Int. J. Ser. C-Mech. Syst. Mach. Elem. Manuf. 2001, 44, 1125–1132. [Google Scholar] [CrossRef]
- Liu, T.; Inoue, Y.; Shibata, K. Measurement of Muscle Motion for Improving Accuracy of Body-mounted Motion Sensor. In Proceedings of the IEEE International Conference on Advanced Intelligent Mechatronics, Xi’an, China, 2–5 July 2008; IEEE: New York, NY, USA; pp. 1325–1330. [Google Scholar]
- Joukov, V.; Karg, M.; Kulic, D. Online Tracking of the Lower Body Joint Angles using IMUs for Gait Rehabilitation. In Proceedings of the IEEE International Conference on Engineering in Medicine and Biology Society; IEEE: New York, NY, USA, 2014; pp. 2310–2313. [Google Scholar]
- Dorschky, E.; Nitschke, M.; Seifer, A.K.; van den Bogert, A.J.; Eskofier, B.M. Estimation of gait kinematics and kinetics from inertial sensor data using optimal control of musculoskeletal models. J. Biomech. 2019. [Google Scholar] [CrossRef] [PubMed]
- Bonnet, V.; Joukov, V.; Kulic, D.; Fraisse, P.; Ramdani, N.; Venture, G. Monitoring of Hip and Knee Joint Angles Using a Single Inertial Measurement Unit During Lower Limb Rehabilitation. IEEE Sens. J. 2016, 16, 1557–1564. [Google Scholar] [CrossRef]
- Caroselli, A.; Bagala, F.; Cappello, A. Quasi-real time estimation of angular kinematics using single-axis accelerometers. Sensors 2013, 13, 918–937. [Google Scholar] [CrossRef]
- Bonnet, V.; Mazza, C.; Fraisse, P.; Cappozzo, A. Real-time estimate of body kinematics during a planar squat task using a single inertial measurement unit. IEEE Trans. Biomed. Eng. 2013, 60, 1920–1926. [Google Scholar] [CrossRef]
- Fasel, B.; Sporri, J.; Chardonnens, J.; Kroll, J.; Muller, E.; Aminian, K. Joint Inertial Sensor Orientation Drift Reduction for Highly Dynamic Movements. IEEE J. Biomed. Health Inform. 2017. [Google Scholar] [CrossRef]
- Frank, J.W.; Matteo, G.; Giovanni, B.; Erik, M.; Jasper, R.; Bert-Jan, F.v.B.; Peter, H.V. Estimation of Vertical Ground Reaction Forces and Sagittal Knee Kinematics During Running Using Three Inertial Sensors. Front. Physiol. 2018, 9. [Google Scholar] [CrossRef]
- Cooper, G.; Sheret, I.; McMillian, L.; Siliverdis, K.; Sha, N.; Hodgins, D.; Kenney, L.; Howard, D. Inertial sensor-based knee flexion/extension angle estimation. J. Biomech. 2009, 42, 2678–2685. [Google Scholar] [CrossRef] [PubMed]
- Ibata, Y.; Kitamura, S.; Motoi, K.; Sagawa, K. Measurement of three-dimensional posture and trajectory of lower body during standing long jumping utilizing body-mounted sensors. In Proceedings of the IEEE International Conference on Engineering in Medicine and Biology Society, Osaka, Japan, 3–7 July 2013; pp. 4891–4894. [Google Scholar] [CrossRef]
- Cockcroft, J.; Muller, J.H.; Scheffer, C. A Novel Complimentary Filter for Tracking Hip Angles During Cycling Using Wireless Inertial Sensors and Dynamic Acceleration Estimation. IEEE Sens. J. 2014, 14, 8. [Google Scholar] [CrossRef]
- Ferraris, F.; Grimaldi, U.; Parvis, M. Procedure for effortless in-field calibration of three-axis rate gyros and accelerometers. Sens. Mater. 1995. [Google Scholar]
- Tedaldi, D.; Pretto, A.; Menegatti, E. A robust and easy to implement method for IMU calibration without external equipments. In Proceedings of the Conference proceedings of IEEE International conference on Robotics and Automation, Hong Kong, China, 31 May–7 June 2014; pp. 3042–3049. [Google Scholar]
- Bruyninckx, H.; De Schutter, J. Symbolic differentiation of the velocity mapping for a serial kinematic chain. Mech. Mach. Theory 1996, 31, 135–148. [Google Scholar] [CrossRef]
- Uicker, J.J.J.; Denavit, J.; Hartenberg, R.S. An Iterative Method for the Displacement Analysis of Spatial Mechanisms. J. Appl. Mech. 1964, 31, 309–314. [Google Scholar] [CrossRef]
- Sabatini, A.M. Quaternion-based strap-down integration method for applications of inertial sensing to gait analysis. Med. Biol. Eng. Comput. 2005, 43, 94–101. [Google Scholar] [CrossRef]
- Fasel, B.; Sporri, J.; Schutz, P.; Lorenzetti, S.; Aminian, K. Validation of functional calibration and strap-down joint drift correction for computing 3D joint angles of knee, hip, and trunk in alpine skiing. PLoS ONE 2017, 12, e0181446. [Google Scholar] [CrossRef]
- Favre, J.; Jolles, B.M.; Siegrist, O.; Aminian, K. Quaternion-based fusion of gyroscopes and accelerometers to improve 3D angle measurement. Electron. Lett. 2006, 42, 612–614. [Google Scholar] [CrossRef]
- Mahony, R.; Hamel, T.; Pflimlin, J.M. Nonlinear complementary filters on the special orthogonal group. IEEE Trans. Autom. Control 2008, 53, 1203–1218. [Google Scholar] [CrossRef]
- Winter, D.A. Biomechanics and Motor Control of Human Movement. In Biomechanics and Motor Control of Human Movement; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Crabolu, M.; Pani, D.; Raffo, L.; Conti, M.; Cereatti, A. Functional estimation of bony segment lengths using magneto-inertial sensing: Application to the humerus. PLoS ONE 2018, 13. [Google Scholar] [CrossRef] [PubMed]
- Olsson, F.; Halvorsen, K. Experimental evaluation of joint position estimation using inertial sensors. In Proceedings of the 20th International Conference on Information Fusion, Xi’an, China, 10–13 July 2017; pp. 354–361. [Google Scholar]
- Frick, E.; Rahmatalla, S. Joint Center Estimation Using Single-Frame Optimization: Part 2: Experimentation. Sensors 2018, 18, 2563. [Google Scholar] [CrossRef] [PubMed]
- Frick, E.; Rahmatalla, S. Joint Center Estimation Using Single-Frame Optimization: Part 1: Numerical Simulation. Sensors 2018, 18, 1089. [Google Scholar] [CrossRef] [PubMed]
- Andriacchi, T.P.; Alexander, E.J. Studies of human locomotion: Past, present and future. J. Biomech. 2000, 33, 1217–1224. [Google Scholar] [CrossRef]
- Morris, J.R.W. Accelerometry—A technique for the measurement of human body movements. J. Biomech. 1973, 6, 729–736. [Google Scholar] [CrossRef]
- Grisetti, G.; Ku, X.; Mmerle, R.; Stachniss, C.; Burgard, W. A Tutorial on Graph-Based SLAM. IEEE Intell. Transp. Syst. Mag. 2010, 2, 31–43. [Google Scholar] [CrossRef]
- Lai, Y.-C.; Lin, H.-S.; Pan, H.-F.; Chang, W.-N.; Hsu, C.-J.; Renn, J.-H. Impact of foot progression angle on the distribution of plantar pressure in normal children. Clin. Biomech. 2014, 29, 196–200. [Google Scholar] [CrossRef]
- De Vroey, H.; Staes, F.; Deklerck, J.; Vereecke, E.; Van Damme, G.; Vanrenterghem, J.; Hallez, H.; Claeys, K. Comparing UKA and TKA lower limb kinematics during gait one year after surgery. In Proceedings of the 18th ESSKA Congress, Glasgow, UK, 9–12 May 2018; pp. 279–280. [Google Scholar]
- Taetz, B.; Bleser, G.; Miezal, M. Towards Self-Calibrating Inertial Body Motion Capture. In Proceedings of the Conference of IEEE International Conference on Information Fusion, Heidelberg, Germany, 5–8 July 2016; pp. 1751–1759. [Google Scholar]
- Olsson, F.; Seel, T.; Lehmann, D.; Halvorsen, K. Joint axis estimation for fast and slow movements using weighted gyroscope and acceleration constraints. arXiv 2019, arXiv:1903.07353. [Google Scholar]
- Madgwick, S.O.H.; Harrison, A.J.L.; Vaidyanathan, R. Estimation of IMU and MARG orientation using a gradient descent algorithm. In Proceedings of the 2011 IEEE International Conference on Rehabilitation Robotics, Zurich, Switzerland, 29 June–1 July 2011; pp. 1–7. [Google Scholar]
- Kok, M.; Schön, T.B. A Fast and Robust Algorithm for Orientation Estimation Using Inertial Sensors. IEEE Signal Process Lett. 2019, 26, 1673–1677. [Google Scholar] [CrossRef]
- Wu, G.; Cavanagh, P.R. ISB recommendations for standardization in the reporting of kinematic data. J. Biomech. 1995, 28, 1257–1261. [Google Scholar] [CrossRef]
- Wu, G.; Siegler, S.; Allard, P.; Kirtley, C.; Leardini, A.; Rosenbaum, D.; Whittle, M.; D’Lima, D.D.; Cristofolini, L.; Witte, H.; et al. ISB recommendation on definitions of joint coordinate system of various joints for the reporting of human joint motion—part I: Ankle, hip, and spine. J. Biomech. 2002, 35, 543–548. [Google Scholar] [CrossRef]
- Grood, E.S.; Suntay, W.J. A joint coordinate system for the clinical description of three-dimensional motions: Application to the knee. J. Biomech. Eng. 1983, 105, 136–144. [Google Scholar] [CrossRef] [PubMed]
- Andriacchi, T.P.; Dyrby, C.O. Interactions between kinematics and loading during walking for the normal and ACL deficient knee. J. Biomech. 2005, 38, 293–298. [Google Scholar] [CrossRef] [PubMed]
- Georgoulis, A.D.; Papadonikolakis, A.; Papageorgiou, C.D.; Mitsou, A.; Stergiou, N. Three-Dimensional Tibiofemoral Kinematics of the Anterior Cruciate Ligament-Deficient and Reconstructed Knee during Walking. Am. Int. J. Sports Med. 2003, 31, 75–79. [Google Scholar] [CrossRef] [PubMed]
- Hewett, T.E.; Myer, G.D.; Ford, K.R.; Heidt, R.S.; Colosimo, A.J.; McLean, S.G.; van den Bogert, A.J.; Paterno, M.V.; Succop, P. Biomechanical Measures of Neuromuscular Control and Valgus Loading of the Knee Predict Anterior Cruciate Ligament Injury Risk in Female Athletes: A Prospective Study. Am. Int. J. Sports Med. 2005, 33, 492–501. [Google Scholar] [CrossRef] [PubMed]
- Dzialo, C.M.; Pedersen, P.H.; Simonsen, C.W.; Jensen, K.K.; de Zee, M.; Andersen, M.S. Development and validation of a subject-specific moving-axis tibiofemoral joint model using MRI and EOS imaging during a quasi-static lunge. J. Biomech. 2018, 72, 71–80. [Google Scholar] [CrossRef] [PubMed]
- Donnelly, C.J.; Lloyd, D.G.; Elliott, B.C.; Reinbolt, J.A. Optimizing whole-body kinematics to minimize valgus knee loading during sidestepping: Implications for ACL injury risk. J. Biomech. 2012, 45, 1491–1497. [Google Scholar] [CrossRef]
- Szczerbik, E.; Kalinowska, M. The influence of knee marker placement error on evaluation of gait kinematic parameters. Acta Bioeng. Biomech. 2011, 13, 43–46. [Google Scholar]
- Callewaert, B.; Labey, L.; Leardini, A.; Bellemans, J.; Desloovere, K.; Scheys, L. High versus normal body-mass index: Effects On 3D kinematics and kinetics during daily-life motor tasks. Gait & Posture 2013, 38, S111. [Google Scholar] [CrossRef]
- Clément, J.; Dumas, R.; Hagemeister, N.; de Guise, J.A. Soft tissue artifact compensation in knee kinematics by multi-body optimization: Performance of subject-specific knee joint models. J. Biomech. 2015, 48, 3796–3802. [Google Scholar] [CrossRef]
- Clément, J.; de Guise, J.A.; Fuentes, A.; Hagemeister, N. Comparison of soft tissue artifact and its effects on knee kinematics between non-obese and obese subjects performing a squatting activity recorded using an exoskeleton. Gait & Posture 2018, 61, 197–203. [Google Scholar] [CrossRef]
- Von Marcard, T.; Henschel, R.; Black, M.J.; Rosenhahn, B.; Pons-Moll, G. Recovering Accurate 3D Human Pose in The Wild Using IMUs and a Moving Camera. In Computer Vision – ECCV 2018; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Reenalda, J.; Maartens, E.; Homan, L.; Buurke, J.H. Continuous three dimensional analysis of running mechanics during a marathon by means of inertial magnetic measurement units to objectify changes in running mechanics. J. Biomech. 2016, 49, 3362–3367. [Google Scholar] [CrossRef] [PubMed]
- Reenalda, J.; Maartens, E.; Buurke, J.H.; Gruber, A.H. Kinematics and shock attenuation during a prolonged run on the athletic track as measured with inertial magnetic measurement units. Gait & Posture 2019, 68, 155–160. [Google Scholar] [CrossRef]
- Teufl, W.; Miezal, M.; Taetz, B.; Frohlich, M.; Bleser, G. Validity, Test-Retest Reliability and Long-Term Stability of Magnetometer Free Inertial Sensor Based 3D Joint Kinematics. Sensors 2018, 18, 1980. [Google Scholar] [CrossRef]
| Ref. | Participants | Protocol | Sensor Set-Up | ||||
|---|---|---|---|---|---|---|---|
| Number and Sex, Type, Age | Activity | Duration | DoF Joint of Interest | Placement | Modalities | ||
| [23] | 5M 3F, healthy, | Gait (Treadmill) | 30s | 1DoF knee | thigh, shank | 1D GYR, 2D ACC | |
| range: 44-70 mean = 58.7 | (2–4 km/h) | ||||||
| [25] | 10M, healthy, | Gait | 10s | 3DoF knee | thigh, shank | 3D GYR, 3D ACC | |
| range: 23-40 mean = 29 | |||||||
| [26] | 8M, healthy, | Gait | 5s * | 3DoF knee | thigh, shank | 3D GYR, 3D ACC | |
| range 19–28 mean = 26 | |||||||
| [16] | 27, healthy, | Gait (Treadmill) (0,15 m/s–2 m/s) | 6s * | 1DoF knee, | thigh, shank, foot | 2× 2D ACC | |
| mean = 26 SD = 1,5 | 1DoF ankle | ||||||
| [27] | 10, healthy, | Gait | 3s * | 1DoF knee, | thigh, shank, foot | 2× 2D ACC | |
| mean = 31 SD = 4 | (slow, normal, fast) | 1DoF ankle | |||||
| [28] | 6M 2F, healthy, | Gait | 10s * | 2DoF hip | close to the hip, thigh | 2× 3D ACC, | |
| mean = 25 SD = 3 | (slow, normal, fast) | 1× 3D ACC | |||||
| [42] | 6, European cup level alpine ski racers, ND | Alpine ski racing | 90s * | 3DoF hip, | sternum, sacrum, thigh (lateral mid-distance between the knee and hip joint center), shank (tibial plateau) | 3D GYR, 3D ACC | |
| 3DoF knee | |||||||
| [29] | ND | Gait | 35s * | 3DoF knee | pelvis, thigh, shank, foot | 3D GYR, 3D ACC, 3D MAG | |
| [30] | 8, healthy, ND | Gait | ND | 1DoF hip, | shank, foot | 3D GYR, 3D ACC | |
| (slow, normal, fast) | 1DoF knee, | ||||||
| 1DoF ankle | |||||||
| [31] | 8, healthy, ND | Gait | 12s * | 1DoF hip, | shank, foot | 3D GYR, 3D ACC | |
| (self-selected speed) | 1DoF knee, 1DoF ankle | ||||||
| [43] | 8M, healthy experienced runners, mean = 25.1 SD = 5.2 | Running (Treadmill) | 180s | 1DoF knee | pelvis, shank | 3D GYR, 3D ACC, 3D MAG | |
| (10 km/h–14 km/h) | |||||||
| [32] | 2M, healthy, range: 23–25 | Leg exercises, gait | 8s * | 3DoF ankle | 3DoF ankle | 3D GYR, 3D ACC, 3D MAG | |
| [40] | 1M, ND, 29 | Squat | 11s * | 1DoF knee | thigh, shank | 1D ACC | |
| [20] | 1, transfemoral amputee, 40 | Gait | 6s * | 1DoF knee, 1DoF ankle | thigh, shank, foot | 3D GYR, 3D ACC | |
| [33] | 3M, healthy, range: 23–28 | Gait | 10s * | 2DoF hip, 1DoF knee | thigh, shank | 3D GYR, 3D ACC | |
| [34] | 5M, healthy, range: 22–27 | Gait | ND | 1DoF hip, 1DoF knee, 1DoF ankle | pelvis, thigh, shank, foot | 3D GYR, 3D ACC | |
| [24] | 5M, healthy, mean = 27.6 SD = 3.4 | Gait (Treadmill), | 15min | 1DoF hip, 1DoF knee, 1DoF ankle | lower back, thigh, shank, foot | 3D GYR, 3D ACC, 3D MAG, pressure insoles | |
| Stair walking | |||||||
| [35] | 6, healthy, > = 18 | Gait | ND | 1DoF hip, 1DoF knee | center of lumbar, thigh (most distal), shank (most distal) | 1D ACC, 1D GYR | |
| (Cadence range: 60-120 step/min) | |||||||
| [36] | 1, healthy, ND | Gait (self-selected speed) | 2s * | 1DoF knee | thigh, shank | 2 × 3D ACC, PSECR insole | |
| [17] | 7F 3M/3F 9M, healthy/unilateral ankle osteoarthritis, mean = 60 SD = 15/mean = 61 SD = 13 | Gait (Treadmill) | 5min | 3DoF shank-hindfoot, 3DoF hindfoot-forefoot, 3DoF shank-forefoot, 3DoF forefoot-toes | shank, hindfoot, forefoot, toes | 3D GYR, 3D ACC | |
| (2 km/h–5 km/h) | |||||||
| [45] | 1M, healthy, 23 | Standing | 5s * | 1DoF hip, 1DoF knee, 1DoF ankle | chest, right thigh, right shank | 3D GYR, 3D ACC, 3D MAG, pressure insole | |
| long jump | |||||||
| [18] | 12M 8F, healthy, mean = 23 | Functional rehabilitation exercises | ND | 3DoF (stationary base), 2DoF knee, 1DoF | hip (height of the anterior superior iliac spine), thigh (near the knee), calf (near the ankle) | 3D GYR, 3D ACC | |
| [41] | 5M 3F, healthy, mean = 32.5 SD = 9.9 | Squat | ND | 1DoF hip, 1DoF knee, 1DoF ankle | lower back | 1D GYR, 2D ACC | |
| [39] | 9M 1F, healthy, mean = 25 SD = 3 | Functional exercise | ND | 3DoF hip, 1DoF knee | shank | 1D GYR, 2D ACC | |
| [37] | 5, healthy, range: 19–25 | Gait | ND | 3DoF hip, 1DoF knee, 1DoF ankle | waist, hip, knee | 3D GYR, 3D ACC | |
| [46] | 1, ND, ND | Cycling | 5min | 3DoF hip | pelvis, thigh | 3D GYR, 3D ACC, 3D MAG | |
| [21] | 2, 1 healthy and 1 incomplete SCI subject, ND | Gait | 50s * | 1DoF knee | thigh, shank | 1D GYR, FSR | |
| [19] | 5 healthy/28 CP, 3M 2F/17M 3M 2F/17M 11F, healthy/CP, mean = 26 SD = 2.0/(18 subjects mean 7.5 sd = 3.1 and 10 subjects mean 5.5 sd 3.5) | Leg movements in supine position | 30s * | 1DoF knee, 1DoF ankle | thigh, shank, foot | 3D GYR, 3D ACC | |
| [22] | 3 and 2, healthy and stroke patients, ND and rang: 67:77 | Gait | 80s | 3DoF hip, 1DoF knee | pelvis, thigh, shank | 3D GYR, 3D ACC | |
| [44] | 5M 3F, healthy, mean = 30 SD = 6 | Gait, running | 5min | 1DoF knee | thigh, shank | 3D GYR, 3D ACC | |
| [38] | 10M, healthy, mean = 27.1 sd = 2.6 | Gait, running | ND | 1DoF hip, 1DoF knee, 1DoF ankle | lower back, lateral thigh, lateral shank, and upper midfoot. | 3D GYR, 3D ACC | |
| Ref. | Pre-Processing | Additional Information | Signal Processing | ||||
|---|---|---|---|---|---|---|---|
| Sensor Calibration | Filter, Type, Order, Cut-Off, Input Data | Prior Knowledge | Assumptions | Initialization and Sensor-Segment Alignment | Information Fusion | Drift Compensation | |
| [23] | ND | Savitzky-Golay, LP, 3, ND, GYR ACC | Position sensor w.r.t. joint center (Photography) | Same acceleration in joint center, Sensor-to-segment mounting assumptions | (INI) Static: 5s (knees extended) and 5s (knees flexed) (S-S) assumptions | Virtual sensors in joint center | N/A |
| [25] | ND | ND | ND | ND | (INI) Static: 10s stand still, Functional: hip AA. | Strap-down integration [53] | ACC gravity compensation, during characteristic samples |
| [26] | ND | ND | ND | ND | (INI) Static: stand still Functional: hip AA, (S-S) Passive shank movements in frontal and sagittal plane | Strap-down integration [53] | ACC gravity compensation, during characteristic samples |
| [16] | ACC | ND | ND | Tangential and centripetal acceleration from redundant ACC set-up, Periodicity | (INI) Static: 2s stand still before and after a trial | N/A | BP filtering |
| [27] | ND | ND | Position sensor w.r.t. joint center | Tangential and centripetal acceleration from redundant ACC set-up | (INI) Static: 2s stand still before and after a trial | N/A | ACC gravity compensation, during characteristic samples, Nonlinear optimization |
| [28] | ND | ND, LP, ND, 20Hz, ACC | Position sensor w.r.t. joint center | Tangential and centripetal acceleration from redundant ACC set-up, Same acceleration in joint center | ND | N/A | N/A |
| [42] | GYR, ACC [47] | ND, LP, ND, 100, GYR ACC | ND | Same acceleration in joint center | (INI) Static: stand still (S-S)[52] | Strap-down integration [53] | ACC gravity compensation, during characteristic samples, Multi-sensor drift correction |
| [29] | GYR | ND | Manual measuring: Orientation sensor on body segment, Position sensor w.r.t. joint center | Segments are connected to each other at all time and Sensors can move slightly w.r.t. body segment | (INI) Static: stand still pose (ACC and MAG) (S-S) prior information | Constraint optimization, Strap-down integration | Exploit assumptions |
| [30] | ND | ND | Subject specific trained model | Periodicity | ND | Regression: GRNN | N/A |
| [31] | ND | ND | Subject specific trained model | ND | ND | Regression: GRNN | N/A |
| [43] | ND | (No inertial data was filtered) | Subject specific trained model | ND | ND | Regression: ANN, two-layer (250 and 100 neurons) | N/A |
| [32] | GYR, ACC [47] | Butterworth, LP, 2, 5Hz, ACC GYR | ND | Assume same discrepancies in magnetic field interference for both segments | (S-S) Functional: two leg movements. | Strap-down integration | ACC gravity compensation, during characteristic samples, MAG readings |
| [40] | ND | ND | Stereo-photogrammetric: Segment lengths, Orientation sensor on body segment, Position sensor w.r.t. joint center | Feet are supposed rigidly connected to the ground, Pendulum motion | (S-S) prior information | N/A | N/A |
| [20] | ND | ND | ND | Same acceleration in joint center | N/A | Complementary filter | Exploit assumptions |
| [33] | GYR, ACC | Moving average, LP, ND, 15 point at 100Hz, ACC GYR | Segment lengths | Same acceleration in joint center, Pendulum motion thigh around the hip, constant velocity in walking speed | (S-S) Static: two poses (standing upright and sitting flat with outstretched legs) | Pendulum model | N/A |
| [34] | GYR | Butterworth, LP, 4, 12Hz, GYR | Segment lengths, Orientation sensor on body segment (sagittal image) | ND | (INI) Static: two poses (standing upright and sitting flat with outstretched legs) (S-S) prior knowledge | Strap-down integration | ACC gravity compensation, during characteristic samples |
| [24] | ND | ND | Optical reference: Segment lengths, Position sensor w.r.t. joint center | One foot on the ground at all time with zero acceleration at contact point. | ND | Recursive EKF | ACC gravity compensation, during characteristic samples, Exploit assumptions |
| [35] | ND | ND | Position sensor w.r.t. joint center | Symmetry, Drift linearly accumulates during integration, ACC measured most distal at a segment equals the joint center acceleration, Same acceleration in joint center | ND | Strap-down integration | ACC gravity compensation, during characteristic samples, Modeling and correcting drift as linear accumulating |
| [36] | ND | ND, BP, ND, function of PSECR skin motion frequency content, ACC | Position sensor w.r.t. joint center, total pressure, CoP between sensor and skin | Same acceleration in joint center | ND | N/A | N/A |
| [17] | ND | ND | Orientation sensor on body segment (Optical motion capture system) | Periodicity | (S-S) prior information | Strap-down integration | ACC gravity compensation, during characteristic samples, Azimuth zeroing cycle-by- cycle. |
| [45] | ND | ND | Segment lengths | Symmetry, Periodicity | (INI) Static: stand still pose. | Strap-down integration, displacement from ACC double integration | Exploit assumption Symmetry |
| [18] | GYR, ACC [47] | ND | Segment lengths (Optical motion capture system), RoM, (anthropometric data) | DH convention | ND | EKF | Exploit assumptions & prior information |
| [41] | ND | ND | Segment lengths, RoM | Periodicity, perfect sagittal symmetry | ND | Inverse kinematics, displacement from ACC double integration | Exploit assumptions |
| [39] | ND | Butterworth, LP, ND, 2Hz, squared GYR | RoM, Segment lengths (manually measured), Initial joint angle (measured by goniometer) | Periodicity, DH convention | (INI) prior information | Constraint optimization | Exploit assumptions |
| [37] | GYR | ND | Segment lengths, Orientation sensor on body segment, (Manual annotation) Spatio-temporal data. | One foot on the ground at all time, kinematic chain model [49] | (S-S) prior information | EKF | Exploit assumptions |
| [46] | ND | Butterworth, LP, 4, 15Hz, ACC | Position sensor w.r.t. joint center, Orientation sensor on body segment | Pendulum motion of thigh segment around the hip CoR | (S-S) prior information | Adapted complimentary filter [54] | Exploit assumptions, MAG readings |
| [21] | GYR | Butterworth, LP, 4, 4Hz, GYR | Spatio-temporal data (FSR measurements) | Sensor-to-segment mounting assumptions | (S-S) assumptions | N/A | HP filtering kinematic estimates, resetting during mid-stance in gait cycle. |
| [19] | ND | Butterworth, LP, 2, 10Hz, GYR ACC | ND | Movements outside sagittal plane occur only at full extension | ND | Strap-down integration | ACC measuring gravity during characteristic samples. Correction for movements outside of sagittal plane. |
| [22] | GYR, ACC [48] | ND, LP, ND, 10Hz, GYR ACC | ND | Periodicity, kinematic chain model [49] | ND | Adapted EKF | Exploit assumption Periodicity |
| [44] | ND | ND | Sensor orientation difference adjacent segments, Initial sensor orientation (Optical motion capture system) | ND | (CAL and S-S) prior information | EKF | Exploit Joint DoF constraint. |
| [38] | GYR, ACC [47] | ND | Segment masses, measured segment lengths, center of mass locations, moments of inertia [55] | Periodicity, constrain translational joint movement | (S-S) ND (I-I) initial guess | Constraint optimization | Exploit assumptions |
| Ref. | Reference | Accuracy | |||
|---|---|---|---|---|---|
| Method | Joint [Measure, Unit] | Sagittal | Frontal | Transversal | |
| [23] | Ultra-sound based motion measurement | knee [RMSE, deg] | 1.3 | ||
| [25] | Magnetic tracking device | knee [RMSE mean (SD), deg] | 1.5 (0.4) * | 1.7 (0.5) * | 1.6 (0.5) * |
| [26] | Magnetic tracking device | knee [RMSE mean (SD), deg] | 1.3 (0.5) * | 2.0 (0.6) * | 2.0 (0.9) * |
| [16] | Flexible goniometer | knee [RMSE median, deg] | 5 | ||
| ankle [RMSE median, deg] | 3.5 | ||||
| [27] | Optical motion capture system | knee [RMSE median, deg] | 3 | ||
| ankle [RMSE median, deg] | 2.8 | ||||
| [28] | Optical motion capture system | hip [RMSE, deg] | 4.1 | 4.9 | |
| [42] | High definition camera’s | hip [RMSE, deg] | 6.0 (1.5) * | ND | ND |
| knee [RMSE, deg] | 4.8 (1.7) * | ND | ND | ||
| [29] | Optical motion capture system | knee | graph only | graph only | graph only |
| [30] | Optical motion capture system | hip | *,*,* | ||
| knee | *,*,* | ||||
| ankle | *,*,* | ||||
| [31] | Optical motion capture system | hip [correlation] | (0.7-0.89) *,*,* | ||
| knee [correlation] | (0.7-0.89) *,*,* | ||||
| ankle [correlation] | (0.7-0.89) *,*,* | ||||
| [43] | Optical motion capture system | knee [mean RMSE, deg] | <5 *,*,* | ||
| [32] | Optical motion capture system | ankle [RMSE, deg] | [0,1] *,* | [1–2.5] *,* | [2.5–4.5] *,* |
| [40] | Mechanical pendulum setup and Optical motion capture system | knee [RMSE mean (SD), deg] | 1.01 (0.11) | ||
| [20] | Optical motion capture system | knee [RMSE healthy|prosthesis mean (SD), deg] | 3.30 (1.20)|0.71 (0.19) | ||
| Ankle [RMSE healthy|prosthesis, deg] | 1.62 (0.57)|0.81 (0.16) | ||||
| [33] | Optical motion capture system | hip [RMSE, deg] | 8.72 | 4.96 | |
| knee [RMSE, deg] | 6.79 | ||||
| [34] | Optical motion capture system | hip [RMSE, deg] | 10.14 | ||
| knee [RMSE, deg] | 7.88 | ||||
| ankle [RMSE, deg] | 9.75 | ||||
| [24] | Optical motion capture system | hip (median over all described conditions, deg) | <5 | ||
| knee (median over all described conditions, deg) | <5 | ||||
| ankle (median over all described conditions, deg) | <5 | ||||
| [35] | Optical motion capture system | hip [RMSE mean (SD), deg] | 5.24 (0.27) | ||
| knee [RMSE mean (SD), deg] | 11.22 (1.09) | ||||
| [36] | Optical motion capture system | knee | graph only | ||
| [17] | Optical motion capture system | shank-hindfoot, hindfoot-forefoot, shank-forefoot, forefoot-toes [RMSE, deg] | [1.4; 2] | [1.4; 2] | [1.4; 2] |
| [45] | Optical motion capture system | hip [RMSE, deg] | 3.92 | ||
| knee [RMSE, deg] | 7.87 | ||||
| ankle [RMSE, deg] | 3.22 | ||||
| [18] | Optical motion capture system | hip [RMSE mean, deg] | 4.3 | 6.5 | 6.5 |
| knee [RMSE mean, deg] | 4.3 | 6.5 | |||
| ankle [RMSE mean, deg] | 4.3 | ||||
| [41] | Optical motion capture system | hip [RMSE mean (SD), deg] | 3.1 (0.9) | ||
| knee [RMSE mean (SD), deg] | 2.0 (1.0) | ||||
| ankle [RMSE mean (SD), deg] | 3.2 (1.0) | ||||
| [39] | Optical motion capture system | hip [RMSE mean (SD), deg] | 3.6 (2.4) | 2.4 (1.0) | 2.7 (1.4) |
| knee [RMSE mean (SD), deg] | 4.0 (3.1) | ||||
| [37] | Optical motion capture system | hip | ND | ND | ND |
| knee [RMSE mean (SD), deg] | 6.20 (1.48) | ||||
| ankle | ND | ||||
| [46] | Optical motion capture system | hip [MAE, deg] | 0.8 | 6.7 | 2.2 |
| [21] | Optical motion capture system | knee [RMSE, deg] | 6.42 | ||
| [19] | Optical motion capture system | knee [RMSE, deg] | <3 | ||
| ankle [RMSE, deg] | <3 | ||||
| [22] | Optical motion capture system | hip [RMSE, deg] | 2.4 | 2.4 | 2.4 |
| knee [RMSE, deg] | 2.4 | ||||
| [44] | Optical motion capture system | knee [RMSE, deg] | |||
| [38] | Optical motion capture system | hip [RMSE mean (SD), deg] | 8.7 | ||
| knee [RMSE mean (SD), deg] | 5.3 | ||||
| ankle [RMSE mean (SD), deg] | 4.6 | ||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Weygers, I.; Kok, M.; Konings, M.; Hallez, H.; De Vroey, H.; Claeys, K. Inertial Sensor-Based Lower Limb Joint Kinematics: A Methodological Systematic Review. Sensors 2020, 20, 673. https://doi.org/10.3390/s20030673
Weygers I, Kok M, Konings M, Hallez H, De Vroey H, Claeys K. Inertial Sensor-Based Lower Limb Joint Kinematics: A Methodological Systematic Review. Sensors. 2020; 20(3):673. https://doi.org/10.3390/s20030673
Chicago/Turabian StyleWeygers, Ive, Manon Kok, Marco Konings, Hans Hallez, Henri De Vroey, and Kurt Claeys. 2020. "Inertial Sensor-Based Lower Limb Joint Kinematics: A Methodological Systematic Review" Sensors 20, no. 3: 673. https://doi.org/10.3390/s20030673
APA StyleWeygers, I., Kok, M., Konings, M., Hallez, H., De Vroey, H., & Claeys, K. (2020). Inertial Sensor-Based Lower Limb Joint Kinematics: A Methodological Systematic Review. Sensors, 20(3), 673. https://doi.org/10.3390/s20030673





