An Experimental Strategy for Characterizing Inductive Electromagnetic Energy Harvesters
Abstract
1. Introduction
2. CT-based Energy Harvesting System Model
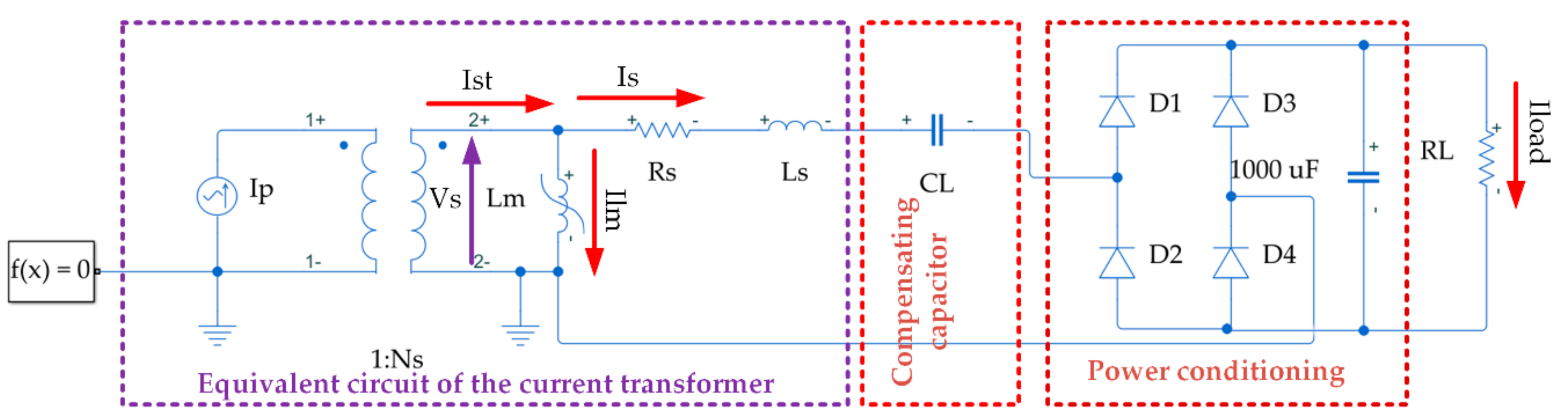
2.1. Equivalent Electrical Circuit of the Energy Harvester
2.2. Linear and Nonlinear Behavior of the Energy Harvester Model.
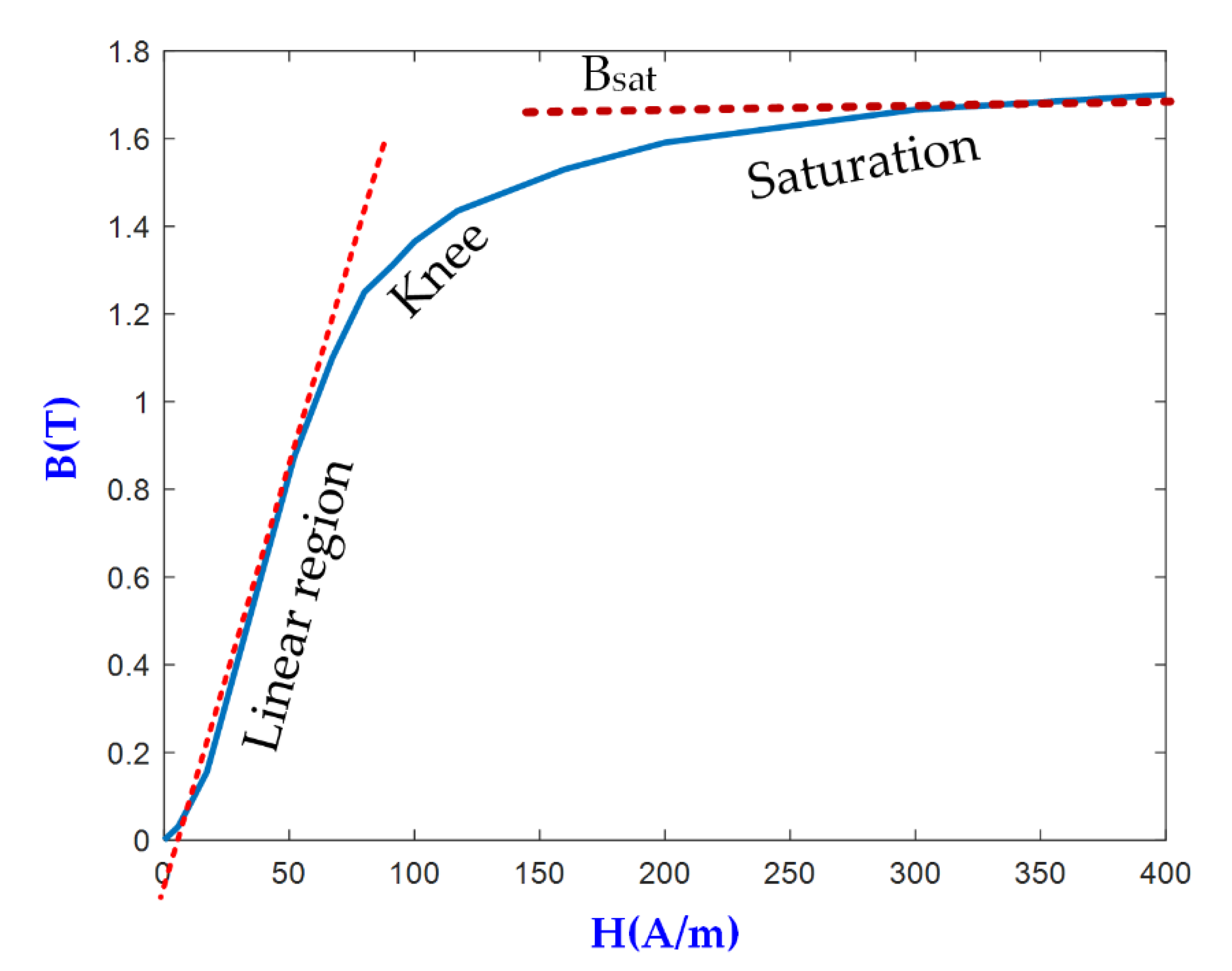
2.3. Saturation Characterization
3. Simulation-Based Characterization of the Inductive Electromagnetic Energy Harvester
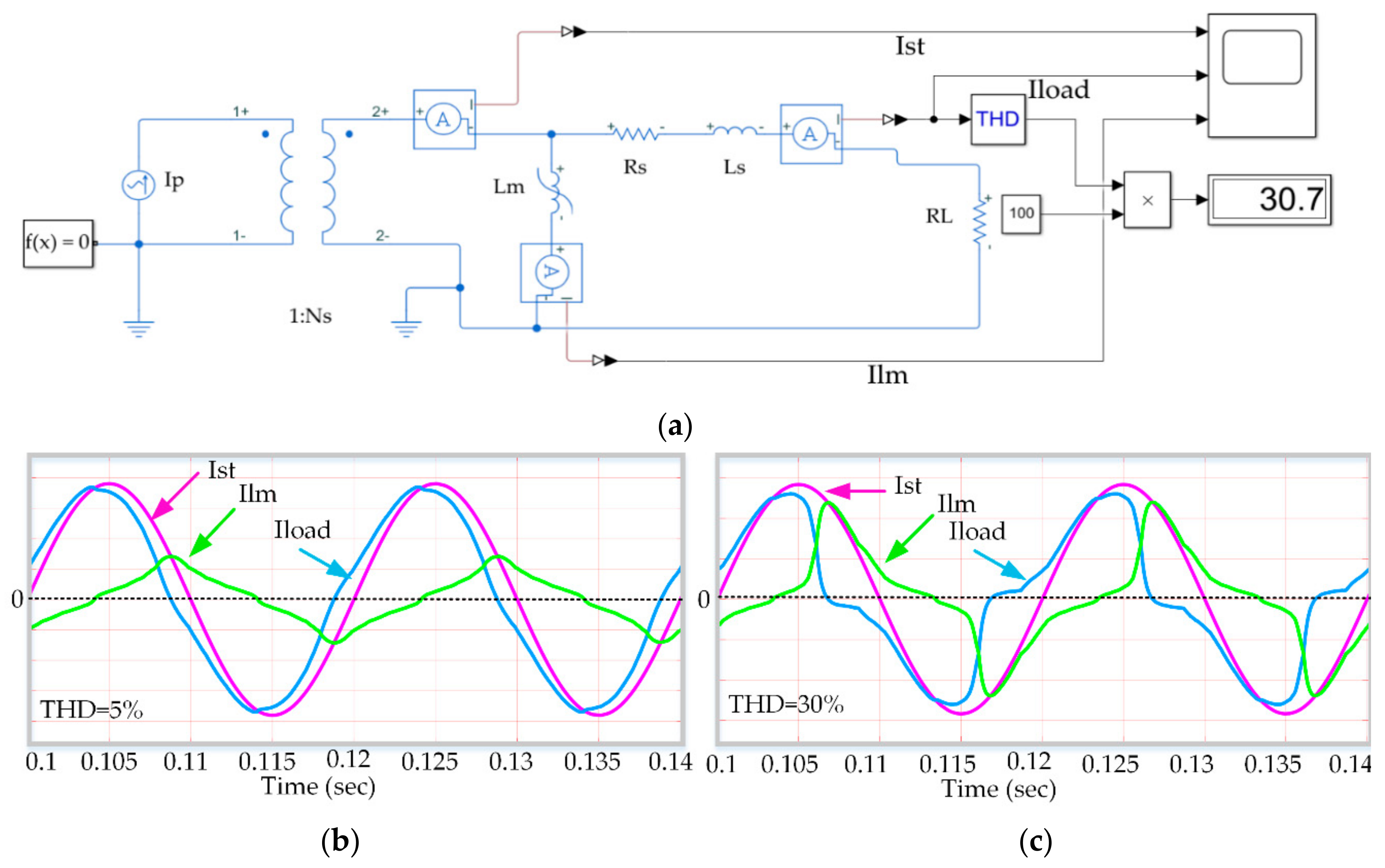
3.1. Model 1. Simulation with an Energy Harvester with Rectifier and Resistive Load Without Reactive Power Compensation.
3.2. Model 2. Simulation with an Energy Harvester with Rectifier and Reactive Power Compensation
4. Verification of the Model Accuracy. Experimental Results and Energy Harvester Prototype
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Weimer, M.A.; Paing, T.S.; Zane, R.A. Remote area wind energy harvesting for low-power autonomous sensors. In Proceedings of the 37th IEEE Power Electronics Specialists Conference, Jeju, Korea, 18–22 June 2006; pp. 1–5. [Google Scholar]
- Orrego, S.; Kourosh, S.; Andre, R.; Kyle, D.; Brett, C.; Rajat, M.; Sung, H.K. Harvesting ambient wind energy with an inverted piezoelectric flag. Appl. Energy 2017, 194, 212–222. [Google Scholar] [CrossRef]
- Perez, M.; Boisseau, S.; Reboud, J.L. Design and performance of a small-scale wind turbine exploiting an electret-based electrostatic conversion. In Proceedings of the Journal of physics: Conference series, Southampton, UK, 12–16 April 2015; 646, p. 012009. [Google Scholar]
- Perez, M.; Boisseau, S.; Geisler, M.; Despesse, G.; Reboud, J.L. A triboelectric wind turbine for small-scale energy harvesting. In Proceedings of the Journal of Physics: Conference Series, Paris, France, 6–9 December 2016; p. 012118. [Google Scholar]
- Li, Y.; Shi, R. An intelligent solar energy-harvesting system for wireless sensor networks. EURASIP J. Bioinf. Syst. Biol. 2015, 1, 179. [Google Scholar] [CrossRef]
- Shaikh, F.K.; Zeadally, S. Energy harvesting in wireless sensor networks: A comprehensive review. Renewable Sustainable Energy Rev. 2016, 55, 1041–1054. [Google Scholar] [CrossRef]
- Habibzadeh, M.; Hassanalieragh, M.; Ishikawa, A.; Soyata, T.; Sharma, G. Hybrid solar-wind energy harvesting for embedded applications: Supercapacitor-based system architectures and design tradeoffs. IEEE Circuits Syst. Mag. 2016, 55, 1041–1054. [Google Scholar] [CrossRef]
- Wei, C.F.; Jing, X.J. A comprehensive review on vibration energy harvesting: Modelling and realization. Renewable Sustainable Energy Rev. 2017, 74, 1–18. [Google Scholar] [CrossRef]
- Nasiri, A.; Zabalawi, S.A.; Jeutter, D.C. A linear permanent magnet generator for powering implanted electronic devices. IEEE Trans. Power Electron. 2011, 26, 192–199. [Google Scholar] [CrossRef]
- Zergoune, Z.; Kacem, N.; Bouhaddi, N. On the energy localization in weakly coupled oscillators for electromagnetic vibration energy harvesting. Smart Mater. Struct. 2019, 28, 07LT02. [Google Scholar] [CrossRef]
- Mahmoudi, S.; Kacem, N.; Bouhaddi, N. Enhancement of the performance of a hybrid nonlinear vibration energy harvester based on piezoelectric and electromagnetic transductions. Smart Mater. Struct. 2014, 23, 075024. [Google Scholar] [CrossRef]
- Abed, I.; Kacem, N.; Bouhaddi, N.; Bouazizi, M.L. Multi-modal vibration energy harvesting approach based on nonlinear oscillator arrays under magnetic levitation. Smart Mater. Struct. 2016, 25, 025018. [Google Scholar] [CrossRef]
- Mann, B.P.; Sims, N.D. Energy harvesting from the nonlinear oscillations of magnetic levitation. J. Sound Vib. 2009, 319, 515–530. [Google Scholar] [CrossRef]
- Drezet, C.; Kacem, N.; Bouhaddi, N. Design of a nonlinear energy harvester based on high static low dynamic stiffness for low frequency random vibrations. Sens. Actuators, A 2018, 283, 54–64. [Google Scholar] [CrossRef]
- Yang, B.; Lee, C.K.; Xiang, W.F.; Xie, J.; He, J.H.; Kotlanka, R.K.; Low, S.P.; Ping, S. Electromagnetic energy harvesting from vibrations of multiple frequencies. J. Micromech. Microeng. 2009, 19, 035001. [Google Scholar] [CrossRef]
- Sari, I.; Balkan, T.; Kulah, H. An electromagnetic micro power generator for wideband environmental vibrations. Sens. Actuators. A 2008, 145, 405–413. [Google Scholar] [CrossRef]
- Yildiz, F.; Coogler, K.L. Low power energy harvesting with a thermoelectric generator through an air conditioning condenser. ASEE Annu. Conf. Expostition 2014, 24, 1. [Google Scholar]
- Hyland, M.; Hunter, H.; Liu, J.; Veety, E.; Vashaee, D. Wearable thermoelectric generators for human body heat harvesting. Appl. Energy 2016, 182, 518–524. [Google Scholar] [CrossRef]
- Lu, Z.S.; Zhang, H.H.; Mao, C.P.; Li, C.M. Silk fabric-based wearable thermoelectric generator for energy harvesting from the human body. Appl. Energy 2016, 164, 57–63. [Google Scholar] [CrossRef]
- Ren, J.; Hu, J.; Zhang, D.Y.; Guo, H.; Zhang, Y.X.; Shen, X.M. RF energy harvesting and transfer in cognitive radio sensor networks: Opportunities and challenges. IEEE Commun. Mag. 2018, 56, 104–110. [Google Scholar] [CrossRef]
- Mishra, D.; De, S.; Jana, S.; Basagni, S.; Chowdhury, K.; Heinzelman, W. Smart RF energy harvesting communications: Challenges and opportunities. IEEE Commun. Mag. 2018, 56, 104–110. [Google Scholar] [CrossRef]
- Soyata, T.; Copeland, L.; Heinzelman, W. RF energy harvesting for embedded systems: A survey of tradeoffs and methodology. IEEE Commun. Mag. 2016, 16, 22–57. [Google Scholar] [CrossRef]
- Chang, K.S.; Kang, S.M.; Park, K.J.; Shin, S.H. Electric field energy harvesting powered wireless sensors for smart grid. J. of Electr. Eng. Technol. 2012, 7, 75–80. [Google Scholar] [CrossRef]
- Cetinkaya, O.; Akan, O.B. Electric-field energy harvesting in wireless networks. IEEE Wirel. Commun. 2017, 24, 34–41. [Google Scholar] [CrossRef]
- Yeesparan, S.; Mohd, Z.B.B.; Norashidah, B.M.D.; Mohamad, H.H. A review of energy harvesting methods for power transmission line monitoring sensors. Int. J. of Eng. Technol. (UAE) 2018, 7, 153–161. [Google Scholar] [CrossRef]
- Guo, F.; Hayat, H.; Wang, J. Energy harvesting devices for high voltage transmission line monitoring. In Proceedings of the IEEE Power Energ. Soc. Gen. Meeting, Detroit, MI, USA, 24–28 July 2011; pp. 1–8. [Google Scholar]
- Zhao, D.S.; Dai, D.; Li, L.C. Electric field energy harvesting for on-line condition-monitoring device installed on high-voltage transmission tower. Electron. Lett 2015, 51, 1692–1693. [Google Scholar] [CrossRef]
- Roscoe, N.M.; Judd, M.D. Harvesting energy from magnetic fields to power condition monitoring sensors. IEEE Sens. J. 2013, 13, 2263–2270. [Google Scholar] [CrossRef]
- Dos, S.P.M.; Vieira, D.A.; Rodriguez, Y.P.M.; Souza, C.P.; Moraes, T.O.; Freire, R.C. Energy harvesting using magnetic induction considering different core materials. In Proceedings of the IEEE International Instrumentation and Measurement Technology Conference (I2MTC) Proceedings, Montevideo, Uruguay, 12–15 May 2014; pp. 942–944. [Google Scholar]
- Hosseinimehr, T.; Tabesh, A. Magnetic field energy harvesting from AC lines for powering wireless sensor nodes in smart grids. IEEE Trans. Ind. Electron. 2016, 63, 4947–4954. [Google Scholar]
- Moon, J.; Leeb, S.B. Analysis model for magnetic energy harvesters. IEEE Trans. Power Electron. 2014, 30, 4302–4311. [Google Scholar] [CrossRef]
- Yuan, S.; Huang, Y.; Zhou, J.F.; Xu, Q.; Song, C.Y.; Yuan, G.Q. A high-efficiency helical core for magnetic field energy harvesting. IEEE Trans. Power Electron. 2016, 32, 5365–5376. [Google Scholar] [CrossRef]
- Liu, Y.D.; Xie, X.L.; Hu, Y.; Qian, Y.; Sheng, G.H.; Jiang, X.C.; Liu, Y.L. A novel high-density power energy harvesting methodology for transmission line online monitoring devices. Rev. Sci. Instrum. 2016, 87, 075119. [Google Scholar] [CrossRef]
- Paul, S.; Chang, J.H. Design of novel electromagnetic energy harvester to power a deicing robot and monitoring sensors for transmission lines. Energy Convers. Manage. 2019, 197, 111868. [Google Scholar] [CrossRef]
- Gupta, V.; Kandhalu, A.; Rajkumar, R.R. Energy harvesting from electromagnetic energy radiating from AC power lines. In Proceedings of the 6th Workshop on Hot Topics in Embedded Networked Sensors, Killarney, Ireland, 28–29 June 2010; p. 17. [Google Scholar]
- Ottman, G.; Hofmann, H.F.; Bhatt, A.C.; Lesieutre, G.A. Adaptive piezoelectric energy harvesting circuit for wireless, remote power supply. In Proceedings of the 20th AIAA Applied Aerodynamics Conference, St. Louis, MO, USA, 24–26 June 2002; 2001; p. 1505. [Google Scholar]
- Qian, Z.N.; Wu, J.; He, X.N.; Lin, Z.Y. Power maximised and anti-saturation power conditioning circuit for current transformer harvester on overhead lines. IET Power Electron. 2018, 11, 2271–2278. [Google Scholar] [CrossRef]
- Lefeuvre, E.; Audigier, D.; Richard, C.; Guyomar, D. Buck-boost converter for sensorless power optimization of piezoelectric energy harvester. IEEE Trans. Power Electron. 2007, 22, 2018–2025. [Google Scholar] [CrossRef]
- Kong, N.A.; Ha, D.S.; Erturk, A.; Inman, D.J. Resistive impedance matching circuit for piezoelectric energy harvesting. J. Intell. Mater. Syst. Struct. 2010, 21, 1293–1302. [Google Scholar] [CrossRef]
- Moghe, R.; Divan, D.; Deepak; Lambert, F. Powering low-cost utility sensors using energy harvesting. In Proceedings of the 14th European Conference on Power Electronics and Applications, Birmingham, UK, 30 August–1 September 2011; pp. 1–10. [Google Scholar]
- LI, P.; Wen, Y.M.; Zhang, Z.Q.; Pan, S.Q. A high-efficiency management circuit using multiwinding upconversion current transformer for power-line energy harvesting. IEEE Trans. Ind. Electron. 2015, 62, 6327–6335. [Google Scholar] [CrossRef]
- Simjee, F.; Chou, P.H. Everlast: long-life, supercapacitor-operated wireless sensor node. In Proceedings of the international symposium on Low power electronics and design, Tegernsee, Germany, 4–6 October 2006; pp. 197–202. [Google Scholar]
- Porcarelli, D.; Spenza, D.; Brunelli, D.; Cammarano, A.; Petrioli, C.; Benini, L. Adaptive rectifier driven by power intake predictors for wind energy harvesting sensor networks. IEEE J. Emerging Sel. Top. Circuits Syst. 2014, 3, 471–482. [Google Scholar] [CrossRef]
- Jiang, X.; Polastre, J.; Culler, D. Perpetual environmentally powered sensor networks. In Proceedings of the 4th international symposium on Information processing in sensor networks, Boise, ID, USA, April 2005; p. 65. [Google Scholar]
- MathWorks Documentation. Available online: https://es.mathworks.com/help/physmod/sps/examples/nonlinear-inductor-characteristics.html (accessed on 25 November 2019).


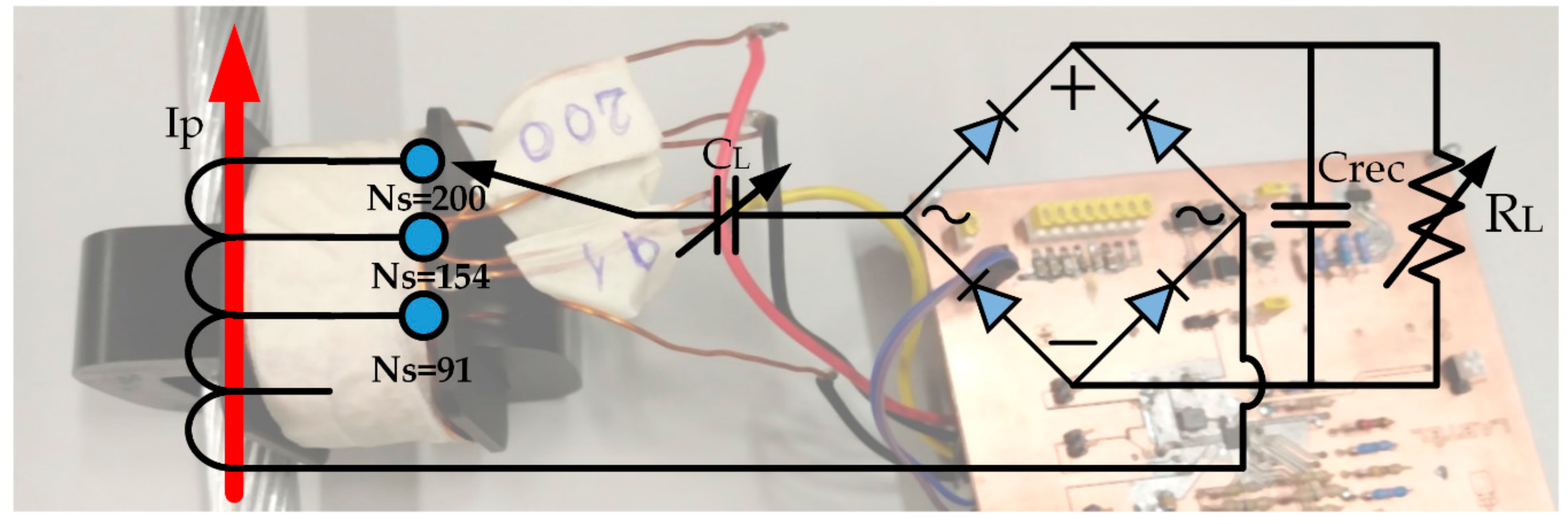
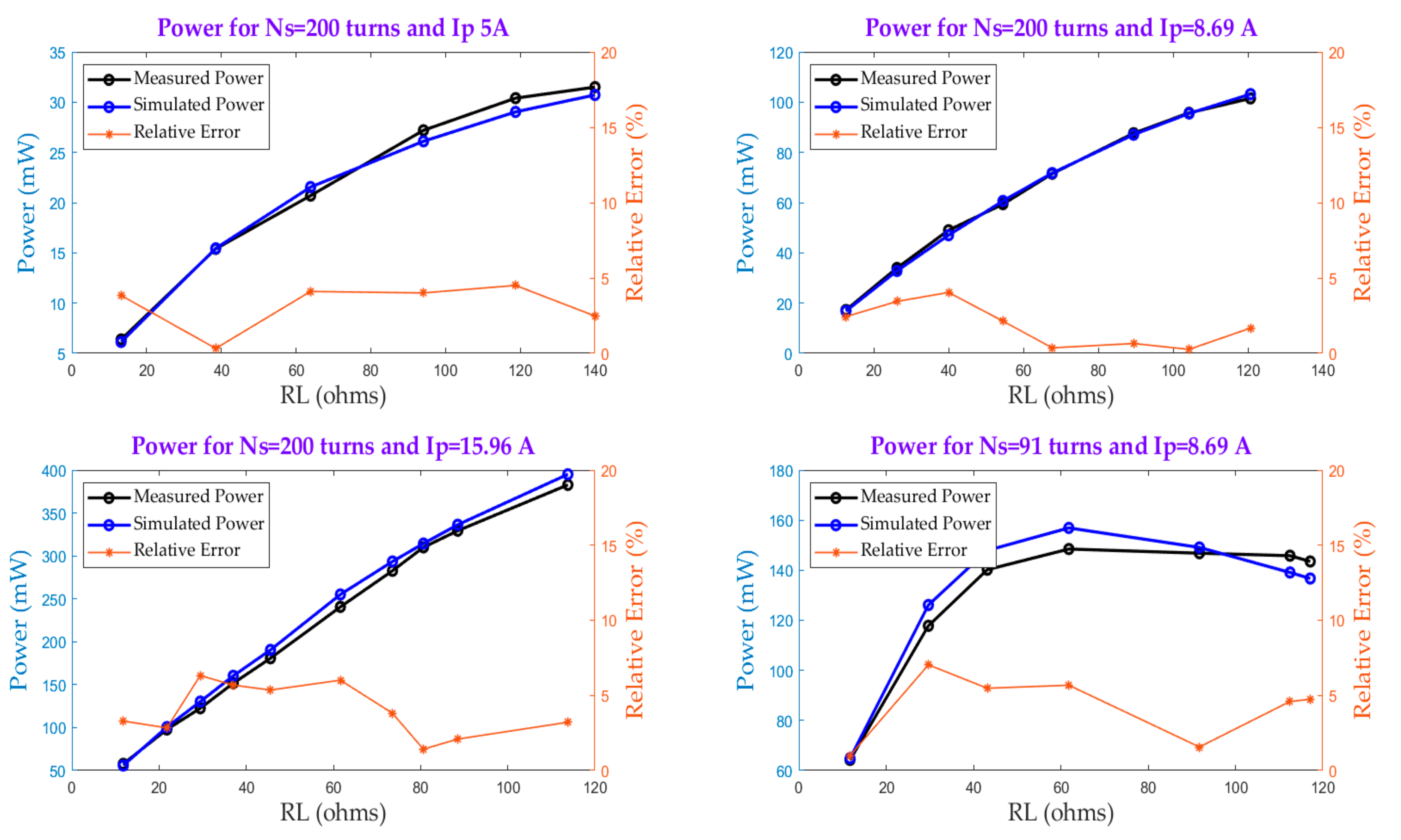
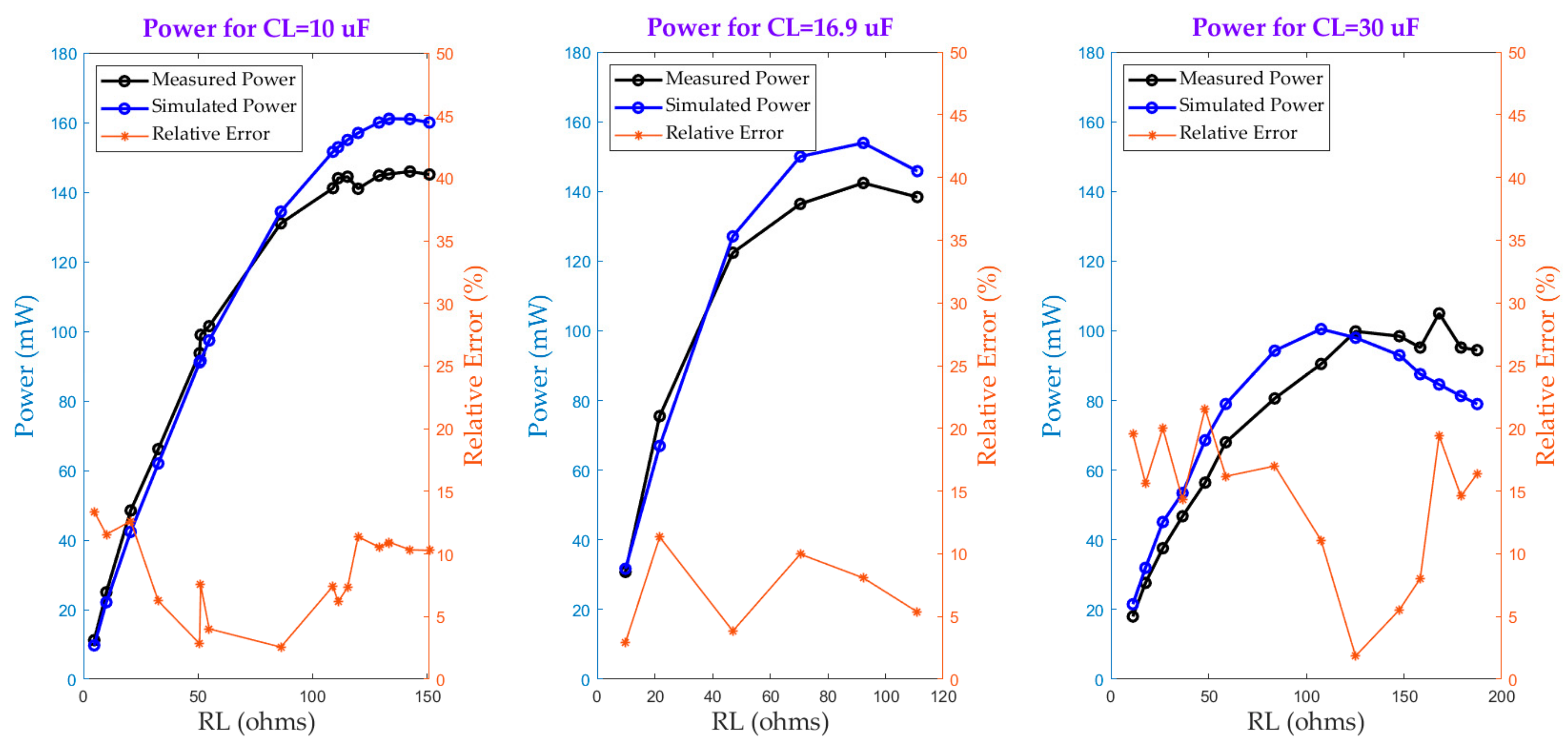
| Ip(A) | RL(Ω) | Vload(V) | Iload(mA) | THD (%) | Power (mW) |
|---|---|---|---|---|---|
| 12 | 65 | 3.21 | 49.42 | 6.3 | 158 |
| 12 | 70 | 3.44 | 49.15 | 5.6 | 169 |
| 13 | 60 | 3.24 | 54.08 | 6.8 | 175 |
| 13 | 65 | 3.49 | 53.81 | 5.8 | 188 |
| 14 | 50 | 2.95 | 59.04 | 6.5 | 174 |
| 14 | 55 | 3.23 | 58.76 | 5.8 | 189 |
| 15 | 40 | 2.56 | 64.05 | 6.3 | 164 |
| 15 | 45 | 2.86 | 63.74 | 6.6 | 182 |
| 15 | 50 | 3.17 | 63.45 | 6.9 | 201 |
| 15 | 55 | 3.47 | 63.16 | 5 | 219 |
| CL(μF) | RL(Ω) | Vload(V) | Iload(mA) | THD (%) | Power (mW) |
|---|---|---|---|---|---|
| 12 | 47 | 2.66 | 56.72 | 7.9 | 151.25 |
| 12 | 37 | 2.35 | 63.76 | 7.2 | 150.43 |
| 13 | 39 | 2.48 | 63.61 | 7.5 | 157.80 |
| 13 | 41 | 2.60 | 63.48 | 7.8 | 165.22 |
| 14 | 31 | 2.16 | 69.76 | 8.7 | 150.89 |
| Parameter | Value | Unit |
|---|---|---|
| Core material | Silicon steel | |
| Magnetic path length (leff) | 19.70 | cm |
| Cross-sectional area (Aeff) | 312 | mm2 |
| Core window area | 1000 | mm2 |
| Weight | 0.420 | Kg |
| Ns | 200, 154, 91 | turns |
| Winding wire diameter | 1 | mm |
| Average length per turn | 80 | mm |
| Maximum height | 25 | mm |
| Saturation magnetic flux density, Bsat | 1.7 | T |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martín Sánchez, P.; Rodríguez Sánchez, F.J.; Santiso Gómez, E. An Experimental Strategy for Characterizing Inductive Electromagnetic Energy Harvesters. Sensors 2020, 20, 647. https://doi.org/10.3390/s20030647
Martín Sánchez P, Rodríguez Sánchez FJ, Santiso Gómez E. An Experimental Strategy for Characterizing Inductive Electromagnetic Energy Harvesters. Sensors. 2020; 20(3):647. https://doi.org/10.3390/s20030647
Chicago/Turabian StyleMartín Sánchez, Pedro, Fco. Javier Rodríguez Sánchez, and Enrique Santiso Gómez. 2020. "An Experimental Strategy for Characterizing Inductive Electromagnetic Energy Harvesters" Sensors 20, no. 3: 647. https://doi.org/10.3390/s20030647
APA StyleMartín Sánchez, P., Rodríguez Sánchez, F. J., & Santiso Gómez, E. (2020). An Experimental Strategy for Characterizing Inductive Electromagnetic Energy Harvesters. Sensors, 20(3), 647. https://doi.org/10.3390/s20030647





