Cross-Frequency Power-Power Coupling Analysis: A Useful Cross-Frequency Measure to Classify ICA-Decomposed EEG
Abstract
1. Introduction
1.1. Background
1.2. Mini-Review on History of Power–Power Coupling Analysis
1.3. Goal of the Current Study
2. Materials and Methods
2.1. Data Acquisition and Preprocessing
2.2. Assessment of Cross-Frequency Power–Power Coupling
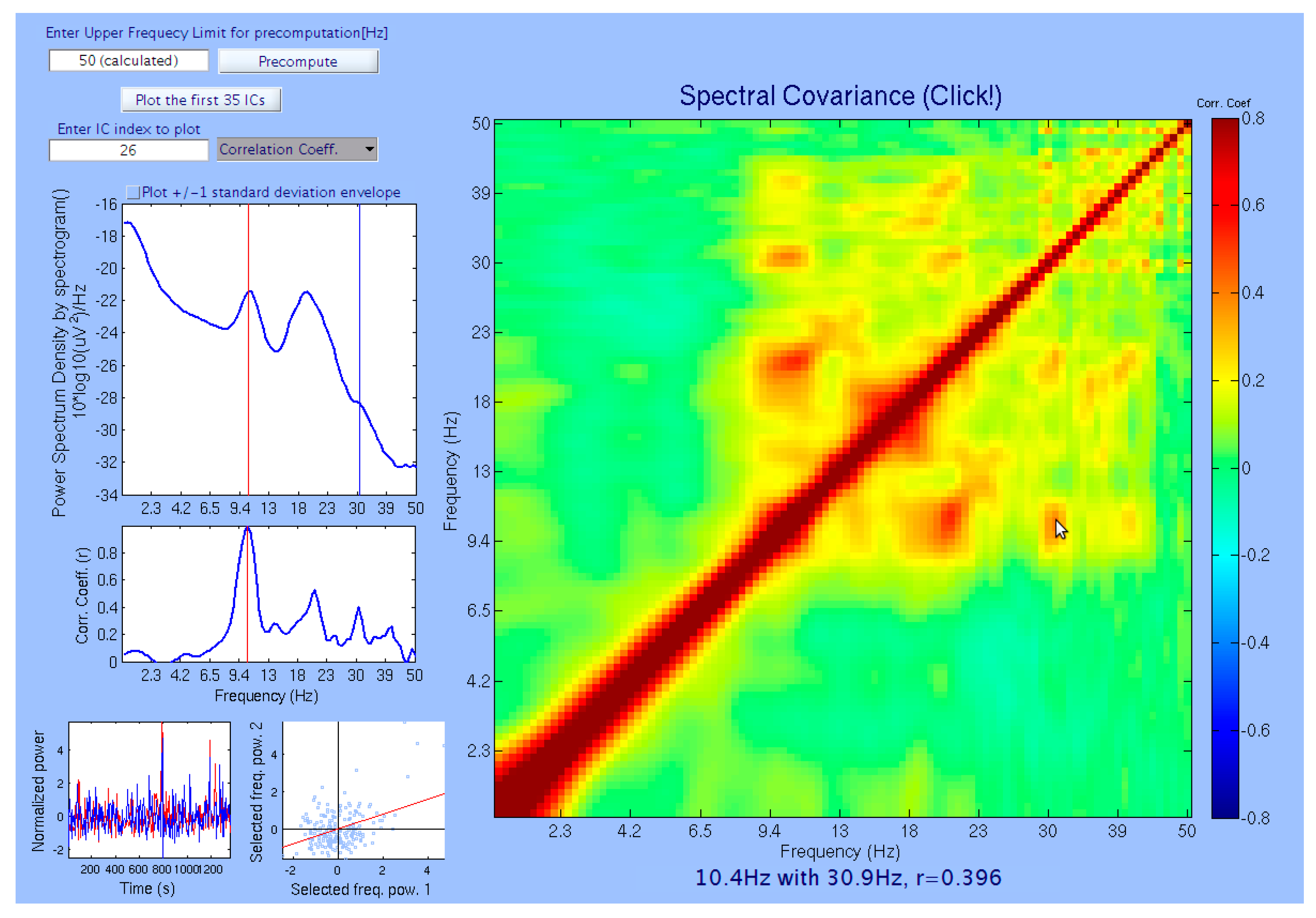
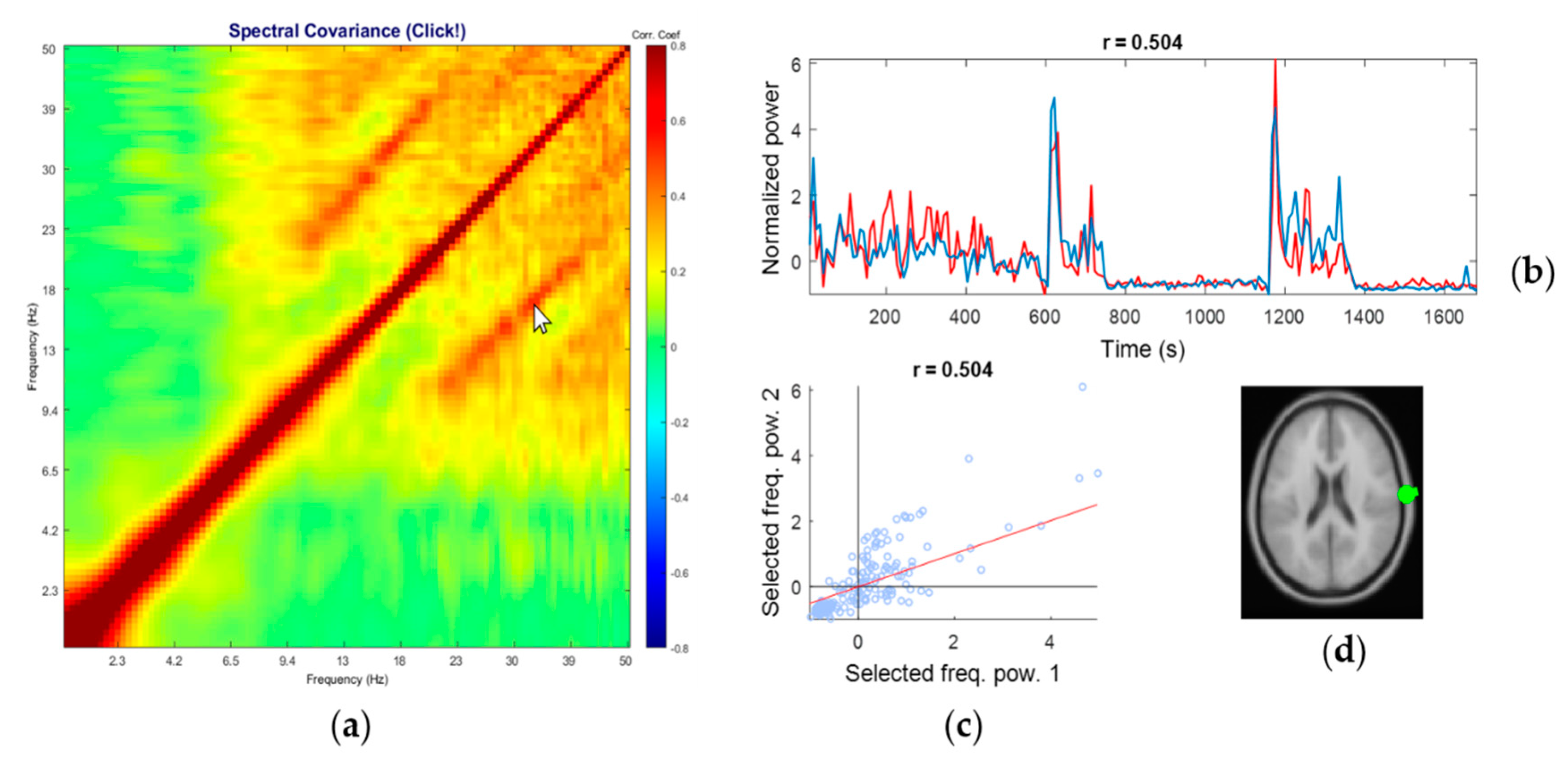
2.3. Visualizations by Power–Power Coupling Analysis Toolbox (PowPowCAT)
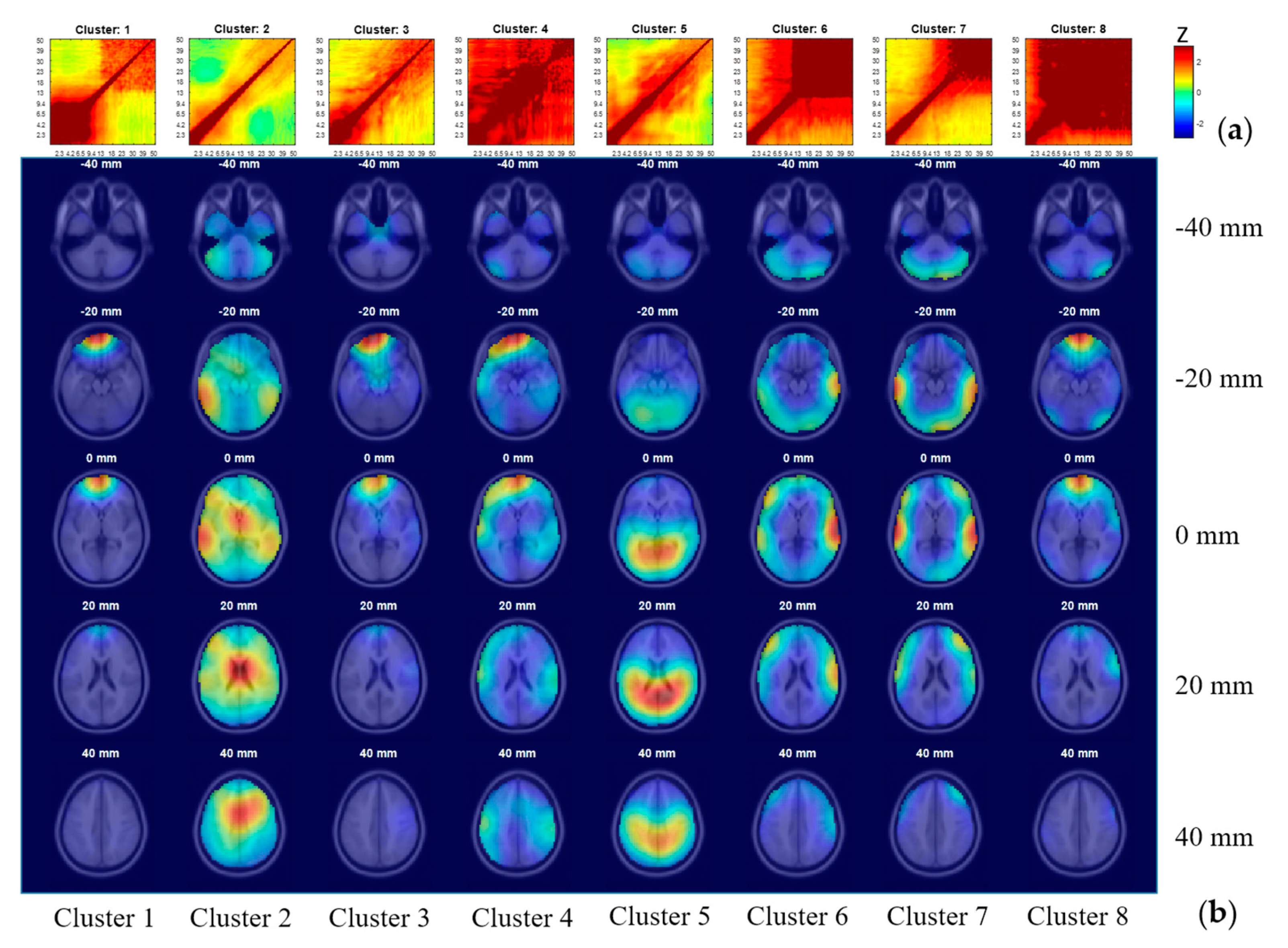
2.4. Clustering ICs Using Comodulogram as Clustering Criterion
3. Results
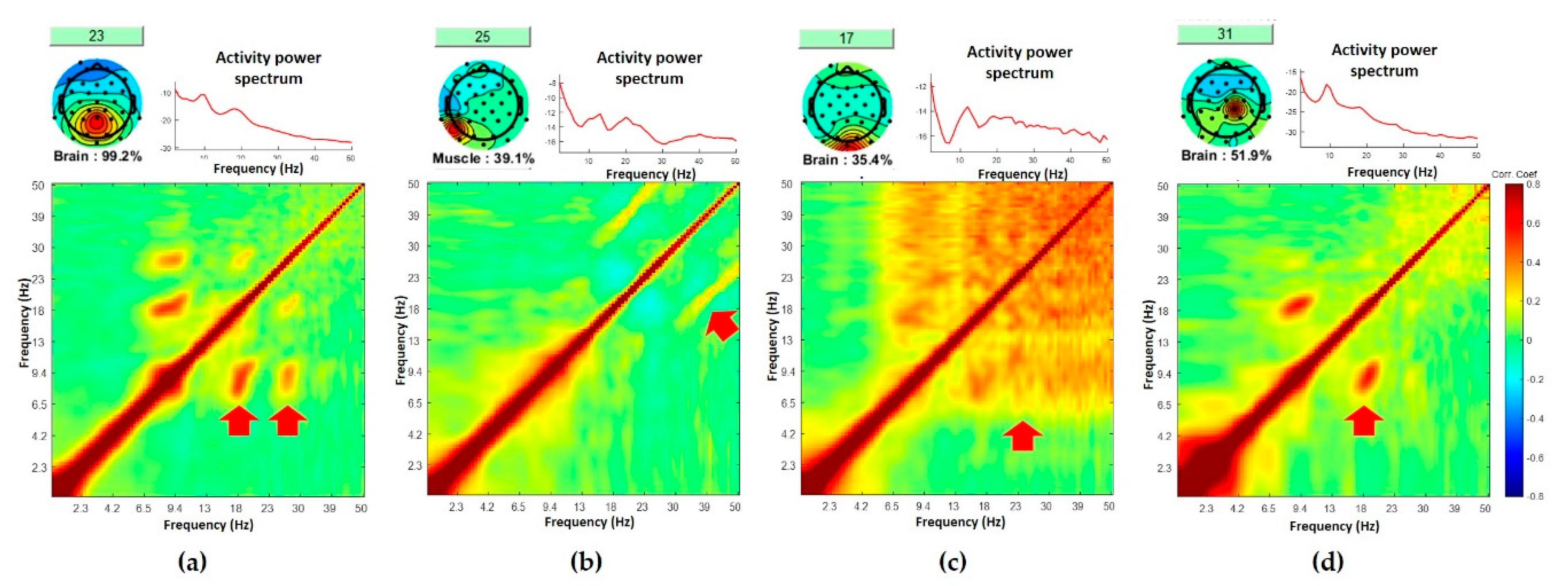
3.1. Standardized Comodulograms for Brain, Eye, and Muscle Classes
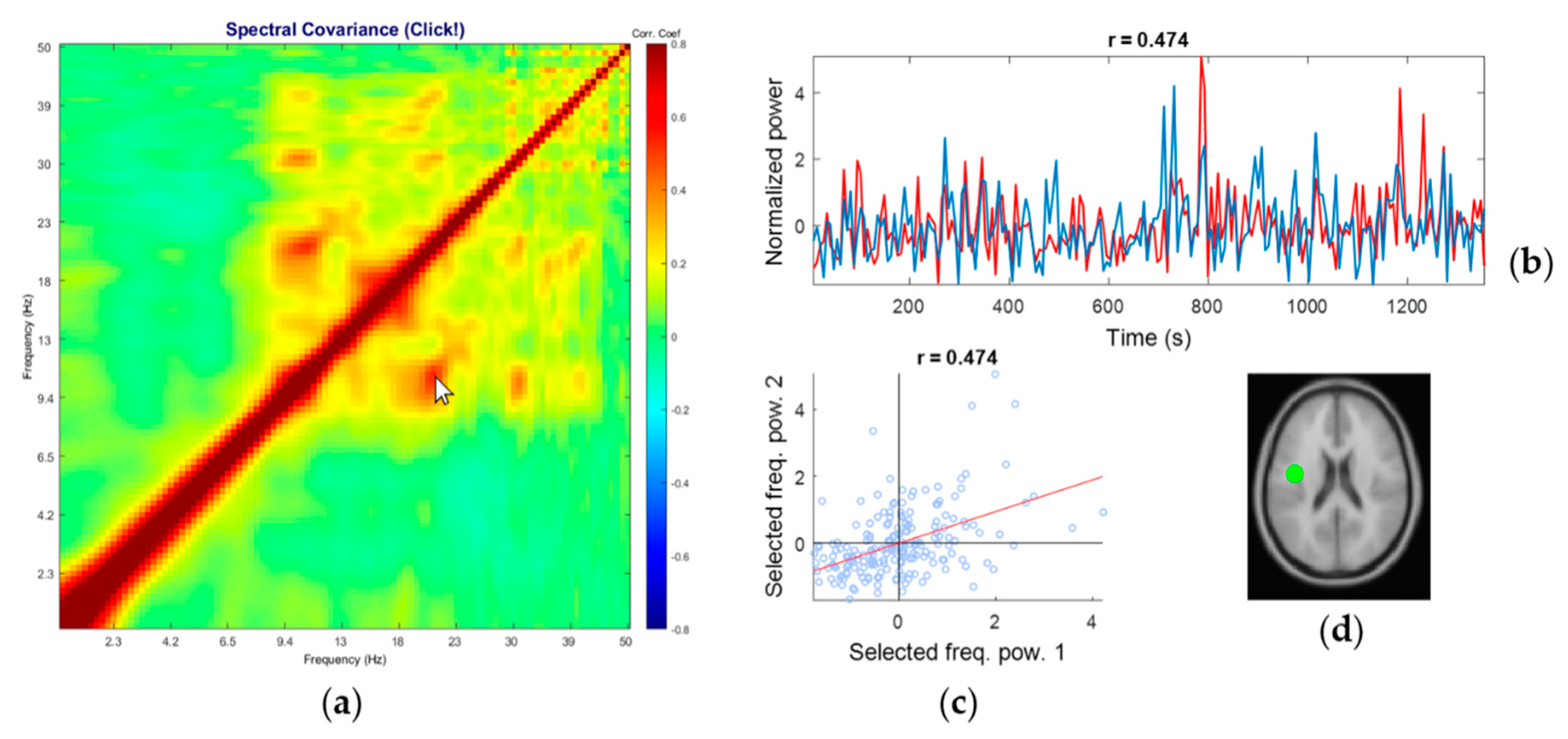
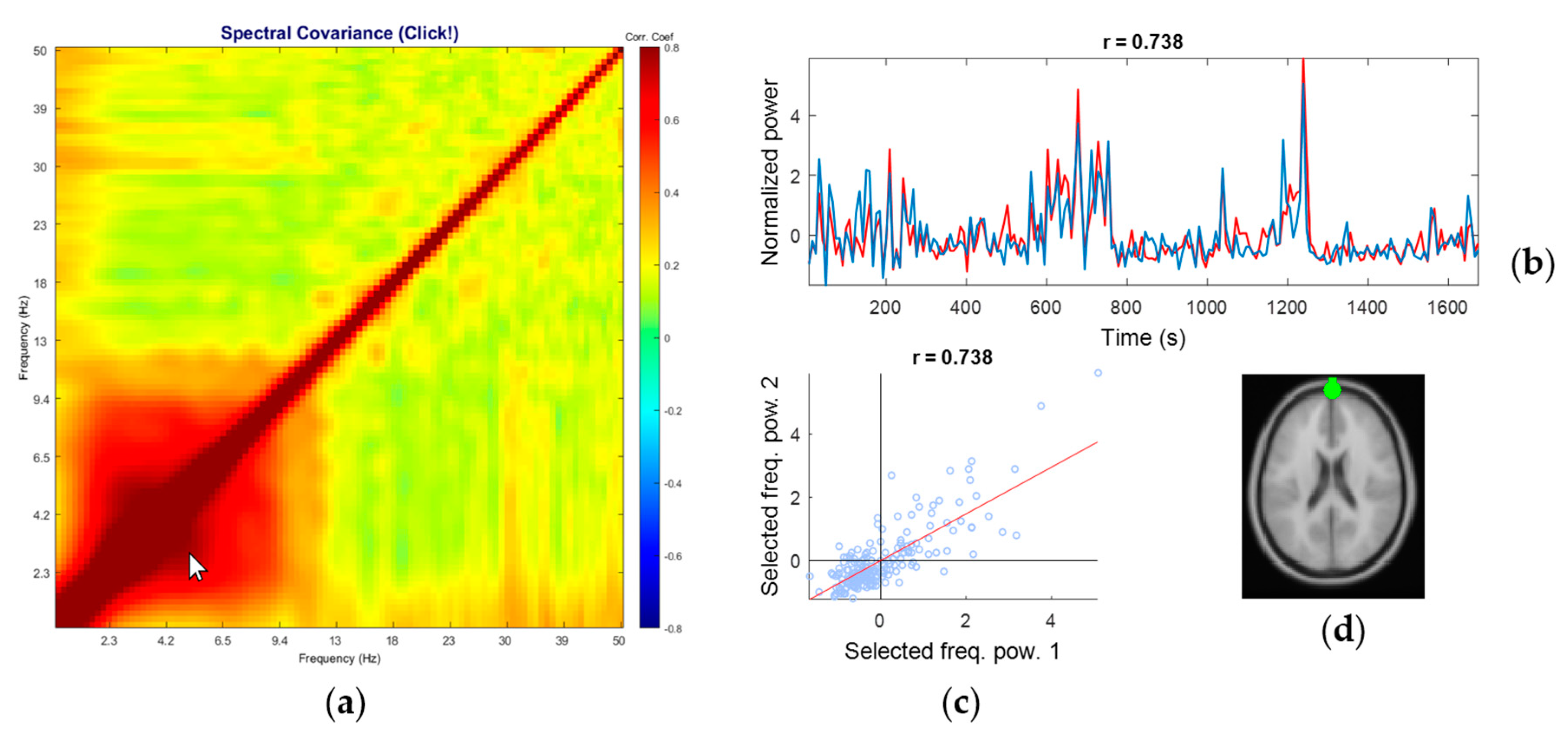
3.2. Representative Comodulogram of Brain Class
3.3. Representative Comodulogram of Eye Class
3.4. Representative Comodulogram of Muscle Class
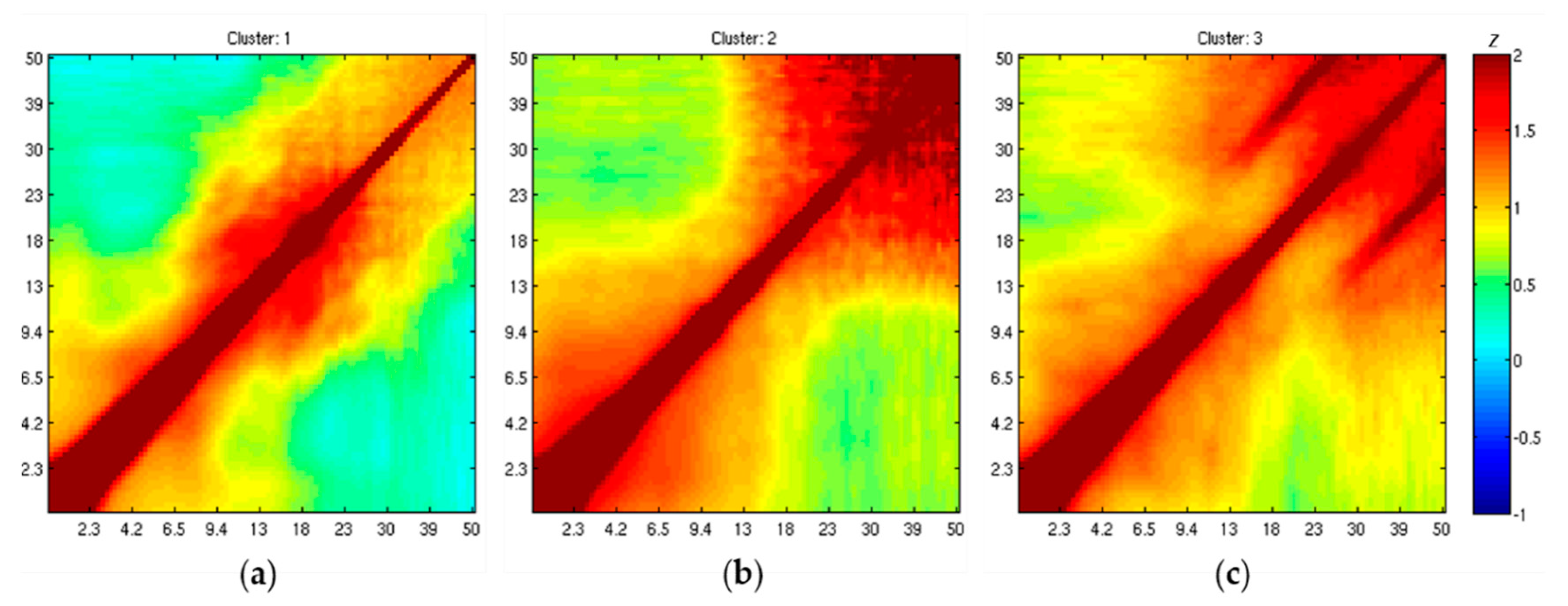
3.5. IC Clustering, According to Comodulogram
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sterman, M.B.; Kaiser, D. Comodulation: A new qEEG analysis metric for assessment of structural and functional disorders of the central nervous system. J. Neurother. 2000, 4, 73–83. [Google Scholar] [CrossRef]
- Gaidica, M.; Hurst, A.; Cyr, C.; Leventhal, D.K. Interactions Between Motor Thalamic Field Potentials and Single-Unit Spiking Are Correlated with Behavior in Rats. Front. Neural Circuits 2020, 14, 52. [Google Scholar] [CrossRef] [PubMed]
- Senzai, Y.; Fernandez-Ruiz, A.; Buzsáki, G. Layer-Specific Physiological Features and Interlaminar Interactions in the Primary Visual Cortex of the Mouse. Neuron 2019, 101, 500–513. [Google Scholar] [CrossRef] [PubMed]
- Khodagholy, D.; Gelinas, J.N.; Buzsáki, G. Learning-enhanced coupling between ripple oscillations in association cortices and hippocampus. Science 2017, 358, 369–372. [Google Scholar] [CrossRef]
- Leventhal, D.K.; Gage, G.J.; Schmidt, R.; Pettibone, J.R.; Case, A.C.; Berke, J.D. Basal Ganglia Beta Oscillations Accompany Cue Utilization. Neuron 2012, 73, 523–536. [Google Scholar] [CrossRef]
- Conde-Moro, A.R.; Rocha-Almeida, F.; Sánchez-Campusano, R.; Delgado-García, J.M.; Gruart, A. The activity of the prelimbic cortex in rats is enhanced during the cooperative acquisition of an instrumental learning task. Prog. Neurobiol. 2019, 183, 101692. [Google Scholar] [CrossRef]
- Watson, B.O.; Levenstein, D.; Greene, J.P.; Gelinas, J.N.; Buzsáki, G. Network Homeostasis and State Dynamics of Neocortical Sleep. Neuron 2016, 90, 839–852. [Google Scholar] [CrossRef]
- Zhou, Y.; Sheremet, A.; Qin, Y.; Kennedy, J.P.; DiCola, N.M.; Maurer, A.P. High-order theta harmonics account for the detection of slow gamma. eNeuro 2019, 6. [Google Scholar] [CrossRef]
- Buzsáki, G.; Buhl, D.; Harris, K.; Csicsvari, J.; Czéh, B.; Morozov, A. Hippocampal network patterns of activity in the mouse. Neuroscience 2003, 116, 201–211. [Google Scholar] [CrossRef]
- Buzsáki, G.; Wang, X.J. Mechanisms of gamma oscillations. Annu. Rev. Neurosci. 2012, 35, 203–225. [Google Scholar] [CrossRef]
- Quilichini, P.; Sirota, A.; Buzsáki, G. Intrinsic circuit organization and theta–gamma oscillation dynamics in the entorhinal cortex of the rat. J. Neurosci. 2010, 30, 11128–11142. [Google Scholar] [CrossRef] [PubMed]
- Sullivan, D.; Csicsvari, J.; Mizuseki, K.; Montgomery, S.; Diba, K.; Buzsáki, G. Relationships between hippocampal sharp waves, ripples, and fast gamma oscillation: Influence of dentate and entorhinal cortical activity. J. Neurosci. 2011, 31, 8605–8616. [Google Scholar] [CrossRef]
- Stujenske, J.; Likhtik, E.; Topiwala, M.; Gordon, J. Fear and safety engage competing patterns of theta-gamma coupling in the basolateral amygdala. Neuron 2014, 83, 919–933. [Google Scholar] [CrossRef] [PubMed]
- Ferraris, M.; Ghestem, A.; Vicente, A.F.; Nallet-Khosrofian, L.; Bernard, C.; Quilichini, P.P. The Nucleus Reuniens Controls Long-Range Hippocampo–Prefrontal Gamma Synchronization during Slow Oscillations. J. Neurosci. 2018, 38, 3026–3038. [Google Scholar] [CrossRef] [PubMed]
- Shirvalkar, P.R.; Rapp, P.R.; Shapiro, M.L. Bidirectional changes to hippocampal theta–gamma comodulation predict memory for recent spatial episodes. Proc. Natl. Acad. Sci. USA 2010, 107, 7054–7059. [Google Scholar] [CrossRef]
- Carlqvist, H.; Nikulin, V.V.; Strömberg, J.O.; Brismar, T. Amplitude and phase relationship between alpha and beta oscillations in the human electroencephalogram. Med. Biol. Eng. Comput. 2005, 43, 599–607. [Google Scholar] [CrossRef]
- Llinás, R.R.; Ribary, U.; Jeanmonod, D.; Kronberg, E.; Mitra, P.P. Thalamocortical dysrhythmia: A neurological and neuropsychiatric syndrome characterized by magnetoencephalography. Proc. Natl. Acad. Sci. USA 1999, 96, 15222–15227. [Google Scholar] [CrossRef]
- Mitra, P.; Bokil, H. Observed Brain Dynamics; Oxford University Press: New York, NY, USA, 2007. [Google Scholar] [CrossRef]
- Llinás, R.R.; Ribary, U.; Jeanmonod, D. Method and System for Diagnosing and Treating Thalamocortical Dysrhythmia. U.S. Patent 6,687,525, 2 February 2004. [Google Scholar]
- Masimore, B.; Kakalios, J.; Redish, A.D. Measuring fundamental frequencies in local field potentials. J. Neurosci. Methods 2004, 138, 97–105. [Google Scholar] [CrossRef]
- Schultheiss, N.W.; Schlecht, M.; Jayachandran, M.; Brooks, D.R.; McGlothan, J.L.; Guilarte, T.R.; Allen, T.A. Awake delta and theta-rhythmic hippocampal network modes during intermittent locomotor behaviors in the rat. Behav. Neurosci. 2020, in press. [Google Scholar] [CrossRef]
- Zhou, Y.; Sheremet, A.; Qin, Y.; Kennedy, J.P.; DiCola, N.M.; Burke, S.N.; Maurer, A.P. Methodological Considerations on the Use of Different Spectral Decomposition Algorithms to Study Hippocampal Rhythms. eNeuro 2019, 6. [Google Scholar] [CrossRef]
- Sheremet, A.; Kennedy, J.P.; Qin, Y.; Zhou, Y.; Lovett, S.D.; Burke, S.N.; Maurer, A.P. Theta-gamma cascades and running speed. J. Neurophysiol. 2019, 121, 444–458. [Google Scholar] [CrossRef] [PubMed]
- Popov, T.; Jensen, O.; Schoffelen, J.-M. Dorsal and ventral cortices are coupled by cross-frequency interactions during working memory. NeuroImage 2018, 178, 277–286. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Hagoort, P.; Jensen, O. Language prediction is reflected by coupling between frontal gamma and posterior alpha oscillations. J. Cogn. Neurosci. 2018, 30, 432–447. [Google Scholar] [CrossRef] [PubMed]
- Bell, A.J.; Sejnowski, T.J. An information-maximization approach to blind separation and blind deconvolution. Neural Comput. 1995, 7, 1129–1159. [Google Scholar] [CrossRef]
- Makeig, S.; Bell, A.J.; Jung, T.P.; Sejnowski, T.J. Independent component analysis of electroencephalographic data. In Advances in Neural Information Processing Systems 8; MIT Press: Cambridge, MA, USA, 1996; pp. 145–151. [Google Scholar]
- Makeig, S.; Jung, T.P.; Bell, A.J.; Ghahremani, D.; Sejnowski, T.J. Blind separation of auditory event-related brain responses into independent components. Proc. Natl. Acad. Sci. USA 1997, 94, 10979–10984. [Google Scholar] [CrossRef]
- Makeig, S.; Westerfield, M.; Jung, T.P.; Enghoff, S.; Townsend, J.; Courchesne, E.; Sejnowski, T.J. Dynamic brain sources of visual evoked responses. Science 2002, 295, 690–694. [Google Scholar] [CrossRef]
- Onton, J.; Makeig, S. Information-based modeling of event-related brain dynamics: Why use ICA to decompose EEG/MEG data? Prog. Brain Res. 2006, 159, 99–120. [Google Scholar] [CrossRef]
- Winkler, I.; Haufe, S.; Tangermann, M. Automatic classification of artifactual ICA-components for artifact removal in EEG signals. Behav. Brain Funct. 2011, 7, 30. [Google Scholar] [CrossRef]
- Winkler, I.; Brandl, S.; Horn, F.; Waldburger, E.; Allefeld, C.; Tangermann, M. Robust artifactual independent component classification for bci practitioners. J. Neural Eng. 2014, 11, 035013. [Google Scholar] [CrossRef]
- Mognon, A.; Jovicich, J.; Bruzzone, L.; Buiatti, M. Adjust: An automatic EEG artifact detector based on the joint use of spatial and temporal features. Psychophysiology 2011, 48, 229–240. [Google Scholar] [CrossRef]
- Nolan, H.; Whelan, R.; Reilly, R. Faster: Fully automated statistical thresholding for EEG artifact rejection. J. Neurosci. Methods 2010, 192, 152–162. [Google Scholar] [CrossRef] [PubMed]
- Bigdely-Shamlo, N.; Kreutz-Delgado, K.; Kothe, C.; Makeig, S. Eyecatch: Data-mining over half a million EEG independent components to construct a fully-automated eye-component detector. In Proceedings of the 2013 35th Annual International Conference of the IEEE Engineering in Medicine and Biology Society EMBC, Osaka, Japan, 3–7 July 2013; pp. 5845–5848. [Google Scholar] [CrossRef]
- Frølich, L.; Andersen, T.S.; Mørup, M. Classification of independent components of EEG into multiple artifact classes. Psychophysiology 2015, 52, 32–45. [Google Scholar] [CrossRef] [PubMed]
- Chaumon, M.; Bishop, D.V.; Busch, N.A. A practical guide to the selection of independent components of the electroencephalogram for artifact correction. J. Neurosci. Methods 2015, 250, 47–63. [Google Scholar] [CrossRef] [PubMed]
- Pion-Tonachini, L.; Kreutz-Delgado, K.; Makeig, S. ICLabel: An automated electroencephalographic independent component classifier, dataset, and website. NeuroImage 2019, 198, 181–197. [Google Scholar] [CrossRef]
- Viola, F.C.; Thorne, J.; Edmonds, B.; Schneider, T.; Eichele, T.; Debener, S. Semi-automatic identification of independent components representing EEG artifact. Clin. Neurophysiol. 2009, 120, 868–877. [Google Scholar] [CrossRef]
- Gabsteiger, F.; Leutheuser, H.; Reis, P.; Lochmann, M.; Eskofier, B.M. SVM for Semi-automatic Selection of ICA Components of Electromyogenic Artifacts in EEG Data. In Proceedings of the 15th International Conference on Biomedical Engineering, Singapore, 4–7 December 2013; Springer: Berlin/Heidelberg, Germany, 2014; pp. 132–135. [Google Scholar] [CrossRef]
- Makeig, S. Auditory event-related dynamics of the EEG spectrum and effects of exposure to tones. Electroencephalogr. Clin. Neurophysiol. 1993, 86, 283–293. [Google Scholar] [CrossRef]
- Delorme, A.; Makeig, S. EEGLAB: An open source toolbox for analysis of single-trial EEG dynamics including independent component analysis. J. Neurosci. Methods 2004, 134, 9–21. [Google Scholar] [CrossRef]
- Miyakoshi, M.; Kanayama, N.; Iidaka, T.; Ohira, H. EEG evidence of face-specific visual self-representation. NeuroImage 2010, 50, 1666–1675. [Google Scholar] [CrossRef]
- Nunez, P.L.; Srinivasan, R. Electric Fields of the Brain: The Neurophysics of EEG, 2nd ed.; Oxford University Press: New York, NY, USA, 2007; pp. 294–298. [Google Scholar]
- Widmann, A.; Schröger, E.; Maess, B. Digital filter design for electrophysiological data—A practical approach. J. Neurosci. Methods 2015, 250, 34–46. [Google Scholar] [CrossRef]
- Palmer, J.A.; Makeig, S.; Kreutz-Delgado, K.; Rao, B.D. Newton method for the ICA mixture model. In Proceedings of the 2008 IEEE International Conference on Acoustics, Speech and Signal Processing, Las Vegas, NV, USA, 31 March–4 April 2008; pp. 1805–1808. [Google Scholar] [CrossRef]
- Delorme, A.; Palmer, J.; Onton, J.; Oostenveld, R.; Makeig, S. Independent EEG Sources Are Dipolar. PLoS ONE 2012, 7, e30135. [Google Scholar] [CrossRef]
- Oostenveld, R.; Fries, P.; Maris, E.; Schoffelen, J.M. Fieldtrip: Open source software for advanced analysis of MEG, EEG, and invasive electrophysiological data. Comput. Intell. Neurosci. 2011, 2011, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Muller, L.; Piantoni, G.; Koller, D.; Cash, S.S.; Halgren, E.; Sejnowski, T.J. Rotating waves during human sleep spindles organize global patterns of activity that repeat precisely through the night. eLife 2016, 5, e17267. [Google Scholar] [CrossRef] [PubMed]
- Rissling, A.J.; Miyakoshi, M.; Sugar, C.A.; Braff, D.L.; Makeig, S.; Light, G.A. Cortical substrates and functional correlates of auditory deviance processing deficits in schizophrenia. NeuroImage Clin. 2014, 6, 424–437. [Google Scholar] [CrossRef] [PubMed]
- Makeig, S.; Westerfield, M.; Townsend, J.; Jung, T.-P.; Courchesne, E.; Sejnowski, T.J. Functionally independent components of early event-related potentials in a visual spatial attention task. Philos. Trans. R. Soc. B Biol. Sci. 1999, 354, 1135–1144. [Google Scholar] [CrossRef] [PubMed]
- Makeig, S.; Debener, S.; Onton, J.; Delorme, A. Mining event-related brain dynamics. Trends Cogn. Sci. 2004, 8, 204–210. [Google Scholar] [CrossRef] [PubMed]
- Groppe, D.M.; Makeig, S.; Kutas, M. Identifying reliable independent components via split-half comparisons. Neuroimage 2009, 45, 1199–1211. [Google Scholar] [CrossRef]
- Jamšek, J.; Paluš, M.; Stefanovska, A. Detecting couplings between interacting oscillators with time-varying basic frequencies: Instantaneous wavelet bispectrum and information theoretic approach. Phys. Rev. E 2010, 81, 036207. [Google Scholar] [CrossRef]
- Lancaster, G.; Iatsenko, D.; Pidde, A.; Ticcinelli, V.; Stefanovska, A. Surrogate data for hypothesis testing of physical systems. Phys. Rep. 2018, 748, 1–60. [Google Scholar] [CrossRef]
- Stankovski, T.; Ticcinelli, V.; McClintock, P.V.E.; Stefanovska, A. Neural Cross-Frequency Coupling Functions, Frontiers in Systems. Neuroscience 2017, 11, 33. [Google Scholar] [CrossRef]
- Herrmann, C.S. Human EEG responses to 1–100 Hz flicker: Resonance phenomena in visual cortex and their potential correlation to cognitive phenomena. Exp. Brain Res. 2001, 137, 346–353. [Google Scholar] [CrossRef]
- Hagemann, D.; Naumann, E. The effects of ocular artifacts on (lateralized) broadband power in the EEG. Clin. Neurophysiol. 2001, 112, 215–231. [Google Scholar] [CrossRef]
- Criswell, E. (Ed.) Cram’s Introduction to Surface Electromyography, 2nd ed.; Jones and Bartlett Learning: Sudbury, MA, USA, 2010. [Google Scholar]
- Anscombe, F.J. Graphs in statistical analysis. Am. Stat. 1973, 27, 17–21. [Google Scholar]
| Clusters | Our Interpretation | Percentage of ICs in Each Class as Labeled by ICLabel | Total Number of ICs | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Brain | Muscle | Eye | Heart | Line Noise | Channel Noise | Other | |||
| 2 | Brain | 52.5 | 23.0 | 1.8 | 0.0 | 13.5 | 0.0 | 9.2 | 282 |
| 3 | Brain | 23.2 | 26.8 | 16.1 | 0.0 | 25.0 | 0.0 | 8.9 | 56 |
| 5 | Brain | 82.0 | 8.7 | 0.0 | 0.0 | 8.7 | 0.0 | 0.7 | 150 |
| 6 | Muscle | 10.4 | 83.1 | 0.0 | 0.0 | 2.6 | 0.0 | 3.9 | 77 |
| 7 | Muscle | 27.6 | 51.5 | 2.2 | 0.0 | 5.2 | 0.0 | 13.4 | 134 |
| 8 | Muscle | 3.3 | 53.3 | 26.7 | 0.0 | 10.0 | 0.0 | 6.7 | 30 |
| 1 | Eye | 3.2 | 0.0 | 83.9 | 0.0 | 6.5 | 0.0 | 6.5 | 31 |
| 4 | Noise | 16.7 | 20.0 | 56.7 | 0.0 | 3.3 | 3.3 | 0.0 | 30 |
| Total | 42.5 | 31.4 | 8.6 | 0.0 | 10.1 | 0.1 | 7.2 | 790 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thammasan, N.; Miyakoshi, M. Cross-Frequency Power-Power Coupling Analysis: A Useful Cross-Frequency Measure to Classify ICA-Decomposed EEG. Sensors 2020, 20, 7040. https://doi.org/10.3390/s20247040
Thammasan N, Miyakoshi M. Cross-Frequency Power-Power Coupling Analysis: A Useful Cross-Frequency Measure to Classify ICA-Decomposed EEG. Sensors. 2020; 20(24):7040. https://doi.org/10.3390/s20247040
Chicago/Turabian StyleThammasan, Nattapong, and Makoto Miyakoshi. 2020. "Cross-Frequency Power-Power Coupling Analysis: A Useful Cross-Frequency Measure to Classify ICA-Decomposed EEG" Sensors 20, no. 24: 7040. https://doi.org/10.3390/s20247040
APA StyleThammasan, N., & Miyakoshi, M. (2020). Cross-Frequency Power-Power Coupling Analysis: A Useful Cross-Frequency Measure to Classify ICA-Decomposed EEG. Sensors, 20(24), 7040. https://doi.org/10.3390/s20247040






