Gravitational-Wave Burst Signals Denoising Based on the Adaptive Modification of the Intersection of Confidence Intervals Rule
Abstract
1. Introduction
2. Materials and Methods
2.1. The LPA Filter Design Method
2.2. The RICI Algorithm
3. Results and Discussion
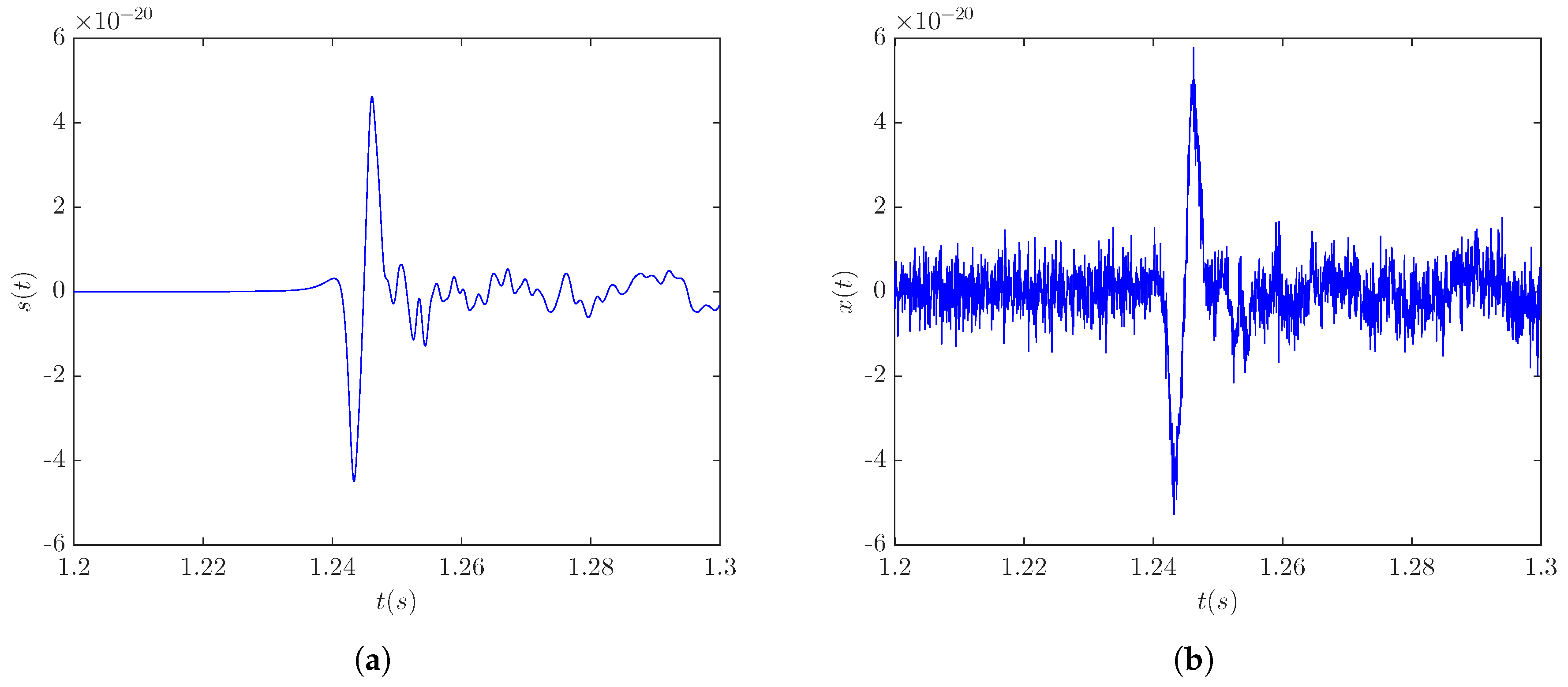
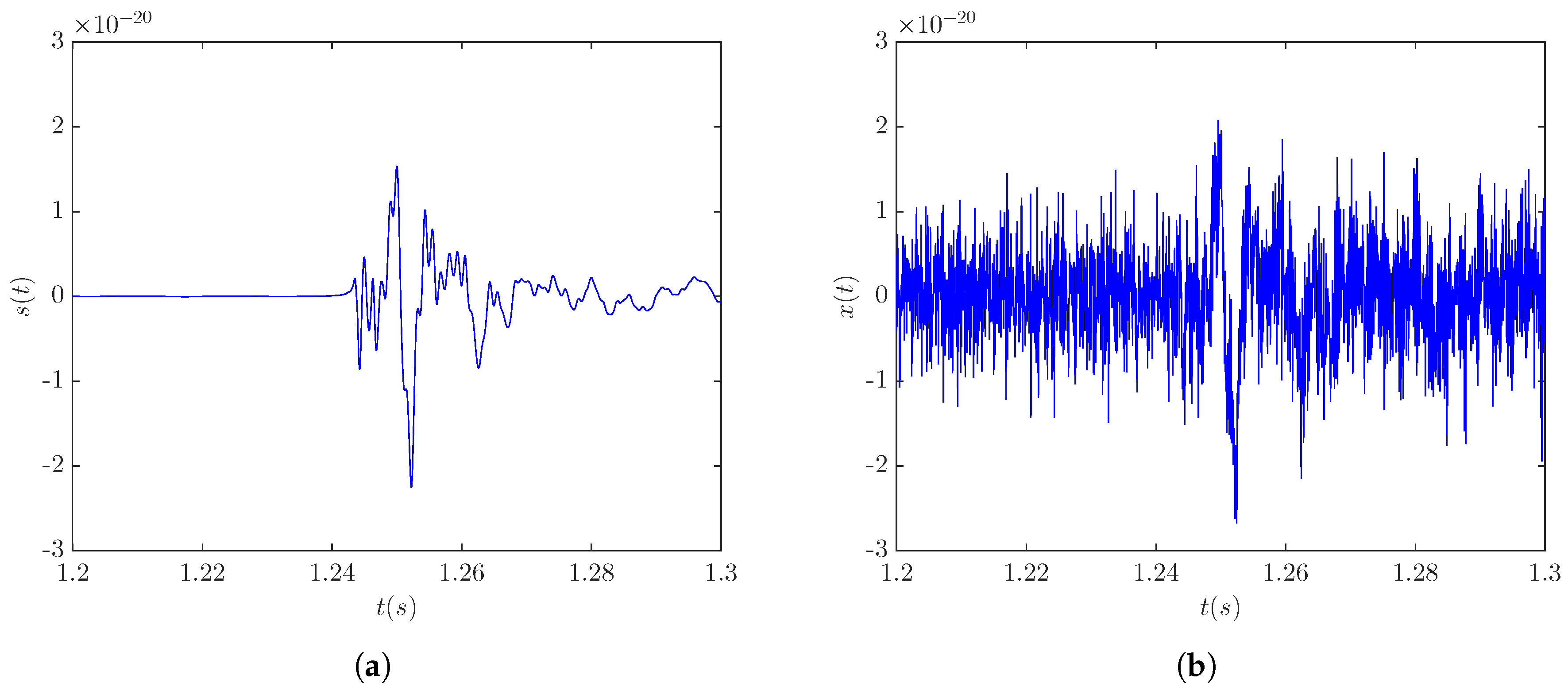
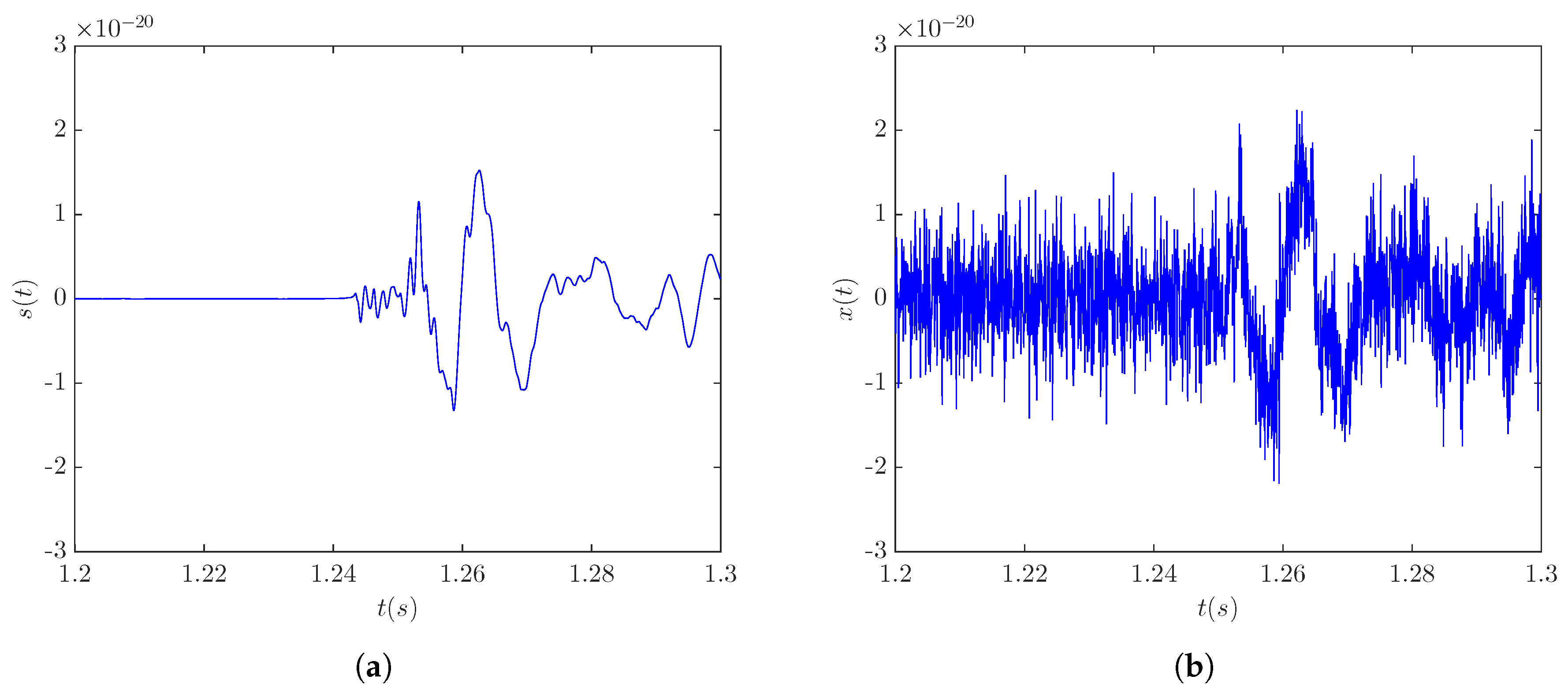
3.1. Data Conditioning
Whitening Procedure
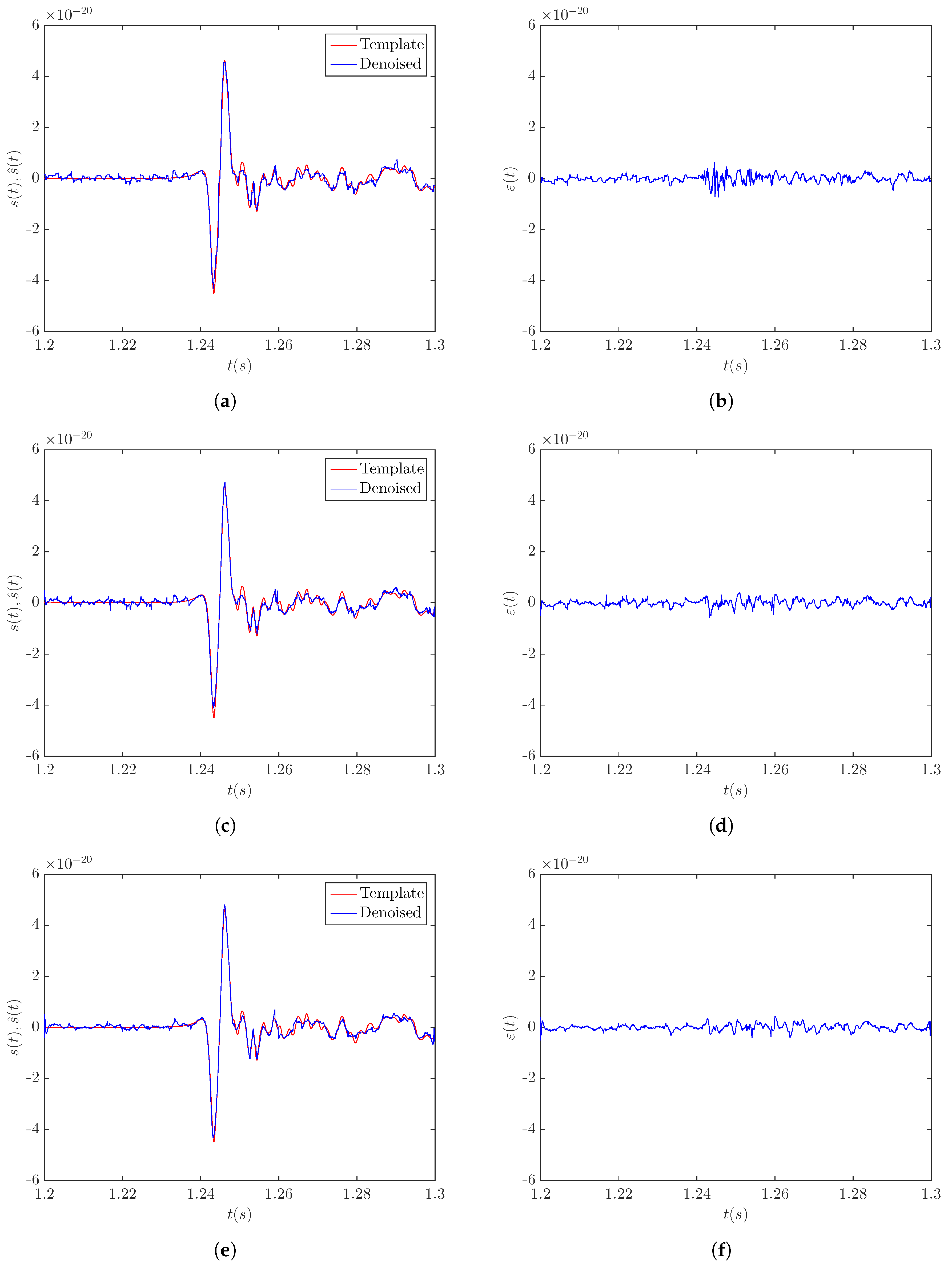
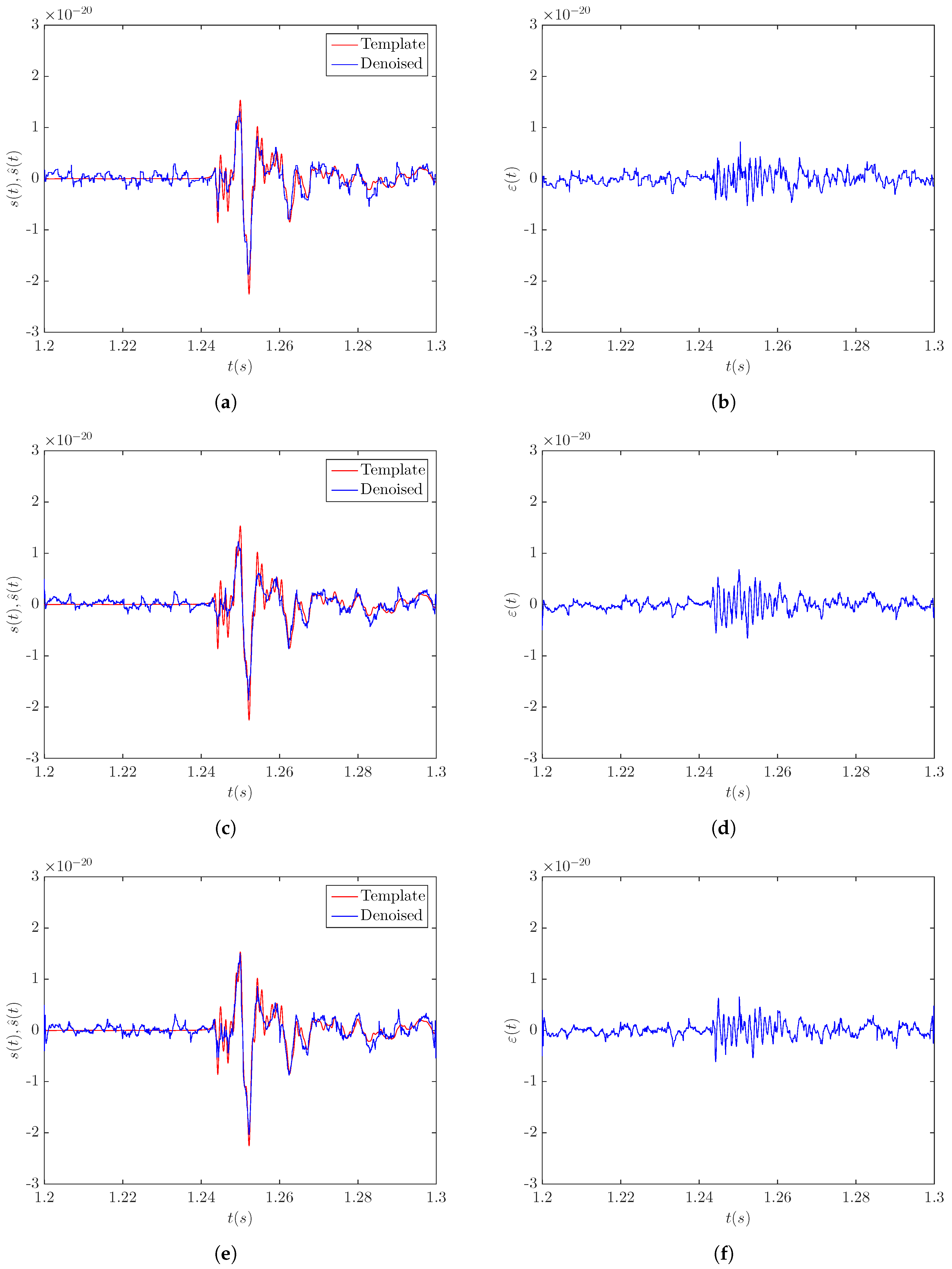
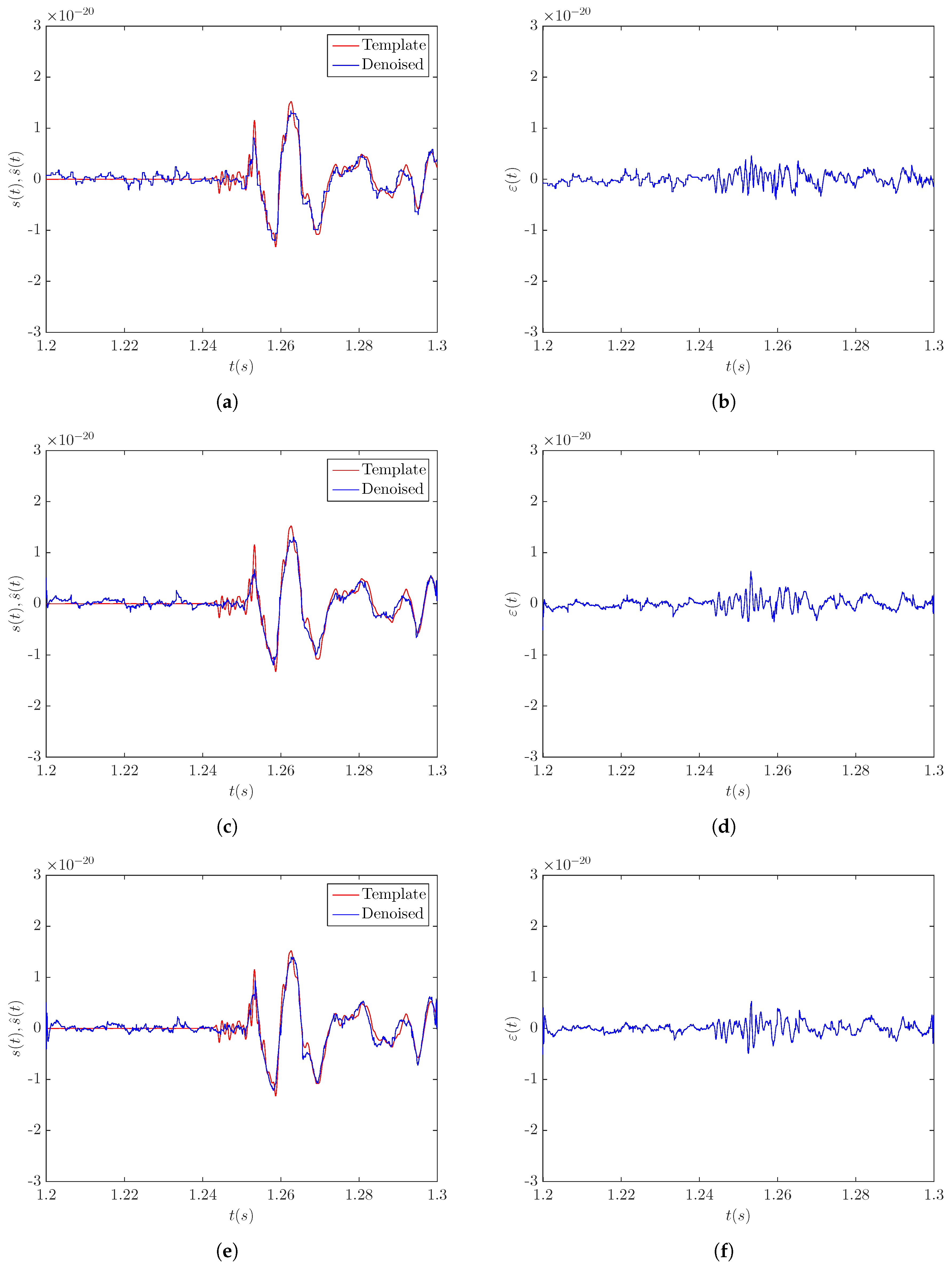
3.2. Data Denoising
3.3. Performance Indices
- Improvement in the signal-to-noise ratio (ISNR):
- Peak signal-to-noise ratio (PSNR):
- Root mean squared error (RMSE):
- Mean absolute error (MAE):
- Maximum absolute error (MAX):
3.4. Case Studies
3.4.1. Case Study—Signal s20a1o05
3.4.2. Case Study—Signal s20a2o09
3.4.3. Case Study—Signal s20a3o15
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AR | autoregressive |
| BBH | binary black holes |
| BNS | binary neutron star |
| CBC | compact binary coalescence |
| CCSN | core collapse supernova |
| CNN | convolutional neural network |
| EGO | European Gravitational Observatory |
| ICI | intersection of confidence intervals |
| ISI | internal seismic isolation |
| ISNR | improvement in the signal-to-noise ratio |
| LIGO | Laser Interferometer Gravitational-Wave Observatory |
| LPA | local polynomial approximation |
| MAE | mean absolute error |
| MAX | maximum absolute error |
| MSE | mean squared error |
| NSBH | neutron star-black hole |
| PCA | principal component analysis |
| PSNR | peak signal-to-noise ratio |
| RICI | relative intersection of confidence intervals |
| RMSE | root mean squared error |
| ROF | Rudin–Osher–Fatemi |
| SNR | signal-to-noise ratio |
| STFT | Short-time Fourier transform |
| SURE | Stein’s unbiased risk estimator |
| TV | total variation |
| WLS | weighted least squares |
References
- Abbott, B.P.; Abbott, R.; Abbott, T.; Abernathy, M.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.; et al. Observation of gravitational-waves from a binary black hole merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.; et al. GW151226: Observation of Gravitational Waves from a 22-Solar-Mass Binary Black Hole Coalescence. Phys. Rev. Lett. 2016, 116, 241103. [Google Scholar] [CrossRef] [PubMed]
- Aasi, J.; Abbott, B.; Abbott, R.; Abbott, T.; Abernathy, M.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.; et al. Advanced LIGO. Class. Quantum Gravity 2015, 32, 074001. [Google Scholar] [CrossRef]
- Acernese, F.; Agathos, M.; Agatsuma, K.; Aisa, D.; Allemandou, N.; Allocca, A.; Amarni, J.; Astone, P.; Balestri, G.; Ballardin, G.; et al. Advanced Virgo: A second-generation interferometric gravitational wave detector. Class. Quantum Gravity 2014, 32, 024001. [Google Scholar] [CrossRef]
- Acernese, F.; Adams, T.; Agatsuma, K.; Aiello, L.; Allocca, A.; Amato, A.; Antier, S.; Arnaud, N.; Ascenzi, S.; Astone, P.; et al. Advanced Virgo Status. J. Phys. Conf. Ser. 2020, 1342, 012010. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.; Adya, V.B.; Affeldt, C.; et al. GWTC-1: A Gravitational-Wave Transient Catalog of Compact Binary Mergers Observed by LIGO and Virgo during the First and Second Observing Runs. Phys. Rev. X 2019, 9, 031040. [Google Scholar] [CrossRef]
- Akutsu, T.; Ando, M.; Arai, K.; Arai, Y.; Araki, S.; Araya, A.; Aritomi, N.; Asada, H.; Aso, Y.; Atsuta, S.; et al. KAGRA: 2.5 generation interferometric gravitational-wave detector. Nat. Astron. 2019, 3, 35–40. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.; Abernathy, M.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.; et al. Prospects for observing and localizing gravitational-wave transients with Advanced LIGO, Advanced Virgo and KAGRA. Living Rev. Relativ. 2018, 21, 3. [Google Scholar] [CrossRef]
- The Virgo Collaboration. Advanced Virgo. 2020. Available online: http://public.virgo-gw.eu/advanced-virgo/ (accessed on 21 October 2020).
- LIGO’s Interferometer. Available online: https://www.ligo.caltech.edu/page/ligos-ifo (accessed on 7 September 2020).
- Blair, D.G. The Detection of Gravitational Waves; Cambridge University Press: Cambridge, MA, USA, 2005. [Google Scholar]
- Meystre, P.; Scully, M.O. Quantum Optics, Experimental Gravity, and Measurement Theory; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 94. [Google Scholar]
- Kwee, P.; Bogan, C.; Danzmann, K.; Frede, M.; Kim, H.; King, P.; Pöld, J.; Puncken, O.; Savage, R.L.; Seifert, F.; et al. Stabilized high-power laser system for the gravitational-wave detector advanced LIGO. Opt. Express 2012, 20, 10617–10634. [Google Scholar] [CrossRef]
- Mueller, C.L.; Arain, M.A.; Ciani, G.; DeRosa, R.T.; Effler, A.; Feldbaum, D.; Frolov, V.V.; Fulda, P.; Gleason, J.; Heintze, M.; et al. The advanced LIGO input optics. Rev. Sci. Instrum. 2016, 87, 014502. [Google Scholar] [CrossRef]
- LIGO Technology. Available online: https://www.ligo.caltech.edu/page/ligo-technology (accessed on 7 September 2020).
- Matichard, F.; Lantz, B.; Mittleman, R.; Mason, K.; Kissel, J.; Abbott, B.; Biscans, S.; McIver, J.; Abbott, R.; Abbott, S.; et al. Seismic isolation of Advanced LIGO: Review of strategy, instrumentation and performance. Class. Quantum Gravity 2015, 32, 185003. [Google Scholar] [CrossRef]
- Aston, S.; Barton, M.; Bell, A.; Beveridge, N.; Bland, B.; Brummitt, A.; Cagnoli, G.; Cantley, C.; Carbone, L.; Cumming, A.; et al. Update on quadruple suspension design for Advanced LIGO. Class. Quantum Gravity 2012, 29, 235004. [Google Scholar] [CrossRef]
- Cumming, A.; Bell, A.; Barsotti, L.; Barton, M.; Cagnoli, G.; Cook, D.; Cunningham, L.; Evans, M.; Hammond, G.; Harry, G.; et al. Design and development of the advanced LIGO monolithic fused silica suspension. Class. Quantum Gravity 2012, 29, 035003. [Google Scholar] [CrossRef]
- Harry, G.M.; Abernathy, M.R.; Becerra-Toledo, A.E.; Armandula, H.; Black, E.; Dooley, K.; Eichenfield, M.; Nwabugwu, C.; Villar, A.; Crooks, D.; et al. Titania-doped tantala/silica coatings for gravitational-wave detection. Class. Quantum Gravity 2006, 24, 405. [Google Scholar] [CrossRef]
- Granata, M.; Saracco, E.; Morgado, N.; Cajgfinger, A.; Cagnoli, G.; Degallaix, J.; Dolique, V.; Forest, D.; Franc, J.; Michel, C.; et al. Mechanical loss in state-of-the-art amorphous optical coatings. Phys. Rev. D 2016, 93, 012007. [Google Scholar] [CrossRef]
- Martynov, D.V.; Hall, E.D.; Abbott, B.P.; Abbott, R.; Abbott, T.D.; Adams, C.; Adhikari, R.; Anderson, R.A.; Anderson, S.B.; Arai, K.; et al. Sensitivity of the Advanced LIGO detectors at the beginning of gravitational-wave astronomy. Phys. Rev. D 2016, 93, 112004. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.; Abernathy, M.; Acernese, F.; Ackley, K.; Adamo, M.; Adams, C.; Adams, T.; Addesso, P.; et al. Characterization of transient noise in Advanced LIGO relevant to gravitational-wave signal GW150914. Class. Quantum Gravity 2016, 33, 134001. [Google Scholar] [CrossRef]
- Effler, A.; Schofield, R.; Frolov, V.; González, G.; Kawabe, K.; Smith, J.; Birch, J.; McCarthy, R. Environmental influences on the LIGO gravitational-wave detectors during the 6th science run. Class. Quantum Gravity 2015, 32, 035017. [Google Scholar] [CrossRef]
- Sathyaprakash, B.S.; Schutz, B.F. Physics, astrophysics and cosmology with gravitational-waves. Living Rev. Relativ. 2009, 12, 2. [Google Scholar] [CrossRef]
- Usman, S.A.; Nitz, A.H.; Harry, I.W.; Biwer, C.M.; Brown, D.A.; Cabero, M.; Capano, C.D.; Dal Canton, T.; Dent, T.; Fairhurst, S.; et al. The PyCBC search for gravitational-waves from compact binary coalescence. Class. Quantum Gravity 2016, 33, 215004. [Google Scholar] [CrossRef]
- Nitz, A.H.; Dal Canton, T.; Davis, D.; Reyes, S. Rapid detection of gravitational-waves from compact binary mergers with PyCBC Live. Phys. Rev. D 2018, 98, 024050. [Google Scholar] [CrossRef]
- Bose, S.; Pai, A.; Dhurandhar, S. Detection of gravitational-waves from inspiraling, compact binaries using a network of interferometric detectors. Int. J. Mod. Phys. D 2000, 9, 325–329. [Google Scholar] [CrossRef]
- Riles, K. Recent searches for continuous gravitational-waves. Mod. Phys. Lett. A 2017, 32, 1730035. [Google Scholar] [CrossRef]
- Edwards, M.C.; Meyer, R.; Christensen, N. Bayesian parameter estimation of core collapse supernovae using gravitational-wave simulations. Inverse Probl. 2014, 30, 114008. [Google Scholar] [CrossRef][Green Version]
- Engels, W.J.; Frey, R.; Ott, C.D. Multivariate regression analysis of gravitational-waves from rotating core collapse. Phys. Rev. D 2014, 90, 124026. [Google Scholar] [CrossRef]
- Edwards, M.C.; Meyer, R.; Christensen, N. Bayesian semiparametric power spectral density estimation with applications in gravitational-wave data analysis. Phys. Rev. D 2015, 92, 064011. [Google Scholar] [CrossRef]
- Powell, J.; Gossan, S.E.; Logue, J.; Heng, I.S. Inferring the core-collapse supernova explosion mechanism with gravitational-waves. Phys. Rev. D 2016, 94, 123012. [Google Scholar] [CrossRef]
- Powell, J.; Szczepanczyk, M.; Heng, I.S. Inferring the core-collapse supernova explosion mechanism with three-dimensional gravitational-wave simulations. Phys. Rev. D 2017, 96, 123013. [Google Scholar] [CrossRef]
- Thrane, E.; Coughlin, M. Detecting Gravitational-Wave Transients at 5σ: A Hierarchical Approach. Phys. Rev. Lett. 2015, 115, 181102. [Google Scholar] [CrossRef]
- Klimenko, S.; Vedovato, G.; Drago, M.; Salemi, F.; Tiwari, V.; Prodi, G.A.; Lazzaro, C.; Ackley, K.; Tiwari, S.; Da Silva, C.F.; et al. Method for detection and reconstruction of gravitational-wave transients with networks of advanced detectors. Phys. Rev. D 2016, 93, 042004. [Google Scholar] [CrossRef]
- Littenberg, T.B.; Kanner, J.B.; Cornish, N.J.; Millhouse, M. Enabling high confidence detections of gravitational-wave bursts. Phys. Rev. D 2016, 94, 044050. [Google Scholar] [CrossRef]
- Kanner, J.B.; Littenberg, T.B.; Cornish, N.; Millhouse, M.; Xhakaj, E.; Salemi, F.; Drago, M.; Vedovato, G.; Klimenko, S. Leveraging waveform complexity for confident detection of gravitational-waves. Phys. Rev. D 2016, 93, 022002. [Google Scholar] [CrossRef]
- Lynch, R.; Vitale, S.; Essick, R.; Katsavounidis, E.; Robinet, F. Information-theoretic approach to the gravitational-wave burst detection problem. Phys. Rev. D 2017, 95, 104046. [Google Scholar] [CrossRef]
- Cuoco, E.; Powell, J.; Cavaglià, M.; Ackley, K.; Bejger, M.; Chatterjee, C.; Coughlin, M.; Coughlin, S.; Easter, P.; Essick, R.; et al. Enhancing Gravitational-Wave Science with Machine Learning. arXiv 2020, arXiv:2005.03745. [Google Scholar]
- Torres-Forné, A.; Marquina, A.; Font, J.A.; Ibáñez, J.M. Denoising of gravitational-wave signals via dictionary learning algorithms. Phys. Rev. D 2016, 94, 124040. [Google Scholar] [CrossRef]
- Ormiston, R.; Nguyen, T.; Coughlin, M.; Adhikari, R.X.; Katsavounidis, E. Noise reduction in gravitational-wave data via deep learning. Phys. Rev. Res. 2020, 2, 033066. [Google Scholar] [CrossRef]
- Wei, W.; Huerta, E. Gravitational-wave denoising of binary black hole mergers with deep learning. Phys. Lett. B 2020, 800, 135081. [Google Scholar] [CrossRef]
- George, D.; Huerta, E. Deep Learning for real-time gravitational-wave detection and parameter estimation: Results with Advanced LIGO data. Phys. Lett. B 2018, 778, 64–70. [Google Scholar] [CrossRef]
- Kim, K.; Harry, I.W.; Hodge, K.A.; Kim, Y.M.; Lee, C.H.; Lee, H.K.; Oh, J.J.; Oh, S.H.; Son, E.J. Application of artificial neural network to search for gravitational-wave signals associated with short gamma-ray bursts. Class. Quantum Gravity 2015, 32, 245002. [Google Scholar] [CrossRef]
- Gebhard, T.; Kilbertus, N.; Parascandolo, G.; Harry, I.; Schölkopf, B. CONVWAVE: Searching for gravitational-waves with fully convolutional neural nets. In Proceedings of the Workshop on Deep Learning for Physical Sciences (DLPS) at the 31st Conference on Neural Information Processing Systems (NIPS), Long Beach, CA, USA, 4–7 December 2017; pp. 1–6. [Google Scholar]
- Gabbard, H.; Williams, M.; Hayes, F.; Messenger, C. Matching Matched Filtering with Deep Networks for Gravitational-Wave Astronomy. Phys. Rev. Lett. 2018, 120, 141103. [Google Scholar] [CrossRef]
- Kim, K.; Li, T.G.F.; Lo, R.K.L.; Sachdev, S.; Yuen, R.S.H. Ranking candidate signals with machine learning in low-latency searches for gravitational-waves from compact binary mergers. Phys. Rev. D 2020, 101, 083006. [Google Scholar] [CrossRef]
- George, D.; Shen, H.; Huerta, E.A. Classification and unsupervised clustering of LIGO data with Deep Transfer Learning. Phys. Rev. D 2018, 97, 101501. [Google Scholar] [CrossRef]
- Razzano, M.; Cuoco, E. Image-based deep learning for classification of noise transients in gravitational-wave detectors. Class. Quantum Gravity 2018, 35, 095016. [Google Scholar] [CrossRef]
- Powell, J.; Trifirò, D.; Cuoco, E.; Heng, I.S.; Cavaglià, M. Classification methods for noise transients in advanced gravitational-wave detectors. Class. Quantum Gravity 2015, 32, 215012. [Google Scholar] [CrossRef]
- Mukund, N.; Abraham, S.; Kandhasamy, S.; Mitra, S.; Philip, N.S. Transient classification in LIGO data using difference boosting neural network. Phys. Rev. D 2017, 95, 104059. [Google Scholar] [CrossRef]
- Powell, J.; Torres-Forné, A.; Lynch, R.; Trifirò, D.; Cuoco, E.; Cavaglià, M.; Heng, I.S.; Font, J.A. Classification methods for noise transients in advanced gravitational-wave detectors II: Performance tests on Advanced LIGO data. Class. Quantum Gravity 2017, 34, 034002. [Google Scholar] [CrossRef]
- Huerta, E.A.; Allen, G.; Andreoni, I.; Antelis, J.M.; Bachelet, E.; Berriman, G.B.; Bianco, F.B.; Biswas, R.; Kind, M.C.; Chard, K.; et al. Enabling real-time multi-messenger astrophysics discoveries with deep learning. Nat. Rev. Phys. 2019, 1, 600–608. [Google Scholar] [CrossRef]
- Cavaglia, M.; Gaudio, S.; Hansen, T.; Staats, K.; Szczepańczyk, M.; Zanolin, M. Improving the background of gravitational-wave searches for core collapse supernovae: A machine learning approach. Mach. Learn. Sci. Technol. 2020, 1, 015005. [Google Scholar] [CrossRef]
- Torres, A.; Marquina, A.; Font, J.A.; Ibáñez, J.M. Total-variation-based methods for gravitational-wave denoising. Phys. Rev. D 2014, 90, 084029. [Google Scholar] [CrossRef]
- Rudin, L.I.; Osher, S.; Fatemi, E. Nonlinear total variation based noise removal algorithms. Physica 1992, 60, 259–268. [Google Scholar] [CrossRef]
- Chambolle, A. An algorithm for total variation minimization and applications. J. Math. Imaging Vis. 2004, 20, 89–97. [Google Scholar] [CrossRef]
- Goldstein, T.; Osher, S. The split Bregman method for L1-regularized problems. SIAM J. Imaging Sci. 2009, 2, 323–343. [Google Scholar] [CrossRef]
- Lee, K.J.; Lee, B. Sequential Total Variation Denoising for the Extraction of Fetal ECG from Single-Channel Maternal Abdominal ECG. Sensors 2016, 16, 1020. [Google Scholar] [CrossRef]
- Xiong, N.; Liu, R.W.; Liang, M.; Wu, D.; Liu, Z.; Wu, H. Effective Alternating Direction Optimization Methods for Sparsity-Constrained Blind Image Deblurring. Sensors 2017, 17, 174. [Google Scholar] [CrossRef]
- Boutemedjet, A.; Deng, C.; Zhao, B. Edge-Aware Unidirectional Total Variation Model for Stripe Non-Uniformity Correction. Sensors 2018, 18, 1164. [Google Scholar] [CrossRef] [PubMed]
- Du, Q.; Xu, H.; Ma, Y.; Huang, J.; Fan, F. Fusing Infrared and Visible Images of Different Resolutions via Total Variation Model. Sensors 2018, 18, 3827. [Google Scholar] [CrossRef] [PubMed]
- Chen, B.; Abascal, J.F.P.J.; Soleimani, M. Electrical Resistance Tomography for Visualization of Moving Objects Using a Spatiotemporal Total Variation Regularization Algorithm. Sensors 2018, 18, 1704. [Google Scholar] [CrossRef] [PubMed]
- Torres-Forné, A.; Cuoco, E.; Marquina, A.; Font, J.A.; Ibáñez, J.M. Total-variation methods for gravitational-wave denoising: Performance tests on Advanced LIGO data. Phys. Rev. D 2018, 98, 084013. [Google Scholar] [CrossRef]
- Katkovnik, V. A new method for varying adaptive bandwidth selection. IEEE Trans. Signal Process. 1999, 47, 2567–2571. [Google Scholar] [CrossRef]
- Katkovnik, V.; Egiazarian, K.; Astola, J. Adaptive window size image de-noising based on intersection of confidence intervals (ICI) rule. J. Math. Imaging Vis. 2002, 16, 223–235. [Google Scholar] [CrossRef]
- Katkovnik, V.; Egiazarian, K.; Astola, J. Adaptive Varying Scale Methods in Image Processing; TTY Monistamo: Tampere, Finland, 2003; Volume 19. [Google Scholar]
- Katkovnik, V. Multiresolution local polynomial regression: A new approach to pointwise spatial adaptation. Digit. Signal Process. 2005, 15, 73–116. [Google Scholar] [CrossRef][Green Version]
- Katkovnik, V.; Egiazarian, K.; Astola, J. Local Approximation Techniques in Signal and Image Processing; The International Society for Optical Engineering: Washington, DC, USA, 2006. [Google Scholar]
- Katkovnik, V.; Shmulevich, I. Kernel density estimation with adaptive varying window size. Pattern Recognit. Lett. 2002, 23, 1641–1648. [Google Scholar] [CrossRef]
- Goldenshluger, A.; Nemirovski, A. On spatially adaptive estimation of nonparametric regression. Math. Meth. Stat. 1997, 6, 135–170. [Google Scholar]
- Sucic, V.; Lerga, J.; Vrankic, M. Adaptive filter support selection for signal denoising based on the improved ICI rule. Digit. Signal Process. 2013, 23, 65–74. [Google Scholar] [CrossRef]
- Stankovic, L. Performance analysis of the adaptive algorithm for bias-to-variance tradeoff. IEEE Trans. Signal Process. 2004, 52, 1228–1234. [Google Scholar] [CrossRef]
- Lerga, J.; Vrankic, M.; Sucic, V. A Signal Denoising Method Based on the Improved ICI Rule. IEEE Signal Process. Lett. 2008, 15, 601–604. [Google Scholar] [CrossRef]
- Lerga, J.; Sucic, V.; Sersic, D. Performance analysis of the LPA-RICI denoising method. In Proceedings of the 6th International Symposium on Image and Signal Processing and Analysis, Salzburg, Austria, 16–18 September 2009; pp. 28–33. [Google Scholar] [CrossRef]
- Dimmelmeier, H.; Ott, C.D.; Marek, A.; Janka, H.T. Gravitational-wave burst signal from core collapse of rotating stars. Phys. Rev. D 2008, 78, 064056. [Google Scholar] [CrossRef]
- Cuoco, E.; Calamai, G.; Fabbroni, L.; Losurdo, G.; Mazzoni, M.; Stanga, R.; Vetrano, F. On-line power spectra identification and whitening for the noise in interferometric gravitational-wave detectors. Class. Quantum Gravity 2001, 18, 1727–1751. [Google Scholar] [CrossRef]
- Cuoco, E.; Losurdo, G.; Calamai, G.; Fabbroni, L.; Mazzoni, M.; Stanga, R.; Guidi, G.; Vetrano, F. Noise parametric identification and whitening for LIGO 40-m interferometer data. Phys. Rev. D 2001, 64, 122002. [Google Scholar] [CrossRef]
- Cuoco, E.; Cella, G.; Guidi, G.M. Whitening of non-stationary noise from gravitational-wave detectors. Class. Quantum Gravity 2004, 21, S801–S806. [Google Scholar] [CrossRef]
- Kay, S.M. Modern Spectral Estimation: Theory and Application; Prentice-Hall: Englewood Cliffs, NJ, USA, 1988. [Google Scholar]
- Acernese, F.; Amico, P.; Alshourbagy, M.; Antonucci, F.; Aoudia, S.; Astone, P.; Avino, S.; Babusci, D.; Ballardin, G.; Barone, F.; et al. Gravitational-waves by gamma-ray bursts and the Virgo detector: The case of GRB 050915a. Class. Quantum Gravity 2007, 24, S671. [Google Scholar] [CrossRef]
- Chambolle, A.; Caselles, V.; Cremers, D.; Novaga, M.; Pock, T. An introduction to total variation for image analysis. Theor. Found. Numer. Methods Sparse Recovery 2010, 9, 227. [Google Scholar]
- Chambolle, A.; Pock, T. A first-order primal-dual algorithm for convex problems with applications to imaging. J. Math. Imaging Vis. 2011, 40, 120–145. [Google Scholar] [CrossRef]
- Mousavi, S.M.; Langston, C.A. Adaptive noise estimation and suppression for improving microseismic event detection. J. Appl. Geophy. 2016, 132, 116–124. [Google Scholar] [CrossRef]
- Donoho, D.L.; Johnstone, J.M. Ideal spatial adaptation by wavelet shrinkage. Biometrika 1994, 81, 425–455. [Google Scholar] [CrossRef]
- Donoho, D.L.; Johnstone, I.M. Minimax estimation via wavelet shrinkage. Ann. Stat. 1998, 26, 879–921. [Google Scholar] [CrossRef]
| Perform. Index | LPA-RICI | LPA-RICI | LPA-RICI | LPA-ICI | TV | Neigh STFT | sym5 Wavelet SURE, Level 6 | db13 Wavelet SURE, Level 5 | coif1 Wavelet SURE, Level 7 |
|---|---|---|---|---|---|---|---|---|---|
| ISNR (db) | 11.1639 | 11.8899 | 12.6307 | 8.9827 | 7.3205 | 5.7691 | 10.1766 | 12.1502 | 9.7551 |
| PSNR (db) | 30.3510 | 31.0770 | 31.8178 | 28.1813 | 26.5192 | 24.9562 | 29.3636 | 31.3373 | 28.9421 |
| RMSE | 0.0304 | 0.0279 | 0.0257 | 0.0390 | 0.0472 | 0.0565 | 0.0340 | 0.0271 | 0.0357 |
| MAE | 0.0225 | 0.0212 | 0.0195 | 0.0258 | 0.0310 | 0.0377 | 0.0246 | 0.0193 | 0.0255 |
| MAX | 0.1642 | 0.1293 | 0.1100 | 0.2377 | 0.3011 | 0.2972 | 0.3372 | 0.1719 | 0.4001 |
| Perform. Index | LPA-RICI | LPA-RICI | LPA-RICI | LPA-ICI | TV | Neigh STFT | sym4 Wavelet SURE, Level 6 | db13 Wavelet SURE, Level 5 | coif4 Wavelet SURE, Level 5 |
|---|---|---|---|---|---|---|---|---|---|
| ISNR (db) | 13.3754 | 13.4002 | 14.0397 | 11.6172 | 9.4346 | 10.2554 | 11.4397 | 12.6607 | 10.4296 |
| PSNR (db) | 26.5485 | 26.5733 | 27.2127 | 24.7953 | 22.6127 | 23.4284 | 24.6127 | 25.8338 | 23.6026 |
| RMSE | 0.0471 | 0.0469 | 0.0436 | 0.0576 | 0.0740 | 0.0674 | 0.0588 | 0.0511 | 0.0660 |
| MAE | 0.0364 | 0.0357 | 0.0326 | 0.0388 | 0.0439 | 0.0419 | 0.0379 | 0.0369 | 0.0421 |
| MAX | 0.2309 | 0.2200 | 0.2200 | 0.4277 | 0.4876 | 0.5204 | 0.7805 | 0.3323 | 0.8102 |
| Perform. Index | LPA-RICI | LPA-RICI | LPA-RICI | LPA-ICI | TV | Neigh STFT | sym3 Wavelet SURE, Level 7 | db3 Wavelet SURE, Level 7 | coif1 Wavelet SURE, Level 7 |
|---|---|---|---|---|---|---|---|---|---|
| ISNR (db) | 15.5200 | 15.3378 | 15.6755 | 14.2550 | 12.5169 | 13.8119 | 13.1240 | 13.1240 | 11.4983 |
| PSNR (db) | 22.6734 | 22.4912 | 22.8289 | 21.4124 | 19.6743 | 20.9653 | 20.2774 | 20.2774 | 18.6518 |
| RMSE | 0.0735 | 0.0751 | 0.0722 | 0.0850 | 0.1038 | 0.0895 | 0.0969 | 0.0969 | 0.1168 |
| MAE | 0.0537 | 0.0570 | 0.0551 | 0.0547 | 0.0618 | 0.0471 | 0.0644 | 0.0644 | 0.0775 |
| MAX | 0.4227 | 0.4399 | 0.4399 | 0.6901 | 0.6482 | 1.0478 | 1.4032 | 1.4032 | 1.5769 |
| Perform. Index | LPA-ICI | TV | Neigh STFT | sym5 Wavelet SURE, Level 6 | db13 Wavelet SURE, Level 5 | coif1 Wavelet SURE, Level 7 |
|---|---|---|---|---|---|---|
| ISNR | 40.61% | 72.54% | 118.94% | 24.12% | 3.95% | 29.48% |
| PSNR | 12.90% | 19.98% | 27.49% | 8.36% | 1.53% | 9.94% |
| RMSE | 34.10% | 45.55% | 54.51% | 24.41% | 5.17% | 28.01% |
| MAE | 24.42% | 37.10% | 48.28% | 20.73% | −1.04% | 23.53% |
| MAX | 53.72% | 63.47% | 62.99% | 67.38% | 36.01% | 72.51% |
| Perform. Index | LPA-ICI | TV | Neigh STFT | sym4 Wavelet SURE, Level 6 | db13 Wavelet SURE, Level 5 | coif4 Wavelet SURE, Level 5 |
|---|---|---|---|---|---|---|
| ISNR | 20.85% | 48.81% | 36.90% | 22.73% | 10.89% | 34.61% |
| PSNR | 9.75% | 20.34% | 16.15% | 10.56% | 5.34% | 15.30% |
| RMSE | 24.31% | 41.08% | 35.31% | 25.85% | 14.68% | 33.94% |
| MAE | 15.98% | 25.74% | 22.20% | 13.98% | 11.65% | 22.57% |
| MAX | 48.56% | 54.88% | 57.72% | 71.81% | 33.79% | 72.85% |
| Perform. Index | LPA-ICI | TV | Neigh STFT | sym3 Wavelet SURE, Level 7 | db3 Wavelet SURE, Level 7 | coif1 Wavelet SURE, Level 7 |
|---|---|---|---|---|---|---|
| ISNR | 9.96% | 25.23% | 13.49% | 19.44% | 19.44% | 36.33% |
| PSNR | 6.62% | 16.03% | 8.89% | 12.58% | 12.58% | 22.40% |
| RMSE | 15.06% | 30.44% | 19.33% | 25.49% | 25.49% | 38.18% |
| MAE | −0.73% | 10.84% | −16.99% | 14.44% | 14.44% | 28.90% |
| MAX | 36.26% | 32.14% | 58.02% | 68.65% | 68.65% | 72.10% |
| Execution Time (s) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Distance (kpc) | LPA-RICI | LPA-RICI | LPA-RICI | LPA-ICI | TV | Neigh STFT | Symlet Wavelet | Daubechies Wavelet | Coiflet Wavelet |
| 5 | 0.3245 | 0.4239 | 0.7288 | 3.0619 | 0.0154 | 0.7661 | 0.0061 | 0.0059 | 0.0046 |
| 10 | 0.4839 | 0.5923 | 1.3046 | 4.6105 | 0.0162 | 0.7967 | 0.0073 | 0.0086 | 0.0055 |
| 20 | 0.8352 | 0.8296 | 1.3178 | 7.3022 | 0.0160 | 0.7457 | 0.0058 | 0.0059 | 0.0058 |
| Perform. Index | LPA-RICI | LPA-RICI | LPA-RICI | LPA-ICI | TV | Neigh STFT | sym4 Wavelet SURE, Level 6 | db6 Wavelet SURE, Level 6 | coif1 Wavelet SURE, Level 7 |
|---|---|---|---|---|---|---|---|---|---|
| ISNR (db) | 12.1897 | 11.8699 | 12.2523 | 11.0513 | 12.4081 | 10.4299 | 11.2266 | 11.6597 | 12.2478 |
| PSNR (db) | 21.1651 | 20.8453 | 21.2277 | 20.0267 | 21.3835 | 19.4053 | 20.2021 | 20.6351 | 21.2232 |
| RMSE | 0.0596 | 0.0619 | 0.0592 | 0.0680 | 0.0582 | 0.0730 | 0.0666 | 0.0634 | 0.0592 |
| MAE | 0.0443 | 0.0428 | 0.0424 | 0.0416 | 0.0412 | 0.0438 | 0.0470 | 0.0439 | 0.0405 |
| MAX | 0.3201 | 0.3030 | 0.2913 | 0.3627 | 0.2985 | 0.5463 | 0.4402 | 0.3855 | 0.2391 |
| Perform. Index | LPA-RICI | LPA-RICI | LPA-RICI | LPA-ICI | TV | Neigh STFT | sym4 Wavelet SURE, Level 6 | db13 Wavelet SURE, Level 5 | coif1 Wavelet SURE, Level 7 |
|---|---|---|---|---|---|---|---|---|---|
| ISNR (db) | 13.7334 | 13.5924 | 14.2997 | 13.1394 | 13.9226 | 7.8194 | 11.1812 | 12.0025 | 12.5731 |
| PSNR (db) | 17.1611 | 17.0201 | 17.7275 | 16.5671 | 17.3504 | 11.2472 | 14.6089 | 15.4303 | 16.0009 |
| RMSE | 0.0946 | 0.0961 | 0.0886 | 0.1012 | 0.0925 | 0.1868 | 0.1269 | 0.1154 | 0.1081 |
| MAE | 0.0704 | 0.0667 | 0.0636 | 0.0581 | 0.0595 | 0.0802 | 0.0887 | 0.0870 | 0.0735 |
| MAX | 0.5082 | 0.5237 | 0.4489 | 0.5831 | 0.6238 | 2.3191 | 0.8801 | 0.6794 | 0.6437 |
| Perform. Index | LPA-RICI | LPA-RICI | LPA-RICI | LPA-ICI | TV | Neigh STFT | sym4 Wavelet SURE, Level 6 | db13 Wavelet SURE, Level 5 | coif1 Wavelet SURE, Level 7 |
|---|---|---|---|---|---|---|---|---|---|
| ISNR (db) | 17.2693 | 15.9216 | 15.8755 | 16.1431 | 17.3306 | 8.8306 | 13.2998 | 12.4740 | 13.8150 |
| PSNR (db) | 14.8028 | 13.4551 | 13.4090 | 13.6766 | 14.8641 | 6.3641 | 10.8333 | 10.0075 | 11.3485 |
| RMSE | 0.1241 | 0.1449 | 0.1456 | 0.1412 | 0.1232 | 0.3277 | 0.1959 | 0.2155 | 0.1846 |
| MAE | 0.0698 | 0.1012 | 0.1084 | 0.0769 | 0.0759 | 0.1072 | 0.1145 | 0.1572 | 0.1059 |
| MAX | 0.6685 | 0.9006 | 0.9006 | 0.9036 | 0.7929 | 4.0053 | 3.0110 | 1.3596 | 2.7521 |
| Perform. Index | LPA-ICI | TV | Neigh STFT | sym4 Wavelet SURE, Level 6 | db6 Wavelet SURE, Level 6 | coif1 Wavelet SURE, Level 7 |
|---|---|---|---|---|---|---|
| ISNR | 10.87% | −1.26% | 17.47% | 9.14% | 5.08% | 0.04% |
| PSNR | 6.00% | −0.73% | 9.39% | 5.08% | 2.87% | 0.02% |
| RMSE | 12.94% | −1.72% | 18.90% | 11.11% | 6.62% | 0.00% |
| MAE | −1.92% | −2.91% | 3.20% | 9.79% | 3.42% | −4.69% |
| MAX | 19.69% | 2.41% | 46.68% | 33.83% | 24.44% | −21.83% |
| Perform. Index | LPA-ICI | TV | Neigh STFT | sym4 Wavelet SURE, Level 6 | db13 Wavelet SURE, Level 5 | coif1 Wavelet SURE, Level 7 |
|---|---|---|---|---|---|---|
| ISNR | 8.83% | 2.71% | 82.87% | 27.89% | 19.14% | 13.73% |
| PSNR | 7.00% | 2.17% | 57.62% | 21.35% | 14.89% | 10.79% |
| RMSE | 12.45% | 4.22% | 52.57% | 30.18% | 23.22% | 18.04% |
| MAE | −9.47% | −6.89% | 20.70% | 28.30% | 26.90% | 13.47% |
| MAX | 23.01% | 28.04% | 80.64% | 48.99% | 33.93% | 30.26% |
| Perform. Index | LPA-ICI | TV | Neigh STFT | sym4 Wavelet SURE, Level 6 | db13 Wavelet SURE, Level 5 | coif1 Wavelet SURE, Level 7 |
|---|---|---|---|---|---|---|
| ISNR | 6.98% | −0.35% | 95.56% | 29.85% | 38.44% | 25.00% |
| PSNR | 8.23% | −0.41% | 132.60% | 36.64% | 47.92% | 30.44% |
| RMSE | 12.11% | −0.73% | 62.13% | 36.65% | 42.41% | 32.77% |
| MAE | 9.23% | 8.04% | 34.89% | 39.04% | 55.60% | 34.09% |
| MAX | 26.02% | 15.69% | 83.31% | 77.80% | 50.83% | 75.71% |
| Execution Time (s) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Distance (kpc) | LPA-RICI | LPA-RICI | LPA-RICI | LPA-ICI | TV | Neigh STFT | Symlet Wavelet | Daubechies Wavelet | Coiflet Wavelet |
| 5 | 0.3427 | 0.5322 | 0.6698 | 4.7678 | 0.0231 | 0.7854 | 0.0054 | 0.0054 | 0.0058 |
| 10 | 0.4770 | 0.7887 | 1.2294 | 9.5808 | 0.0218 | 0.7553 | 0.0054 | 0.0071 | 0.0059 |
| 20 | 0.1670 | 1.0763 | 1.3092 | 12.6891 | 0.0231 | 0.7768 | 0.0042 | 0.0071 | 0.0058 |
| Perform. Index | LPA-RICI | LPA-RICI | LPA-RICI | LPA-ICI | TV | Neigh STFT | sym4 Wavelet SURE, Level 6 | db25 Wavelet SURE, Level 4 | coif4 Wavelet SURE, Level 5 |
|---|---|---|---|---|---|---|---|---|---|
| ISNR (db) | 12.9255 | 12.9800 | 12.8344 | 10.7381 | 9.6876 | 7.2057 | 10.5605 | 11.8525 | 10.0418 |
| PSNR (db) | 22.4275 | 22.4820 | 22.3364 | 20.2401 | 19.1895 | 16.7077 | 20.0624 | 21.3545 | 19.5438 |
| RMSE | 0.0756 | 0.0751 | 0.0764 | 0.0973 | 0.1098 | 0.1461 | 0.0993 | 0.0856 | 0.1054 |
| MAE | 0.0590 | 0.0557 | 0.0546 | 0.0641 | 0.0774 | 0.0877 | 0.0679 | 0.0676 | 0.0671 |
| MAX | 0.3054 | 0.4222 | 0.3502 | 0.4744 | 0.4466 | 0.7650 | 1.0834 | 0.3646 | 1.2784 |
| Perform. Index | LPA-RICI | LPA-RICI | LPA-RICI | LPA-ICI | TV | Neigh STFT | sym8 Wavelet SURE, Level 5 | db4 Wavelet SURE, Level 6 | coif4 Wavelet SURE, Level 5 |
|---|---|---|---|---|---|---|---|---|---|
| ISNR (db) | 15.6555 | 15.4472 | 14.9058 | 12.9291 | 11.9438 | 10.3813 | 11.3717 | 12.6203 | 10.7677 |
| PSNR (db) | 19.1655 | 18.9571 | 18.4157 | 16.4390 | 15.4537 | 13.8912 | 14.8816 | 16.1303 | 14.2776 |
| RMSE | 0.1101 | 0.1128 | 0.1200 | 0.1507 | 0.1688 | 0.2020 | 0.1803 | 0.1561 | 0.1932 |
| MAE | 0.0845 | 0.0850 | 0.0890 | 0.1002 | 0.1123 | 0.1223 | 0.1102 | 0.1044 | 0.1194 |
| MAX | 0.6060 | 0.6680 | 0.6680 | 0.9034 | 0.6923 | 1.2354 | 2.1975 | 0.9295 | 2.3395 |
| Perform. Index | LPA-RICI | LPA-RICI | LPA-RICI | LPA-ICI | TV | Neigh STFT | sym5 Wavelet SURE, Level 6 | db6 Wavelet SURE, Level 6 | coif1 Wavelet SURE, Level 7 |
|---|---|---|---|---|---|---|---|---|---|
| ISNR (db) | 18.0346 | 17.6215 | 17.6932 | 15.4138 | 15.7267 | 9.0143 | 12.0204 | 12.6513 | 11.3468 |
| PSNR (db) | 15.5324 | 15.1193 | 15.1910 | 12.9116 | 13.2245 | 6.5121 | 9.5182 | 10.1491 | 8.8446 |
| RMSE | 0.1673 | 0.1754 | 0.1740 | 0.2262 | 0.2182 | 0.4725 | 0.3343 | 0.3108 | 0.3612 |
| MAE | 0.1299 | 0.1335 | 0.1284 | 0.1415 | 0.1411 | 0.2302 | 0.2236 | 0.1835 | 0.2325 |
| MAX | 0.7221 | 1.3360 | 1.3360 | 1.4224 | 0.9131 | 3.1182 | 3.8350 | 3.7716 | 4.7470 |
| Perform. Index | LPA-ICI | TV | Neigh STFT | sym4 Wavelet SURE, Level 6 | db25 Wavelet SURE, Level 4 | coif4 Wavelet SURE, Level 5 |
|---|---|---|---|---|---|---|
| ISNR | 20.88% | 33.99% | 80.14% | 22.91% | 9.51% | 29.26% |
| PSNR | 11.08% | 17.16% | 34.56% | 12.06% | 5.28% | 15.03% |
| RMSE | 22.82% | 31.60% | 48.60% | 24.37% | 12.27% | 28.75% |
| MAE | 13.10% | 28.04% | 36.49% | 17.97% | 17.60% | 16.99% |
| MAX | 11.00% | 5.46% | 44.81% | 61.03% | −15.80% | 66.97% |
| Perform. Index | LPA-ICI | TV | Neigh STFT | sym8 Wavelet SURE, Level 5 | db4 Wavelet SURE, Level 6 | coif4 Wavelet SURE, Level 5 |
|---|---|---|---|---|---|---|
| ISNR | 21.09% | 31.08% | 50.80% | 37.67% | 24.05% | 45.39% |
| PSNR | 16.59% | 24.02% | 37.97% | 28.79% | 18.82% | 34.23% |
| RMSE | 26.94% | 34.77% | 45.50% | 38.94% | 29.47% | 43.01% |
| MAE | 15.67% | 24.76% | 30.91% | 23.32% | 19.06% | 29.23% |
| MAX | 32.92% | 12.47% | 50.95% | 72.42% | 34.80% | 74.10% |
| Perform. Index | LPA-ICI | TV | Neigh STFT | sym5 Wavelet SURE, Level 6 | db6 Wavelet SURE, Level 6 | coif1 Wavelet SURE, Level 7 |
|---|---|---|---|---|---|---|
| ISNR | 17.00% | 14.68% | 100.07% | 50.03% | 42.55% | 58.94% |
| PSNR | 20.30% | 17.45% | 138.52% | 63.19% | 53.04% | 75.61% |
| RMSE | 26.04% | 23.33% | 64.59% | 49.96% | 46.17% | 53.68% |
| MAE | 8.20% | 7.94% | 43.57% | 41.91% | 29.21% | 44.13% |
| MAX | 49.23% | 20.92% | 76.84% | 81.17% | 80.85% | 84.79% |
| Execution Time (s) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Distance (kpc) | LPA-RICI | LPA-RICI | LPA-RICI | LPA-ICI | TV | Neigh STFT | Symlet Wavelet | Daubechies Wavelet | Coiflet Wavelet |
| 5 | 0.4498 | 0.7315 | 0.9687 | 3.8876 | 0.0163 | 0.7809 | 0.0054 | 0.0162 | 0.0051 |
| 10 | 0.6978 | 0.8143 | 1.1634 | 4.9161 | 0.0169 | 0.7755 | 0.0050 | 0.0054 | 0.0050 |
| 20 | 0.8756 | 1.0480 | 2.3415 | 10.5730 | 0.0169 | 0.7700 | 0.0054 | 0.0055 | 0.0058 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lopac, N.; Lerga, J.; Cuoco, E. Gravitational-Wave Burst Signals Denoising Based on the Adaptive Modification of the Intersection of Confidence Intervals Rule. Sensors 2020, 20, 6920. https://doi.org/10.3390/s20236920
Lopac N, Lerga J, Cuoco E. Gravitational-Wave Burst Signals Denoising Based on the Adaptive Modification of the Intersection of Confidence Intervals Rule. Sensors. 2020; 20(23):6920. https://doi.org/10.3390/s20236920
Chicago/Turabian StyleLopac, Nikola, Jonatan Lerga, and Elena Cuoco. 2020. "Gravitational-Wave Burst Signals Denoising Based on the Adaptive Modification of the Intersection of Confidence Intervals Rule" Sensors 20, no. 23: 6920. https://doi.org/10.3390/s20236920
APA StyleLopac, N., Lerga, J., & Cuoco, E. (2020). Gravitational-Wave Burst Signals Denoising Based on the Adaptive Modification of the Intersection of Confidence Intervals Rule. Sensors, 20(23), 6920. https://doi.org/10.3390/s20236920






