Body-Worn IMU Human Skeletal Pose Estimation Using a Factor Graph-Based Optimization Framework
Abstract
1. Introduction
2. Problem Formulation
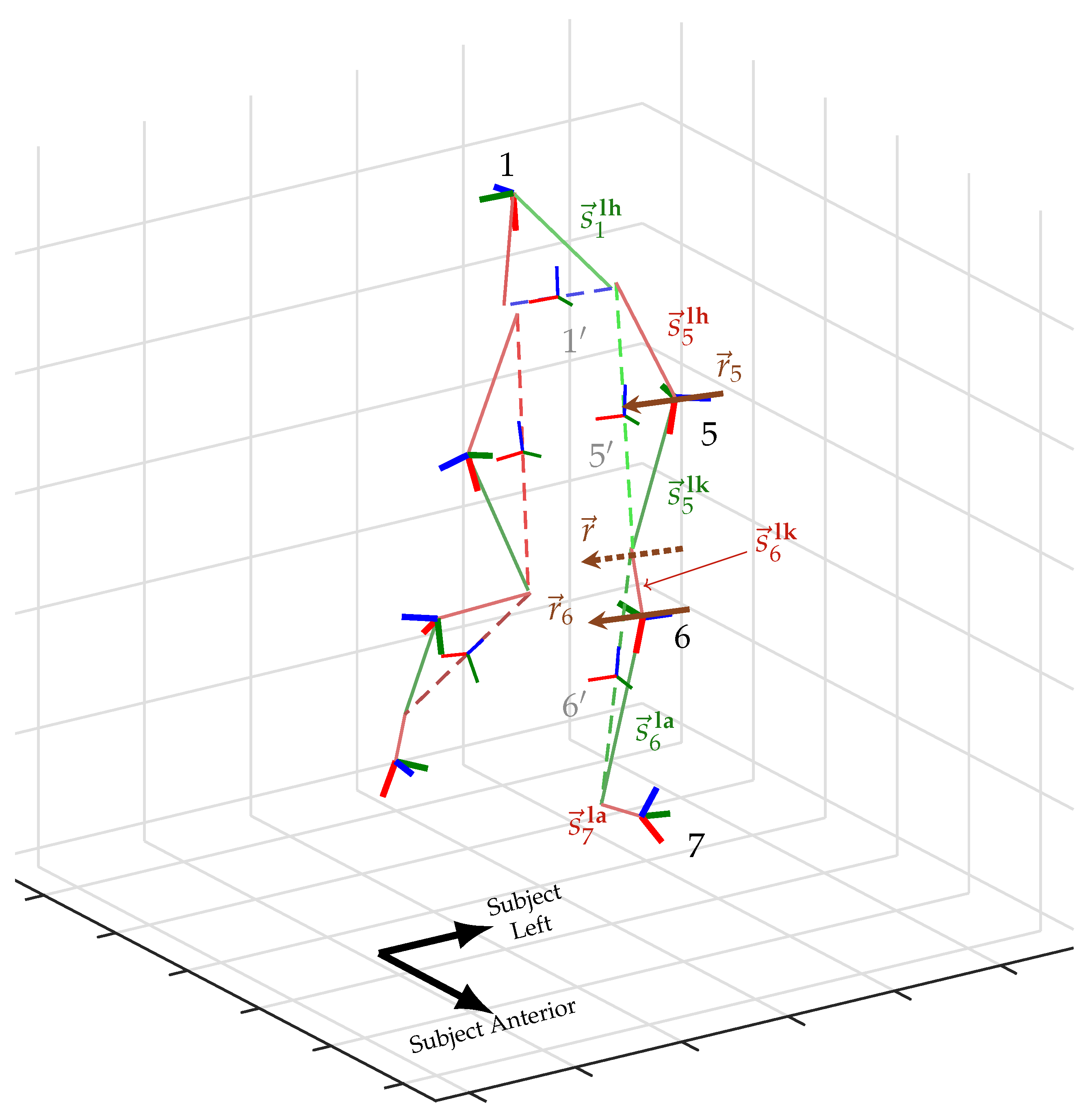
2.1. Estimated Variables, Derived Quantities, and Notation
- Discrete time-series pose trajectory of each IMU: , , , , , , for . It should be noted that a pose from frame A to the navigation frame, may equivalently be expressed in terms of its orientation and position components;
- Discrete time-series velocities of each IMU: , , , , , , ∈ for ;
- Discrete time-series angular velocities of each IMU: , , , , , , for ;
- Discrete time-series accelerometer and gyroscope biases for each IMU: , , , , , , ∈ for ;
- The (static) hinge axis of the right knee, expressed in the right thigh and right shank IMU frame, respectively: ∈, and similar for the (static) axis of the left knee expressed in its respective thigh and shank frame: ∈;
- The (static) vector from the IMU frame to each adjacent joint center, i.e., the vector from the
- –
- lumbar IMU frame to the right hip rotation center: ,
- –
- right thigh IMU to the right hip center: ,
- –
- right thigh IMU to the right knee center: ,
- –
- right shank IMU to the right knee center: ,
- –
- right shank IMU to the right ankle center: ,
- –
- right foot IMU to the right ankle center:
- –
- lumbar IMU frame to the left hip rotation center: ,
- –
- left thigh IMU to the left hip center: ,
- –
- left thigh IMU to the left knee center: ,
- –
- left shank IMU to the left knee center: ,
- –
- left shank IMU to the left ankle center: ,
- –
- left foot IMU to the left ankle center: .
- Discrete time-series orientations of the anatomical pelvic, right femur, right tibial, left femur, and left tibial segments: , , , , for ;
- The time-series flexion/extension, internal/external rotation, and abduction/adduction joint angles of the knee.
- z: positive in the proximal direction;
- y: positive in the anterior direction;
- x: positive to the subject’s right.
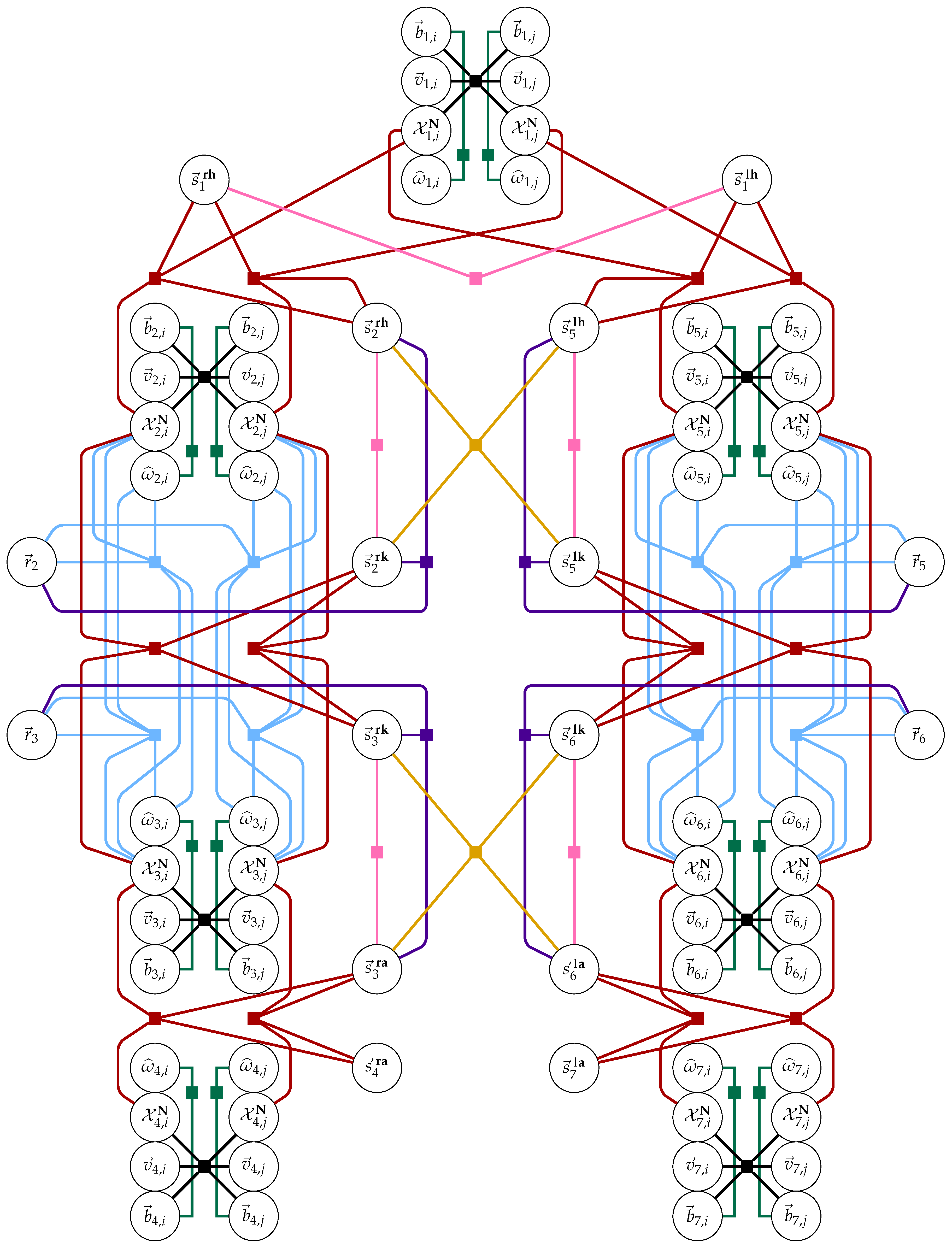
2.2. Model
2.2.1. IMU Dynamics Model
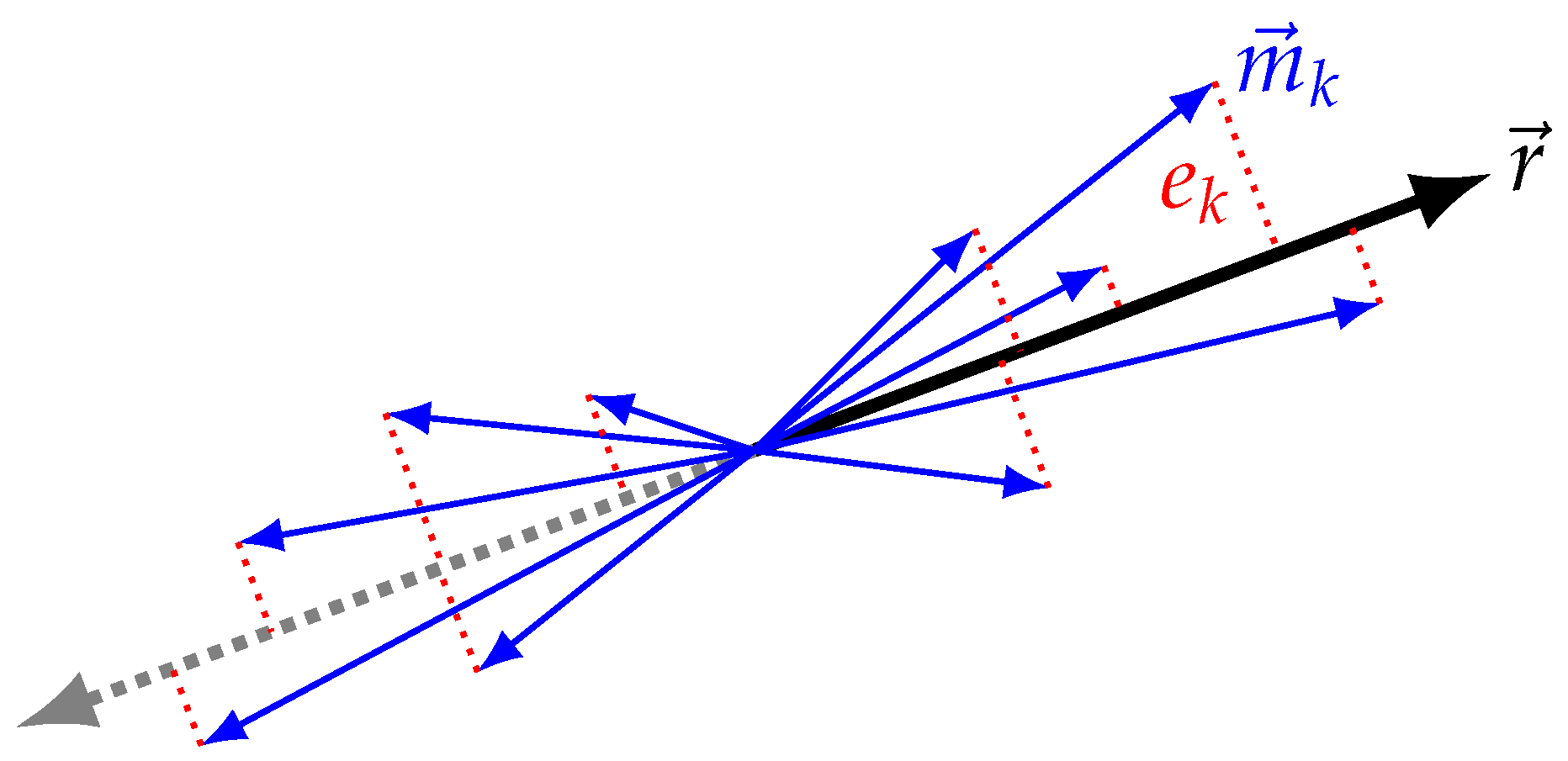
2.2.2. Knee Pseudo-Hinge Kinematics
2.2.3. Constrained Joint Centers of Rotation
2.2.4. Angle Between the Knee Rotation Axis and Femur/Tibia Proximal
2.2.5. Femur Length, Tibia Length, and Pelvic Width from Anthropometry
2.2.6. Maximum/Minimum Anthropometric Lengths
2.2.7. Femur and Tibia Length Discrepancy
2.2.8. Full Problem Representation
2.2.9. Model Identifiability
- (Structural nonidentifiability #1) Gauge freedom [89] of the solution in absolute position, velocity, and heading. The proposed model does not have an absolute reference for position, velocity, or heading (i.e., GPS or magnetometers). Therefore, the estimated solution is correct up to a constant offset in these degrees of freedom. This nonidentifiability is addressed through the use of priors to anchor the solution, as detailed in Section 3.7;
- (Structural nonidentifiability #2) Knee axis sign ambiguity: Both the positive and negative sign of knee axes and are equivalent nonunique solutions to Equations (8) and (9), respectively. This manifests as discrete equivalent-error local minima per leg. These equivalent local minima are disambiguated post-hoc, detailed in Section 3.9.
- (Practical nonidentifiability #1) (a) A trivial nonidentifiability of static vector and knee axis variables occurs when there is no motion of the subject—the proposed method does require human motion. (b) Similarly, static vectors to the hip and ankle joints must sufficiently explore all DOF of the joints. The solution to the constrained joint center of rotation model (Equation (10)) is only identifiable and unique when both IMUs flanking the joint sufficiently rotate in multiple DOF relative to the joint center;
- (Practical nonidentifiability #2) Discerning heading relationship between IMUs flanking the hip and ankle joints. In a magnetometer-free estimation framework, the heading relationship between IMUs must be derived from human kinematics alone. It is possible the constrained joint center of rotation model Equation (10) provides the necessary information. However, in conditions where one or more of the static vectors from the IMU to neighboring joint centers is generally vertical, i.e., orthogonal to the heading plane, then the associated IMU’s orientation trajectory becomes underconstrained and all constant-offset heading solutions are viable. This situation may occur, for example, in upright walking gait with small step length. In the case of the 1DOF knee, this heading relationship between thigh and shank IMUs is well defined by hinge model Equation (8).
3. Materials and Methods
3.1. Participants
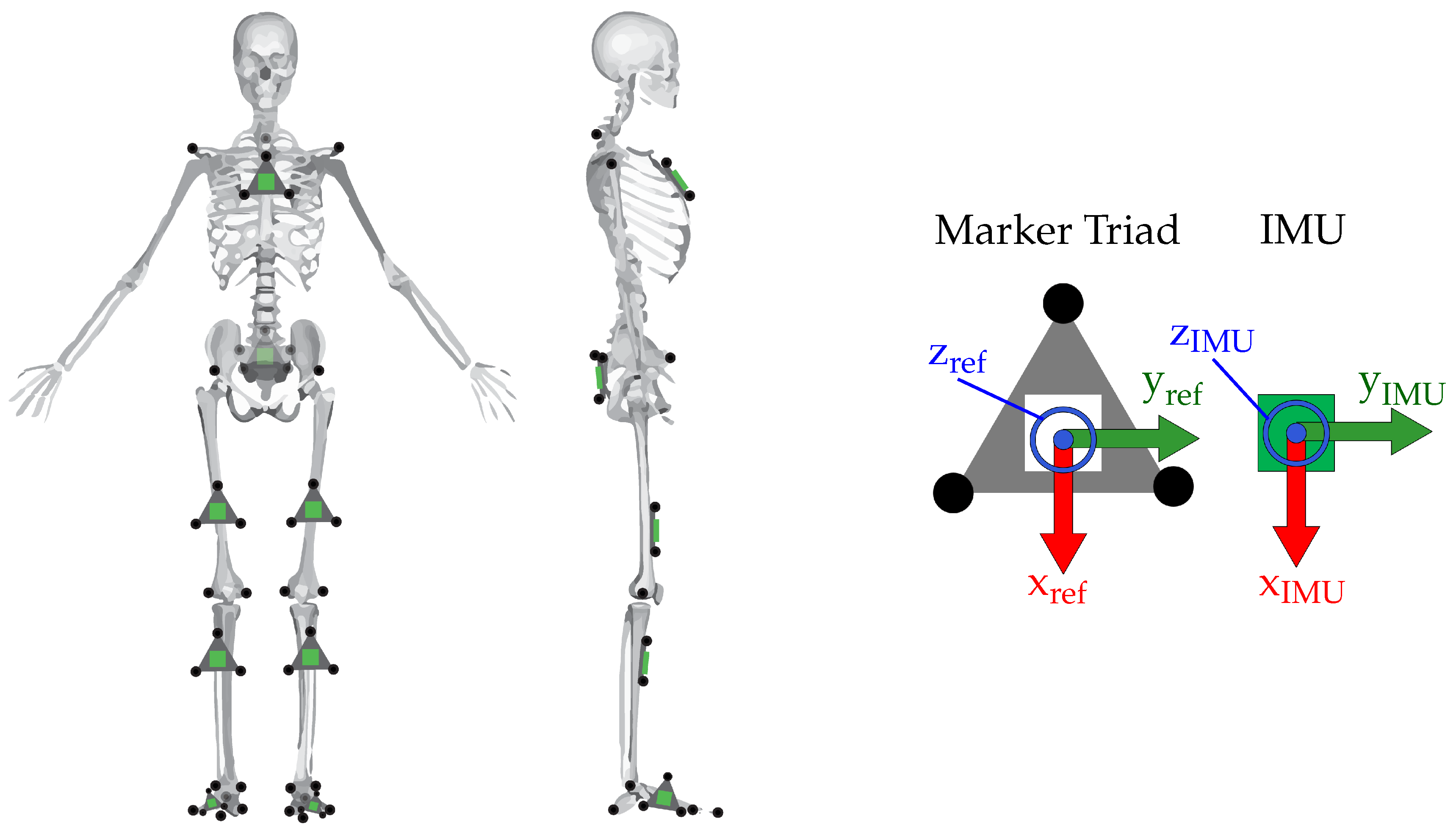
3.2. Study Protocol
- Ankle calibration: Lift your right foot so that it is hovering a few inches off the ground. Perform three ankle flexion/extension cycles within maximum range of comfort. Then, while foot is lifted a few inches off ground, rotate the front of your foot in a circle three times within maximum range of comfort. Repeat for left ankle;
- Knee calibration: Stand on left foot while keeping both thighs as vertical as possible. Swing right foot behind you (flexing the knee), at least 90 degrees, then return right foot to ground (extending the knee). Do this three times. Repeat for left knee;
- Hip calibration: From standard pose, while keeping knee and ankle neutral, swing your straight right leg up in front of you to maximum range of comfort and return to ground (flexion/extension of hip) three times. Then, perform an adduction/abduction of hip by swinging straight right leg out to lateral side of the body to maximum range of comfort and then returning foot to ground three times. Finally, perform internal/external rotation of hip by keeping foot near to ground and rotating your foot in and out three times to maximum range of comfort while keeping your ankle and knee stiff. Repeat for left hip;
- Torso calibration: From neutral pose, bend down and touch your toes and come back up. Then, twist your torso (forward-left torso twist-forward-right torso twist-forward) to maximum range of comfort. Finally, a side-to-side bend: Up-left-up-right-up.
3.3. Data Processing
3.4. Derivation and Processing of Knee Angles
3.5. Selection of Noise Parameters
3.6. Selection of Anthropometric Priors
3.7. Other Priors
3.8. Initialization
3.9. Hinge Axis Direction Disambiguation
- (Step #1)
- Ensuring both knee axes are pointed in the same direction. First, the sign of is adjusted to ensure it points to the same side as . Both knee axes are transformed into the global frame for all points in time through estimated IMU orientations and . For each point in time, the angle between the knee axes in the world frame is computed. If the median of this distribution is greater than 90 degrees, we conclude that the knee axes point in opposite directions, and the sign of is flipped. Otherwise, we conclude that knee axes are pointed in the same direction;
- (Step #2)
- Ensuring both axes are pointed to the subject’s right. After Step #1, both knee axes will point to either the subject’s left or the subject’s right. However, if both axes point to the subject’s left, then the knee flexion/extension angle as derived in Section 3.4 will have the incorrect sign. Per the ISB-recommended knee angle convention (if both knee axes point to the subject’s right), the range of motion (ROM) of the knee angle should fall approximately in [+10,−150]. If both knee axes point to the subject’s left, this ROM will fall in [+150,−10]. Therefore, after Step #1 the knee angle is computed. If the median knee angle is greater than +20, it is concluded that both knee axes must have been pointing to the subject’s left. Then both axes’ signs are flipped and the angle is recomputed.
3.10. Statistical Analysis
4. Results and Discussion
Future Work and Limitations
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Han, F.; Reily, B.; Hoff, W.; Zhang, H. Space-time representation of people based on 3D skeletal data: A review. Comput. Vis. Image Underst. 2017, 15, 85–105. [Google Scholar] [CrossRef]
- Liu, Z.; Zhu, J.; Bu, J.; Chen, C. A survey of human pose estimation: The body parts parsing based methods. J. Vis. Commun. Image Represent. 2015, 32, 10–19. [Google Scholar] [CrossRef]
- Van der Kruk, E.; Reijne, M.M. Accuracy of human motion capture systems for sport applications; state-of-the-art review. Eur. J. Sport Sci. 2018, 18, 806–819. [Google Scholar] [CrossRef]
- Sarafianos, N.; Boteanu, B.; Ionescu, B.; Kakadiaris, I.A. 3D Human pose estimation: A review of the literature and analysis of covariates. Comput. Vis. Image Underst. 2016, 152, 1–20. [Google Scholar] [CrossRef]
- Ceseracciu, E.; Sawacha, Z.; Cobelli, C. Comparison of markerless and marker-based motion capture technologies through simultaneous data collection during gait: Proof of concept. PLoS ONE 2014, 9, e87640. [Google Scholar] [CrossRef]
- Delp, S.L.; Anderson, F.C.; Arnold, A.S.; Loan, P.; Habib, A.; John, C.T.; Guendelman, E.; Thelen, D.G. OpenSim: Open source to create and analyze dynamic simulations of movement. IEEE Trans. Bio-Med Eng. 2007, 54, 1940–1950. [Google Scholar] [CrossRef]
- Davis, R.B.; Õunpuu, S.; Tyburski, D.; Gage, J.R. A gait analysis data collection and reduction technique. Hum. Mov. Sci. 1991, 10, 575–587. [Google Scholar] [CrossRef]
- Kadaba, M.P.; Ramakrishnan, H.K.; Wootten, M.E. Measurement of Lower-Extremity Kinematics during Level Walking. J. Orthop. Res. 1990, 8, 383–392. [Google Scholar] [CrossRef]
- Field, M.; Stirling, D.; Naghdy, F.; Pan, Z. Motion capture in robotics review. In Proceedings of the 2009 IEEE International Conference on Control and Automation, ICCA, Christchurch, New Zealand, 9–11 December 2009. [Google Scholar] [CrossRef]
- Ahmad, N.; Ghazilla, R.A.R.; Khairi, N.M.; Kasi, V. Reviews on Various Inertial Measurement Unit (IMU) Sensor Applications. Int. J. Signal Process. Syst. 2013, 1, 256–262. [Google Scholar] [CrossRef]
- Allerton, D.J.; Jia, H. A review of multisensor fusion methodologies for aircraft navigation systems. J. Navig. 2005, 58, 405–417. [Google Scholar] [CrossRef]
- Hays, K.M.; Schmidt, R.G.; Wilson, W.A.; Campbell, J.D.; Heckman, D.W.; Gokhale, M.P. A submarine navigator for the 21st century. In Proceedings of the IEEE PLANS, Position Location and Navigation Symposium, Palms Springs, CA, USA, 15–18 April 2002. [Google Scholar] [CrossRef]
- Zhao, J. A Review of Wearable IMU (Inertial-Measurement-Unit)-based Pose Estimation and Drift Reduction Technologies. J. Phys. Conf. Ser. 2018, 1087. [Google Scholar] [CrossRef]
- Jimenez, A.R.; Seco, F.; Prieto, J.C.; Guevara, J. Indoor Pedestrian navigation using an INS/EKF framework for yaw drift reduction and a foot-mounted IMU. In Proceedings of the 2010 7th Workshop on Positioning, Navigation and Communication, WPNC’10, Dresden, Germany, 11–12 March 2010. [Google Scholar] [CrossRef]
- Ilyas, M.; Cho, K.; Baeg, S.H.; Park, S. Drift reduction in IMU-only pedestrian navigation system in unstructured environment. In Proceedings of the 2015 10th Asian Control Conference: Emerging Control Techniques for a Sustainable World, ASCC 2015, Kota Kinabalu, Malaysia, 31 May–3 June 2015. [Google Scholar] [CrossRef]
- Ilyas, M.; Cho, K.; Baeg, S.H.; Park, S. Drift reduction in pedestrian navigation system by exploiting motion constraints and magnetic field. Sensors 2016, 16, 1455. [Google Scholar] [CrossRef]
- Borenstein, J.; Ojeda, L.; Kwanmuang, S. Heuristic reduction of gyro drift in IMU-based personnel tracking systems. Opt. Photonics Glob. Homel. Secur. Biom. Technol. Hum. Identif. 2009, 7306. [Google Scholar] [CrossRef]
- Yang, D.; Woo, J.K.; Najafi, K.; Lee, S.; Mitchell, J.; Challoner, D. 2ppm Frequency Drift and 300x Reduction of Bias Drift of Commercial 6-Axis Inertial Measurement Units Using a Low-Power Oven-Control Micro Platform. In Proceedings of the 2015 IEEE SENSORS, Busan, Korea, 1–4 November 2015; pp. 1–4. [Google Scholar] [CrossRef]
- Nerino, R.; Contin, L.; Gonçalves Da Silva Pinto, W.J.; Massazza, G.; Actis, M.; Capacchione, P.; Chimienti, A.; Pettiti, G. A BSN based service for post-surgical knee rehabilitation at home. In Proceedings of the BODYNETS 2013—8th International Conference on Body Area Networks, Brussels, Belgium, 30 September–2 October 2013. [Google Scholar] [CrossRef]
- Nerino, R.; Contin, L.; Tirri, A.; Massazza, G.; Chimienti, A.; Pettiti, G.; Cau, N.; Cimolin, V. An improved solution for knee rehabilitation at home. In Proceedings of the BODYNETS 2014—9th International Conference on Body Area Networks, Brussels, Belgium, 29 September–1 October 2014. [Google Scholar] [CrossRef]
- Vienne, A.; Barrois, R.P.; Buffat, S.; Ricard, D.; Vidal, P.P. Inertial sensors to assess gait quality in patients with neurological disorders: A systematic review of technical and analytical challenges. Front. Psychol. 2017, 8, 817. [Google Scholar] [CrossRef]
- Caldas, R.; Mundt, M.; Potthast, W.; Buarque de Lima Neto, F.; Markert, B. A systematic review of gait analysis methods based on inertial sensors and adaptive algorithms. Gait Posture 2017, 52, 204–210. [Google Scholar] [CrossRef]
- Glowinski, S.; Łosiński, K.; Kowiański, P.; Waśkow, M.; Bryndal, A.; Grochulska, A. Inertial sensors as a tool for diagnosing discopathy lumbosacral pathologic gait: A preliminary research. Diagnostics 2020, 10, 342. [Google Scholar] [CrossRef]
- Nguyen, L.N.N.; Rodríguez-Martín, D.; Català, A.; Pérez-López, C.; Samà, A.; Cavallaro, A. Basketball activity recognition using wearable inertial measurement units. ACM Int. Conf. Proc. Ser. 2015, 1–6. [Google Scholar] [CrossRef]
- Dadashi, F.; Arami, A.; Crettenand, F.; Millet, G.P.; Komar, J.; Seifert, L.; Aminian, K. A hidden Markov model of the breaststroke swimming temporal phases using wearable inertial measurement units. In Proceedings of the 2013 IEEE International Conference on Body Sensor Networks, BSN, Cambridge, MA, USA, 6–9 May 2013. [Google Scholar] [CrossRef]
- Clark, W.W.; Romeiko, J.R. Inertial Measurements of Sports Motion. U.S. Patent No. 8,944,939, 3 February 2015. [Google Scholar]
- Dadashi, F.; Crettenand, F.; Millet, G.P.; Aminian, K. Front-crawl instantaneous velocity estimation using a wearable inertial measurement unit. Sensors 2012, 12, 2927. [Google Scholar] [CrossRef]
- Vitali, R.V.; Cain, S.M.; Ojeda, L.V.; Potter, M.V.; Zaferiou, A.M.; Davidson, S.P.; Coyne, M.E.; Hancock, C.L.; Mendoza, A.; Stirling, L.A.; et al. Body-worn IMU array reveals effects of load on performance in an outdoor obstacle course. PLoS ONE 2019, 14, e0214008. [Google Scholar] [CrossRef]
- Xu, R.; Agarwal, P.; Kumar, S.; Krovi, V.N.; Corso, J.J. Combining skeletal pose with local motion for human activity recognition. In Proceedings of the International Conference on Articulated Motion and Deformable Objects), Mallorca, Spain, 11–13 July 2012. [Google Scholar] [CrossRef]
- Koskimäki, H.; Huikari, V.; Siirtola, P.; Laurinen, P.; Röning, J. Activity recognition using a wrist-worn inertial measurement unit: A case study for industrial assembly lines. In Proceedings of the 17th Mediterranean Conference on Control and Automation, Thessaloniki, Greece, 24–26 June 2009. [Google Scholar] [CrossRef]
- Chinimilli, P.T.; Redkar, S.; Zhang, W. Human activity recognition using inertial measurement units and smart shoes. In Proceedings of the American Control Conference, Seattle, WA, USA, 24–26 May 2017. [Google Scholar] [CrossRef]
- Storm, F.A.; Heller, B.W.; Mazzà, C. Step detection and activity recognition accuracy of seven physical activity monitors. PLoS ONE 2015, 10, e0118723. [Google Scholar] [CrossRef]
- Bayat, A.; Pomplun, M.; Tran, D.A. A study on human activity recognition using accelerometer data from smartphones. Procedia Comput. Sci. 2014, 34, 450–457. [Google Scholar] [CrossRef]
- Lim, S.; D’Souza, C. A narrative review on contemporary and emerging uses of inertial sensing in occupational ergonomics. Int. J. Ind. Ergon. 2020, 76, 102937. [Google Scholar] [CrossRef]
- Fineman, R.A.; McGrath, T.M.; Kelty-Stephen, D.G.; Andrew, A.F.; Stirling, L.A. Objective metrics quantifying fit and performance in spacesuit assemblies. Aerosp. Med. Hum. Perform. 2018, 89, 985–995. [Google Scholar] [CrossRef]
- Vitali, R.V.; Perkins, N.C. Determining anatomical frames via inertial motion capture: A survey of methods. J. Biomech. 2020, 109832. [Google Scholar] [CrossRef]
- Luinge, H.J.; Veltink, P.H.; Baten, C.T.M. Estimating orientation with gyroscopes and accelerometers. Technol. Health Care 1999, 7, 455. [Google Scholar] [CrossRef]
- Mayagoitia, R.E.; Nene, A.V.; Veltink, P.H. Accelerometer and rate gyroscope measurement of kinematics: An inexpensive alternative to optical motion analysis systems. J. Biomech. 2002, 35, 537–542. [Google Scholar] [CrossRef]
- Favre, J.; Luthi, F.; Jolles, B.M.; Siegrist, O.; Najafi, B.; Aminian, K.; Ne, K.; Favre, E.J.; Najafi, A.B.; Aminian, A.K.; et al. A new ambulatory system for comparative evaluation of the three-dimensional knee kinematics, applied to anterior cruciate ligament injuries. Knee Surg. Sport. Traumatol. Arthrosc. 2006, 14, 592–604. [Google Scholar] [CrossRef]
- Favre, J.; Jolles, B.; Siegrist, O.; Animian, K. Quaternion-based fusion of gyroscopes and accelerometers to improve 3D angle measurement. Inst. Eng. Technol. 2006, 42, 612–614. [Google Scholar] [CrossRef]
- Kok, M.; Hol, J.D.; Schön, T.B. An optimization-based approach to human body motion capture using inertial sensors. Ifac Proc. Vol. (IFAC-PapersOnline) 2014, 19, 79–85. [Google Scholar] [CrossRef]
- Roetenberg, D.; Luinge, H.; Slycke, P. Xsens MVN: Full 6DOF human motion tracking using miniature inertial sensors. Xsens Motion Technol. 2009, 1. Available online: https://me.queensu.ca/People/Deluzio/JAM/files/12.17.10_Yang.pdf (accessed on 1 December 2020).
- Favre, J.; Jolles, B.M.; Aissaoui, R.; Aminian, K. Ambulatory measurement of 3D knee joint angle. J. Biomech. 2008, 41, 1029–1035. [Google Scholar] [CrossRef]
- Favre, J.; Aissaoui, R.; Jolles, B.M.; de Guise, J.A.; Aminian, K. Functional calibration procedure for 3D knee joint angle description using inertial sensors. J. Biomech. 2009, 42, 2330–2335. [Google Scholar] [CrossRef] [PubMed]
- Zhu, R.; Zhou, Z. A real-time articulated human motion tracking using tri-axis inertial/magnetic sensors package. IEEE Trans. Neural Syst. Rehabil. Eng. 2004, 12, 295–302. [Google Scholar] [CrossRef] [PubMed]
- Luinge, H.J.; Veltink, P.H.; Baten, C.T.M. Ambulatory measurement of arm orientation. J. Biomech. 2007, 40, 78–85. [Google Scholar] [CrossRef] [PubMed]
- O’Donovan, K.J.; Kamnik, R.; O’Keeffe, D.T.; Lyons, G.M. An inertial and magnetic sensor based technique for joint angle measurement. J. Biomech. 2007, 40, 2604–2611. [Google Scholar] [CrossRef]
- Cooper, G.; Sheret, I.; McMillian, L.; Siliverdis, K.; Sha, N.; Hodgins, D.; Kenney, L.; Howard, D. Inertial sensor-based knee flexion/extension angle estimation. J. Biomech. 2009, 42, 2678–2685. [Google Scholar] [CrossRef]
- Tadano, S.; Takeda, R.; Miyagawa, H. Three dimensional gait analysis using wearable acceleration and gyro sensors based on quaternion calculations. Sensors 2013, 13, 9321–9343. [Google Scholar] [CrossRef] [PubMed]
- Cutti, A.G.; Ferrari, A.; Garofalo, P.; Raggi, M.; Cappello, A.; Ferrari, A. ‘Outwalk’: A protocol for clinical gait analysis based on inertial and magnetic sensors. Med. Biol. Eng. Comput. 2010, 48, 17–25. [Google Scholar] [CrossRef]
- Vitali, R.V.; Cain, S.M.; McGinnis, R.S.; Zaferiou, A.M.; Ojeda, L.V.; Davidson, S.P.; Perkins, N.C. Method for estimating three-dimensional knee rotations using two inertial measurement units: Validation with a coordinate measurement machine. Sensors 2017, 17, 1970. [Google Scholar] [CrossRef] [PubMed]
- Adamowicz, L.; Gurchiek, R.; Ferri, J.; Ursiny, A.; Fiorentino, N.; McGinnis, R. Validation of Novel Relative Orientation and Inertial Sensor-to-Segment Alignment Algorithms for Estimating 3D Hip Joint Angles. Sensors 2019, 19, 5143. [Google Scholar] [CrossRef]
- Müller, P.; Bégin, M.A.; Schauer, T.; Seel, T. Alignment-Free, Self-Calibrating Elbow Angles Measurement Using Inertial Sensors. IEEE J. Biomed. Health Inform. 2017, 21, 312–319. [Google Scholar] [CrossRef]
- McGrath, T.; Fineman, R.; Stirling, L. An Auto-Calibrating Knee Flexion-Extension Axis Estimator Using Principal Component Analysis with Inertial Sensors. Sensors 2018, 18, 1882. [Google Scholar] [CrossRef]
- Seel, T.; Schauer, T. Joint Axis and Position Estimation from Inertial Measurement Data by Exploiting Kinematic Constraints. In Proceedings of the IEEE International Conference on Control Applications, Dubrovnik, Croatia, 3–5 October 2012. [Google Scholar]
- Seel, T.; Raisch, J.; Schauer, T. IMU-based joint angle measurement for gait analysis. Sensors 2014, 14, 6891–6909. [Google Scholar] [CrossRef]
- Salehi, S.; Bleser, G.; Reiss, A.; Stricker, D. Body-IMU autocalibration for inertial hip and knee joint tracking. Bodynets Int. Conf. Body Area Netw. 2015, 51–57. [Google Scholar] [CrossRef]
- Taetz, B.; Bleser, G.; Miezal, M. Towards self-calibrating inertial body motion capture. In Proceedings of the FUSION 2016—19th International Conference on Information Fusion, Heidelberg, Germany, 5–8 July 2016. [Google Scholar]
- Miezal, M.; Taetz, B.; Bleser, G. Real-time inertial lower body kinematics and ground contact estimation at anatomical foot points for agile human locomotion. In Proceedings of the IEEE International Conference on Robotics and Automation, Singapore, 29 May–3 June 2017. [Google Scholar] [CrossRef]
- Miezal, M.; Bleser, G.; Schmitz, N.; Stricker, D. A generic approach to inertial tracking of arbitrary kinematic chains. In Proceedings of the BODYNETS 2013—8th International Conference on Body Area Networks, Boston, MA, USA, 30 September–2 October 2013. [Google Scholar] [CrossRef]
- Miezal, M.; Taetz, B.; Schmitz, N.; Bleser, G. Ambulatory inertial spinal tracking using constraints. In Proceedings of the BODYNETS 2014—9th International Conference on Body Area Networks, London, UK, 29 September–1 October 2014. [Google Scholar] [CrossRef]
- Miezal, M.; Taetz, B.; Bleser, G. On inertial body tracking in the presence of model calibration errors. Sensors 2016, 16, 1132. [Google Scholar] [CrossRef]
- Kok, M.; Pakazad, S.K.; Schon, T.B.; Hansson, A.; Holz, J.D. A scalable and distributed solution to the inertial motion capture problem. In Proceedings of the FUSION 2016—19th International Conference on Information Fusion, Heidelberg, Germany, 5–8 July 2016. [Google Scholar]
- Pakazad, S.; Hansson, A.; Andersen, M. Distributed Primal-dual Interior-point Methods for Solving Loosely Coupled Problems Using Message Passing. arXiv 2015, arXiv:1502.06384. [Google Scholar]
- Leutenegger, S.; Lynen, S.; Bosse, M.; Siegwart, R.; Furgale, P. Keyframe-based visual-inertial odometry using nonlinear optimization. Int. J. Robot. Res. 2015, 34, 314–334. [Google Scholar] [CrossRef]
- Lupton, T.; Sukkarieh, S. Visual-inertial-aided navigation for high-dynamic motion in built environments without initial conditions. IEEE Trans. Robot. 2012. [Google Scholar] [CrossRef]
- Carlone, L.; Kira, Z.; Beall, C.; Indelman, V.; Dellaert, F. Eliminating conditionally independent sets in factor graphs: A unifying perspective based on smart factors. In Proceedings of the Proceedings—IEEE International Conference on Robotics and Automation, Hong Kong, China, 31 May–7 June 2014. [Google Scholar] [CrossRef]
- Forster, C.; Carlone, L.; Dellaert, F.; Scaramuzza, D. IMU preintegration on manifold for efficient visual-inertial maximum-a-posteriori estimation. Robot. Sci. Syst. 2015. [Google Scholar] [CrossRef]
- Warner, F.W. Foundations of Differentiable Manifolds and Lie Groups; Springe: Berlin, Germany, 1983. [Google Scholar] [CrossRef]
- Blanco, J.L. A Tutorial on SE(3) Transformation Parameterizations and On-Manifold Optimization; Technical Report; University of Malaga: Malaga, Spain, 2010. [Google Scholar]
- Kok, M.; Hol, J.D.; Schön, T.B. Using inertial sensors for position and orientation estimation. arXiv 2017, arXiv:1704.06053. [Google Scholar] [CrossRef]
- Dellaert, F. Factor Graphs and GTSAM: A Hands-On Introduction; Technical Report; Georgia Institute of Technology: Atlanta, GA, USA, 2012. [Google Scholar]
- Kschischang, F.R.; Frey, B.J.; Loeliger, H.A. Factor graphs and the sum-product algorithm. IEEE Trans. Inf. Theory 2001, 47, 498–519. [Google Scholar] [CrossRef]
- Roetenberg, D.; Luinge, H.J.; Baten, C.T.M.; Veltink, P.H. Compensation of magnetic disturbances improves inertial and magnetic sensing of human body segment orientation. IEEE Trans. Neural Syst. Rehabil. Eng. 2005, 13, 395–405. [Google Scholar] [CrossRef]
- De Vries, W.H.; Veeger, H.E.; Baten, C.T.; van der Helm, F.C. Magnetic distortion in motion labs, implications for validating inertial magnetic sensors. Gait Posture 2009, 29, 535–541. [Google Scholar] [CrossRef]
- Laidig, D.; Schauer, T.; Seel, T. Exploiting kinematic constraints to compensate magnetic disturbances when calculating joint angles of approximate hinge joints from orientation estimates of inertial sensors. In Proceedings of the IEEE International Conference on Rehabilitation Robotics, London, UK, 17–20 July 2017; pp. 971–976. [Google Scholar] [CrossRef]
- Chow, J.C. Drift-free indoor navigation using simultaneous localization and mapping of the ambient heterogeneous magnetic field. Int. Arch. Photogramm. Remote. Sens. Spat. Inf. Sci. ISPRS Arch. 2017. [Google Scholar] [CrossRef]
- Kok, M.; Schon, T.B. Magnetometer calibration using inertial sensors. IEEE Sensors J. 2016, 16, 5679–5689. [Google Scholar] [CrossRef]
- Lee, J.K.; Jeon, T.H. Magnetic Condition-Independent 3D Joint Angle Estimation Using Inertial Sensors and Kinematic Constraints. Sensors 2019, 19, 5522. [Google Scholar] [CrossRef]
- Laidig, D.; Lehmann, D.; Begin, M.A.; Seel, T. Magnetometer-free Realtime Inertial Motion Tracking by Exploitation of Kinematic Constraints in 2-DoF Joints. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, EMBS, Berlin, Germany, 23–27 July 2019. [Google Scholar] [CrossRef]
- Wu, G.; Cavanagh, P.R. ISB recommendations for standardization in the reporting of kinematic data. J. Biomech. 1995, 28, 1257–1261. [Google Scholar] [CrossRef]
- Grood, E.S.; Suntay, W.J. A Joint Coordinate System for the Clinical Description of Three-Dimensional Motions: Application to the Knee. J. Biomech. Eng. 1983, 105, 136. [Google Scholar] [CrossRef]
- Wu, G.; Siegler, S.; Allard, P.; Kirtley, C.; Leardini, A.; Rosenbaum, D.; Whittle, M.; D’Lima, D.D.; Cristofolini, L.; Witte, H.; et al. ISB recommendation on definitions of joint coordinate system of various joints for the reporting of human joint motion—part I: Ankle, hip, and spine. J. Biomech. 2002, 35, 543–548. [Google Scholar] [CrossRef]
- Hollister, A.M.; Jatana, S.; Singh, A.K.; Sullivan, W.W.; Lupichuk, A.G. The axes of rotation of the knee. Clin. Orthop. Relat. Res. 1993, 290, 259–268. [Google Scholar] [CrossRef]
- Shultz, S.J.; Nguyen, A.D. Bilateral asymmetries in clinical measures of lower-extremity anatomic characteristics. Clin. J. Sport Med. 2007, 17, 357–361. [Google Scholar] [CrossRef]
- Ugochukwu, E.; Ugbem, L.; Ijomone, O.; Ebi, O. Estimation of Maximum Tibia Length from its Measured Anthropometric Parameters in a Nigerian Population. J. Forensic Sci. Med. 2016, 2, 222. [Google Scholar] [CrossRef]
- Pierre, M.A.; Zurakowski, D.; Nazarian, A.; Hauser-Kara, D.A.; Snyder, B.D. Assessment of the bilateral asymmetry of human femurs based on physical, densitometric, and structural rigidity characteristics. J. Biomech. 2010, 43, 2228–2236. [Google Scholar] [CrossRef]
- Raue, A.; Becker, V.; Klingmüller, U.; Timmer, J. Identifiability and observability analysis for experimental design in nonlinear dynamical models. Chaos 2010, 20, 045105. [Google Scholar] [CrossRef]
- Triggs, B.; McLauchlan, P.F.; Hartley, R.I.; Fitzgibbon, A.W. Bundle adjustment—A modern synthesis. In International Workshop on Vision Algorithms; Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Berlin/Heidelberg, Germany, 2000; Volume 1883, pp. 298–372. [Google Scholar] [CrossRef]
- Seth, A.; Hicks, J.L.; Uchida, T.K.; Habib, A.; Dembia, C.L.; Dunne, J.J.; Ong, C.F.; DeMers, M.S.; Rajagopal, A.; Millard, M.; et al. OpenSim: Simulating musculoskeletal dynamics and neuromuscular control to study human and animal movement. PLoS Comput. Biol. 2018, 14, e1006223. [Google Scholar] [CrossRef]
- Moré, J.J. The Levenberg-Marquardt algorithm: Implementation and theory. In Numerical Analysis; Springer: Berlin/Heidelberg, Germany, 1978; pp. 105–116. [Google Scholar] [CrossRef]
- Delp, S.L.; Loan, J.P.; Hoy, M.G.; Zajac, F.E.; Topp, E.L.; Rosen, J.M. An Interactive Graphics-Based Model of the Lower Extremity to Study Orthopaedic Surgical Procedures. IEEE Trans. Biomed. Eng. 1990, 37, 757–767. [Google Scholar] [CrossRef]
- Yamaguchi, G.T.; Zajac, F.E. A planar model of the knee joint to characterize the knee extensor mechanism. J. Biomech. 1989, 22, 1–10. [Google Scholar] [CrossRef]
- Anderson, F.C.; Pandy, M.G. A dynamic optimization solution for vertical jumping in three dimensions. Comput. Methods Biomech. Biomed. Eng. 1999, 2, 201–231. [Google Scholar] [CrossRef]
- Anderson, F.C.; Pandy, M.G. Dynamic optimization of human walking. J. Biomech. Eng. 2001, 123, 381–390. [Google Scholar] [CrossRef]
- Seidel, G.K.; Marchinda, D.M.; Dijkers, M.; Soutas-Little, R.W. Hip joint center location from palpable bony landmarks-A cadaver study. J. Biomech. 1995, 28, 995–998. [Google Scholar] [CrossRef]
- Paquette, S.; Gordon, C.; Bradtmiller, B. Anthropometric Survey (ANSUR) II Pilot Study: Methods and Summary Statistics; Anthrotch, US Army Natick Soldier Research, Development and Engineering Center: Natick, MA, USA, 2009. [Google Scholar]
- Rabari, Y.B.; Sanap, A.; Prasad, D.V.; Thadeshwar, K.H. The distance of the centre of femoral head relative to the midline of the pelvis: A prospective X-ray study of 500 adults. Int. J. Res. Orthop. 2017, 3, 565. [Google Scholar] [CrossRef]
- Zhang, Z.; Gallego, G.; Scaramuzza, D. On the Comparison of Gauge Freedom Handling in Optimization-Based Visual-Inertial State Estimation. IEEE Robot. Autom. Lett. 2018, 3, 2710–2717. [Google Scholar] [CrossRef]
- Carlone, L.; Tron, R.; Daniilidis, K.; Dellaert, F. Initialization techniques for 3D SLAM: A survey on rotation estimation and its use in pose graph optimization. In Proceedings of the IEEE International Conference on Robotics and Automation, Seattle, WA, USA, 26–30 May 2015. [Google Scholar] [CrossRef]
- Desloovere, K.; Wong, P.; Swings, L.; Callewaert, B.; Vandenneucker, H.; Leardini, A. Range of motion and repeatability of knee kinematics for 11 clinically relevant motor tasks. Gait Posture 2010, 32, 597–602. [Google Scholar] [CrossRef]
- Lafortune, M.A.; Cavanagh, P.R.; Sommer 3rd, H.J.; Kalenak, A. Three-dimensional kinematics of the human knee during walking. J. Biomech. Eng. 1992, 25, 347–357. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Lebel, K.; Boissy, P.; Nguyen, H.; Duval, C. Autonomous quality control of joint orientation measured with inertial sensors. Sensors 2016, 16, 1037. [Google Scholar] [CrossRef]
- Lebel, K.; Hamel, M.; Duval, C.; Nguyen, H.; Boissy, P. Camera pose estimation to improve accuracy and reliability of joint angles assessed with attitude and heading reference systems. Gait Posture 2018, 59, 199–205. [Google Scholar] [CrossRef]
- Zimmermann, T.; Taetz, B.; Bleser, G. IMU-to-segment assignment and orientation alignment for the lower body using deep learning. Sensors 2018, 18, 302. [Google Scholar] [CrossRef]
- Zhang, Z. Parameter estimation techniques: A tutorial with application to conic fitting. Image Vis. Comput. 1997, 15, 59–76. [Google Scholar] [CrossRef]

| Segment | ||
|---|---|---|
| Left femur | 96 | 2.4 |
| Left tibia | 88 | 1.2 |
| Right femur | 84 | 2.4 |
| Right tibia | 92 | 1.2 |
| Constraint | Source | ||||
|---|---|---|---|---|---|
| Tibial length | 0.411 | 0.026 | 0.344 | 0.479 | ANSUR II [97], Calf Link |
| Femur length | 0.394 | 0.030 | 0.326 | 0.480 | ANSUR II [97], Thigh Link |
| Femoral head separation | 0.187 | 0.009 | 0 | 0.409 | Rabari et al. [98], ANSUR II [97], Hip Breadth |
| Sacrum | RThigh | RShank | RFoot | LThigh | LShank | LFoot | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Subject | P | C | P | C | P | C | P | C | P | C | P | C | P | C |
| 1 | 0.96 | 1.31 | 1.49 | 1.46 | 1.58 | 1.51 | 2.05 | 3.28 | 1.31 | 0.60 | 1.13 | 1.73 | 1.90 | 2.03 |
| 2 | 1.08 | 1.20 | 1.56 | 2.12 | 0.95 | 1.65 | 1.72 | 2.67 | 1.38 | 1.63 | 0.97 | 2.26 | 1.23 | 1.82 |
| 3 | 2.56 | 1.12 | 2.60 | 2.00 | 1.81 | 1.20 | 2.50 | 2.22 | 1.43 | 2.12 | 1.95 | 3.43 | 2.09 | 1.91 |
| 4 | 1.42 | 2.07 | 1.20 | 0.60 | 1.71 | 1.67 | 1.06 | 4.34 | 0.92 | 0.83 | 0.84 | 1.27 | 2.11 | 1.58 |
| 5 | 1.33 | 1.64 | 1.05 | 1.02 | 1.15 | 1.01 | 1.08 | 3.45 | 0.99 | 0.94 | 0.88 | 1.01 | 2.17 | 2.11 |
| 6 | 0.24 | 0.16 | 0.72 | 0.88 | 1.60 | 1.41 | 1.81 | 1.60 | 0.66 | 0.55 | 0.46 | 0.74 | 0.67 | 0.86 |
| 7 | 2.02 | 0.39 | 2.12 | 1.22 | 2.74 | 1.74 | 1.90 | 2.46 | 2.11 | 0.96 | 1.98 | 0.84 | 1.94 | 0.75 |
| 8 | 2.03 | 0.28 | 1.75 | 1.16 | 1.72 | 1.71 | 3.48 | 1.49 | 2.50 | 0.28 | 2.23 | 1.04 | 2.01 | 0.89 |
| 9 | 0.87 | 0.52 | 1.30 | 1.35 | 2.25 | 2.19 | 1.16 | 1.69 | 0.43 | 0.59 | 0.37 | 0.74 | 0.61 | 0.61 |
| 10 | 0.68 | 0.80 | 0.45 | 0.65 | 1.55 | 1.29 | 1.41 | 1.55 | 0.59 | 1.31 | 0.55 | 1.20 | 0.75 | 1.35 |
| 11 | 0.39 | 0.29 | 0.77 | 0.60 | 1.21 | 1.28 | 2.16 | 1.86 | 0.59 | 0.55 | 0.51 | 0.58 | 0.59 | 1.18 |
| 12 | 3.98 | 1.87 | 4.38 | 0.42 | 3.26 | 1.22 | 5.26 | 1.48 | 4.70 | 0.58 | 4.19 | 0.63 | 4.24 | 1.05 |
| Mean | 1.46 | 0.97 | 1.62 | 1.12 | 1.79 | 1.49 | 2.13 | 2.34 | 1.47 | 0.91 | 1.34 | 1.29 | 1.69 | 1.35 |
| Sacrum | RThigh | RShank | RFoot | LThigh | LShank | LFoot | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Subject | P | C | P | C | P | C | P | C | P | C | P | C | P | C |
| 1 | 3.45 | 0.59 | 2.92 | 2.19 | 3.19 | 1.47 | 2.79 | 2.43 | 2.42 | 1.62 | 2.60 | 1.43 | 2.92 | 1.05 |
| 2 | 1.17 | 1.02 | 0.40 | 4.70 | 2.07 | 2.30 | 0.60 | 1.14 | 0.70 | 0.71 | 0.43 | 3.90 | 0.38 | 0.96 |
| 3 | 4.15 | 0.57 | 3.24 | 3.48 | 4.14 | 1.69 | 4.12 | 1.40 | 3.09 | 0.90 | 3.66 | 5.07 | 3.74 | 2.93 |
| 4 | 2.52 | 1.17 | 2.92 | 2.03 | 3.49 | 1.70 | 2.68 | 1.49 | 2.44 | 1.04 | 2.63 | 4.42 | 2.48 | 0.86 |
| 5 | 2.36 | 1.32 | 0.76 | 0.74 | 1.94 | 1.67 | 0.93 | 0.77 | 1.03 | 1.38 | 1.22 | 1.60 | 1.06 | 0.79 |
| 6 | 0.50 | 0.88 | 0.75 | 1.77 | 2.07 | 2.06 | 1.87 | 1.86 | 0.56 | 1.76 | 1.34 | 3.36 | 0.96 | 3.49 |
| 7 | 0.51 | 1.00 | 1.26 | 2.31 | 2.61 | 2.45 | 1.24 | 2.02 | 1.26 | 1.89 | 1.25 | 1.06 | 0.68 | 1.66 |
| 8 | 0.78 | 0.77 | 1.03 | 2.06 | 1.52 | 1.54 | 1.21 | 1.67 | 0.75 | 1.36 | 0.67 | 3.98 | 0.54 | 2.15 |
| 9 | 2.72 | 0.92 | 2.35 | 3.50 | 3.19 | 1.78 | 2.66 | 1.56 | 2.38 | 1.25 | 1.74 | 4.94 | 2.12 | 2.11 |
| 10 | 0.81 | 0.81 | 1.65 | 2.64 | 1.43 | 2.03 | 1.05 | 1.71 | 1.60 | 2.31 | 1.02 | 3.03 | 0.83 | 2.38 |
| 11 | 0.99 | 1.23 | 1.43 | 1.03 | 1.72 | 2.26 | 1.44 | 1.88 | 1.17 | 1.90 | 0.79 | 1.30 | 0.93 | 5.16 |
| 12 | 0.51 | 1.13 | 1.44 | 1.20 | 2.03 | 1.14 | 1.55 | 1.51 | 0.67 | 1.89 | 1.36 | 3.77 | 0.83 | 1.58 |
| Mean | 1.71 | 0.95 | 1.68 | 2.30 | 2.45 | 1.84 | 1.84 | 1.62 | 1.51 | 1.50 | 1.56 | 3.16 | 1.46 | 2.09 |
| Source | Sum Sq. | d.f. | Mean Sq. | F | p |
|---|---|---|---|---|---|
| Subject | 3.04 | 11 | 0.28 | 5.09 | <0.001 |
| IMU | 2.56 | 6 | 0.43 | 7.86 | <0.001 |
| Model | 2.0 × 10 | 1 | 2.0 × 10 | 0.04 | 0.85 |
| DOF | 0.79 | 1 | 0.79 | 14.58 | <0.001 |
| IMU*Model | 0.92 | 6 | 0.15 | 2.82 | 0.01 |
| Error | 16.83 | 310 | 0.05 | ||
| Total | 24.14 | 335 |
| Subject | Lumbar RThigh | RThigh RShank | RShank RFoot | Lumbar LThigh | LThigh LShank | LShank LFoot |
|---|---|---|---|---|---|---|
| 1 | 16.92 | 0.92 | 3.21 | 8.79 | 4.35 | 2.23 |
| 2 | 8.28 | 0.90 | 2.33 | 7.30 | 0.66 | 2.74 |
| 3 | 4.86 | 2.79 | 3.20 | 5.27 | 2.84 | 3.67 |
| 4 | 5.93 | 1.84 | 2.30 | 6.04 | 1.83 | 2.65 |
| 5 | 13.53 | 1.27 | 2.72 | 1.36 | 2.68 | 3.34 |
| 6 | 4.86 | 2.29 | 2.87 | 5.25 | 3.38 | 3.79 |
| 7 | 9.90 | 0.73 | 2.38 | 8.58 | 0.57 | 2.68 |
| 8 | 11.44 | 0.49 | 2.52 | 10.73 | 1.46 | 1.90 |
| 9 | 13.65 | 0.92 | 2.45 | 10.99 | 0.68 | 3.07 |
| 10 | 8.51 | 1.17 | 1.94 | 4.72 | 1.96 | 2.61 |
| 11 | 10.19 | 0.97 | 2.40 | 6.11 | 1.53 | 3.12 |
| 12 | 5.75 | 0.47 | 2.42 | 6.81 | 1.89 | 2.49 |
| Mean | 9.49 | 1.23 | 2.56 | 6.83 | 1.98 | 2.86 |
| Std | 3.71 | 0.69 | 0.36 | 2.58 | 1.11 | 0.54 |
| RMSE | Peak Error | |||
|---|---|---|---|---|
| Subject | RKnee F/E | LKnee F/E | RKnee F/E | LKnee F/E |
| 1 | 2.17 | 2.08 | 8.83 | 6.00 |
| 2 | 3.28 | 7.09 | 8.70 | 10.85 |
| 3 | 5.37 | 10.30 | 21.84 | 15.42 |
| 4 | 2.37 | 3.34 | 8.45 | 9.13 |
| 5 | 4.61 | 6.74 | 10.66 | 11.37 |
| 6 | 4.28 | 4.33 | 18.69 | 10.41 |
| 7 | 3.32 | 5.60 | 9.75 | 11.85 |
| 8 | 3.11 | 4.92 | 15.45 | 13.94 |
| 9 | 3.83 | 7.71 | 14.45 | 12.51 |
| 10 | 2.95 | 3.97 | 10.67 | 7.85 |
| 11 | 4.22 | 2.31 | 11.24 | 9.46 |
| 12 | 2.19 | 4.10 | 9.46 | 8.30 |
| Mean | 3.47 | 5.21 | 12.35 | 10.59 |
| Std | 1.01 | 2.40 | 4.34 | 2.66 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
McGrath, T.; Stirling, L. Body-Worn IMU Human Skeletal Pose Estimation Using a Factor Graph-Based Optimization Framework. Sensors 2020, 20, 6887. https://doi.org/10.3390/s20236887
McGrath T, Stirling L. Body-Worn IMU Human Skeletal Pose Estimation Using a Factor Graph-Based Optimization Framework. Sensors. 2020; 20(23):6887. https://doi.org/10.3390/s20236887
Chicago/Turabian StyleMcGrath, Timothy, and Leia Stirling. 2020. "Body-Worn IMU Human Skeletal Pose Estimation Using a Factor Graph-Based Optimization Framework" Sensors 20, no. 23: 6887. https://doi.org/10.3390/s20236887
APA StyleMcGrath, T., & Stirling, L. (2020). Body-Worn IMU Human Skeletal Pose Estimation Using a Factor Graph-Based Optimization Framework. Sensors, 20(23), 6887. https://doi.org/10.3390/s20236887





