Multi-User Precoder Designs for RGB Visible Light Communication Systems
Abstract
:1. Introduction
1.1. Organization
1.2. Notation
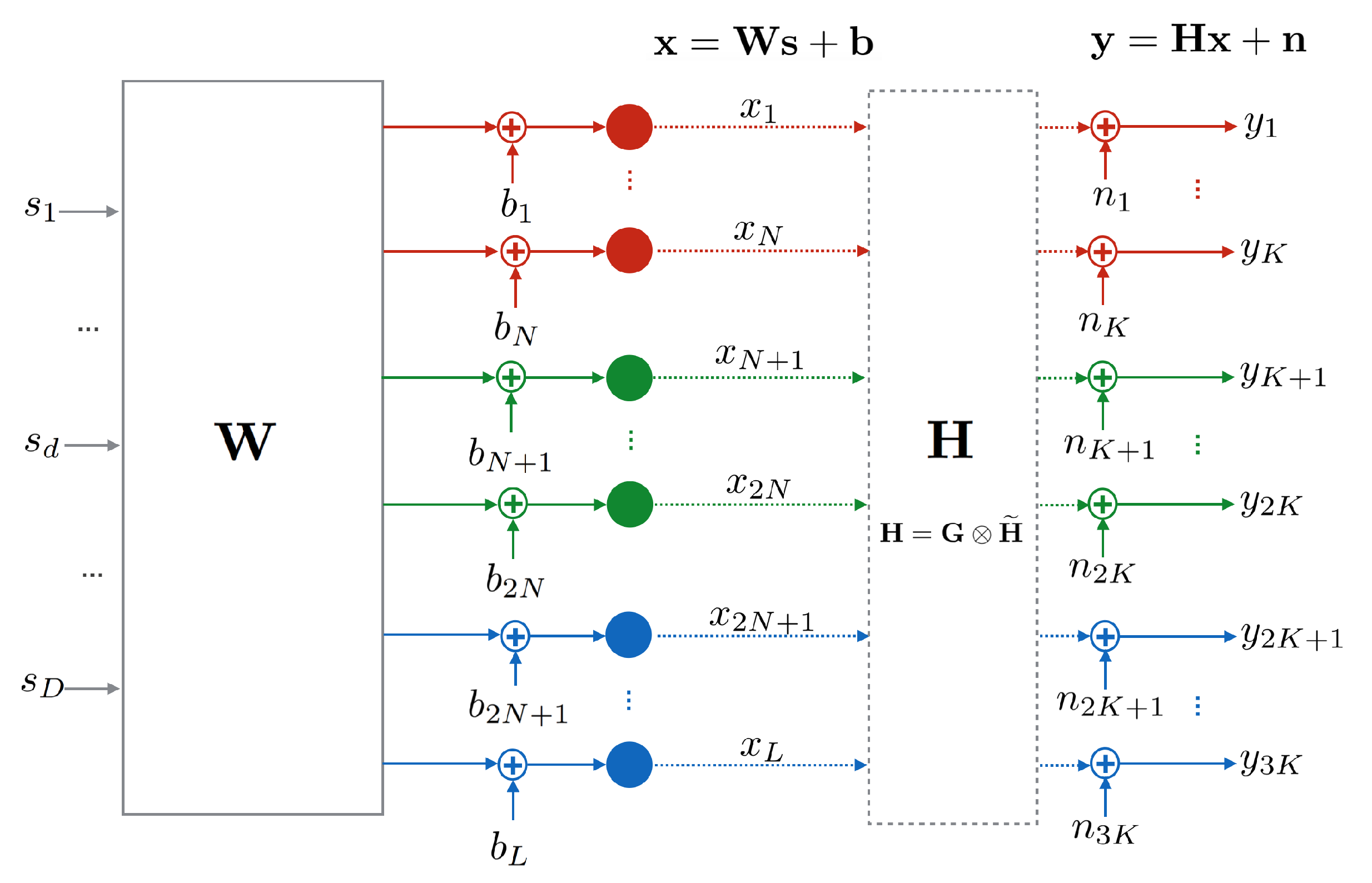
2. System Model
3. Optical and Electrical Constraints
3.1. White Color Constraint
3.2. Instantaneous Optical Power Constraint
3.3. Average Radiated Optical Power Constraint
4. RGB-LED Based Zero Forcing Precoding
4.1. Zero Forcing Precoding with Pseudoinverse
4.2. Optimal Zero Forcing Precoding for Maximum Weighted Sum Rate
5. PWLED Based Zero Forcing Precoding
5.1. Zero Forcing Precoding with Pseudoinverse
5.2. Optimal Zero Forcing Scheme for Maximum Weighted Sum-Rate
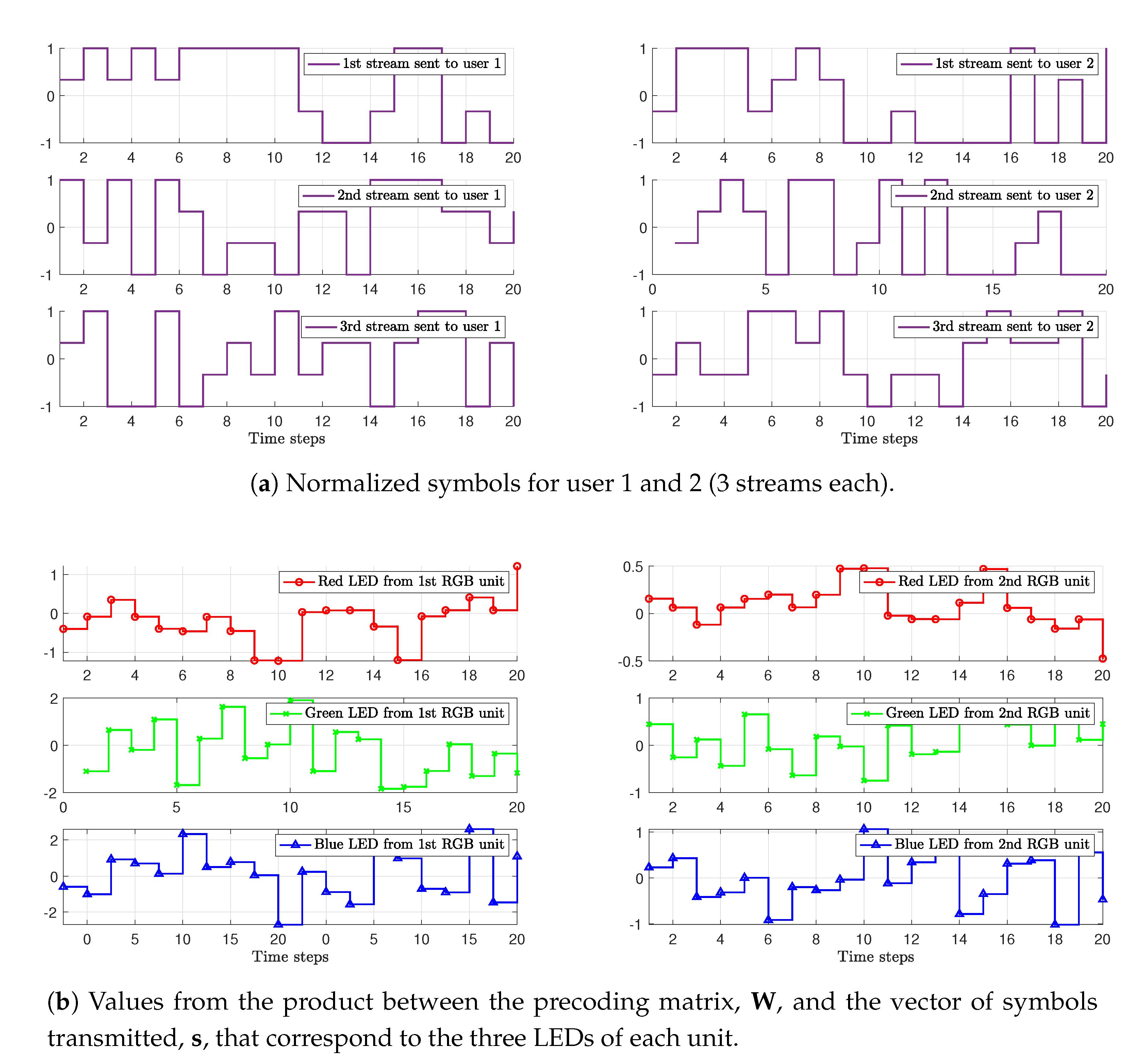
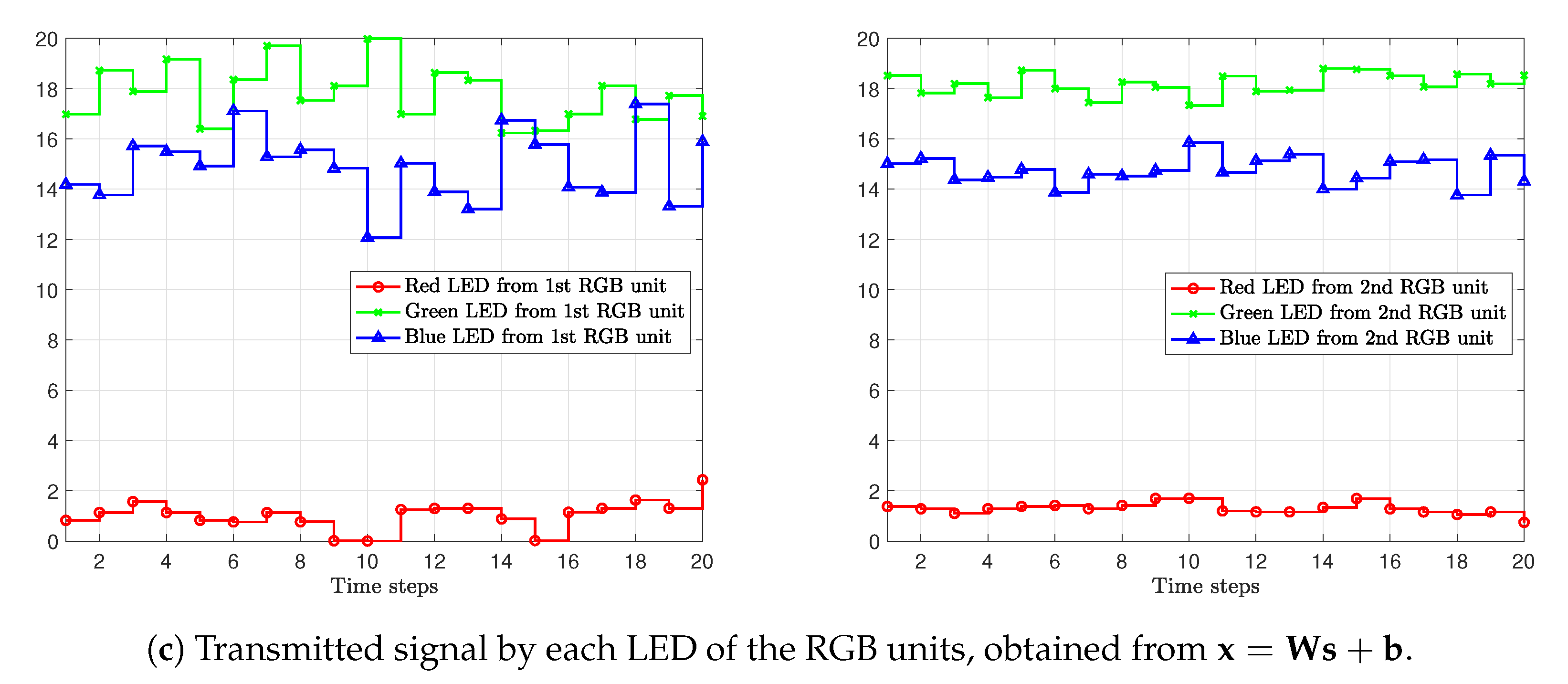
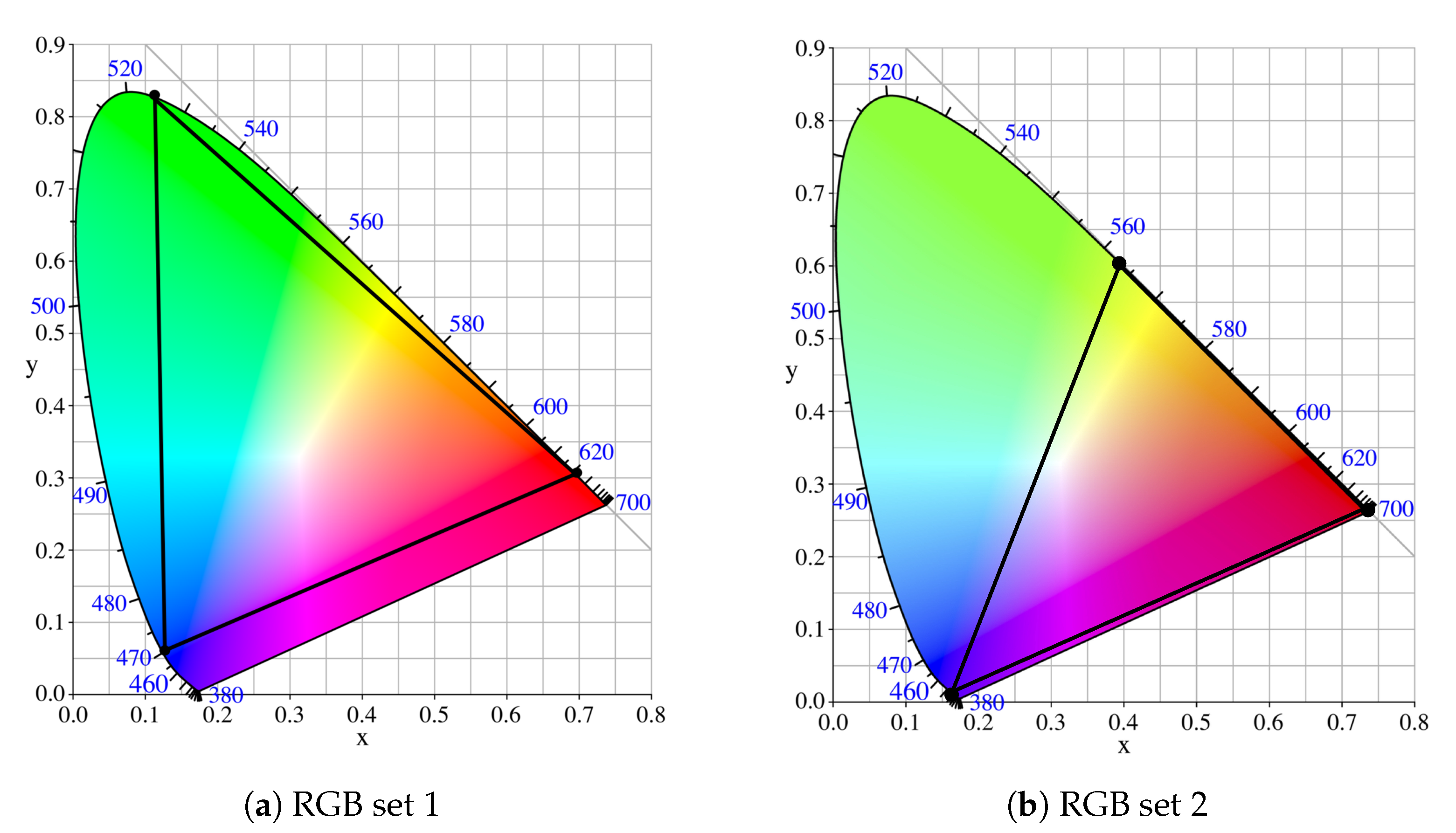
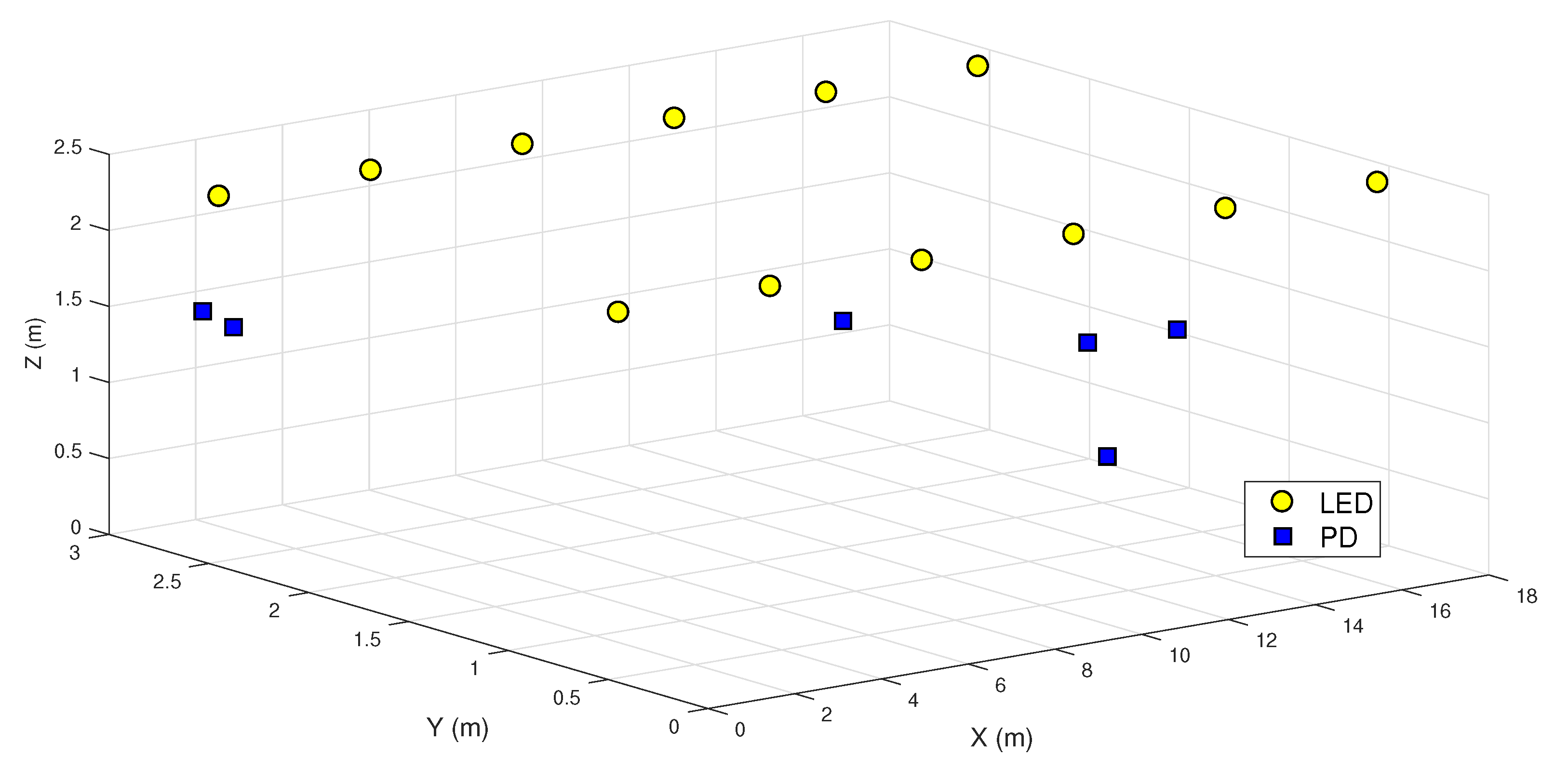
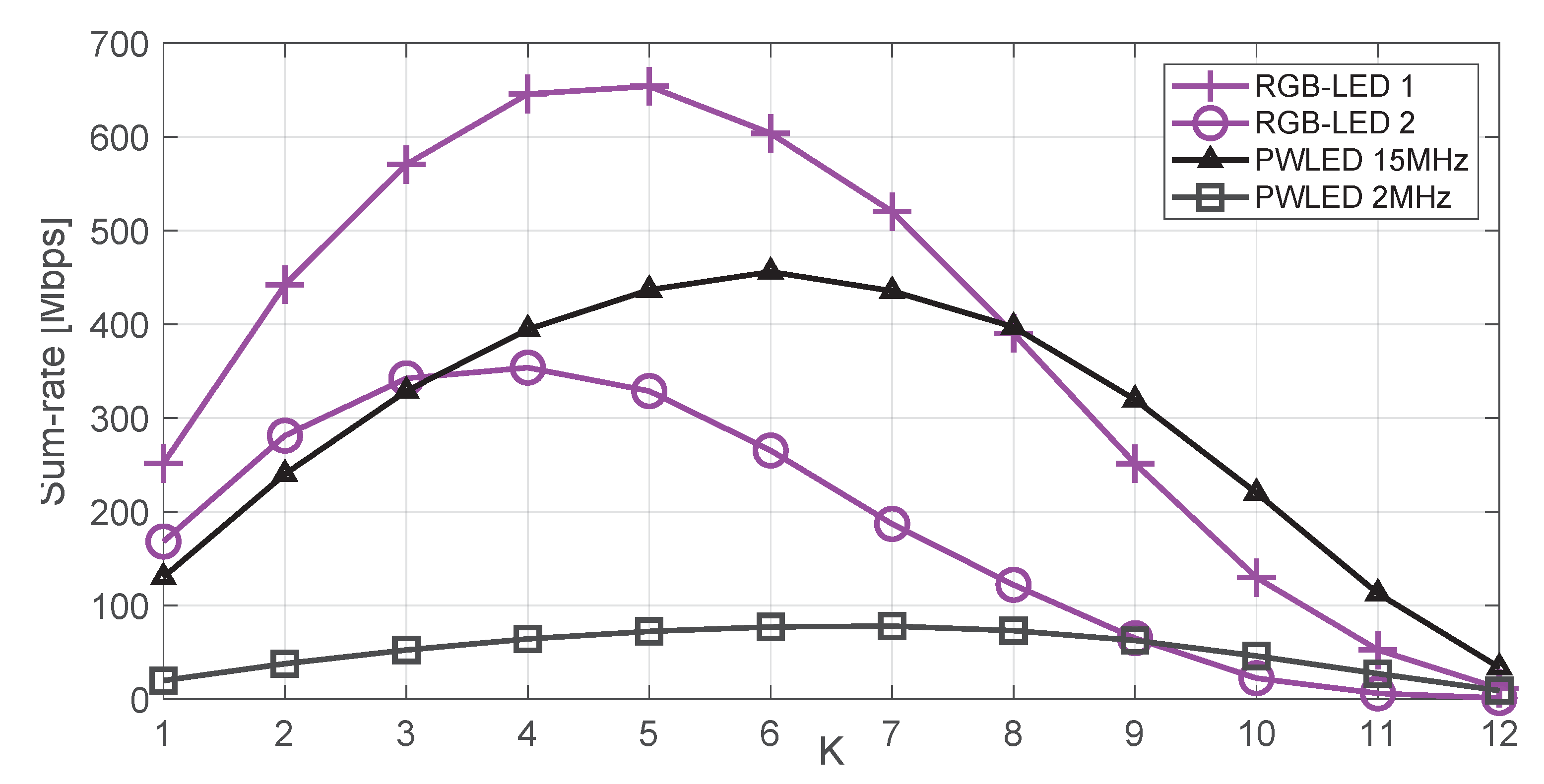
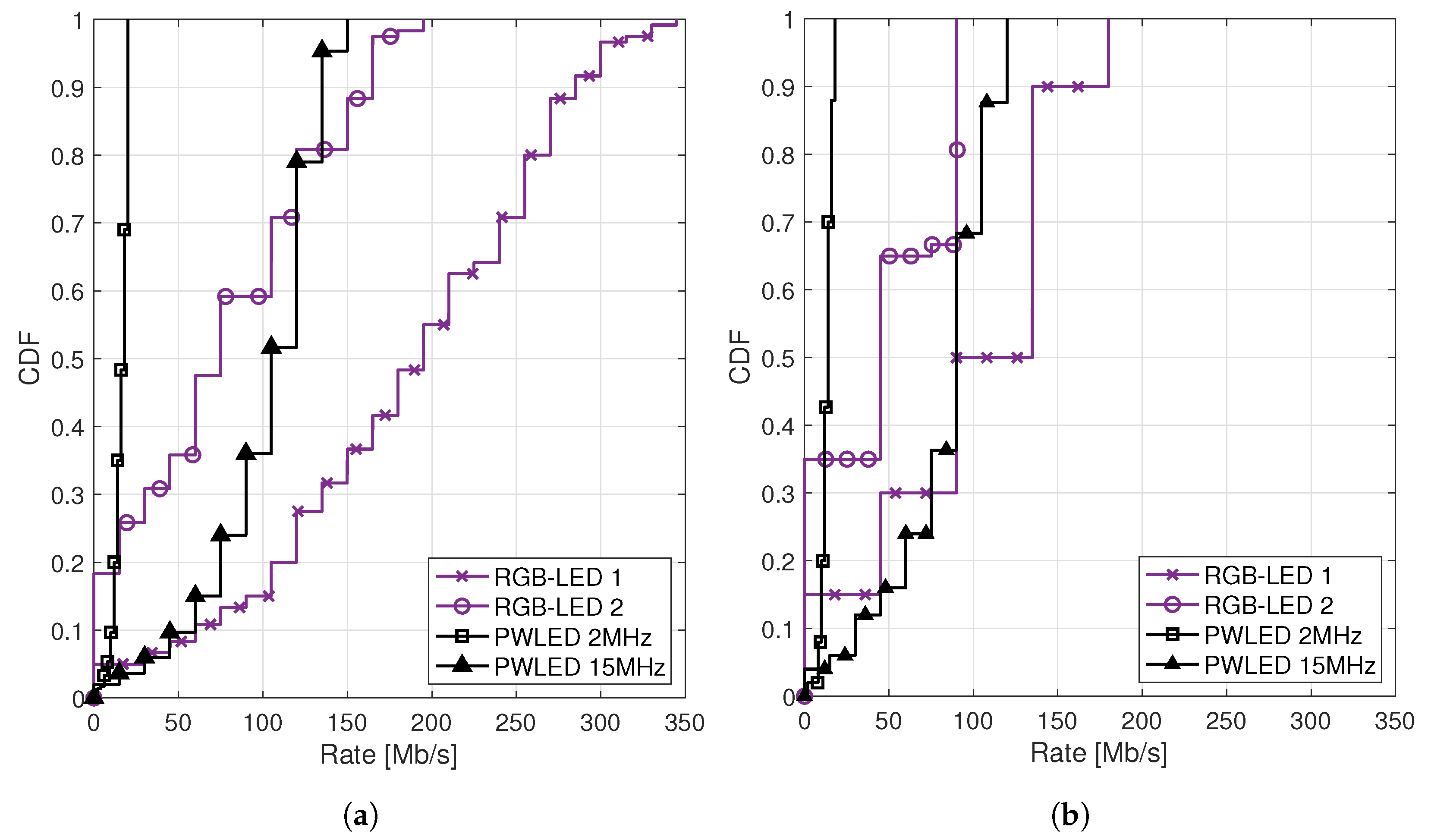
6. Numerical Results
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Dimitrov, S.; Haas, H. Principles of LED Light Communications; Torwards Networked Li-Fi; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
- Viñals, R. Multi-User MISO for Visible Light Communication. Master’s Thesis, Universitat Politecnica de Catalunya, Barcelona, Spain, September 2016. [Google Scholar]
- Yu, Z.; Baxley, R.J.; Zhou, G.T. Multi-User MISO Broadcasting for indoor Visible Light Communication. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013. [Google Scholar]
- Shen, H.; Deng, Y.; Xu, W.; Zhao, C. Rate-Maximized Zero-Forcing Beamforming for VLC Multiuser MISO Downlinks. IEEE Photonics J. 2016, 8, 1–13. [Google Scholar] [CrossRef]
- Pham, T.V.; Minh, H.L.; Ghassemlooy, Z.; Hayashi, T.; Pham, A.T. Sum-Rate Maximization of Multi-User MIMO Visible Light Communications. In Proceedings of the IEEE ICC, Workshop on Visible Light Communications and Networking (VLCN), London, UK, 8–12 June 2015. [Google Scholar]
- Yang, H.; Chen, J.; Wang, Z.; Yu, C. Performance of a Precoding MIMO System for Decentralized Multiuser Indoor Visible Light Communications. IEEE Photonics J. 2014, 5, 7800211. [Google Scholar] [CrossRef]
- Shen, H.; Deng, Y.; Xu, W.; Zhao, C. Rate Maximization for Downlink Multiuser Visible Light Communications. IEEE Access 2016, 4, 6567–6573. [Google Scholar] [CrossRef]
- Sun, Z.; Yu, H.; Tian, Z.; Zhu, Y. Linear Precoding for MU-MISO VLC Systems With Noisy Channel State Information. IEEE Commun. Lett. 2018, 22, 732–735. [Google Scholar] [CrossRef]
- Vinals, R.; Munoz, O.; Agustin, A.; Vidal, J. Cooperative Linear Precoding for Multi-User MISO Visible Light Communications. In Proceedings of the GLOBECOM 2017—2017 IEEE Global Communications Conference, Singapore, 4–8 December 2017; pp. 1–7. [Google Scholar]
- Zhao, L.; Cai, K.; Jiang, M. Multiuser Precoded MIMO Visible Light Communication Systems Enabling Spatial Dimming. J. Light. Technol. 2020, 38, 5624–5634. [Google Scholar] [CrossRef]
- Chen, C.; Zhong, W.; Yang, H.; Du, P. On the Performance of MIMO-NOMA-Based Visible Light Communication Systems. IEEE Photonics Technol. Lett. 2018, 30, 307–310. [Google Scholar] [CrossRef]
- Haigh, P.A.; Son, T.T.; Bentley, E.; Ghassemlooy, Z.; Minh, H.L.; Chao, L. Development of a Visible Light Communications System for Optical Wireless Local Area Networks. In Proceedings of the Computing, Communications and Applications Conference (ComComAp), Hong Kong, China, 11–13 June 2012. [Google Scholar]
- Ghassemlooya, Z.; Minh, H.L.; Haigh, P.A.; Burton, A. Development of visible light communications: Emerging technology and integration aspects. In Proceedings of the Optics and Photonics Taiwan International Conference (OPTIC), Taipei, Taiwan, 6–8 December 2012. [Google Scholar]
- Grobe, L.; Paraskevopoulos, A.; Hilt, J.; Schulz, D.; Lassak, F.; Hartlieb, F.; Kottke, C.; Jungnickel, V.; Langer, K.D.; Institute, H.H. High-Speed Visible Light Communication Systems. IEEE Commun. Mag. 2013, 51, 60–66. [Google Scholar] [CrossRef]
- Cossu, G.; Khalid, A.M.; Choudhury, P.; Corsini, R.; Ciaramella, E. 3.4 Gbit/s visible optical wireless transmission based on RGB LED. Opt. Express 2012, 20, B501–B506. [Google Scholar] [CrossRef] [PubMed]
- Murata, N.; Kozawa, Y.; Umeda, Y. Digital Color Shift Keying with multi-color LED array. IEEE Photonics J. 2016, 8, 1–13. [Google Scholar] [CrossRef] [Green Version]
- IEEE. IEEE Standard for Local and metropolitan area networks—Part 15.7: Short-Range Optical Wireless Communications—Redline. In IEEE Std 802.15.7-2018 (Revision of IEEE Std 802.15.7-2011)—Redline; IEEE: Piscataway, NJ, USA, 2019; pp. 1–670. [Google Scholar]
- Monteiro, E.; Hranilovic, S. Design and implementation of color-shift keying for visible light communications. J. Light. Technol. 2014, 32, 2053–2060. [Google Scholar] [CrossRef] [Green Version]
- Drost, R.J.; Sadler, B.M. Constellation Design for Color-Shift Keying Using Billiards Algorithms. In Proceedings of the IEEE Globecom Workshop on Optical Wireless Communications, Miami, FL, USA, 6–10 December 2010. [Google Scholar]
- Monteiro, E.; Hranilovic, S. Constellation Design for Color-Shift Keying Using Interior Point Methods. In Proceedings of the 3rd IEEE Workshop on Optical Wireless Communications, Anaheim, CA, USA, 3–7 December 2012. [Google Scholar]
- Singh, R.; O’Farrell, T.; David, J. An enhanced color shift keying modulation scheme for high-speed wireless visible light communications. J. Light. Technol. 2014, 32, 2582–2592. [Google Scholar] [CrossRef]
- Jain, S.; Mitra, R.; Bhatia, V. Multivariate-KLMS based Post-Distorter for Nonlinear RGB-LEDs for Color-Shift Keying VLC. In Proceedings of the 2019 IEEE 30th Annual International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC), Istanbul, Turkey, 8–11 September 2019; pp. 1–6. [Google Scholar]
- Luna-Rivera, J.; Perez-Jimenez, R.; Rabadan-Borjes, J.; Rufo-Torres, J.; Guerra, V.; Suarez-Rodriguez, C. Multiuser CSK scheme for indoor visible light communications. Opt. Soc. Am. 2014, 22, 24256–24267. [Google Scholar] [CrossRef] [PubMed]
- Zhang, D.F.; Yu, H.Y.; Zhu, Y.J. A multi-user joint constellation design of color-shift keying for VLC downlink broadcast channels. Opt. Commun. 2020, 473, 126001. [Google Scholar] [CrossRef]
- Xiao, Y.; Zhu, Y.J.; Sun, Z.G. Linear Precoding Designs for MIMO VLC Using Multi-Color LEDs under Multiple Lighting Constraints. Crystals 2018, 8, 408. [Google Scholar] [CrossRef] [Green Version]
- Luna-Rivera, J.M.; Perez-Jimenez, R.; Rabadan-Borjes, J.A.; Rufo-Torres, J.F.; Guerra, V.; Suarez-Rodriguez, C. Multiuser scheme for indoor visible light communications using RGB LEDs. In Proceedings of the 3rd IEEE International Work-Conference on Bioinspired Intelligence, Liberia, Costa Rica, 16–18 July 2014; pp. 119–123. [Google Scholar] [CrossRef]
- Sewaiwar, A.; Chung, Y. High-performance TDM-MIMO-VLC Using RGB LEDs in Indoor Multiuser Environments. Curr. Opt. Photonics 2017, 1, 289–294. [Google Scholar]
- Xiao, Y.; Zhu, Y.; Zhang, Y.; Sun, Z. Linear Optimal Signal Designs for Multi-Color MISO-VLC Systems Adapted to CCT Requirement. IEEE Access 2018, 6, 75519–75530. [Google Scholar] [CrossRef]
- Wang, X.; Wang, L.; Jian, K.; Wang, C.; Yue, C.P. A RGB LED PAM-4 Visible Light Communication Transmitter Based on a System Design with Equalization. In Proceedings of the 2020 IEEE International Conference on Artificial Intelligence and Computer Applications (ICAICA), Dalian, China, 27–29 June 2020; pp. 798–801. [Google Scholar] [CrossRef]
- Kwon, T.H.; Kim, J.E.; Kim, Y.H.; Kim, K.D. Color-Independent Visible Light Communications Based on Color Space: State of the Art and Potentials. Electronics 2018, 7, 190. [Google Scholar] [CrossRef] [Green Version]
- Komine, T.; Nakagawa, M. Fundamental analysis for visible-light communication system using LED lights. IEEE Trans. Consum. Electron. 2004, 50, 100–107. [Google Scholar] [CrossRef]
- Pathak, P.H.; Feng, X.; Hu, P.; Mohapatra, P. Visible Light Communication, Networking, and Sensing: A Survey, Potential and Challenges. IEEE Commun. Surv. Tutorials 2015, 17, 2047–2077. [Google Scholar] [CrossRef]
- Chung, S.T.; Vishwanath, S.; Goldsmith, A. Degrees of Freedom in Adaptive Modulation: A Unified View. IEEE Trans. Commun. 2001, 49, 1561–1571. [Google Scholar] [CrossRef]
- Singh, R.; O’Farrell, T.; David, J.P.R. Performance Evaluation of IEEE 802.15.7 CSK Physical Layer. In Proceedings of the Globecom Workshop—Optical Wireless Communications, Atlanta, GA, USA, 9–13 June 2013. [Google Scholar]
- Arnon, S.; Barry, J.R.; Karagiannidis, G.K.; Schober, R.; Uysal, M. Advanced Optical Wireless Communication Systems; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Hranilovic, S. Wireless Optical Communication Systems; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Kahn, J.M.; Barry, J.R. Wireless Infrared Communication. Proc. IEEE 1997, 85, 265–298. [Google Scholar] [CrossRef] [Green Version]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Haigh, P.A.; Ghassemlooy, Z.; Le Minh, H.; Rajbhandari, S.; Arca, F.; Tedde, S.F.; Hayden, O.; Papakonstantinou, I. Exploiting Equalization Techniques for Improving Data Rates in Organic Optoelectronic Devices for Visible Light Communications. J. Light. Technol. 2012, 30, 3081–3088. [Google Scholar] [CrossRef]
- Grubor, J.; Randel, S.; Langer, K.D.; Walewski, J.W. Broadband Information Broadcasting Using LED-Based Interior Lighting. J. Lightw. Technol. 2008, 26, 3883–3892. [Google Scholar] [CrossRef] [Green Version]
- Schanda, J. (Ed.) Colorimetry: Understanding the CIE System; Wiley: Hoboken, NJ, USA, 2007. [Google Scholar]
- NEMA ANSLG ANSI. C78.377–2008: Specifications for the Chromaticity of Solid State Lighting Products; ANSI, American National Standard Institute: Washington, DC, USA, 2008. [Google Scholar]
- Mobley, C. Ocean Optics Web Book. Available online: https://oceanopticsbook.info/view/photometry-and-visibility/chromaticity (accessed on 19 November 2020).
- CIE International Commission on Illumination. CIE Standard Illuminants for Colorimetry; ISO 10526:1999/CIE S005/E; Multiple; Distributed through American National Standards Institute (ANSI): Evanston, IL, USA, 23 August 2007. [Google Scholar]


| RF | VLC | Impact on VLC Systems | |
|---|---|---|---|
| Bandwidth | From 3 Hz to 3000 GHz. | From 380 to 780 THz | Massive unused free bandwidth is available. |
| Spectrum regulation | Strict | None | Worldwide compatibility. |
| EM interference | Possible interference with electronic devices. | No interference with electronic devices. | VLC can be used safely in hospitals, planes, etc. |
| Surface penetration | It penetrates walls and other surfaces. It is strongly attenuated in water. | Can not propagate through opaque barriers but propagates through water. | Less coverage. Securely deployed. Suitable for underwater communications. |
| Channel model | The data-carrying signal modulates the complex- valued bipolar electric field radiated by an antenna. | The signal modulates the intensity of the optical emitter (IM/DD). | The channel input needs to be real-valued and positive. Positive channel model. |
| The channel input, , represents | Amplitude | Optical power | |
| Average power proportional to |
| RGB | White | |||
|---|---|---|---|---|
| LED parameters | ||||
| Number of transmitters | N | 12 | ||
| Number of LEDs | L | 36 | 12 | |
| Maximum transmitted optical power | R | |||
| G | ||||
| B | ||||
| Minimum transmitted optical power | R | |||
| G | ||||
| B | ||||
| Maximum average optical power | ||||
| Bandwidth | R | |||
| G | ||||
| B | ||||
| Semi-angle at half power | ||||
| Center luminous intensity | ||||
| PD parameters | ||||
| Number of users | K | 6 | ||
| Field of View | ||||
| Detector physical area of a PD | ||||
| Gain of the optical filter | 1 | |||
| Refractive index of the concentrator | ||||
| Responsivity | [16] | |||
| Noise parameters noise-related parameters can be found in [31] | ||||
| Set 1 | Set 2 | |||||
|---|---|---|---|---|---|---|
| Wavelength | Wavelength | |||||
| Red | ||||||
| Green | ||||||
| Blue | ||||||
| Precoders | RGB | White | ||
|---|---|---|---|---|
| Set 1 | Set 2 | |||
| Optimal precoder | 1185 | 525 | 98 | 630 |
| Pseudoinverse | 810 | 270 | 84 | 540 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Viñals, R.; Muñoz, O.; Agustín, A.; Vidal, J. Multi-User Precoder Designs for RGB Visible Light Communication Systems. Sensors 2020, 20, 6836. https://doi.org/10.3390/s20236836
Viñals R, Muñoz O, Agustín A, Vidal J. Multi-User Precoder Designs for RGB Visible Light Communication Systems. Sensors. 2020; 20(23):6836. https://doi.org/10.3390/s20236836
Chicago/Turabian StyleViñals, Roser, Olga Muñoz, Adrián Agustín, and Josep Vidal. 2020. "Multi-User Precoder Designs for RGB Visible Light Communication Systems" Sensors 20, no. 23: 6836. https://doi.org/10.3390/s20236836






