Galileo Broadcast Ephemeris and Clock Errors Analysis: 1 January 2017 to 31 July 2020
Abstract
1. Introduction
2. Anomaly Monitoring
2.1. Data Cleansing
- Least-Significant Bit (LSB) recovery to remove potential errors in the decoding of navigation messages and convert the values to double-precision floating-point numbers.
- Classify the GPS URA values to cope with the different URAs appearing in the RINEX files (e.g., some receivers use URA indices instead of URA values, and the same URA index may correspond to three possible values in meters).
- Duplication removal and majority voting to select the most likely message as the one shared by the largest number of stations, after removing duplicates. In this step, the navigation data are classified as robust parameters (most ephemeris and clock parameters) and fragile parameters (Transmission Time of Message (TTOM), PRN, URA, Issue of Data Clock (IODC)). The robust parameters are used to identify the candidates of navigation messages. Their associated fragile parameters are then selected as those shared by the largest number of stations.
- TTOM recovering. The TTOM is not a parameter broadcast in the navigation message. The record given in RINEX navigation files is not the TTOM but the first reception time of the message by the receiver collecting data. The correct TTOM cannot be determined by the oldest one because some IGS receivers may provide an incorrect TTOM older than the actual one. On the other hand, since the IGS stations are not evenly distributed, neither can it be determined simply by the most frequent one. A procedure is then defined to retrieve the TTOM.
- Minority discard. After the previous steps, few navigation messages can still have errors in their robust parameters, and a uniqueness criterion is applied to select the final candidates.
- There is only a single Issue of Data Navigation (IOD) to identify the ephemeris, satellite clock correction parameters and SISA, instead of the two IODC and Issue of Data Ephemeris (IODE) of GPS navigation data.
- The following parameters are not linked to the IOD:
- ⚬
- The Broadcast Group Delay (BGD) values;
- ⚬
- The navigation Data Validity Status (DVS);
- ⚬
- The signal Health Status (HS).
In RINEX navigation files [13], DVS and HS are embedded in the 8 bits of the Satellite Vehicle (SV) health flag for the different signals E1B, E5a, and E5b. Thus, SV health = 0 means that DVS and HS are OK.Note: in the GPS, the Total Group Delay (TGD) and SV health are linked to the IODC. - Galileo broadcast navigation message update [9]:
- ⚬
- The typical refresh rate of navigation data ranges from 10 min to 3 h, and each message must be associated with a different IOD;
- ⚬
- The maximum nominal broadcast period of a healthy navigation message data set is currently 4 h;
- ⚬
- The message Validity Duration (VD) is 4 h.
- Minority discard step:In the case of GPS satellites, candidates are selected according to a uniqueness criterion based on PRN—IODC, i.e., the one confirmed by the larger number of stations having the same PRN—IODC. As the IODC may be occasionally reused by a satellite within the same day, a backup uniqueness criterion based on PRN and Time-of-Clock (Toc) is also applied, i.e., PRN—Toc.In the case of Galileo satellites, the previous uniqueness criterion, based on checking the PRN—IODC, cannot be applied. This is because the IOD may be repeated within the same day.Thence, with Galileo satellites, for each Data Source’s value in the RINEX file, the uniqueness is based only on the PRN—Toc criterion. This criterion is applied to all robust parameters, except SV health (i.e., DVS, HS) and BGDs, as they are not linked to the IOD.
2.2. Anomaly Detection: Space Approach
- The WC URE exceeds the NTE threshold;
- The most recent navigation data set broadcast on a Healthy SIS by the Galileo satellite is used, where Healthy SIS, means:The RINEX field SV health [13] is 0, i.e., DVS = “Navigation Data Valid” and HS = “Signal OK”, and SISA ≠ NAPA (NAPA = No Accuracy Prediction Available);
- The Age of Ephemeris (AoE) is smaller than or equal to 4 h Toe, i.e., h;
- The precise orbits and clocks are available and healthy.Note: in the GPS the validity period is given from TTOM and Fit Interval (FI) by , where FI is typically 4 h.
2.3. Anomaly Verification: Ground Approach
- A set of 10 or more active stations having the satellite in view during the whole anomaly event, or as long as possible, is selected. These stations should experience as large anomalous UREs as possible. The algorithm for station selection presented in Section 4.2 of [12] has been implemented in this study.
- For each selected station (, the Instantaneous SIS URE (IURE) is computed from the prefit residual ( of the Ionosphere-Free (IF) combination of Galileo C1 and C5 code measurements [15]. That is, for each satellite, j = 1,…, N in view from the receiver (rec):where and are the geometric range and the satellite clock offset computed with the broadcast ephemeris, is the tropospheric delay estimated using the UNB-3 nominal model and the simple mapping function implemented in the gLAB tool [16], and is the IF combination of unsmoothed code measurements. Satellites below deg of elevation are excluded.The IURE for the anomalous satellite (sat) is then computed as:where is the receiver clock offset estimated as the weighted average of the prefit residuals of all satellites in view, excluding the anomalous satellite (sat) (see Equation (4.7) in [12]).A configurable sampling rate of 300 s has been used in this study.
- Following [12], the Galileo satellite is set as “anomalous” when all the following conditions are fulfilled:
- The IURE exceeds the NTE threshold;
- The most recent navigation data broadcast on a Healthy SIS by the Galileo satellite are used, where Healthy SIS means:The RINEX field SV health is 0, i.e., DVS = “Navigation Data Valid” and HS = “Signal OK” and SISA ≠ NAPA.
- The broadcast navigation message is within its validity time, i.e., ;
- The signal was tracked with an acceptable SNR, i.e., the RINEX SNR flag value ≥4.
2.4. Decision Criterion
3. Data Sets
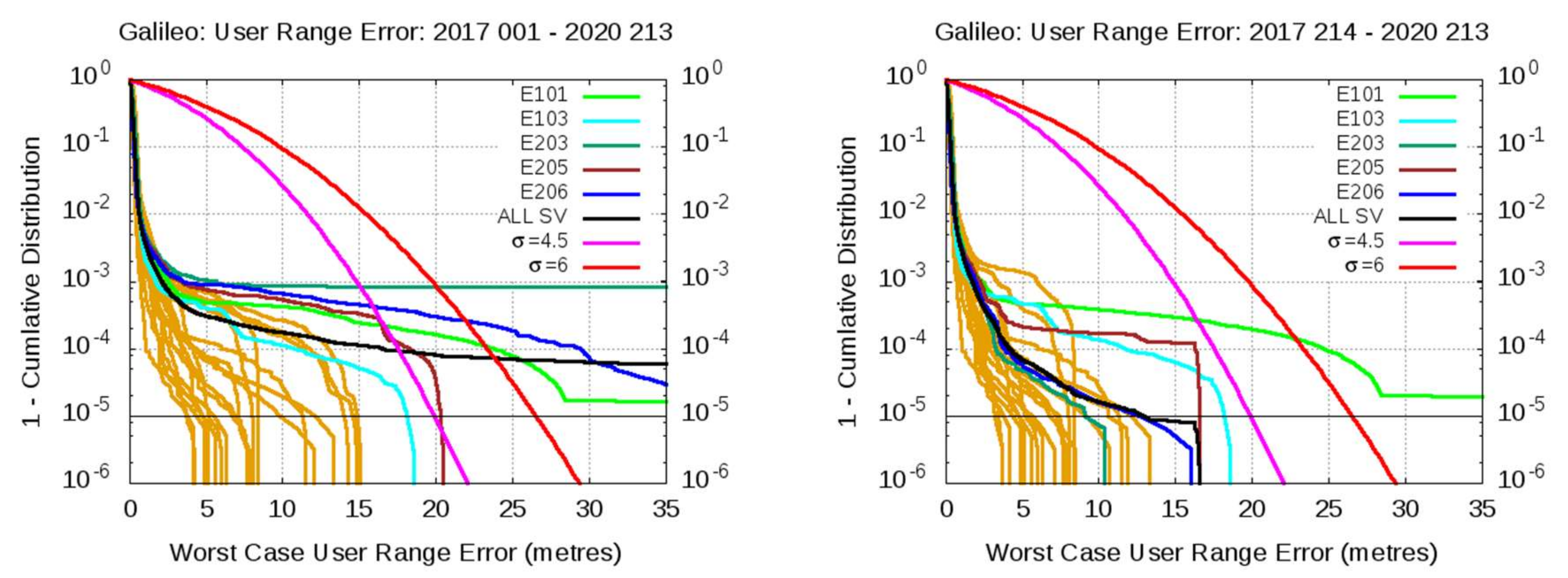
4. Observed Error Distribution
4.1. Identification of Potential SISE Events
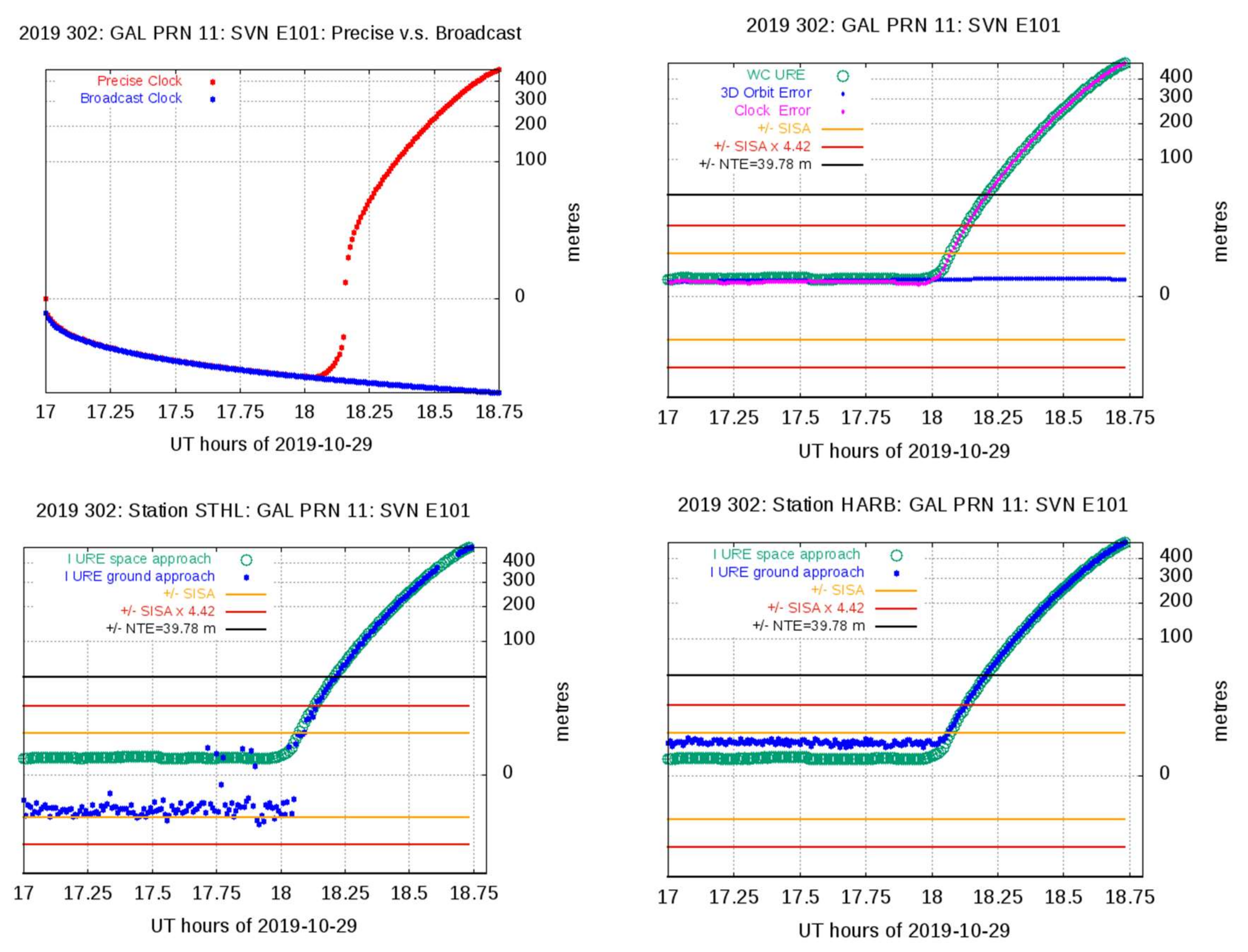
Galileo IOV E101 Satellite Event on 29 October 2019
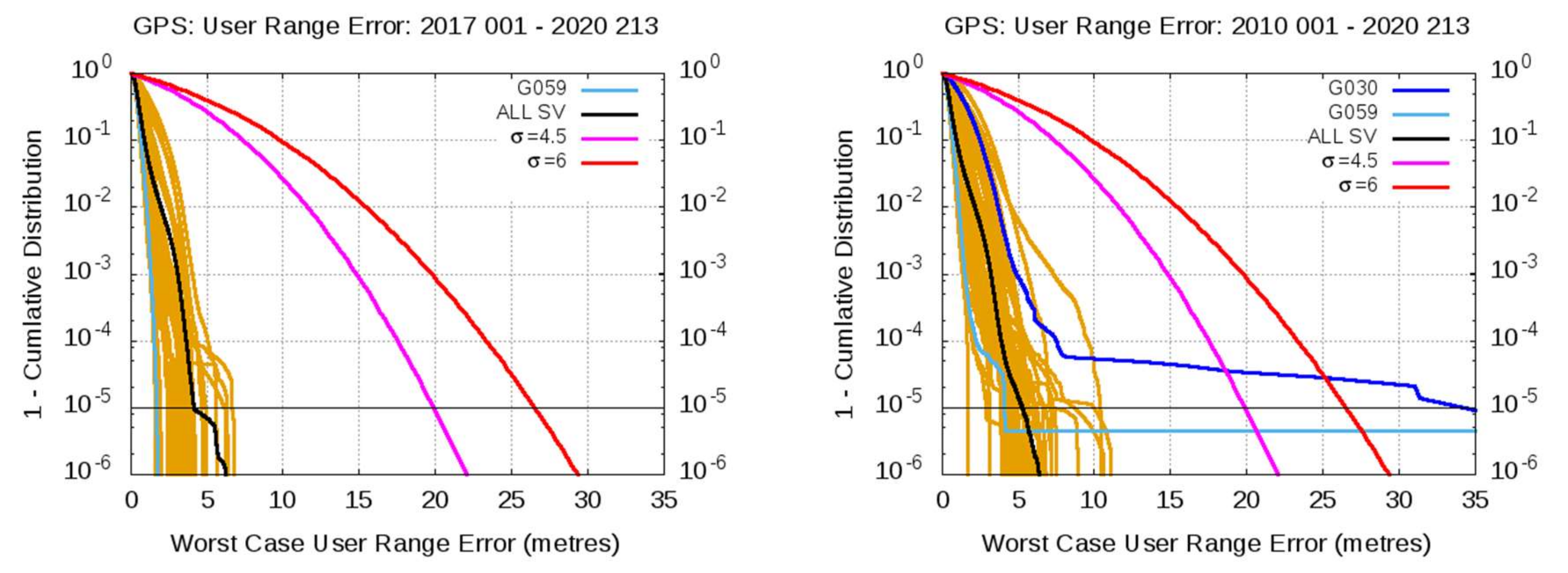
4.2. GPS Satellites: Events Exceeding the 4.42 × IAURA Threshold
4.3. Signal-in-Space Error Overbounding
5. Observed Nominal Accuracy
- The WC URE is under the 4.42 × SISA threshold;
- The most recent navigation data set broadcast on a Healthy SIS by the Galileo satellite is used, where Healthy SIS means:The RINEX field SV health is 0, i.e., DVS = “Navigation Data Valid” and HS = “Signal OK” and SISA ≠ NAPA;
- Broadcast navigation message is within its validity time, i.e., ;
- The precise orbits and clocks are available and healthy.
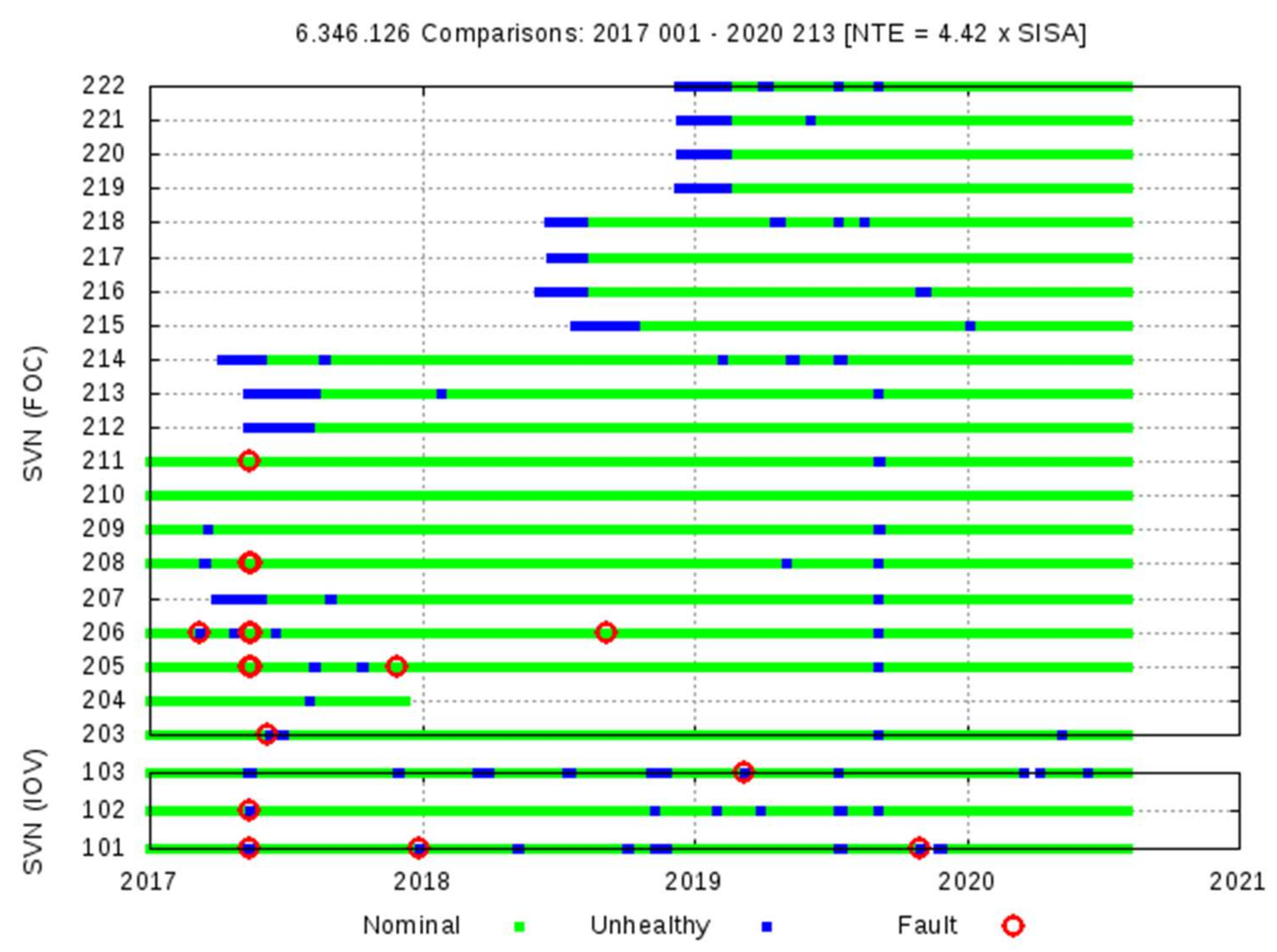
6. Observed Fault Probabilities
- (1)
- (2)
- NTE = 4.17 × 6 = 25.04 m threshold recently proposed to the ICAO NSP on April 2020 [10].
6.1. Observed Fault Probabilities Based on NTE = 39.78 m
- (overbound of SISE) lower than 9 m;
- lower than 1 × 10−5/sat;
- lower than 1 × 10−4.
6.2. Observed Fault Probabilities Based on NTE = 25.04 m
- (overbound of SISE) lower than 6 m;
- lower than 3 × 10−5/sat;
- lower than 1 × 10−4.
6.3. Extrapolation to Galileo Full Operational Capability
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- European GNSS Service Centre (GSA). Available online: https://www.gsc-europa.eu/system-service-status/constellation-information (accessed on 21 October 2020).
- GNSS. Phase II of the GNSS Evolutionary Architecture Study. Panel Report; FAA, 2010. Available online: http://www.faa.gov/about/office_org/headquarters_offices/ato/service_units/techops/navservices/gnss/library/documents/media/GEASPhaseII_Final.pdf. (accessed on 8 November 2020).
- Blanch, J.; Walker, T.; Enge, P.K.; Lee, Y.; Pervan, B.; Rippl, M.; Spletter, A.; Kropp, V. Baseline advanced RAIM user algorithm and possible improvements. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 713–732. [Google Scholar] [CrossRef]
- Walter, T.; Joerger, M.; Pervan, B. Determination of fault probabilities for ARAIM. In Proceedings of the 2016 IEEE/ION Position, Location and Navigation Symposium (PLANS), Savannah, GA, USA, 11–16 April 2016; pp. 451–461, Corrected Version. [Google Scholar]
- Galluzo, G.; Wallner, S.; Pericacho, J.G.; Criado, O.; García, C.; Sobrero, F.J.; Brieden, P.; Binder, K.; Battista, G.; Odriozola, M.; et al. Prototyping of galileo URA determination with TGVF and extended galileo performance characterisation for SoL applications. In Proceedings of the 33rd International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2020), Online Conference, 21–25 September 2020; pp. 1462–1475. [Google Scholar]
- Walter, T.; Blanch, J.; Choi, M.J.; Reid, T.; Enge, P. Incorporating GLONASS into aviation RAIM receivers. In Proceedings of the ION International Technical Meeting, San Diego, CA, USA, 3 January 2013; pp. 239–249. [Google Scholar]
- Working Group C-ARAIM Technical Subgroup. EU-U.S. Cooperation on Satellite Navigation. Milestone 3 Report. 2016. Available online: https://insidegnss.com/wp-content/uploads/2016/11/ARAIM-milestone-3-report.pdf (accessed on 25 November 2020).
- United States Department of Defense. Global Positioning System Standard Positioning Service Performance Standard. Available online: https://www.gps.gov/technical/ps/2020-SPS-performance-standard.pdf (accessed on 25 November 2020).
- European GNSS (Galileo) Open Service—Service Definition Document, Issue 1.1. May 2019. Available online: https://www.gsc-europa.eu/sites/default/files/sites/all/files/Galileo-OS-SDD_v1.1.pdf (accessed on 25 November 2020).
- Chatre, E.; Boyero, J.P.; Martini, I.; Sgammini, M.; Wallner, S.; Cosson, F.; Brieden, P.; Laura, D.; Canestri, D. Galileo performance characterization for horizontal ARAIM. In Proceedings of the ICAO Navigation System Panel (NSP), Online Conference, 20–24 April 2020. Information paper. [Google Scholar]
- Walter, T.; Blanch, J. KEYNOTE—Characterization of GNSS clock and ephemeris errors to support ARAIM. In Proceedings of the ION 2015 Pacific PNT Meeting, Honolulu, HI, USA, 20–23 April 2015; pp. 920–931. [Google Scholar]
- Heng, L. Safe Satellite Navigation with Multiple Constellations: Global Monitoring of GPS and GLONASS Signal-in-Space Anomalies. Ph.D. Dissertation, Stanford University, Stanford, CA, USA, 2012. [Google Scholar]
- Guurter, W. RINEX: The Receiver Independent Exchange Format, version 2.11; Astronomical Institute, University of Berne: Bern, Switzerland, 2012; Available online: ftp://igs.org/pub/data/format/rinex211.txt (accessed on 21 October 2020).
- Global Positioning System Wing (GPSW). Interface Specification IS-GPS-200E. 2010. Available online: https://www.navcen.uscg.gov/pdf/gps/IS-GPS-200E_Final_08Jun10.pdf (accessed on 25 November 2020).
- Sanz, J.; Juan Zornoza, J.M.; Hernández-Pajares, M. GNSS Data Processing, Volume 1: Fundamentals and Algorithms; ESA TM-23/1; ESA Communications: Noordwijk, The Netherlands, 2013; Available online: https://gage.upc.edu/gnss_book (accessed on 25 November 2020)ISBN 9789292217.
- Ibáñez, D.; Rovira-Garcia, A.; Alonso, M.T.; Sanz, J.; Juan, J.M.; González-Casado, G.; Lopez-Martínez, M. EGNOS 1046 Maritime Service Assessment. Sensors 2020, 20, 276. [Google Scholar] [CrossRef] [PubMed]
- Montenbruck, O.; Steigenberger, P.; Prange, L.; Deng, Z.; Zhao, Q.; Perosanz, F.; Romero, I.; Noll, C.; Stürze, A.; Weber, G.; et al. The Multi-GNSS Experiment (MGEX) of the International GNSS Service (IGS)—Achievements, prospects and challenges. Adv. Space Res. 2017, 59, 1671–1697. [Google Scholar] [CrossRef]
- ANTEX Files Server. European GNSS Service Centre. April 2019. Available online: https://www.gsc-europa.eu/sites/default/files/sites/all/files/GSAT_2023.atx.txt (accessed on 21 October 2020).
- National Geospatial Agency Server. Available online: ftp://ftp.nga.mil/pub2/gps/apcpe (accessed on 25 November 2020).
- European GNSS (Galileo) Open Service—Signal-In-Space Interface Control Document, Issue 1.3. December 2016. Available online: https://www.gsc-europa.eu/sites/default/files/sites/all/files/Galileo-OS-SIS-ICD.pdf (accessed on 25 November 2020).
- NAGU. Available online: https://www.gsc-europa.eu/system-status/user-notifications-archive (accessed on 25 November 2020).
- Cedric, R.; Bonhoure, B.; Suard, N.; Mabilleau, M.; Vuillaume, J.; Dulery, C.; Lapeyre, D.; Sauce, C. Galileo ephemeris consolidation and control analysis—GECCO. In Proceedings of the 28th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2015), Tampa, FL, USA, 14–18 September 2015. [Google Scholar]
- Serenad Server from CNES. Available online: ftp://serenad-public.cnes.fr/SERENAD0/FROM_NTMFV2 (accessed on 25 November 2020).
- Juan, J.M.; Sanz, J.; Rovira-Garcia, A.; González-Casado, G.; Ventura-Traveset, J.; Cacciapuoti, L.; Schoenemann, E. A New Approach to Improve Satellite Clock Estimates, Removing the Inter-day Jumps. In Proceedings of the 51st Annual Precise Time and Time Interval Systems and Applications Meeting, San Diego, CA, USA, 21–24 January 2020; pp. 279–301. [Google Scholar] [CrossRef]
- Walter, T.; Rife, J.; Blanch, J. Treatment of Biased Error Distributions in SBAS. In Proceedings of the 2004 International Symposium on GNSS/GPS, Sydney, Australia, 6–8 December 2004. [Google Scholar]
- DeCleene, B. Defining pseudorange integrity—Overbounding. In Proceedings of the 13th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GPS 2000), Salt Lake City, UT, USA, 19–22 September 2000; pp. 1916–1924. [Google Scholar]
- Brieden, P.; Wallner, S.; Canestri, E.; Joly, D.; Sanz, J.; Martini, I.; Nuckelt, A.; Battista, G.; Lauria, D.; Luongo, F.; et al. Galileo characterization as input to H-ARAIM and SBAS DFMC. In Proceedings of the 32nd International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2019), Miami, FL, USA, 16–20 September 2019; pp. 2819–2841. [Google Scholar]
- Guo, F.; Li, X.; Zhang, X.; Wang, J. Assessment of precise orbits and clock products for Galileo, Beidou and QZSS from IGS Multi-GNSS Experiment (MGEX). GPS Solut. 2017, 21, 279–290. [Google Scholar] [CrossRef]






| Potential Anomalies Found with Space Approach (NTE = 4.42 × SISA) | Potential Anomalies Found with Ground Approach | Final Decision | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| YYDOY | SVN | PRN | Start Time | Duration (min) | Anomaly | WC URE (m) | SISA (m) | Start Time | Duration (min) | WC URE (m) | Ref. Station | Num. of Stations that Decide | Algorithm Decision | |||||
| Type | Value (m) | Anom. | Nominal | Untrack | ||||||||||||||
| 17066 | E206 | 30 | 7 March 2017 | 03:15 | 40 | clock | 340.9 | 341.9 | 3.12 | 03:21 | 38.5 | 341.9 | SEYG | 11 | 0 | 39 | TRUE | TRUE |
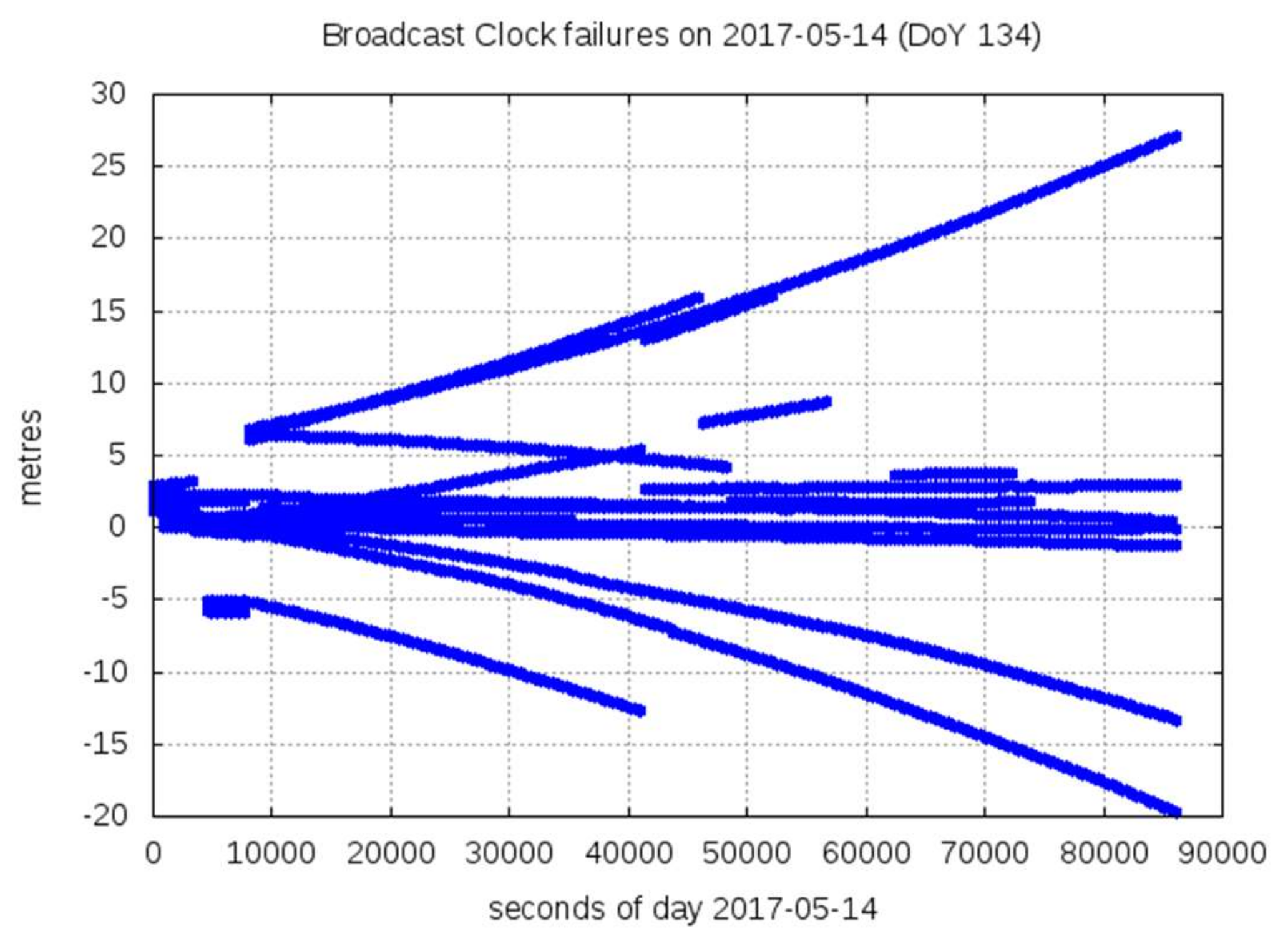
| 17134 | E101 | 11 | 14 May 2017 | 13:30 | 60 | clock | 14.9 | 15.0 | 3.12 | 11:42 | 287.5 | 17.6 | WGTN | 11 | 1 | 39 | PARADOX | TRUE |
| 17134 | E102 | 12 | 14 May 2017 | 12:20 | 25 | clock | 14.4 | 14.4 | 3.12 | 10:25 | 144.5 | 14.4 | WGTN | 13 | 0 | 37 | TRUE | TRUE |
| 17134 | E205 | 24 | 14 May 2017 | 17:35 | 395 | clock | 20.3 | 20.3 | 3.12 | 15:38 | 309.5 | 16.9 | YEL2 | 24 | 3 | 23 | PARADOX | TRUE |
| 17134 | E206 | 30 | 14 May 2017 | 13:30 | 625 | clock | 26.6 | 26.9 | 3.12 | 20:17 | 222.0 | 26.9 | YEL2 | 22 | 0 | 28 | TRUE | TRUE |
| 17134 | E208 | 08 | 14 May 2017 | 23:35 | 25 | clock | 13.8 | 14.2 | 3.12 | 23:45 | 9.5 | 14.1 | RGDG | 1 | 7 | 42 | PARADOX | TRUE |
| 17134 | E211 | 02 | 14 May 2017 | 11:55 | 30 | clock | 14.6 | 14.9 | 3.12 | 08:59 | 150.5 | 14.3 | MAYG | 9 | 6 | 35 | PARADOX | TRUE |
| 17135 | E205 | 24 | 15 May 2017 | 00:00 | 70 | clock | 20.6 | 20.6 | 3.12 | 00:03 | 66.5 | 20.6 | RGDG | 11 | 1 | 38 | PARADOX | TRUE |
| 17135 | E206 | 30 | 15 May 2017 | 00:00 | 190 | clock | 31.4 | 36.7 | 3.12 | 00:03 | 157.0 | 33.3 | YEL2 | 9 | 0 | 41 | TRUE | TRUE |
| 17135 | E208 | 08 | 15 May 2017 | 00:00 | 105 | clock | 15.1 | 15.1 | 3.12 | 01:02 | 47.5 | 15.1 | RGDG | 5 | 7 | 38 | PARADOX | TRUE |
| 17157 | E203 | 26 | 6 June 2017 | 05:50 | 1085 | clock | 491.3 | 491.9 | 3.12 | 12:27 | 163.5 | 491.9 | YEL2 | 31 | 0 | 19 | TRUE | TRUE |
| 17158 | E203 | 26 | 7 June 2017 | 00:00 | 430 | clock | 460.4 | 472.8 | 3.12 | 01:09 | 360.5 | 472.8 | YEL2 | 21 | 0 | 29 | TRUE | TRUE |
| 17332 | E205 | 24 | 28 November 2017 | 06:45 | 185 | clock | 16.2 | 16.6 | 3.12 | 07:27 | 144.5 | 16.6 | YEL2 | 17 | 1 | 32 | PARADOX | TRUE |
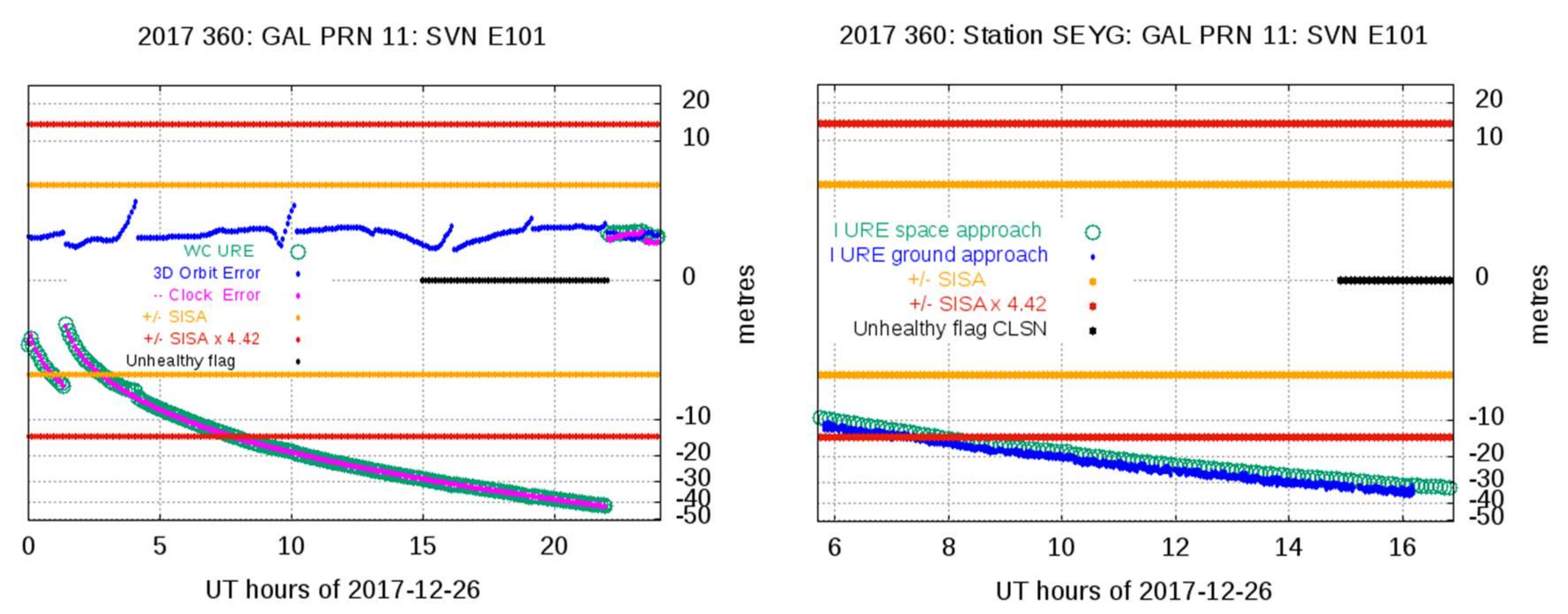
| 17360 | E101 | 11 | 26 December 2017 | 07:45 | 385 | clock | 27.2 | 27.2 | 3.12 | 05.48 | 140.5 | 14.7 | VIGO | 28 | 7 | 15 | PARADOX | TRUE |
| 18248 | E206 | 30 | 5 September 2018 | 02:20 | 10 | eph. | 18.8 | 17.8 | 3.12 | 02:08 | 21.5 | 17.8 | TLSE | 20 | 7 | 23 | PARADOX | TRUE |
| 19066 | E103 | 19 | 7 March 2019 | 12:15 | 125 | eph. | 22.2 | 18.8 | 3.12 | 14:03 | 17.5 | 18.8 | KIRU | 8 | 0 | 42 | TRUE | TRUE |
| 19302 | E101 | 11 | 29 October 2019 | 18.10 | 30 | clock | 431.9 | 432.1 | 3.12 | 18:08 | 36.0 | 432.1 | STHL | 18 | 0 | 32 | TRUE | TRUE |
| Events found with Space Approach (NTE = 4.42 × IAURA) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| YYDOY | SVN | PRN | Start Time | Duration (min) | Anomaly | WC URE (m) | IAURA (m) | ||
| Type | Value (m) | ||||||||
| 10053 | G030 | 30 | 22 February 2010 | 20:55 | 20 | clock | 42.8 | 42.9 | 3.40 |
| 10115 | G039 | 09 | 25 April 2010 | 19:45 | 10 | eph. | 44.9 | 11.3 | 2.40 |
| 12169 | G059 | 19 | 17 June 2012 | 00:15 | 20 | eph. | 1899.0 | 451.5 | 2.40 |
| From 1 January 2017 to 31 July 2020: gAGE Consolidated Broadcast + MGEX Precise Orbits and Clocks | |||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Radial (cm) | Along-Track (cm) | Cross-Track (cm) | Clock (cm) | WC URE (cm) | N. Samples | IURE (cm) (Acum. Dodec.) | |||||||||||||||||||||
| SVN | 68th | 95th | 68th | 95th | 68th | 95th | 68th | 95th | 68th | 95th | 68th | 95th | N. Sampl. | ||||||||||||||
| IOV | E101 | 5.1 | 13 | 28 | 15 | −5.5 | 28 | 59 | 32 | −0.1 | 18 | 35 | 18 | −5.3 | 17 | 38 | 25 | 15.6 | 24 | 44 | 27 | 353,796 | 10.3 | 17 | 35 | 24 | 2,446,525 |
| IOV | E102 | 8.6 | 16 | 32 | 15 | −9.6 | 30 | 65 | 32 | 0.3 | 19 | 37 | 19 | −17.1 | 25 | 46 | 26 | 33.3 | 38 | 56 | 26 | 366,125 | 25.4 | 31 | 48 | 24 | 2,568,002 |
| IOV | E103 | 3.1 | 12 | 25 | 15 | −6.8 | 33 | 70 | 52 | 1.8 | 20 | 40 | 21 | −9.3 | 18 | 38 | 18 | 19.0 | 27 | 46 | 25 | 353,354 | 12.5 | 18 | 37 | 17 | 2,462,407 |
| FOC | E203 | 13.7 | 20 | 40 | 18 | −7.1 | 26 | 57 | 34 | 0.0 | 17 | 34 | 17 | −2.1 | 16 | 35 | 21 | 20.6 | 28 | 50 | 24 | 360,845 | 15.5 | 22 | 43 | 20 | 2,533,431 |
| FOC | E204 | 7.0 | 14 | 30 | 28 | −6.5 | 28 | 64 | 35 | −0.5 | 17 | 35 | 28 | 11.2 | 20 | 43 | 27 | −5.2 | 21 | 45 | 33 | 97,644 | −4.4 | 15 | 36 | 26 | 679,576 |
| FOC | E205 | 10.3 | 15 | 31 | 14 | −3.3 | 24 | 53 | 28 | 1.6 | 16 | 32 | 16 | 4.0 | 13 | 30 | 24 | 8.7 | 17 | 33 | 28 | 365,578 | 6.2 | 12 | 27 | 24 | 2,542,545 |
| FOC | E206 | 9.4 | 15 | 30 | 14 | −4.2 | 25 | 54 | 29 | 0.6 | 16 | 33 | 17 | 5.8 | 14 | 32 | 25 | 5.6 | 17 | 33 | 28 | 364,742 | 3.6 | 11 | 26 | 24 | 2,526,134 |
| FOC | E207 | 9.3 | 14 | 28 | 13 | −7.5 | 25 | 52 | 26 | −0.5 | 16 | 32 | 16 | 10.1 | 17 | 36 | 15 | −0.9 | 16 | 31 | 19 | 326,371 | −0.9 | 11 | 24 | 14 | 2,293,869 |
| FOC | E208 | 11.7 | 17 | 34 | 15 | −6.9 | 25 | 54 | 35 | 0.6 | 15 | 32 | 16 | −1.1 | 13 | 30 | 27 | 17.0 | 24 | 42 | 30 | 364,725 | 12.6 | 18 | 36 | 26 | 2,532,747 |
| FOC | E209 | 11.3 | 17 | 33 | 14 | −2.5 | 24 | 54 | 30 | 1.0 | 17 | 33 | 17 | 1.0 | 11 | 28 | 14 | 13.9 | 22 | 40 | 19 | 363,586 | 10.3 | 16 | 34 | 15 | 2,556,984 |
| FOC | E210 | 10.2 | 15 | 31 | 14 | −6.0 | 25 | 54 | 28 | 1.8 | 16 | 33 | 17 | 2.6 | 16 | 36 | 18 | 10.1 | 19 | 44 | 22 | 362,894 | 7.4 | 13 | 37 | 18 | 2,522,405 |
| FOC | E211 | 11.6 | 17 | 34 | 16 | −2.2 | 24 | 52 | 28 | 1.4 | 16 | 32 | 16 | −0.8 | 13 | 31 | 25 | 16.1 | 23 | 44 | 30 | 362,281 | 12.3 | 17 | 38 | 26 | 2,517,599 |
| FOC | E212 | 11.0 | 17 | 36 | 15 | −3.8 | 24 | 54 | 28 | −0.1 | 16 | 32 | 16 | −1.9 | 12 | 28 | 14 | 17.3 | 23 | 43 | 19 | 307,404 | 12.7 | 17 | 37 | 16 | 2,160,517 |
| FOC | E213 | 11.6 | 17 | 37 | 17 | −4.5 | 24 | 53 | 33 | 1.3 | 16 | 33 | 17 | −1.0 | 13 | 29 | 15 | 17.0 | 23 | 43 | 21 | 306,383 | 12.5 | 17 | 37 | 17 | 2,137,544 |
| FOC | E214 | 13.4 | 20 | 41 | 17 | −3.2 | 24 | 52 | 32 | 1.4 | 17 | 33 | 17 | −5.9 | 14 | 30 | 16 | 24.5 | 30 | 52 | 21 | 323,637 | 19.2 | 24 | 46 | 18 | 2,255,881 |
| FOC | E215 | 5.6 | 11 | 24 | 13 | −1.5 | 23 | 49 | 26 | 1.3 | 17 | 33 | 17 | 4.3 | 13 | 29 | 16 | 2.5 | 15 | 27 | 19 | 181,434 | 1.2 | 9 | 20 | 14 | 1,258,327 |
| FOC | E216 | 5.8 | 11 | 24 | 12 | −2.7 | 22 | 49 | 26 | 0.9 | 15 | 31 | 16 | 1.6 | 12 | 28 | 14 | 6.6 | 15 | 28 | 16 | 199,853 | 4.1 | 10 | 21 | 12 | 1,385,543 |
| FOC | E217 | 5.3 | 11 | 22 | 11 | −3.0 | 24 | 49 | 26 | −0.3 | 16 | 33 | 17 | 4.6 | 13 | 28 | 15 | 1.9 | 14 | 26 | 18 | 202,319 | 0.7 | 9 | 19 | 14 | 1,407,647 |
| FOC | E218 | 6.0 | 11 | 24 | 13 | −4.6 | 23 | 48 | 32 | 0.8 | 16 | 31 | 16 | 3.2 | 13 | 30 | 16 | 4.9 | 15 | 28 | 18 | 199,516 | 2.8 | 9 | 22 | 12 | 1,382,738 |
| FOC | E219 | 6.0 | 13 | 26 | 13 | −2.0 | 25 | 53 | 29 | −0.3 | 17 | 33 | 17 | 6.1 | 17 | 33 | 16 | 0.7 | 16 | 28 | 17 | 147,133 | −0.1 | 9 | 21 | 11 | 1,029,590 |
| FOC | E220 | 5.3 | 12 | 25 | 13 | −5.2 | 24 | 50 | 30 | −0.5 | 18 | 33 | 17 | 2.8 | 15 | 31 | 15 | 4.7 | 16 | 28 | 17 | 144,999 | 2.5 | 9 | 21 | 11 | 1,000,198 |
| FOC | E221 | 5.6 | 13 | 25 | 12 | −4.6 | 24 | 52 | 26 | 0.0 | 18 | 33 | 17 | 3.8 | 15 | 32 | 15 | 3.7 | 16 | 28 | 16 | 145,985 | 1.7 | 10 | 21 | 11 | 1,022,116 |
| FOC | E222 | 4.8 | 13 | 26 | 16 | −2.1 | 25 | 54 | 52 | −1.0 | 17 | 33 | 19 | 1.6 | 15 | 32 | 20 | 5.9 | 17 | 31 | 25 | 144,747 | 3.1 | 10 | 23 | 14 | 998,716 |
| ALL | IOV | 5.6 | 14 | 29 | 15 | −7.3 | 30 | 65 | 40 | 0.7 | 19 | 38 | 19 | −10.6 | 20 | 41 | 24 | 22.7 | 31 | 51 | 27 | 1,073,275 | 16.2 | 23 | 42 | 23 | 7,476,934 |
| ALL | FOC | 9.7 | 15 | 32 | 15 | −4.3 | 24 | 53 | 31 | 0.6 | 16 | 33 | 17 | 1.8 | 14 | 32 | 20 | 10.7 | 20 | 41 | 24 | 5,272,076 | 7.7 | 14 | 34 | 20 | 36,744,107 |
| ALL | ALL | 9.0 | 15 | 32 | 15 | −4.8 | 25 | 55 | 32 | 0.6 | 17 | 34 | 17 | −0.3 | 15 | 34 | 21 | 12.7 | 22 | 44 | 25 | 6,345,351 | 9.2 | 15 | 36 | 21 | 44,221,041 |
| From 1 January 2017 to 31 July 2020: gAGE Consolidated Broadcast + MGEX Precise Orbits and Clocks | |||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Radial (cm) | Along-Track (cm) | Cross-Track (cm) | Clock (cm) | WC URE (cm) | N. Samples | IURE (cm) (Acum. Dodec.) | |||||||||||||||||||||
| SVN | 68th | 95th | 68th | 95th | 68th | 95th | 68th | 95th | 68th | 95th | 68th | 95th | N. Sampl. | ||||||||||||||
| IIA | G034 | −0.6 | 18 | 36 | 18 | 6.4 | 96 | 225 | 110 | 0.3 | 53 | 98 | 51 | −6.1 | 62 | 155 | 72 | 8.2 | 87 | 187 | 93 | 184,456 | 3.3 | 63 | 158 | 74 | 1,300,383 |
| IIR | G041 | −1.1 | 11 | 24 | 12 | 49.3 | 106 | 226 | 102 | 0.2 | 41 | 81 | 41 | −7.7 | 28 | 64 | 31 | 11.7 | 54 | 100 | 54 | 360,479 | 7.0 | 32 | 71 | 35 | 2,639,671 |
| IIR | G043 | −0.1 | 10 | 21 | 11 | 18.9 | 86 | 192 | 92 | −0.4 | 36 | 72 | 37 | −3.2 | 36 | 88 | 43 | 3.8 | 59 | 115 | 62 | 365,426 | 3.0 | 39 | 93 | 45 | 2,454,557 |
| IIR | G044 | 1.4 | 13 | 27 | 13 | −9.6 | 85 | 188 | 92 | 0.4 | 38 | 78 | 39 | −5.2 | 82 | 218 | 97 | 9.0 | 104 | 244 | 115 | 365,428 | 6.6 | 83 | 219 | 98 | 2,400,351 |
| IIR | G045 | 0.5 | 14 | 30 | 15 | 12.7 | 104 | 226 | 112 | 1.5 | 54 | 107 | 54 | −3.3 | 26 | 59 | 30 | 6.9 | 56 | 99 | 56 | 365,310 | 5.3 | 33 | 72 | 36 | 2,399,917 |
| IIR | G046 | 2.8 | 14 | 29 | 14 | −52.1 | 118 | 267 | 120 | −0.9 | 47 | 93 | 47 | −2.2 | 37 | 95 | 45 | 8.1 | 69 | 136 | 71 | 365,141 | 6.6 | 43 | 105 | 50 | 2,472,920 |
| IIR | G047 | 1.9 | 13 | 26 | 14 | −5.8 | 92 | 196 | 101 | 0.4 | 33 | 64 | 33 | −5.1 | 23 | 48 | 23 | 12.3 | 45 | 78 | 44 | 365,233 | 7.5 | 27 | 57 | 28 | 2,473,181 |
| IIR | G048 | 0.9 | 13 | 26 | 13 | −4.7 | 88 | 193 | 94 | 0.9 | 54 | 105 | 53 | 2.6 | 38 | 87 | 42 | −3.9 | 62 | 118 | 63 | 363,994 | −1.8 | 41 | 92 | 45 | 2,324,785 |
| IIR | G050 | 1.7 | 13 | 26 | 13 | 2.7 | 79 | 170 | 85 | 0.1 | 34 | 67 | 34 | 4.4 | 26 | 54 | 27 | −3.3 | 45 | 78 | 44 | 364,960 | −3.0 | 27 | 59 | 29 | 2,376,931 |
| IIR | G051 | 0.8 | 10 | 22 | 11 | 2.3 | 84 | 180 | 90 | 0.0 | 48 | 105 | 51 | 0.2 | 23 | 49 | 24 | 1.5 | 46 | 80 | 46 | 365,291 | 2.0 | 27 | 58 | 29 | 2,468,535 |
| IIR | G052 | 1.2 | 12 | 24 | 12 | 0.0 | 83 | 183 | 91 | −0.1 | 38 | 81 | 40 | −5.0 | 38 | 91 | 43 | 8.5 | 60 | 118 | 62 | 364,962 | 5.7 | 40 | 95 | 45 | 2,343,561 |
| IIR | G053 | 0.1 | 14 | 28 | 14 | 18.4 | 117 | 267 | 128 | 0.4 | 35 | 72 | 36 | 1.4 | 52 | 145 | 66 | −1.3 | 79 | 180 | 89 | 365,110 | −1.5 | 53 | 146 | 67 | 2,390,098 |
| IIR | G054 | 1.1 | 12 | 24 | 12 | −13.5 | 92 | 197 | 99 | 1.3 | 54 | 97 | 51 | −4.2 | 31 | 86 | 41 | 6.9 | 56 | 114 | 61 | 110,854 | 6.4 | 35 | 90 | 43 | 749,849 |
| IIR | G055 | 0.1 | 12 | 24 | 12 | 9.9 | 95 | 212 | 103 | 0.1 | 34 | 71 | 36 | 2.5 | 21 | 43 | 22 | −4.7 | 44 | 78 | 43 | 364,942 | −2.2 | 25 | 53 | 26 | 2,395,559 |
| IIR | G056 | 1.2 | 13 | 26 | 13 | −15.9 | 77 | 163 | 80 | −0.3 | 35 | 71 | 36 | −2.3 | 22 | 46 | 23 | 6.3 | 42 | 72 | 41 | 365,333 | 3.8 | 25 | 53 | 26 | 2,438,184 |
| IIR | G057 | 1.6 | 15 | 30 | 15 | 7.8 | 120 | 263 | 130 | −0.1 | 50 | 95 | 49 | 3.9 | 40 | 111 | 54 | −8.3 | 70 | 152 | 78 | 364,843 | −3.4 | 43 | 118 | 57 | 2,312,041 |
| IIR | G058 | 1.0 | 15 | 28 | 15 | 11.6 | 87 | 189 | 93 | −0.5 | 39 | 77 | 39 | −5.1 | 24 | 49 | 25 | 11.0 | 46 | 80 | 45 | 365,127 | 6.4 | 28 | 58 | 29 | 2,448,912 |
| IIR | G059 | 1.1 | 11 | 24 | 12 | 10.2 | 85 | 182 | 90 | −0.7 | 45 | 83 | 43 | 2.7 | 23 | 50 | 24 | −2.6 | 46 | 80 | 45 | 365,432 | 0.0 | 27 | 58 | 29 | 2,649,750 |
| IIR | G060 | 2.1 | 12 | 24 | 12 | −19.9 | 90 | 192 | 93 | 0.7 | 47 | 87 | 46 | 0.2 | 22 | 47 | 23 | 3.1 | 47 | 80 | 46 | 330,981 | 1.4 | 27 | 58 | 29 | 2,201,256 |
| IIR | G061 | −0.5 | 12 | 26 | 13 | 31.8 | 102 | 230 | 108 | 0.9 | 40 | 79 | 40 | −2.2 | 24 | 55 | 27 | 3.1 | 52 | 94 | 52 | 365,266 | 2.5 | 30 | 65 | 32 | 2,418,084 |
| IIF | G062 | −0.9 | 21 | 42 | 21 | 23.1 | 101 | 221 | 110 | −0.2 | 43 | 83 | 42 | 5.0 | 27 | 53 | 26 | −8.9 | 57 | 101 | 57 | 365,034 | −4.8 | 37 | 76 | 38 | 2,626,341 |
| IIF | G063 | 1.5 | 18 | 38 | 19 | −21.3 | 106 | 232 | 113 | −0.6 | 50 | 90 | 47 | 5.8 | 36 | 79 | 41 | −6.7 | 66 | 119 | 66 | 363,301 | −5.4 | 44 | 95 | 48 | 2,385,276 |
| IIF | G064 | 0.4 | 16 | 32 | 16 | 16.4 | 82 | 182 | 89 | 0.1 | 32 | 65 | 33 | 5.8 | 25 | 51 | 25 | −7.7 | 50 | 87 | 49 | 365,008 | −5.3 | 32 | 67 | 33 | 2,448,277 |
| IIF | G065 | 0.0 | 25 | 51 | 26 | 19.5 | 103 | 238 | 117 | −0.6 | 33 | 67 | 33 | 0.8 | 120 | 243 | 121 | 1.2 | 148 | 275 | 145 | 365,176 | −1.3 | 123 | 248 | 124 | 2,446,742 |
| IIF | G066 | 0.4 | 16 | 31 | 16 | −13.8 | 81 | 176 | 88 | −0.4 | 39 | 77 | 39 | 1.8 | 22 | 43 | 22 | −1.6 | 49 | 82 | 47 | 364,855 | −0.8 | 31 | 62 | 32 | 2,457,384 |
| IIF | G067 | 0.5 | 19 | 37 | 19 | 7.2 | 103 | 233 | 113 | −0.1 | 33 | 71 | 35 | 7.3 | 26 | 55 | 26 | −9.6 | 56 | 99 | 55 | 365,087 | −6.3 | 36 | 73 | 36 | 2,324,301 |
| IIF | G068 | 1.0 | 15 | 31 | 15 | 6.5 | 75 | 173 | 86 | 0.6 | 32 | 65 | 33 | 1.1 | 24 | 54 | 29 | 0.3 | 46 | 87 | 49 | 365,082 | 0.6 | 29 | 66 | 34 | 2,373,489 |
| IIF | G069 | 0.5 | 18 | 37 | 19 | 0.6 | 93 | 204 | 104 | −0.3 | 38 | 76 | 39 | −10.2 | 41 | 85 | 42 | 15.3 | 67 | 115 | 64 | 365,002 | 13.3 | 46 | 95 | 47 | 2,425,257 |
| IIF | G070 | 0.7 | 13 | 28 | 14 | −3.7 | 88 | 202 | 100 | 0.5 | 36 | 72 | 36 | −2.3 | 19 | 41 | 22 | 5.3 | 45 | 82 | 46 | 365,017 | 3.1 | 27 | 59 | 30 | 2,568,890 |
| IIF | G071 | −0.5 | 19 | 37 | 19 | 9.9 | 94 | 210 | 107 | 0.2 | 42 | 83 | 42 | −0.5 | 26 | 55 | 27 | 0.5 | 56 | 98 | 56 | 364,879 | 0.7 | 36 | 75 | 38 | 2,338,517 |
| IIF | G072 | 1.3 | 22 | 45 | 22 | −30.8 | 112 | 244 | 118 | −0.2 | 47 | 89 | 47 | −0.2 | 96 | 207 | 101 | 2.3 | 126 | 242 | 126 | 364,969 | 2.4 | 99 | 213 | 104 | 2,312,670 |
| IIF | G073 | 0.2 | 14 | 29 | 14 | −5.4 | 92 | 203 | 103 | 0.6 | 48 | 92 | 47 | −8.1 | 24 | 54 | 25 | 13.2 | 52 | 90 | 50 | 365,041 | 9.4 | 32 | 68 | 32 | 2,463,582 |
| IIA | ALL | −0.6 | 18 | 36 | 18 | 6.4 | 96 | 225 | 110 | 0.3 | 53 | 98 | 51 | −6.1 | 62 | 155 | 72 | 8.2 | 87 | 187 | 93 | 184,456 | 3.3 | 63 | 158 | 74 | 1,300,383 |
| IIR | ALL | 0.9 | 13 | 26 | 13 | 3.6 | 93 | 209 | 103 | 0.2 | 41 | 85 | 43 | −1.3 | 29 | 83 | 42 | 3.5 | 54 | 114 | 62 | 6,644,112 | 2.7 | 33 | 88 | 45 | 44,358,142 |
| IIF | ALL | 0.4 | 18 | 38 | 19 | 0.7 | 94 | 212 | 106 | 0.0 | 39 | 79 | 40 | 0.5 | 32 | 118 | 53 | 0.3 | 61 | 150 | 75 | 4,378,451 | 0.5 | 41 | 122 | 58 | 29,170,726 |
| ALL | ALL | 0.7 | 14 | 31 | 16 | 2.5 | 94 | 210 | 104 | 0.1 | 41 | 83 | 42 | −0.7 | 31 | 97 | 47 | 2.3 | 56 | 130 | 68 | 11,207,019 | 1.8 | 36 | 103 | 51 | 74,829,251 |
| From 1 January 2010 to 31 July 2020: gAGE Consolidated Broadcast + NGA Precise Orbits and Clocks | |||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Radial (cm) | Along-Track (cm) | Cross-Track (cm) | Clock (cm) | WC URE (cm) | N. Samples | IURE (cm) (Acum. Dodec.) | |||||||||||||||||||||
| SVN | 68th | 95th | 68th | 95th | 68th | 95th | 68th | 95th | 68th | 95th | 68th | 95th | N. Samples | ||||||||||||||
| IIA | G023 | −2.2 | 25 | 46 | 24 | 19.8 | 100 | 230 | 112 | 0.1 | 42 | 86 | 44 | −2.1 | 61 | 131 | 65 | 1.8 | 80 | 156 | 82 | 634,169 | 1.1 | 55 | 128 | 62 | 4,080,462 |
| IIA | G024 | −0.5 | 42 | 77 | 41 | −11.1 | 152 | 329 | 170 | 0.5 | 41 | 84 | 42 | −1.3 | 141 | 280 | 142 | 5.0 | 169 | 305 | 165 | 182,285 | 1.1 | 132 | 265 | 133 | 1,230,973 |
| IIA | G026 | −2.5 | 15 | 35 | 18 | 14.2 | 103 | 252 | 123 | −0.7 | 38 | 77 | 39 | 3.8 | 47 | 117 | 57 | −8.0 | 75 | 156 | 81 | 521,082 | −6.0 | 52 | 125 | 61 | 3,485,740 |
| IIA | G027 | −1.4 | 83 | 126 | 74 | 15.2 | 251 | 473 | 247 | −1.5 | 46 | 88 | 45 | 7.0 | 197 | 355 | 188 | −0.9 | 220 | 365 | 208 | 252,287 | −11.0 | 158 | 301 | 155 | 1,819,735 |
| IIA | G030 | −2.5 | 24 | 50 | 25 | 26.3 | 114 | 269 | 130 | −0.3 | 33 | 67 | 34 | 6.5 | 134 | 259 | 133 | −8.4 | 161 | 290 | 156 | 141,581 | −9.7 | 133 | 259 | 132 | 986,392 |
| IIA | G033 | −1.8 | 26 | 51 | 26 | −1.0 | 120 | 257 | 129 | −0.7 | 41 | 81 | 41 | −1.4 | 129 | 255 | 129 | 1.4 | 154 | 283 | 151 | 480,756 | 0.3 | 126 | 253 | 127 | 3,229,855 |
| IIA | G034 | −1.8 | 17 | 35 | 18 | 6.1 | 101 | 228 | 113 | 0.0 | 39 | 79 | 40 | 0.5 | 68 | 159 | 76 | −1.8 | 91 | 190 | 97 | 796,131 | −2.7 | 68 | 161 | 77 | 5,337,739 |
| IIA | G035 | −0.8 | 22 | 49 | 25 | 6.5 | 88 | 196 | 99 | −0.3 | 47 | 91 | 46 | −3.0 | 146 | 308 | 156 | 4.8 | 171 | 335 | 175 | 161,036 | 2.5 | 147 | 309 | 156 | 1,053,649 |
| IIA | G036 | −1.9 | 16 | 35 | 18 | 6.1 | 111 | 248 | 123 | −0.4 | 41 | 81 | 41 | −8.7 | 75 | 187 | 86 | 9.2 | 102 | 219 | 109 | 433,611 | 6.4 | 77 | 189 | 88 | 2,905,140 |
| IIA | G038 | −1.8 | 29 | 56 | 29 | −8.1 | 128 | 276 | 140 | 1.4 | 81 | 138 | 75 | −0.7 | 135 | 265 | 134 | 0.6 | 165 | 297 | 160 | 505,126 | −0.6 | 132 | 262 | 132 | 3,305,906 |
| IIA | G039 | −2.5 | 42 | 73 | 40 | 22.8 | 155 | 312 | 158 | −0.2 | 34 | 69 | 36 | 2.6 | 141 | 273 | 139 | −2.7 | 168 | 298 | 162 | 453,215 | −5.6 | 132 | 260 | 132 | 2,996,678 |
| IIA | G040 | −1.7 | 20 | 41 | 21 | −4.1 | 105 | 237 | 121 | −0.8 | 38 | 76 | 38 | 5.3 | 123 | 245 | 123 | −7.3 | 148 | 276 | 146 | 579,819 | −7.0 | 124 | 249 | 125 | 3,866,837 |
| IIR | G041 | −0.5 | 12 | 24 | 12 | 10.5 | 96 | 210 | 104 | 0.3 | 43 | 85 | 43 | −3.7 | 28 | 65 | 33 | 5.5 | 53 | 99 | 55 | 1,093,820 | 4.1 | 32 | 72 | 36 | 7,527,301 |
| IIR | G043 | 0.5 | 11 | 23 | 12 | −7.0 | 86 | 190 | 95 | −0.4 | 42 | 83 | 42 | −1.9 | 35 | 83 | 41 | 3.3 | 56 | 112 | 60 | 1,098,316 | 3.0 | 38 | 89 | 44 | 7,174,694 |
| IIR | G044 | 0.8 | 13 | 27 | 13 | −16.3 | 91 | 199 | 97 | 0.3 | 42 | 84 | 42 | −3.3 | 94 | 224 | 104 | 6.0 | 117 | 250 | 123 | 1,099,057 | 4.5 | 95 | 225 | 105 | 7,283,867 |
| IIR | G045 | 0.1 | 14 | 28 | 14 | 3.1 | 102 | 224 | 112 | 1.3 | 54 | 105 | 54 | −2.3 | 27 | 60 | 31 | 4.9 | 55 | 99 | 56 | 1,098,722 | 3.8 | 32 | 71 | 36 | 7,176,231 |
| IIR | G046 | 0.1 | 14 | 28 | 14 | −21.1 | 108 | 239 | 117 | −1.1 | 44 | 88 | 44 | 0.1 | 43 | 116 | 55 | −0.5 | 71 | 151 | 78 | 1,097,737 | 1.3 | 47 | 122 | 58 | 7,480,736 |
| IIR | G047 | 0.8 | 13 | 26 | 13 | −5.2 | 93 | 204 | 102 | 0.6 | 49 | 103 | 51 | 3.5 | 40 | 139 | 63 | −3.9 | 65 | 169 | 82 | 1,097,713 | −1.9 | 43 | 140 | 64 | 7,427,244 |
| IIR | G048 | 0.3 | 13 | 27 | 14 | −3.2 | 84 | 186 | 92 | 0.8 | 55 | 103 | 54 | 0.5 | 36 | 83 | 40 | −0.9 | 59 | 112 | 61 | 1,097,593 | 0.4 | 38 | 88 | 43 | 6,982,467 |
| IIR | G050 | 0.2 | 13 | 25 | 13 | −1.3 | 80 | 168 | 86 | 0.0 | 34 | 68 | 35 | 1.2 | 25 | 52 | 26 | −0.9 | 44 | 77 | 44 | 1,098,283 | −1.4 | 27 | 57 | 28 | 7,163,104 |
| IIR | G051 | 0.0 | 11 | 23 | 12 | −10.9 | 89 | 195 | 97 | −0.2 | 48 | 96 | 49 | −0.5 | 23 | 51 | 26 | 1.2 | 48 | 84 | 48 | 1,097,335 | 1.8 | 28 | 60 | 30 | 7,391,918 |
| IIR | G052 | 0.6 | 12 | 25 | 12 | 0.0 | 90 | 198 | 98 | −0.2 | 41 | 83 | 42 | −2.5 | 42 | 105 | 50 | 4.2 | 65 | 134 | 70 | 1,098,270 | 3.0 | 44 | 109 | 52 | 7,038,834 |
| IIR | G053 | 0.0 | 13 | 28 | 14 | 2.6 | 114 | 254 | 126 | 0.6 | 51 | 105 | 53 | 1.9 | 49 | 142 | 65 | −1.4 | 78 | 179 | 89 | 1,098,471 | −1.6 | 52 | 144 | 66 | 7,290,358 |
| IIR | G054 | −0.3 | 13 | 26 | 14 | 6.6 | 93 | 204 | 101 | 1.5 | 50 | 96 | 50 | −2.9 | 26 | 70 | 36 | 3.6 | 51 | 103 | 57 | 844,431 | 3.5 | 30 | 76 | 39 | 5,909,974 |
| IIR | G055 | −0.3 | 12 | 25 | 13 | −3.6 | 94 | 203 | 101 | −0.1 | 40 | 81 | 41 | 1.3 | 21 | 44 | 22 | −2.5 | 45 | 77 | 44 | 1,098,372 | −1.2 | 25 | 53 | 26 | 7,146,200 |
| IIR | G056 | −0.3 | 13 | 25 | 13 | −8.1 | 81 | 174 | 87 | −0.3 | 42 | 83 | 43 | −2.0 | 22 | 46 | 23 | 3.5 | 43 | 74 | 42 | 1,098,440 | 2.8 | 25 | 54 | 27 | 7,302,290 |
| IIR | G057 | 0.2 | 15 | 29 | 15 | 14.8 | 118 | 265 | 130 | −0.2 | 46 | 93 | 47 | 3.3 | 41 | 115 | 56 | −9.1 | 71 | 156 | 80 | 1,098,204 | −2.6 | 44 | 122 | 59 | 6,966,483 |
| IIR | G058 | 0.2 | 15 | 28 | 15 | 9.3 | 97 | 212 | 106 | −0.3 | 38 | 76 | 39 | −2.8 | 24 | 50 | 26 | 6.1 | 48 | 84 | 48 | 1,098,471 | 3.6 | 28 | 60 | 31 | 7,377,606 |
| IIR | G059 | 0.0 | 11 | 23 | 11 | −4.1 | 83 | 179 | 90 | −0.8 | 47 | 89 | 46 | −0.4 | 24 | 54 | 26 | 0.8 | 47 | 83 | 47 | 1,098,801 | 1.8 | 28 | 62 | 30 | 7,516,062 |
| IIR | G060 | 1.2 | 12 | 24 | 12 | −10.5 | 85 | 181 | 89 | 0.5 | 45 | 89 | 45 | 0.2 | 22 | 46 | 23 | 1.8 | 45 | 77 | 44 | 1,064,220 | 0.6 | 26 | 55 | 27 | 7,109,733 |
| IIR | G061 | −0.6 | 11 | 23 | 11 | 15.4 | 85 | 194 | 94 | 0.8 | 43 | 83 | 43 | −2.0 | 25 | 56 | 30 | 2.6 | 49 | 88 | 50 | 1,098,004 | 2.4 | 29 | 64 | 33 | 7,292,988 |
| IIF | G062 | −0.5 | 18 | 36 | 18 | 5.6 | 92 | 201 | 103 | −0.3 | 38 | 75 | 38 | 0.7 | 21 | 46 | 23 | −1.5 | 51 | 90 | 51 | 1,029,880 | −0.5 | 31 | 67 | 33 | 7,452,310 |
| IIF | G063 | 0.9 | 16 | 33 | 16 | −25.8 | 102 | 223 | 108 | 0.2 | 45 | 84 | 44 | 0.5 | 25 | 64 | 32 | 1.0 | 55 | 105 | 58 | 909,943 | 0.5 | 34 | 80 | 40 | 5,988,329 |
| IIF | G064 | 0.0 | 16 | 32 | 17 | 21.9 | 81 | 183 | 92 | 0.1 | 34 | 70 | 35 | 1.8 | 23 | 50 | 27 | −2.4 | 49 | 89 | 51 | 636,049 | −1.9 | 31 | 67 | 35 | 4,251,589 |
| IIF | G065 | −0.2 | 23 | 47 | 24 | 8.9 | 105 | 236 | 117 | −0.2 | 36 | 71 | 36 | 0.3 | 112 | 234 | 115 | 0.9 | 140 | 267 | 139 | 798,327 | −1.2 | 115 | 240 | 118 | 5,375,499 |
| IIF | G066 | 0.4 | 16 | 31 | 16 | −11.9 | 87 | 189 | 98 | −0.3 | 35 | 71 | 36 | 1.1 | 20 | 42 | 21 | −0.7 | 48 | 83 | 48 | 734,798 | −0.3 | 30 | 62 | 32 | 4,952,788 |
| IIF | G067 | 0.6 | 17 | 36 | 18 | 0.1 | 94 | 216 | 107 | −0.1 | 37 | 76 | 38 | 3.3 | 23 | 50 | 24 | −3.5 | 52 | 94 | 52 | 633,047 | −1.8 | 32 | 69 | 34 | 4,037,496 |
| IIF | G068 | 0.6 | 15 | 33 | 16 | 7.3 | 80 | 182 | 91 | 0.5 | 34 | 68 | 35 | −1.0 | 22 | 52 | 27 | 2.8 | 47 | 89 | 50 | 604,580 | 2.2 | 30 | 66 | 34 | 3,923,233 |
| IIF | G069 | 0.8 | 17 | 37 | 19 | −4.0 | 94 | 214 | 110 | −0.1 | 37 | 75 | 38 | −6.5 | 32 | 78 | 37 | 10.8 | 61 | 112 | 62 | 579,700 | 9.2 | 40 | 90 | 44 | 3,850,647 |
| IIF | G070 | 0.5 | 14 | 33 | 17 | −2.9 | 92 | 215 | 108 | 0.5 | 36 | 74 | 37 | −2.4 | 21 | 47 | 25 | 5.2 | 48 | 93 | 52 | 449,579 | 3.2 | 29 | 66 | 35 | 3,162,919 |
| IIF | G071 | −0.7 | 19 | 38 | 19 | 10.5 | 96 | 213 | 108 | 0.4 | 39 | 79 | 40 | −0.7 | 24 | 53 | 26 | 0.5 | 56 | 97 | 56 | 542,495 | 0.4 | 35 | 74 | 38 | 3,473,748 |
| IIF | G072 | 1.2 | 22 | 44 | 22 | −34.2 | 112 | 246 | 119 | −0.1 | 46 | 87 | 46 | 0.5 | 93 | 201 | 98 | 1.3 | 123 | 238 | 124 | 509,746 | 1.5 | 96 | 209 | 101 | 3,231,799 |
| IIF | G073 | 0.2 | 14 | 31 | 16 | −5.3 | 90 | 204 | 105 | 0.5 | 50 | 95 | 49 | −9.4 | 24 | 56 | 25 | 15.3 | 53 | 95 | 52 | 475,901 | 10.6 | 33 | 71 | 34 | 3,211,411 |
| IIA | ALL | −1.9 | 24 | 61 | 30 | 7.3 | 118 | 277 | 136 | −0.2 | 42 | 91 | 45 | 0.5 | 99 | 242 | 113 | −0.9 | 126 | 269 | 134 | 5,141,098 | −2.4 | 96 | 234 | 110 | 34,299,106 |
| IIR | ALL | 0.2 | 13 | 26 | 13 | −1.6 | 93 | 206 | 102 | 0.1 | 45 | 90 | 46 | −0.6 | 31 | 93 | 46 | 1.2 | 55 | 124 | 65 | 20,574,260 | 1.5 | 35 | 97 | 48 | 136,558,090 |
| IIF | ALL | 0.3 | 17 | 37 | 19 | −2.4 | 94 | 211 | 107 | 0.0 | 39 | 78 | 39 | −0.6 | 29 | 113 | 51 | 1.8 | 59 | 148 | 73 | 7,904,045 | 1.3 | 38 | 120 | 56 | 52,911,768 |
| ALL | ALL | −0.1 | 15 | 35 | 18 | −0.4 | 96 | 219 | 109 | 0.1 | 43 | 87 | 44 | −0.4 | 36 | 141 | 62 | 1.1 | 63 | 172 | 81 | 33,619,403 | 0.8 | 41 | 141 | 63 | 223,768,964 |
| Events Found with Space Approach Using NTE = 39.78 m | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| YYDOY | SVN | PRN | Start Time | Duration (min) | Anomaly | WC URE (m) | SISA (m) | ||
| Type | Value (m) | ||||||||
| 17066 | E206 | 30 | 07 March 2017 | 03:15 | 40 | clock | 340.9 | 341.9 | 3.12 |
| 17157 | E203 | 26 | 06 June 2017 | 05:50 | 1085 | clock | 491.3 | 491.9 | 3.12 |
| 17158 | 07 June 2017 | 00:00 | 430 | clock | 460.4 | 472.8 | 3.12 | ||
| 19302 | E101 | 11 | 29 October 2019 | 18.10 | 30 | clock | 431.9 | 432.1 | 3.12 |
| Year | Number Satellite Fault Events | Faults Duration (h) | Total Signal Valid Hours | ||||
|---|---|---|---|---|---|---|---|
| IOV | FOC | Total | IOV | FOC | Total | ||
| 1 August 2017–31 December 2017 | 0 | 0 | 0 | 0 | 0 | 0 | 0.54 × 105 |
| Full 2017 | 0 | 2 | 2 | 0 | 25.9 | 25.9 | 1.12 × 105 |
| Full 2018 | 0 | 0 | 0 | 0 | 0 | 0 | 1.34 × 105 |
| Full 2019 | 1 | 0 | 1 | 0.5 | 0 | 0.5 | 1.76 × 105 |
| 1 January 2020–31 July 2020 | 0 | 0 | 0 | 0 | 0 | 0 | 1.07 × 105 |
| Years | Total Satellite Fault Events | Total Valid (h) | Estimated Mean Fault Rate | Average Fault Duration | MTTN (h) | Psat (/sat) | ||
|---|---|---|---|---|---|---|---|---|
| IOV | FOC | Total | (/sat/h) | (h) | ||||
| 1 January 2017–31 July 2020 | 1 | 2 | 3 | 5.28 × 105 | 6.6 × 10−6 | 8.81 | 8.81 | 5.8 × 10−5 |
| 1 August 2017–31 July 2020 | 1 | 0 | 1 | 4.70 × 105 | 3.2 × 10−6 | 0.50 | 1.00 | 3.2 × 10−6 |
| Years | Total Satellite Fault Events | Total Valid (h) | Estimated Mean Fault Rate | Average Fault Duration | MTTN (h) | Psat (/sat) | ||
|---|---|---|---|---|---|---|---|---|
| IOV | FOC | Total | (/sat/h) | (h) | ||||
| 1 January 2017–31 July 2020 | 2 | 2 | 4 | 5.28 × 105 | 8.5 × 10−6 | 9.13 | 9.13 | 7.8 × 10−5 |
| 1 August 2017–31 July 2020 | 2 | 0 | 2 | 4.70 × 105 | 5.3 × 10−6 | 0.42 | 1.00 | 5.3 × 10−6 |
| Date | SVN | PRN | Extrapolated to FOC | |
|---|---|---|---|---|
| Exposure Time (min) | WC URE (m) | |||
| 6 June 2017 | E203 | 26 | 50 | >40 |
| 29 October 2019 | E101 | 11 | 35 | >40 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alonso, M.T.; Sanz, J.; Juan, J.M.; Rovira García, A.; Casado, G.G. Galileo Broadcast Ephemeris and Clock Errors Analysis: 1 January 2017 to 31 July 2020. Sensors 2020, 20, 6832. https://doi.org/10.3390/s20236832
Alonso MT, Sanz J, Juan JM, Rovira García A, Casado GG. Galileo Broadcast Ephemeris and Clock Errors Analysis: 1 January 2017 to 31 July 2020. Sensors. 2020; 20(23):6832. https://doi.org/10.3390/s20236832
Chicago/Turabian StyleAlonso, María Teresa, Jaume Sanz, José Miguel Juan, Adrià Rovira García, and Guillermo González Casado. 2020. "Galileo Broadcast Ephemeris and Clock Errors Analysis: 1 January 2017 to 31 July 2020" Sensors 20, no. 23: 6832. https://doi.org/10.3390/s20236832
APA StyleAlonso, M. T., Sanz, J., Juan, J. M., Rovira García, A., & Casado, G. G. (2020). Galileo Broadcast Ephemeris and Clock Errors Analysis: 1 January 2017 to 31 July 2020. Sensors, 20(23), 6832. https://doi.org/10.3390/s20236832







