1. Introduction
Industrial processes show some characteristics that make difficult their regulation, for instance multivariable interactions between controlled and manipulated variables, non-measurable state variables, non-measurable disturbances, uncertain and time-varying parameters, restrictions in manipulated variables and nonlinearities, among others [
1,
2,
3]. Modern control strategies involve the use of compensators that comprise a state feedback and an observer [
4]. Observers are used to reconstruct the unmeasured state variables, since they are either unmeasurable (e.g., when they have no physical sense) or there is no technical and/or economical viability to use high-priced sensors, from the input–output behavior [
5,
6].
State observers and soft sensors are being used more often nowadays in control systems to achieve different objectives in several industries. For instance, Liu [
7] presented a robust adaptive observer for multiple-input multiple-output nonlinear systems with unknown parameters, uncertain nonlinearities, disturbances and unmodeled dynamics; Ciccio et al. [
8] proposed a new nonlinear observer-based controller for time-delay nonlinear systems; Fernandes et al. [
9] proposed a motion control system for a underwater vehicle using a MIMO PID controller aided by a high-gain observer; Turki et al. [
10] developed a backstepping control for a tank process based on adaptive observers; Aguilar-Garnica et al. [
11] designed and applied a reset observer in order to provide on-line estimation of the concentration of Free Fatty Acids from temperature measurements within a continuous stirred tank reactor; Eleiwi and Laleg-Kirati [
12] presented a nonlinear observer-based Lyapunov control for a membrane distillation process; Kleindienst et al. [
13] used the measurement of temperature at one single point of a silicon wafer to estimate the remaining wafer temperature profile using a state observer; and Lisci et al. [
14] developed a geometric observer to design a model-based soft sensor for the estimation of quality indexes in a bioreactor. Sheng et al. [
15] went further and showed how smart soft sensors can be combined with machine learning techniques to significantly save human resources and improve performance under complex industrial conditions. Although there are several estimation techniques, as stated in [
16], it is difficult to select the proper one for specific applications; hence, the authors performed a review of observers recently used in process control and classified them into six classes.
Several studies for control systems have been performed using tanks because of their reconfiguration possibilities and easiness to visualize variables [
17,
18]. Hou et al. [
19] provided a method for designing nonlinear state observers that can be used to design observers for models of induction motors and three-tank systems. Hou et al. [
20] performed the observability analysis and observer synthesis for a three-tank water process taking into account singularities of nonlinear observers. Pan et al. [
21] addressed the nonlinear control design problem for a state-coupled two-tank liquid level system. Korbicz and Witczak [
22] designed a bank of extended unknown input observers for fault diagnosis of a two-tank system. Zhou et al. [
23] designed three receding horizon predictive control strategies for a three-tank system based on the structural characteristics of a hybrid pseudo-linear RBF-ARX model. Prajapati and Roy [
24] used unknown input observers for fault detection and isolation in a three-coupled tank system. Li et al. [
25] proposed and evaluated an energy-efficient data transmission scheme for remote state estimation in a two-tank system. More recently, Arasu and Prakash [
26] designed and implemented predictor-corrector based control schemes for a single input-single output nonlinear lab-scale conical tank system. Patel and Shah [
27] developed a fault-tolerant controller for nonlinear systems that was implemented and validated on a computer model of a three interconnected conical tank system. Zhao and Zhang [
28] proposed an inverse tangent functional nonlinear feedback control and carried out a case study related to the water tank level control system. Most of the referenced works rely on two types of tanks: cascade tanks, where the input flow goes into the first tank, and the level of each tank depends on the level of the previous tank, such as the benchmark quadruple tank system [
29,
30,
31], and interacting tanks, where the input flow additionally depends on the current level [
32,
33].
High-gain observers have been considered to estimate the state in processes with nonlinear dynamics because they have robust estimation properties and disturbance rejection capabilities [
34,
35,
36,
37,
38]. Regarding process control using HGOs, some works have been reported in literature. For instance, Lafont et al. [
39] designed an adaptive high-gain observer for wastewater treatment systems. Turki et al. [
40] introduced an output-feedback control scheme that combines nonlinear backstepping control with an adaptive high-gain observer in a two-tank process. Banerjee and Jana [
41] synthesized an estimator-based hybrid control scheme that consists of a high gain nonlinear observer and the extended generic model controller and tested it in reactive distillation column. Gouta et al. [
42] reported the nonlinear control design for a state coupled two-tank liquid level system which combines a nonlinear generalized predictive controller with a high-gain observer. Ayadi et al. [
43] implemented a high-gain observer which provides a full state estimation (position, velocity, temperatures and pressures) in an electropneumatic system. Wang et al. [
44] proposed a sliding-mode dynamic surface control strategy based on a high-gain observer for glue mixing and dosing control in the particleboard process.
Although some reported works in the literature about observer design show plant tests in fixed lab rigs, just a few provide either the complete observability analysis or the use of robust industrial instruments. This work addresses the complete observability analysis, in the Herman–Krener sense, for a three-tank process that combines tanks in series, interaction and nonlinear weirs and the design and implementation of a high-gain observer that guarantees convergence of the state estimation. The validation and comparison to the Extended Kalman Filter, of this observer, was performed using both simulations and real tests in a multipurpose experimental station that uses industrial instrumentation and provides flexibility to change dynamics and nonlinear behavior, as briefly addressed in [
18].
The organization of the paper is as follows. In
Section 2, the plant is described and a state–space model is analyzed.
Section 3 shows the observability analysis of the set-up using the notions in [
45].
Section 4 contains the design of the high-gain observer. Numerical simulations are provided in
Section 5. The experimental results for the multipurpose station are presented in
Section 6. Finally, conclusions are presented in
Section 7.
2. Process Modeling
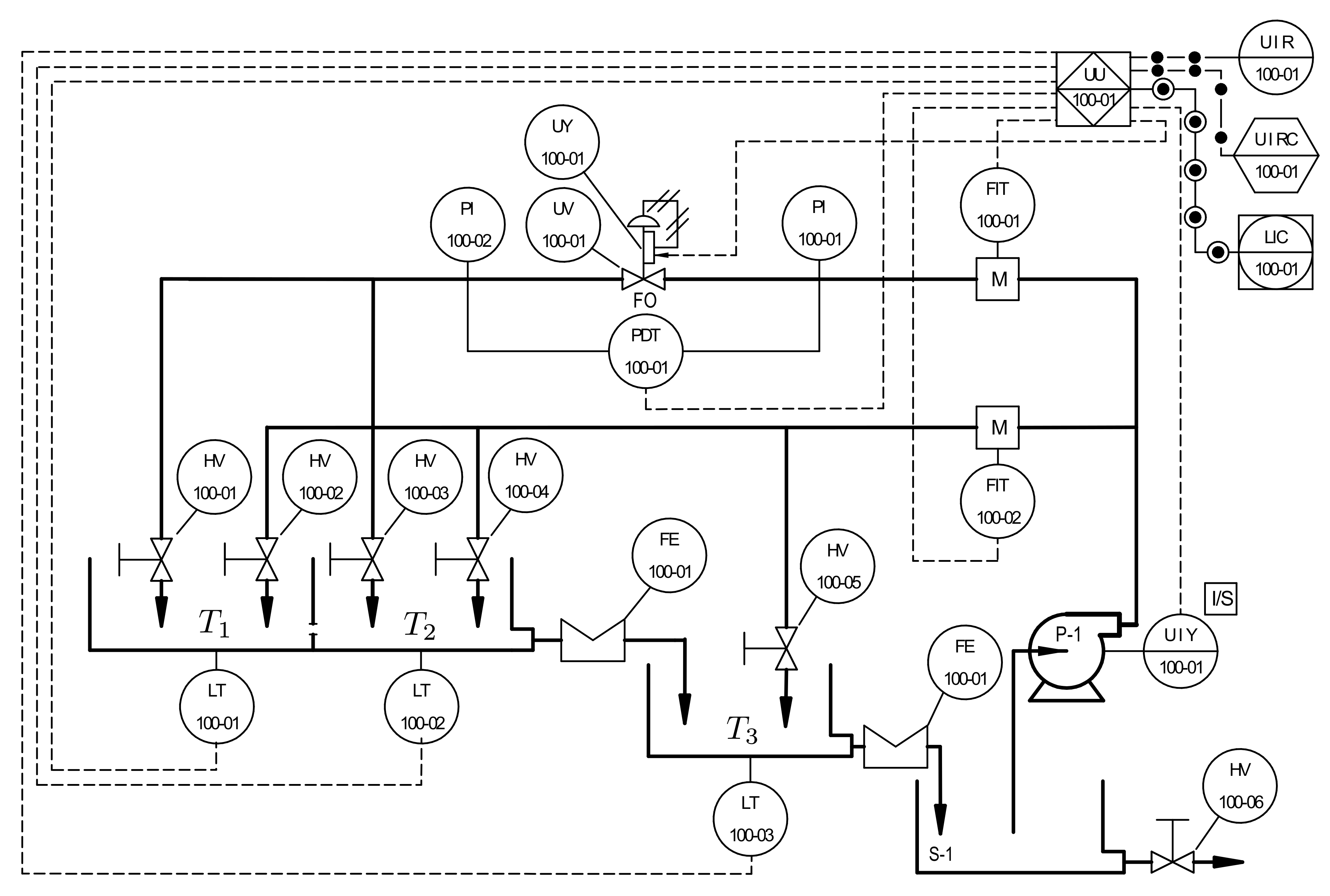
As addressed in [
18], the process comprises three tanks arranged as shown in
Figure 1. The system consists of three tanks,
,
, and
, and each tank is equipped with a real level transmitter (LT). The two interacting Tanks
and
are connected in series with the third Tank
. An electrical pump (P-1) is used to provide water supply into the system through two different branches, namely main and secondary, and, to measure the flow through the branches, each branch is equipped with an electromagnetic flow transmitter (FIT). Flow regulation in the main branch is achieved with the help of a control valve (UV-UY), which allows the manipulation of input flow to Tank
. Using a manual valve (HV) located in the secondary branch, disturbances to the system are injected at Tank
. In this paper, the input to the system is the flow regulated by the control valve, whereas the output of the system is the level in Tank
(see [
46,
47,
48] for further details about the process).
The mathematical model can be obtained performing a mass balance in each tank, which is given by [
18]
where
and
are the input and output mass flows, respectively, and
denotes the accumulation of mass in the tank. Assuming environment conditions, the density of water (the fluid process) is constant; therefore, Equation (
1) becomes
where
and
are the input and output volumetric flows, respectively,
A is the cross-section area and
is the level variation in that tank.
Applying Equation (
2) for Tanks
,
, and
yields
with
the input flow to Tank
and
the output flow from Tank
,
, where
and
are the cross-section areas and water levels of Tank
,
, respectively, and
is the coupling orifice constant. In Equation (
3),
is the absolute value function and
is the sign function, that is,
and
The output flow from Tank
to Tank
can be chosen according to the sharp crested weir type. The general formula for the weir [
49] can be written as
where
is the coefficient of the weir for Tank
and
is the distance from the bottom of the tank to the crest of the weir in Tank
;
is the order of the weir, which depends on the shape; and
is the Heaviside step function, that is,
In addition, since the zeros of the sensors can be calibrated to match the lower boundary of each weir and the working space is always above this level, for each
, Equation (
4) can be written as
.
To get a state–space realization of the system, let us define the state vector as
and define the function
as
. The water level in the three tanks is non-negative, i.e.,
,
. Then, the state–space representation of the plant is given by
where the state vector
and the scalar input
is the input flow, i.e.,
. The drift and control vector fields are given by
with
,
and
is given by
where
,
, is the
ith column of the
identity matrix
. The output function is linear, that is,
with
. In addition, recall that
,
,
,
,
,
,
and
are all known, nonzero positive constants and hence
A and
K are nonsingular matrices. Consequently, from Equation (
6), the equilibrium points are given by those points where
vanishes, that is,
; from Equation (
8) it follows that
.
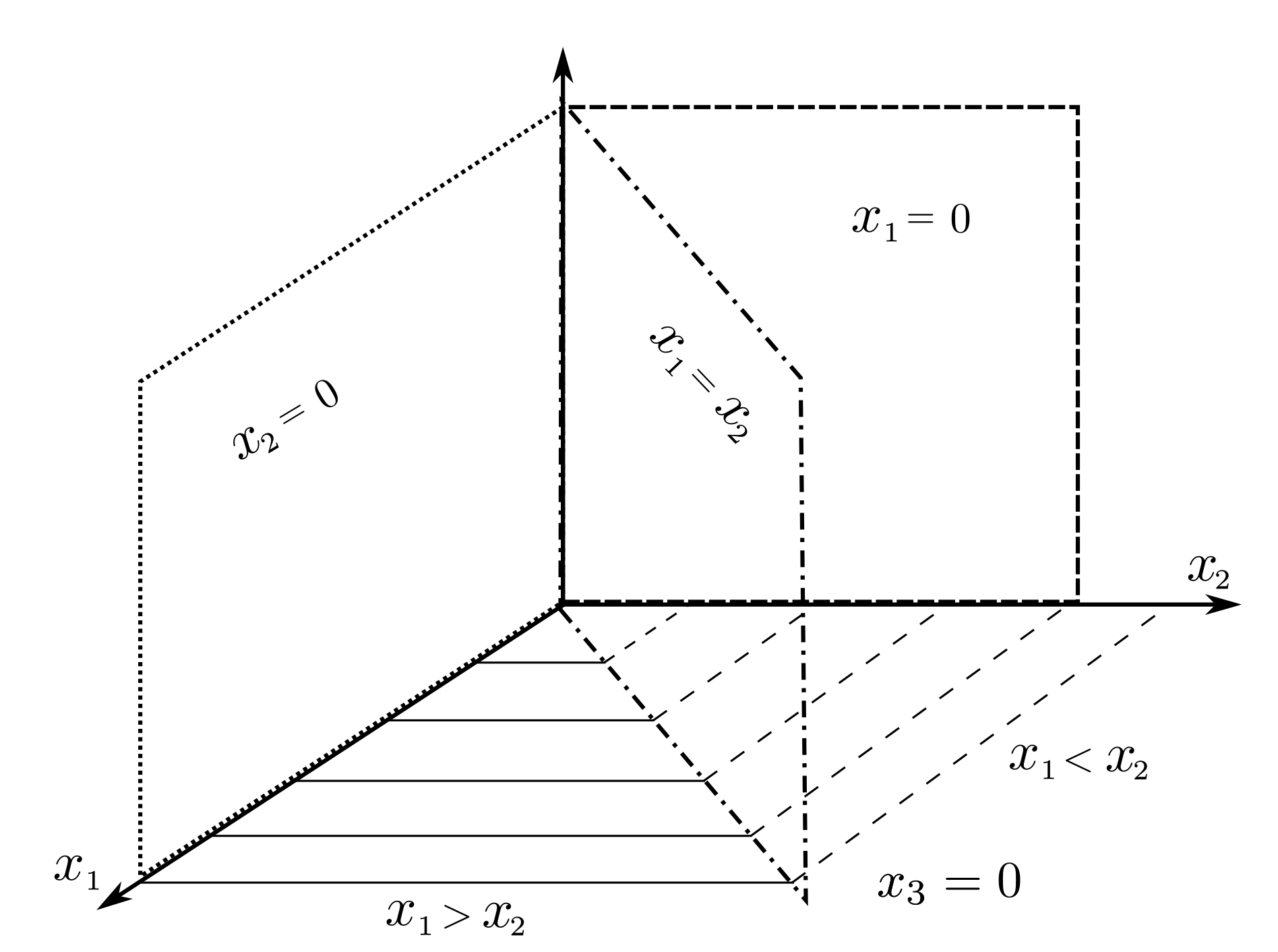
From
Figure 1, it can be noticed that the level in the third tank only depends on the output flow of the second Tank
. Therefore, the complete system can be seen as the interconnection of two systems in cascade: two interacting tanks and the lower tank. Hence, the phase portrait is used in order to analyze the behaviour of the two interacting Tanks
and
. To this end,
,
, and
. Referring to
Figure 2,
and
, respectively, denote regions where the level in
is greater than that of
, the level in
is lower than in
and the levels in Tanks
and
are equal.
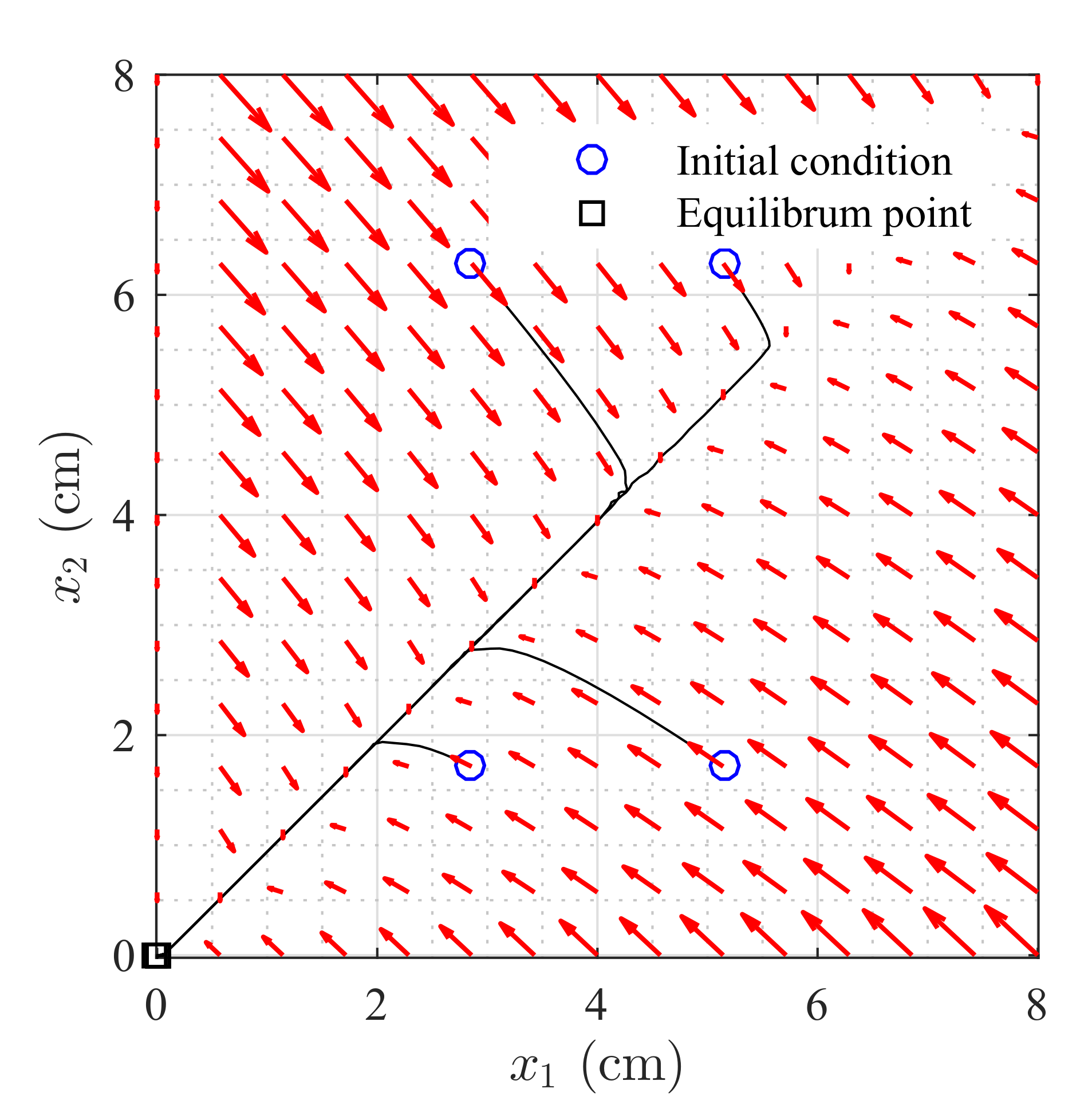
Figure 3 shows the phase portrait of the levels in Tanks
and
without the input. As it is shown, trajectories starting from different initial conditions in the regions
and
approach the equilibrium point (origin). Nevertheless, this depends on the value of
, since a large value correspond to almost zero restriction between the two tanks, transforming the two tanks into a single one.
3. Observability Analysis
Consider a general nonlinear system
defined on
, where
is a smooth and complete vector field on
, the input vector
takes values in a compact subset
of
containing zero in its interior and the output function
has smooth components
.
Two states
are
indistinguishable for the system in Equation (
9) if, for every admissible input
, the solutions of Equation (
9) satisfying the initial conditions
and
produce identical output-time histories. In other words,
are indistinguishable for the system in Equation (
9), if and only if
for every
and input
, where
denotes the solution of the system in Equation (
9) at time
t for the initial condition
and the input
. Given
, let us denote
as the set of all points that are indistinguishable from
with respect to the system in Equation (
9).
The following definitions from [
45] are used. The system in Equation (
9) is
observable at if
, and it is
observable if
for every
. The system in Equation (
9) is
weakly observable at if
is an isolated point of
. The system in Equation (
9) is
weakly observable if it is weakly observable at every
. Clearly, observability implies weak observability.
The following assumptions are made:
Assumption 1. Let us assume that the plant operates in the region Assumption 2. The input flowis bounded (above and below), i.e.,and enters into the plant through Tank, whereis the maximum input flow.
The implications of Assumption 2 are the following. The maximum input flow
ensures no water overflow from the tanks, which is true since the plant was designed to avoid liquid overtopping the tank’s physical limit [
46,
47]. Additionally, water always flows from Tank
to Tank
and finally to Tank
. Then, it is assumed that there are no disturbances, i.e., the only water input into the system is located at the first tank. In addition, it ensures that the level in each tank is bounded, that is
,
, where
is the maximum level in the
ith tank.
Given
, let
denote the set of indistinguishable states from the initial condition
for the unactuated system in Equation (
9). Our next result characterizes this set.
Proposition 1. For the unactuated system in Equation (9),
for every.
Proof. First, observe that, in this case,
. Consider
and let
be such that
. Then,
for all
, which implies that
. Now,
for all
also implies that
, where
is the Lie-derivative of the function
h along the vector field
. Recall that
, where ∇ is the gradient operator. Using this, we have
Hence,
yields
Since , the last equation implies that , and substituting immediately implies that .
Next,
yields
Since
and
, the last equation becomes
Simplifying yields . This implies that , and hence . Thus, it has been shown that implies that . In other words, . This completes the proof. □
Proposition 1 implies that the unactuated system in Equation (
9) is observable in the Herman–Krener sense. Given
, let
denote the set of indistinguishable states from the initial condition
for the actuated system in Equation (
9). Clearly,
. Consequently,
, and hence the actuated system in Equation (
9) is also observable in the sense of Herman–Krener. Thus, it has been shown that the three-tank system with the knowledge of the input and the water level in Tank
is observable in the sense of Herman–Krener. A high-gain observer is proposed in the following section.
4. Observer Design
Consider the nonlinear system of the form
where
denotes the state vector,
is the input vector,
is the output vector,
and
is of the form
which is a globally Lipschitz nonlinear function that contains the nonlinearities of the system.
Consider
and let
be such that the matrix
is Hurwitz. Referring to Besançon [
50], for the system in Equation (
10), the observer is given by
where
. This form of observer is called
high-gain observer (HGO), and it has good robust estimation properties and disturbance rejection capabilities [
51]. The idea is to use a high-gain constant in order to generate a fast response in the observer and reduce the effect of the nonlinear error. Nevertheless, due to the high gain, the observer is very sensitive to noise and the transient response, when the estimation is far from the true value, can cause peaks in the prediction. However, this drawback can be solved by filtering the output signal or introducing a saturation function in the feedback control law [
52,
53], making them a good solution for state estimation.
To obtain an observer of the form of Equation (
11), the system in Equation (
5) must be transformed into its observability canonical form. According to Besançon [
54], any control affine system satisfying the observability rank condition can be turned into the form Equation (
10) using a diffeomorphism
given by
where
, with
.
Thus, the control affine system is related to its observability canonical form. To design an observer for the original plant and to avoid the inverse transformation of the observer obtained for the canonical form, it is recalled the definition of system equivalence used in [
50].
Definition 1. (System equivalence).For each,
consider the systemsdefined onwith input,
outputand’s
are smooth vector fields.
The two systemsandare (state–space) equivalent
if there exists a diffeomorphism such that .
In other words, if
is a trajectory of
, then
is a trajectory of
, that is,
Consider the systems
and
and suppose
is an observer for the system
. Then,
is an observer for the system
. Using the concept of system equivalence and by transforming the system into its observability canonical form, a HGO is proposed for the three-tank system.
Proposition 2. Consider the three-tank system in Equation (5) and suppose that Assumption 1 holds. Definewithand letbe such thatis Hurwitz. Then is an asymptotic observer for the system in Equation (5), where Proof. To check the observability rank condition, the Jacobian matrix of
must be full rank. The Jacobian is given by
where
Thus, is nonsingular if and only if , which is true if and only if . Under Assumption 1, it now follows that the Jacobian has full rank.
Applying the diffeomorphism
to the observer in Equation (
12) yields
where
and
. According to Besançon [
54],
where
is Lipschitz with respect to
, that is, there exists a
such that
for all
, and
Using Equation (
14) in Equation (
13) yields
Next, define
. Then, the error dynamics is given by
where
. Inspired by the work of Hann et al. [
55], the following Lyapunov function is defined
where
is such that
with
being the identity matrix of size
. This quadratic form was chosen in order to be positive definite and radially unbounded. Then,
Using Equation (
15) in Equation (
17) yields
while substituting Equation (
16) in the above yields
where
is the Euclidean norm in
. Since
is Lipschitz with respect to
, it follows that
and hence
By selecting , it follows that the . This completes the proof. □
5. Simulation Results
The first validation stage of the HGO was performed with simulations for full-state estimation in system. Such simulations were carried out using MATLAB
®, which is a high-performance language developed by MathWorks
®. To get similar behavior to the real plant, a sample period of
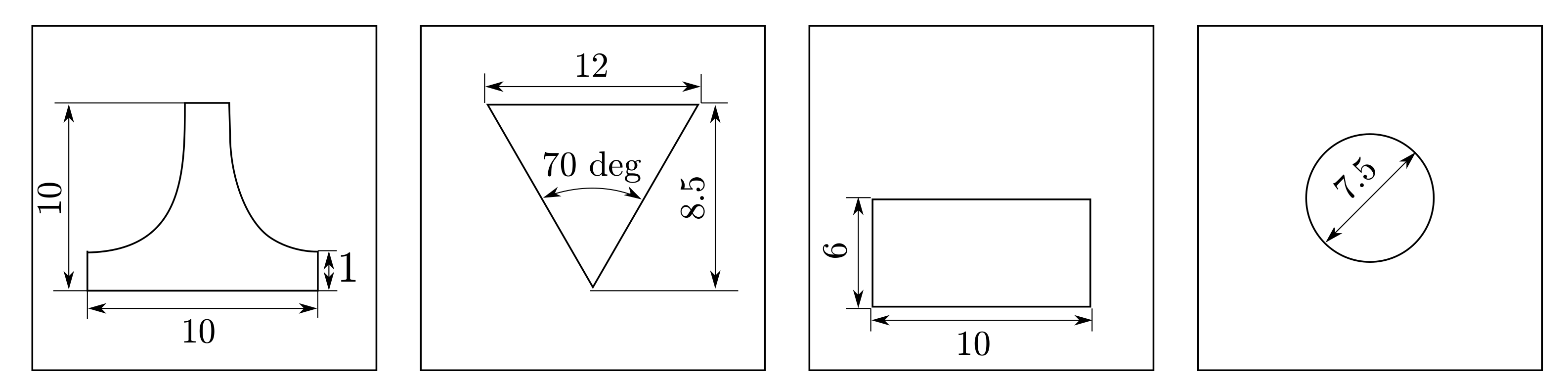
was selected. Different nonlinearities were tested by selecting different kind of weirs that are available for the configuration of the plant: linear, v-notch, rectangular and circular (see
Figure 4).
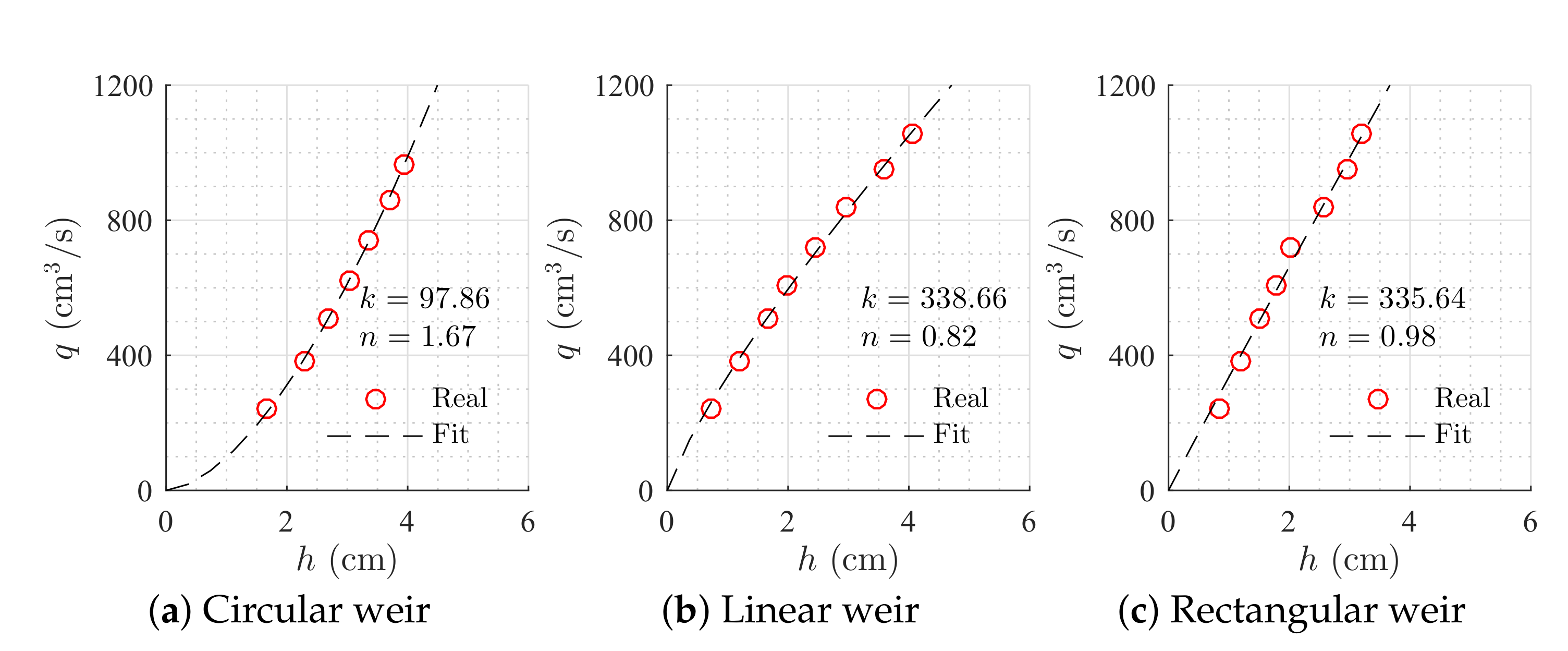
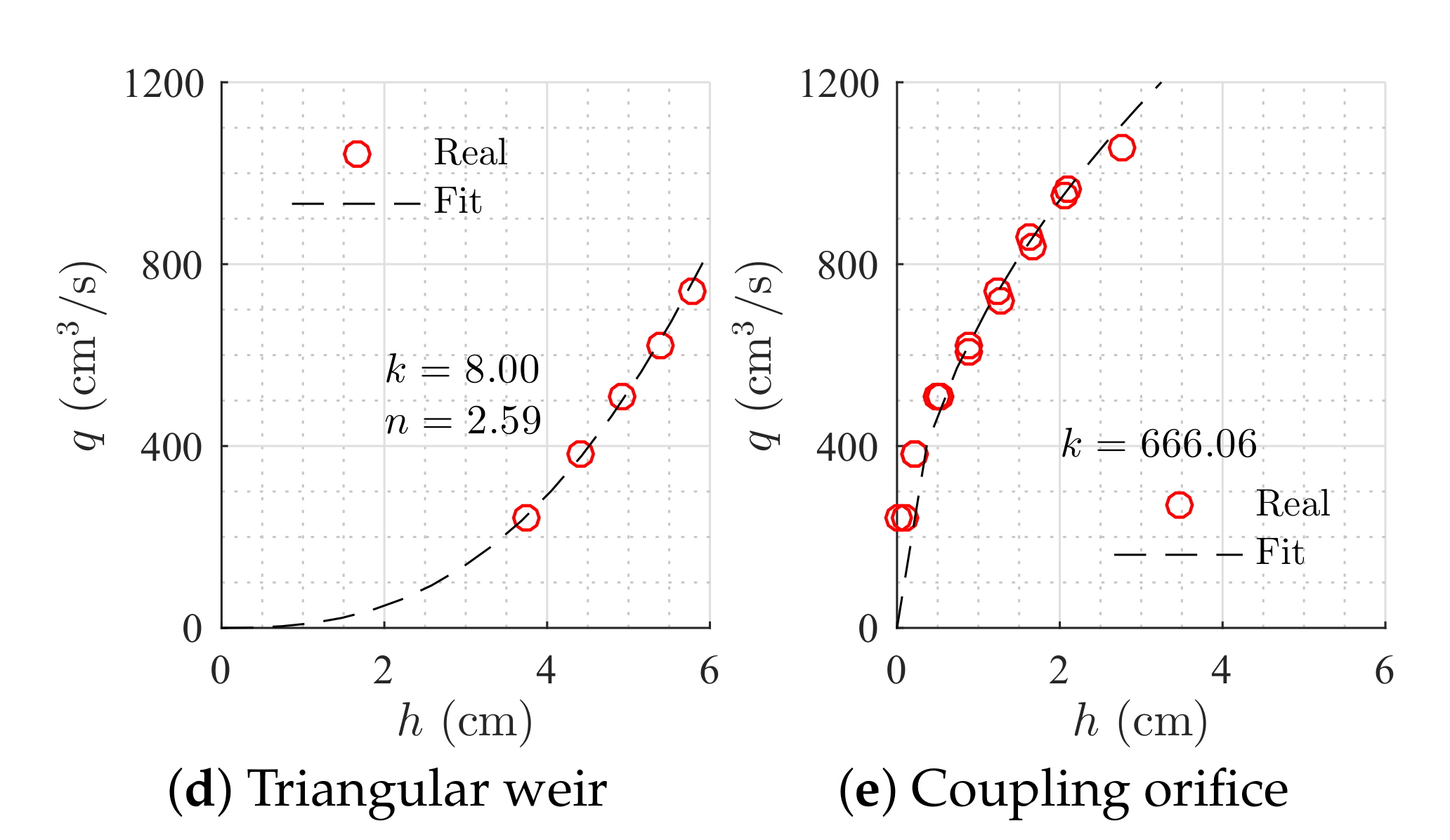
Constant parameters were obtained measuring tanks’ areas and performing an open-loop test to get the coefficient and the exponential of Equation (
4) for each weir (
Table 1 and
Table 2). The input flow was set to a constant value of
, and levels were measured for each steady-state condition. Then, the weirs’ parameters were computed using the MATLAB
® fitting toolbox,
Figure 5. For the simulation, sensor noise was implemented through a Gaussian distribution with
cm standard deviation. Additionally, a deviation of 5% in all the parameters of the system was taken into account.
Step inputs of 25% of the total flow capacity were simulated every 50s approximately. The gain was chosen such that is Hurwitz and as the high-gain observer parameter. Two different sets of weirs were used at the outputs of Tanks and . The first set comprised a rectangular weir in the upper tank and a linear in the lower, and the second set comprised a v-notch weir in the upper tank and a circular in the lower.
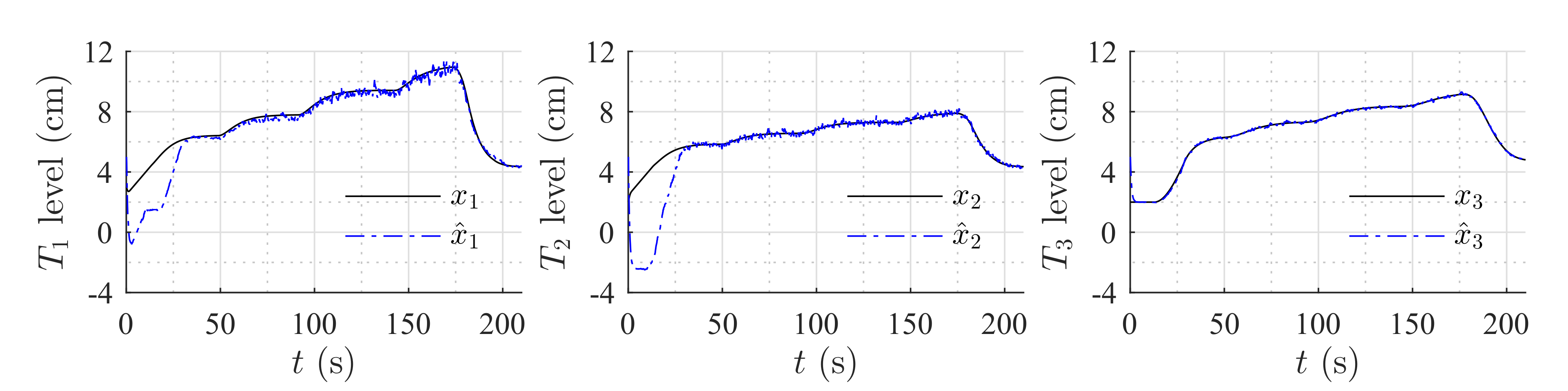
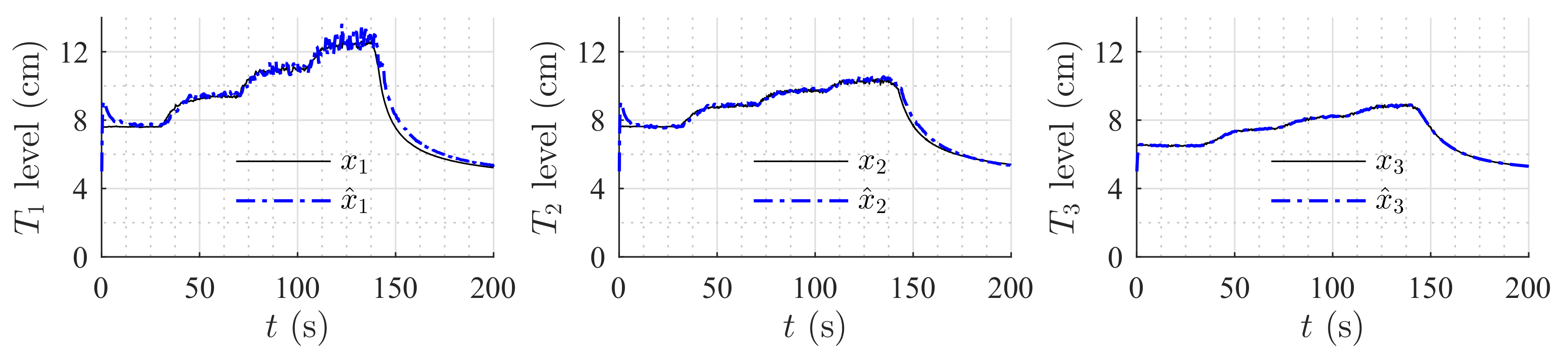
Figure 6 shows the estimation of the level in each tank for the first set of weirs.
Figure 7 shows the estimation of the level in each tank for the second set of weirs. The same parameters were used in both simulations, but the observer’s parameters changed according to the exponential and coefficient of each weir. The observer converges slowly to the desired value, since poles were placed near to the imaginary axis. In both simulations, level estimations are affected by noise, as expected for a HGO.
6. Experimental Results
The second stage of validation of the HGO was performed through full-state estimation in the real process. The experimental set-up is shown in
Figure 8. This three-tank system has different control technologies: PLC, industrial controller and PC with LabVIEW
®. In this case, the PLC controller was used as the DAQ system, and is connected through Ethernet to a LabVIEW
® interface [
48], in which the compensator (controller+observer) was implemented.
Since the real plant is a complete experimental station, all variables were measured with real sensors, as indicated in
Figure 1; hence, the state estimation can be compared to real measurements of the levels in all the tanks. The sample time for the PLC and LabVIEW
® program was set to
. As in simulations, step inputs of 25% of the total flow capacity were manually performed every 50
approximately. The gain
was again chosen such that
is Hurwitz and
as the high-gain observer parameter. Two different sets of weirs were used at the outputs of Tanks
and
. The first set comprised a rectangular weir in the upper tank and a linear in the lower, and the second set comprised a v-notch weir in the upper tank and a circular in the lower one.
6.1. High-Gain Observer Performance
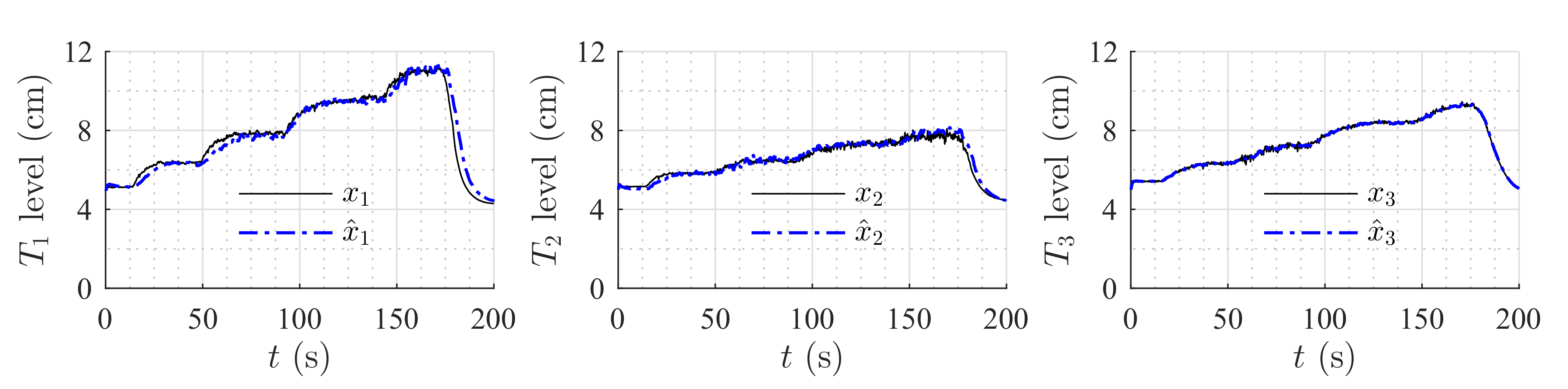
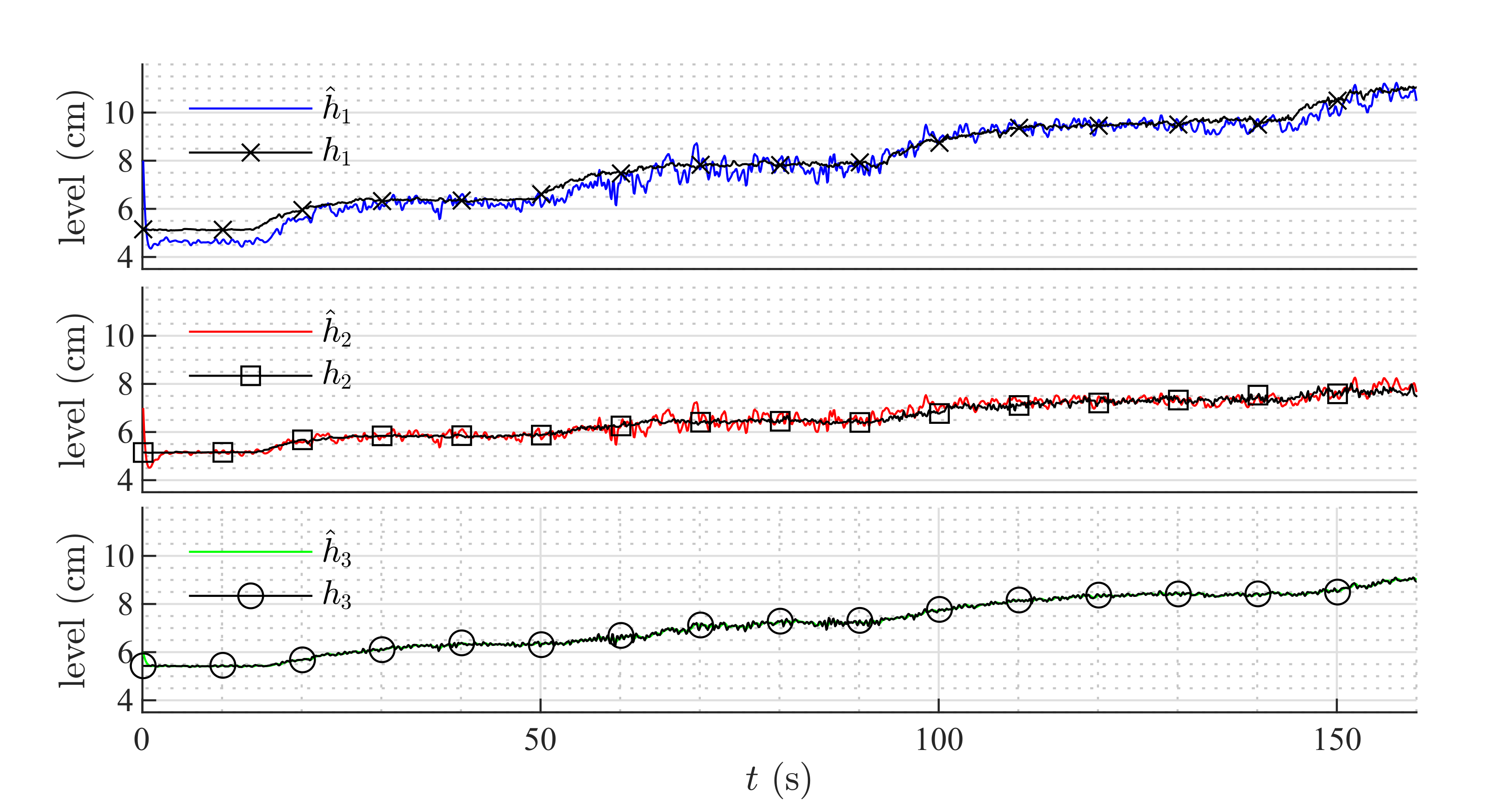
Figure 9 and
Figure 10 show the estimation of the level in each tank for the first and second set of weirs, respectively. As can be noticed, the observer converges to the measurements. In both experiments, level estimations are affected by noise, but the level estimation for Tank
, considered as the output (controlled variable) behaves very similar to the real measurement. Noise in the real process is mainly caused by the configuration of the system, in which several waves are produced by the input flow (see
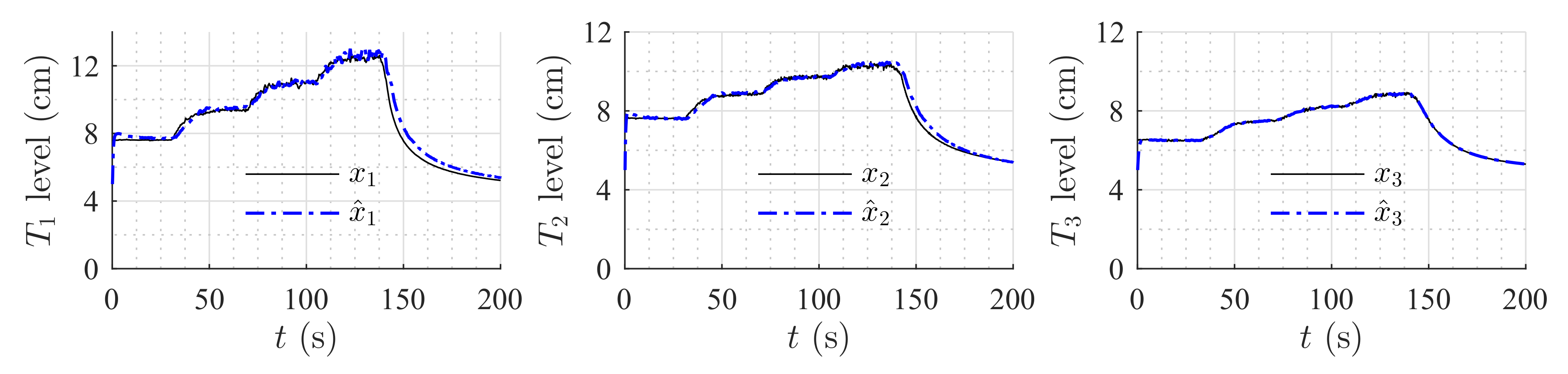
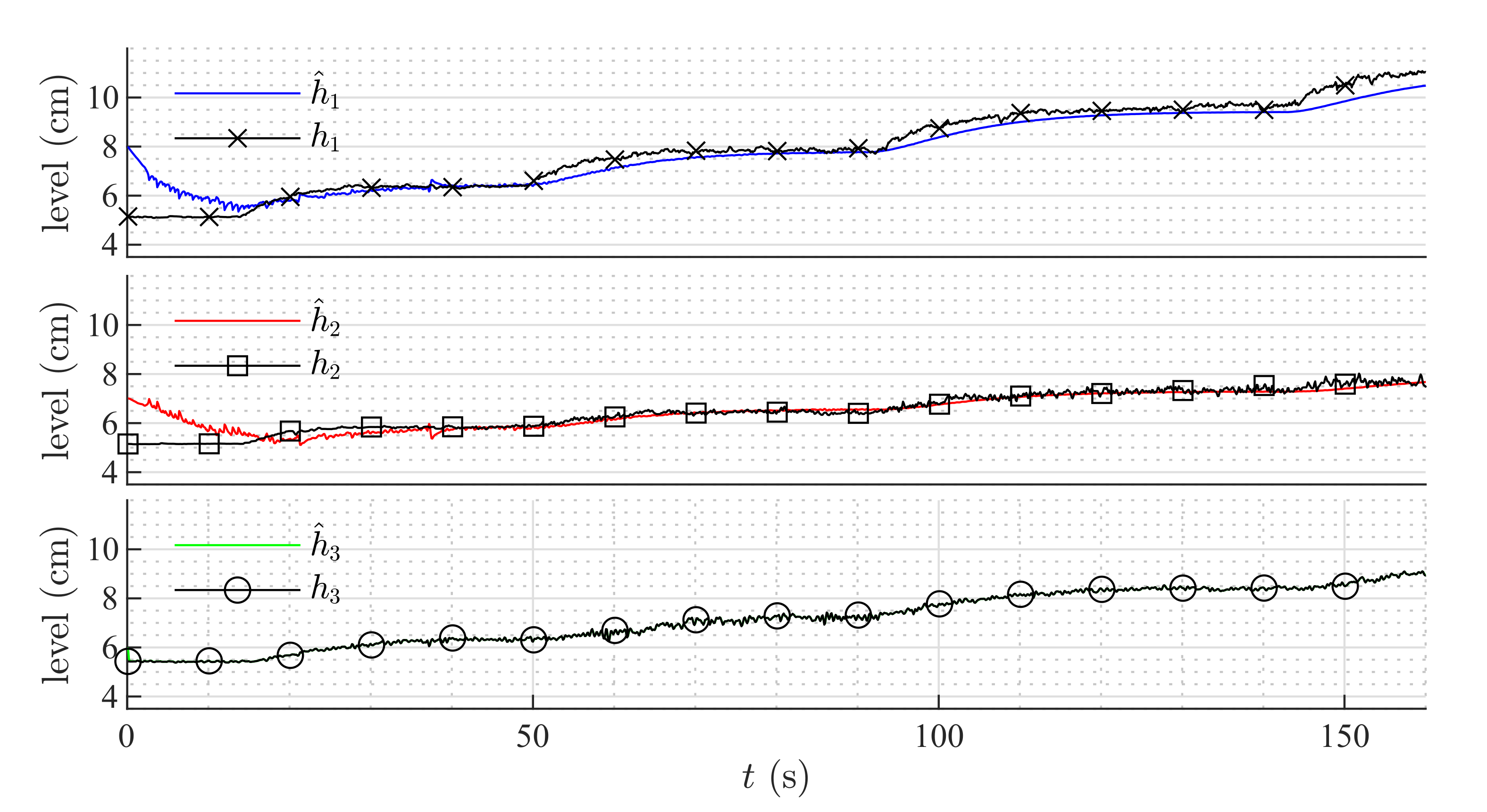
Figure 8). Two more experiments were conducted using an HGO with higher gain,
.
Figure 11 and
Figure 12 show how the state estimation is affected in a more noticeable way.
After , the system enters into an unobservable zone of the state space, and the estimation provided by the HGO diverges. This happens because the level in Tank goes below the minimum height of the weir, and, therefore, there is not flow from Tank to Tank . A faster observer response can be achieved by increasing the gain , which can result in a noisy estimation of the state, but it can still perform well when used in a complete compensator that includes the state feedback.
6.2. Robustness Analysis
To test the robustness of the observer, two different experiments were carried out. In the first experiment, a variation of 30% of all parameters was made (tanks areas and weir constants). In this scenario, the HGO was compared to the well-known Luenberger observer [
56] and the Extended Kalman Filter (EKF) [
57].
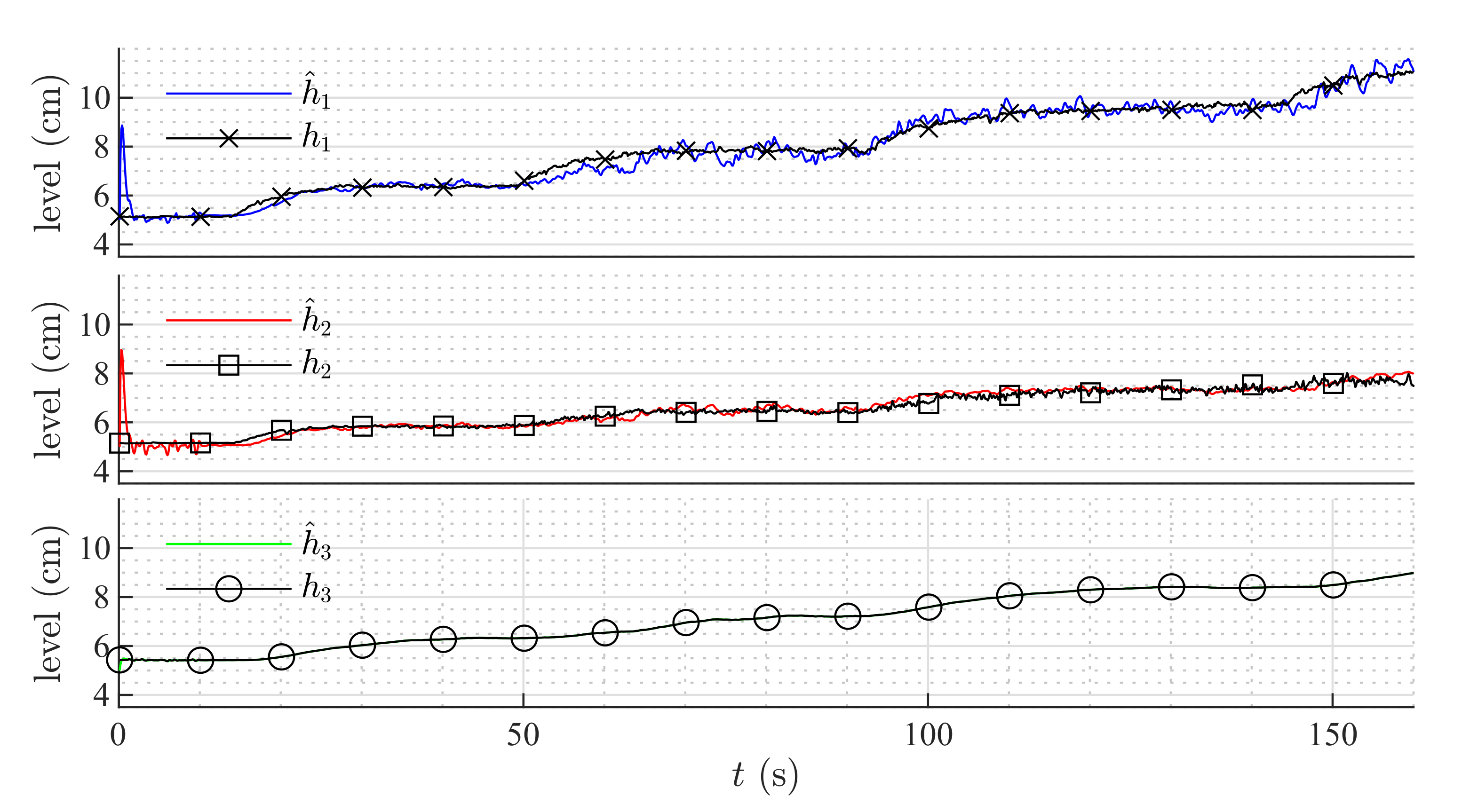
Table 3 shows the mean squared error for the three observers; as can be noticed, the HGO obtained the best performance in the real process for the complete range of the tank levels despite the 30% variation in the model parameters.
Figure 13,
Figure 14 and
Figure 15 show the estimation for all levels with each observer. The HGO shows better performance and robustness than the other two observers. For instance, it can be seen how, for the low-level section, the estimation provided by the HGO converges in less than 2 s while Luenberger and EKF estimations are deviated from the measurement and converge after more than 20 s. It is important to point out that asymptotic estimation has been proved for the HGO, which is not the case for the EKF.
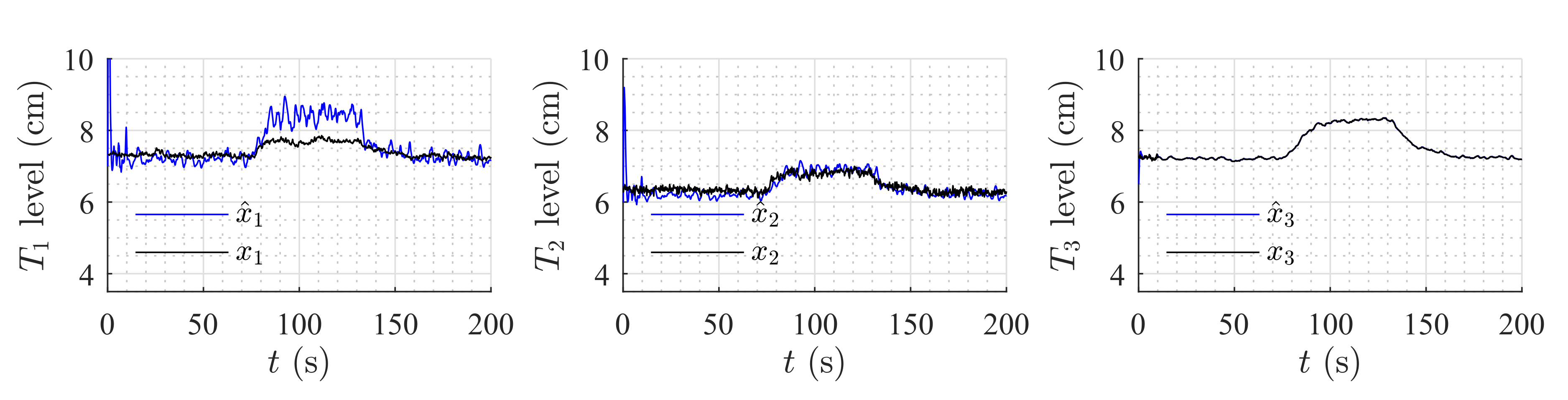
In the second experiment, an unmeasured temporary input flow went into the first and second tanks.
Figure 16 and
Figure 17 show the estimation of the level in each tank for a temporary input flow to the first and second tank, respectively. As was expected, the output of the system changed (level in Tank 3), and therefore the estimation should change. Recall that the level of tank
i depends on the inflow of the previous tank, which depends on the level of such tank. Therefore, it can been seen in
Figure 16 that the estimated level in Tank 2 is similar to the actual value, but higher for Tank 1. Now, when the perturbation was introduced in Tank 1, as was expected, the estimation converges to the real values of all levels (see
Figure 17).